1 Introduction

Abundant achievements have been made in the research of flow in concentric and eccentric annuli. For example, Snyder and Goldstein studied fully developed flows in eccentric annuli and proposed an exact solution for the velocity distribution [1]. The flow in the annulus has been proved to be useful as a mode for longitudinal flows in tube bundles. Satellite thrusters usually consist of concentric components to mix oxidizer and combustion. However, the problem of tube misalignment often happens. It is essential to master characteristics of capillary-driven flow in eccentric annuli under microgravity.

Since the substantial Lucus–Washburn equation was derived [2], capillary-driven flows in tubes and other kinds of containers have been widely studied. Levine et al. [3] derived the dynamic equation of capillary rise in cylindrical tubes and the convective loss at the tube entrance was considered for the first time. Stange et al. [4] presented a more comprehensive dynamic equation by considering the meniscus reorientation, the dynamic contact angle and the development of flows. Chen et al. [5] analyzed flows in oval tubes and proposed a new flow mode in which the entire flow can be divided into two regions. Capillary-driven flows in tubes with varying cross section [6,7,8,9,10], in complex containers [11] and in containers with axisymmetric geometries [12] were also deeply analyzed. The inverse problem of capillary imbibition [13], the oscillatory regime of capillary rise [14] and the effects of dynamic contact angle and initial liquid volume on capillary-driven flows [15, 16] were discussed in detail as well.

The capillary-driven flow in corners has also attracted much attention. Weislogel and Lichter [17] proposed a dynamic model of the capillary flow in sharp inner corners(尖内角). It was further extended to interior corners with different wettability [18] and rounded interior corners [19]. Capillary flows in the interior corner formed by cylindrical and planar walls [20], in the narrow gap between two vertical plates making a small angle [21], in the curved interior corner [22], in the narrow and tilting corner [23], and in the small corner formed by two curved corners [24] were also explored in detail, and the dynamic equations of flows in these situations were presented.

The capillary rise behavior of liquid between parallel plates was studied by Dreyer et al. [25]. They divided the whole flow process into three regions. The lattice Boltzmann method based on field mediators was adopted by Wolf et al. [26] to simulate the capillary rise behavior between parallel plates. Liquid penetration through the metal wire mesh between parallel plates was analyzed by Weng et al. [27]. Klatte et al. [28] explored steady capillary-driven flows in open channels, and a fast numerical procedure was proposed. Equilibrium capillary surfaces [29, 30] and influences of the capillarity on a creeping film flow [31] were also explored. Theories of capillary-driven flows and numerical simulations were adopted to analyze liquid behaviors in propellant tanks under microgravity and optimize propellant management devices (PMD) [32,33,34,35].

However, capillary-driven flows in eccentric annuli have not been studied yet, and the influences of eccentricity on the capillary flow are still unknown. In this study, a theory for the capillary rise in eccentric annuli under microgravity is developed, and the effects of the dynamic contact angle, the pressure loss force at the entrance, the friction force and the curved liquid surface in the reservoir are all considered. The theory has been verified by numerical simulation based on the volume of fluid (VOF) method. Besides, the differential equation is transformed into a sum of forces acting on the control volume. Effects of different forces are discussed in detail, and the influences of eccentricity on the capillary flow are deeply analyzed.

2 Theoretical analysis

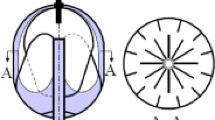
The vertical cross-sectional view of the theoretical model is shown in Fig. 1. The eccentric annulus is immersed into the liquid vertically from above with the immersion depth of h0. The radius of the curved free surface of the liquid inside the reservoir is \(R_{r}\), which is calculated from the distance a between the wetting barriers and the distance b between the centerline of the free surface inside the reservoir and the centerline of the annulus. Figure 2 shows a horizontal cross-sectional view of the annulus. The inner and outer radii of the annulus are ri and ro, respectively. The distance between the centers of inner and outer tubes is e. The dynamic contact angles on the inner and outer walls are αi and αo, respectively. The bipolar coordinate system is selected for the theoretical analysis of this model, as Fig. 2 shows. The inner and outer surfaces of the annulus are thus represented by lines of constant η, which will be designated as ηi and ηo, respectively. The coordinates (ξ, η) are defined by the transformation

$$ x + iy = {\text{ic}}\cot (\frac{\xi + i\eta }{2}) $$
(1a)
$$ c = r_{i} \sinh \eta_{i} = r_{o} \sinh \eta_{o} $$
(1b)
$$ \cosh \eta_{i} = \frac{1}{\gamma }\frac{{\gamma \left( {1 + \phi^{2} } \right) + \left( {1 - \phi^{2} } \right)}}{2\phi } $$
(1c)
$$ \cosh \eta_{o} = \frac{{\gamma \left( {1 - \phi^{2} } \right) + \left( {1 + \phi^{2} } \right)}}{2\phi } $$
(1d)
$$ \gamma = \frac{{r_{i} }}{{r_{o} }} $$
(1e)
$$ \phi = \frac{e}{{r_{o} - r_{i} }} $$
(1f)
Fig. 1
figure 1

Vertical cross-sectional view of capillary-driven flow in the eccentric annulus

Full size image
Fig. 2
figure 2

Horizontal cross-sectional view of an eccentric annulus

Full size image

The liquid in the annulus is set to be Control Volume 1 (CV1). The climbing height is represented by h, and the average velocity of the meniscus is \(\mathop h\limits^{ \cdot }\). The flow is assumed to be fully developed Poiseuille flow and the stress that acts on the free surface is neglected. The liquid is assumed to be isothermal during the flow process.

According to reference 1, the velocity field in the z-direction u in the horizontal cross section of the annulus is

$$ u\left( {\xi ,\eta ,t} \right) = - \frac{{c^{2} }}{\mu }\frac{dp}{{dz}}\left\{ {F + E\eta - \frac{\coth \eta }{2} + \sum\limits_{n = 1}^{\infty } {\left[ {A_{n} e^{n\eta } + \left( {B_{n} - \coth \eta } \right)e^{ - n\eta } } \right]\cos n\xi } } \right\} $$
(2)
$$ F = \frac{{\eta_{i} \coth \eta_{o} - \eta_{o} \coth \eta_{i} }}{{2\left( {\eta_{i} - \eta_{o} } \right)}} $$
$$ E = \frac{{\coth \eta_{i} - \coth \eta_{o} }}{{2\left( {\eta_{i} - \eta_{o} } \right)}} $$
$$ A_{n} = \frac{{\coth \eta_{i} - \coth \eta_{o} }}{{e^{{2n\eta_{i} }} - e^{{2n\eta_{o} }} }} $$
$$ B_{n} = \frac{{e^{{2n\eta_{i} }} \coth \eta_{o} - e^{{2n\eta_{o} }} \coth \eta_{i} }}{{e^{{2n\eta_{i} }} - e^{{2n\eta_{o} }} }} $$

where E, F, An and Bn are constants decided by ηi and ηo.

The boundary condition is

$$ \left. {u\left( {\xi ,\eta ,t} \right)} \right|_{{\eta = \eta_{i} }} = \left. {u\left( {\xi ,\eta ,t} \right)} \right|_{{\eta = \eta_{o} }} = 0 $$
(3)

The volume flux rate across a horizontal cross section is

$$ \pi \left( {r_{o}^{2} - r_{i}^{2} } \right)\mathop {{\text{ }}h}\limits^{ \cdot } = \int_{{\eta _{i} }}^{{\eta _{o} }} {\int_{0}^{{2\pi }} {\frac{{uc^{2} }}{{\left( {\cosh \eta - \cos \xi } \right)^{2} }}{\text{d}}\xi {\text{d}}\eta } } $$
(4)

From Eq. 4, the velocity field can be expressed as follows

$$ u = \frac{{\pi \left( {r_{o}^{2} - r_{i}^{2} } \right)}}{{2c^{2} I}}\mathop {{\text{ }}h}\limits^{ \cdot } \left\{ {F + E\eta - \frac{{\coth \eta }}{2} + \sum\limits_{{n = 1}}^{\infty } {\left[ {A_{n} e^{{n\eta }} + \left( {B_{n} - \coth \eta } \right)e^{{ - n\eta }} } \right]\cos n\xi } } \right\} $$
(5)
$$ I = \int_{{\eta_{i} }}^{{\eta_{o} }} {\int_{0}^{\pi } {\frac{{F + E\eta - \frac{\coth \eta }{2} + \sum\limits_{n = 1}^{\infty } {\left[ {A_{n} e^{n\eta } + \left( {B_{n} - \coth \eta } \right)e^{ - n\eta } } \right]\cos n\xi } }}{{\left( {\cosh \eta - \cos \xi } \right)^{2} }}{\text{d}}\xi {\text{d}}\eta } } $$

The same method proposed in reference [4] is adopted here to derive the dynamic equation. The N-S equation for the z component in the Cartesian coordinate system is

$$ \frac{\partial u}{{\partial t}} + u\frac{\partial u}{{\partial z}} + v\frac{\partial u}{{\partial x}} + w\frac{\partial u}{{\partial y}} = - \frac{1}{\rho }\frac{dp}{{dz}} + \nu \left( {\frac{{\partial^{2} u}}{{\partial z^{2} }} + \frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) + g_{z} $$
(6)

where ρ is the liquid density, ν is the kinematic viscosity, gz is the gravity component in the z direction, v and w are velocity components in the x- and y-directions, respectively. The velocity components in x- and y-directions are both zero, and u is independent of z. In space, the magnitude of gravity is less than 10–4 g, as a result, for the liquid on the satellite, the Bond number is much smaller than 1. Therefore, gzcan be neglected. After simplification, Eq. 6 can be transformed into the bipolar coordinate system, which is written as

$$ \frac{{c^{2} }}{{\left( {\cosh \eta - \cos \xi } \right)^{2} }}\frac{\partial u}{{\partial t}} + \frac{{c^{2} }}{{\left( {\cosh \eta - \cos \xi } \right)^{2} }}u\frac{\partial u}{{\partial z}} = - \frac{1}{\rho }\frac{{{\text{d}}p}}{{{\text{d}}z}}\frac{{c^{2} }}{{\left( {\cosh \eta - \cos \xi } \right)^{2} }} + \nu \left( {\frac{{\partial^{2} u}}{{\partial \xi^{2} }} + \frac{{\partial^{2} u}}{{\partial \eta^{2} }}} \right) $$
(7)

Integrating Eq. 7 with respect to η and ξ across the entire horizontal cross section of the eccentric annulus, we can obtain

$$ \begin{gathered} \frac{\partial }{\partial t}\iint\limits_{\Omega } {u\frac{{c^{2} }}{{\left( {\cosh \eta - \cos \xi } \right)^{2} }}{\text{d}}\xi {\text{d}}\eta } + \frac{{c^{2} }}{{\left( {\cosh \eta - \cos \xi } \right)^{2} }}\iint\limits_{\Omega } {u\frac{\partial u}{{\partial z}}}{\text{d}}\xi {\text{d}}\eta = ... \hfill \\ \iint\limits_{\Omega } { - \frac{1}{\rho }\frac{{{\text{d}}p}}{{{\text{d}}z}}\frac{{c^{2} }}{{\left( {\cosh \eta - \cos \xi } \right)^{2} }}}{\text{d}}\xi {\text{d}}\eta + \iint\limits_{\Omega } {\nu \left( {\frac{{\partial^{2} u}}{{\partial \xi^{2} }} + \frac{{\partial^{2} u}}{{\partial \eta^{2} }}} \right)}\frac{{c^{2} }}{{\left( {\cosh \eta - \cos \xi } \right)^{2} }}{\text{d}}\xi {\text{d}}\eta \hfill \\ \end{gathered} $$
(8)

where \(\Omega\) represents the entire horizontal cross section of the eccentric annulus. Combined with Eqs. 4, 8 is integrated with respect to z from z = –h0 to z = h, and then, the following equation is obtained.

$$ \begin{aligned} \pi \left( {r_{o}^{2} - r_{i}^{2} } \right)\mathop h\limits^{ \cdot \cdot } & = - \frac{1}{\rho }\iint\limits_{\Omega } {\left[ {p\left( {h,t} \right) - p\left( { - h_{0} ,t} \right)} \right]\frac{{c^{2} }}{{\left( {\cosh \eta - \cos \xi } \right)^{2} }}}{\text{d}}\xi {\text{d}}\eta \\ & + \int_{{ - h_{0} }}^{h} {\iint\limits_{\Omega } {\nu \left( {\frac{{\partial^{2} u}}{{\partial \xi^{2} }} + \frac{{\partial^{2} u}}{{\partial \eta^{2} }}} \right)}} \frac{{c^{2} }}{{\left( {\cosh \eta - \cos \xi } \right)^{2} }}{\text{d}}\xi {\text{d}}\eta \\ \end{aligned} $$
(9)

The velocity distribution u is independent of z, so the second term on the left side of (9) vanishes.

The liquid–gas interface in the annulus is defined as the upper control surface of the Control Volume 1(CV 1). The upper control surface of CV 1 is considered to be equivalent to a horizontal plane with z = h. The pressure on the upper control surface is

$$ p\left( {h,t} \right) = p_{0} + p_{\sigma } $$
(10)

where p0 is the air pressure, and pσ is the capillary pressure, which is written as

$$ \pi \left( {r_{o}^{2} - r_{i}^{2} } \right)p_{\sigma } = - 2\pi \sigma \left( {r_{i} \cos \alpha_{i} + r_{o} \cos \alpha_{o} } \right) $$
(11)

When the static contact angle of liquid is 0, there exits an empirical equation for the dynamic contact angle, which is written as

$$ {\text{cos}}\alpha_{d} = 1 - 2\tanh \left[ {4.96 * (\frac{{\mu \mathop h\limits^{ \cdot } }}{\sigma })^{0.702} } \right] $$
(12)

where μ is the dynamic viscosity of the liquid, and σ is the surface tension of liquid. This equation is presented by Jiang et al. [36], and it has been widely adopted.

With the same method adopted in reference (25), according to the geometric relationship, an approximate formula is given for calculating Rr, which is written as

$$ R_{r} = { - }\frac{{a^{3} b}}{{6\left( {r_{o}^{2} - r_{i}^{2} } \right)h}} $$
(13)

According to the velocity distribution in the annulus, it can be known that \(\left. {\frac{\partial u}{{\partial \eta }}} \right|_{{\eta = \eta_{i} }} > 0\) on the inner wall and \(\left. {\frac{\partial u}{{\partial \eta }}} \right|_{{\eta = \eta_{o} }} < 0\) on the outer wall. Using the plus sign for the case of inner wall and the minus sign for the case of outer wall will give positive values for both cases. The friction forces on the inner and outer walls are

$$ F_{i} = 2\left( {h_{0} + h} \right)\int_{0}^{\pi } {\left. {\mu \frac{\partial u}{{\partial \eta }}} \right|_{{\eta = \eta_{i} }} } {\text{d}}\xi $$
(14a)
$$ F_{o} = - 2\left( {h_{0} + h} \right)\int_{0}^{\pi } {\left. {\mu \frac{\partial u}{{\partial \eta }}} \right|_{{\eta = \eta_{o} }} } {\text{d}}\xi $$
(14b)

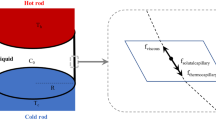
To calculate the pressure at the entrance of the annulus, it is necessary to build the Control Volume 2 (CV 2) around the entrance in the reservoir. The analysis is based on an equivalent circular entrance, whose radius reequals \(\sqrt {{\text{r}}_{o}^{2} - r_{i}^{2} }\), as shown in Fig. 3. In CV 2, we have

$$ I_{{\text{c}}} = I_{{\text{e}}} - I_{{\text{l}}} + \Sigma F $$
(15)

where Ic is the rate of change of total momentum in CV 2, Ie is the flux of momentum entering CV 2, Il is the flux of momentum leaving CV 2, and ΣF is the sum of forces acting on CV 2. The similar analysis as described in reference 24 is adopted here, and the pressure force at the entrance is obtained as below,

$$ x_{2} = \pi r_{e}^{2} \left( {p_{0} + p_{r} } \right) - 2\pi \mu r_{e} \mathop {{\text{ }}h}\limits^{ \cdot } - \left( {\frac{7}{{12}} + \frac{{A_{l} }}{3}} \right)\pi r_{e}^{3} \rho \mathop {{\text{ }}h}\limits^{{ \cdot \cdot }} + \frac{1}{6}\pi r_{e}^{2} \rho \mathop {h^{2} }\limits^{ \cdot } - I $$
(16)
$$ p_{r} = \frac{\sigma }{{R_{r} }} $$
$$ I_{l} = \rho \int_{{\eta_{i} }}^{{\eta_{o} }} {\int_{0}^{2\pi } {\frac{{\rho u^{2} c^{2} }}{{\left( {\cosh \eta - \cos \xi } \right)^{2} }}{\text{d}}\xi {\text{d}}\eta } } $$
$$ A_{l} = \frac{{\int_{{\eta_{i} }}^{{\eta_{o} }} {\int_{0}^{2\pi } {\frac{{\rho u\frac{{{\text{d}}u}}{{{\text{d}}t}}c^{2} }}{{\left( {\cosh \eta - \cos \xi } \right)^{2} }}{\text{d}}\xi {\text{d}}\eta } } }}{{\pi r_{e}^{2} \mathop h\limits^{ \cdot } \mathop h\limits^{ \cdot \cdot } }} $$
Fig. 3
figure 3

An equivalent entrance and the CV 2

Full size image

Inserting Eqs. 10–16 into Eq. 8, the second-order differential equation for the height of the meniscus is obtained as below,

$$ \mathop {{\text{ }}h}\limits^{{ \cdot \cdot }} = \frac{1}{{\pi \rho r_{e}^{2} \left[ {h + h_{0} + \left( {\frac{7}{{12}} + \frac{{A_{l} }}{{3\rho }}} \right)r_{e} } \right]}}\left[ \begin{gathered} 2\pi \sigma \left( {r_{i} \cos \alpha _{i} + r_{o} \cos \alpha _{o} } \right) + \frac{\sigma }{{R_{r} }}\pi \left( {r_{o}^{2} - r_{i}^{2} } \right) \hfill \\ - 2\pi \mu r_{e} \mathop {{\text{ }}h}\limits^{ \cdot } + \frac{1}{6}\pi r_{e}^{2} \rho \mathop {h^{2} }\limits^{ \cdot } - I_{l} - F_{i} - F_{o} \hfill \\ \end{gathered} \right] $$
(17)

This equation can be solved using the fourth-order Runge–Kutta method with the initial conditions, \(h\left( {t = 0} \right) = \mathop h\limits^{ \cdot } \left( {t = 0} \right) = 0\).

3 Results and discussion

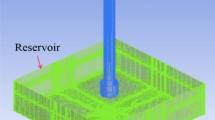
Figure 4 shows a mesh model established for numerical simulation in Fluent. Instead of a circular cylinder, a square cylinder is chosen as the reservoir for convenience. The square cylinder that has a width of 142 mm and an equivalent radius of 80 mm is used in the theoretical analysis. This simplification is acceptable because the influences of capillary pressure of the free surface in the reservoir are very small and can be neglected. The height of the model is 220 mm, and the number of grids is about 1.1 million. Boundary layers are established in the regions near all walls. The height of the first boundary layer is about 0.08 mm. The expansion ratio between two adjacent layers is 1.2.

Fig. 4
figure 4

3D Mesh model established for numerical simulation

Full size image

Three kinds of silicone oil named by their kinematic viscosities (SF 1, SF 2 and SF 5) are used in the simulation. The liquid properties are shown in Table 1. The laminar flow is chosen as the flow mode in the simulation as the Re number is much smaller than 2000. Simulation parameters are listed in Table 2.

Table 1 Liquid properties (25℃)
Full size table
Table 2 Numerical settings
Full size table

A simulation result is shown in Fig. 5a and b. In Fig. 5a, the red part represents the liquid distribution. Once the simulation begins, the liquid flows upwards quickly into the annulus. And after 2.4 s, the liquid almost reaches the top of the annulus. In Fig. 5b, the yellow surface represents the gas–liquid interface. At t = 0 s, all the liquid is at the bottom of the annulus. After the simulation starts, the liquid climbs upwards continuously and forms a concave surface in the annulus. Owing to the eccentricity, the free surface in the annulus is not on the same level, and it is higher on the narrow side. As shown in Fig. 6, we define h = (h1 + h2 + h3 + h4)/4 as the final climbing height. On the other hand, when the liquid climbs upward after the simulation starts, the liquid surface develops from a horizontal plane into an inclined curved surface. But this only occurs at the beginning of the flow. The shape of the gas–liquid interface is changing rapidly, and the duration is very short. Therefore, the effect of this process is negligible. In a fully developed capillary-driven flow, the free surface configuration almost keeps the same. The error caused by this simplification is acceptable compared to the flow distance.

Fig. 5
figure 5

A numerical result of capillary-driven flow with the liquid of SF 1 and ri = 5 mm, ro = 8 mm, e = 1.5 mm and h0 = 15 mm. a Liquid distribution in the vertical cross section of the annulus. b Height of free surface vs time

Full size image
Fig. 6
figure 6

Meniscus height at different positions

Full size image

Figure 7 shows the theoretical and numerical results of meniscus height vs time. The expression of velocity field contains a sum of an infinite series. To reduce calculation time and ensure accuracy at the same time, n in the expression of velocity field is set to be 3. The solid curves and square signs represent theoretical and numerical results, respectively. And the results of different liquids are plotted in different colors. Eight sizes of annuli with a wide range of eccentricity are selected. Numerical results are all in good agreement with corresponding theoretical ones.

Fig. 7
figure 7

Comparison between theoretical and numerical results. a ri = 2 mm, ro = 4 mm, e = 0.5 mm, h0 = 15 mm, b ri = 2 mm, ro = 4 mm, e = 1.0 mm, h0 = 15 mm, c ri = 3 mm, ro = 6 mm, e = 0.8 mm, h0 = 15 mm, d ri = 3 mm, ro = 6 mm, e = 1.6 mm, h0 = 15 mm, e ri = 5 mm, ro = 8 mm, e = 0.8 mm, h0 = 20 mm, e ri = 5 mm, ro = 8 mm, e = 1.5 mm, h0 = 20 mm, f ri = 6 mm, ro = 8 mm, e = 0.6 mm, h0 = 15 mm, g ri = 6 mm, ro = 8 mm, e = 1.2 mm, h0 = 15 mm

Full size image

Equation (17) can also be expressed as a sum of forces acting on CV 1, which is written as.

$$ F_{{ca}} = F_{{ia}} + F_{{ir}} + F_{{cr}} + F_{{fa}} + F_{{fr}} + F_{{pl}} $$
(18)

The meanings of the force terms are:

\( {\text{capillary}}\,\,{\text{force}}\,\,{\text{in}}\,\,{\text{the}}\,\,{\text{annulus}}\,\,F_{{ca}} = 2\pi \left( {r_{i} \cos \alpha _{i} + r_{o} \cos \alpha _{o} } \right)\sigma \).

\( {\text{inertia}}{\mkern 1mu} {\mkern 1mu} {\text{force}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\text{in}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\text{the}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\text{reservoir}}\,\,\,F_{{ir}} = \rho \pi r_{e}^{2} \left[ {\left( {\frac{7}{{12}} + \frac{{A_{l} }}{{3\rho }}} \right)r_{e} + h_{0} } \right]\mathop {{\text{ }}h}\limits^{{ \cdot \cdot }} \).

\( {\text{pressure}}\,\,{\text{loss}}\,\,{\text{force}}\,\,{\text{a}}\,\,{\text{tthe}}\,\,{\text{entrance}}\,\,F_{{pl}} = I_{l} - \frac{1}{6}\rho \pi r_{e}^{2} \mathop {h^{2} }\limits^{ \cdot } \).

\( {\text{friction }}\,\,{\text{force}}\,\,{\text{ in}}\,\,{\text{ the}}\,\,{\text{ annulus }}\,\,F_{{fa}} {\text{ }} = {\text{ }}F_{i} {\text{ }} + {\text{ }}F_{o} \).

\( {\rm capillary\,\,\, force\,\,\, in\,\,\, the\,\,\, reservoir} \,\,\,F_{cr} = \frac{{6\pi r_{e}^{4} }}{{a^{3} b}}\sigma h\).

\( {\rm friction\,\,\, force \,\,\,in \,\,\,the \,\,\,reservoir}\,\,\,F_{fr} = 2\pi \mu r_{e} \mathop h\limits^{ \cdot }\).

\( {inertia \,\,\,force \,\,\,in \,\,\,the \,\,\,annulus}\,\,\,F_{ia} = \rho \pi r_{e}^{2} h\mathop h\limits^{ \cdot \cdot }\).

The development of different forces vs time is shown in Fig. 8. The liquid is SF 1, with ri = 3 mm, ro = 6 mm, e = 0.8 mm, and h0 = 15 mm. The capillary force in the annulus always plays a dominant role. The inertia force in the reservoir has a maximum value at the beginning and decreases rapidly. The pressure loss force at the entrance increases with time until it reaches the maximum value and then decreases with time thereafter. The friction force in the annulus increases with time, and finally, it will be close to the capillary force in the annulus. In a flow for a long period of time, it can be considered that the flow is governed by the friction force and the capillary force in the annulus. While in the beginning of a capillary flow, the inertia force in the reservoir and the pressure loss force at the entrance should also be considered; otherwise, the theoretical results will have unacceptable deviations. In some previous study of capillary-driven flows [9], the pressure loss at the entrance is neglected and the deviation between theoretical and experimental results in the beginning of flow is unacceptable. The capillary force in the reservoir is too small to identify under this condition.

Fig. 8
figure 8

Development of forces vs time for SF 1, ri = 3 mm, ro = 6 mm, e = 0.8 mm, and h0 = 15 mm

Full size image

The liquid flow speed increases as the eccentricity increases due to the decrease of the friction force in the annulus. For example, as shown in Fig. 7a, after 2.4 s, the theoretical flow distance of SF 1 is 142.7 mm, while in Fig. 7b, it is 155.7 mm. The maximum flow speed of liquid also increases as the eccentricity increases. As shown in Table 3, in the annulus with ri = 3 mm and ro = 6 mm, when e = 0.8 mm, the maximum speed is 66.3 mm/s for SF 2, while it is 71.0 mm/s when e = 1.6 mm. The development of the friction force in the annulus is shown in Fig. 9a and b. Figure 9a shows the results of SF 1, and Fig. 9b shows the results of SF 5. The black curves represent the results of the case with ri = 5 mm and ro = 8 mm. The blue curves represent the results of the case with ri = 3 mm and ro = 6 mm. The red curves represent the results of the case with ri = 2 mm and ro = 4 mm. And the values of eccentricity are labeled in the lower right corners of the figures. It can be seen that, for different liquids or annuli with different values of \(\gamma\), the increase in eccentricity will lead to the decrease of the friction force in the annulus, which leads to the increase in liquid flow speed. Besides, the longer the flow distance of the liquid, the smaller the difference between the friction forces in different annuli.

Table 3 Numerical parameters
Full size table
Fig. 9
figure 9

Development of friction forces vs time. The black curves represent the case ri = 5 mm ro = 8 mm; the blue curves represent the case ri = 3 mm, ro = 6 mm; the red curves represent the case ri = 2 mm, ro = 4 mm. a Liquid SF 1. b Liquid SF 5

Full size image

4 Conclusions

An exact differential equation for capillary-driven flow in an eccentric annulus under microgravity is proposed for the first time and verified by numerical simulation. Eight sizes of eccentric annuli and three types of silicone oil are adopted. The theoretical results are in good agreement with numerical results. Capillary-driven flows in eccentric annuli under microgravity can be predicted accurately with this equation.

The development of different forces is analyzed comprehensively, and different flow features are obtained. Besides, the effects of eccentricity on flow resistance and flow speed are discussed. The flow resistance in the annulus decreases with the increase in eccentricity, which leads to the increase in flow speed.

This can deepen people’s understanding and fill the gap in the knowledge of capillary-driven flow. The conclusions proposed in this paper will be helpful for liquid management under microgravity, especially for the design of tube bundles.