Introduction

The application of an alternating electric field to a non-isothermal dielectric fluid provides thermoelectric buoyancy due to an electric gravity. In spherical and cylindrical configurations, this gravity can provide a central force field which is of most interest for geophysical and astrophysical study, where radial forces play a predominant role (Yavorskaya et al. 1984; Hart et al. 1986; Futterer et al. 2013). In the present work, we investigated the cylindrical geometry which has also such an application if we consider the flow at the equatorial region of planetary systems. Another application for this geometry is the control of the heat transfer by dielectrophoretic force. In particular, the heat transfer and its control under reduced gravity condition are in the focus of attention of researchers (Evgeridis et al. 2011; Lotto et al. 2017). Experiments have been performed under Earth’s gravity conditions (Chandra and Smylie 1972), and many theoretical and numerical works have been done considering microgravity conditions in order to focus on the effects of the thermoelectric buoyancy (Takashima 1980; Malik et al. 2012; Yoshikawa et al. 2013; Travnikov et al. 2015, 2016).

During the last years, many experiments have been conducted during parabolic flight campaigns, which is a convenient way to get reasonable duration of weightlessness environments (Futterer et al. 2016; Meyer et al. 2017). These experiments have been performed for several annular geometries, for various fluids, and for different intensities of the axial gravity. In this framework, the study of the effects of the combined action of the Archimedean and thermoelectric buoyancies was performed through a linear stability analysis in order to predict the critical threshold, as well as the temporal and spatial structure of the flow. Numerical simulations have also been performed while taking into account the temporal variation of axial gravity within a parabolic flight. In these simulations, the effect of the thermoelectric buoyancy was only considered during microgravity, but in practice, this buoyancy force can also be active all along a parabola.

This theoretical and numerical work come together with the newest results of parabolic flight experiments which are presented in the corresponding article of this issue.

The article is organized as follows. Section “Problem Formulation” gives the problem formulation both for the linear stability theory and for the direct numerical simulation. Section “Linear Stability Results” is dedicated to the results obtained from the linear stability analysis and Section “Numerical Results” gives the results from the numerical simulations. The last section addresses a conclusion of this work.

Problem Formulation

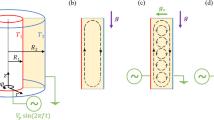
We consider an incompressible dielectric fluid of density ρ, kinematic viscosity ν, thermal diffusivity κ and permittivity ε, confined between two vertical coaxial cylinders. The inner and outer cylinders are of radii R1 and R2 = R1 + d and are maintained at the temperatures T1 and T2 < T1 respectively. An electric potential of the form \(\sqrt {2} V_{0} \sin (2 \pi f t)\) is applied between the two cylinders, producing a radial electric field E (Fig. 1). The temperature difference ΔT = T1 − T2 induces a radial stratification of the density and of its permittivity, which can be modelized by ρ = ρ2(1 − α𝜃) and ε = ε2(1 − e𝜃) respectively, where α is the thermal expansion coefficient, e is the coefficient of thermal variation of the permittivity, and 𝜃 = T − T2 is the temperature deviation from the reference temperature T2. ρ2 and ε2 are the density and the permittivity at the reference temperature, respectively. Earth’s gravity will act on the density stratification to give the Archimedean buoyancy.

Fig. 1
figure 1

Sketch of the annular geometry

Full size image

Due to the electric field, a dielectric fluid will undergo the electrohydrodynamic (EHD) force which is given by (Landau and Lifshitz 1984):

$$ \mathbf{F}_{EHD} = \rho_{e} \mathbf{E} - \frac{1}{2} \mathbf{E}^{2} \mathbf{\nabla} \varepsilon + \mathbf{\nabla} \left[ \frac{1}{2} \rho \left( \frac{\partial \varepsilon}{\partial \rho} \right)_{\theta} \mathbf{E}^{2} \right], $$
(1)

where ρe is the electric charge density. The first term of Eq. 1 is the electrophoretic force and corresponds to the Coulomb force acting on free charges. Most of the time, this term is the dominant one, but for an alternating electric field with frequency much larger than the inverse of relaxation time of free charges τe = ε/σe, where σe is the electric conductivity, there is no accumulation of charges. Thus the electrophoretic force is negligible. The third term of Eq. 1, called the electrostrictive force, is a gradient that will not affect the dynamic of the fluid, unless the fluid is compressible or has free surfaces. This term will be injected into the pressure gradient of the momentum equation. The second term of Eq. 1 called the dielectrophoretic (DEP) force is proportional to the permittivity gradient. Using the Boussinesq approximation for the permittivity, the DEP force can be recast as:

$$ \mathbf{F}_{DEP} = \mathbf{\nabla}\left( \frac{\varepsilon_{2} e \mathbf{E}^{2} \theta}{2}\right) - \rho\alpha\theta\mathbf{g}_{e} . $$
(2)

Since it is a gradient, the first term of Eq. 2 will not affect the dynamics of the fluid and will also be included into the pressure gradient of the momentum equation. The second term of Eq. 2 is analogue to a thermal buoyancy induced by an effective electric gravity ge given by:

$$ \mathbf{g}_{e} = \mathbf{\nabla}\left( \frac{e\varepsilon_{2}\mathbf{E}^{2}}{2\alpha\rho_{2}}\right) $$
(3)

and can be interpreted as the energy stored between the two cylindrical electrodes. As in the Rayleigh-Bénard problem, the DEP force induces instabilities if the electric Rayleigh number L = αΔTged3/νκ is larger than a critical value (Yoshikawa et al. 2013).

Flow Equations

The governing equations for the velocity field u = (u, v, w), temperature 𝜃 and electric potential ϕ are the continuity equation, the momentum equations, the energy equation and Gauss’ law for electricity

$$\begin{array}{@{}rcl@{}} && \mathbf{\nabla} \cdot \mathbf{u} = 0 \end{array} $$
(4a)
$$\begin{array}{@{}rcl@{}} && \frac{\partial \mathbf{u}}{\partial t} + \mathbf{u} \cdot \mathbf{\nabla}\mathbf{u} = -\mathbf{\nabla}\pi + \nu{\Delta}\mathbf{u} - \alpha\theta \left( \mathbf{g}+\mathbf{g}_{e} \right) \end{array} $$
(4b)
$$\begin{array}{@{}rcl@{}} && \frac{\partial \theta}{\partial t} + \mathbf{u} \cdot \mathbf{\nabla}\theta = \kappa{\Delta} \theta \end{array} $$
(4c)
$$\begin{array}{@{}rcl@{}} && \mathbf{\nabla} \cdot \left( \varepsilon\mathbf{E}\right) = 0 \quad \text{with} \quad \mathbf{E} = -\mathbf{\nabla} \phi , \end{array} $$
(4d)

where π, the generalized pressure, is given by:

$$ \pi = \frac{p}{\rho_{2}} + gz - \frac{e \theta \varepsilon_{2} \mathbf{E}^{2}}{2 \rho_{2}} - \frac{1}{2} \left( \frac{\partial \varepsilon}{\partial \rho} \right)_{\theta} \mathbf{E}^{2} . $$
(5)

Since the frequency of the electric potential is also assumed to be high compared to the inverse of the viscous diffusion time τν = d2/ν and of the thermal diffusion time τκ = d2/κ, only the temporal average of the thermoelectric buoyancy affects the fluid motion. Thus we reduce the problem with an a.c. electric field to the one with an effective static tension V 0. In this assumption, the boundary conditions at the two cylindrical walls read:

$$ \left\lbrace \begin{array}{l l l l} \mathbf{u} = \mathbf{0}, & \theta = {\Delta}T, & \phi = V_{0} & \text{at} \: r = R_{1} \\ \mathbf{u} = \mathbf{0}, & \theta = 0, & \phi = 0 & \text{at} \: r = R_{2} . \end{array} \right. $$
(6)

Nondimensionalizing with scales d of length, τν of time, ΔT of temperature and V 0 of electric tension, Eqs. 4a–d reads:

$$\begin{array}{@{}rcl@{}} && \mathbf{\nabla} \cdot \mathbf{u} = 0 \end{array} $$
(7a)
$$\begin{array}{@{}rcl@{}} && \frac{\partial \mathbf{u}}{\partial t} + \mathbf{u} \cdot \mathbf{\nabla} \mathbf{u} = - \mathbf{\nabla} \pi + {\Delta} \mathbf{u} + \text{Gr} \theta \mathbf{e}_{z} - \frac{{\gamma_{e}} {V_{E}^{2}}}{\text{Pr}} \theta \mathbf{g}_{e} \end{array} $$
(7b)
$$\begin{array}{@{}rcl@{}} && \frac{\partial \theta}{\partial t} + \mathbf{u} \cdot \mathbf{\nabla} \theta = \frac{1}{\text{Pr}} {\Delta} \theta \end{array} $$
(7c)
$$\begin{array}{@{}rcl@{}} &&\mathbf{\nabla} \cdot \left[ \left( 1 - {\gamma_{e}} \theta \right) \mathbf{\nabla} \phi \right] = 0 , \end{array} $$
(7d)

where Pr = ν/κ is the Prandtl number, Gr = αΔTgd3/ν2 is the Grashof number, \(V_{E}=V_{0} / \sqrt {\rho _{2} \nu \kappa / \varepsilon _{2}}\) is the dimensionless electric potential, and γe = eΔT is the thermoelectric parameter. The boundary conditions (6) then become:

$$ \left\lbrace \begin{array}{l l l l} \mathbf{u} = \mathbf{0}, & \theta = 1, & \phi = 1 & \text{at} \: r = \eta / (1-\eta) \\ \mathbf{u} = \mathbf{0}, & \theta = 0, & \phi = 0 & \text{at} \: r = 1 / (1-\eta) , \end{array} \right. $$
(8)

where η = R1/R2 is the radius ratio between the two cylinders. The Galileo number \(\text {Ga} = \sqrt {g d^{3}} / \nu \) is a characteristics of the flow configuration and it allows to make the axial gravity intensity constant. Therefore, Gr only varies with the temperature. The Rayleigh number Ra = PrGr will also be used to characterize the Archimedean buoyancy. Additionally we introduce δ = α/e, which is a dimensionless fluid property and thermally links the two thermal buoyancies.

Base State

Considering a stationary axisymmetric and axially invariant state (cylinders of infinite length), integration of the energy (7c) and that of the Gauss’ law (7d) give the base temperature and the base electric potential respectively:

$$ {\Theta}(r) = \frac{\ln\left[(1-\eta)r\right]} {\ln(\eta)} \; , \quad {\Phi}(r) = \frac {\ln(1-{\gamma_{e}} {\Theta}(r))}{\ln(1-{\gamma_{e}})} . $$
(9)

Considering the condition of zero axial volume flux, the axial component of the momentum (7b) yields the following expression for the base axial velocity (Choi and Korpela 1980):

$$\begin{array}{@{}rcl@{}} W(r) &=& \text{Gr} \left( A \left[ \left( 1 - \eta \right)^{2} r^{2} - 1 + \left( 1 - \eta \right)^{2} {\Theta} \right]\right.\\ &&\quad\quad\left.- \frac{r^{2} \left( 1 - \eta \right)^{2} - \eta^{2}}{4 \left( 1 - \eta \right)^{2}} {\Theta} \right) , \end{array} $$
(10)

where the coefficient A is:

$$A = \frac{(1 - \eta^{2})(1 - 3\eta^{2}) - 4\eta^{4}\ln(\eta)}{16 (1 - \eta)^{2} \left[ (1 - \eta^{2})^{2} + (1 - \eta^{4})\ln(\eta) \right]} . $$

The base electric gravity is radially oriented and is defined as positive when it is centripetal. Therefore the base electric gravity is given by (Yoshikawa et al. 2013):

$$\begin{array}{@{}rcl@{}} G_{e}(r) &=& \frac {1} {(\ln\eta)^{2} r^{3}}F(r,\gamma_{e},\eta) \quad \text{with}\\ \quad F &=& \frac {{\gamma_{e}^{2}} \left[ 1 - \gamma_{e} \left( {\Theta} + 1 / \ln(\eta) \right) \right]} {\left[ \ln \left( 1 - \gamma_{e} \right) \right]^{2} \left( 1 - \gamma_{e} {\Theta} \right)^{3}} . \end{array} $$
(11)

The base electric gravity behaves like the inverse of r3 and is inhomogeneous because of curvature. The factor F corresponds to the thermoelectric coupling. It describes different behaviours depending on the direction of the temperature gradient and on η. In outward heating (γe > 0), the base electric gravity is always centripetal. Nevertheless for inward heating (γe < 0) the basic electric gravity can change its sign within the gap when η is sufficiently large, i.e. for low curvature. In this study we consider the case of outward heating.

Linear Stability Analysis

We linearised the equations about the base state. The perturbations are developed into normal modes of complex growth rate s, azimuthal mode number n and axial wavenumber k: \((\hat {u},\hat {v},\hat {w},\hat {\pi },\hat {\theta },\hat {\phi })e^{st+in\varphi +ikz}\), where the complex amplitudes of perturbations, indicated with a hat, depend only on the radial position. Equations 7a–d are thus written as follows:

$$\begin{array}{@{}rcl@{}} 0 &=& \left( D + \frac{1}{r} \right) \hat{u} + \frac{in}{r}\hat{v} + ik\hat{w} \end{array} $$
(12a)
$$\begin{array}{@{}rcl@{}} s\hat{u} &=& \left( {\Delta} - \frac{1}{r^{2}} - ikW \right)\hat{u} - \frac{2in}{r^{2}}\hat{v} -D\hat{\pi}\\ &&- \frac{\gamma_{e} {V_{E}^{2}}}{\text{Pr}} \left( -\hat{\theta}G_{e} + \hat{g}_{e,r}{\Theta} \right) \end{array} $$
(12b)
$$\begin{array}{@{}rcl@{}} s\hat{v} &= &\frac{2in}{r^{2}}\hat{u} + \left( {\Delta} - \frac{1}{r^{2}} - ikW \right)\hat{v} - \frac{in}{r}\hat{\pi}\\ &&- \frac{\gamma_{e} {V_{E}^{2}}}{\text{Pr}} \hat{g}_{e,\varphi}{\Theta} \end{array} $$
(12c)
$$\begin{array}{@{}rcl@{}} s\hat{w} &= &\left( DW \right)\hat{u} + \left( {\Delta} - ikW \right)\hat{w} - ik\hat{\pi} + \text{Gr} \hat{\theta} \\ &&- \frac {\gamma_{e} {V_{E}^{2}}}{\text{Pr}} \hat{g}_{e,z}{\Theta} \end{array} $$
(12d)
$$\begin{array}{@{}rcl@{}} s\hat{\theta} &=& -\left( D{\Theta} \right)\hat{u} + \left( \frac{1}{Pr}{\Delta} - ikW \right) \hat{\theta} \end{array} $$
(12e)
$$\begin{array}{@{}rcl@{}} 0 &=& - {\gamma_{e}} \left[ D {\Phi} D + \frac{1}{r} D {\Phi} + \left( D^{2} {\Phi} \right) \right] \hat{\theta}\\ &&+ \left[ \left( 1 - {\gamma_{e}} {\Theta} \right) {\Delta} - {\gamma_{e}} D {\Theta} D \right] \hat{\phi} , \end{array} $$
(12f)

where D = d/dr is the radial derivative operator, and Δ = d2/dr2 + d/rdr − (n2/r2 + k2) is the Laplacian operator. The perturbation electric gravity \((\hat {g}_{e,r},\hat {g}_{e,\varphi },\hat {g}_{e,z})\) has been introduced:

$$\begin{array}{@{}rcl@{}} \hat{g}_{e,r} &=& \left( D {\Phi} D^{2} + D^{2} {\Phi} D \right) \hat{\phi} \:,\quad \hat{g}_{e,\varphi} = \frac{in}{r} D {\Phi} D \hat{\phi} \:,\\ \hat{g}_{e,z} &=& i k D {\Phi} D \hat{\phi} . \end{array} $$
(13)

The boundary conditions for the perturbations are homogeneous and read:

$$ \hat{u} = \hat{v} = \hat{w} = D\hat{u} = \hat{\theta} = \hat{\phi} = 0 \quad \text{at} \: r = \frac{\eta}{1-\eta} \: \text{and} \: \frac{1}{1-\eta} . $$
(14)

Equations 12a–f together with boundary conditions (14) are invariant by the operation \((n,\hat {v})\rightarrow (-n,-\hat {v})\). It means that once the eigenvalue s and its corresponding eigenfunctions \((\hat {u},\hat {v},\hat {w},\hat {\pi },\hat {\theta },\) \(\hat {\phi })\) are known for a given mode (n, k), the mode (−n, k) will give the same eigenvalue s with eigenfunctions \((\hat {u},-\hat {v},\hat {w},\hat {\pi },\hat {\theta },\hat {\phi })\). The stability condition of both modes are identical.

The eigenvalue problem is discretized by a Chebyshev spectral collocation method and is solved by a QZ decomposition. To ensure the convergence of the computation, the order of Chebyshev polynomials is set to 30.

Numerical Simulation

Unsteady 3D direct numerical simulations (DNS) are performed using the finite elements code COMSOL Multiphysics v3.5. The code has been used to simulate the temporal evolution of the axial gravity during parabolic flights (Pletser et al. 2016). During one parabola, the experiment successively undergoes a 1g phase of about one minute, a 1.8g phase of 20s, followed by a microgravity phase of 22s, and another 1.8g phase of 20s. The duration of the microgravity phase is short for such experiments, therefore it is of most interest to have an insight of the effects of the previous phases of gravity on the flow behaviour during the microgravity phase. For these simulations, the cylindrical annulus has an inner radius of R1 = 5mm, an outer radius of R2 = 10mm, and a height of l = 30mm. It yields to a radius ratio of η = 0.5 and an aspect ratio of Γ = l/d = 6, which corresponds to the experimental geometry. The top and bottom surfaces of the cylindrical annulus are supposed to be adiabatic with perfect electric insulation. The working fluid has the physical properties of silicone oil AK5, which is the fluid used during the parabolic flight campaigns (Meyer et al. 2017). It has a Prandtl number of Pr = 65 and a ratio between the thermal coefficients of δ = 1.01. Under 1g condition, the Galileo number is Ga = 228.

Figure 2 shows the evolution of the three normalized components of the acceleration, measured by Novespace inside the airplane, during the first half of a parabola (the first hypergravity phase and some seconds of microgravity). Only the axial component of the acceleration gz has been taken into account for the simulations. An analytical function is used to modelize the axial gravity, which is given by:

$$\begin{array}{@{}rcl@{}} g_{z}(t) &=& \frac{\arctan \left[ 1.4 \left( t - 1.9 \right) \right]}{\pi} \cdot t + 1.3875 \quad \text{for} \quad t \leq 10s \\ g_{z}(t) &=& \frac{\arctan \left[ 1.4 \left( 22.5 - t \right) \right]}{\pi / 2} \cdot t + 0.8978 \quad \text{for} \quad\!\!\! t > 10s . \end{array} $$

The model gives empirically the variation of the axial gravity from the 1g phase to the μg phase, passing through the hypergravity phase. Then gz is zero during the μg phase, and the second hypergravity phase is symmetric to the first one.

Fig. 2
figure 2

Temporal behaviour of the gravity components inside the airplane during the first part of a parabola. For simulations, the axial gravity has been modelized with an analytical function. The gravity is below 0.01g after t = 356.5s, and this lasts up to t = 378s

Full size image

Linear Stability Results

The eigenvalue s = σ + iω is computed for a given set of parameters (η,Pr,Ga, δ, Gr, V E, n, k). The state where the maximum value of the growth rate’s real part σ is equal to zero is called the marginal state. Marginal curves can be plotted in a diagram spanned by (k, V E) or (k,Gr) for various azimuthal mode number n. The global minimum of these curves corresponds to the critical state denoted by (Grc, V Ec, nc, kc, ωc) where ωc is the critical frequency of vortices propagation. The angle Ψ of modes with respect to the azimuthal direction and the total wave number q are defined as:

$$\begin{array}{@{}rcl@{}} q_{c} &=& \sqrt{ k_{\varphi}^{2} + k^{2} }, \quad {\Psi} = \frac{180}{\pi} \arctan \frac{k_{\varphi}}{k} \quad \text{where} \\ k_{\varphi} &=& \frac{2n_{c}(1-\eta)}{1+\eta} . \end{array} $$
(15)

The total wavenumber of the critical mode qc gives the wavenumber measured along the transverse direction to the rolls at the median surface between the two electrodes.

Stability Parameters

In the absence of electric tension, critical modes develop either as hydrodynamic mode (HM) or thermal mode (TM) depending on the Prandtl number and on the curvature of the cylindrical annulus (Bahloul et al. 2000). These modes are both axisymmetric (nc = 0) and oscillatory (ωc≠ 0) and are distinguishable by their wavelengths. Figure 3 shows variations of the critical parameters as functions of V E for Pr = 10. For this value of the Prandtl number, TM are critical in the absence of electric potential. Applying a small electric tension, thermal modes remain critical, and the corresponding critical parameters are nearly independent from V E until a certain value of V E denoted by \(V_{E}^{*}\). At \(V_{E}^{*}\), two modes of different nature have the same growth rate and are thus critical at the same time. The points (\(V_{E}^{*},\text {Ra}^{*}\)) are called codimension-2 points. Beyond this particular value of the dimensionless electric potential, the threshold strongly decreases with the electric potential (Fig. 3a). The axial wavenumber becomes equal to zero (Fig. 3b), which means that the vortices take the form of axially aligned columns. The number of columns (Fig. 3c) depends on the radius ratio and corresponds to the maximum number m of vortices of the gap size, given by m = [π(1 + η)/2(1 − η)]. The angle of CM with respect to the azimuthal direction is Ψ = 90∘ (Fig. 3d). These columnar modes (CM) are stationary (Fig. 3e). For large values of V E, another codimension-2 point (\(V_{E}^{**},\text {Ra}^{**}\)) indicates the transition from columnar modes to electric modes (EM) which are stationary and helical. Indeed the axial wavenumber of EM is different from zero and increases with increasing V E. Depending on the radius ratio, the azimuthal mode number can gradually decrease from its value for CM to its value for the microgravity case (Yoshikawa et al. 2013). Indeed, for large values of V E, the Archimedean buoyancy is negligible compared to the dielectrophoretic effect, and the problem is equivalent to the case of microgravity condition. The angle of EM with respect to the azimuthal direction decreases with increasing V E and tends to Ψ = 60∘. The critical Rayleigh number of both CM and EM is proportional to \(V_{E}^{-2}\). The fact that the threshold behaviour does not change at the codimension-2 point (\(V_{E}^{**},\text {Ra}^{**}\)) indicates that both modes are of the same nature, i.e. they originate from the thermoelectric convection. For all the regimes, the curvature of the annulus has a destabilizing effect.

Fig. 3
figure 3

Variations of (a) the critical Rayleigh number, b the critical axial wavenumber, c the critical azimuthal mode number, d the angle of modes with respect to the azimuthal direction and e the critical frequency with the dimensionless electric potential for different values of η and for Pr = 10, Ga = 1370 and δ = 1

Full size image

Figure 4a shows the variation of the critical Rayleigh number with the dimensionless electric potential for η = 0.5 and for various values of Pr. For low values of V E, HM are found in case Pr = 0.72 while TM are found for Pr = 10 and Pr = 100. The critical parameters of TM and HM are affected by the Prandtl number, as it is described in Bahloul et al. (2000). For all values of V E, the Prandtl number has a stabilizing effect. The wavenumber of CM and EM are not modified by Pr, in the sense that the Prandtl number only changes the position of the codimension-2 points between HM or TM and CM and between CM and EM. Indeed the larger the Prandtl number, the larger the dimensionless electric potential at the codimension-2 points.

Fig. 4
figure 4

Variations of (a) the critical Rayleigh number and b the critical Grashof number with the dimensionless electric potential for different values of Pr and for η = 0.5, Ga = 1370 and δ = 1

Full size image

Figure 4b shows the variation of the critical Grashov number with the dimensionless electric potential for the same set of parameters. In this case, the threshold of HM or TM decreases with increasing the Prandtl number. However, the critical Grashof number of CM and EM is not affected by Pr. The independence of the threshold of CM and EM with Pr confirms their electric nature since this independence characterises the thermoelectric buoyancy (Yoshikawa et al. 2013).

Experimental Configuration

Experiments have been performed in laboratory, as well as during parabolic flight campaigns. For these experiments, the cylindrical annulus has a radius ratio of η = 0.5, and an aspect ratio of Γ = 6 or Γ = 20. The working fluid is silicone oil AK5, whose properties have been given in Section “Numerical Simulation”. Figure 5 shows the stability diagram spanned by Ra and L considering an infinite aspect ratio. For low values of L, the critical modes are thermal modes and the variation of their threshold with L is weak, indicating that the modes are not affected by the dielectrophoretic buoyancy. On the other hand, the critical electric Rayleigh number L for CM and EM is nearly independent from Ra, indicating that those modes are not affected by the Archimedean buoyancy.

Fig. 5
figure 5

Variations of the critical Rayleigh number with the electric Rayleigh number for η = 0.5, Ga = 228, δ = 1.01 and Pr = 65

Full size image

Additionally, we derived an equation for kinetic energy from the linearised momentum equations (12b–12d) by multiplying them with \(\hat {u}^{*}\), \(\hat {v}^{*}\) and \(\hat {w}^{*}\) respectively, where the asterisks mean complex conjugate, and by adding the resulting equations. The remaining equation is integrated over the volume and over a period of oscillation, then one can find:

$$ 2 s K = W_{Hy} + W_{Th} + W_{BG} + W_{PG} - D_{\nu} , $$
(16)

where K is the kinetic energy and reads:

$$ K = \int \frac{|\hat{u}|^{2} + |\hat{v}|^{2} + |\hat{w}|^{2}}{2} dV . $$
(17)

The terms WHy and WTh are related to the action of the axial gravity, and corresponds to the power performed by the shear stress and to the power performed by the Archimedean buoyancy respectively. The two contributions are given by:

$$ W_{Hy} = - \int \hat{u} \hat{w}^{*} \frac{\partial W}{\partial r} dV \; , \quad W_{Th} = \text{Gr} \int \hat{\theta} \hat{w}^{*} dV . $$
(18)

WBG and WPG are concerned with the thermoelectric buoyancy. They represent the power performed by the base electric gravity and the one performed by the perturbation electric gravity, respectively. The two terms are given by:

$$\begin{array}{@{}rcl@{}} W_{BG} \!&=&\! \frac{{\gamma_{e}} {V_{E}^{2}}}{\text{Pr}} \int \hat{\theta} G_{e} \hat{u}^{*} dV \; , \\ W_{PG} \!&=&\! - \frac{{\gamma_{e}} {V_{E}^{2}}}{\text{Pr}} \int {\Theta} \left( \hat{u}^{*} \hat{g}_{e,r} \,+\, \hat{v}^{*} \hat{g}_{e,\varphi} \,+\, \hat{w}^{*} \hat{g}_{e,z} \right) dV . \end{array} $$
(19)

The last term Dν is the rate of viscous energy dissipation and reads:

$$ D_{\nu} = \int {\Phi}_{\nu} dV , $$
(20)

where Φν is:

$$\begin{array}{@{}rcl@{}} {\Phi}_{\nu} \!&=&\! \left\vert D\hat{u} \right\vert^{2} \,+\, \left\vert \frac{in\hat{u}}{r} - \frac{\hat{v}}{r} \right\vert^{2} \,+\, k^{2} \left\vert \hat{u} \right\vert^{2} \,+\, \left\vert D\hat{v} \right\vert^{2} \,+\, \left\vert \frac{in\hat{v}}{r} + \frac{\hat{u}}{r} \right\vert^{2} \\ &&\!+ k^{2} \left\vert \hat{v} \right\vert^{2} + \left\vert D\hat{w} \right\vert^{2} + \left\vert \frac{in\hat{w}}{r} \right\vert^{2} + k^{2} \left\vert \hat{w} \right\vert^{2} . \end{array} $$

The rate of viscous dissipation completely balances the other terms, since there is no temporal variation of kinetic energy at the onset of instabilities.

Figure 6 shows the variation of the power terms of Eq. 16 with the dimensionless electric potential. For low values of V E, critical modes are TM and the term WTh is the dominant one. For large values of V E, the power WBG is the main contribution to the energy transfer from the base state to perturbations. In the intermediate case, for columnar modes, both WTh and WBG are important. WHy also contributes to the energy transfer. However, its magnitude is one order of magnitude lower than the other terms. The power input by the perturbation electric gravity is negligible for the whole range of parameters. The value of Dν is equivalent to the sum of the other power terms. Its lower value for CM compared to TM or EM indicates that columnar modes need less energy to be sustained.

Fig. 6
figure 6

Energy generation terms normalized by twice the kinetic energy K as functions of the dimensionless electric potential V E. The curves have been obtained for Ga = 228, δ = 1.01, Pr = 64.6 and η = 0.5

Full size image

Numerical Results

In all simulations, the electric field is only applied during microgravity in order to focus on the effect of a purely central force field. But during the parabolic flight experiments, the DEP force has also been active all along a parabola (Meyer et al. 2017). The hypergravity phase starts after 330 seconds of normal gravity phase. Therefore we ensure an established base flow, which has the form of an axisymmetric monocellular convection cell, at the beginning of the parabola.

Figure 7 shows the evolution in time of the Nusselt numbers computed numerically at the inner and outer cylinders as the ratio of heat flux at inner/outer cylinder and heat flux of the conductive state. The evolution starts from the 1g phase and stops at the end of the μg phase. During the 1g phase, the Nusselt number is Nu(1g) = 2.67 for both cylinders, since the base flow already increases the heat flux at the surfaces compared to the conductive state. The hypergravity phase reinforces the base flow, and increases the Nusselt numbers compared to the 1g phase. During the change of gravity intensity, the Nusselt number at the inner cylinder is slightly lower than that of the outer cylinder, which indicates a unsteady transition from 1g to hypergravity concerning the heat transfer. Passing from hypergravity to μg condition, the Nusselt numbers start to decrease because of the dissipation of the base flow by viscous effects. The dissipation process keeps going during the first seconds of microgravity, until the Nusselt numbers start to grow. The resulting minimum of the Nusselt numbers is larger than one, which means that the DEP force starts to affect the flow while the base flow produced by the previous hypergravity phase has not been completely dissipated. The growth of the Nusselt numbers indicate the development of instability inside the gap due to the DEP buoyancy. Vortices occur inside the gap and are responsible for heat transfer enhancement.

Fig. 7
figure 7

Nusselt number at the inner and outer cylinder as a function of time. The gravity is 10− 2g at t = 360s and lasts 18s. The temperature difference is ΔT = 10K and the dimensionless electric potential, only applied during μg, is V E = 1832 (L = 22064)

Full size image

Figure 8 shows the temperature profile in the (r, φ) plane and its derivative with respect to the azimuthal direction for the same parameters as for Fig. 7. The profiles exhibit a non-axisymmetric pattern with 8 modes in the azimuthal direction, which is quantitatively comparable to Shadowgraph measurements (see the article dedicated to experiments from this issue by Meier et al.). The instability starts at the inner cylinder and develops in radial direction outward. The maximum of the Nusselt numbers during microgrvity phase (Fig. 7) corresponds to the point where the instability touches the outer cylinder. Then the Nusselt numbers decrease again, likely to converge to a stationary state which is not observed due to the short duration of the microgravity phase. All along the μg phase, the Nusselt number at the inner cylinder is larger than that at the outer cylinder which indicates that the heat transfer during this phase is transient.

Fig. 8
figure 8

Temperature profile and its azimuthal derivative in the (r, φ) plane at the end of the microgravity phase and at z = 14mm above the bottom surface. The temperature difference is ΔT = 10K and the dimensionless electric tension, only applied during μg, is V E = 1832 (L = 22064)

Full size image

A series of simulations have been performed for Gr = 530 (ΔT = 10K) and Gr = 265 (ΔT = 5K) with various values of the electric potential. The Nusselt numbers is computed at the inner and outer cylinders, and averaged over the last nine seconds of the μg phase. Their development as functions of the electric Rayleigh number L is shown in Fig. 9. If L < 700, the Nusselt numbers are nearly constant and are slightly larger than one, which corresponds to the quasi-conductive regime. Nu larger than one might have its origin in inert reminiscences of the previous hypergravity phase. If L > 700, the Nusselt numbers increase with increasing L because of the occurrence of instabilities which enhance the heat transfer. The Nusselt number at the inner cylinder is always larger than that of the outer cylinder, which could be partly explained by the fact that the intensity of the electric gravity is larger at the inner cylinder than at the outer one. At some values of the electric Rayleigh number, there are two slightly different values of the Nusselt number. This corresponds to the two different ΔT which were used for the simulations. Indeed, the base flow originated from the previous gravity phase takes less time to dissipate if the temperature difference between the two cylinders is lower, which results in a lower value of the Nusselt number even for the same value of L.

Fig. 9
figure 9

Nusselt number at the inner and outer cylinders, time averaged during the second half of the microgravity phase, as a function of the electric Rayleigh number. Several values of V E have been simulated both for ΔT = 5K and for ΔT = 10K

Full size image

Conclusion

The flow of a dielectric fluid confined in a vertical cylindrical annulus subjected to the axial Archimedean buoyancy and to the radial dielectrophoretic force has been investigated in the framework of parabolic flight experiments. A linear stability analysis has been performed. If the electric tension between the two cylinders is sufficiently large, it is found that non-axisymmetric modes can be critical. These modes are stationary and can either be columnar or helical. Their threshold is proportional to \(V_{E}^{-2}\), but in terms of electric Rayleigh number, the threshold is nearly not affected by the Archimedean buoyancy. The energy analysis showed that columnar modes need less energy to be sustained than thermal modes, critical for weak electric potentials, and than the electric modes, critical at high electric potentials. In addition to the theoretical study, numerical simulations have been performed with an axial gravity varying in time, that corresponds to the parabolic flight scenario. In simulations, the DEP force was active only during microgravity conditions. It was found that the base flow provided by the previous hypergravity phase is not completely dissipated during the microgravity phase and affects the evaluation of the heat transfer. One μg phase lasts 22s. It is sufficient to observe the development of non-axisymmetric instabilities, but it is still too short to become stationary.