Numerical Investigation of Transonic Non-ideal Gas Flows Around a Circular Cylinder at High Reynolds Number

Abstract

High Reynolds transonic ideal and non-ideal gas flows around a smooth circular cylinder are investigated by means of Large Eddy Simulations over a range of Mach numbers encompassing the drag divergence. The global aerodynamic performance of the cylinder in both air and a dense vapor are compared, as well as the influence of the thermodynamic behavior of the working fluid on the wake development. The drag divergence is delayed in the dense vapor flow compared to air, and the overall pressure drag is increased due to the lower back pressure. Loss generation mechanisms are also studied via entropy production in the boundary layer and by means of a loss breakdown analysis commonly used in turbomachinery. The specific entropy production rate is found to be lower in the dense gas flow compared to air. Finally, the momentum loss coefficient is reduced upon suppressing unsteady transonic vortex shedding.

1 Introduction

In the recent years, increased attention has been given to Organic Rankine Cycle (ORC) systems, which find their use in small-scale applications such as waste-heat recovery (Colonna et al. 2015). ORC machines are based on Rankine’s thermodynamic cycle, but they work with molecularly complex organic fluids characterized by high molar mass instead of water. Furthermore, the thermodynamic operating conditions are such that the calorically and thermally perfect gas model is no longer valid. These non-ideal thermodynamic states are typically located in the dense vapor region, defined as the thermodynamic region in the vapor phase where the fundamental derivative of gas dynamics (Thompson 1971):

$$\begin{aligned} \Gamma := \frac{v^3}{2c^2}\frac{\partial ^2 p}{\partial v^2}\vert _s = 1+\frac{\rho }{c}\frac{\partial c}{\partial \rho }\vert _s \end{aligned}$$

(1)

is lower than one. The fundamental derivative characterizes the variations of the speed of sound $c=\sqrt{(\partial p/\partial \rho )_s}$ with density $\rho =1/v$ through isentropic processes, where v is the specific volume, p is the pressure and s is the entropy. Furthermore, the main component in an ORC, the expander, is often a turbine. Due to size constraints on ORC machines, only a small number of turbine stages is possible, leading to high pressure ratios. Thus, typical flow regimes encountered in ORC turbines are often transonic or supersonic (Wheeler and Ong 2013). Compressibility strongly affects the flow around the blades, and especially the developing boundary layers or the detached free mixing layers near rounded trailing edges (TE) (Passmann 2021). Shock waves and flow separation developing around the TE can typically account for one third of the total blade mechanical losses in air (Denton 1993). Optimal TE shapes are not circular (Melzer and Pullan 2019), yet, due to mechanical integrity requirements of the blade a rounded end is commonly used to evenly distribute the load. Therefore, an appropriate prototype for studying TE loss mechanisms is represented by the flow around a circular cylinder (Sieverding and Manna 2020).

Circular cylinders at various flow regimes are of interest for many other engineering applications (Achenbach 1968; Zdravkovich 1997). The incompressible high Reynolds number flow around a smooth circular cylinder has become a classical fluid mechanics problem and has served to develop experimental and numerical methods. On the other hand, the compressible regime has received dimmer attention. In transonic flow regimes (for Mach numbers $M\ge 0.6$), locally supersonic zones exist in the vicinity of the cylinder, allowing shock waves to form near the walls (Rodriguez 1984), as well as shocklets in the recirculating flow (Hong et al. 2014). Supersonic expansion fans occurring on either sides of the cylinder delay boundary layer separation. This favorable pressure gradient further decreases the pressure on the cylinder surface so that when the flow finally detaches, the back pressure is low, leading to high pressure drag $C_{d,p}$. The same mechanism is found around supersonic turbine round TEs (Sieverding et al. 1980). As the Mach number is increased, pressure drag continuously rises and reaches a maximum for a critical Mach number $M_{cr}$ (Gowen and Perkins 1953; Macha 1977): this is the so-called drag divergence.

Few studies on transonic cylinder flows encompassing the drag divergence conditions exist in the literature, both experimental and numerical, and they are focused on air, modeled as an ideal gas. Experimental studies have measured the pressure drag $C_{d,p}$ at various Mach numbers within the range $0.9\le M\le 1.0$ (Welsh 1953; Gowen and Perkins 1953; Macha 1977; Murthy and Rose 1978). According to the experimental setting, the peak drag was measured in the range $M_{cr}=0.95\div 1.0$. The results were found to be sensitive to the spanwise extent of the cylinder and to blockage effects. The flow topology was also strongly affected by the Mach number but similar topologies did not always correspond to the same Mach number in different experiments, because of flow sensitivity to experimental uncertainties, such as surface roughness and levels of freestream turbulence. Instantaneous flow visualisations report different unsteady wake shapes either alternating in time at identical Mach number, or quickly switching from one topology to another over a very slight change in inlet conditions (Rodriguez 1984; van Dyke 1982). With the aim of explaining this phenomenon, Hirsch (2007) mentions the non uniqueness of the viscous flow in the transonic regime around smooth cylinders. Alternating long/short shear layer regimes (Dyment 1982) are a good example. More recently, numerical investigations have been performed on the drag divergence of air flows past smooth cylinders. Xu et al. (2009) investigated the range $0.85\le M\le 0.98$ at a Reynolds number based on the cylinder diameter $\text{Re} _{D} =2.0\times 10^5$ using Detached Eddy Simulation (DES), and the peak in $C_{d,p}$ is obtained at $M_{cr}=0.9$. Similar observations are made by Xia et al. (2016) using Constrained LES (CLES) over a wide range of Mach numbers at $\text{Re} _{D} =4\times 10^4,1\times 10^6$. We summarize the integrated drag coefficients from the literature in Fig. 1. The figure illustrates the large scatter in the range $M\ge 0.8$, both in $C_{d,p}$ and $M_{cr}$. The present authors previously performed low-fidelity Unsteady Reynolds-Averaged Navier–Stokes (URANS) computations of the cylinder drag divergence in both air and the dense gas Novec 649 (Matar et al. 2023); some of the results are shown in Fig. 1. The predictions are in rather good agreement on the divergence Mach number $M_{cr}$ with the experimental data of Welsh for air (Welsh 1953), but the computed peak value is more similar to the peak $C_{d,p}$ measured by Murthy and Rose (1978) and Macha (1977); still, it remains within the wide literature disparities. On the other hand, the dense gas results show significantly higher values of $C_{d,p}$ over the whole Mach number range. The reason was found to be the lower back pressure, due to the lower isentropic exponent of the gas (Matar et al. 2023). On the other hand, the $M_{cr}$ was identical to the one in air. Therefore, the thermodynamic behavior of the gas plays a crucial role in the aerodynamic performance of the cylinder in addition to the Mach and Reynolds numbers.

Fig. 1

Pressure drag coefficient against Mach number

With the aim of better understanding the strong coupling between compressibility effects and turbulent wake development, we undertook a numerical study of transonic cylinder flows by using high-fidelity, wall-resolved Large Eddy Simulations. Two working fluids are considered: the first one is an organic vapor, Novec 649, used as a working fluid in ORCs, and the second one is air at standard conditions. The Novec 649 was used in an experimental campaign conducted in the CLOWT (Closed-loop Organic Wind Tunnel) facility at FH Muenster (Reinker et al. 2021), which allowed to validate our previous URANS simulations (Matar et al. 2023) for $M=0.16 \div 0.6$. In addition to shedding light on transonic cylinder aerodynamics over a range of conditions little studied in the recent literature, including the effect of the thermodynamic behavior of the working fluids, we also take benefit of this simple geometry to investigate loss mechanisms also common to turbine blades.

The paper is organized as follows. In Sect. 2, we describe the numerical methods. Then, the characteristics of the aerodynamic fields are investigated for different Mach numbers, both for air and for Novec 649. In Sect. 3.2, a study of loss-generating mechanisms is performed, leading to systematic comparisons between ideal and non-ideal gas flows. Conclusions are given in Sect. 4.

2 Methods

2.1 Working Fluids and Thermodynamic Conditions

Transonic flows past cylinders are investigated both for a dense organic vapor and for air. The dense vapor chosen for this study is the fluorinated ketone Novec 649 by 3 M due its practicability, low toxicity and inflammability, as well as high thermal stability. Some useful properties of the dense working fluid are given in Table 1. While its vapor phase contains a $\Gamma \le 1$ region, as shown in Fig. 2, it does not feature an inversion region (Thompson 1971), i.e. $\Gamma _{\min}\ge 0$ everywhere in the vapor region. Due to the high density of the working fluid, only mildly non-ideal thermodynamic conditions are accessible in the CLOWT experimental facility (Reinker et al. 2021), which are also selected for the present simulations. Even so, the deviations from the ideal gas behavior are large enough to make the ideal gas law inaccurate, and the behavior of the dense gas is therefore modeled by the Peng-Robinson equation of state (Peng and Robinson 1976) improved by Stryjek and Vera (1986), along with a power-law approximation of the specific heat at constant volume in the dilute gas limit

$$\begin{aligned} C_{v,\infty }(T) = C_{v,\infty }(T_c)\left( \frac{T}{T_c}\right) ^n \end{aligned}$$

(2)

where $T_c$ is the critical temperature. Dynamic viscosity and thermal conductivity coefficient are computed using the Chung–Lee–Starling models (Chung et al. 1988).

For air, we use the thermally and calorically perfect gas model along with the Sutherland law for viscosity and a constant Prandtl number of 0.71.

The inflow conditions ’IC’ used for Novec 649 are summarized in Table 2 and are indicated by the cross symbol in the Clapeyron diagram of the organic vapor in Fig. 2. The symbols indicate the minimum reduced volume reached in the computational domain for each Mach number. On the one hand, we can expect opposite behavior of the speed of sound with density as $\Gamma \le 1$, on the other hand, the $p-v$ space explored remains in the diluted gas region.

Table 1 Novec 649 properties 3M: Novec 649 (Engineered fluid 2009)

Fig. 2

Clapeyron diagram of Novec 649. $P_r=P/P_c$ and $v_r=\rho _c/\rho$ are the reduced pressure and volume, respectively. The thick black line is the liquid–vapor saturation curve, the grey lines with inlines are the $\Gamma$ iso-contours and the thin dotted curves are the isotherms

Table 2 Thermodynamic conditions used at the computational domain inflow for the dense gas computations

2.2 Numerical Methods

Compressible LES are carried out using the in-house finite-difference solver MUSICAA (Bienner et al. 2022). The inviscid fluxes are discretized by means of 10th-order centred differences whereas 4th-order is used for viscous fluxes. The scheme is supplemented with a 10th-order selective filter to eliminate grid-to-grid oscillations, along with a low-order shock capturing term activated locally by a combination of Jameson’s shock sensor and Ducros’ dilatation/vorticity sensor. The filter also acts as a regularization term draining energy at subgrid scales, so that no explicit subgrid-scale model is used (implicit LES). A four-stage Runge-Kutta algorithm is used for time integration and high-order implicit residual smoothing (Cinnella and Content 2016), modified as in Bienner et al. (2022), is applied to relax stability constraints on the time step. This allows CFL values of 5 for air and 7 for the dense gas in the current computations. Adiabatic no-slip conditions are applied at the cylinder wall, and non-reflecting Tam & Dong’s conditions are imposed at the inflow and outflow boundaries.

2.3 Computational Setup

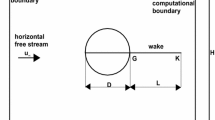
The mesh is a multi-block curvilinear grid where a polar grid is fitted to the cylinder surrounded by H–blocks. The computational domain extends from $-10D$ to 30D and from $-10D$ to 10D in the streamwise and transverse directions respectively, where D is the cylinder diameter. A close-up view of the mesh around the cylinder is shown in Fig. 3a. The wall normal first cell height $n_1=1.3\times 10^{-4}D$ corresponds to a flow wall unit $n^+_{avg}\approx 1$ and it was estimated using the von Kármán integral equation for a turbulent boundary layer as well as existing values from the literature (Lehmkuhl et al. 2014; Cheng et al. 2017; Breuer 2000). The cylinder surface is discretized with $N_\theta =1\,500$ points to obtain a good description of the boundary layer separation mechanism. The two-dimensional mesh is then extruded in the spanwise direction z over 1D and discretized by 250 planes, leading to a resolution of $z^+\approx 30$. Figure 3b shows the resulting tangential $t^+$ and normal $n^+$ wall units evolutions against angular position. Furthermore, Fig. 4 shows the power spectrum density of the transverse velocity component v signal taken in the near wake (0.75D, 0) in the $M=0.7$ Novec 649 flow, and indicates a resolution extending beyond $S_t\ge 200$.

An additional coarser mesh is designed with half the resolution in the azimuthal direction to assess the convergence level of the spatial discretization. The predicted Strouhal number $S_t=\frac{fD}{U_{in}}$, where f is the frequency and $U_{in}$ the inlet velocity, associated with the vortex shedding corresponds to the peak in power density and is $S_{t,vs}\approx 0.188$ in both cases. The distribution of the averaged friction coefficient $C_f=\frac{\tau _w}{1/2\rho _{in}U_{in}^2}$, where $\tau _w$ is the wall shear stress and $\rho _{in}$ the inlet density, in Fig. 5a against angular position also shows only mild evolution between the fine and coarse mesh. Finally, the boundary layer velocity profiles at two stations are shown in Fig. 5b; overall, first order statistics are reasonably well converged to consider the solution independent of the mesh for several Mach numbers. The mesh characteristics are summarized in Table 3.

Fig. 3

a Close-up view of the mesh (one in five lines shown) and b normal $n^+$ and tangential $t^+$ grid resolutions in wall units

Fig. 4

Power spectrum density (PSD) of the instantaneous transverse velocity component signal at $(x,y)=(0.75D,0)$

Fig. 5

a Friction coefficient $C_f$ against angular position $\theta$ and b boundary layer velocity profile at (Left) $\theta =30$°and (Right) $\theta =60$°

Table 3 Mesh characteristics

To further assess the spatial resolution of the grid, we inspect auto-correlation functions in the spanwise direction. The separated shear layers quickly transition to turbulence and there the spanwise resolution is crucial. Several resolution criteria for LES have been inspected by Davidson (2009), and one that emerged as adequate was the resolution of the correlation decay in the direction of interest. Indeed, a minimum number of grid points must be contained within the correlation decay region to show that the largest turbulence scales are well resolved. About 6–10 points within the decay region is deemed satisfactory (Davidson 2009). Hence we show in Fig. 6 the auto-correlation functions of the three velocity components along the spanwise direction computed using time signals from each location along the span, using the definition

$$\begin{aligned} R_{\phi \phi }(z) = \frac{\langle \phi '(\varvec{x},t) \phi '(\varvec{x}+\delta z,t) \rangle }{\langle \phi '(\varvec{x},t)^2 \rangle } \end{aligned}$$

(3)

where $\phi '=\phi -\bar{\phi }$ is the fluctuating signal and $\langle \cdot \rangle$ is a time-averaging operator. Here, we focus on the length scale we can resolve using LES just downstream the boundary layer separation point, where an unsteady shear layer transitions to turbulence. There, the structures are expected to be small and thus provide a good estimate of the actual resolution. Therefore, we place the numerical probe in the average passing of the shear layer.

Fig. 6

a Auto-correlation functions along cylinder span and b zoom on correlation decay region where the vertical lines indicate the computed integral scale for each velocity component

Figure 6a shows that all three velocity components (u, v, w in the streamwise, transverse and spanwise directions respectively) auto-correlation functions decay quickly, indicating that the local mean flow features three-dimensional structures. This stems from the unsteady motion of the shear layer, which transitions at intermittent locations. A zoom on the decay region is provided in Fig. 6b, where the integral length scale (vertical lines) has been indicated for each component. The latter was computed using the definition

$$\begin{aligned} \Lambda_{\phi} =\int ^\infty _0R_{\phi\phi}(z)dz \end{aligned}$$

(4)

In practice, the upper integration limit is finite and the first zero-crossing of the function is used here, as in Kurian and Fransson (2009), O’Neill et al. (2004). The decay is steeper in the case of v compared to the other components, hence its auto-correlation function is be used as reference. The computed integral scale $\Lambda _v\le 5$ grid points, however the decay region is described by 9 points which is within the aforementioned criterion for LES resolution. Thus, we consider that the spanwise resolution is sufficient.

In the following simulations, flow statistics are collected over 25 vortex sheddings, corresponding to over 150 flow units $t^*=D/U_{in}$. The evolutions of the lift and pressure drag coefficients, $C_l$ and $C_{d,p}$ respectively, against $t^*$ for the $M=0.7$ dense gas flow are given in Fig. 7. While longer integration times may be needed to better converge the flow statistics, computational resource constraints imposed to divide 1,500,000 CPU hours among the 6 inlet conditions simulated.

Fig. 7

Lift $C_l$ and drag coefficients $C_d$ against characteristic flow time $t^*=D/U_{in}$

3 Results

3.1 Effect of Mach Number

3.1.1 Wake Development

As mentioned in the introduction, the drag divergence of the circular cylinder is characterised by a sharp change in the shape of the near wake. The stronger gas compressibility governs the main changes as the Mach number increases; hence, we expect the drag divergence to be dependent on the gas thermodynamic behavior. We show in Fig. 8 instantaneous snapshots of both air and Novec 649 flows, at all inflow Mach numbers at stake. Transonic vortex shedding occurs in most cases, where the shed vortices achieve local supersonic flow which in turn allows shock waves. There are two types of compression waves: those attached to the cylinder surface, and those standing normal to the principal flow direction further downstream on the shear layers. The former have their foot located at the boundary layer separation point and both form a coupled system: they oscillate over the surface between the front and aft sections of the cylinder. Additionally, noise is generated by the transitioning shear layers, especially visible in Fig. 8b ($M=0.8$, air).

Fig. 8

Q–criterion iso-contour colored by local velocity magnitude as well as shock waves detected using the method from Pagendram (Ziniu et al. 2013). Left: air, right: Novec 649. Top to bottom: $M=0.7$, $M=0.8$, $M=0.9$

As the Mach number increases, the standing shocks move further downstream in the wake, until an abrupt change of configuration is observed in air, characterized by a closed recirculation region behind the cylinder, associated with a fishtail-shaped shock system and suppression of vortex shedding. For Novec 649 the qualitative behavior is similar to the one observed for air, but shifted toward higher values of the Mach number. As a consequence, at $M=0.9$ the Novec flow still exhibits an open wake, and the fishtail shock configuration is not observed.

The delayed drag divergence in Novec 649 is a typical effect of dense gases operating under thermodynamic conditions such that the fundamental derivative $\Gamma \le 1$. As shown in Fig. 9, where the time-averaged speed of sound fields are presented along with the recirculation region and the sonic line, the speed of sound varies inversely to that of air (as evidenced by the color map), and it increases while the flow expands. In turn, this limits the increase in Mach number compared to the perfect gas case. As a result, the extent of the supersonic region is smaller, which ultimately leads to a delay in the drag divergence. This effect can be quantified by introducing the generalized transonic similarity parameter $K=(1-M^2)/(\Gamma _{in}D)^{2/3}$ (Hayes 2016). Although derived in the small transonic perturbation limit and hence not strictly valid for a bluff body such as a cylinder, the parameter allows to estimate an equivalent Mach number for a flow of Novec 649 to achieve the same K as an air flow at a given Mach number, knowing that $\Gamma =1.2$ everywhere for air:

$$\begin{aligned} M_{Novec}=\left[ 1-\left( \frac{\Gamma _{in}}{1.2}\right) ^{2/3} \left(1-M_{air}^2 \right)\right] ^{1/2} \end{aligned}$$

(5)

According to this rough estimate, similarity with air flow at $M=0.9$ in air requires an inflow Mach number of about 0.92 for Novec 649 at the present thermodynamic conditions.

Fig. 9

Speed of sound c mean field and grey contours (the color map is centered around the inlet value). The thick black line is the sonic line $M=1$, and the thick black dotted line is the null streamwise velocity component iso-contour $u=0$. Left: air, right: Novec 649. Top to bottom: $M=0.7$, $M=0.8$, $M=0.9$

3.1.2 Wall Quantities

The time- and spanwise-averaged pressure coefficient $C_p=\frac{P(\theta )-P_{in}}{1/2\rho _{in}U_{in}^2}$ is reported in Fig. 10 for air and Novec 649 at various Mach numbers. In the figures for air, we also report experimental data from Macha (1977), as well as the CLES of Xia et al. (2016). For Novec 649, we include the experimental measurements from Reinker et al. (2021) performed in CLOWT for a cylindrical Pitot tube immersed in Novec 649 cross flow, at a closeby Mach number ($M=0.65$) and somewhat higher Reynolds number ($3.4\times 10^5$). At $M=0.7$ (Fig. 10a) the present LES of Novec 649 shows a globally lower pressure on the aft portion of the cylinder compared to data for air. This is mostly due to the lower isentropic exponent of the dense gas which induces a stronger dilation of the gas. The present LES of air shows a trend similar to the literature data, however the back pressure is somewhat underestimated. Nevertheless, the present computations agree with the experimental measurements on the absence of a minimum of $C_p$, contrary to the simulations of Xia et al. (2016). In Reinker’s experiments for Novec 649 (Reinker et al. 2021) a local minumum is also observed: geometrical defects present on the cylinder surface (discussed in Cinnella et al. 2021) fix the separation point to the apex, which results in a pronounced $C_{p,min}$ and affects the aft section pressure. In the case of a smooth circular cylinder in a transonic cross flow (such as the present LES), the separation point accompanies the vortex shedding and oscillates over a large angular range, typical of compressibility/turbulence coupling (Dyment 1982). The resulting $C_p$ curves are essentially flattened, as are the ones obtained in the present study. Similar comments can be made at $M=0.8$ (Fig. 10b) except that the literature experimental measurements lie within the numerical disparities. Finally, at $M=0.9$ the experiments show a large deviation from the present and literature computations in air. This may be caused by a surface defect fixing the separation to an early position. Nevertheless, we see that a constant pressure plateau is reached just downstream flow separation, characteristic of the quasi-steady wake shown in Fig. 8c. Overall, the dense gas flow exhibits a pressure distribution similar to air at lower Mach number.

Figure 11a and b show the time- and spanwise-averaged friction coefficient evolution against angular position for air and Novec 649 respectively. As M increases, both the $C_f$ peak on the front section $\theta \le 90$°and the mean boundary layer separation point $\theta _{sep}$ (corresponding to $C_f(\theta _{sep})=0$) are displaced further downstream. This is a consequence of the favorable pressure gradient enhanced by the growing supersonic expansion with Mach number. At $M=0.9$ in air, the $C_f$ shows a distinct $\theta _{sep}$ due to the quasi-steady nature of the flow, followed by a plateau at a value near zero. For all other cases, the mean $\theta _{sep}$ is not well captured as it covers a large angular range during each vortex shedding.

Fig. 10

Pressure coefficients for air and Novec 649 at a $M=0.7$, b $M=0.8$ and c $M=0.9$. Line styles: $M=0.7$; $M=0.8$; $-\cdot$ $M=0.9$; present LES air; $\square$ Macha (1977); $\cdot \cdot$ $\text{Re} _{D} =1\times 10^6$; Xia et al. (2016); $\bullet$ Reinker et al. (2021)

Fig. 11

Wall friction coefficient from a air and b Novec 649 flows (for line styles see Fig. 10)

3.1.3 Boundary Layer Profiles

Boundary layer profiles are given for each inlet Mach number in Fig. 12 for Novec 649 (top) and air (bottom). The similarity variable $n^*=\frac{n}{x}Re_x^{-0.5}$ has been used, where n is the coordinate normal to the wall. At this station, the boundary layer is laminar. In the Novec 649 flows, the dynamic boundary layer height remains almost constant with Mach number as shown by Fig. 12a (top), but deviations in tangential velocity $u/U_{in}$ exist due to the local pressure gradient. Figure 12b (top) highlights one key aspect of dense gas thermodynamics: due to the high heat capacity of such fluids, mean temperature variations are much smaller compared to a perfect gas. The maximum deviation from the wall temperature is less than $0.3\%$. The mean fluctuations $T_{rms}/T_{in}$ are also very small, less than $0.05\%$ of the inlet temperature as shown in Fig. 12c (top). As observed in Gloerfelt et al. (2020), this behavior also results in decoupled thermodynamics and hydrodynamics; Fig. 12d (top) shows indeed the very low values of the Eckert number $E_c$ indicating weak self-heating, and therefore small influence of the thermal boundary layer on the hydrodynamic boundary layer. Below are given the same plots for air. The velocity profile is affected by the local pressure gradient in the same way as in the dense gas flow and the boundary layer height is similar: the Mach number range covered in the present study is too small to highlight differences between ideal and dense gase hydrodynamic boundary layer thickness. However, the temperature variations and mean fluctuations in Fig. 12b and c (bottom) are more than one order of magnitude higher than the dense gas boundary layer. The same can be said about $E_c$, which shows that friction heating is much stronger in the light gas flow.

Fig. 12

Boundary layer profile at $\theta =30$°a wall tangential velocity, b temperature, c temperature mean fluctuations, d Eckert number. Top: Novec 649, bottom: air (for line styles see Fig. 10)

3.1.4 Boundary Layer Separation Motion

In practice, the vortex shedding in the wake induces a quasi-periodic oscillation of the separation point and of the shock system (Dyment 1982). To showcase this phenomenon, we provide in Fig. 13a and b the conditional average of the $C_p$ only when lift is positive, corresponding to times where separation is likely to occur at the front and aft sections of the top and bottom of the cylinder, here shown for 0° $\le \theta \le 180$°and 180° $\le \theta \le 360$°respectively. This allows to view the pressure distribution when the separation point is at its approximate average front and rear locations, indicated by the vertical lines. In both gases, as M increases, separation is delayed due to the stronger supersonic expansion of the flow past the curved wall. Moreover, the wake thickness $\Delta \theta$ decreases when M increases, in agreement with the onset of drag divergence. However, the back pressure coefficient $C_{p,b}=C_p(180$°) clearly increases with M for Novec 649, whereas it varies only slightly for air: this is of major importance for turbine TE study as a large portion of losses are attributable to the low back pressure, as discussed later.

Fig. 13

Pressure coefficient conditional average from a Novec 649 and b air computations (for line styles see Fig. 10)

3.1.5 Drag Coefficient

Finally, Fig. 14 summarizes the pressure drag coefficients $C_{d,p}$ against some literature data. The underestimated back pressure in the present LES for air leads to a higher $C_{d,p}$ at $M=0.7$ and $M=0.8$, and the drag peak seems to correspond to that found by Xu et al. (2009). Most of all, we observe the same trend as that predicted by the URANS from the previous work (Matar et al. 2023): due to the lower back pressure reached in the dense vapor computations, the pressure drag exerted on the cylinder is stronger at $M=0.7$ and $M=0.8$. However, no distinguishable peak in drag can be observed in this case, which supports the claim that drag divergence is delayed and the critical Mach number is higher with respect to the ideal gas.

Fig. 14

Pressure drag coefficient $C_{d,p}$ against Mach number M: present LES Novec 649; present LES air; URANS Novec 649 and URANS air (Matar et al. 2023); $\text{Re} _{D} =4\times 10^4$ and $\text{Re} _{D} =1\times 10^6$ from Xia et al. (2016); $--$ data from Welsh (1953); $-\cdot$ data from Macha (1977)

3.2 Loss Mechanisms

In this section, we examine some of the processes responsible for loss generation in the vicinity of the cylinder for both the dense and perfect gas flows. First, the generation of entropy in the near wall flow is investigated, then a loss breakdown analysis commonly used in turbomachinery is carried out.

3.2.1 Entropy Generation

The mechanisms responsible for entropy production inside the boundary layer have been studied in the case of flat plate boundary layers in laminar, transitional and turbulent states, as well as under different pressure gradients (Ghasemi et al. 2014). Typically, the rate of entropy generation in an unsteady boundary layer is computed in volumetric form and, in the case of adiabatic surfaces, is assumed to consist of two contributions: the lost work of the mean viscous forces, referred to as viscous dissipation, and the unsteady kinetic energy dissipated in the form of heat. In the present study, the boundary layer developing on the cylinder is mostly laminar in all cases, due to the high speed flows. Moreover, up to two thirds of pointwise entropy generation is located in the viscous region of turbulent boundary layers. Therefore, the viscous dissipation mechanism should dominate. Here, we compute the so-called approximate form of the pointwise volumetric entropy generation (Ghasemi et al. 2014)

$$\begin{aligned} \dot{S}'''^+ = \left( \frac{\partial u^+}{\partial n^+} + \overline{u'v'}^+ \right) \frac{\partial u^+}{\partial n^+} \end{aligned}$$

(6)

where $^+$ indicates non-dimensional wall flow quantity, $\dot{S}'''^+=\frac{T\nu \dot{S'''}}{\rho u_\tau ^4}$, n is the wall normal coordinate and $\overline{u'v'}$ is the cross-correlation of the two-dimensional velocity vector.

We show in Fig. 15a–c the $\dot{S}'''^+$ profiles at several stations on the cylinder ($\theta =15,45,60$°) for all Mach numbers, both in air and Novec 649.

Fig. 15

a–c Pointwise volumetric entropy production rate and d–f Pointwise specific entropy production per characteristic time, at $\theta =15,45,60$°(for line styles see Fig. 10)

At $\theta =15$°, the profiles collapse to a self-similar solution, which corresponds to that found in favorable pressure gradient boundary layers (Ghasemi et al. 2014). The small deviations may be due to the different local pressure gradients. At $\theta =45$°, the $M=0.9$ flows of air and Novec 649 exhibit additional $\dot{S}'''^+$ occurring further away from the wall; upon not including the cross-correlation terms $\overline{u'v'}$ in Eq. (6), the differences vanish while the other curves remain mostly unchanged, indicating that local mean fluctuations are also responsible for entropy increase at this station. Finally, as the region of separation point oscillation is approached for both $M=0.7$ air and Novec 649 flows, the mean boundary layer encounters an adverse pressure gradient which enhances local entropy generation above the value computed at the wall.

To further compare the entropy production rates between fluids, we report in Fig. 15d–f the pointwise entropy generation rate per unit mass, normalized by the gas constant R of each fluid as well as the flow advection characteristic time, i.e. $\dot{s}^*/R=\frac{S'''D}{U_{in}\rho R}$. This gives the specific entropy produced at a given position across the boundary layer per characteristic time. We see that the generation rate is higher in air compared to the dense gas at every station, especially in the viscous dominated region of the boundary layer. We have seen in Fig. 12b that, due to the weakened coupling between hydrodynamics and thermodynamics of dense vapors, near wall temperature gradients are reduced compared to air. Therefore, viscous dissipation generates less heat and in turn contributes less to local entropy generation.

3.2.2 Loss Breakdown

Loss analysis is a design tool used in turbomachinery, which consists in breaking down the total loss into its multiple sources. Denton (1993) gives a review of certain major aspects of loss mechanisms in turbine flows, including the flow around the TE. A loss coefficient $\zeta$ (from here on designated by "Denton loss") was derived as

$$\begin{aligned} \zeta = \frac{-C_{p,b}t}{w} + \frac{2\theta ^*}{w} + \left( \frac{\delta ^*+t}{w}\right) ^2 \end{aligned}$$

(7)

where $C_{p,b}=(P_b-P_{in})/(P_{0,1}-P_{in})$ is the back pressure coefficient, t the TE thickness, w the blade pitch, and $\delta ^*$ and $\theta ^*$ are the displacement and momentum thickness respectively. This expression allows to breakdown TE loss into three sources: the first term gives the profile loss, the second term gives the momentum loss due to the growing boundary layer, and the third term gives the loss due to blockage of the vane passage also caused by the boundary layers. In typical high pressure turbine flows, the boundary layer height just before separation is of the order of the TE thickness, and therefore generates loss levels comparable to the profile loss (Leggett et al. 2018). In the present study, the boundary layer is only a fraction of the cylinder diameter and hence the low pressure behind the cylinder is the strongest contributor. Nevertheless, this analysis is carried out here to highlight the evolution of loss with Mach number for both air and dense gas flows. Additionally, because the present flow is open as opposed to internal, the blade pitch is not defined so the loss coefficient $\zeta$ is expressed in unit length (equivalent to setting the pitch to an arbitrary unit length). This precludes the computation of the third term, which is still dependent on w. This term is not relevant in the present unconfined flow and will not be considered in the following.

First, the boundary layer thickness is required to compute the momentum and displacement thicknesses. For zero pressure gradient flat plate flows, it can be simply defined as $\delta _{99}=y(0.99U_{e})$, where y is a coordinate normal to the wall, and $U_e$ the external flow velocity, while here a different definition must be followed as large pressure gradients, both favorable and adverse exist. We choose one based on local spanwise vorticity, labeled $-y\Omega _z$ (Griffin et al. 2021; Vinuesa et al. 2016), which consists in evaluating this function through the boundary layer and finding the location where it reaches a threshold, commonly set to $C_\Omega =0.02$. Then, the angular position of the evaluation of $\delta ^*$ and $\theta ^*$ needs to be fixed for the comparison to be relevant. In the theory, Eq. (7) is derived for a row of square TEs; hence, the boundary layer separation point is fixed to the TE corner, and the thicknesses are evaluated just upstream. In the case of the cylinder, this can be viewed under two different scopes: either the cylinder is used to simulate a TE, either we study the loss associated to the whole cylinder. The former suggests that the angular position at which $\delta ^*$ and $\theta ^*$ are computed should be representative of the position just upstream a turbine blade TE, while the latter simply fixes that point at the cylinder apex $\theta =90^\circ$. As the present boundary layers cannot be representative of those developing at the end of turbine blades, we choose the latter option and perform the analysis specifically on the cylinder loss.

Fig. 16

a Boundary layer shape factor (for line styles see Fig. 10) and b (left axis) $\circ$ back pressure coefficient $C_{p,b}$ and (right axis) $\blacktriangle$ percentage of Denton loss attributed to momentum deficit $\zeta _\theta /\zeta$

Denton also proposed a modification of the first term of Eq. (7) in the case of separated flow at the TE, where the geometrical thickness t is replaced with $(t+\delta ^*)$ to take into account the large separated boundary layer and the contribution of its low pressure to form drag. Therefore, we inspect the boundary layer quality by means of the the shape factor $H=\delta ^*/\theta ^*$ to assess whether the modification is appropriate. Figure 16a shows the shape factor against angular position. We see that H is not far from the Blasius boundary layer value $H=2.59$ on the front section of the cylinder for all cases, but quickly diverges as the shock oscillation region is approached. After an initial collapse, implying a relative increase in momentum thickness, H rises due to an adverse pressure gradient. We stress that the mean boundary layer separation point is located after $\theta >90$°, therefore the increase in H before that point is due to the mean adverse pressure gradient and the flow is locally still not separated. Nevertheless, the boundary layer thickness rapidly increases and cannot be neglected. The $M=0.9$ air flow is the exception and clearly shows delayed and more local separation. Therefore, it is relevant to use the modification of the form loss term in all cases except the latter.

Upon computing $\zeta$, it was found that $\approx 99\%$ of the Denton loss is caused by the low back pressure, as expected. To make the graphs meaningful, we simply give in Fig. 16b the value of $-C_{p,b}$ on the left axis and the percentage of loss due to momentum deficit $\zeta _\theta /\zeta$ on the right axis, as a function of the Mach number. We see that the profile loss decreases for both dense and ideal gas flows as the Mach number rises, except between $M=0.8$ and $M=0.9$ in air. Note that transonic vortex shedding gradually weakens in this M range, indicating that the latter may be detrimental to the cylinder performance. Moreover, form loss are greater in the dense gas flow, consistently with the increased pressure drag of the whole cylinder. On the other hand, $\zeta _\theta /\zeta$ is comparable between air and Novec 649 below $M=0.8$, but then collapses as the boundary layer remains attached at $M=0.9$ in air, where vortex shedding is essentially suppressed. Similarly, this indicates that the oscillations of the separation point, at the origin of the large region of thickening boundary layer, should be reduced in the view to increase cylinder performance.

4 Conclusion

High Reynolds transonic ideal and non-ideal gas flows around a circular cylinder were investigated numerically using implicit Large Eddy Simulation (LES). Three inlet Mach numbers encompassing the drag divergence were simulated in air and a dense vapor Novec 649 in diluted conditions.

It was shown that the thermodynamic behavior of the gas affects the flow near the cylinder in several ways. The fish-tail like shock wave system is not obtained in the dense gas flow, which indicates a delay in drag divergence compared to air. This is due to the fundamental derivative which requires the speed of sound to increase during the initial expansion of the fluid, limiting the local rise in Mach number. Moreover, the pressure on the aft section of the cylinder is lower in the dense gas flow, primarily due to the lower value of the equivalent isentropic exponent. This also results in a systematically lower back pressure, which essentially drives the pressure drag to higher values.

The decoupled thermodynamics and hydrodynamics were evidenced in Novec 649 by inspecting the developing boundary layers in each fluid. It was seen that in the case of the organic vapor, in agreement with previous works (Gloerfelt et al. 2020), the thermal boundary layer has little effect on the dynamic one and self-heating is largely weakened, due to the high heat capacity.

Some loss mechanisms were explored, specifically entropy generation inside the boundary layer, and form and momentum loss. Because of the similarities between a circular cylinder and a turbine blade trailing edge, the latter were obtained by means of a loss analysis common in turbomachinery. The pointwise specific entropy production rate was found to be lower in the dense gas compared to air. Using the Denton loss breakdown analysis, we found that transonic vortex shedding, responsible for wake thickening, is the main contributor to momentum loss and should essentially be suppressed to increase the cylinder performance.

In future works, similar studies will be conducted on full turbine blades at thermodynamic states representative of ORC operating conditions. Further investigations will be performed via wall-resolved implicit LES to understand the coupled effects of turbulence development inside a high-pressure vane passage and compressibility on the global performance of the profile.