Introduction

Thermo-solutocapillary convection is driven by surface tension gradient due to the variation of temperature and solute concentration at free surface. This phenomenon widely exists in crystal growth process, welting process, and many other industrial processes. The most widely studied model associated with the thermo-solutocapillary convection is a liquid bridge with temperature and solute concentration differences between two disks. As early as 1969, Levich and Krylov (1969) had made an analysis of the coupling of thermocapillary convection and solutocapillary convection. The first time numerical investigation of thermo-solutocapillary convection in liquid bridge or float zone is by You and Hu (1992), they found that the solutal Marangoni number has obvious influence on the streamline function and the solute distribution but has relatively slight effect on the temperature distribution. Wanschura et al. (1995) made a linear stability analysis of thermo- and solutocapillary convection in a cylindrical liquid bridge, and they obtained critical Reynolds numbers for different parameter variations. Artemyev et al. (2001) numerically investigated the heat mass transfer processes in germanium crystal growth by the floating zone method under microgravity conditions, the thermal and solutal kinds of Marangoni convection in the molten zone was considered. Walker et al. (2002) numerically investigated the thermo-solutocapillary convection under a strong magnetic field. Joly et al. (2004) investigated the transport dynamics and stability limit of the axisymmetric steady flow driven by a surface tension variation in a liquid bridge configuration, in which the thermal and solutal Marangoni effect were included. Minakuchi et al. (2004) numerically studied the effect of solutal Marangoni convection during the SixGe1−x crystal growth by the floating-zone technique under zero gravity, the results show that the contribution of the solutal Marangoni convection to the flow structure was significant although the strength of the solutal Marangoni convection is much weaker than that of the thermal Marangoni convection. Lin et al. (2005) numerically investigated Marangoni flows in a floating zone of germanium-silicon crystals, the competition between the thermocapillary and solutocapillary flows in the floating zones was qualitatively examined, and in their model the static deformable free surface was used. Lyubimova et al. (2007a, b, 2011a, b ) made a lot of investigation on thermo-solutocapillary convection in float zone crystal growth, they studied the flow structure and flow instability of the convection, and obtained the effect of constant axial magnetic field on the thermosolutocapillary convection Recently, Minakuchi et al. (2012, 2014) studied the thermo-solutal Marangoni convection occurring in a liquid bridge of a silicon-germanium system under zero gravity, and they also investigated the relative contributions of thermal and solutal Marangoni convections on transport structures in a liquid bridge under zero gravity.

The literatures show that the thermo-solutocapillary convection in liquid bridge or float zone has been investigated extensively, however, all the above studies were dedicated to the situation of nondeformable free surface or static deformable free surface, and the dynamic deformation of free surface was neglected in order to avoid the simulation complexity associated with the unknown free surface shapes. It is well known that the deformation of free surface has an important influence on the pure thermocapillary convection, in particular for the onset of the oscillatory flow in liquid bridge (Sim et. al 2004). Microgravity experiment by Koster (1994) indicated that, a detailed investigation of thermocapillary convection in multilayered fluid systems needed to take account for finite interface deformations in conjunction with a suitable dynamic contact line condition. Moreover, the dynamic deformation of free surface in pure thermocapillary convection of liquid bridge has been considered by many investigators (Kuhlmann and Nienhuser (2002); Kawajia et al. (2006); Liang et al. (2014)).

To the authors’ knowledge, the dynamic deformation of free surface in the numerical simulation of thermo-solutocapillary convection has not been considered. Therefore, in the present work we report on the simulations of steady thermo-solutocapillary convection with a deformable free surface in axisymmetric liquid bridge by level set method, and the effects of thermal to solutal Marangoni number ratio and Marangoni number on the thermo-solutocapillary convection are discussed.

Physical and Mathematical Models

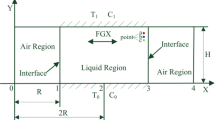
The liquid bridge with radius R0 and height H is suspended between two coaxial disks and surrounded by the gas in a cylindrical container with radius 2R0 and height H as shown in Fig. 1. The Aspect ratio of the liquid bridge is A =H/R0=1.2. The liquid bridge is filled with a binary fluid, which is a two-component mixture working medium. The interface between the fluid and gas is a deformable free surface. Different temperatures and concentrations are applied at the upper disk (T1, C1) and lower disk (T2, C2), where T 1>T 2 and C 1>C 2. The no-slip boundary condition is adopted for the upper and lower disks, and the surface tension force acts on the free surface. All the thermal properties are assumed to be constant except for the surface tension, and the surface tension is allowed to vary linearly with the liquid temperature and solute concentration. Thus the surface tension can be formulated as,

$$\sigma =\sigma_{0} -\gamma_{T} ({T-T_{0}} )-\gamma_{C} ({C-C_{0}} ) $$

where σ 0=σ(T0,C 0), γ T=−(∂ σ/∂ T), γ C =−(∂ σ/∂ C) T . Thermophysical properties of the fluid are estimated at the reference temperature T0 and concentration C0, which are set to be equal to T1 and C1, respectively. Moreover, only the liquid surface tension increases with concentration and decreases with temperature are considered. The fluid flow is assumed to be laminar, and buoyancy effects are neglected in present study.

Fig. 1
figure 1

Physical model

Full size image

The nondimensional variables of velocity, temperature, solute concentration, coordinates, time and pressure are defined as \(\boldsymbol {V}=\frac {\boldsymbol {u}}{U}, \varTheta =\frac {T-T_{1}} {T_{2} -T_{1}} ,C^{\ast } =\frac {C-C_{1}} {C_{2} -C_{1}} , (R,Z)=\frac {(r, z )}{R_{0}} , \tau =\frac {tU}{R_{0}} , P=p/\left ({\rho _{l} U^{2}} \right )\), respectively. Here, U=γ T Δ T/μ l is characteristic velocity. The level set method is employed to capture the free surface implicitly by introducing a smooth level set function, with the zero level set as the free surface, positive value outside the free surface, and negative value inside the free surface. Then, the non-dimensional Navier-Stokes equations governing the thermo-solutocapillary convection are expressed as follows:

$$ \nabla \cdot \textit{\textbf{V}}=0 $$
(1)
$$\begin{array}{@{}rcl@{}} \frac{\partial \textit{\textbf{V}}}{\partial \tau}+\nabla \cdot (\textit{\textbf{VV}})&=&-\frac{1}{\tilde{\rho} }\nabla P+\frac{1}{\tilde{\rho} Re}\nabla \cdot (\tilde{\mu}\nabla \textit{\textbf{V}}) \\ &&+\frac{1}{\tilde{\rho}Re}\nabla \cdot (\tilde{\mu}\nabla \textit{\textbf{V}})^{T}+\frac{1}{\tilde{\rho}Re}\left(\nabla_{s} \varTheta +\frac{\nabla_{s} C^{\ast}}{R_{\sigma} } \right)\delta (\phi) \\ &&+\frac{1}{\tilde{\rho} Re}\left( {\frac{1}{Ca}+\varTheta +\frac{C^{\ast}}{R_{\sigma} }} \right)\frac{k(\phi )\delta (\phi )\nabla \phi} {\tilde{\rho}} \end{array} $$
(2)
$$ \frac{\partial {\Theta}} {\partial \tau} +\textit{\textbf{V}}\cdot \nabla {\Theta} =\frac{1}{\tilde{{\rho} }\tilde{{C}}_{p} Ma}\nabla \cdot ({\tilde{\lambda}\nabla {\Theta}} ) $$
(3)
$$ \frac{\partial \mathrm{C}^{\ast} }{\partial \tau} +\textit{\textbf{V}}\cdot \nabla C^{\ast} =\frac{1}{LeMa}\nabla \cdot (\tilde{\mathrm{D}}\nabla C^{\ast}) $$
(4)
$$ \frac{\partial \phi} {\partial \tau} +\textit{\textbf{V}}\cdot \nabla \phi=0 $$
(5)

where \(\tilde {\mu }=\mu /\mu _{l} \), \(\tilde {\rho }=\rho /\rho _{l} \), \(\tilde {\lambda }=\lambda /\lambda _{l} \), \(\tilde {D}=D/D_{l} \) and \(\tilde {C}_{p} =C_{p} /C_{pl} \) are the dimensionless viscosity, density, thermal conductivity, solute diffusivity, and specific heat, respectively. ϕ is the Level set function, δ is the smeared-out Dirac delta function, and ∇ s =(I−nn)⋅∇ is free surface gradient operator. The dimensionless parameters are defined as follows: thermal Marangoni number \(Ma_{T} =\frac {\gamma _{T} \varDelta TR_{0}} {\mu _{l} \alpha _{l}} \), Solutal Marangoni number \(Ma_{C} =\frac {\gamma _{C} \varDelta CR_{0}} {\mu _{l} \alpha _{l}} \), Marangoni number M a=|M a T|, Reynolds number \(Re=\frac {UR_{0}} {\nu _{l}} \), Capillary number C a=|C a T CaC|, \(\text {Ca}_{\mathrm {T}} =\frac {\gamma _{T} \cdot \varDelta T}{\sigma _{0}} \) and \(\text {Ca}_{\mathrm {C}} =\frac {\gamma _{c} \cdot \varDelta C}{\sigma _{0}} \), the ratio of thermal Marangoni number to solutal Marangoni \(R_{\sigma } =\frac {\gamma _{T} \cdot {\Delta } T}{\gamma _{C} \cdot {\Delta } C}\), Prandtl number \(\text {Pr}=\frac {\nu _{l}} {\alpha _{l}} \) and Lewis number \(\text {Le}=\frac {\alpha _{l}} {D_{l}} \). The Marangoni number equals to the product of Reynolds number and Prandtl number, namely Ma = Pr ∗Re. The subscripts of g and l note the gas and liquid, respectively. The continuum surface force (CSF) model (Brackbill et al. 1992) is used to reformulate the surface tension as a volume force, and the fourth and fifth terms at the right hand of the momentum equation are the tangential and normal surface tension, respectively.

The corresponding physical variants can be expressed as

$$\begin{array}{@{}rcl@{}} \tilde{\rho}&=&\eta_{\rho} +(1-\eta_{\rho} )H(\phi ), \\ \tilde{\mu}&=&\eta_{\mu} +(1-\eta_{\mu} )H(\phi ) \end{array} $$
(6)

where η ρ =ρ g/ρ l ,η μ =μ g /μ l , H(ϕ) is the smeared-out Heaviside function defined by

$$ H(\phi )=\left\{ \begin{array}{llll} 1 \\ \frac{1}{2}+\frac{\phi} {2\xi} +\frac{1}{2\pi} sin \left(\frac{\pi \phi} {\xi}\right) \\ 0 \\ \end{array} \right. \quad \begin{array}{l} \phi < -\xi \\ -\xi \leq \phi \leq \xi \\ \phi > \xi \\ \end{array} $$
(7)

where ξ is a tunable parameter that determines the size of the bandwidth of numerical smearing. A typical good value is ξ=1.5Δ R, and Δ R is the grid step spacing in R-direction

To keep the level set function as a distance function from the front, an approach based on solving the hyperbolic partial differential equation has been presented in reference (Sussman et al. 1994). The reinitialization equation is

$$ \phi_{Y} =sign\left(\phi_{0}\right)\left( {1-\left| {\nabla \phi} \right|} \right), \quad \phi \left(R,0 \right)=\phi_{0} \left( R \right) $$
(8)

Where \(\left | {\nabla \phi } \right |=\sqrt {\phi _{R}^{2} +\phi _{Z}^{2}} \), and the sign function \(sign_{\xi } \left (\phi _{0} \right )=\frac {\phi } {\sqrt {\phi ^{2}+\xi ^{2}}}\).

Moreover, in order to make the total mass completely satisfy the mass conservation in time, the mass conserving procedure proposed by Liang et al. (2011) is used.

Boundary and Initial Conditions

$$ \varTheta =0, C^{\ast}=0,\textit{\textbf{V}}=0, \frac{\partial \phi} {\partial \mathrm{Z}}=0 \qquad \text{at} \ \ Z=0 $$
$$ \varTheta =1, C^{\ast}=1,\textit{\textbf{V}}=0, \frac{\partial \phi} {\partial Z}=0 \qquad \text{at} \ \ Z=1.2 $$
$$ V_{\mathrm{R}}=0, \frac{\partial \mathrm{V}_{Z}} {\partial \mathrm{R}}=0,\frac{\partial \varTheta} {\partial \mathrm{R}}\,=\,0,\frac{\partial C^{\ast}}{\partial \mathrm{R}}\!=0, \frac{\partial \phi} {\partial R}\!=0 \quad \text{at} \ \ R=0 $$
$$ V_{\mathrm{R}}=0, V_{\mathrm{z}}=0, \frac{\partial \varTheta} {\partial \mathrm{R}}=0, \frac{\partial C^{\ast}}{\partial \mathrm{R}}=0, \frac{\partial \phi} {\partial R}=0 \quad \text{at} \ \ R=2 $$
$$ \varTheta =0, C^{\ast}=0,\textit{\textbf{V}}=0, \phi\left( \textit{1},Z\right)=0, P=0 \quad \text{at} \ \ \tau =0 $$

In this paper, we consider the contact conditions of interface with the upper and lower disks is contact points fixed.

Computational Method

In this article we use the Runge-Kutta Crank-Nicholson (RKCN) projection method presented by Ni et al. (2003) to solve the governing equations The Crank-Nicholson implicit technique is employed to update the diffusion term, and the low storage three-stage Runge-Kutta technique is employed to update the convective term. This method has second-order temporal accuracy for variable-density unsteady incompressible flows. The diffusion term in momentum equation is discretized using standard central difference schemes, while the convective term is discretized by high-order compact schemes. The convective term in the level set equation using the third-order essentially nonoscillatory (ENO) scheme. The non-dimensional time step for all the simulations is 1×10−3. This detailed description of the computational method can refer to our previous paper (Zhou and Huang 2010) The numerical code is validated by comparing computed surface deformation of pure thermocapillary convection with those from Sim et al. (2004) in Fig. 2. The parameters for the simulation are Pr =1, A = 1, Ca = 0.05 and Re = 1 The numerical results at Bi = are in good agreement with Sim’s results

Fig. 2
figure 2

Comparison of free surface deformation in liquid bridge with Sim’s results

Full size image

The axisymmetric liquid bridge is discretized with a uniform mesh, and this mesh is determined by refining the mesh size until convergence and constancy of flow velocity, temperature, concentration and free surface deformation is achieved. The grid number 200\(^{\mathrm {R}_{\ast }}\)200 Z is used, which is found to be sufficient to accurately capture the free surface, temperature, solute concentration and flow fields.

Results and Discussions

In the liquid bridge, both the temperature and solute concentration differences between the upper and lower disks produce a surface tension gradient at free surface, so the thermocapillary and solutocapillary convection can be induced. The numerical simulations are carried out for Prandtl number Pr = 1, Lewis number Le = 100, Capillary number Ca = 0.1, Marangoni number 1 ≤ Ma ≤ 100 and thermal to solutal Marangoni number ratio −10≤R σ ≤−0.1. All the simulations start from the all-zero initial field V =P=Θ=C ∗= 0 and the thermo-solutocapillary convection is considered to be fully developed as the velocity, temperature, solute concentration and free surface deformation keep constant in computational process, namely the final steady thermo-solutocapillary convection. The convergence criteria can be defined as follows: for each time step the quotient \(Q=\frac {\left | {\varphi ^{n+1}-\varphi ^{n}} \right |}{\left | {\varphi _{max}^{n}} \right |}\) is calculated for all dependent variables in all grid points, and the index n + 1 denotes a discrete point of time which follows the point of time n after a time step Δτ. If Q ≤10−5 is valid for all variables in all grid points the thermo-solutocapillary convection is interpreted as a steady flow. In our simulations, the density ratio, dynamic viscosity ratio, thermal conductivity ratio, solute diffusivity ratio and specific heat ratio of gas and liquid are η ρ =2×10−4, η μ =3×10−3, η λ =10−3, η D=10−3 and \(\eta _{C_{p}} =5\), respectively. The initial shape of the free surface of liquid bridge is a vertical non-deformable plane, and the computational results at the time of τ= 500 are given in the paper.

Influence of Thermal to Solutal Marangoni Number Ratio

The streamlines distribution of thermo-solutocapillary convection under different R σ with Ca = 0.1, Le = 100, Ma = 1 is shown in Fig. 3, in which solid lines denote clockwise rotating cell and dashed lines denote anticlockwise rotating cell. As R σ =-0.1, the flow field consists of one anticlockwise rotating convective cell, and from the fluid flow direction at free surface we can know that this convection is driven by solutocapillary effect. As R σ =−1, the flow field consists of one anticlockwise and one clockwise rotating convective cells, and the lower and upper convective cells are driven by thermocapillary and solutocapillary effects, respectively. As R σ =−10, the flow field consists of one clockwise rotating convective cell, which is driven by thermocapillary effect.

Fig. 3
figure 3

Streamlines distribution with Ca =0.1, Le =100, Ma =1 and various R σ

Full size image

Figure 4 gives free surface deformations and surface pressure distribution under different R σ with Ca = 0.1, Le = 100 and Ma = 1. It can be seen that the free surfaces is almost asymmetric about the central point (R = 1, Z = 0.6) of free surface. As R σ =−1 the free surface deformation is very small, the order of magnitude is O(10 −6), whose amplified figure is shown in Fig. 4b. Meanwhile, the free surface bulges out near the lower and upper disks and bulges in at the central region of the liquid bridge. As R σ <−1, the free surfaces bulge out near the lower disk and bulge in near the upper disk, and with the decrease of R σ the free surface deformation increases. The surface deformation is O(10 −3), and its maximum value is 0.0011 at R σ =−10, Ca = 0.1, Le = 100 and Ma = 1. As R σ >−1, the free surfaces bulge out near the upper disk and bulge in near the lower disk, and the free surface deformation increases with the increase of R σ . The free surface deformation is mainly caused by surface pressure gradient, so the mechanism of free surface deformation can be explained by the surface pressure distribution The corresponding surface pressure distribution of Fig. 4a is shown in Fig. 4c. As R σ =−1, the surface pressure approximates to zero, this means the pressure gradient is zero, therefore this surface pressure distribution does not induce a obvious free surface deformation. As R σ <−1, the surface pressure decreases along z axis, namely the pressure gradient is negative, this leads to the free surface bulges out near the lower disk. Meanwhile, the absolute pressure gradient increases with R σ decreasing, so the free surface deformation increases with the decrease of R σ . As R σ >−1, the change tendency of surface pressure and pressure gradient along Z axis is opposite to that of R σ <−1.

Fig. 4
figure 4

Free surface deformations (a), amplified figure of R σ =-1 (b) and surface pressure (c) distribution with Ca = 0.1, Le = 100, Ma = 1 and various R σ

Full size image

Figure 5 shows surface axial velocity distribution with Ca = 0.1, Le = 100, Ma = 1 and various R σ . As R σ =−1, the axial velocity is very small. As R σ <−1, the surface axial velocity is negative, this means the free surface fluid flow from the upper disk to the lower disk, and it’s magnitude increases with R σ decreasing. As R σ >−1, the surface axial velocity is positive, which means the free surface fluid flow from the lower disk to the upper disk, and it’s magnitude increases with R σ increasing. Figure 5b shows non-dimensional surface tension distribution under different R σ with Ca = 0.1, Le = 100, and Ma = 1. As R σ =−1, the non-dimensional surface tension is unit, this means that the thermocapillary forces is balanced by solutocapillary forces at free surface. As R σ <−1, the non-dimensional surface tension is monotous decreasing, and it increases with R σ decreasing. As R σ >−1, the non-dimensional surface tension is monotous increasing, and it increases with R σ increasing.

Fig. 5
figure 5

Surface axial velocity (a) and surface tension (b) distribution with Ca = 0.1, Le = 100, Ma = 1 and various R σ

Full size image

Influence of Marangoni Number

Figure 6 shows streamlines distribution under different Marangoni number with R σ =−1, Ca = 0.1, Le = 100. As Ma = 1, the streamlines distribution is shown in Fig. 3b, the flow field consists of one anticlockwise and one clockwise rotating convective cells, and the size of the both cells are comparable. With Marangoni number increasing, the size of the lower convective cell increases, but that of the upper convective cell decreases. At the same time, the flow field is dominated by the lower cell, which is driven thermocapillary effect. This reason can be attributed to the thermal diffusivity is larger than that of mass diffusivity, which causes the convective cell driven by thermocapillary effect is formed before that driven by solutocapillary effect. Moreover, with Marangoni number increasing the temperature gradient is more quickly established across the surface and the clockwise rotating convective cell is generated, and this leads to the convective cell driven by solutocapillary effect is confined in the upper corner.

Fig. 6
figure 6

Streamlines distribution with R σ =-1, Ca = 0.1, Le = 100, and various Ma

Full size image

Figure 7 shows free surface deformations and surface pressure distribution under various Marangoni numbers with R σ =−1, Le = 100 and Ca = 0.1. We can see that the free surface deformations near the upper and lower disks almost equals to each other at R σ =−1, Ma = 1, Le = 100 and Ca = 0.1, as shown in Fig. 4b. However, Fig. 7a shows that, as the Marangoni number increases the deformation near the lower disk increases deeply, but that near the upper disk decreases. Meanwhile, the maximal free surface deformation point travels to the lower disk, and the free surface deformation of Ma = 100 is less than that of Ma = 50. In Fig. 7b, the absolute value of pressure gradients at zone 1 and zone 2 is larger than that at the central region as Ma = 10, this leads to the free surface bulges out near the upper and lower disks. As Ma = 50 and 100, the obvious surface pressure gradient just occurs near the lower disk, this causes the free surface bulges out near the lower disk. Moreover, even if the pressure gradient near the lower disk of Ma = 100 is larger than that of Ma = 50, but the boundary effect of the lower dick damps the free surface deformation, which results in the free surface deformation in case Ma = 100 is smaller.

Fig. 7
figure 7

Free surface deformations (a) and surface pressure (b) distribution with R σ =-1, Le = 100, Ca = 0.1, and various Ma

Full size image

In the next, we shall discuss the effect of Marangoni number in the case of R σ =−10. With the increase of Marangoni number the flow fields remain unchanged, and similar to Fig. 3c, so we do not give the flow fields under various Marangoni numbers here. Figure 8 shows free surface deformations and surface pressure with R σ =−10, Le = 100, Ca = 0.1 and various Ma. For different Marangoni numbers, the free surfaces bulge out near the lower disk and bulge in near the upper disk. As Marangoni number increases, the free surface deformation near the upper disk is reduced, and the length between the maximal point and the minimal point also is reduced. Therefore, the free surface deformation is reduced with the increase of Marangoni number. The surface pressures distribution in Fig. 8b show that, the absolute of pressure gradient decreases with Marangoni number increasing, then results in the free surface deformation decreases.

Fig. 8
figure 8

Free surfaces (a) and surface pressure (b) distribution with R σ =-10, Le = 100, Ca = 0.1 and various Ma

Full size image

Figure 9 shows surface axial velocity and surface tension distribution under various Marangoni numbers with R σ =−10, Le = 100 and Ca = 0.1. With Marangoni number increasing the surface axial velocity increases, and the inhomogeneity is enlarged. As for the non-dimensional surface tension, it manifests as linear variation along z axis. However, with Marangoni number increasing the distortion of the surface tension increases, particularly near the lower disk, which means the thermocapillary convection is enhanced as Marangoni number increases.

Fig. 9
figure 9

Surface axial velocity (a) and surface tension (b) distribution with R σ =−10, Le = 100, Ca = 0.1, and various Ma

Full size image

Conclusions

In this paper, steady thermo-solutocapillary convection in a liquid bridge with dynamic deformable free surface under zero gravity condition is numerically simulated, and the effects of thermal to solutal Marangoni number ratio and Marangoni number on the flow and free surface deformation are discussed. The following conclusions were drawn:

  1. 1)

    As −10≤R σ <−1, the free surface bulges out near the lower disk and bulges in near the upper disk under low Marangoni number, and the flow field exists one anti-clockwise rotating convective cell which is driven by thermocapillary effect. With the increase of Marangoni number the free surface deformation decreases.

  2. 2)

    As R σ =−1, the free surface bulges out near the lower and upper disks and bulges in at the central region of the liquid bridge under low Marangoni number, the flow field consists of one clockwise and one anti-clockwise rotating convective cells, them are driven by solutocapillary and thermocapillary convection, respectively. With the increase of Marangoni number the free surface deformation mode is changed.

  3. 3)

    As −1<R σ ≤−0.01, the free surface bulges out near the upper disk and bulges in near the lower disk, and the flow field consists of one clockwise rotating convective cell, which is driven by solutocapillary effect.