Effect of Horizontal Vibrations on Thermo-Solutocapillary Convection and Free Surface of Liquid Bridge

Abstract

In this study, effect of lateral vibrations on the thermo-solutocapillary convection and surface behavior in a liquid bridge of toluene/n-hexane solution has been studied numerically under microgravity. The Navier-Stokes equations coupled with the concentration diffusion equation are solved on a staggered grid, and the level set approach is used to capture the deformation of free surface. Present results indicate the interface deformation is convex below the midheight of the liquid bridge and relatively complex at the upper height of the liquid bridge under different frequency vibrations. The lateral vibrations restrain radial and axial velocities on the surface under lateral vibrations with frequencies of 5 Hz and 10 Hz. While the radial and axial velocities on the surface increase under the lateral vibration with frequency of 15 Hz, which illustrates that the effect of lateral vibrations on the free surface has uncertainty.

Introduction

The floating zone method is a commonly used method in the industrial production of high quality crystals, and the oscillatory thermo-solutocapillary convection is found to be the main cause of micron-scale impurity fringes in the grown crystals using the floating zone. To suppress oscillatory thermo-solutocapillary convection, external vibrations, magnetic fields, and shearing airflow have been adopted to control the oscillations. The liquid bridge is a simplified model of the floating zone method, therefore, studies on the influence of external vibration on the liquid bridge have been carried out through theoretical analyses, simulations and experiments. Sanz and Diez (1989) considered the linear non-axisymmetric oscillations of a liquid bridge. The plateau technique was used to obtain the resonant frequencies of the liquid bridge when lateral perturbations were imposed. Zhang and Alexander (1990) found that the liquid bridge deviated from its initial equilibrium position when a single frequency axial vibration was applied to the liquid bridge. This action of deviation depended on the vibration acceleration, and an ideal method was found to judge the limits of the liquid bridge deviation. Anilkumar and Grugel (1993) investigated a novel end-wall oscillation model for thermo-solutocapillary convection in a semi-floating silicon-oil bridge under constant gravity. It was found that the surface flow velocity depended on the vibration amplitude, frequency, the length of the bridge and the viscosity of the silicone oil. Tang and Hu (1995) discussed the influence of high-frequency vibration (15-100 Hz) on thermalcapillary convection and critical Marangoni number in the semi-floating zone. It was pointed out that when the frequency of the applied vibration force was large enough, the temperature response amplitude that changed with time would disappear. Moreover, the fluctuation of the liquid bridge interface caused by inertial action also disappeared. Nicolas and Vega (1996) investigated the nonlinear and non-viscous reverberations of axisymmetric oscillations caused by an axial vibration, and they proposed a mathematical form of the amplitude, which could well predict the pressure field, velocity field, and interface oscillation. Lyubimov and Lyubimov (1997) applied a high-frequency axial vibration to an isothermal liquid bridge and found two reverse flows of pulsation and constancy. Furthermore, based on Boussinesq’s approximation, a numerical study was conducted to investigate the use of high-frequency axial vibration to control thermal capillary convection (Lyubimov et al. 2002). Kanashima et al. (2005) studied the effect of g-jitters on the interface deformation caused by oscillating thermal capillary convection. The vibration test was conducted on a table which was driven by a piezoelectric actuator so as to obtain a reasonable range of amplitudes and frequencies. Experimental results showed that in the period of the convective oscillation, the deformation characteristics of the free interface could be distinguished clearly according to the applied harmonic and non-harmonic g-jitter frequencies. Kawaji et al. (2006) measured the critical temperature difference in a Marangoni convection with and without small disturbances. A three-dimensional numerical model was developed to predict the interface oscillation behavior under single and multiple oscillations in space environment. Liang et al. (2011) investigated the influence of gravity jitter on a multiphase flow system using theoretical and experimental methods. Their study indicated that the response frequency of the liquid bridge depended on the size and physical parameters of the liquid bridge and that there was a triangular coupling relationship between the surface vibration, internal flow, and temperature oscillation. Tatyana et al. (2014) conducted a numerical study based on the Boussinesq method to evaluate the influence of high-frequency oscillations on thermocapillary convection and the linear stability of an axisymmetric liquid bridge in a semi-floating zone. It was found that the average vorticity could be obtained on the dynamic boundary layer, and the applied vibration could stabilize the flow. They also revealed the influence of different oscillation amplitudes and the Prandtl number on the Weber number. Yang et al. (2015) studied the thermocapillary convection and surface behavior in a high Prandtl number bridge under an external horizontal vibration. Results showed that the cell flow in the liquid bridge was not symmetrical because of the horizontal vibration. Changing the direction of acceleration of the horizontal vibration would lead to a change in the direction of rotation of the transverse eddy flow and thereby affect the surface flow velocity. Lyubimova et al. (2017) carried out a numerical study of thermo-solutocapillary convection controlled by an axial vibration in a liquid bridge under zero gravity. It was shown that vibration produced a stabilizing effect, increasing the critical Marangoni number of all unstable modes. However, this effect was different in different modes, and the liquid bridge could become unstable at high vibration intensity.

It is difficult to capture small deformations of the free surface in a liquid bridge using existing methods of free surface tracking (Zhou and Huai, 2015), therefore, the existing studies on thermo-solutocapillary convection in liquid bridges did not consider the dynamic surface deformation. Moreover, studies about the effects of vibrations on thermo-solutocapillary convection and free surface of liquid bridge have not been found so far in the existing literatures. Therefore, the present work establishes a model of thermo-solutocapillary convection for a toluene/hexane solution under external horizontal vibrations considering the dynamic surface deformation. The SIMPLE algorithm is used to solve the control equations, and the level set method is used to track the tiny changes in the two-phase free interface. The applied lateral vibrations are used to simulate the external acceleration caused by the gravity jitter which exists in microgravity environment.

Physical and Mathematical Models

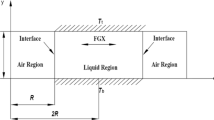
The physical model of liquid bridge is shown in Fig. 1, and the cylindrical liquid bridge with radius R = 5 mm and height H = 5 mm is suspended initially between two coaxial disks and surrounded by the gas in a rectangular container with radius 2R and height H. The aspect ratio of the liquid bridge is Ar = H/R = 1.0. Different temperatures and concentrations are applied at the upper disk (T₁, C₁) and lower disk (T₀, C₀), respectively, where T₁ > T₀ and C₁ > C₀. In addition, according to the specific research contents, some monitoring points are arranged at different positions of liquid bridge.

Fig. 1

Schematic of liquid bridge model and layout of monitoring points

Governing Equations

The general governing equations are given by the following non-dimensional mass conservation, Navier-Stokes, energy conservation and solute diffusion equations, which are solved on a staggered grid.

$$ {\displaystyle \begin{array}{c}\nabla \cdotp V=0\\ {}\overline{\rho}\left[\partial V/\partial \overline{t}+\nabla \left(V\cdotp V\right)\right]=-\nabla \overline{P}+\left[{Ca}_T{\nabla}_s\varTheta +{Ca}_C{\nabla}_s{C}^{\prime}\right]/ We+\left[1-{Ca}_T\varTheta -{Ca}_c{C}^{\prime}\right]\left[\kappa \delta (d)\boldsymbol{n}\right]/ We\end{array}} $$

(1)

$$ +\nabla \cdotp \left(2\overline{\mu}\boldsymbol{D}\right)/\mathit{\operatorname{Re}}+ FGX $$

(2)

$$ \mathrm{\partial \Theta }/\partial \overline{t}+V\cdotp \nabla \varTheta ={\nabla}^2\varTheta / Ma $$

(3)

$$ \partial {C}^{\prime }/\partial \overline{t}+V\cdotp \nabla {C}^{\prime }={\nabla}^2{C}^{\prime }/ Le\cdot Ma $$

(4)

Where Θ and C′ are dimensionless temperature and concentration, respectively, and we take Θ = (T–T₀)/(T₁–T₀) and C′ = (C–C₀)/(C₁–C₀). Here κ, δ, d, and φ are the curvature of the interface, the dirac delta function, the normal distance to the interface, and the level set function, respectively. n and D are the unit normal vector at the interface and the viscous stress tensor, respectively. V = (u, v) is dimensionless fluid velocity, u(u = u_s/U) and v(v = v_s/U) are dimensionless radial and axial velocity, respectively, U = (σ_T·ΔT)/μ_l is characteristic velocity under microgravity, and L is the characteristic length and we take L = 2R. The dimensionless time, pressure, density and viscosity are defined as⁻t = (t·U)/L,⁻P=P/(ρ_l·U²),⁻ρ = ρ/ρ_l,⁻μ = μ/μ_l, respectively. ∇_s = (I-nn)·∇ is free interface gradient operator, The interface tension σ is considered as a linear function of temperature and concentration, σ = σ₀-σ_T(T-T₀)-σ_C(C-C₀), where σ₀ is a reference value of surface tension, σ_T = −∂σ/∂T, σ_C = −∂σ/∂C.

The dimensionless density ratio ρ_g /ρ_l and viscosity ratio μ_g /μ_l are the key parameters. The subscripts of g and l note the gas and liquid, respectively. Reynolds number Re = (ρ_lUL)/μ_l, Weber number We = (ρ_lU²L)/σ, Prandtl number Pr = μ_l /(ρ_lα), Marangoni number Ma = RePr, thermal Capillary number Ca_T = (σ_T·ΔT)/σ₀, solutal Capillary number Ca_C = (σ_C·ΔC)/σ₀, Lewis Number Le = α/D_l, α and D_l are the thermal and solutal diffusivity. The associated dimensionless thermal and solutal Marangoni numbers can be defined as Ma_T = −σ_T·ΔT·L/(αμ_l) and Ma_C = σ_C·ΔC·L/(αμ_l), respectively, and Ma = |Ma_T|. FGX is the volume force introduced by the lateral acceleration, FGX = g_xL/U², where g_x = Aω²sinωt, A is the vibration amplitude, ω is the angular frequency, ω = 2πf, and f is the vibration frequency. The second term at the right hand of the momentum equation includes the thermal capillary force and the concentration capillary force, respectively. The third and fifth terms at the right hand of the momentum equation are the surface tension force (Continuum surface force model, Brackbill et al. 1992) and the volume force introduced by the horizontal vibration, respectively.

Level Set Function and its Formulation

The level set method was originally introduced by Osher and Sethian (1988) to numerically predict the moving interface Γ(t) between two fluids. Instead of explicitly tracking the interface, the level set method implicitly captures the interface by introducing a smooth signed distance from the interface in the entire computational domain. The level set function φ(x, t) is taken to be positive outside the liquid bridge, zero on the interface and negative inside the liquid bridge. The interface motion is predicted by solving the following convection equation for the level set function of φ(x, t) given by,

$$ {\varphi}_t+V\cdotp \nabla \varphi =0 $$

(5)

$$ V\cdotp \nabla \varphi ={\left( u\varphi \right)}_x+{\left( v\varphi \right)}_y $$

(6)

Sussman et al. (1994) adopted a second-order ENO method (Mulder et al. 1992) for the approximation of the convective terms as follows,

$$ {\displaystyle \begin{array}{c}{\left( u\varphi \right)}_x+{\left( v\varphi \right)}_y=\left({u}_{i+1/2,j}+{u}_{i-1/2,j}\right)\left({\varphi}_{i+1/2,j}-{\varphi}_{i-1/2,j}\right)/(2h)\\ {}+\left({\phi}_{i+1/2,j}+{\phi}_{i-1/2,j}\right)\left({u}_{i+1/2,j}-{u}_{i-1/2,j}\right)/(2h)\\ {}+\left({v}_{i,j+1/2}+{v}_{i,j-1/2}\right)\left({\phi}_{i,j+1/2}-{\phi}_{i,j-1/2}\right)/(2h)\\ {}+\left({\phi}_{i,j+1/2}+{\phi}_{i,j-1/2}\right)\left({v}_{i,j+1/2}-{v}_{i,j-1/2}\right)/(2h)\end{array}} $$

(7)

For smooth data, we have (ϕ_{i + 1/2, j} + ϕ_{i-1/2, j}) ≈ (ϕ_{i, j + 1/2} + ϕ_{i, j-1/2}). In addition, we have (u_{i + 1/2, j}-u_{i-1/2, j}) ≈ (v_{i, j + 1/2}-v_{i, j-1/2}) because V is numerically divergence free. Thus,

$$ {\displaystyle \begin{array}{c}{\left( u\varphi \right)}_x+{\left( v\varphi \right)}_y\approx \left({u}_{i+1/2,j}+{u}_{i-1/2,j}\right)\left({\varphi}_{i+1/2,j}+{\varphi}_{i-1/2,j}\right)/(2h)\\ {}+\left({v}_{i,j+1/2}+{v}_{i,j-1/2}\right)\left({\phi}_{i,j+1/2}+{\phi}_{i,j-1/2}\right)/(2h)\end{array}} $$

(8)

For computing u_{i + 1/2, j} (similarly for u_{i, j + 1/2}, ϕ_{i + 1/2, j},...), a second-order ENO scheme is used as follows,

Define

$$ m\left(a,b\right)\kern1em \equiv \left\{\begin{array}{c}\kern1em a\kern1em if\kern1em \left|a\right|\kern1em \le \kern1em \left|b\right|\\ {}b\kern1.5em otherwise\end{array}\right.\kern6em $$

(9)

Let

$$ {\displaystyle \begin{array}{l}{u}_L\equiv {u}_{i,j}+m\left({u}_{i+1,j}-{u}_{i,j},{u}_{i,j}-{u}_{i-1,j}\right)/2\\ {}{u}_R\equiv {u}_{i+1,j}+m\left({u}_{i+2,j}-{u}_{i+1,j},{u}_{i+1,j}-{u}_{i,j}\right)/2\\ {}{u}_M\equiv \left({u}_L+{u}_R\right)/2\end{array}} $$

(10)

Thus,

$$ {u}_{i+1/2,j}=\left\{\begin{array}{c}{u}_M\kern0.4em if\ {u}_L\le 0,{u}_R\ge 0\\ {}{u}_R\kern0.5em if\ {u}_M\le 0,{u}_R\le 0\\ {}{u}_L\kern0.4em if\ {u}_M\ge 0,{u}_R\ge 0\end{array}\right. $$

(11)

Boundary and Numerical Conditions

The upper and lower disks of the liquid bridge are maintained at constant concentrations C₁, C₀ and temperatures T₁, T₀, respectively and a concentration difference ∆C and temperatures difference ∆T, respectively. The non-slip condition is used for all walls of the computational domain. It is assumed that there is no heat and mass transfer at outer edges of the ambient air. For the distance function, the gradient at all solid walls is assumed to be zero. The following boundary conditions should be satisfied. The continuum surface force (CSF) model is employed to treat the surface tension force at the interface in the present work, and the effect of surface tension is continuously distributed on the free surface instead of being treated as the boundary condition of the interface when the CSF model is used.

$$ \mathrm{Upper}\ \mathrm{disk}\ \left(\mathrm{Y}=\mathrm{H}\right):\varTheta =1,{C}^{\prime }=1,V\left(u,v\right)=0,\partial \varphi /\partial Y=0 $$

(12)

$$ \mathrm{Lower}\ \mathrm{disk}\ \left(\mathrm{Y}=0\right):\varTheta =0,{C}^{\prime }=0,V\left(u,v\right)=0,\partial \varphi /\partial Y=0 $$

(13)

$$ \mathrm{Outer}\ \mathrm{edge}\ \mathrm{of}\ \mathrm{gas}\ \mathrm{phase}\ \left(\mathrm{X}=0\ \mathrm{and}\ \mathrm{X}=4\mathrm{R}\right):\mathrm{\partial \Theta }/\partial X=0,\partial {C}^{\prime }/\partial X=0,V\left(u,v\right)=0,\partial \varphi /\partial X=0 $$

(14)

Results and Discussion

In this study, the effect of lateral vibrations on thermo-solutocapillary convection in a liquid bridge is investigated under microgravity. There are few studies about the thermo-solutocapillary convection for medium Prandtl fluid, therefore, the toluene/n-hexane solution (0.24/0.76) is selected as the working fluid in this work. Computational conditions adopted are Ma = 748, Pr = 5.54, D = 5 mm, Ar = H/R = 1. The temperature difference and concentration difference between two discs are ΔT = 0.1 °C, ΔC = 0.05 g/g, respectively. The thermal capillary number is Ca_T = 0.00045, and the solute capillary number is Ca_C = −0.021, and we define R_σ = (Ca_T·ΔT)/(Ca_C·ΔC).

The applied lateral vibration is mainly used to simulate the gravity jitter which exists when the space floating zone method is used to produce high-quality semiconductors. In this work, the lateral vibration with an acceleration of 20 mg (1 mg = 10⁻³ g) is applied, which is just the magnitude of real microgravity level. The oscillating mode of the applied lateral vibration conforms to the sinusoidal function with frequencies ranged from 5 Hz to 15 Hz.

Code Validation

To validate the procedure, we compare our results with those presented by Zhou et al. (2015). The numerical simulation is carried out for fluid with Prandtl number Pr = 1, and the other parameters adopted are shown in Table 1.

Table 1 Parameters for the comparison

Figure 2 and Fig. 3 present the surface deformation of liquid bridge and surface velocity in axial direction, respectively, and the present results are in good agreement with those presented by Zhou et al. (2015). Figure 4 shows the isolines of concentration obtained in the present work.

Fig. 2

Comparison of surface deformation on right side

Fig. 3

Free surface velocity in axial direction (Ma = 50)

Fig. 4

Present isolines of concentration (Ma = 50)

The existing studies on thermo-solutocapillary convection in liquid bridges under microgravity did not consider the surface deformation, while the free surface deforms indeed in the actual space floating zone. In the present work, thermo-solutocapillary convection in a liquid bridge under the lateral vibration is investigated considering the free surface deformation. Figure 5 depicts the temperature gradient on the free surface of the liquid bridge with or without considering the free surface deformation under an acceleration of 20 mg. The free surface on right side is selected as the research object. As shown in Fig. 5, the temperature gradients on the free surface are different with or without considering the free surface deformation at heights from 0.2 to 0.7 as well as 0.8 to 1.0 away from the lower disk, indicating that it is necessary to consider the free surface deformation in the research on thermo-solutocapillary convection. In addition, the temperature gradients on the free surface are the driving force for the thermocapillary convection. The temperature gradients on the free surface are small at height of 0.0 to 0.3 away from the lower disk and then increase rapidly at height of 0.3 to 1.0 away from the lower disk, implying that thermocapillary convection is weak in the vicinity of the lower disk and becomes strong in the vicinity of the middle height and upper disk.

Fig. 5

Temperature gradient on free surface with and without considering free surface deformation (Ma = 748, Pr = 5.54, D = 5 mm, H/R = 1, FGX = 20 mg)

Effect of Horizontal Vibration on Velocity Vectors inside the Liquid Bridge

Figure 6 illustrates the velocity vectors inside the liquid bridge at a fully developed state when lateral vibrations with frequencies of 0 Hz, 5 Hz, 10 Hz and 15 Hz are applied. A pair of flow cells in opposite flow directions can be found inside the liquid bridge under different vibration frequencies. The effect of lateral vibrations on the fluid flow in the liquid bridge can be found from the enlarged views of velocity vectors in the liquid bridge. Based on careful observation, the velocity vectors near the central axis of liquid bridge show a tendency of moving to the left and to the right rather than a downward trend at vibration frequencies of 0 Hz and 15 Hz, respectively, indicating that the oscillation has occurred inside the liquid bridge at vibration frequencies of 0 Hz and 15 Hz. However, when the lateral vibrations with frequencies of 5 Hz and 10 Hz are introduced, the velocity vector arrows point downward symmetrically, illustrating that there is no oscillation inside the liquid bridge. It is confirmed that the lateral vibrations with frequencies of 5 Hz and 10 Hz restrain the oscillation inside the liquid bridge, while the lateral vibration with frequency of 15 Hz strengthens the oscillation inside the liquid bridge. Therefore, the influence of lateral vibrations on the fluid flow in the liquid bridge is uncertain.

Fig. 6

Velocity vectors at different vibrational frequencies (Ma = 748, Pr = 5.54, D = 5 mm, H/R = 1, FGX = 20 mg)

Effect of Horizontal Vibration on Velocity and Deformation on Free Surface

Figure 7 shows the radial and axial velocities on the free surface of the liquid bridge. At the height from 0 to 0.6, the radial velocities at different vibration frequencies experiences a transition from negative values to positive ones (Fig. 7a), however, the radial velocities at the vibration frequencies of 0 Hz and 15 Hz present larger oscillation comparing with those at 5 Hz and 10 Hz at the height from 0.6 to 1.0. On the whole, the radial velocities on the surface decrease when lateral vibrations with frequencies of 5 Hz and 10 Hz are applied, indicating that the surface flow and bulk return flow becomes slow down at this time, that is, the lateral vibration restrains radial velocities on the surface under lateral vibrations with frequencies of 5 Hz and 10 Hz. It can be observed from Fig. 7b that the axial velocities on the surface present approximately parabolic forms, and the axial velocities on the surface are all positive under different vibration frequencies. The axial velocity gradients at the height from 0 to 0.2 and from 0.8 to 1.0 are significantly greater than those from 0.2 to 0.8 under different vibration frequencies due to the wall effect at the lower and upper disks. Under the vibration frequencies of 0 Hz, 5 Hz and 10 Hz, the axial velocities on the surface decrease, which implies that the introduction of lateral vibration suppress the axial velocity on the surface. While, the axial velocities on the surface increase under the vibration frequency of 15 Hz, which illustrates that the effect of vibration on the free surface has uncertainty.

Fig. 7

Variation of radial and axial velocities on free surface (Ma = 748, Pr = 5.54, D = 5 mm, H/R = 1, FGX = 20 mg)

Figure 8 illustrates the free surface deformation under different vibration frequencies when the thermo-solutocapillary convection is considered to be fully developed. The interface deformation is convex at heights below 0.54 (mid height of the liquid bridge) under lateral vibrations with frequencies of 0 Hz, 5 Hz, 10 Hz, and 15 Hz. At heights higher than 0.54, the interface deformation is basically concave, which is relatively complex under lateral vibrations with frequencies of 0 Hz, 5 Hz, 10 Hz, and 15 Hz, indicating that surface flow is more active on the free surface of the upper part in the liquid bridge.

Fig. 8

Surface deformation of the liquid bridge with different lateral vibrations (Ma = 748, Pr = 5.54, D = 5 mm, H/R = 1, FGX = 20 mg)

Figures 9 illustrates the temperature isolines in the liquid bridge with vibration (f = 10 Hz) in the steady thermo-solutocapillary convection. The temperature isolines from X = 2.0 (center axis) to X = 2.5 present approximately a horizontal distribution, indicating that the temperature diffusion in the middle part of the liquid bridge is relatively uniform and the heat conduction is the main heat transfer pattern. The temperature gradients increase near the free surface (X = 3.0) at the same height in the liquid bridge because the convective heat transfer dominates the heat transfer process near the free surface.

Fig. 9

Temperature isolines under horizontal vibration with f = 10 Hz (Ma = 748, Pr = 5.54, D = 5 mm, H/R = 1, FGX = 20 mg)

Effect of Horizontal Vibration on Radial Velocity at Hot Corner

The hot corner is a special and representative area in the liquid bridge because the oscillatory thermo-solutocapillary convection originates from hot corner, therefore, monitoring points a, b, c are set at the hot corner to monitor the velocity oscillations, which are shown in Fig. 1, and the location of each monitoring point can be found in Table 2. Monitoring points a, b and c locate at the same vertical line away from the upper disk.

Table 2 Layout of monitoring points

Figures 10, 11, and 12 show oscillations of radial velocity and PSD chart of radial velocity oscillation at monitoring points a, b, and c, respectively. In the period of t = 275 to 321, the radial velocity experiences steady but irregular disturbance when the lateral vibration is not introduced (f = 0 Hz). After lateral vibrations are introduced (f = 5 Hz, 10 Hz and 15 Hz), radial velocities maintain basically certain values at monitoring points a, b, and c. Radial velocities start to oscillate at about t = 321 with or without external vibration. The period and amplitude of velocity oscillation are different at different vibration frequencies at monitoring points a, b, and c. The periods at point a are T = 23, 27, and 29 at three vibration frequencies of 5 Hz, 10 Hz, and 15 Hz, respectively, while the period is T = 18 at the vibration frequency of 0 Hz, that is, in the case of no lateral vibration in Fig. 10a. At point b in Fig. 11a, the periods are T = 21, 27 and 32 at three vibration frequencies of 5 Hz, 10 Hz, and 15 Hz, respectively. At point c, the periods are T = 25, 19, and 28 at three vibration frequencies of 5 Hz, 10 Hz, and 15 Hz, respectively, while the period is T = 14 at the vibration frequency of 0 Hz in Fig. 12a. It can be seen that the periods of radial velocity oscillation successively increase with increasing vibration frequency at monitoring points a and b, while this observation does not apply to monitoring point c. The further away from the upper disk of the bridge, the larger the oscillation amplitude. From the distribution of the PSD at monitoring points a, b, and c in Figs. 10b-12b, multiple peaks of different sizes appear in the PSD, indicating that the velocities at such points fluctuate greatly. After the introduction of lateral vibrations with f = 5 Hz and 10 Hz, the peak values are smaller than those when no vibration (f = 0 Hz) is introduced, indicating that the lateral vibration suppresses the oscillation of lateral velocity under the lateral vibrations with f = 5 Hz and 10 Hz, while the uncertainty can be seen when the lateral vibration with f = 15 Hz is introduced.

Fig. 10

(a) Oscillation of radial velocity and (b) PSD chart of radial velocity oscillation at monitoring point a (Ma = 748, Pr = 5.54, D = 5 mm, H/R = 1, FGX = 20 mg)

Fig. 11

(a) Oscillation of radial velocity and (b) PSD chart of radial velocity oscillation at monitoring point b (Ma = 748, Pr = 5.54, D = 5 mm, H/R = 1, FGX = 20 mg)

Fig. 12

(a) Oscillation of radial velocity and (b) PSD chart of radial velocity oscillation at monitoring point c (Ma = 748, Pr = 5.54, D = 5 mm, H/R = 1, FGX = 20 mg)

Conclusions

In this paper, effect of lateral vibrations on the thermo-solutocapillary convection and surface behavior in a liquid bridge of toluene/n-hexane solution has been studied numerically under microgravity. From present results, it can be concluded that the lateral vibrations restrain radial and axial velocities on the surface under lateral vibrations with frequencies of 5 Hz and 10 Hz. While the radial and axial velocities on the surface increase under the vibration frequencies of 15 Hz, which illustrates that the effect of vibration on the free surface has uncertainty. Moreover, the introduction of lateral vibration intensifies the diffusion of temperature and concentration on the interface, which results in the decrease in temperature and concentration differences on the interface. Therefore, surface flow becomes weak because the flow generation on the interface is due to the temperature and concentration gradients on the interface.