Dynamics of an eco-epidemiological system with disease in competitive prey species

Abstract

The objective of the present paper is to investigate the dynamics of an eco-epidemiological system with predator’s hyperbolic mortality and Holling type II functional response. The local stability, global stability of the ecosystem near biologically feasible equilibria have been thoroughly investigated. The boundedness and positivity of solutions for the model are also derived. Threshold values for a few parameters, which determine the feasibility and stability of some equilibria are calculated and a threshold is identified for the disease to die out. The existence of Hopf bifurcation around the coexistence equilibrium is shown. Finally, numerical illustrations are performed in order to validate some of the important analytical findings.

1 Introduction

In the literature of mathematical biology, there are several areas of research among which epidemiology is an emerging area which combines both ecological and eco-epidemiological issues. In recent times, disease in the predator–prey system is one of the most important fields of research. The effect of disease is the crucial topic in ecological systems from both experimental and mathematical points of view. The pioneering work of Lotka–Volterra on predator–prey model and the popular work of Kermack–McKendrick opened a new door to epidemiology. Then numerous mathematical models already have been proposed to study the spread and control of infectious disease and the interactions between predator and prey population.

Functional response on prey population is the key element in predator–prey interaction. Functional response is the rate at which the number of prey consumed by one predator. There are some important types of functional responses used to model predator–prey interaction, such as Beddington–DeAngelis , Crowley–Martin, Ivlev, Michaelis–Menten, Hassell–Varley, Holling type-I, i.e., simple mass action law, Holling type II, III, IV. Population models with such functional responses are widely studied in ecological literature (cf. [1,2,3,4,5,6,7,8,9]). Many research works on three species systems like two prey one predator are investigated in [10,11,12,13,14], tritrophic food chain models in [15,16,17].

Important studies on infectious disease have been studied in [18,19,20,21,22,23,24]. Species do not exist alone at all. They live in a community of other species. In mathematical biology, the predator–prey model systems for transmissible disease are essential field of study in their own right. From early papers [25], disease mainly spreading only in the prey species are studied in [26,27,28] and only in predator species in [29,30,31]. The predator–prey model with modified Leslie–Gower Holling type II scheme was introduced in [32, 33]. The Leslie–Gower model with Holling type II response function with disease in predator is discussed in [34] and disease in prey in [35]. Also Leslie–Gower model with Holling type III response mechanism with disease in predator is investigated in [36].

The rate of mortality plays an important role in population ecology. It is observed that when population density is low, the linear rate dominates the mortality which is used in many biological models such as [37,38,39]. If population density is relatively high, the quadratic rate dominates the mortality [40,41,42]. Again, if the population density is large, hyperbolic rate dominates the mortality, [43,44,45,46,47,48,49].

In [50], the linear mortality of predator and strong Allee effect in prey is considered. In [51], authors considered linear mortality of predator. The authors considered Leslie–Gower predator prey model and ratio dependent functional response in [52]. In [53], disease transmission follows saturation incidence kinetics and the system includes prey refuge.

In this paper, an eco-epidemiological model consisting of three species, namely, the susceptible prey, the infected prey (which becomes infective by some virus) and their common predator population is considered. The present paper deals with the study of dynamics of an eco-epidemiological system with disease in competitive prey species. The novelty of our study is lying on the consideration of hyperbolic mortality of predator, Holling type II functional mechanism for predation and disease in competitive prey species and hence in that sense this model is distinct from the models, which have been studied already.

The outline of this article is as follows: In Sect. 2, an eco-epidemiological model has been proposed with detailed explanation. Section 3 contains positivity and boundedness of solutions of the model. In Sect. 4, the existence and feasibility of the equilibria are analyzed. The system behavior around axial and boundary equilibria are investigated in Sect. 5. Persistence of the system is discussed in Sect. 6. In Sect. , local and global stability of the coexistence equilibria are done. Numerical simulation has been carried out in Sect. 8 for justification of the analytical findings. The article comes to an end with a discussion in Sect. 9.

2 Mathematical model formulation

We consider the following assumptions in order to construct our model system:

• A transmissible disease is incorporated to only among the competitive prey species. Let the total prey population N is divided into in two sub-classes, namely, susceptible prey population (x) and the infected prey population (y) in the presence of disease. The total prey population at any time t is $N(t) = x(t) + y(t)$.

• The disease transmits horizontally with simple mass action incidence rate $\beta xy$, where $\beta$ is the force of infection. The susceptible prey population x grows logistically with intrinsic growth rate $r_1 > 0$ and carrying capacity $r_1/s_1$ in the absence of predator population.

• The infected prey population neither recover from the disease nor reproduce. They contribute to inter and intra-specific competition at a lower rate $s_2$ than that of sound ones, i.e., $s_1 > s_2$.

• Predator consumes both healthy and infected prey at different rates. Since the escape ability of healthy prey is higher than infected prey, $c_1 \le c_2$.

• Hyperbolic mortality rate is considered for predator population.

• Holling type-II response mechanism is considered between the interacting populations.

Thus, the model based on our assumptions takes the following form:

$$\begin{aligned}&\frac{dx}{dt}=r_1x-s_1x(x+y)-\frac{c_1xz}{x+y+k_1}-\beta x y\equiv xF_1(x,y,z), \end{aligned}$$

(2.1a)

$$\begin{aligned}&\frac{dy}{dt}=\beta xy-s_2y(x+y)-\frac{c_2yz}{x+y+k_1} -\delta y \equiv yF_2(x,y,z), \end{aligned}$$

(2.1b)

$$\begin{aligned}&\frac{dz}{dt}=\left( \frac{e_1c_1x+e_2c_2y}{x+y+k_1} - \frac{c_3z}{z+k_2}\right) z \equiv zF_3(x,y,z), \nonumber \\&x(0)\ge 0,\quad y(0)\ge 0,\quad z(0)\ge 0, \end{aligned}$$

(2.1c)

where the term $\frac{c_3z^2}{z+k_2}$ is for hyperbolic mortality, which dominates the mortality for large population density [45, 49]. Also $k_1, k_2$ are the half saturation constants for the competitive prey and predator population respectively. The parameters $\delta$ and $c_3$ represent the mortality rate of infected prey and hyperbolic death rate of predator respectively. The parameters $e_1$ and $e_2$ are the conversion factors of consumed susceptible and infected prey respectively. Others parameters are already specified with their biological meanings at the beginning of model formulation. It is to be note that, all the system parameters are positive.

3 Preliminaries

3.1 Positive invariance

Theorem 3.1

Every solution of the system (2.1) with initial conditions exists in the interval $(0,+\infty )$ and $x(t)\ge 0$, $y(t)\ge 0$, $z(t)\ge 0$ for all $t\ge 0$.

Proof

As $xF_1, \ yF_2, \ zF_3$ are completely continuous functions and locally Lipschitzian on ${\mathbb {R}}^{3 }_+$, the solution with positive initial condition exists and unique on $[0,\xi )$ where $0<\xi <\infty$ (cf. [54]). From the system (2.1), we have $x(t)=x(0)e^{\int _{0}^{t}F_1(x(s),y(s),z(s)) ds}\ge 0$, $y(t)=y(0)e^{\int _{0}^{t} F_2(x(s),y(s),z(s)) ds}\ge 0$, $z(t)=z(0)e^{\int _{0}^{t} F_3(x(s),y(s),z(s)) ds}\ge 0$, where $x(0)=x_0\ge 0$, $y(0)=y_0\ge 0$, $z(0)=z_0\ge 0$. Hence the proof of the theorem is completed. $\square$

3.2 Boundedness

Theorem 3.2

All the solutions of the system which initiate in ${\mathbb {R}}_{+}^{3}$ are uniformly bounded if $e_1>e_2$ and $c_3>\mu >\delta$.

Proof

Defining a function $\Omega =e_1x+e_2y+z$, we have

$$\begin{aligned} \frac{d\Omega }{dt}+\mu \Omega= & {} e_1\frac{dx}{dt}+e_2\frac{dy}{dt}+\frac{dz}{dt}+\mu (e_1x+e_2y+z)\\\le & {} (\mu e_1x+e_1r_1x-e_1s_1x^2)+(\mu e_2-e_2 \delta -e_2s_2y)y+\frac{z\big (\mu (z+k_2)-c_3z\big )}{z+k_2}\\\le & {} \bigl ((\mu e_1+e_1r_1)-e_1s_1x\bigr )x+\bigl ((\mu e_2-e_2\delta )-e_2s_2y\bigr )y+\bigl (\mu k_2-(c_3-\mu )z\bigr )z\\\le & {} \frac{e_1(\mu + r_1)^2}{4s_1}+\frac{e_2(\mu -\delta )^2}{4s_2}+\frac{\mu ^2 k_2^2}{4(c_3-\mu )}=\rho . \end{aligned}$$

Therefore, one can find a positive number $\rho$, such that $\frac{d\Omega }{dt}+\mu \Omega \le \rho$. By the theory of differential inequality (cf. [55]), one can easily obtain the inequality $0<\Omega (x,y,z)\le \frac{\rho }{\mu }(1-e^{-ut})+\Omega \big (x(0),y(0),z(0)\big )e^{-\mu t}$. Taking limit $t\rightarrow \infty$ on both sides, we have

$$\begin{aligned} \lim _{t\rightarrow \infty }\Omega \le \frac{\rho }{\mu }. \end{aligned}$$

Hence, all the solutions of the system that starting from ${\mathbb {R}}_{+}^{3}$ are confined for all future time in the compact region

$$\begin{aligned} \Gamma =\left\{ {(x,y,z)\in {\mathbb {R}}_{+}^{3}:\Omega (t) \le \frac{\rho }{\mu }+\epsilon , \forall \epsilon >0}\right\} . \end{aligned}$$

$\square$

3.3 Natural disease control

It is better to eliminate disease naturally (as [52]) from the model system. The infected prey will be removed from the ecosystem if the per capita death rate of infected prey exceeds $\frac{\beta r_1}{s_1}$, where $\beta$ denotes force of infection, $s_1$ be the competition rate and $\delta$ be the mortality rate of infected prey.

Proposition 3.3

The disease will be eradicated from the system (2.1) if the condition $\frac{\beta r_1}{s_1}< \delta$ hold.

Proof

From the second sub-equation of the system (2.1), we have

$$\begin{aligned} \frac{dy}{dt}\le & {} \beta xy-\delta y \le y\left( \frac{\beta r_1}{s_1}-\delta \right) ,\, \hbox {by using the upper bound of } x =\frac{r_1}{s_1}. \end{aligned}$$

Hence, $\frac{dy}{dt}$ becomes negative if $\frac{\beta r_1}{s_1}< \delta$, consequently infected prey population $y(t)\rightarrow 0$ as $t \rightarrow 0$. $\square$

4 Equilibria and their feasibility

The system (2.1) has the following equilibrium points:

$\text {(i) } E_0(0,0,0), \, \text {(ii) }E_1(0,-\frac{\delta }{s_2},0), \ \text {(iii) }E_2(\frac{r_1}{s_1},0,0),$  $\text {(iv) }E_3(\frac{\beta \delta +\delta s_1+r_1s_2}{\beta (\beta +s_1-s_2)},\frac{\beta r_1-\delta s_1-r_1s_2}{\beta (\beta +s_1-s_2)},0),$   $\text {(v) }E_4(0,y_4,z_4), \text {(vi) }E_5(x_5,0,z_5) \text { and}\, \text {(vii) }E_*(x_*,y_*,z_*).$ The interior equilibrium is $E_*(x_*,y_*,z_*)$, the components are as follows:

$x_*=\frac{y_*(c_1s_2-c_2(s_1+\beta ))+c_1\delta +c_2r_1}{c_1(\beta -s_2)+c_2s_1},$$z_*=-\frac{\big (r_1(s_2-\beta )+y_*\beta (s_1-s_2+\beta )+s_1\delta \big )\big (c_2(r_1+k_1s_1-y_*\beta ) +c_1(-k_1s_2+(k_1+y_*)\beta +\delta )\big )}{\big (c_2s_1+c_1(-s_2+\beta )\big )^2}$ and $y_*$ is a positive root of the cubic polynomial equation

$$\begin{aligned} A_1y^3+3B_1y^2+3C_1y+D_1=0, \end{aligned}$$

(4.1)

where $A_1$, $3B_1$, $3C_1$, $D_1$ are given in Appendix (10).

The Eq. (4.1) possesses exactly one positive root if $G_1^2+4H_1^3>0$, where $G_1=A_1^2D_1+3A_1B_1C_1+2B_1^3$, $H_1=A_1C_1-B_1^2$. Using Cardano’s method we obtain the root as $\frac{1}{A_1}(p_1-(\frac{H_1}{p_1}-B_1))$, where $p_1$ is one of the three values of $\bigl (\frac{1}{2}(-G_1+\sqrt{G_1^2+4H_1^3})\bigr )^\frac{1}{3}$. The interior equilibrium point exists if $\bigl (\frac{c_1}{c_2}-\frac{s_1}{s_2}\bigr )>\frac{\beta }{s_2} >1$, provided $\frac{c_2r_1+c_1k_1\beta +c_1\delta }{c_2k_1s_2}<\frac{y_*(c_2-c_1)}{c_2k_1s_2}+1$.

Obviously, the equilibrium point $E_1(0,-\frac{\delta }{s_2},0)$ is not biologically feasible, but the axial equilibrium $E_2(\frac{r_1}{s_1},0,0)$ is feasible. The equilibrium point $E_3$ is biologically feasible under the conditions $s_1>s_2$ and $\beta r_1> \delta s_1+ r_1s_2$. As $z_4=-\frac{(s_2y_4+\delta )(y_4+k_1)}{c_2}<0,$ the boundary equilibrium point $E_4(0,y_4,z_4)$ is not biologically feasible.

For the equilibrium point $E_5(x_5,0,z_5)$, $z_5=\frac{k_2e_1c_1x_5}{k_1c_3+(c_3-e_1c_1)x_5}$ and $x_5$ is the root of the cubic equation

$$\begin{aligned} A_2y^3+3B_2y^2+3C_2y+D_2=0, \end{aligned}$$

(4.2)

where $A_2=c_1e_1s_1-c_3s_1$,   $3B_2=c_1e_1k_1s_1-c_1e_1r_1-2c_3k_1s_1+c_3r_1$, $3C_2=-c_1^2e_1k_2-c_1e_1k_1r_1-c_3k_1^2s_1+2c_3k_1r_1$, $D_2=c_3k_1^2r_1$.

The Eq. (4.2) has exactly one positive root if $G_2^2+4H_2^3>0$, where $G_2=A_2^2D_2+3A_2B_2C_2+2B_2^3$, $H_2=A_2C_2-B_2^2$. Using Cardano’s method we obtain the root as $\frac{1}{A_2}\bigl (p_2-(\frac{H_2}{p_2}-B_2)\bigr )$, where $p_2$ is one of the three values of $\bigl (\frac{1}{2}(-G_2+\sqrt{G_2^2+4H_2^3})\bigr )^\frac{1}{3}$. Hence, $E_5$ is biologically feasible if $c_3>e_1c_1$.

5 System behaviour near boundary equilibria

Let $J_i$ denotes the Jacobian matrix at the equilibrium point $E_i, \ i= 0,1,2,3,5$.

5.1 $E_0$

The eigenvalues of the Jacobian matrix $J_0$ are $0, \ r_1$, $-\delta$ and equilibrium point $E_0$ is unstable in nature.

5.2 $E_1$

The equilibrium point $E_1$ is not biologically feasible and so, we do not go for stability analysis.

5.3 $E_2$

The eigenvalues of the Jacobian matrix $J_2$ are $-r_1, \ \frac{c_1e_1r_1}{(k_1+\frac{r_1}{s_1})s_1}, \ -\frac{r_1s_2}{s_1}+\frac{r_1\beta }{s_1}-\delta$. Since one pair of the eigenvalues of $J_2$ are of opposite sign, $E_2$ is saddle in nature.

5.4 $E_3$

One of the eigenvalues of the Jacobian matrix $J_3$ is $\frac{c_1e_1x_3+c_2e_2y_3}{k_1+x_3+y_3}$ which is always positive and therefore, $E_3$ is unstable.

5.5 $E_4$

The equilibrium point $E_4$ is not biologically feasible and so, we do not go for stability analysis.

5.6 $E_5(x_5,0,z_5)$

The Jacobian matrix at $J_5=(n_{ij})_{3\times 3}$, $i,j=1,2,3$, where

$$\begin{aligned}&n_{11}=r_{1}-2s_{1}x_5+\frac{c_1x_5z_5}{(x_5+k_1)^2}-\frac{c_1z_5}{x_5+k_1}, \ n_{12}=-s_{1}x_5+\frac{c_1x_5z_5}{(x_5+k_1)^2}\\&\quad -x_5\beta , \ n_{13}=-\frac{c_1x_5}{x_5+k_1}, \ \\&n_{21}=0, \ n_{22}=-s_2x_5-\frac{c_2z_5}{x_5+k_1}+x_5\beta -\delta , \ n_{23}=0, \ \\&n_{31}=-\frac{c_1e_1x_5z_5}{(x_5+k_1)^2}+\frac{c_1e_1z_5}{x_5+k_1}, \ \\&n_{32}=-\frac{c_1e_1x_5z_5}{(x_5+k_1)^2}+\frac{c_2e_2z_5}{x_5+k_1}, \ n_{33}=\frac{c_1e_1x_5}{x_5+k_1}+\frac{c_3z_5^2}{x_5+k_2}-\frac{2c_3z_5}{x_5+k_2}. \end{aligned}$$

The eigenvalues of $J_5$ are

$$\begin{aligned} \lambda _{1,2}=\frac{n_{11}+n_{33}\pm \sqrt{(n_{11}+n_{33})^2-4(n_{11}n_{33}-n_{31}n_{13})}}{2}, \text { and}\, \lambda _3=n_{22}.\nonumber \\ \end{aligned}$$

(5.1)

So, $E_5$ will be stable if  (i) $n_{22}<0$, (ii) $n_{11}+n_{33}<0$ and $(n_{11}n_{33}-n_{31}n_{13})>0$.

Proposition 5.1

The system (2.1) experiences Hopf bifurcation around $E_5$ while the parameter $s_1$ crosses its critical value $s_1=-\frac{c_3z_5(z_5+2k_2)}{x_5(z_5+k_2)^2}+\frac{c_1(e_1(x_5+k_1)+z_5)}{(x_5+k_1)^2}=s_1^{[hb]}$.

Proof

From (5.1) we have $\lambda _3$ is real, $\lambda _1$, $\lambda _2$ are purely imaginary iff there is a critical value of $s_1=s_1^{[hb]}=-\frac{c_3z_5(z_5+2k_2)}{x_5(z_5+k_2)^2}+\frac{c_1(e_1(x_5+k_1)+z_5)}{(x_5+k_1)^2}$. But for $i=1,2$, the real part ${\text {Re}}\Bigl (\frac{d\lambda _i}{ds_1}\Bigr )|_{s_1=s_1^{[hb]}}=x_5\ne 0$. So, the system undergoes Hopf bifurcation around $E_5$ for some critical value of the parameter $s_1=s_1^{[hb]}$. $\square$

6 Persistence

Definition 6.1

If there exists a compact set $D\subset \Gamma =\{(x,y,z): x>0, y>0, z>0\}$ in which all the solutions of the system (2.1) eventually enter and remain in D, then system (2.1) is called persistent.

Proposition 6.1

The system (2.1) is persistent if the following conditions are fulfilled:

• (i) $\beta (\gamma _1+\gamma _2+\delta )>\gamma _2s_2$,

• (ii) $s_1c_3(k_1+x_5)<r_1c_1e_1, \ \beta x_5>s_2x_5+\delta .$

Proof

Under the conditions (i) and (ii) the trivial, axial and boundary equlibria are repeller. Therefore, using the method of average Lyapunav function (see [56]), one can show that the system is persistent via considering a function of the form $V(x,y,z)=x^{\gamma _1}y^{\gamma _2}z^{\gamma _3}$, where $\gamma _i=1,2,3$ are positive constants.

$\square$

7 System behaviour near the coexistence equilibrium $E_*(x_*,y_*,z_*)$

The Jacobian matrix $J_*(x_*,y_*,z_*) =(\alpha _{ij})_{3\times 3}$, where $\alpha _{ij}$ are as follows:

$$\begin{aligned}&\alpha _{11}=-s_{1}x_*+\frac{c_1x_*z_*}{(x_*+y_*+k_1)^2}, \\&\alpha _{12}=-s_{1}x_*+\frac{c_1x_*z_*}{(x_*+y_*+k_1)^2}-x_*\beta , \ \alpha _{13}=-\frac{c_1x_*}{x_*+y_*+k_1}, \ \\&\alpha _{21}=-s_{2}y_*+\frac{c_2y_*z_*}{(x_*+y_*+k_1)^2}+y_*\beta , \\&\alpha _{22}=-s_{2}y_*+\frac{c_2y_*z_*}{(x_*+y_*+k_1)^2}, \ \alpha _{23}=-\frac{c_2y_*}{x_*+y_*+k_1}, \ \\&\alpha _{31}=\frac{\big (-c_2e_2y_*+c_1e_1(k_1+y_*)\big )z_*}{(x_*+y_*+k_1)^2},\\&\alpha _{32}=\frac{\big (-c_1e_1x_*+c_2e_2(k_1+x_*)\big )z_*}{(x_*+y_*+k_1)^2},\\&\alpha _{33}=\frac{-k_2(c_1e_1x_*+c_2e_2y_*)}{(x_*+y_*+k_1)(z_*+k_2)}. \end{aligned}$$

7.1 Local stability

The characteristic equation for $J_*$ is given by $\lambda ^3+k_1\lambda ^2+k_2\lambda +k_3=0$, where 

$$\begin{aligned} k_1= & {} -\alpha _{11}-\alpha _{22}-\alpha _{33}=\text {trace} (J_*), \\ k_2= & {} \alpha _{11}\alpha _{22}+\alpha _{11}\alpha _{33}+\alpha _{22}\alpha _{33}-\alpha _{13}\alpha _{31}-\alpha _{23}\alpha _{32} -\alpha _{21}\alpha _{12}\\= & {} \text {Sum of the second order principal minors of} J_*, \\ k_3= & {} \alpha _{11}\alpha _{23}\alpha _{32}+\alpha _{12}\alpha _{21}\alpha _{33}+\alpha _{13}\alpha _{22}\alpha _{31} -\alpha _{11}m_{22}\alpha _{33}-\alpha _{12}\alpha _{23}\alpha _{31}\\&-\alpha _{13}\alpha _{21}\alpha _{32} =-\det (J_*), \end{aligned}$$

If $k_1>0$, $k_3>0$ and $k_1k_2-k_3>0$, by Routh–Hurwitz criterion, the co-existence equilibrium $E_*(x_*,y_*,z_*)$ is locally asymptotically stable.

7.2 Global stability

Theorem 7.1

Let $\frac{dX}{dt}= f(X)$ where $X=(x,y,z)^\mathrm{T}$ and $f(X)=\left( f_1(X),f_2(X),f_3(X)\right) ^\mathrm{T}$. Assuming D is simply connected domain in ${\mathbb {R}}_+^3$, there exist a compact absorbing set $K \subset D$ and the system (2.1) has a unique interior equilibrium $E_*=(x_*,y_*,z_*)$ in D, then the unique equilibrium $E_*$ of the system (2.1) is globally stable in D if $\min {\bigl (\Delta _1,\Delta _2\bigr )}>0$.

Proof

Define the function $Q(x)=\text {diag}(1, \frac{y}{z}, \frac{yx^2}{z})= \left( \begin{array}{ccc} 1 &{} 0 &{} 0\\ 0 &{} \frac{y}{z} &{} 0\\ 0 &{} 0 &{} \frac{yx^2}{z} \end{array}\right)$ and we get $Q^{-1}(x)= \left( \begin{array}{ccc} 1 &{} 0 &{} 0\\ 0 &{} \frac{z}{y} &{} 0\\ 0 &{} 0 &{} \frac{z}{yx^2} \end{array}\right)$. Therefore, $Q_fQ^{-1}(x)= \left( \begin{array}{ccc} 0 &{} 0 &{} 0\\ 0 &{} \frac{{\dot{y}}}{y}-\frac{{\dot{z}}}{z} &{} 0\\ 0 &{} 0 &{} \frac{2{\dot{x}}}{x}+\frac{{\dot{y}}}{y}-\frac{{\dot{z}}}{z} \end{array}\right)$

The second compound matrix is

$$\begin{aligned} A^{[2]}=\left( \begin{array}{ccc} A_{11} &{} A_{12} &{} A_{13}\\ A_{21} &{} A_{22} &{} A_{23}\\ A_{31} &{} A_{32} &{} A_{33} \end{array}\right) = \left( \begin{array}{ccc} a_{11}+a_{22} &{} a_{23} &{} -a_{13}\\ a_{32} &{} a_{11}+a_{33} &{} a_{12}\\ -a_{31} &{} a_{21} &{} a_{22}+a_{33} \end{array}\right) \end{aligned}$$

with the entries

$$\begin{aligned}&A_{11}=\frac{xzc_1}{(x+y+k_1)^2}+\frac{yzc_2}{(x+y+k_1)^2}-xs_1-ys_2,\\&A_{12}=\frac{yc_2}{x+y+k_1}, \ A_{13}=-\frac{xc_1}{x+y+k_1},\\&A_{21}=\frac{z(-xc_1e_1+c_2e_2(x+k_1))}{x+y+k_1}, \\&A_{22}=\frac{xzc_1}{(x+y+1)^2}-\frac{(xc_1e_1+yc_2e_2)k_2}{(x+y+k_1)(z+k_2)}-xs_1, \\&A_{23}=-x\beta +\frac{xzc_1}{(x+y+k_1)^2}-xs_1, \\&A_{31}=-\frac{z(-yc_2e_2+c_1e_1(y+k_1))}{(x+y+k_1)^2}, \\&A_{32}=y\beta +\frac{zyc_2}{(x+y+k_1)^2}-ys_2, \\&A_{33}=\frac{yzc_2}{(x+y+k_1)^2}-\frac{(xc_1e_1+yc_2e_2)k_2}{(x+y+k_1)(z+k_2)}-ys_2. \ \hbox {Also, } \\&B=Q_fQ^{-1}+QA^{[2]}Q^{-1}=\left[ {\begin{array}{cc } B_{11} &{} B_{12} \\ B_{21} &{} B_{22} \end{array}}\right] ,\hbox { where } B_{22}=\left[ {\begin{array}{cc } \beta _{11} &{} \beta _{12} \\ \beta _{21} &{} \beta _{22} \end{array}}\right] ,\\&B_{11}=\frac{c_1 x z}{\left( k_1+x+y\right) {}^2}+\frac{c_2 y z}{\left( k_1+x+y\right) {}^2}-s_1 x-s_2 y,\\&B_{12}=\left( -\frac{c_2 z}{k_1+x+y},\frac{c_1 z}{x y \left( k_1+x+y\right) }\right) , \\&B_{21}=\left( \frac{y \left( c_2 e_2 \left( k_1+x\right) -c_1 e_1 x\right) }{\left( k_1+x+y\right) {}^2},-\frac{x^2 y \left( c_1 e_1 \left( k_1+y\right) -c_2 e_2 y\right) }{\left( k_1+x+y\right) {}^2}\right) ^\mathrm{T},\\&\beta _{11}= \frac{c_1 x \left( z-\frac{e_1 k_2 \left( k_1+x+y\right) }{k_2+z}\right) }{\left( k_1+x+y\right) {}^2}-\frac{c_2 e_2 k_2 y}{\left( k_2+z\right) \left( k_1+x+y\right) }-s_1 x+\frac{{\dot{y}}}{y}-\frac{{\dot{z}}}{z},\\&\beta _{12}=-\frac{\beta -\frac{c_1 z}{\left( k_1+x+y\right) {}^2}+s_1}{x},\\&\beta _{21}=x^2 y \left( \beta +\frac{c_2 z}{\left( k_1+x+y\right) {}^2}-s_2\right) , \ \beta _{22}=\frac{c_2 y \left( z-\frac{e_2 k_2 \left( k_1+x+y\right) }{k_2+z}\right) }{\left( k_1+x+y\right) {}^2}\\&\quad -\frac{c_1 e_1 k_2 x}{\left( k_2+z\right) \left( k_1+x+y\right) }-s_2 y+\frac{2 {\dot{x}}}{x}+\frac{{\dot{y}}}{y}-\frac{{\dot{z}}}{z}. \end{aligned}$$

Let (u, v, w) denote the vectors in ${\mathbb {R}}_{+}^{3}$, we define its norm $\left| .\right|$ as $\left| x,y,z\right| =\max (\left| x\right| ,\left| y+z\right| )$. Let Lozinski${\check{i}}$ measure with repect to this norm be m. By using the method of estimating m as in [57], we have

$$\begin{aligned} m(B)\le \sup (g_1,g_2) \end{aligned}$$

where

$$\begin{aligned} g_1= & {} m_1(B_{11})+|B_{12}|,\\ g_2= & {} m_1(B_{22})+|B_{21}|, \end{aligned}$$

$|B_{12}|$ and $|B_{21}|$ are matrix norm with repect to the $l_1$ vector norm and $m_1$ be the Lozinski${\check{i}}$ measure with repect to the $l_1$ norm. Here $\left| B_{12}\right| =\max \left( \frac{zc_2}{x+y+1},\frac{zc_1}{xy(x+y+1)}\right) ,$  and  $\left| B_{21}\right| =\max \left( \frac{y(-xc_1e_1+c_2e_2(x+k_1))}{(x+y+k_1)^2},-\frac{x^2y(-yc_2e_2 +c_1e_1(y+k_1))}{(x+y+k_1)^2}\right)$.

Since, the system is uniformly persistent there exists $\sigma >0$ and $\tau >0$ such that for $t>\tau$, $x\ge \sigma , \ y\ge \sigma , \ z\ge \sigma ,$ and as the system is bounded $x+y+z\le M$, i.e., $z\le M-(x+y)=M-2\sigma =M_0$. Also upper bound of $x=\frac{r_1}{s_1}$ and upper bound of $y=\frac{\beta r_1}{s_1s_2}$. Division of first term by second of $\left| B_{12}\right|$ gives $\frac{c_2xy}{c_1}<1$, which implies $\sigma ^2<\frac{c_1}{c_2}$. So, by this condition we obtain $\left| B_{12}\right| =\frac{zc_1}{xy(x+y+1)}$. Subtracting second term from first term of $\left| B_{21}\right|$, we have

$$\begin{aligned}&y\Bigl (\frac{-xc_1e_1+c_1e_2(x+k_1)}{(x+y+k_1)^2}+\frac{x^2(-yc_2e_2+c_1e_1(y+k_1))}{(x+y+k_1)^2}\Bigr )\nonumber \\&\quad =\frac{y(c_1e_2(x+k_1)+c_1e_1(y+k_1)x^2)-(xc_1e_1+x^2)}{(x+y+k_1)^2}\nonumber \\&\quad<0,\, \hbox {if}\, c_1e_2\Big (\frac{r_1}{s_1}+k_1\Big )+c_1e_1\Big (\frac{\beta r_1}{s_1s_2}+k_1\Big )\frac{r_1^2}{s_1^2}< \sigma c_1e_1+\sigma ^3c_2e_2.\nonumber \\ \end{aligned}$$

(7.1)

Therefore, $\left| B_{21}\right| =\frac{y(-xc_1e_1+c_2e_2(x+k_1))}{(x+y+k_1)^2}) \text { by the condition }$(7.1). Thus, we have $m_1(B_{11})=\frac{xzc_1}{(x+y+k_1)^2}+\frac{yzc_2}{(x+y+k_1)^2}-xs_1-ys_2$ and $m_1(B_{22})=\max (\beta _{11}+\beta _{21},\beta _{12}+\beta _{22})$. Here

$$\begin{aligned}&(\beta _{12}+\beta _{22})-(\beta _{11}+\beta _{21}) = \frac{z(c_1+xyc_2)}{x(x+y+k_1)^2)}\\&\quad -\frac{x^2yzc_2}{(x+y+k_1)^2} -\frac{zc_1(3x+2y+2k_1)}{(x+y+k_1)^2}\\&\quad -\frac{(1+x(2+x^2)y)+(1+x^2+2xy)s_1+xys_2}{x}+2r_1+x^2ys_2\\&<\frac{z(c_1+xyc_2)}{x(x+y+k_1)^2)}-\frac{x^2yzc_2}{(x+y+k_1)^2}+2r_1+x^2ys_2\\&<\frac{M_0(c_1+\frac{\beta c_2}{s_2})}{\sigma (2\sigma +k_1)^2}-\frac{\sigma ^4c_2}{(\frac{r_1}{s_1}+\frac{\beta r_1}{s_1s_2}+k_1)^2}+2r_1+\frac{\beta s_1}{r_1}<0 \end{aligned}$$

if $\frac{M_0(c_1+\frac{\beta c_2}{s_2})}{\sigma (2\sigma +k_1)^2}+2r_1+\frac{\beta s_1}{r_1}<\frac{\sigma ^4c_2}{(\frac{r_1}{s_1}+\frac{\beta r_1}{s_1s_2}+k_1)^2}$.

Using this condition one can say that

$$\begin{aligned} m_1(B_{22})= & {} \frac{2{\dot{x}}}{x}+\frac{{\dot{y}}}{y}-\frac{{\dot{z}}}{z}-ys_2-\frac{xc_1e_1k_2}{(x+y+k_1)(z+k_2)}\\&\quad +\frac{yc_2(z-\frac{c_2(x+y+k_1)k_2}{z+k_2})}{(x+y+k_1)^2} - \frac{\beta -\frac{zc_1}{(x+y+k_1)^2}+s_1}{x}. \end{aligned}$$

Now

$$\begin{aligned} g_1= & {} m_1(B_{11})+|B_{12}|\\= & {} \frac{{\dot{y}}}{y}-\left( \beta x-s_2(x+y)-\frac{c_2z}{x+y+k_1}-\delta \right) +\frac{xzc_1}{(x+y+k_1)^2}\\&+\frac{yzc_2}{(x+y+k_1)^2}-xs_1-ys_2+\frac{zc_1}{xy(x+y+k_1)}\\= & {} \frac{{\dot{y}}}{y}-xs_1+xs_2-\beta x+\delta +\frac{z(xc_1+yc_2)}{(x+y+k_1)^2}+\frac{z(c_1+c_2xy)}{xy(x+y+k_1)}\\\le & {} \frac{{\dot{y}}}{y}-\Bigl (xs_1-\delta -xs_2-\frac{z(xc_1+yc_2)}{(x+y+k_1)^2}-\frac{z(c_1+c_2xy)}{xy(x+y+k_1)}\Bigr )\\\le & {} \frac{{\dot{y}}}{y}-\Bigl (\delta s_1-\frac{s_1s_2}{r_1}-\delta -\frac{M_0(\frac{s_1c_1}{r_1}+\frac{\beta r_1c_2}{s_1s_2})}{(2\sigma +k_1)^2}-\frac{M_0(c_1+\frac{\beta c_2}{s_2})}{\sigma ^2(2\sigma +k_1)}\Bigr )\\= & {} \frac{{\dot{y}}}{y}-\Delta _1, \\&\quad \text { where}\\ \Delta _1= & {} \delta s_1-\frac{s_1s_2}{r_1}-\delta -\frac{M_0(\frac{s_1c_1}{r_1}+\frac{\beta r_1c_2}{s_1s_2})}{(2\sigma +k_1)^2}-\frac{M_0(c_1+\frac{\beta c_2}{s_2})}{\sigma ^2(2\sigma +k_1)}; \end{aligned}$$

and

$$\begin{aligned} g_2= & {} m_1(B_{22})+|B_{21}|\\= & {} \frac{{\dot{y}}}{y}+\frac{2{\dot{x}}}{x}-\frac{{\dot{z}}}{z}-(\beta x-s_2(x+y)-\frac{xc_1e_1k_2}{(x+y+k_1)(z+k_2)}\\&+\frac{yc_2(z-\frac{e_2(x+y+k_1)k_2}{z+k_2})}{(x+y+k_1)^2}- ys_2-\frac{\beta -\frac{zc_1}{(x+y+k_1)^2}+s_1}{x}\\&+\frac{y\Big (-xc_1e_1+c_2e_2(x+k_1)\Big )}{x+y+k_1}\\\le & {} \frac{{\dot{y}}}{y}-\Bigl (2y\beta -\frac{z(c_1+xyc_2)}{x(x+y+k_1)^2}-\frac{zc_3}{z+k_2} \Bigr )\\\le & {} \frac{{\dot{y}}}{y}-\Bigl (2\sigma \beta -\frac{M_0(c_1+\frac{\beta c_2)}{s_2}}{\sigma (2\sigma +k_1)^2}-\frac{M_0c_3}{\sigma +k_2} \Bigr )\\= & {} \frac{{\dot{y}}}{y}-\Delta _2, \text { where}\\ \Delta _2= & {} 2\sigma \beta -\frac{M_0(c_1+\frac{\beta c_2)}{s_2}}{\sigma (2\sigma +k_1)^2}-\frac{M_0c_3}{\sigma +k_2}. \end{aligned}$$

Taking $\Delta =\min (\Delta _1,\Delta _2)$, then it is seen that $g_1\le \frac{{\dot{y}}}{y}-\Delta , \ g_2\le \frac{{\dot{y}}}{y}-\Delta$.

Since, $m(B)\le \sup (g_1,g_2)$, we have $m(B)\le \frac{{\dot{y}}}{y}-\Delta .$ No the average value of m(B) is given by

$$\begin{aligned} \frac{1}{t} \int _{0}^{t} m(B)ds \le \frac{1}{t} \int _{0}^{t} m(B)ds+\frac{1}{t}\log \frac{y(t)}{y(0)}-\Delta , \end{aligned}$$

(7.2)

which implies

$$\begin{aligned} \bar{q_2}= \limsup _{t \rightarrow \infty } \sup _{x\in K}\frac{1}{t} \int _{0}^{t} B\big (x,(s,E_*)\big )ds\le -\Delta <0 \text { if }\Delta >0, \end{aligned}$$

Hence following Li and Muldowney [58] there exists a compact absorbing subset K of the simply connected domain D and a non wondering point $E_*$ . Hence the proof is completed. $\square$

Proposition 7.2

The system (2.1) undergoes Hopf bifurcation around the interior equilibrium point $E_*$ while the parameter $c_3$ crosses its critical value $c_3=c_3^{[hb]}$ in the domain

$$\begin{aligned} D_{hb}&=\Bigl \{c_3^{[hb]}\in \mathbb {R^+}:H(c_3^{[hb]})=(k_1(c_3)k_2(c_3)\\&\quad -k_3(c_3))|_{c_3=c_3^{[hb]}}=0 \, \text {with} \,\, k_2(c_3^{[hb]})>0,\,\, \text {and}\,\, \frac{dH(c_3)}{dc_3}|_{c_3=c_3^{[hb]} }\ne 0\Bigr \}. \end{aligned}$$

Proof

The Jacobian matrix at the interior equilibrium $E_*$ is given by $J_*$ and hence the characteristic equation of $J_*$ is

$$\begin{aligned} \lambda ^3+k_1\lambda ^2+k_2\lambda +k_3=0 , \end{aligned}$$

(7.3)

where $k_1$, $k_2$ and $k_3$ are defined in the Sect. (7.1). We have $(k_1k_2-k_3)\arrowvert _{c=c_3^{[hb]}}=0$ is a cubic equation in $c_3^{[hb]}$. From (7.3), we get $(\lambda ^2+k_2)(\lambda +k_1)=0,$ which gives three roots $\lambda _1=i\sqrt{k_2}$, $\lambda _2=-i\sqrt{k_2}$, $\lambda _3=-k_1$. Here $\pm i\sqrt{k_2}$ be a pair of purely imaginary eigenvalues. For all values of $\lambda$, the roots are, in general, of the form $\lambda _1=p(c_3)+iq(c_3)$, $\lambda _2=p(c_3)-iq(c_3)$, $\lambda _3=-k_1(c_3)$. Differentiating the characteristic Eq.  (7.3) with respect to $c_3$, we get

$$\begin{aligned} \frac{d\lambda }{dc_3}= & {} -\frac{\lambda ^2 \dot{k_1}+\lambda \dot{k_2}+\dot{k_3}}{3\lambda ^2+2k_1\lambda +k_2}\arrowvert _{\lambda =i\sqrt{k_2}}\nonumber \\= & {} \frac{\dot{k_3}-k_2\dot{k_1}+i\dot{k_2}\sqrt{k_2}}{2(k_2-ik_1\sqrt{k_2} )} \end{aligned}$$

(7.4)

$$\begin{aligned}= & {} \frac{\dot{k_3}-(k_2\dot{k_1}+k_1\dot{k_2})}{2(k_1^2+k_2)}+\frac{\sqrt{k_2}{(k_1\dot{k_3}+k_2\dot{k_2}-k_1\dot{k_1}k_2)}}{2k_2(k_1^2+k_2))}\nonumber \\= & {} -\frac{\frac{dH}{dc_3}}{2(k_1^2+k_2)}+i\Big (\frac{\sqrt{k_2}\dot{k_2}}{2k_2}-\frac{k_1\sqrt{k_2}\frac{dH}{dc_3}}{2k_2(k_1^2+k_2)}\Big ). \end{aligned}$$

(7.5)

Here $\frac{d{\text {Re}}(\lambda )}{dc_3}\Big |_{c_3= c_3^{[hb]} }= -\frac{\frac{dH}{dc_3}}{2(k_1^2+k_2)}\Big |_{c_3= c_3^{[hb]} }\ne 0.$ Using monotonicity condition of the real part of the complex root $\frac{d{\text {Re}}(\lambda )}{dc_3}\Big |_{c_3=c_3^{[hb]}}\ne 0$ (cf. [59]), the transversality condition $\frac{dH}{dc_3}\ne 0$ of the theorem can be established for the existence of Hopf bifurcation. $\square$

Lemma 7.1

The system (2.1) undergoes a transcritical bifurcation around the equilibrium point $E_2$ at $\delta =\delta ^{[tc]}$, where $\delta ^{[tc]}=\frac{r_1(\beta -s_2)}{s_1}$, provided $\beta >s_2$.

Proof

Writing the governing system (2.1) as $\frac{dX}{dt}= f(X)$, where $X=(x,y,z)^\mathrm{T}$ and $f(X)=\left( f_1(X),f_2(X),f_3(X)\right) ^\mathrm{T}$. There is a zero eigenvalue iff $\det (J_2)=0$, which gives $\delta =\frac{r_1(\beta -s_2)}{s_1}=\delta ^{[tc]}$. The other two eigenvalues are $-r_1,\ \frac{c_1e_1r_1}{r_1+k_1s_1}$. Let v and w be the eigenvectors corresponding to zero eigenvalue of the matrices $J_2$ and $(J_2)^\mathrm{T}$(transpose of $J_2$) respectively. Then we have $v=(-\frac{\beta + s_1}{s_1},1,0)^\mathrm{T}$ and $w=(0,1,0)^\mathrm{T}$. Since $w^\mathrm{T}f_{\delta }(E_2,\delta ^{[tc]})=0$, $w^\mathrm{T}[Df_\delta (E_2,\delta ^{[tc]})v]=-1\ne 0$ and $w^\mathrm{T}[D^2f(E_2,\delta ^{[tc]})(v,v)]=-\frac{2\beta (\beta + s_1-s_2)}{s_1}\ne 0$ if $s_1+\beta \ne s_2$. It is also found that $w^\mathrm{T}[D^3f(E_2,\delta ^{[tc]})(v,v,v)]= 0$ unconditionally. Hence, the system experiences neither Saddle-Node(SN) nor Pitch-fork (PF) bifurcation. But the system experiences Transcritical (TC) bifurcation near the equilibrium point $E_2 =(\frac{r_1}{s_1},0,0)$. $\square$

The expression for $Df(U),\ D^2f(U,U)$ and $D^3f(U,U,U)$ can be obtained analytically (cf. Rudin [60]). Hence the system possesses a transcritical bifurcation (cf. Sotomayor [61]) at $E_2$.

8 Numerical simulation

Analytical studies can never be completed if numerical verification of the derived results is not achieved. With the help of MATLAB-R2011a and Maple-18 numerical simulation has been carried out. In this section, we have presented computer simulations of some solutions of the system (2.1). The analytical findings of the present study are summarized and represented schematically in Table 1. The disease will be wiped out naturally when infected prey mortality exceeds the value 0.172 and if the value of the parameter $c_3$ decreases its value from 1.2 to $c_3=0.90894556.2$, the system (2.1) undergoes Hopf bifurcation around interior equilibrium. Local stability occurs around interior equilibrium when $c_3=1.2$. For larger value of $s_1=0.0185$, $E_5$ is locally asymptotically stable.The system experiences Hopf bifurcation around $E_5$ for $s_1=0.0097669$.

Table 1 Schematic representation of our analytical findings: US $\equiv$ unstable saddle, LAS $\equiv$ locally asymptotically stable, GAS $\equiv$ globally asymptotically stable, HB $\equiv$ Hopf bifurcation

9 Discussion

In present paper, an eco-epidemiological model is considered with hyperbolic mortality rate of predator population. Here an infectious disease is assumed and it is transmitted only in prey population. We have also assumed that prey population does not reproduce, but compete with the susceptible prey population for the same resources. The mode of disease spread follows a simple mass action law.

It is observed that our system is bounded and possesses seven equilibria. The equilibrium point $E_0$, where there is the extinction of all species, exists and is unstable. The equilibrium point $E_2$ corresponds to extinction of infected prey and predator populations $E_2$ exists and it is unstable. The equilibrium point $E_3$ corresponds to the absence of predator population exists if $s_1 > s_2$ and $\beta r_1>\delta s_1 +r_1s_2$ and it also unstable. Furthermore, the equilibrium point $E_5$ corresponds to nonexistence of infected prey population. Also $E_5$ exists if $c_3>e_1 c_1$ and is locally asymptotically stable under some conditions $m_{22}<0$, $m_{11}+m_{33}<0$,  $m_{11}m_{33}-m_{31}m_{13}>0$. Figure 1 indicates that infected prey population goes to extinction. The system undergoes Hopf bifurcation around $E_5$ as the parameter $s_1$ crosses its critical value $s_1^{[hb]}$(see Fig. 2). The system (2.1) experiences transcritical bifurcation at $E_2$ with respect to the parameter $\delta$.

Fig. 1

Stability behaviour around the equilibrium position $E_5$ of the system (2.1) with the initial conditions $x_0=40, \ y_0=10, \ z_0=270$ and parameter values $r=3.25, \ k_1=200, \ k_2=150, \ c_1=2.5, \ c_2=2.84, \ c_3=0.4, \ s_1=0.0185, \ s_2=0.0042, \ \beta =0.0098, \ \delta =0.56, \ e_1=0.70, \ e_2=0.49$. a Time series evolution. b Phase portrait diagram

Fig. 2

Hopf bifurcation behaviour around the equilibrium position $E_5$ of the system (2.1) with the initial conditions $x_0=40, \ y_0=10, \ z_0=270$ and parameter values $r=3.25, \ k_1=200, \ k_2=150, \ c_1=2.5, \ c_2=2.84, \ c_3=0.4, \ s_1=0.0097669, \ s_2=0.0042, \ \beta =0.0098, \ \delta =0.56, \ e_1=0.70, \ e_2=0.49$. a Time series evolution. b Phase portrait diagram

Fig. 3

Stability behaviour of the system (2.1) around the equilibrium position $E_*$ with the initial conditions $x_0=170, \ y_0=10, \ z_0=150$ and parameter values $r=3.25, \ k_1=200, \ k_2=150, \ c_1=2.5, \ c_2=2.84, \ c_3=1.2, \ s_1=0.0055, \ s_2=0.0042, \ \beta =0.0496, \ \delta =0.56, \ e_1=0.70, \ e_2=0.49$. a Time series evolution. b Phase portrait diagram

Fig. 4

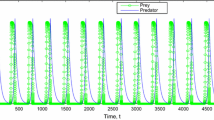
Hopf bifurcation behaviour around the equilibrium position $E_*$ of the system (2.1) with the initial conditions $x_0=48, \ y_0=29, \ z_0=149$ and parameter values $r=3.25, \ k_1=200, \ k_2=150, \ c_1=2.5, \ c_2=2.84, \ c_3=0.90894556, \ s_1=0.0055, \ s_2=0.0042, \ \beta =0.0496, \ \delta =0.56, \ e_1=0.70, \ e_2=0.49$. a Time series evolution. b Phase portrait diagram

The positive equilibrium point $E_*$ is locally asymptotically stable if the Routh–Hurwitz criterion is satisfied. Stability of positive equilibrium point out of that the existence and survival of all species in the ecosystem (see Fig. 3). From the Biological point of view this equilibrium point is very important as it provides actual interaction among all species of the system. Under this situation actual balance is maintained in ecosystem. For this reason ecologists feel interested to observe the stability of positive coexistence equilibrium. The system experiences Hopf bifurcation around interior equilibrium $E_*$ which is shown in Fig. 4. Conditions for persistence of the system are $\beta (\gamma _1+\gamma _2+\delta )>\gamma _2s_2$ and $s_1c_3(k_1+x_5)<r_1c_1e_1, \ \beta x_5>s_2x_5+\delta$. Global stability around the co-existence equilibrium $E_*$ is also investigated with the help of Lozinski${\check{i}}$ measure. Also Fig. 4 shows that the predator population coexists with susceptible and infected prey exhibiting oscillatory balance behavior for the set of system parameters: $r=3.25, \ k_1=200, \ k_2=150, \ c_1=2.5, \ c_2=2.84, \ c_3=0.90894556, \ s_1=0.0055, \ s_2=0.0042, \ \beta =0.0496, \ \delta =0.56, \ e_1=0.70, \ e_2=0.49$. In the real world system, the population dynamics certainly affected by environmental fluctuations. Natural disaster, climate change, pollution also regulate the stability of the ecosystem and then interior stable equilibrium may loose the stability in some ecosystems, which are prone to face such calamities. We have derived parametric restriction $\frac{\beta r_1}{s_1}< \delta$ to control disease naturally. The parameter associated with this model plays a key role for ecological balance. The future work may be carried out to extend the paper assuming that the disease can spread horizontally as well as vertically in the predator population with some delay factors like gestation or maturity delays.

APPENDIX

The coefficients of the Eq. (4.1) are as follows:

$$\begin{aligned} A_1= & {} \beta ^2 (c_2-c_1)(\beta +s_1-s_2)\bigl ((\beta (c_2 c_3-c_1 (c_2 (e_1-e_2)+c_3))) +(c_1 e_1-c_2 e_2)\\&\times (c_1 s_2-c_2 s_1)\bigr ),\\ 3B_1= & {} c_1^3 e_1 \left\{ r_1 \left( \beta -s_2\right) \left( \left( \beta -s_2\right) \left( c_2 k_2+\delta k_1\right) +\delta ^2\right) -\delta s_1 \left( \left( \beta -s_2\right) \left( \delta k_1-2 c_2 k_2\right) +\delta ^2\right) \right\} \\&+\,c_1^2 \left\{ c_2 e_1 \left\{ -2 r_1 s_1 \left( c_2 k_2 \left( s_2-\beta \right) +\delta ^2\right) +\delta s_1^2 \left( c_2 k_2-\delta k_1\right) \right. \right. \\&\left. +\,r_1^2 \left( \beta -s_2\right) \left( 2 \delta +k_1 \left( \beta -s_2\right) \right) \right\} \left. +c_3 \left( \delta +k_1 \left( \beta -s_2\right) \right) {}^2 \left( r_1 \left( s_2-\beta \right) +\delta s_1\right) \right\} \\&+\,c_2 c_1 \left\{ c_2 e_1 r_1 \left( s_1^2 \left( c_2 k_2-\delta k_1\right) -r_1 s_1 \left( \delta +k_1 \left( s_2-\beta \right) \right) +r_1^2 \left( \beta -s_2\right) \right) \right. \\&\left. -\,2 c_3 \left( k_1 s_1+r_1\right) \left( \delta +k_1 \left( \beta -s_2\right) \right) \left( r_1 \left( \beta -s_2\right) -\delta s_1\right) \right\} \\&+\,c_1^4 \delta e_1 k_2 \left( \beta -s_2\right) ^2+c_2^2 c_3 \left( k_1 s_1+r_1\right) ^2 \left( r_1 \left( s_2-\beta \right) +\delta s_1\right) ,\\ 3C_1= & {} e_1 k_2 s_2 \left( s_2-\beta \right) {}^2 c_1^4 -\left\{ e_1 \left( \beta \left( \beta -s_2\right) +s_1 \left( 2 \beta +s_2\right) \right) \delta ^2+e_1 \left( s_2-\beta \right) \left( r_1 \left( \beta +s_2\right) \right. \right. \\&\left. \left. -\,k_1 \left( \beta \left( \beta -s_2\right) +s_1 \left( \beta +s_2\right) \right) \right) \delta +\left( s_2-\beta \right) \left( e_1 k_1 r_1 \left( \beta -s_2\right) s_2\right. \right. \\&\left. \left. +\,c_2 k_2 \left( e_2 \left( s_2-\beta \right) {}^2+e_1 \left( -\beta ^2-s_1 \beta +s_2 \beta +3 s_1 s_2\right) \right) \right) \right\} c_1^3\\&+\,\left\{ k_2 s_1 \left( 3 e_2 \left( s_2-\beta \right) {}^2+e_1 \left( 2 \beta \left( s_2-\beta \right) +s_1 \left( 3 s_2-2 \beta \right) \right) \right) c_2^2\right. \\&\left. +\,\left( e_1 \left( \left( \beta ^2-s_2^2\right) r_1^2-2 k_1 \left( \beta +s_1\right) \left( s_2-\beta \right) {}^2 r_1-4 \beta \delta \left( \beta +s_1-s_2\right) r_1\right. \right. \right. \\&\left. \left. \left. +\,\delta s_1 \left( 2 \beta \delta +s_1 \delta -2 k_1 s_1 s_2\right) \right) -e_2 \left( s_2-\beta \right) \left( k_1 \left( s_2-\beta \right) -\delta \right) \right. \right. \\&\times \left. \left. \left( \delta s_1+r_1 \left( s_2-\beta \right) \right) \right) c_2+\beta c_3 \left( \delta +k_1 \left( \beta -s_2\right) \right) \left( \delta \left( \beta +3 s_1-s_2\right) \right. \right. \\&\left. \left. +\,\left( 2 r_1-k_1 \left( \beta +s_1-s_2\right) \right) \left( s_2-\beta \right) \right) \right\} c_1^2 +c_2 \left\{ -c_2^2 k_2 \left( e_1 \left( \beta +s_1\right) \right. \right. \\&\left. \left. +\,3 e_2 \left( s_2-\beta \right) \right) s_1^2+2 \beta c_3 \left( -s_1 \delta ^2+2 \left( k_1 s_1^2+r_1 \left( \beta +s_1-s_2\right) \right) \delta \right. \right. \\&\left. \left. +\,\left( s_2-\beta \right) \left( -s_1 \left( \beta +s_1-s_2\right) k_1^2+2 r_1 \left( s_2-\beta \right) k_1+r_1^2\right) \right) \right. \\&\left. +\,c_2 \left( \delta e_1 s_1 \left( k_1 s_1 \left( \beta +s_1\right) +r_1 \left( 2 \beta +s_1\right) \right) +e_2 \left( \delta s_1+r_1 \left( s_2-\beta \right) \right) \right. \right. \\&\times \left. \left. \left( \left( r_1+2 k_1 s_1\right) \left( s_2-\beta \right) -\delta s_1\right) +e_1 r_1 \left( k_1 s_1 \left( s_1 \left( s_2-2 \beta \right) +2 \beta \left( s_2-\beta \right) \right) \right. \right. \right. \\&\left. \left. \left. +\,r_1 \left( s_1 \left( s_2-2 \beta \right) +3 \beta \left( s_2-\beta \right) \right) \right) \right) \right\} c_1 +c_2^2 \left\{ c_2^2 e_2 k_2 s_1^3\right. \\&\left. -\,c_2 e_2 \left( r_1+k_1 s_1\right) \left( \delta s_1+r_1 \left( s_2-\beta \right) \right) s_1\right. \\&\left. +\,\beta c_3 \left( r_1+k_1 s_1\right) \left( -2 \delta s_1+k_1 \left( \beta +s_1-s_2\right) s_1+r_1 \left( 3 \beta +s_1-3 s_2\right) \right) \right\} , \\ D_1= & {} c_1^3 e_1 \left\{ c_2 k_2 \left( s_2-\beta \right) \left( -\beta r_1+r_1 s_2-2 \delta s_1\right) +\delta \left( -\delta -\beta k_1+k_1 s_2\right) \right. \\&\times \left. \left( -\beta r_1+r_1 s_2+\delta s_1\right) \right\} +c_1^2 \left\{ c_2^2 e_1 k_2 s_1 \left( 2 \beta r_1-2 r_1 s_2+\delta s_1\right) \right. \\&\left. +c_2 e_1 \left( -\beta r_1+r_1 s_2+\delta s_1\right) \left( k_1 r_1 \left( s_2-\beta \right) -\delta \left( k_1 s_1+2 r_1\right) \right) \right. \\&\left. +c_3 \left( \delta +\beta k_1-k_1 s_2\right) {}^2 \left( -\beta r_1+r_1 s_2+\delta s_1\right) \right\} \\&+c_2 c_1 \left\{ -c_2 e_1 r_1 \left( k_1 s_1+r_1\right) \left( -\beta r_1+r_1 s_2+\delta s_1\right) +c_2^2 e_1 k_2 r_1 s_1^2\right. \\&\left. -2 c_3 \left( k_1 s_1+r_1\right) \left( -\delta -\beta k_1+k_1 s_2\right) \left( -\beta r_1+r_1 s_2+\delta s_1\right) \right\} \\&+c_1^4 \delta e_1 k_2 \left( s_2-\beta \right) ^2 + c_2^2 c_3 \left( k_1 s_1+r_1\right) ^2 \left( r_1 \left( s_2-\beta \right) +\delta s_1\right) . \end{aligned}$$