Global stability of an eco-epidemiological predator-prey model with saturation incidence

Abstract

A delayed predator-prey model with disease in the predator and stage structure for the prey is investigated. By analyzing the corresponding characteristic equations, the local stability of each of feasible equilibria is studied. The existence of Hopf bifurcations at the disease-free equilibrium and the coexistence equilibrium are addressed, respectively. By using Lyapunov functions and LaSalle invariant principle, sufficient conditions are derived for the global stability of the trivial equilibrium, the predator-extinction equilibrium and the disease-free equilibrium, respectively. Further, sufficient conditions are derived for the global attractiveness of the coexistence equilibrium of the proposed system.

1 Introduction

Predator-prey models are important in the modelling of multi-species interactions and have received great attention among theoretical and mathematical biologists. The dynamics of the predator-prey models has been studied by many means, such as the adomian decomposition method (ADM), the variational iteration method (VIM) and the differential transform method (DTM) (see [1, 4, 6–8, 13]). Since the pioneering work of Anderso and May [3] who were the first to propose an eco-epidemiological model by merging the ecological predator-prey model introduced by Lotka and Volterra, great attention has been paid to the modelling and analysis of eco-epidemiological system recently (see [9, 11, 12, 15–18, 21, 22]). In [18], Xiao and Chen discussed a predator-prey model with disease in the prey. Mathematical analysis of the model equations with regard to invariance of nonnegativity, boundedness of solutions, nature of equilibria, permanence and global stability were analyzed. In [21], Zhang and Sun considered a predator-prey model with disease in the predator and Holling-II type functional response. Sufficient conditions were derived for the permanence of the eco-epidemiological system. In [22], Zhang et al. considered the following eco-epidemiological model

$$\begin{aligned} \begin{array}{l} \displaystyle {\dot{x}(t)=rx(t)-ax^2(t)-a_{12}x(t)S(t)},\\ \displaystyle {\dot{S}(t)=a_{21}x(t-\tau )S(t-\tau )-d_3S(t)-\beta S(t)I(t)},\\ \displaystyle {\dot{I}(t)=\beta S(t)I(t)-d_4I(t)}, \end{array} \end{aligned}$$

(1.1)

where x(t), S(t) and I(t) represent the densities of the prey, susceptible (sound) predator and infected predator population at time t, respectively. The parameters $a, a_{12}, a_{21}, d_3, d_4, r$ and $\beta$ are positive constants (see [22]). In system (1.1), the authors assumed that the infectious predator would die of diseases and only the healthy predator had predation capacity, but once infected with the disease, the predator would not be able to recover. By regarding the time delay $\tau$ as the bifurcation parameter and analyzing the characteristic equation of the positive equilibrium, the local asymptotic stability of the positive equilibrium and the existence of a Hopf bifurcation of system (1.1) were investigated in [22].

The above-mentioned works all used bilinear incidence to model disease transmission. However, there are a variety of factors that emphasize the need for a modification of the bilinear incidence. For example, the underlying assumption of homogeneous mixing may not always hold. Incidence rates that increase more gradually than linearly in I and S may arise from saturation effects. It has been strongly suggested by several authors that the disease transmission process may follow saturation incidence. After studying the cholera epidemic spread in Bari in 1973, Capasso and Serio [5] introduced a saturated incidence rate with $\beta IS/(1+\alpha I)$. This incidence rate seems more reasonable than the bilinear incidence rate $\beta SI$, because it includes the behavioral change and crowding effect of the infective individuals and prevents the unboundedness of the contact rate by choosing suitable parameters.

We note that it is assumed in system (1.1) that each individual prey admits the same risk to be attacked by predators. This assumption seems not to be realistic for many animals. In the natural world, there are many species whose individuals pass through an immature stage during which they are raised by their parents, and the rate at which they are attacked by predator can be ignored. Moreover, it can be assumed that their reproductive rate during this stage is zero. Stage-structure is a natural phenomenon and represents, for example, the division of a population into immature and mature individuals. Stage-structured models have received great attention in recent years (see, for example, [2, 16, 19, 20]).

Based on above discussions, in this paper, we incorporate a stage structure for the prey and saturation incidence into the system (1.1). To this end, we study the following differential equations

$$\begin{aligned} \begin{array}{l} \displaystyle {\dot{x}_1(t)=rx_2(t)-(r_1+d_1)x_1(t)},\\ \displaystyle {\dot{x}_2(t)=r_1x_1(t)-d_2x_2(t)-ax_2^2(t)-a_1x_2(t)S(t)},\\ \displaystyle {\dot{S}(t)=a_2x_2(t-\tau )S(t-\tau )-d_3S(t)-bS^2(t)-\frac{\beta S(t)I(t)}{1+\alpha I(t)}},\\ \displaystyle {\dot{I}(t)=\frac{\beta S(t)I(t)}{1+\alpha I(t)}-d_4I(t)}, \end{array} \end{aligned}$$

(1.2)

where $x_1(t)$ and $x_2(t)$ represent the densities of the immature and the mature prey population at time t, respectively. $\tau \ge 0$ represents the time delay due to the gestation of the susceptible predator. The parameters $a, a_1, a_2, b, d_1, d_2, d_3, d_4, r, r_1,$ $\alpha$ and $\beta$ are positive constants in which $d_1$ and $d_2$ are the death rates of the immature and the mature prey, respectively; $d_3$ and $d_4$ are the death rates of the susceptible and infected predator, respectively; a and b are the intra-specific competition rate of the mature prey and the susceptible predator, respectively; $a_1>0$ is the capturing rate of the susceptible predator; $a_2/a_1>0$ is the conversion rate of nutrients into the reproduction of the predator by consuming mature prey; the disease incidence is assumed to be the saturation incidence $\beta SI/(1+\alpha I)$, where $\beta >0$ is called the disease transmission coefficient.

The initial conditions for system (1.2) take the form

$$\begin{aligned} x_1(\theta )= & {} \varphi _1(\theta )\ge 0,\;\;x_2(\theta )=\varphi _2(\theta )\ge 0,\;\;\nonumber \\ S(\theta )= & {} \phi _1(\theta )\ge 0,\;\;I(\theta )=\phi _2(\theta )\ge 0,\;\;\theta \in [-\tau ,0),\nonumber \\&\varphi _1(0)>0,\;\;\varphi _2(0)>0,\;\; \phi _1(0)>0,\;\;\phi _2(0)\nonumber \\&>0,\;\;(\varphi _1(\theta ),\varphi _2(\theta ), \phi _1(\theta ),\phi _2(\theta ))\in {C([-\tau ,0], R_{+0}^4)}, \end{aligned}$$

(1.3)

where $R_{+0}^4=\{(y_1, y_2, y_3, y_4): {y_i\ge {0}},i=1,2,3,4\}.$

It is well known by the fundamental theory of functional differential equations [10] that system (1.2) has a unique solution $(x_1(t), x_2(t), S(t), I(t))$ satisfying initial conditions (1.3). It is easy to show that all solutions of system (1.2) with initial conditions (1.3) are defined on $[0, +\infty )$ and remain positive for all $t\ge 0$.

The organization of this paper is as follows. In the next section, we show the permanence of solutions of model (1.2) with initial conditions (1.3). In Sect. 3, by analyzing the corresponding characteristic equations, we study the local stability of each feasible boundary equilibria of system (1.2) and the existence of Hopf bifurcations of system (1.2) at the disease-free equilibrium. By means of Lyapunov functions and LaSalle invariant principle, we establish sufficient conditions for the global stability of each feasible boundary equilibria of system (1.2). In Sect. 4, by analyzing the corresponding characteristic equation, we discuss the local stability of coexistence equilibrium and the existence of Hopf bifurcations of system (1.2) at the coexistence equilibrium. By means of Lyapunov functions and LaSalle invariant principle, we establish sufficient conditions for the global attractiveness of the coexistence equilibrium. A brief discussion is given in Sect. 5 to conclude this work.

2 Permanence

In this section, we are concerned with the permanence of system (1.2).

Lemma 2.1

Positive solutions of system (1.2) with initial conditions (1.3) are ultimately bounded.

Proof

Let $(x_1(t), x_2(t), S(t), I(t))$ be any positive solution of system (1.2) with initial conditions (1.3). Denote $d=\min \{ d_1, d_2, d_3, d_4\}$. Define

$$\begin{aligned}V(t)=x_1(t-\tau ) +x_2(t-\tau )+\frac{a_1}{a_2}[S(t)+I(t)].\end{aligned}$$

Calculating the derivative of V(t) along positive solutions of system (1.2), it follows that

$$\begin{aligned} \dot{V}(t)= & {} -d_1x_1(t-\tau )-d_2x_2(t-\tau )-ax_2^2(t-\tau )+rx_2(t-\tau )\\&-\,\frac{a_1}{a_2}[d_3S(t)+d_4I(t)]-bS^2(t)\\\le & {} {-d}V(t)-a\left[ x_2(t-\tau )-\frac{r}{2a}\right] ^2-bS^2(t)+\frac{r^2}{4a}\\\le & {} -dV(t)+\frac{r^2}{4a} \end{aligned}$$

which yields $\limsup _{t\rightarrow \infty }V(t)\le {\frac{r^2}{4ad}}.$

If we choose $M_1=r^2/(4ad)$, $M_2=a_2r^2/(4aa_1d)$, then

$$\begin{aligned} \limsup _{t\rightarrow \infty }x_i(t)\le {M_1}(i=1,2), \;\;\limsup _{t\rightarrow \infty }S(t)\le {M_2},\;\; \limsup _{t\rightarrow \infty }I(t)\le {M_2}. \end{aligned}$$

$\square$

Theorem 2.1

Suppose that

$(H_1)\;\;\beta \underline{S}>d_4,$

where $\underline{S}$ is defined in (2.3), then system (1.2) is permanent.

Proof

Let $(x_1(t), x_2(t), S(t), I(t))$ be any positive solution of system (1.2) with initial conditions (1.3). By Lemma 2.1, it follows that $\limsup _{t\rightarrow +\infty }S(t)\le M_2$. Hence, for $\varepsilon >0$ being sufficiently small, there is a $T_0>0$ such that if $t>T_0$, $S(t)<M_2+\varepsilon$. Accordingly, for $\varepsilon >0$ being sufficiently small, we derive from the first and the second equations of system (1.2) that, for $t>T_0$,

$$\begin{aligned} \begin{array}{l} \displaystyle {\dot{x}_1(t)=rx_2(t)-(r_1+d_1)x_1(t)},\\ \displaystyle {\dot{x}_2(t)\ge r_1x_1(t)-d_2x_2(t)-ax_2^2(t)-a_1(M_2+\varepsilon )x_2(t)},\\ \end{array} \end{aligned}$$

(2.1)

which yields

$$\begin{aligned} \displaystyle {\liminf _{t\rightarrow +\infty }x_1(t)\ge \frac{r}{r_1+d_1}\underline{x}_2:=\underline{x}_1,\;\;\liminf _{t\rightarrow +\infty }x_2(t)\ge \frac{rr_1-(r_1+d_1)(d_2+a_1M_2)}{a(r_1+d_1)}:=\underline{x}_2.} \end{aligned}$$

(2.2)

we derive from the third equation of system (1.2), for t sufficiently large, we have

$$\begin{aligned} \displaystyle {\dot{S}(t)\ge b\underline{x}_2S(t-\tau )-d_3S(t)-bS^2(t)-\frac{\beta M_2}{1+\alpha M_2}S(t)} \end{aligned}$$

By Theorem 4.9.1 in [14], one can obtain that

$$\begin{aligned} \displaystyle {\liminf _{t\rightarrow +\infty }S(t)\ge \frac{1}{b}[b\underline{x}_2-d_3-\frac{\beta M_2}{1+\alpha M_2}]:=\underline{S}.} \end{aligned}$$

(2.3)

we derive from the fourth equation of system (1.2), for t sufficiently large, we have

$$\begin{aligned} \displaystyle {\dot{I}(t)\ge \frac{\beta \underline{S}I(t)}{1+\alpha I(t)}-d_4I(t)} \end{aligned}$$

Since $(H_1)$ holds, then

$$\begin{aligned} \displaystyle {\liminf _{t\rightarrow +\infty }I(t)\ge \frac{1}{\alpha d_4}[\beta \underline{S}-d_4]:=\underline{I}.} \end{aligned}$$

(2.4)

The above calculations and Lemma 2.1 imply that system (1.2) is permanent. $\square$

3 Boundary equilibria and their stability

In this section, we discuss the stability of the boundary equilibria and the existence of a Hopf bifurcation at the disease-free equilibrium.

System (1.2) always has a trivial equilibrium $E_0(0, 0, 0, 0)$. If $rr_1>d_2(r_1+d_1),$ then system (1.2) has a predator-extinction equilibrium $E_1(x_1^0, x_2^0, 0, 0)$, where

$\displaystyle {x_1^0=\frac{r[rr_1-d_2(r_1+d_1)]}{a(r_1+d_1)^2},\;\;x_2^0=\frac{rr_1-d_2(r_1+d_1)}{a(r_1+d_1)}}.$

If $a_2x_2^0>d_3$, then system (1.2) has a disease-free equilibrium $E_2(x_1^+, x_2^+, S^+, 0)$, where

$\begin{array}{l} \displaystyle {x_1^+=\frac{r(abx_2^0+a_1d_3)}{(r_1+d_1)(ab+a_1a_2)},\;\;\;\;\;\;x_2^+=\frac{abx_2^0+a_1d_3}{ab+a_1a_2},\;\;\;\;\;\;S^+=\frac{a(a_2x_2^0-d_3)}{ab+a_1a_2}}. \end{array}$

The characteristic equation of system (1.2) at the equilibrium $E_0(0, 0, 0, 0)$ takes the form

$$\begin{aligned} (\lambda +d_3)(\lambda +d_4)[\lambda ^2+(r_1+d_1+d_2)\lambda +d_2(r_1+d_1)-rr_1]=0, \end{aligned}$$

(3.1)

It is readily seen from Eq. (3.1) that if $rr_1<d_2(r_1+d_1)$, then $E_0$ is locally asymptotically stable; if $rr_1>d_2(r_1+d_1)$, then $E_0$ is unstable.

Theorem 3.1

If $rr_1<d_2(r_1+d_1)$, then the trivial equilibrium $E_0(0, 0, 0, 0)$ of system (1.2) is globally asymptotically stable.

Proof

Based on above discussions, we see that if $rr_1<d_2(r_1+d_1)$, then $E_0$ is locally asymptotically stable. Hence, we only prove that all positive solutions of system (1.2) with initial conditions (1.3) converge to $E_0$. Let $(x_1(t), x_2(t), S(t), I(t))$ be any positive solution of system (1.2) with initial conditions (1.3). Define

$$\begin{aligned} V_0(t)=\displaystyle {\frac{r_1}{r_1+d_1}x_1(t)+x_2(t)+\frac{a_1}{a_2}\left[ S(t)+I(t)\right] +a_1\int _{t-\tau }^tx_2(u)S(u)du}. \end{aligned}$$

Calculating the derivative of $V_0(t)$ along positive solutions of system (1.2), it follows that

$$\begin{aligned} \begin{array}{l} \displaystyle {\dot{V}_0(t)}=\displaystyle {-\frac{d_2(r_1+d_1)-rr_1}{r_1+d_1}x_2(t)-ax_2^2(t)-\frac{a_1}{a_2}\left[ d_3S(t)+d_4I(t)\right] -\frac{a_1}{a_2}bS^2(t).} \end{array} \end{aligned}$$

(3.2)

If $rr_1<d_2(r_1+d_1)$, it then follows from (3.2) that $\dot{V}_0(t)\le 0$. By Theorem 5.3.1 in [10], solutions limit to $\Lambda$, the largest invariant subset of $\{\dot{V}_0(t)=0\}$. Clearly, we see from (3.2) that $\dot{V}_0(t)=0$ if and only if $x_2(t)=0, S(t)=0$ and $I(t)=0$. Noting that $\Lambda$ is invariant, for each element in $\Lambda$, we have $x_2(t)=0$. It therefore follows from the second equation of system (1.2) that

$$\begin{aligned} 0=\dot{x}_2(t)=r_1x_1(t), \end{aligned}$$

which yields $x_1(t)=0$. Hence, $\dot{V}_0(t)=0$ if and only if $(x_1(t), x_2(t), y_1(t), y_2(t))=(0,0,0,0)$. Accordingly, the global asymptotic stability of $E_0$ follows from LaSalle invariant principle for delay differential systems. $\Box$

The characteristic equation of system (1.2) at the equilibrium $E_1(x_1^0, x_2^0, 0,0)$ is of the form

$$\begin{aligned} (\lambda +d_4)[\lambda ^2+(r_1+d_1+d_2+2ax_2^0)\lambda +rr_1-d_2(r_1+d_1)](\lambda +d_3-a_2x_2^0e^{-\lambda \tau })=0, \end{aligned}$$

(3.3)

Equation (3.3) always has a negative real root: $\lambda _1=-d_4$. If $rr_1>d_2(r_1+d_1)$, then the equation

$$\begin{aligned} \lambda ^2+(r_1+d_1+d_2+2ax_2^0)\lambda +rr_1-d_2(r_1+d_1)=0 \end{aligned}$$

has two roots with negative real parts. All other roots of Eq. (3.3) are determined by the equation

$$\begin{aligned} \lambda +d_3-a_2x_2^0e^{-\lambda \tau }=0. \end{aligned}$$

(3.4)

Denote $f(\lambda )=\lambda +d_3-a_2x_2^0e^{-\lambda \tau }$. If $a_2x_2^0>d_3$ holds, it is easy to show that, for $\lambda$ real,

$$\begin{aligned} \begin{array}{l} \displaystyle {f(0)=d_3-a_2x_2^0<0,}\;\;\;\; \displaystyle {\lim _{\lambda \rightarrow +\infty }f(\lambda )=+\infty } \end{array} \end{aligned}$$

Hence, $f(\lambda )=0$ has a positive real root. Therefore, if $a_2x_2^0>d_3$ holds, the equilibrium $E_1(x_1^0, x_2^0, 0,0)$ is unstable.

If $0<a_2x_2^0<d_3,$ we claim that $E_1$ is locally asymptotically stable. Otherwise, there is a root $\lambda$ satisfying $Re\lambda \ge 0$. It follows from (3.4) that

$$\begin{aligned} \displaystyle {Re\lambda =a_2x_2^0e^{-\tau Re\lambda }cos(\tau Im\lambda )-d_3\le a_2x_2^0-d_3}<0, \end{aligned}$$

which is a contradiction. Hence, if $0<a_2x_2^0<d_3,$ then the equilibrium $E_1$ is locally asymptotically stable. $\square$

Theorem 3.2

If $0<a_2x_2^0<d_3,$ then the predator-extinction equilibrium $E_1(x_1^0, x_2^0, 0, 0)$ of system (1.2) is globally asymptotically stable.

Proof

Based on above discussions, we see that if $0<a_2x_2^0<d_3$, then $E_1$ is locally asymptotically stable. Hence, we only prove that all positive solutions of system (1.2) with initial conditions (1.3) converge to $E_1$. Let $(x_1(t), x_2(t), S(t), I(t))$ be any positive solution of system (1.2) with initial conditions (1.3). System (1.2) can be rewritten as

$$\begin{aligned} \dot{x}_1(t)= & {} \frac{r}{x_1^0}[-x_2(t)(x_1(t)-x_1^0)+x_1(t)(x_2(t)-x_2^0)]\nonumber \\ \dot{x}_2(t)= & {} \frac{r_1}{x_2^0}[-x_1(t)(x_2(t)-x_2^0)+x_2(t)(x_1(t)-x_1^0)]\nonumber \\&+\,x_2(t)[-a(x_2(t)-x_2^0)]-a_1x_2(t)S(t)\nonumber \\ \dot{S}(t)= & {} a_2x_2(t-\tau )S(t-\tau )-d_3S(t)-bS^2(t)-\frac{\beta S(t)I(t)}{1+\alpha I(t)}\nonumber \\ \dot{I}(t)= & {} \frac{\beta S(t)I(t)}{1+\alpha I(t)}-d_4I(t) \end{aligned}$$

(3.5)

Define

$$\begin{aligned} \displaystyle {V_{11}(t)=k_1\left( x_1-x_1^0-x_1^0\ln \frac{x_1}{x_1^0}\right) +x_2-x_2^0-x_2^0\ln \frac{x_2}{x_2^0}+k_2(S+I)}. \end{aligned}$$

where $k_1=r_1x_1^0/(rx_2^0)$, $k_2=a_1/a_2$. Calculating the derivative of $V_{11}(t)$ along positive solutions of system (1.2), it follows that

$$\begin{aligned} \dot{V}_{11}(t)= & {} \displaystyle {\frac{k_1(x_1(t)-x_1^0)}{x_1(t)}\dot{x}_1(t)+\frac{x_2(t)-x_2^0}{x_2(t)} \dot{x}_2(t)+k_2\left( \dot{S}(t)+\dot{I}(t)\right) }\nonumber \\= & {} -\frac{r_1}{x_2^0}\left( \sqrt{\frac{x_2(t)}{x_1(t)}}(x_1(t)-x_1^0) -\sqrt{\frac{x_1(t)}{x_2(t)}}(x_2(t)-x_2^0)\right) ^2\nonumber \\&-\,a(x_2(t)-x_2^0)^2+a_1x_2^0S(t)\nonumber \\&-\,a_1x_2(t)S(t)+a_1x_2(t-\tau )S(t-\tau )\nonumber \\&-\,k_2d_3S(t)-k_2bS^2(t)-k_2d_4I(t). \end{aligned}$$

(3.6)

Define

$$\begin{aligned} \displaystyle {V_{1}(t)=V_{11}(t)+a_1\int _{t-\tau }^tx_2(u)S(u)du}. \end{aligned}$$

By calculation, we have that

$$\begin{aligned} \dot{V}_{1}(t)= & {} \displaystyle {-\frac{r_1}{x_2^0}\left( \sqrt{\frac{x_2(t)}{x_1(t)}}(x_1(t)-x_1^0)-\sqrt{\frac{x_1(t)}{x_2(t)}}(x_2(t)-x_2^0)\right) ^2-a(x_2(t)-x_2^0)^2}\nonumber \\&-\,(k_2d_3-a_1x_2^0)S(t)-k_2bS^2(t)-k_2d_4I(t) \end{aligned}$$

(3.7)

It follows from (3.7) that if $a_2x_2^0<d_3$, i.e. $k_2d_3>a_1x_2^0$ holds, then $\dot{V}_1(t)\le 0$. By Theorem 5.3.1 in [10], solutions limit to $\Lambda$, the largest invariant subset of $\{\dot{V}_0(t)=0\}$. Clearly, we see from (3.7) that $\dot{V}_1(t)=0$ if and only if $x_1(t)=x_1^0, x_2(t)=x_2^0, S(t)=0$ and $I(t)=0$. Hence, the only invariant set $M=\{(x_1^0, x_2^0, 0, 0)\}$. Using LaSalle invariant principle for delay differential systems, the global asymptotic stability of $E_1$ follows. $\square$

The characteristic equation of system (1.2) at the equilibrium $E_2(x_1^+, x_2^+, S^+, 0)$ takes the form

$$\begin{aligned} (\lambda +d_4-\beta S^+)[\lambda ^3+g_2\lambda ^2+g_1\lambda +g_0+(f_2\lambda ^2+f_1\lambda +f_0)e^{-\lambda \tau }]=0, \end{aligned}$$

(3.8)

where

$$\begin{aligned} \begin{array}{l} g_0=ax_2^+(r_1+d_1)(d_3+2bS^+),\;\; \;\;g_1=(d_3+2bS^+)(r_1+d_1+c_1)+ax_2^+(r_1+d_1), \\ g_2=r_1+d_1+c_1+d_3+2bS^+, \;\;\;\;\;\;\;\;\;c_1=d_2+2ax_2^++a_1S^+,\\ f_0=a_2x_2^+[a_1S^+(r_1+d_1)-ax_2^+(r_1+d_1)],\\ \displaystyle {f_1=a_2x_2^+[a_1S^+-(r_1+d_1+c_1)],\;\;\;\;\;\;\;\;f_2=-a_2x_2^+.} \end{array} \end{aligned}$$

Clearly, Eq. (3.8) always has a root $\lambda _1=\beta S^+-d_4$. All other roots of Eq. (3.8) are determined by the following equation

$$\begin{aligned} \lambda ^3+g_2\lambda ^2+g_1\lambda +g_0+(f_2\lambda ^2+f_1\lambda +f_0)e^{-\lambda \tau }=0. \end{aligned}$$

(3.9)

When $\tau =0$, Eq. (3.9) reduces to

$$\begin{aligned} \lambda ^3+(g_2+f_2)\lambda ^2+(g_1+f_1)\lambda +g_0+f_0=0. \end{aligned}$$

(3.10)

By calculation, we derive that

$$\begin{aligned} \begin{array}{l} \Delta _1=g_2+f_2=r_1+d_1+c_1+bS^+>0, \\ \Delta _2=(g_1+f_1)(g_2+f_2)-(g_0+f_0)=bS^+(r_1+d_1+c_1)(r_1+d_1+c_1+bS^+)\\ \;\;\;\;\;\;\;\;\;+\;a_1a_2x_2^+S^+(c_1+bS^+)+ax_2^+(r_1+d_1)(r_1+d_1+c_1)>0,\\ \Delta _3=(g_0+f_0)\Delta _2=x_2^+S^+(r_1+d_1)(ab+a_1a_2)\Delta _2>0. \end{array} \end{aligned}$$

Hence, if $0<\beta S^+<d_4$, then the equilibrium $E_2$ is locally asymptotically stable when $\tau =0$.

If $i\omega (\omega >0)$ is a solution of (3.9), separating real and imaginary parts, we have

$$\begin{aligned} \begin{array}{l} f_1\omega \sin \omega \tau +(f_0-f_2\omega ^2)\cos \omega \tau =g_2\omega ^2-g_0,\\ f_1\omega \cos \omega \tau -(f_0-f_2\omega ^2)\sin \omega \tau =\omega ^3-g_1\omega \end{array} \end{aligned}$$

(3.11)

Squaring and adding the two equations of (3.11), it follows that

$$\begin{aligned} \omega ^6+h_2\omega ^4+h_1\omega ^2+h_0=0. \end{aligned}$$

(3.12)

By calculation, we derive that

$$\begin{aligned} \begin{array}{l} h_2=g_2^2-2g_1-f_2^2=c_1^2+(r_1+d_1)^2+2rr_1+bS^+(2d_3+3bS^+)>0,\\ \displaystyle { h_1=g_1^2-2g_0g_2+2f_0f_2-f_1^2}\\ \displaystyle {\;\;\;\;\;=[ax_2^+(r_1+d_1)]^2+a_1S^+(d_3+bS^+)^2(2d_2+4ax_2^++a_1S^+)>0},\\ \displaystyle {h_0=g_0^2-f_0^2=x_2^+S^+(r_1+d_1)(ab+a_1a_2)(g_0-f_0)} \end{array} \end{aligned}$$

Note that if $g_0>f_0$, equation (3.12) has no positive real roots. Accordingly, by Theorem 3.4.1 in Kuang [14], we see that if $0<\beta S^+<d_4$ and $g_0>f_0$, then $E_2$ is locally asymptotically stable for all $\tau \ge 0.$ If $0<\beta S^+<d_4$ and $g_0<f_0$, then equation (3.12) has a unique positive root $\omega _0$. That is, equation (3.9) has a pair of purely imaginary roots of the form $\pm i\omega _0$. Denote

$$\begin{aligned} \tau _k= & {} \frac{1}{\omega _0}\arccos \frac{f_1\omega _0(\omega _0^3-g_1\omega _0)+(f_0-f_2\omega _0^2)(g_2\omega _0^2-g_0)}{(f_1\omega _0)^2+(f_0-f_2\omega _0^2)^2}\nonumber \\&+\,\frac{2k\pi }{\omega _0},\;k=0,1,2,\cdots . \end{aligned}$$

(3.13)

By Theorem 3.4.1 in Kuang [14], we see that if $0<\beta S^+<d_4$ and $g_0<f_0$, then $E_2$ remains stable for $\tau <\tau _0$.

We now claim that

$\left. \displaystyle {\frac{d(Re(\lambda ))}{d\tau }}\right| _{\tau =\tau _0}>0$

This will show that there exists at least one eigenvalue with positive real part for $\tau >\tau _0$. Moreover, the conditions for the existence of a Hopf bifurcation [10] are then satisfied yielding a periodic solution. To this end, differentiating Eq. (3.9) with respect to $\tau$, it follows that

$$\begin{aligned} \left( \frac{d\lambda }{d\tau }\right) ^{-1}=\displaystyle {\frac{3\lambda ^2+2g_2\lambda +g_1}{-\lambda (\lambda ^3+g_2\lambda ^2+g_1\lambda +g_0)}+ \frac{2f_2\lambda +f_1}{\lambda (f_2\lambda ^2+f_1\lambda +f_0)}-\frac{\tau }{\lambda }}. \end{aligned}$$

Hence, a direct calculation shows that

$$\begin{aligned} \begin{array}{l} \displaystyle {sign\left\{ \frac{d(Re\lambda )}{d\tau }\right\} _{\lambda =i\omega _0}=sign\left\{ Re\left( \frac{d\lambda }{d\tau }\right) ^{-1}\right\} _{\lambda =i\omega _0}}\\ \displaystyle {=sign\left\{ \frac{3\omega _0^4+2(g_2^2-2g_1)\omega _0^2+g_1^2-2g_0g_2}{(\omega _0^3-g_1\omega _0)^2+(g_0-g_2\omega _0^2)^2}+\frac{-2f_2^2\omega _0^2+2f_2f_0-f_1^2}{(f_1\omega _0)^2+(f_2\omega _0^2-f_0)^2}\right\} .}\\ \end{array} \end{aligned}$$

We derive from (3.11) that

$$\begin{aligned} (\omega _0^3-g_1\omega _0)^2+(g_0-g_2\omega _0^2)^2=(f_1\omega _0)^2+(f_2\omega _0^2-f_0)^2 \end{aligned}$$

Hence, it follows that

$$\begin{aligned} sign\left\{ \frac{d(Re\lambda )}{d\tau }\right\} _{\lambda =i\omega _0}=sign\left\{ \frac{3\omega _0^4+2h_2\omega _0^2+h_1}{(f_1\omega _0)^2+(f_2\omega _0^2-f_0)^2}\right\} >0. \end{aligned}$$

Therefore, the transversal condition holds and a Hopf bifurcation occurs at $\omega =\omega _0, \tau =\tau _0$.

In conclusion, we have the following results.

Theorem 3.3

For system (1.2), assume $0<\beta S^+<d_4$ holds, we have the following:

• (i) If $g_0>f_0$, then the disease-free equilibrium $E_2(x_1^+, x_2^+, S^+,0,)$ is locally asymptotically stable for all $\tau \ge 0$;

• (ii) If $g_0<f_0$, then there exists a positive number $\tau _0$, such that $E_2$ is locally asymptotically stable if $0<\tau <\tau _0$ and is unstable if $\tau >\tau _0$. Further, system (1.2) undergoes a Hopf bifurcation at $E_2$ when $\tau =\tau _0$.

Theorem 3.4

Let $0<\beta S^+<d_4$ hold, then the disease-free equilibrium $E_2$ is globally asymptotically stable provided

$(H_2)\;\displaystyle {\underline{x}_2>\frac{a_1}{a}S^+.}$

Here, $\underline{x}_2$ is defined in Theorem 2.1.

Proof

It is easy to see that if $(H_2)$ holds, then $ax_2^+>a_1S^+$. It follows from (3.8) that $g_0-f_0=x_2^+(r_1+d_1)[ad_3+2abS^++a_2(ax_2^+-a_1S^+)]>0$ holds. By Theorem 3.3, we see that if $0<\beta S^+<d_4$ and $(H_1)$ hold, then the equilibrium $E_2(x_1^+. x_2^+, S^+, 0)$ is locally asymptotically stable. Hence, it suffices to show that all positive solutions of system (1.2) with initial conditions (1.3) converge to $E_2$. We achieve this by constructing a global Lyapunov function. Let $(x_1(t), x_2(t), S(t), I(t))$ be any positive solution of system (1.2) with initial conditions (1.3). System (1.2) can be rewritten as

$$\begin{aligned} \begin{array}{l} \displaystyle {\dot{x}_1(t)=\frac{r}{x_1^+}[-x_2(t)(x_1(t)-x_1^+)+x_1(t)(x_2(t)-x_2^+)]}\\ \displaystyle {\dot{x}_2(t)=\frac{r_1}{x_2^+}[-x_1(t)(x_2(t)-x_2^+)+x_2(t)(x_1(t)-x_1^+)]+x_2(t)[-a(x_2(t)-x_2^+)]}\\ \;\;\;\;\;\;\;\;\;\;\;\;\displaystyle {+a_1S^+x_2(t)-a_1x_2(t)S(t)}\\ \displaystyle {\dot{S}(t)=a_2x_2(t-\tau )S(t-\tau )-d_3S(t)-bS^2(t)-\frac{\beta S(t)I(t)}{1+\alpha I(t)}}\\ \displaystyle {\dot{I}(t)=\frac{\beta S(t)I(t)}{1+\alpha I(t)}-d_4I(t)} \end{array} \end{aligned}$$

(3.14)

Define

$$\begin{aligned} V_{21}(t)= & {} k_3\left( x_1-x_1^+-x_1^+\ln \frac{x_1}{x_1^+}\right) +x_2-x_2^+-x_2^+\ln \frac{x_2}{x_2^+}\\&+\,k_4\left( S-S^+-S^+\ln \frac{S}{S^+}\right) +k_4I. \end{aligned}$$

where $k_3=r_1x_1^+/(rx_2^+)$, $k_4=a_1/a_2$.

Calculating the derivative of $V_{21}(t)$ along positive solutions of system (1.2), it follows that

$$\begin{aligned} \begin{array}{l} \displaystyle {\dot{V}_{21}(t)}=\displaystyle {k_3\frac{x_1(t)-x_1^+}{x_1(t)}\dot{x}_1(t)+\frac{x_2(t)-x_2^+}{x_2(t)}\dot{x}_2(t)+k_4\frac{S(t)-S^+}{S(t)}\dot{S}(t)+k_4\dot{I}(t)}\\ \;\;\;\;\;\;\;\;\;\; \displaystyle {=-\frac{r_1}{x_2^+}\left( \sqrt{\frac{x_2(t)}{x_1(t)}}(x_1(t)-x_1^+)-\sqrt{\frac{x_1(t)}{x_2(t)}}(x_2(t)-x_2^+)\right) ^2-a(x_2(t)-x_2^+)^2}\\ \;\;\;\;\;\;\;\;\;\; \;\;\;\;\displaystyle {-a_1x_2(t)S(t)+a_1x_2(t-\tau )S(t-\tau )-k_4\left( d_4-\frac{\beta S^+}{1+\alpha I(t)}\right) I(t)+\;a_1x_2^+S^+}\\ \;\;\;\;\;\;\;\;\;\; \;\;\;\;\displaystyle {-\frac{a_1S^+}{S(t)}x_2(t-\tau )S(t-\tau )+\;a_1S^+(x_2(t)-x_2^+)-\;k_4b(S(t)-S^+)^2} \end{array} \end{aligned}$$

(3.15)

Define

$$\begin{aligned} \begin{array}{l} \displaystyle {V_{2}(t)=V_{21}(t)+a_1\int _{t-\tau }^t\left[ x_2(u)S(u)-x_2^+S^+-x_2^+S^+\ln \frac{x_2(u)S(u)}{x_2^+S^+}\right] du}. \end{array} \end{aligned}$$

By calculation, we have that

$$\begin{aligned}&{\dot{V}_{2}(t)}=\displaystyle {-\frac{r_1}{x_2^+}\left( \sqrt{\frac{x_2(t)}{x_1(t)}}(x_1(t)-x_1^+)-\sqrt{\frac{x_1(t)}{x_2(t)}}(x_2(t)-x_2^+)\right) ^2-k_4b(S(t)-S^+)^2 }\nonumber \\&\quad {-a_1x_2^+S^+\left[ \frac{x_2(t-\tau )S(t-\tau )}{x_2^+S(t)}-1-\ln \frac{x_2(t-\tau )S(t-\tau )}{x_2^+S(t)}\right] }\nonumber \\&\quad {-a_1x_2^+S^+\left[ \frac{x_2^+}{x_2(t)}-1-\ln \frac{x_2^+}{x_2(t)}\right] -k_4(d_4-\frac{\beta S^+}{1+\alpha I(t)})I(t)}\nonumber \\&\quad {-(x_2(t)-x_2^+)^2\left[ a-\frac{a_1S^+}{x_2(t)}\right] } \end{aligned}$$

(3.16)

It follows from (3.16) that if $0<\beta S^+<d_4$ and $(H_1)$ hold true, then $\dot{V}_2(t)\le 0$ with equality if and only if $x_1(t)=x_1^+, x_2(t)=x_2^+, S(t)=S^+, I(t)=0$ Using LaSalle invariant principle for delay differential systems, the global asymptotic stability of the equilibrium $E_2$ of system (1.2) follows. $\square$

4 Coexistence equilibrium and its stability

In this section, we discuss the stability of the coexistence equilibrium.

It is easy to show that if $\beta S^+>d_4$, system (1.2) has a unique coexistence equilibrium $E^*(x_1^*, x_2^*, S^*, I^*)$, where

$$\begin{aligned} x_1^*= & {} \frac{r}{r_1+d_1}x_2^*,\;\;\;\;x_2^*=\frac{rr_1-d_2(r_1+d_1)}{a(r_1+d_1)}-\frac{a_1}{a}S^*,\\ S^*= & {} \frac{1}{2}\Delta +\sqrt{\frac{1}{4}\Delta ^2+\frac{ad_4}{\alpha (ab+a_1a_2)}},\;\;\;\;I^*=\frac{\beta S^*-d_4}{\alpha d_4},\\ \Delta= & {} S^+-\frac{a\beta }{\alpha (ab+a_1a_2)}. \end{aligned}$$

The characteristic equation of system (1.2) at the equilibrium $E^*$ is of the form

$$\begin{aligned} \lambda ^4+p_3\lambda ^3+p_2\lambda ^2+p_1\lambda +p_0+(q_3\lambda ^3+q_2\lambda ^2+q_1\lambda +q_0)e^{-\lambda \tau }=0, \end{aligned}$$

(4.1)

where

$\begin{array}{l} \displaystyle {p_3=r_1+d_1+c_2+c_3+\frac{d_4\alpha I^*}{1+\alpha I^*}},\\ \displaystyle {p_2=\frac{d_4\alpha I^*}{1+\alpha I^*}(r_1+d_1+c_2+c_3)+c_3(r_1+d_1+c_2)+\frac{d_4\beta I^*}{(1+\alpha I^*)^2}+ax_2^*(r_1+d_1)},\\ \displaystyle {p_1=(r_1+d_1+c_2)\left( \frac{c_3d_4\alpha I^*}{1+\alpha I^*}+\frac{d_4\beta I^*}{(1+\alpha I^*)^2}\right) +ax_2^*(r_1+d_1)\left( c_3+\frac{d_4\alpha I^*}{1+\alpha I^*}\right) },\\ \displaystyle {p_0=ax_2^*(r_1+d_1)\left( \frac{c_3d_4\alpha I^*}{1+\alpha I^*}+\frac{d_4\beta I^*}{(1+\alpha I^*)^2}\right) },\\ \displaystyle {q_3=-a_2x_2^*},\;\;\;\;\;\; \displaystyle {q_2=-a_2x_2^*\left( r_1+d_1 +d_2+2ax_2^*+\frac{d_4\alpha I^*}{1+\alpha I^*}\right) },\\ \displaystyle {q_1=-a_2x_2^*\left[ (r_1+d_1+c_2)\frac{d_4\alpha I^*}{1+\alpha I^*}+ax_2^*(r_1+d_1)-a_1S^*(r_1+d_1+\frac{d_4\alpha I^*}{1+\alpha I^*})\right] ,}\\ \displaystyle {q_0=-a_2x_2^*\frac{d_4\alpha I^*}{1+\alpha I^*}[ax_2^*(r_1+d_1)-a_1S^*(r_1+d_1)],}\\ \displaystyle {c_2=d_2+2ax_2^*+a_1S^*, c_3=a_2x_2^*+bS^*}. \end{array}$

When $\tau =0$, Eq. (4.1) becomes

$$\begin{aligned} \lambda ^4+(p_3+q_3)\lambda ^3+(p_2+q_2)\lambda ^2+(p_1+q_1)\lambda +p_0+q_0=0. \end{aligned}$$

(4.2)

It is easy to show that

$$\begin{aligned} \triangle _1= & {} p_3+q_3=r_1+d_1+c_2+bS^*+\frac{d_4\alpha I^*}{1+\alpha I^*}>0,\\ \triangle _2= & {} (p_3+q_3)(p_2+q_2)-(p_1+q_1)\\= & {} ax_2^*(r_1+d_1)(r_1+d_1+c_2)+a_1a_2x_2^*S^*(c_2+bS^*)\\&+\,bS^*(r_1+d_1+c_2+bS^*)\left( r_1+d_1+c_2+\frac{d_4\alpha I^*}{1+\alpha I^*}\right) \\&+\,\frac{d_4\beta I^*}{(1+\alpha I^*)^2}\left( bS^*+\frac{d_4\alpha I^*}{1+\alpha I^*}\right) \\&\frac{d_4\alpha I^*}{1+\alpha I^*}(r_1+d_1+c_2)\left( r_1+d_1+c_2+bS^*+\frac{d_4\alpha I^*}{1+\alpha I^*}\right) >0,\\ \triangle _3= & {} (p_1+q_1)\triangle _2-(p_0+q_0)(p_3+q_3)^2 \\ \triangle _4= & {} (p_0+q_0)\triangle _3 \end{aligned}$$

Note $p_0+q_0>0$, hence, if $\triangle _3>0$, we have $\triangle _4>0$. By the Routh-Hurwitz criterion, we know that if $\beta S^+>d_4$ and $\triangle _3>0$ hold, the coexistence equilibrium $E^*$ of system (1.2) is locally asymptotically stable when $\tau =0$.

Substituting $\lambda =i\nu (\nu >0)$ into (4.1) and separating the real and imaginary parts, one obtains that

$$\begin{aligned} \begin{array}{l} (q_3\nu ^3-q_1\nu )\sin \nu \tau +(q_2\nu ^2-q_0)\cos \nu \tau =\nu ^4-p_2\nu ^2+p_0,\\ (q_3\nu ^3-q_1\nu )\cos \nu \tau -(q_2\nu ^2-q_0)\sin \nu \tau =p_1\nu -p_3\nu ^3. \end{array} \end{aligned}$$

(4.3)

Squaring and adding the two equations of (4.3), it follows that

$$\begin{aligned} \nu ^8+\hat{h}_3\nu ^6+\hat{h}_2\nu ^4+\hat{h}_1\nu ^2+\hat{h}_0=0, \end{aligned}$$

(4.4)

where

$$\begin{aligned} \begin{array}{l} \hat{h}_3=p_3^2-2p_2-q_3^2,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \hat{h}_2=p_2^2+2p_0-2p_1p_3-q_2^2+2q_1q_3,\\ \hat{h}_1=p_1^2-2p_0p_2-q_1^2+2q_0q_2,\;\;\;\;\;\;\hat{h}_0=p_0^2-q_0^2. \end{array} \end{aligned}$$

Letting $z=\nu ^2$, Eq. (4.4) can be written as

$$\begin{aligned} \hat{h}(z):=z^4+\hat{h}_3z^3+\hat{h}_2z^2+\hat{h}_1z+\hat{h}_0=0. \end{aligned}$$

(4.5)

If $\hat{h}_i>0(i=0,1,2,3)$, then $\hat{h}(z)$ has always no positive roots. Hence, under these conditions, Eq. (4.4) has no purely imaginary roots for any $\tau >0$ and accordingly, the equilibrium $E^*$ is locally asymptotically stable for all $\tau \ge 0$.

If $\hat{h}_i>0(i=1,2,3)$ and $\hat{h}_0<0$, then Eq. (4.5) has one positive root $z^*$. Accordingly, Eq. (4.4) has one positive roots $\nu _0=\sqrt{z^*}$. From (4.3) one can get the corresponding $\tau ^{(j)}>0$ such that (4.1) has a pair of purely imaginary roots $\pm i\nu _0$ given by

$$\begin{aligned} \tau ^{(j)}= & {} \frac{1}{\nu _0}\arccos \frac{(q_2\nu _0^2-q_0)(\nu _0^4-p_2\nu _0^2+p_0)+(q_3\nu _0^3-q_1\nu _0)(p_1\nu _0-p_3\nu _0^3)}{(q_2\nu _0^2-q_0)^2+(q_3\nu _0^3-q_1\nu _0)^2}+\frac{2j\pi }{\nu _0},\\ j= & {} 0,1,2,\cdots \end{aligned}$$

Differentiating the two sides of (4.1) with respect to $\tau$, it follows that

$$\begin{aligned} \left( \frac{d\lambda }{d\tau }\right) ^{-1}=\displaystyle {\frac{4\lambda ^3+3p_3\lambda ^2+2p_2\lambda +p_1}{-\lambda (\lambda ^4+p_3\lambda ^3+p_2\lambda ^2+p_1\lambda +p_0)}+ \frac{3q_3\lambda ^2+2q_2\lambda +q_1}{\lambda (q_3\lambda ^3+q_2\lambda ^2+q_1\lambda +q_0)}-\frac{\tau }{\lambda }}. \end{aligned}$$

After some algebra, one obtains that

$$\begin{aligned}&sign\left\{ \frac{dRe\lambda }{d\tau }\right\} _{\tau =\tau ^{(j)}}=sign\left\{ Re\left( \frac{d\lambda }{d\tau }\right) ^{-1}\right\} _{\tau =\tau ^{(j)}}\\&\quad =sign\left\{ -\frac{(p_1-3p_3\nu _0^2)(p_3\nu _0^2-p_1)+2(p_2-2\nu _0^2)(\nu _0^4-p_2\nu _0^2+p_0)}{\nu _0^2(p_1-p_3\nu _0^2)^2 +(\nu _0^4-p_2\nu _0^2+p_0)^2}\right. \\&\qquad \left. +\frac{(q_1-3q_3\nu _0^2)(q_3\nu _0^2-q_1)+2q_2\nu _0(q_0-q_2\nu _0^2)}{(q_0-q_2\nu _0^2)^2+(q_1\nu _0-q_3\nu _0^3)^2}\right\} \\ \end{aligned}$$

We derive from (4.3) that

$\nu _0^2(p_1-p_3\nu _0^2)^2+(\nu _0^4-p_2\nu _0^2+p_0)^2=(q_0-q_2\nu _0^2)^2+(q_1\nu _0-q_3\nu _0^3)^2.$ Hence, it follows that

$\begin{array}{l} \displaystyle {sign\left\{ \frac{dRe\lambda }{d\tau }\right\} _{\tau =\tau ^{(j)}}=sign\left\{ \frac{4\nu _0^6+3\hat{h}_3\nu _0^4+2\hat{h}_2\nu _0^2+\hat{h}_1}{(q_2\nu _0^2-q_0)^2+(q_1\nu _0-q_3\nu _0^3)^2}\right\} >0}\\ \end{array}$

From what has been discussed above, we have the following results.

Theorem 4.1

Assume that $\beta S^+>d_4$ and $\triangle _3>0$ hold, we have

• (i) If $\hat{h}_i>0(i=0,1,2,3)$, then the coexistence equilibrium $E^*$ is locally asymptotically stable for all $\tau \ge 0$.

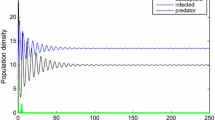
• (ii) If $\hat{h}_i>0(i=1,2,3)$ and $\hat{h}_0<0$, then there exists a positive number $\tau ^{(0)}$, such that $E^*$ is locally asymptotically stable if $0<\tau <\tau ^{(0)}$ and is unstable if $\tau >\tau ^{(0)}$. Further, system (1.2) undergoes a Hopf bifurcation at $E_2$ when $\tau =\tau ^{(0)}$.

Now, we are concerned with the global attractiveness of the coexistence equilibrium $E^*$.

Theorem 4.2

Assume that $\beta S^+>d_4$, then the coexistence equilibrium $E^*(x_1^*, x_2^*, S^*, I^*)$ of system (1.2) is globally attractive provided

$(H_3)\;\displaystyle {\underline{x}_2>\frac{a_1}{a}S^*,\;\;\underline{I}>[\alpha \beta (I^*)^2-4bS^*(1+\alpha I^*)]/[4\alpha bS^*(1+\alpha I^*)]}$ Here, $\underline{x}_2$ and $\underline{I}$ are defined in Theorem 2.1.

Proof

Let $(x_1(t), x_2(t), S(t), I(t))$ be any positive solution of system (1.2) with initial conditions (1.3). System (1.2) can be rewritten as

$$\begin{aligned} \dot{x}_1(t)= & {} \frac{r}{x_1^*}[-x_2(t)(x_1(t)-x_1^*)+x_1(t)(x_2(t)-x_2^*)]\nonumber \\ \dot{x}_2(t)= & {} \frac{r_1}{x_2^*}[-x_1(t)(x_2(t)-x_2^*)+x_2(t)(x_1(t)-x_1^*)]\nonumber \\&+\,x_2(t)[-a(x_2(t)-x_2^*)]+a_1S^*x_2(t)-a_1x_2(t)S(t)\nonumber \\ \dot{S}(t)= & {} a_2x_2(t-\tau )S(t-\tau )-d_3S(t)-bS^2(t)-\frac{\beta S(t)I(t)}{1+\alpha I(t)}\nonumber \\ \dot{I}(t)= & {} \frac{\beta S(t)I(t)}{1+\alpha I(t)}-d_4I(t) \end{aligned}$$

(4.6)

Define

$$\begin{aligned} V_{31}(t)= & {} k_5\left( x_1-x_1^*-x_1^*\ln \frac{x_1}{x_1^*}\right) +x_2-x_2^*-x_2^*\ln \frac{x_2}{x_2^*}+k_6\left( S-S^*-S^*\ln \frac{S}{S^*}\right) \\&+\,k_6\left( I-I^*-I^*\ln \frac{I}{I^*}\right) . \end{aligned}$$

where $k_5=r_1x_1^*/(rx_2^*), k_6=a_1/a_2$.

Calculating the derivative of $V_{31}(t)$ along positive solutions of system (1.2), it follows that

$$\begin{aligned} \displaystyle {\dot{V}_{31}(t)}= & {} \displaystyle {k_5\frac{x_1(t)-x_1^*}{x_1(t)}\dot{x}_1(t)+\frac{x_2(t)-x_2^*}{x_2(t)}\dot{x}_2(t)+k_6\frac{S(t)-S^*}{S(t)}\dot{S}(t)+k_6\frac{I(t)-I^*}{I(t)}\dot{I}(t)}\nonumber \\= & {} -\frac{r_1}{x_2^*}\left( \sqrt{\frac{x_2(t)}{x_1(t)}}(x_1(t)-x_1^*)-\sqrt{\frac{x_1(t)}{x_2(t)}}(x_2(t)-x_2^*)\right) ^2-a(x_2(t)-x_2^*)^2\nonumber \\&+\,a_1S^*(x_2(t)-x_2^*)-a_1(x_2(t)-x_2^*)S(t)+a_1 x_2(t-\tau )S(t-\tau )\frac{S(t)-S^*}{S(t)}\nonumber \\&-\,k_6d_3(S(t)-S^*)-k_6bS(t)(S(t)-S^*)-\frac{k_6\beta I(t)(S(t)-S^*) }{1+\alpha I(t)}\nonumber \\&+\frac{k_6\beta S(t)(I(t)-I^*)}{1+\alpha I(t)}-k_6d_4(I(t)-I^*) \end{aligned}$$

(4.7)

Define

$$\begin{aligned} \begin{array}{l} \displaystyle {V_{3}(t)=V_{31}(t)+a_1\int _{t-\tau }^t\left[ x_2(u)S(u)-x_2^*S^*-x_2^*S^*\ln \frac{x_2(u)S(u)}{x_2^*S^*}\right] du}. \end{array} \end{aligned}$$

By calculation, we have that

$$\begin{aligned} \dot{V}_{3}(t)= & {} \displaystyle {-\frac{r_1}{x_2^*}\left( \sqrt{\frac{x_2(t)}{x_1(t)}}(x_1(t)-x_1^*)-\sqrt{\frac{x_1(t)}{x_2(t)}}(x_2(t)-x_2^*)\right) ^2}\nonumber \\&\displaystyle {-a_1x_2^*S^*\left[ \frac{x_2(t-\tau )S(t-\tau )}{x_2^*S(t)}-1-\ln \frac{x_2(t-\tau )S(t-\tau )}{x_2^*S(t)}\right] }\nonumber \\&\displaystyle {-a_1x_2^*S^*\left[ \frac{x_2^*}{x_2(t)}-1-\ln \frac{x_2^*}{x_2(t)}\right] -\frac{k_6\alpha \beta S^*}{(1+\alpha I^*)(1+\alpha I(t))}}\nonumber \\&\left[ (I(t)- I^*)-\frac{I^*(S(t)-S^*)}{2S^*}\right] ^2-(x_2(t)-x_2^*)^2\left( a-\frac{a_1S^*}{x_2(t)}\right) \nonumber \\&\displaystyle {-k_6(S(t)-S^*)^2\left[ b-\frac{\alpha \beta (I^*)^2}{4S^*(1+\alpha I^*)}\cdot \frac{1}{1+\alpha I(t)}\right] } \end{aligned}$$

(4.8)

Note that the function $g(x)=x-1-\ln x$ is always non-negative for any $x>0$, and $g(x)=0$ if and only if $x=1$. Hence, if $x_2(t)>a_1S^*/a$ and $I(t)>[\alpha \beta (I^*)^2-4bS^*(1+\alpha I^*)]/[4\alpha bS^*(1+\alpha I^*)]$ for $t\ge T$, we have $-(x_2(t)-x_2^*)^2\left[ a-\frac{a_1S^*}{x_2(t)}\right] \le 0$ and $-k_6(S(t)-S^*)^2\left[ b-\frac{\alpha \beta (I^*)^2}{4S^*(1+\alpha I^*)}\cdot \frac{1}{1+\alpha I(t)}\right] \le 0$ with equality if and only if $x_2(t)=x_2^*$ and $S(t)=S^*$. This, together with (4.8), implies that if $(H_3)$ holds, then $\dot{V}_{3}(t)\le 0$ with equality if and only if $x_1(t)=x_1^*, x_2(t)=x_2^*, S(t)=S^*$ and $I(t)=I^*$. Therefore, the global attractiveness of $E^*$ follows from LaSalle invariant principle for delay differential systems. This completes the proof. $\square$

5 Conclusion

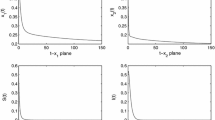
In this paper, we have incorporated a stage structure for the prey and time delay due to the gestation of the predator into an eco-epidemiological model. By analyzing the corresponding characteristic equations, the local stability of each of feasible equilibria of system (1.2) has been established, respectively. It has been shown that, under some conditions, the time delay may destabilize both the disease-free equilibrium and the coexistence equilibrium of the eco-epidemiological system and cause the population to fluctuate. By means of Lyapunov functions and LaSalle invariant principle, sufficient conditions were obtained for the global asymptotic stability of each of feasible equilibria of system (1.2), respectively. By Theorem 3.1, we see that if $rr_1<d_2(r_1+d_1)$, then both the prey population and the predator population go to extinction. By Theorem 3.2, we see that if $0<a_2x_2^0<d_3$ holds, the prey population persists and the predator population goes to extinction. By Theorem 3.4, we see that if $0<\beta S^+<d_4$ and $\underline{x}_2>a_1S^+/a$ hold, that is the disease transmission coefficient $\beta$ is sufficiently small and the prey population is always abundant enough, the disease among the predator population dies out and in this case, the prey and the sound predator coexist. By Theorem 4.2, we see that if $\beta S^+>d_4$ and $(H_3)$ hold, that is the prey population is always abundant enough and the disease transmission coefficient $\beta$ is sufficiently large, the coefficient equilibrium is a global attractor of the system (1.2). In this case, the disease spreading in the predator becomes endemic and the prey, sound predator and the infected predator coexist.