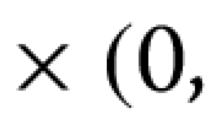Galerkin finite element schemes with fractional Crank–Nicolson method for the coupled time-fractional nonlinear diffusion system

Abstract

This paper deals with two fractional Crank–Nicolson–Galerkin finite element schemes for coupled time-fractional nonlinear diffusion system. The first scheme is iterative and is based on Newton’s method, while the other one is a linearized scheme. Existence-uniqueness results of the fully discrete solution for both schemes are discussed. In addition, a priori bounds and a priori error estimates are derived for proposed schemes using a new discrete fractional Grönwall-type inequality. Both the schemes yield $O({\varDelta } t^2)$ accuracy in time and hence, superior to $O({\varDelta } t^{2-\alpha })$ accurate L1 scheme existing in the literature. Moreover, three different numerical examples are provided to illustrate the theoretical estimates .

1 Introduction

Time-fractional parabolic partial differential equations (TFPDEs) model many real-world problems like anomalous diffusion in the transport process, entropy, hydrology, and single-molecular protein dynamics (Dumitru et al. 2012; Hajipour et al. 2019; Jin et al. 2018; Kou 2008). In this paper, we consider the following coupled time-fractional nonlinear diffusion system with unknowns u and v.

Find $(u,v)=(u(x,t),v(x,t)),$ $x\in {\varOmega }$ and $t>0$, such that

$$\begin{aligned} ^C{D}^{\alpha }_{t}u-{\varDelta }{u}&= F_{1}(u,v) \quad \text{ in } \quad {\varOmega }\times (0,T], \end{aligned}$$

(1a)

$$\begin{aligned} ^C{D}^{\alpha }_{t}v-{\varDelta }{v}&= F_{2}(u,v) \quad \text{ in }\quad {\varOmega }\times (0,T], \end{aligned}$$

(1b)

$$\begin{aligned} u(x,t)&=v(x,t)=0 \quad \text{ on }\quad \partial {{\varOmega }}\times (0,T], \end{aligned}$$

(1c)

$$\begin{aligned} u(x,0)&=0, \quad v(x,0)=0 \quad \text{ in } \quad {\varOmega }, \end{aligned}$$

(1d)

where ${{\varOmega }}$ is a bounded domain in ${\mathbb {R}}^d$ $(d=1,2,3)$ with smooth boundary $\partial {\varOmega }$, T is a positive constant, and $F_{1}(u,v),$ $F_{2}(u,v)$ are forcing terms. The following hypotheses are made throughout the paper on forcing terms $F_1,\ F_2.$

$H1: F_{i}:{\mathbb {R}}^2 \rightarrow {\mathbb {R}}$ is Lipschitz continuous with $|F_i(u_1,v_1)-F_i(u_2,v_2)|\le L_i\big ( |u_1-u_2|+|v_1-v_2|\big )$ for $u_1,$ $v_1,$ $u_2,$ $v_2$ $\in {\mathbb {R}},$ and $L_i>0$, $i=1,2.$

$H2: F_{i}\in C^2({\mathbb {R}}^2)$ for $i=1,2.$

Here, $^C{D}^{\alpha }_{t}\varphi$ denotes the $\alpha ^{th}$ order $(0<\alpha < 1)$ Caputo fractional derivative of the function $\varphi (t)$ and it is defined as: (Kilbas et al. 2006):

$$\begin{aligned} \begin{aligned} ^{C}{D}^{\alpha }_{t}\varphi (t):=\frac{1}{{\varGamma }(1-\alpha )}\int _{0}^{t}(t-s)^{-\alpha }\frac{\partial \varphi (s)}{\partial s}\mathrm{d}s,\\ \end{aligned} \end{aligned}$$

where ${\varGamma }(\cdot )$ denotes the Gamma function.

The following relation can be utilized to express Caputo fractional derivatives in terms of Riemann–Liouville fractional derivatives: (Kilbas et al. 2006)

$$\begin{aligned} ^CD^{\alpha }_{t}\varphi (t)=\ ^RD^{\alpha }_{t}\big (\varphi (t)-\varphi (0)\big ), \end{aligned}$$

(2)

where the Riemann–Liouville fractional derivative $^RD^{\alpha }_{t}\varphi$ is defined as:

$$\begin{aligned} ^RD^{\alpha }_{t}\varphi (t) :=\frac{1}{{\varGamma }(1-\alpha )}\frac{\mathrm{d}}{\mathrm{d}t}\int _{0}^{t}(t-s)^{-\alpha }\varphi (s)\mathrm{d}s. \end{aligned}$$

Note that when $\varphi (0)=0$, Caputo and Riemann–Liouville fractional derivatives coincide. Therefore, based on the relation (2), we can also express (1a)–(1d) in terms of Riemann–Liouville fractional derivative.

The above coupled time-fractional nonlinear diffusion system (1a)–(1d) can be considered as an extension of the scalar time-fractional nonlinear diffusion equation studied by Jin et al. (2018), Li et al. (2018),Liao et al. (2019), and Liao et al. (2018). Consequently, this problem can be employed to describe several natural phenomena in engineering, biology, and physics (Kilbas et al. 2006; Li et al. 2015; Podlubny 1999; West 2007).

There are various papers in the literature which focus on problems involving more than one unknown function. Sun et al. (2017) and Li et al. (2018) solved the classical coupled nonlinear Schrödinger system and space-fractional coupled nonlinear Schrödinger system, respectively, with different numerical techniques. Recently, the nonlocal coupled parabolic problem was studied by applying classical Crank–Nicolson method in temporal direction and finite element method (FEM) in the spatial direction (Chaudhary 2018).

The fractional Crank–Nicolson method was first time developed by Dimitrov (2014) for solving time-fractional diffusion equation. This method is popular for recovering $O({\varDelta } t^2)$ accuracy in time. Moreover, Gao et al. (2015) applied this method to address other time-fractional diffusion equations. Furthermore, Wang et al. (2016) solved nonlinear fractional cable equation using fractional Crank–Nicolson–Galerkin FEM. Later on, Jin et al. (2017) analyzed this method and obtained $O({\varDelta } t^2)$ accuracy in time for subdiffusion equation in case of both smooth and nonsmooth problem data.

Li et al. (2018) solved nonlinear TFPDEs by L1-Galerkin FEM. Subsequently, Jin et al. (2018) considered the same nonlinear problem and proved the existence-uniqueness and regularity of solution at continuous as well as discrete levels. Moreover, they utilized the L1 method and backward Euler convolution quadrature with FEM to solve the problem. In these two works, error analysis is done in terms of newly developed fractional Grönwall-type inequality. It is well known that, for a sufficiently smooth solution, the L1 scheme is $O({\varDelta } t^{2-\alpha })$ accurate (Lin and Xu 2007) and backward Euler convolution quadrature [Gr$\ddot{\mathrm {u}}$nwald–Letnikov (GL) approximation] is $O({\varDelta } t)$ accurate (Podlubny 1999). To recover $O({\varDelta } t^2)$ accuracy, Kumar et al. (2018) have solved nonlinear TFPDEs using fractional Crank–Nicolson–Galerkin FEM. Furthermore, for error analysis, they also established a new discrete fractional Grönwall-type inequality for backward Euler convolution quadrature.

Motivated by the above-mentioned literature, we solve coupled time-fractional nonlinear diffusion system by two different fully discrete schemes. The first scheme is based on Newton’s method (iterative) and the second scheme is a linearized scheme (noniterative). To the best of our knowledge, this is the first attempt to consider Galerkin finite element schemes with fractional Crank–Nicolson method for solving the coupled time-fractional diffusion system. We study the well-posedness results for iterative and noniterative schemes in detail. To obtain a priori bound and a priori error estimate for the iterative scheme, we use discrete fractional Grönwall inequality developed by Kumar et al. (2018). Furthermore, we generalize the discrete fractional Grönwall inequality (Kumar et al. 2018) to derive these estimates for the linearized scheme. The generalized Grönwall inequality in this paper can be utilized in the analysis of other linearized schemes based on backward Euler convolution quadrature.

The rest of the paper is organized as follows. Section 2 presents the fractional Crank–Nicolson–Galerkin finite element scheme based on Newton’s method and discuss its well-posedness results and an error estimate. In Sect. 3, we propose another linearized Crank–Nicolson–Galerkin finite element scheme for solving the problem (1a)–(1d). Existence-uniqueness results are studied, and a priori bound, convergence estimate are derived in terms of new discrete fractional Grönwall inequality. Section 4 demonstrates the performance of the given schemes through three numerical examples. Section 5 concludes the paper.

Throughout the paper, $C>0$ denotes a generic constant which can take different values at different occurrences, but is independent of step size h and ${\varDelta } t.$

2 Fractional Crank–Nicolson–Galerkin finite element scheme based on Newton’s method

Let ${\mathcal {T}}_h$ be a quasi-uniform shape regular triangulation of domain ${\varOmega }$. In addition, let $X_h$ be the finite-dimensional subspace of $H^{1}_{0}({\varOmega })$ consisting of continuous functions on closure $\bar{{\varOmega }}$ of ${\varOmega }$ which are linear in each triangle ${T}_k\in {\mathcal {T}}_h$ and vanish on $\partial {\varOmega },$ that is:

$$\begin{aligned} X_h:=\{v\in C(\bar{{\varOmega }}): v_{|T_{k}} \ \text {is a linear polynomial} \ \forall \ T_{k}\in {\mathcal {T}}_{h}, \ \text{ and } \ v_{|{\partial {\varOmega }}}=0 \}. \end{aligned}$$

Let $\{P_i\}_{i=1}^{M}$ be the interior vertices of ${\mathcal {T}}_h$ and $\phi _i(x)$ be the pyramid function in $X_h$ which takes the value 1 at each interior vertex but vanishes at other vertices. Then, $\{\phi _i(x)\}_{i=1}^{M}$ form a basis for the space $X_h.$ Furthermore, assume that $0=t_0<t_1<t_2\ldots <t_N=T$ be a given partition of time interval [0, T] with step length ${\varDelta } t=\frac{T}{N}$ for some positive integer N.

Based on the discussion in Gao et al. (2015), the following second-order approximation to the Riemann–Liouville fractional derivative at point $(t_n-\frac{\alpha {\varDelta } t}{2})$ holds:

$$\begin{aligned} ^RD^{\alpha }_{{\varDelta } t}\varphi (t_n)= \ ^RD^{\alpha }_{t_{n-\frac{\alpha }{2}}}\varphi (t)+O \left( {\varDelta } t^2 \right) , \end{aligned}$$

(3)

where $^RD^{\alpha }_{{\varDelta } t}$ is the discrete fractional differential operator defined as

$$\begin{aligned} ^RD^{\alpha }_{{\varDelta } t} \ \varphi (t_n):={{\varDelta } t}^{-\alpha }\sum _{i=0}^{n} w^{(\alpha )}_{n-i} \ \varphi (t_i), \end{aligned}$$

(4)

and the weights $w^{(\alpha )}_i$ are given by $w^{(\alpha )}_i=(-1)^i\frac{{\varGamma }(\alpha +1)}{{\varGamma }(i+1){\varGamma }(\alpha -i+1)}.$ More details about applications of the approximation (3) can be found in Gao et al. (2015), Kumar et al. (2018), Liu et al. (2018), and Wang et al. (2016).

Remark 1

The approximation (3) gives $O({\varDelta } t^2)$ convergence order under the following regularity assumption and certain compatibility conditions (Gao et al. 2015) on the function $\varphi$:

$$\begin{aligned} \varphi \in C^3[0,T], \ \ \text{ and } \ \ \varphi (0)=0, \ \varphi _t(0)=0, \ \ \varphi _{tt}(0)=0. \end{aligned}$$

(5)

In general, for smooth problem data, the exact solution of time-fractional partial differential equations may be weakly singular near $t=0$. Therefore, straightforward implementation (without regularity assumption and compatibility conditions) of schemes based on approximation (3) provides $O({\varDelta } t)$ accuracy (Jin et al. 2017). In this work, we obtain $O({\varDelta } t^2)$ accuracy in time under the regularity assumption and compatibility conditions given in (5) on the solution (u, v) of the problem (1a)–(1d).

With the above approximation (3) to the Riemann–Liouville fractional derivative in time and standard Galerkin FEM in space, we present fully discrete fractional Crank–Nicolson–Galerkin finite element scheme to approximate the solution $(u(t_n),v(t_n))$ of problem (1a)–(1d) by $(U_h^n,V_h^n),$ $n=1,2,3,\ldots ,N$. For convenience, we set $U_h^{n,\alpha }=(1-\frac{\alpha }{2})U_h^{n}+\frac{\alpha }{2}U_h^{n-1}$ and $V_h^{n,\alpha }=(1-\frac{\alpha }{2})V_h^{n}+\frac{\alpha }{2}V_h^{n-1},$ then the fractional Crank–Nicolson finite element scheme is used to seek $U_h^{n},\ V_h^{n}\in X_h$, such that

$$\begin{aligned} \begin{aligned} \langle ^RD^{\alpha }_{{\varDelta } t}U_h^{n}, w_{h}\rangle +\langle \nabla U_h^{n,\alpha }, \nabla w_{h}\rangle&=\langle F_{1}(U_h^{n,\alpha },V_h^{n,\alpha }), w_{h}\rangle ,\quad \forall w_{h}\in X_{h},\\ \langle ^RD^{\alpha }_{{\varDelta } t}V_h^{n}, \omega _{h}\rangle +\langle \nabla V_h^{n,\alpha }, \nabla \omega _{h}\rangle&=\langle F_{2}(U_h^{n,\alpha },V_h^{n,\alpha }), \omega _{h}\rangle ,\quad \forall \omega _{h}\in X_h,\\ U_h^0&=0,\ V_h^0=0.\\ \end{aligned} \end{aligned}$$

(6)

Observe that, for $\alpha =1,$ scheme (6) recovers the classical Crank–Nicolson scheme for the coupled diffusion system. Thus, fractional Crank–Nicolson scheme can be seen as an extension of classical Crank–Nicolson scheme for TFPDEs.

The discrete fractional operator $^RD^{\alpha }_{{\varDelta } t}$ can be employed to re-write scheme (6) as follows:

$$\begin{aligned} \begin{aligned} {{\varDelta } t^{-\alpha }}w_0^{(\alpha )}\langle U_h^{n},w_h\rangle +\langle \nabla U_h^{n,\alpha }, \nabla w_{h}\rangle&=\langle F_{1}(U_h^{n,\alpha },V_h^{n,\alpha }), w_{h}\rangle -{{\varDelta } t^{-\alpha }}\sum _{j=1}^{n-1}w_{n-j}^{(\alpha )}\langle U_h^{j},w_h\rangle ,\\ {{\varDelta } t^{-\alpha }}w_0^{(\alpha )} \langle V_h^{n},\omega _h\rangle +\langle \nabla V_h^{n,\alpha }, \nabla \omega _{h}\rangle&=\langle F_{2}(U_h^{n,\alpha },V_h^{n,\alpha }), \omega _{h}\rangle -{{\varDelta } t^{-\alpha }}\sum _{j=1}^{n-1}w_{n-j}^{(\alpha )}\langle V_h^{j},\omega _h\rangle .\\ \end{aligned} \end{aligned}$$

(7)

The fully discrete formulation (6) (or (7)) provides us a system of nonlinear equations. There are several iterative techniques to deal with the above system of nonlinear equations. In particular, we use Newton’s method to solve the system (6) (or (7)). With the help of M-dimensional basis of $X_h$, $\{\phi _i \}_{1\le i\le M},$ associated with nodes of ${\mathcal {T}}_h$, we can write solution $(U_h^n,V_h^n)$ of (6) [or (7)] as

$$\begin{aligned} U_h^n=\sum _{i=1}^{M}\beta _{i}^n\phi _i,\quad V_h^n=\sum _{i=1}^{M}\gamma _{i}^n\phi _i, \quad \text{ for } \ \beta _{i}^n, \gamma _{i}^n\in {\mathbb {R}}. \end{aligned}$$

(8)

Define $\varvec{\beta ^n}$ := $[\beta _1^n, \beta _2^n,\ldots ,\beta _M^n]^{\prime }$ and $\varvec{\gamma ^n}$ := $[\gamma _1^n, \gamma _2^n,\ldots ,\gamma _M^n]^{\prime }$.

Using the value of $U_h^n,\ V_h^n$ from (8) into (7), we get the following nonlinear algebraic equations:

$$\begin{aligned} \begin{aligned} H_{1i}(\varvec{\beta ^n}, \varvec{\gamma ^n})&= H_{1i}(U_h^n, V_h^n)=0,\quad 1\le i\le M,\\ H_{2i}(\varvec{\beta ^n}, \varvec{\gamma ^n})&= H_{2i}(U_h^n, V_h^n)=0,\quad 1\le i\le M,\\ \end{aligned} \end{aligned}$$

(9)

where

$$\begin{aligned} \begin{aligned} H_{1i}(U_h^n, V_h^n)&={{\varDelta } t^{-\alpha }}w_0^{(\alpha )}\langle U_h^{n},\phi _i\rangle +\langle \nabla U_h^{n,\alpha }, \nabla \phi _i\rangle -\langle F_{1}(U_h^{n,\alpha },V_h^{n,\alpha }), \phi _i\rangle \\&\quad +{{\varDelta } t^{-\alpha }}\sum _{j=1}^{n-1}w_{n-j}^{(\alpha )}\langle U_h^{j},\phi _i\rangle ,\\ H_{2i}( U_h^n, V_h^n)&={{\varDelta } t^{-\alpha }}w_0^{(\alpha )}\langle V_h^{n},\phi _i\rangle +\langle \nabla V_h^{n,\alpha }, \nabla \phi _i\rangle -\langle F_{2}(U_h^{n,\alpha },V_h^{n,\alpha }), \phi _i\rangle \\&\quad +{{\varDelta } t^{-\alpha }}\sum _{j=1}^{n-1}w_{n-j}^{(\alpha )}\langle V_h^{j},\phi _i\rangle .\\ \end{aligned} \end{aligned}$$

(10)

Utilizing Newton’s method in (9), the following matrix system is obtained for the correction term:

$$\begin{aligned} \begin{aligned} J \left[ \begin{array}{c} \varvec{\beta ^n} \\ \varvec{\gamma ^n} \end{array} \right] =\left[ \begin{array}{cc} A1 &{} \quad B1 \\ C1 &{} \quad D1 \end{array} \right] \left[ \begin{array}{c} \varvec{\beta ^n} \\ \varvec{\gamma ^n} \end{array} \right] =\left[ \begin{array}{c} \varvec{H_1} \\ \varvec{H_2} \end{array} \right] , \end{aligned} \end{aligned}$$

(11)

where $\varvec{H_1}=[H_{11}, H_{12},\ldots ,H_{1M}]^{\prime },$ $\varvec{H_2}=[H_{21}, H_{22},\ldots ,H_{2M}]^{\prime }$ and entries of $A1=A1_{(M\times M)},$ $B1=B1_{(M\times M)},$ $C1=C1_{(M\times M)},$ $D1=D1_{(M\times M)}$ are given by the following:

$$\begin{aligned} \begin{aligned} (A1)_{li}&=\frac{\partial H_{1i}(U_h^n, V_h^n)}{\partial \beta _{l}^{n}}={{\varDelta } t^{-\alpha }}w_0^{(\alpha )}\langle \phi _l,\phi _i\rangle +\Big (1-\frac{\alpha }{2}\Big )\langle \nabla \phi _l , \nabla \phi _i\rangle \\&\quad -\Big (1-\frac{\alpha }{2}\Big )\Big \langle \frac{\partial F_{1}(U_h^{n,\alpha },V_h^{n,\alpha })}{\partial U^{n}_{h}}\phi _l, \phi _i\Big \rangle ,\\ (B1)_{li}&=\frac{\partial H_{1i}(U_h^n, V_h^n)}{\partial \gamma _{l}^{n}}=-\Big (1-\frac{\alpha }{2}\Big )\Big \langle \frac{\partial F_{1}(U_h^{n,\alpha },V_h^{n,\alpha })}{\partial V^{n}_{h}}\phi _l, \phi _i\Big \rangle ,\\ (C1)_{pi}&=\frac{\partial H_{2i}(U_h^n, V_h^n)}{\partial \beta _{p}^{n}}=-\Big (1-\frac{\alpha }{2}\Big )\Big \langle \frac{\partial F_{2}(U_h^{n,\alpha },V_h^{n,\alpha })}{\partial U^{n}_{h}}\phi _p, \phi _i\Big \rangle ,\\ (D1)_{pi}&=\frac{\partial H_{2i}(U_h^n, V_h^n)}{\partial \gamma _{p}^{n}}={{\varDelta } t^{-\alpha }}w_0^{(\alpha )}\langle \phi _p,\phi _i\rangle +\Big (1-\frac{\alpha }{2}\Big )\langle \nabla \phi _p, \nabla \phi _i\rangle \\&\quad -\Big (1-\frac{\alpha }{2}\Big )\Big \langle \frac{\partial F_{2}(U_h^{n,\alpha },V_h^{n,\alpha })}{\partial V^{n}_{h}}\phi _p, \phi _i\Big \rangle ,\\ \end{aligned} \end{aligned}$$

where $1\le i,\ l,\ p\le M.$

The matrices A1 and D1 take the similar form as Galerkin matrix for the following semi-linear elliptic equation:

$$\begin{aligned} \begin{aligned} \langle u, v\rangle +k_1\langle \nabla u,\nabla v\rangle =k_2\langle f(u),v\rangle , \end{aligned} \end{aligned}$$

(12)

where $k_1, \ k_2$ are positive constants. Therefore, A1 and D1 are sparse matrices. In addition, it is not difficult to check that B1, C1 are sparse matrices too, and consequently, J is a sparse matrix. Thus, for a given initial guess and an initial solution, we can solve the above matrix system using the Sherman–Morrison Woodbury formula and block elimination algorithm (Chaudhary 2018; Govaerts and Pryce 1990).

Now, in the following, we prove the existence-uniqueness of the fully discrete solution $(U_h^n,V_h^n)$. The following proposition is required to prove the existence of solution $(U_h^n,V_h^n)$ for the scheme (6) [or (7)].

Proposition 1

(Chaudhary 2018; Thomée 1984) Let ${\mathcal {H}}$ be a finite-dimensional Hilbert space with scalar product $\langle \cdot ,\cdot \rangle$ and norm $|\cdot |.$ Let $S:{\mathcal {H}}\rightarrow {\mathcal {H}}$ be a continuous map, such that

$$\begin{aligned} \langle S(v),v\rangle> 0 \quad \forall v\in {\mathcal {H}}\quad \text{ with }\quad |v|=\rho ,\quad \rho > 0.\\ \end{aligned}$$

Then, there exists $w\in {\mathcal {H}}$, such that

$$\begin{aligned} S(w)=0 \quad \text{ and }\quad |w|< \rho . \end{aligned}$$

Theorem 1

Let $U^0_{h},\ U^1_{h},\ldots , U^{n-1}_{h}$ and $V^0_{h},\ V^1_{h},\ldots , V^{n-1}_{h}$ are given. Then for all $1\le n\le N,$ there exists a unique solution $(U^n_{h},V^n_{h})$ of the problem (6).

Proof

We know $X_h$ is the finite-dimensional Hilbert space with scalar product $\langle \cdot , \cdot \rangle .$ For $(X, Y)\in {X_h\times X_h},$ let

$$\begin{aligned} \langle (X, Y),(X, Y)\rangle _{X_h\times X_h} =\langle X,Y\rangle +\langle X,Y\rangle . \end{aligned}$$

Clearly, $\big (X_h\times X_h,\langle \cdot ,\cdot \rangle _{X_h\times X_h}\big )$ is the product Hilbert space.

From (7), we have

$$\begin{aligned} \begin{aligned}&\langle U_h^{n},w_h\rangle +{{\varDelta } t}^{\alpha }\langle \nabla U_h^{n,\alpha }, \nabla w_{h}\rangle -{{\varDelta } t}^{\alpha } \langle F_{1}(U_h^{n,\alpha },V_h^{n,\alpha }), w_{h}\rangle + \sum _{j=1}^{n-1}w_{n-j}^{(\alpha )}\langle U_h^{j},w_h\rangle =0,\\&\langle V_h^{n},\omega _h\rangle + {{\varDelta } t}^{\alpha } \langle \nabla V_h^{n,\alpha }, \nabla \omega _{h}\rangle -{{\varDelta } t}^{\alpha } \langle F_{2}(U_h^{n,\alpha },V_h^{n,\alpha }), \omega _{h}\rangle +\sum _{j=1}^{n-1}w_{n-j}^{(\alpha )}\langle V_h^{j},\omega _h\rangle =0.\\ \end{aligned} \end{aligned}$$

(13)

Multiplying by $(1-\frac{\alpha }{2})$ in (13) to get

$$\begin{aligned} \begin{aligned}&\langle U_h^{n,\alpha },w_h\rangle +\left( 1-\frac{\alpha }{2}\right) {{\varDelta } t}^{\alpha }\langle \nabla U_h^{n,\alpha }, \nabla w_{h}\rangle -\left( 1-\frac{\alpha }{2}\right) {{\varDelta } t}^{\alpha } \langle F_{1}\left( U_h^{n,\alpha },V_h^{n,\alpha }\right) , w_{h}\rangle \\&\quad +\left( 1-\frac{\alpha }{2}\right) \sum _{j=1}^{n-1}w_{n-j}^{\left( \alpha \right) }\langle U_h^{j},w_h\rangle -\frac{\alpha }{2}\langle U_h^{n-1},w_h\rangle =0,\\&\langle V_h^{n,\alpha },\omega _h\rangle + \left( 1-\frac{\alpha }{2}\right) {{\varDelta } t}^{\alpha } \langle \nabla V_h^{n,\alpha }, \nabla \omega _{h}\rangle -\left( 1-\frac{\alpha }{2}\right) {{\varDelta } t}^{\alpha } \langle F_{2}\left( U_h^{n,\alpha },V_h^{n,\alpha }\right) , \omega _{h}\rangle \\&\quad +\left( 1-\frac{\alpha }{2}\right) \sum _{j=1}^{n-1}w_{n-j}^{\left( \alpha \right) }\langle V_h^{j},\omega _h\rangle -\frac{\alpha }{2}\langle V_h^{n-1},w_h\rangle =0.\\ \end{aligned} \end{aligned}$$

(14)

Equations (13) and (14) are equivalent in the sense that the solution of (13) is the solution of (14) and vice versa.

Define operator $G:X_h \times X_h\rightarrow X_h \times X_h$, such that

$$\begin{aligned} G(X_{1}^{n,\alpha }, X_{2}^{n,\alpha }):=(G_1(X_{1}^{n,\alpha }, X_{2}^{n,\alpha }),G_2(X_{1}^{n,\alpha }, X_{2}^{n,\alpha })), \end{aligned}$$

(15)

where $G_1:X_h\times X_h\rightarrow X_h$ and $G_2:X_h\times X_h\rightarrow X_h$ are defined by the following:

$$\begin{aligned} \begin{aligned} \langle G_1(X^{n,\alpha }_{1},X^{n,\alpha }_{2}),w_1\rangle&:=\langle X^{n,\alpha }_{1},w_1\rangle +\left( 1-\frac{\alpha }{2}\right) {{\varDelta } t}^{\alpha }\langle \nabla X^{n,\alpha }_{1},\nabla w_1\rangle \\&\quad -\left( 1-\frac{\alpha }{2}\right) {{\varDelta } t}^{\alpha }\langle F_1(X^{n,\alpha }_{1},X^{n,\alpha }_{2}),w_1\rangle \\&\quad +\left( 1-\frac{\alpha }{2}\right) \sum _{j=1}^{n-1}w^{(\alpha )}_{n-j}\langle U^{j}_{h},w_1\rangle \\&\quad -\frac{\alpha }{2}\langle U_h^{n-1},w_1\rangle , \end{aligned} \end{aligned}$$

(16)

and

$$\begin{aligned} \begin{aligned} \langle G_2\left( X^{n,\alpha }_{1},X^{n,\alpha }_{2}\right) ,w_2\rangle&:=\langle X^{n,\alpha }_{2},w_2\rangle +\left( 1-\frac{\alpha }{2}\right) {{\varDelta } t}^{\alpha }\langle \nabla X^{n,\alpha }_{2},\nabla w_2\rangle \\&\quad -\left( 1-\frac{\alpha }{2}\right) {{\varDelta } t}^{\alpha }\langle F_2\left( X^{n,\alpha }_{1},X^{n,\alpha }_{2}\right) ,w_2\rangle \\&\quad +\left( 1-\frac{\alpha }{2}\right) \sum _{j=1}^{n-1}w_{n-j}^{\left( \alpha \right) }\langle V^{j}_{h},w_2\rangle \\&\quad -\frac{\alpha }{2}\langle V_h^{n-1},w_2\rangle . \end{aligned} \end{aligned}$$

(17)

Since $G_1$ and $G_2$ are continuous maps, therefore, G is also continuous. By choosing $w_1=X^{n,\alpha }_{1}$ in Eq. (16), we get

$$\begin{aligned} \begin{aligned} \langle G_1\left( X^{n,\alpha }_{1},X^{n,\alpha }_{2}\right) ,X^{n,\alpha }_{1}\rangle&=\langle X^{n,\alpha }_{1},X^{n,\alpha }_{1}\rangle +\left( 1-\frac{\alpha }{2}\right) {\varDelta } t^{\alpha }\langle \nabla X^{n,\alpha }_{1},\nabla X^{n,\alpha }_{1}\rangle \\&\quad -\left( 1-\frac{\alpha }{2}\right) {\varDelta } t^{\alpha }\langle F_1\left( X^{n,\alpha }_{1},X^{n,\alpha }_{2}\right) ,X^{n,\alpha }_{1}\rangle \\&\quad +\left( 1-\frac{\alpha }{2}\right) \sum _{j=1}^{n-1}w_{n-j}^{\left( \alpha \right) }\langle U^{j}_{h},X^{n,\alpha }_{1}\rangle \\&\quad -\frac{\alpha }{2}\langle U_h^{n-1},X^{n,\alpha }_{1}\rangle . \end{aligned} \end{aligned}$$

(18)

From the hypothesis H1,  we have

$$\begin{aligned} \Vert F_i(X_1^{n,\alpha }, X_2^{n,\alpha })\Vert \le L_i(\Vert X_1^{n,\alpha }\Vert +\Vert X_2^{n,\alpha }\Vert )+\Vert F_i(0,0)\Vert , \quad \text{ for } \ \ i=1,2, \end{aligned}$$

which implies that

$$\begin{aligned} \Vert F_i(X_1^{n,\alpha }, X_2^{n,\alpha }\Vert \le a_i (1+\Vert X_1^{n,\alpha }\Vert +\Vert X_2^{n,\alpha }\Vert ), \quad \ a_i>0, \ i=1,2. \end{aligned}$$

(19)

Using (19) and $w_j^{(\alpha )}< 0,$ $1\le j\le n$ in (18) to get

$$\begin{aligned} \begin{aligned} \langle G_1(X^{n,\alpha }_{1},X^{n,\alpha }_{2}),X^{n,\alpha }_{1}\rangle&\ge \Vert X^{n,\alpha }_{1}\Vert ^2+\left( 1-\frac{\alpha }{2}\right) {\varDelta } t^{\alpha }\Vert \nabla X^{n,\alpha }_{1}\Vert ^2\\&\quad -\left( 1-\frac{\alpha }{2}\right) {\varDelta } t^{\alpha } a_1(1+\Vert X^{n,\alpha }_{1}\Vert +\Vert X^{n,\alpha }_{2}\Vert )\Vert X^{n,\alpha }_{1}\Vert \\&\quad +\left( 1-\frac{\alpha }{2}\right) \sum _{j=1}^{n-1}w_{n-j}^{(\alpha )}\Vert U^{j}_{h}\Vert \Vert X^{n,\alpha }_{1}\Vert -\frac{\alpha }{2} \Vert U_h^{n-1}\Vert \Vert X^{n,\alpha }_{1}\Vert . \end{aligned} \end{aligned}$$

(20)

Since $(1-\frac{\alpha }{2}){\varDelta } t^{\alpha }\Vert \nabla X^n_{i}\Vert > 0,$ we write (20) as

$$\begin{aligned} \begin{aligned} \langle G_1(X^{n,\alpha }_{1},X^{n,\alpha }_{2}),X^{n,\alpha }_{1}\rangle&\ge \Big (\Big (1-\Big (1-\frac{\alpha }{2}\Big ){\varDelta } t^{\alpha } a_1\Big )\Vert X^{n,\alpha }_{1}\Vert -\Big (1-\frac{\alpha }{2}\Big ){\varDelta } t^{\alpha } a_1(1+\Vert X^{n,\alpha }_{2}\Vert )\\&\quad +\Big (1-\frac{\alpha }{2}\Big )\sum _{j=1}^{n-1}w_{n-j}^{(\alpha )}\Vert U^{j}_{h}\Vert -\frac{\alpha }{2}\Vert U_h^{n-1}\Vert \Big )\Vert X^{n,\alpha }_{1}\Vert . \end{aligned} \end{aligned}$$

In the similar manner, we get the following inequality for $G_2$:

$$\begin{aligned} \begin{aligned} \langle G_2(X^{n,\alpha }_{1},X^{n,\alpha }_{2}),X^{n,\alpha }_{2}\rangle&\ge \Big (\Big (1-\Big (1-\frac{\alpha }{2}\Big ){\varDelta } t^{\alpha } a_2\Big )\Vert X^{n,\alpha }_{2}\Vert -\Big (1-\frac{\alpha }{2}\Big ){\varDelta } t^{\alpha } a_2(1+\Vert X^{n,\alpha }_{1}\Vert )\\&\quad +\Big (1-\frac{\alpha }{2}\Big )\sum _{j=1}^{n-1}w_{n-j}^{(\alpha )}\Vert V^{j}_{h}\Vert -\frac{\alpha }{2}\Vert V_h^{n-1}\Vert \Big )\Vert X^{n,\alpha }_{2}\Vert . \end{aligned} \end{aligned}$$

Assume that if the following inequalities hold:

$$\begin{aligned} \begin{aligned}&\left( 1-\left( 1-\frac{\alpha }{2}\right) {\varDelta } t^{\alpha } a_1\right) \Vert X^{n,\alpha }_{1}\Vert -\left( 1-\frac{\alpha }{2}\right) {\varDelta } t^{\alpha } a_1\left( 1+\Vert X^{n,\alpha }_{2}\Vert \right) \\&\quad +\left( 1-\frac{\alpha }{2}\right) \sum _{j=1}^{n-1}w_{n-j}^{\left( \alpha \right) }\Vert U^{j}_{h}\Vert -\frac{\alpha }{2}\Vert U_h^{n-1}\Vert>0,\\&\left( 1-\left( 1-\frac{\alpha }{2}\right) {\varDelta } t^{\alpha } a_2\right) \Vert X^{n,\alpha }_{2}\Vert -\left( 1-\frac{\alpha }{2}\right) {\varDelta } t^{\alpha } a_2\left( 1+\Vert X^{n,\alpha }_{1}\Vert \right) \\&\quad +\left( 1-\frac{\alpha }{2}\right) \sum _{j=1}^{n-1}w_{n-j}^{\left( \alpha \right) }\Vert V^{j}_{h}\Vert -\frac{\alpha }{2}\Vert V_h^{n-1}\Vert >0, \end{aligned} \end{aligned}$$

then $\langle G_i(X^{n,\alpha }_{1},X^{n,\alpha }_{2}),X^{n,\alpha }_{i}\rangle >0$ for $i=1,2$.

Now, choosing ${\varDelta } t^{\alpha }<\frac{1}{(1-\frac{\alpha }{2})(a_1+a_2)},$ then $\exists$ $X^{n,\alpha }_{1},$ $X^{n,\alpha }_{2}$, such that

$$\begin{aligned}&\Vert X^{n,\alpha }_{1}\Vert>\frac{1}{\Big (1-\Big (1-\frac{\alpha }{2}\Big ){\varDelta } t^{\alpha }(a_1+a_2)\Big )}\Bigg (\Big (1-\frac{\alpha }{2}\Big ){\varDelta } t^{\alpha } a_1\Big (1-\Big (1-\frac{\alpha }{2}\Big )\\&\quad \sum _{j=1}^{n-1}w^{(\alpha )}_{n-j}\Vert V^{j}_{h}\Vert +\frac{\alpha }{2}\Vert V_h^{n-1}\Vert \Big )\\&\quad -\Big (1-\Big (1-\frac{\alpha }{2}\Big ){\varDelta } t^{\alpha } a_2\Big )\Big (\Big (1-\frac{\alpha }{2}\Big )\sum _{j=1}^{n-1}w^{(\alpha )}_{n-j}\Vert U^{j}_{h}\Vert -\frac{\alpha }{2}\Vert U_h^{n-1}\Vert \Big )\Bigg ),\\&\Vert X^{n,\alpha }_{2}\Vert >\frac{1}{\Big (1-\Big (1-\frac{\alpha }{2}\Big ){\varDelta } t^{\alpha }(a_1+a_2)\Big )}\Bigg (\Big (1-\frac{\alpha }{2}\Big ){\varDelta } t^{\alpha } a_2\Big (1-\Big (1-\frac{\alpha }{2}\Big )\\&\quad \sum _{j=1}^{n-1}w^{(\alpha )}_{n-j}\Vert U^{j}_{h}\Vert +\frac{\alpha }{2}\Vert U_h^{n-1}\Vert \Big )\\&\quad -\Big (1-\Big (1-\frac{\alpha }{2}\Big ){\varDelta } t^{\alpha } a_1\Big )\Big (\Big (1-\frac{\alpha }{2}\Big )\sum _{j=1}^{n-1}w^{(\alpha )}_{n-j}\Vert V^{j}_{h}\Vert -\frac{\alpha }{2}\Vert V_h^{n-1}\Vert \Big )\Bigg ), \end{aligned}$$

which implies that $\langle G_i(X^{n,\alpha },X^{n,\alpha }),X^{n,\alpha }_{i}\rangle >0$ for $i=1,2.$ Therefore, with

$\Vert (X_{1}^{n,\alpha }, X_{2}^{n,\alpha })\Vert _{X_h\times X_h}=\sqrt{\Vert X_{1}^{n,\alpha }\Vert ^2+\Vert X_2^{n,\alpha }\Vert ^2}=\rho ,$ we have

$$\begin{aligned} \begin{aligned}&\langle G(X_{1}^{n,\alpha }, X_{2}^{n,\alpha }),(X_{1}^{n,\alpha }, X_{2}^{n,\alpha })\rangle _{X_h\times X_h}=\langle G_1(X_{1}^{n,\alpha }, X_{2}^{n,\alpha }),X_{1}^{n,\alpha }\rangle \\&\quad +\langle G_2(X_{1}^{n,\alpha }, X_{2}^{n,\alpha }), X_{2}^{n,\alpha }\rangle >0. \end{aligned} \end{aligned}$$

Hence, Proposition 1 guarantees the existence of fully discrete solution $(U_h^n,V_h^n)$.

Next, we prove the uniqueness of the solution $(U^{n,\alpha }_{h},V^{n,\alpha }_{h})$ for problem (14). Let $(U^{n,\alpha }_{h1},V^{n,\alpha }_{h1})$ and $(U^{n,\alpha }_{h2},V^{n,\alpha }_{h2})$ be two solutions of problem (14). For simplicity, we denote $U_1=U^{n,\alpha }_{h1},$ $V_1=V^{n,\alpha }_{h1},$ $U_2=U^{n,\alpha }_{h2},$ and $V_2=V^{n,\alpha }_{h2}.$ Then, from (14), we obtain

$$\begin{aligned} \begin{aligned} \langle U_1-U_2,w_h\rangle +\Big (1-\frac{\alpha }{2}\Big ){\varDelta } t^{\alpha }\langle \nabla (U_1-U_2), \nabla w_{h}\rangle&=\Big (1-\frac{\alpha }{2}\Big ){\varDelta } t^{\alpha }\Big (\langle F_{1}(U_1,V_1),w_{h} \rangle \\&\quad -\langle F_{1}(U_2,V_2), w_{h}\rangle \Big ),\\ \langle V_1-V_2,\omega _h\rangle +\Big (1-\frac{\alpha }{2}\Big ){\varDelta } t^{\alpha }\langle \nabla (V_1-V_2), \nabla \omega _{h}\rangle&=\Big (1-\frac{\alpha }{2}\Big ){\varDelta } t^{\alpha }\Big (\langle F_{2}(U_1,V_1), \omega _{h} \rangle \\&\quad -\langle F_2(U_2,V_2), \omega _{h}\rangle \Big ).\\ \end{aligned} \end{aligned}$$

(21)

Setting $w_h=U_1-U_2=r,$ $\omega _{h}=V_1-V_2=s$ in (21) and using hypothesis H1,  we obtain

$$\begin{aligned} \Vert r\Vert ^2&\le \left( 1-\frac{\alpha }{2}\right) {\varDelta } t^{\alpha }L_1(\Vert r\Vert +\Vert s\Vert )\Vert r\Vert , \end{aligned}$$

(22)

$$\begin{aligned} \Vert s\Vert ^2&\le \left( 1-\frac{\alpha }{2}\right) {\varDelta } t^{\alpha }L_2(\Vert r\Vert +\Vert s\Vert )\Vert s\Vert . \end{aligned}$$

(23)

Adding (22) and (23), we get

$$\begin{aligned} \Vert r\Vert ^2+\Vert s\Vert ^2\le \frac{\Big (1-\frac{\alpha }{2}\Big ){\varDelta } t^{\alpha }}{2}\Big ((3L_1+L_2)\Vert r\Vert ^2+(L_1+3L_2)\Vert s\Vert ^2\Big ). \end{aligned}$$

Taking ${\varDelta } t^{\alpha }<1$ sufficiently small, such that $\Big (1-\frac{(1-\frac{\alpha }{2}){\varDelta } t^{\alpha }}{2}\max \{(3L_1+L_2),(L_1+3L_2)\}\Big )>0,$ we get

$$\begin{aligned} \Vert r\Vert ^2+\Vert s\Vert ^2\le 0. \end{aligned}$$

This completes the proof. $\square$

2.1 Error analysis

Here, we derive a priori bound and a priori error estimate for the fully discrete scheme (6). In this regard, we first recall some known results.

Lemma 1

(Kumar et al. 2018) Let $\{a^n,\ b^n| \ n\ge 0\}$ be nonnegative sequences and $\mu _1$ and $\mu _2$ be nonnegative constants. For $a^0=0$ and

$$\begin{aligned} ^RD^{\alpha }_{{\varDelta } t}a^n\le \mu _1 a^n + \mu _2 a^{n-1}+b^n,\quad n\ge 1, \end{aligned}$$

(24)

there exists a positive constant ${\varDelta } t^*$, such that, when ${\varDelta } t\le {\varDelta } t^*,$

$$\begin{aligned} a^n\le 2\Big (\frac{t_n^{\alpha }}{\alpha } \ \max _{0\le i\le n}b^i\Big )E_{\alpha }(2 {\varGamma } (\alpha ) \mu t_n^{\alpha }), \quad 1\le n\le N, \end{aligned}$$

where $E_{\alpha }(z)$=$\sum _{j=0}^{\infty }\frac{z^j}{{\varGamma }(1+j\alpha ) }$ is the Mittag–Leffler function and $\mu =\mu _1+\frac{\mu _2}{\alpha }.$

Lemma 2

(Kumar et al. 2018) For any sequence $\{\mathrm{e}^k\}_{k=0}^{N}\subset X_h$, the following inequality holds:

$$\begin{aligned} \left\langle ^RD^{\alpha }_{{\varDelta } t}\mathrm{e}^{k},\left( 1-\frac{\alpha }{2}\right) \mathrm{e}^k+\frac{\alpha }{2}\mathrm{e}^{k-1}\right\rangle \ge \frac{1}{2} \ ^RD^{\alpha }_{{\varDelta } t}\Vert \mathrm{e}^k\Vert ^2,\quad \text{ for } \quad 1\le k\le N. \end{aligned}$$

(25)

In the following theorem, we provide a priori bound for the fully discrete solution $(U^n_{h},V^n_{h})$.

Theorem 2

Let $(U_h^n,V_h^n)$ be the solution of fully discrete scheme (6). Then, there exists a positive constant ${{\varDelta } t}^{*}$, such that when ${\varDelta } t\le {{\varDelta } t}^{*},$ the solution $(U_h^n,V_h^n)$ satisfies

$$\begin{aligned} \Vert U_h^n\Vert +\Vert V_h^n\Vert \le C, \end{aligned}$$

(26)

where $n= 1,2,\ldots ,N$ and C is a positive constant independent of h and ${\varDelta } t.$

Proof

From (6), we have

$$\begin{aligned} \langle ^RD^{\alpha }_{{\varDelta } t}U_h^{n}, w_{h}\rangle +\langle \nabla U_h^{n,\alpha }, \nabla w_{h}\rangle =\langle F_{1}(U_h^{n,\alpha },V_h^{n,\alpha }), w_{h}\rangle ,\quad \forall w_{h}\in X_{h}. \end{aligned}$$

(27)

Setting $w_{h}=U_h^{n,\alpha }$ in (27) to obtain

$$\begin{aligned} \langle ^RD^{\alpha }_{{\varDelta } t}U_h^{n},U_h^{n,\alpha }\rangle +\Vert \nabla U_h^{n,\alpha }\Vert ^2\le \frac{1}{2}\big (\Vert F_{1}(U_h^{n,\alpha },V_h^{n,\alpha })\Vert ^2+\Vert U_h^{n,\alpha }\Vert ^2\big ). \end{aligned}$$

(28)

Using (19) in (28) to get

$$\begin{aligned} \langle ^RD^{\alpha }_{{\varDelta } t}U_h^{n},U_h^{n,\alpha }\rangle +\Vert \nabla U_h^{n,\alpha }\Vert ^2 \le C\big ((1+\Vert U_h^{n,\alpha }\Vert +\Vert V_h^{n,\alpha }\Vert )^2+\Vert U_h^{n,\alpha }\Vert ^2\big ). \end{aligned}$$

(29)

For $a,b\ge 0,$ using the fact $(a+b)^2\le 2(a^2+b^2)$ in (29), we have

$$\begin{aligned} \langle ^RD^{\alpha }_{{\varDelta } t}U_h^{n},U_h^{n,\alpha }\rangle \le C\big (1+\Vert U_h^{n,\alpha }\Vert ^2+\Vert V_h^{n,\alpha }\Vert ^2\big ). \end{aligned}$$

(30)

Using Lemma 2 in (30), we have

$$\begin{aligned} {^RD}^{\alpha }_{{\varDelta } t}\Vert U_h^{n}\Vert ^2\le C\big (1+\Vert U_h^{n,\alpha }\Vert ^2+\Vert V_h^{n,\alpha }\Vert ^2\big ). \end{aligned}$$

(31)

Similarly, the estimate for $V_h^{n}$ is given by

$$\begin{aligned} {^RD}^{\alpha }_{{\varDelta } t}\Vert V_h^{n}\Vert ^2\le C\big (1+\Vert V_h^{n,\alpha }\Vert ^2+\Vert U_h^{n,\alpha }\Vert ^2\big ). \end{aligned}$$

(32)

Adding (31) and (32) to get

$$\begin{aligned} \begin{aligned} {^RD}^{\alpha }_{{\varDelta } t}(\Vert U_h^{n}\Vert ^2+\Vert V_h^{n}\Vert ^2)&\le C\big (1+\Vert U_h^{n,\alpha }\Vert ^2+\Vert V_h^{n,\alpha }\Vert ^2\big )\\&=C\Big (1+\big (1-\frac{\alpha }{2}\big )^2(\Vert U_h^{n}\Vert ^2+\Vert V_h^{n}\Vert ^2)\\&\quad +\big (\frac{\alpha }{2}\big )^2(\Vert U_h^{n-1}\Vert ^2+\Vert V_h^{n-1}\Vert ^2)\Big ). \end{aligned} \end{aligned}$$

(33)

Using Lemma 1 in (33), one can find a positive constant ${{\varDelta } t}^*$, such that when ${\varDelta } t\le {{\varDelta } t}^*$, then

$$\begin{aligned} \begin{aligned} \Vert U_h^{n}\Vert ^2+\Vert V_h^{n}\Vert ^2&\le C,\\ \Vert U_h^{n}\Vert +\Vert V_h^{n}\Vert&\le C. \end{aligned} \end{aligned}$$

This completes the proof. $\square$

Next, we derive the error estimate for the scheme (6). Direct comparison between $u(x,t_n)=u^n(x)\ \text{ and }\ U_h^n,$ $v(x,t_n)=v^n(x)\ \text{ and }\ V_h^n$ may not yield optimal convergence. Therefore, we need to define Ritz projection $R_h:H^1_0({\varOmega })\rightarrow X_h$ which satisfies (Thomée 1984):

$$\begin{aligned} \langle \nabla w,\nabla v_h\rangle =\langle \nabla R_h w,\nabla v_h\rangle , \quad \forall w\in H_0^1({\varOmega }),\ v_h\in X_h. \end{aligned}$$

(34)

We now mention the following approximation results for $R_h$ which is significant in the derivation of a priori error estimate.

Theorem 3

(Rannacher and Scott 1982) There exists a positive constant C, independent of h, such that

$$\begin{aligned} \Vert w-R_hw\Vert _j\le \mathrm{Ch}^{i-j}\Vert w\Vert _i \ , \quad \forall w\in H^{i}\cap H_0^1, \quad j=0 ,\ 1; \ i=1, \ 2. \end{aligned}$$

(35)

Using an intermediate projection $R_h,$ we can write the error as follows:

$$\begin{aligned} \begin{aligned} u^n(x)-U_h^n=u^n-U_h^n&=(u^n -R_hu^n)+(R_hu^n-U_h^n)=\rho _{1h}^n+\theta _{1h}^n,\\ v^n(x)-V_h^n=v^n-V_h^n&=(v^n-R_hv^n)+(R_hv^n-V_h^n)=\rho _{2h}^n+\theta _{2h}^n.\\ \end{aligned} \end{aligned}$$

In the following theorem, we give the detailed proof of a priori error estimate for the fully discrete scheme (6).

Theorem 4

Let $(u^n, v^n)$ be the solution of (1a)–(1d) and $(U_h^n,V_h^n)$ be the solution of fully discrete scheme (6). Then, there exists a positive constant ${{\varDelta } t}^{*}$, such that when ${\varDelta } t\le {{\varDelta } t}^{*},$ the solution $(U_h^n,V_h^n)$ satisfies

$$\begin{aligned} \Vert u^n-U_h^n\Vert +\Vert v^n-V_h^n\Vert \le C\big ({\varDelta } t^{2}+h^2\big ), \end{aligned}$$

(36)

where $n= 1,2,\ldots ,N$ and C is a positive constant independent of h and ${\varDelta } t.$

Proof

From (1a)–(1b), it is easy to see that the exact solution $(u^n,v^n)$ satisfies the following equations with truncation errors $E_1^{n}, \ E_2^n$:

$$\begin{aligned}&^RD^{\alpha }_{{\varDelta } t}u^n-{\varDelta } u^{n-\frac{\alpha }{2}}=F_1 \left( u^{n,\alpha },v^{n,\alpha } \right) +E_1^n, \end{aligned}$$

(37)

$$\begin{aligned}&^RD^{\alpha }_{{\varDelta } t}v^n-{\varDelta } v^{n-\frac{\alpha }{2}}=F_2 \left( u^{n,\alpha },v^{n,\alpha } \right) +E_2^n, \end{aligned}$$

(38)

where $E_1^{n}$ and $E_2^n$ are given by

$$\begin{aligned} \begin{aligned} E_1^n&=\,^RD^{\alpha }_{{\varDelta } t}u^n- \ ^RD^{\alpha }_{{\varDelta } t_{n-\frac{\alpha }{2}}}u+F_1 \left( u^{n-\frac{\alpha }{2}},v^{n-\frac{\alpha }{2}} \right) -F_1(u^{n,\alpha },v^{n,\alpha }),\\ E_2^n&=\,^RD^{\alpha }_{{\varDelta } t}v^n- \ ^RD^{\alpha }_{{\varDelta } t_{n-\frac{\alpha }{2}}}v+F_2(u^{n-\frac{\alpha }{2}},v^{n-\frac{\alpha }{2}})-F_2(u^{n,\alpha },v^{n,\alpha }). \end{aligned} \end{aligned}$$

Moreover

$$\begin{aligned} \begin{aligned} \Vert E_1^n\Vert&\le \Vert ^RD^{\alpha }_{{\varDelta } t}u^n- \ ^RD^{\alpha }_{{\varDelta } t_{n-\frac{\alpha }{2}}}u\Vert +\Vert F_1(u^{n-\frac{\alpha }{2}},v^{n-\frac{\alpha }{2}})-F_1(u^{n,\alpha },v^{n,\alpha })\Vert ,\\ \Vert E_2^n\Vert&\le \Vert ^RD^{\alpha }_{{\varDelta } t}v^n- \ ^RD^{\alpha }_{{\varDelta } t_{n-\frac{\alpha }{2}}}v\Vert +\Vert F_2(u^{n-\frac{\alpha }{2}},v^{n-\frac{\alpha }{2}})-F_2(u^{n,\alpha },v^{n,\alpha })\Vert . \end{aligned} \end{aligned}$$

(39)

Using (3), hypothesis H1, and simple application of Taylor expansion in (39), errors are bounded by

$$\begin{aligned} \begin{aligned} \Vert E_1^n\Vert \le C ({\varDelta } t^2), \ \ \Vert E_2^n\Vert \le C ({\varDelta } t^2). \end{aligned} \end{aligned}$$

(40)

Furthermore, for any $w_h\in X_h,$ the estimate for ${\theta _{1h}^n}$ is given by

$$\begin{aligned} \begin{aligned} \langle ^RD^{\alpha }_{{\varDelta } t}{\theta _{1h}^n},w_h\rangle +\langle \nabla {\theta _{1h}^{n,\alpha },\nabla w_h}\rangle&=\langle ^RD^{\alpha }_{{\varDelta } t}{R_hu^n},w_h\rangle +\langle \nabla {R_hu^{n,\alpha }},\nabla w_h\rangle \\&\quad -\langle ^RD^{\alpha }_{{\varDelta } t}{U_h^n},w_h\rangle -\langle \nabla {U_h^{n,\alpha }},\nabla w_h\rangle .\\ \end{aligned} \end{aligned}$$

Based on (34), (6), and (37), we get

$$\begin{aligned} \begin{aligned} \langle ^RD^{\alpha }_{{\varDelta } t}{\theta _{1h}^n},w_h\rangle +\langle \nabla {\theta _{1h}^{n,\alpha },\nabla w_h}\rangle&=\langle ^RD^{\alpha }_{{\varDelta } t}({R_hu^n}-u^n),w_h\rangle +\langle \nabla ({u^{n,\alpha }}-u^{n-\frac{\alpha }{2}}),\nabla w_h\rangle \\&\quad +\langle F_{1}(u^{n,\alpha },v^{n,\alpha })- F_{1}(U_h^{n,\alpha },V_h^{n,\alpha }),w_h\rangle +\langle E_1^{n},w_h\rangle . \end{aligned} \end{aligned}$$

(41)

Setting $w_h=\theta _{1h}^{n,\alpha }$ in (41) to get

$$\begin{aligned} \langle ^RD^{\alpha }_{{\varDelta } t}{\theta _{1h}^n},\theta _{1h}^{n,\alpha }\rangle\le & {} \frac{1}{2} \Vert ^RD^{\alpha }_{{\varDelta } t}\rho _{1h}^n\Vert ^2+\frac{1}{2} \Vert \theta _{1h}^{n,\alpha }\Vert ^2+\frac{1}{2}\Vert \nabla ({u^{n,\alpha }}-u^{n-\frac{\alpha }{2}})\Vert ^2 \nonumber \\&+\frac{L_1}{2}\big (\Vert {u^{n,\alpha }}-U_h^{n,\alpha }\Vert +\Vert {v^{n,\alpha }}-V_h^{n,\alpha }\Vert \big )^2+\frac{L_1}{2}\Vert \theta _{1h}^{n,\alpha }\Vert ^2 \nonumber \\&+\frac{1}{2}\Vert E_1^{n}\Vert ^2+\frac{1}{2} \Vert \theta _{1h}^{n,\alpha }\Vert ^2 \nonumber \\\le & {} \left( \frac{L_1}{2}+1\right) \Vert \theta _{1h}^{n,\alpha }\Vert ^2+2 L_1\left( \Vert \theta _{1h}^{n,\alpha }\Vert ^2+\Vert \rho _{1h}^{n,\alpha }\Vert ^2+\Vert \theta _{2h}^{n,\alpha }\Vert ^2+\Vert \rho _{2h}^{n,\alpha }\Vert ^2\right) \nonumber \\&+\frac{1}{2} \Vert ^RD^{\alpha }_{{\varDelta } t}\rho _{1h}^n\Vert ^2+\frac{1}{2}\Vert \nabla ({u^{n,\alpha }}-u^{n-\frac{\alpha }{2}})\Vert ^2+\frac{1}{2}\Vert E_1^{n}\Vert ^2. \end{aligned}$$

(42)

Note that

$$\begin{aligned} \begin{aligned} \Vert ^RD^{\alpha }_{{\varDelta } t}{\rho _{1h}^n}\Vert&\le \Vert ^RD^{\alpha }_{{\varDelta } t}{\rho _{1h}^n}-{^R{D}}^{\alpha }_{t_{n-\frac{\alpha }{2}}}\rho _{1h}\Vert +\Vert ^RD^{\alpha }_{t_{n-\frac{\alpha }{2}}}{\rho _{1h}}\Vert \le C({\varDelta } t^{2}+h^2),\\ \end{aligned} \end{aligned}$$

(43)

and

$$\begin{aligned} \begin{aligned} \Vert \nabla (u^{n-\frac{\alpha }{2}}-u^{n,\alpha })\Vert&\le \left( 1-\frac{\alpha }{2}\right) \left( \frac{\alpha }{2}\right) {\varDelta } t\int _{t_{n-1}}^{t_{n}}\Vert \nabla u_{tt}(s)\Vert \mathrm{d}s\le C{\varDelta } t^2.\\ \end{aligned} \end{aligned}$$

(44)

Using (40), (43), and (44) in (42), we get

$$\begin{aligned} {^RD}^{\alpha }_{{\varDelta } t}\Vert {\theta _{1h}^n}\Vert ^2\le \big ({5L_1+2}\big )\Vert \theta _{1h}^{n,\alpha }\Vert ^2+4L_1\Vert \theta _{2h}^{n,\alpha }\Vert ^2+C\big ({\varDelta } t^{2}+h^2\big )^2. \end{aligned}$$

(45)

Similarly, we can obtain the estimate for ${\theta _{2h}^n}$

$$\begin{aligned} {^RD}^{\alpha }_{{\varDelta } t}\Vert {\theta _{2h}^n}\Vert ^2\le \big ({5L_2+2}\big )\Vert \theta _{2h}^{n,\alpha }\Vert ^2+4L_2\Vert \theta _{1h}^{n,\alpha }\Vert ^2+C\big ({\varDelta } t^{2}+h^2\big )^2. \end{aligned}$$

(46)

Adding (45) and (46) yields

$$\begin{aligned} {^RD}^{\alpha }_{{\varDelta } t}(\Vert {\theta _{1h}^n}\Vert ^2+\Vert {\theta _{2h}^n}\Vert ^2)\le & {} (5L1+4L_2+2)\Vert \theta _{1h}^{n,\alpha }\Vert ^2\\&\quad +(4L_1+5L_2+2)\Vert \theta _{2h}^{n,\alpha }\Vert ^2+C\big ({\varDelta } t^{2}+h^2\big )^2. \end{aligned}$$

Next, we have

$$\begin{aligned} \begin{aligned} {^RD}^{\alpha }_{{\varDelta } t}\left( \Vert {\theta _{1h}^n}\Vert ^2+\Vert {\theta _{2h}^n}\Vert ^2\right)&\le \mu _1 \left( \Vert \theta _{1h}^n\Vert ^2+\Vert \theta _{2h}^n\Vert ^2 \right) \\&\quad +\mu _2 \left( \Vert \theta _{1h}^{n-1}\Vert ^2+\Vert \theta _{2h}^{n-1}\Vert ^2\right) +C\Big ({\varDelta } t^{2}+h^2\Big )^2, \end{aligned} \end{aligned}$$

(47)

where

$$\begin{aligned} \begin{aligned} \mu _1&= 2\left( 1-\frac{\alpha }{2}\right) ^2\max \Big \{(5L_1+4L_2+2),(4L_1+5L_2+2)\Big \},\\ \mu _2&= \frac{\alpha ^2}{2}\max \Big \{(5L_1+4L_2+2),(4L_1+5L_2+2)\Big \}. \end{aligned} \end{aligned}$$

Using Lemma 1 in (47), one can find a positive constant ${{\varDelta } t}^*$, such that, when ${\varDelta } t\le {{\varDelta } t}^*$, then

$$\begin{aligned} \begin{aligned} \Vert {\theta _{1h}^n}\Vert ^2+\Vert {\theta _{2h}^n}\Vert ^2&\le C\big ({\varDelta } t^{2}+h^2\big )^2,\\ \Vert {\theta _{1h}^n}\Vert +\Vert {\theta _{2h}^n}\Vert&\le C\big ({\varDelta } t^{2}+h^2\big ). \end{aligned} \end{aligned}$$

Now, an application of triangular inequality and Theorem 3 completes the proof of Theorem 4. $\square$

3 Linearized Fractional Crank–Nicolson-Galerkin finite element scheme

A disadvantage of the scheme (6) is that it yields a nonlinear system of equations at each time level. To solve such system of equations, we need an iterative method. Thus, to avoid iterations at each time step, we propose a new linearized fractional Crank–Nicolson–Galerkin finite element scheme in which the forcing terms $F_1, \ F_2$ are obtained by extrapolation from $(U_h^{n-1},V_h^{n-1})$ and $(U_h^{n-2},V_h^{n-2}).$ Precisely, we use $\bar{U}_h^{n,\alpha }=(2-\frac{\alpha }{2})U_h^{n-1}-(1-\frac{\alpha }{2})U_h^{n-2}$ and $\bar{V}_h^{n,\alpha }=(2-\frac{\alpha }{2})V_h^{n-1}-(1-\frac{\alpha }{2})U_h^{n-2}$ for $n=2,3,\ldots ,N.$

Now the noniterative scheme is: to find $U_h^{n},\ V_h^{n}\in X_h$, such that for all $1\le n\le N$:

$$\begin{aligned} \begin{aligned} \langle ^RD^{\alpha }_{{\varDelta } t}U_h^{n}, w_{h}\rangle +\langle \nabla U_h^{n,\alpha }, \nabla w_{h}\rangle&=\langle F_{1}(\bar{U}_h^{n,\alpha },\bar{V}_h^{n,\alpha }), w_{h}\rangle ,\quad \forall w_{h}\in X_{h},\\ \langle ^RD^{\alpha }_{{\varDelta } t}V_h^{n}, \omega _{h}\rangle +\langle \nabla V_h^{n,\alpha }, \nabla \omega _{h}\rangle&=\langle F_{2}(\bar{U}_h^{n,\alpha },\bar{V}_h^{n,\alpha }), \omega _{h}\rangle ,\quad \forall \omega _{h}\in X_h,\\ \end{aligned} \end{aligned}$$

(48)

with

$$\begin{aligned} \begin{aligned} \langle ^RD^{\alpha }_{{\varDelta } t}U_h^{1}, w_{h}\rangle +\langle \nabla U_h^{1,\alpha }, \nabla w_{h}\rangle&=\langle F_{1}(U_h^{0},V_h^{0})+F_{1u}(U_h^{0},V_h^{0})(U_h^{1,\alpha }-U_h^{0}),w_h\rangle \\&\quad +\langle F_{1v}(U_h^{0},V_h^{0})(V_h^{1,\alpha }-V_h^{0}), w_{h}\rangle ,\quad \forall w_{h}\in X_{h},\\ \langle ^RD^{\alpha }_{{\varDelta } t}V_h^{1}, \omega _{h}\rangle +\langle \nabla V_h^{1,\alpha }, \nabla \omega _{h}\rangle&=\langle F_{2}(U_h^{0},V_h^{0})+F_{2u}(U_h^{0},V_h^{0})(U_h^{1,\alpha }-U_h^{0}),w_h\rangle \\&\quad +\langle F_{2v}(U_h^{0},V_h^{0})(V_h^{1,\alpha }-V_h^{0}), w_{h}\rangle ,\quad \forall \omega _{h}\in X_h,\\ U_h^0&=0,\quad V_h^0=0,\\ \end{aligned} \end{aligned}$$

(49)

where $F_{iu}(U_h^0,V_h^0)=\frac{\partial F_i(u,v)}{\partial u}|_{(u,v)=(U_h^0,V_h^0)}$ and $F_{iv}(U_h^0,V_h^0)=\frac{\partial F_i(u,v)}{\partial v}|_{(u,v)=(U_h^0,V_h^0)}$ for $i=1,2.$

After using the value of the discrete fractional differential operator $^RD^{\alpha }_{{\varDelta } t},$ it can be observed that the coefficient matrix (Galerkin matrix) corresponding to the linear system (48) is positive definite. Therefore, the existence-uniqueness of the solution $(U_h^n,V_h^n)$ for the above linearized scheme for $n\ge 2$ follows immediately. By the simple application of Proposition 1, the existence-uniqueness of solution $(U_h^1,V_h^1)$ for the system (49) can be obtained in a similar manner as the existence-uniqueness for the solution $(U_h^n,V_h^n)$ of the Scheme (6).

3.1 Error analysis

In this part, we provide a priori bound and convergence estimates for the new linearized fractional Crank–Nicolson–Galerkin finite element scheme (48)–(49). For this purpose, we first need to generalize the fractional Grönwall-type inequality given in Lemma 1. We also require the following results for the generalization of the fractional Grönwall-type inequality.

Define $g_{n}^{(\alpha )}:=\sum _{i=0}^{n} w^{(\alpha )}_i,$ then $g^{(\alpha )}_0=w^{(\alpha )}_0$ and $w^{(\alpha )}_i=g^{(\alpha )}_i - g^{(\alpha )}_{i-1}$ for $1\le i\le n,$ where $w^{(\alpha )}_i$ are defined in (4). Since weights $w^{(\alpha )}_i$ possess the following properties:

$$\begin{aligned} w^{(\alpha )}_0=1, \quad -1<w^{(\alpha )}_1<w^{(\alpha )}_2< \cdots<w^{(\alpha )}_i< \cdots <0,\quad \sum _{i=0}^{\infty }w^{(\alpha )}_i=0; \end{aligned}$$

(50)

therefore, $g^{(\alpha )}_{i-1} > g^{(\alpha )}_{i}$ for $i\ge 1$. Using the definition of $g^{(\alpha )}_n,$ we can re-write (4) as follows:

$$\begin{aligned} ^RD^{\alpha }_{{\varDelta } t}\varphi (t_n)={{\varDelta } t}^{-\alpha }\sum _{i=1}^{n} \left( g_i^{(\alpha )}-g_{i-1}^{(\alpha )}\right) \varphi (t_{n-i})+{\varDelta } t^{-\alpha } g_0^{(\alpha )}\varphi (t_n). \end{aligned}$$

(51)

If $\varphi (0)=0,$ then, from (51), we get

$$\begin{aligned} ^RD^{\alpha }_{{\varDelta } t}\varphi (t_n)={{\varDelta } t}^{-\alpha }\sum _{i=1}^{n} g_{n-i}^{(\alpha )}\delta \varphi (t_i), \end{aligned}$$

(52)

where $\delta \varphi (t_i)=\varphi (t_i)-\varphi (t_{i-1})$ $\forall \ i=1,2,\ldots ,n.$

Lemma 3

(Kumar et al. 2018) Consider the sequence $\{\phi _n\}$ given by

$$\begin{aligned} \phi _0=1, \quad \phi _n=\sum _{i=1}^{n}\left( g^{(\alpha )}_{i-1}-g^{(\alpha )}_i \right) \ \phi _{n-i},\quad n\ge 1. \end{aligned}$$

(53)

Then, $\{\phi _n\}$ satisfies the following properties:

$$\begin{aligned}&\mathrm{(i)}\quad 0<\phi _n<1, \quad \sum _{i=j}^{n}\phi _{n-i} \ g^{(\alpha )}_{i-j}=1, \quad 1\le j\le n, \end{aligned}$$

(54)

$$\begin{aligned}&\mathrm{(ii)} \quad \frac{1}{{\varGamma } \alpha } \sum _{i=1}^{n}\phi _{n-i} \le \frac{n^{\alpha }}{{\varGamma } (1+\alpha )}, \end{aligned}$$

(55)

$$\begin{aligned}&\mathrm{(iii)} \ \frac{1}{{\varGamma } \alpha {\varGamma } (1+(k-1)\alpha )} \sum _{i=1}^{n-1}\phi _{n-i}\ i^{(k-1)\alpha } \le \frac{n^{k \alpha }}{{\varGamma } (1+ k \alpha )}, \end{aligned}$$

(56)

where $k=1,2,\ldots$.

Lemma 4

(Kumar et al. 2018) Consider the matrix

$$\begin{aligned} W = 2\mu {\varDelta } t^{\alpha } \left[ \begin{array}{ccccc} 0&{} \quad \phi _1&{} \quad \cdots &{} \quad \phi _{n-2} &{} \quad \phi _{n-1} \\ 0&{} \quad 0&{} \quad \cdots &{} \quad \phi _{n-3} &{} \quad \phi _{n-2} \\ \vdots &{} \quad \vdots &{} \quad \ddots &{} \quad \vdots &{} \quad \vdots \\ 0&{} \quad 0&{} \quad \cdots &{} \quad 0 &{} \quad \phi _1 \\ 0&{} \quad 0&{} \quad \cdots &{} \quad 0 &{} \quad 0 \\ \end{array} \right] _{n\times n}. \end{aligned}$$

(57)

Then, W satisfies the following properties:

$$\begin{aligned}&\mathrm{(i)} \quad W^l=0, \quad l\ge n, \\&\mathrm{(ii)}\quad W^k \varvec{e}\le \frac{1}{{\varGamma }(1+k\alpha )}[(2{\varGamma } (\alpha )\mu t_n^{\alpha })^k,(2{\varGamma } (\alpha )\mu t_{n-1}^{\alpha })^k,\ldots ,(2{\varGamma } (\alpha )\mu t_1^{\alpha })^k]^{\prime }, \\&\qquad {k=0,1,2,\ldots ,}\\&\mathrm{(iii)} \quad \sum _{k=0}^{l}W^k \varvec{e}=\sum _{k=0}^{n-1}W^k \varvec{e}\le [E_{\alpha }(2{\varGamma } (\alpha )\mu t_n^{\alpha }),E_{\alpha }(2{\varGamma } (\alpha )\mu t_{n-1}^{\alpha }),\ldots ,E_{\alpha }(2{\varGamma } (\alpha )\mu t_1^{\alpha })]^{\prime },\\&\quad l\ge n, \end{aligned}$$

where $\varvec{e}=[1,1,..,1]^{\prime }\in {\mathbb {R}}^n$.

Now, we state, with proof, the fractional Grönwall-type inequality which is relevant in the analysis of linearized-type fully discrete schemes for TFPDEs.

Lemma 5

Let $\{a^n| \ n\ge -1\}$ and $\{b^n| \ n\ge 0\}$ be nonnegative sequences with $a^{-1}= a^{0}=0$ and $\mu _i \ (i=1,2,3)$ be nonnegative constants. For

$$\begin{aligned} ^RD^{\alpha }_{{\varDelta } t}a^1\le \mu _1 a^1 + \mu _2 a^{0}+b^1, \end{aligned}$$

and

$$\begin{aligned} ^RD^{\alpha }_{{\varDelta } t}a^n\le \mu _1 a^n + \mu _2 a^{n-1}+\mu _3 a^{n-2}+b^n,\quad n\ge 2, \end{aligned}$$

(58)

there exists a positive constant ${\varDelta } t^*$, such that, when ${\varDelta } t\le {\varDelta } t^*,$

$$\begin{aligned} a^n\le 2\Big (\frac{t_n^{\alpha }}{\alpha } \ \max _{0\le i\le n}b^i\Big )E_{\alpha }(2 {\varGamma } (\alpha ) \mu t_n^{\alpha }), \quad 1\le n\le N, \end{aligned}$$

(59)

where $E_{\alpha }(z)$=$\sum _{j=0}^{\infty }\frac{z^j}{{\varGamma }(1+j\alpha ) }$ is the Mittag–Leffler function and $\mu =\mu _1+\frac{\mu _2}{\alpha }+\frac{2\mu _3}{\alpha (1-\alpha )}.$

Proof

From the definition of discrete fractional differential operator (52), we re-write (58) as

$$\begin{aligned} \sum _{j=1}^{i}g^{(\alpha )}_{i-j}\delta a^j\le {\varDelta } t^{\alpha }(\mu _1 a^i + \mu _2 a^{i-1}+\mu _3 a^{i-2})+{\varDelta } t^{\alpha }b^i. \end{aligned}$$

(60)

Multiplying by $\phi _{n-i}$ in (60), and taking sum for i from 1 to n to get

$$\begin{aligned} \sum _{i=1}^{n}\phi _{n-i}\sum _{j=1}^{i}g^{(\alpha )}_{i-j}\delta a^j\le {\varDelta } t^{\alpha }\sum _{i=1}^{n}\phi _{n-i}(\mu _1 a^i + \mu _2 a^{i-1}+\mu _3 a^{i-2})+{\varDelta } t^{\alpha }\sum _{i=1}^{n}\phi _{n-i}b^i.\nonumber \\ \end{aligned}$$

(61)

Using properties (54) and (55) of sequence $\{\phi _n\}$ from Lemma 3, we get

$$\begin{aligned} \sum _{i=1}^{n}\phi _{n-i}\sum _{j=1}^{i}g^{(\alpha )}_{i-j}\delta a^j=\sum _{j=1}^{n}\delta a^j\sum _{i=j}^{n}\phi _{n-i}g^{(\alpha )}_{i-j}=\sum _{j=1}^{n}\delta a^j=a^n, \end{aligned}$$

and

$$\begin{aligned} {\varDelta } t^{\alpha }\sum _{i=1}^{n}\phi _{n-i}b^i\le {\varDelta } t^{\alpha } \max _{1\le i\le n} b^{i}\sum _{i=1}^{n}\phi _{n-i}\le \frac{(n{\varDelta } t)^{\alpha }}{\alpha }\max _{1\le i\le n} b^{i}\le \frac{t_n^{\alpha }}{\alpha }\max _{0\le i\le n} b^{i}. \end{aligned}$$

For convenience, set ${\varPsi }_n=\frac{t_n^{\alpha }}{\alpha }\max _{0\le i\le n} b^{i}.$ Also note that ${\varPsi }_k\le {\varPsi }_n$ for $n\ge k\ge 1,$ then we have

$$\begin{aligned} a^n\le 2 {\varPsi }_n +2 {\varDelta } t^{\alpha }\left( \mu _{1}\sum _{i=1}^{n-1}\phi _{n-i}a^{i}+\mu _{2}\sum _{i=2}^{n}\phi _{n-i}a^{i-1}+\mu _{3}\sum _{i=3}^{n}\phi _{n-i}a^{i-2}\right) ,\quad n\ge 1,\nonumber \\ \end{aligned}$$

(62)

when ${\varDelta } t\le \root \alpha \of {\frac{1}{2\mu _1}}.$

Let $\varvec{V}=[a^n, a^{n-1},\ldots , a^1]^{\prime }$; then, we can write (62) in a vector form by

$$\begin{aligned} \varvec{V}\le (\mu _{1}W_{1}+\mu _{2}W_{2}+\mu _{3}W_{3})\varvec{V}+2 {\varPsi }_n \varvec{e}, \end{aligned}$$

(63)

where

$$\begin{aligned} W_1 = 2{\varDelta } t^{\alpha } \left[ \begin{array}{cccccc} 0&{} \quad \phi _1&{} \quad \phi _2&{} \quad \cdots &{} \quad \phi _{n-2} &{} \quad \phi _{n-1} \\ 0&{} \quad 0&{} \quad \phi _1&{} \quad \cdots &{} \quad \phi _{n-3} &{} \quad \phi _{n-2} \\ \vdots &{} \quad \vdots &{} \quad \ddots &{} \quad \vdots &{} \quad \vdots &{} \quad \vdots \\ 0&{} \quad 0&{} \quad 0&{} \quad \cdots &{} \quad \phi _1 &{} \quad \phi _2 \\ 0&{} \quad 0&{} \quad 0&{} \quad \cdots &{} \quad 0 &{} \quad \phi _1 \\ 0&{} \quad 0&{} \quad 0&{} \quad \cdots &{} \quad 0 &{} \quad 0 \\ \end{array} \right] _{n\times n}, \end{aligned}$$

$$\begin{aligned} W_2 = 2{\varDelta } t^{\alpha } \left[ \begin{array}{cccccc} 0&{} \quad \phi _0&{} \quad \phi _1&{} \quad \cdots &{} \quad \phi _{n-3} &{} \quad \phi _{n-2} \\ 0&{} \quad 0&{} \quad \phi _0&{} \quad \cdots &{} \quad \phi _{n-4} &{} \quad \phi _{n-3} \\ \vdots &{} \quad \vdots &{} \quad \ddots &{} \quad \vdots &{} \quad \vdots &{} \quad \vdots \\ 0&{} \quad 0&{} \quad 0&{} \quad \cdots &{} \quad \phi _0 &{} \quad \phi _1 \\ 0&{} \quad 0&{} \quad 0&{} \quad \cdots &{} \quad 0 &{} \quad \phi _0 \\ 0&{} \quad 0&{} \quad 0&{} \quad \cdots &{} \quad 0 &{} \quad 0 \\ \end{array} \right] _{n\times n}, \end{aligned}$$

and

$$\begin{aligned} W_3 = 2{\varDelta } t^{\alpha } \left[ \begin{array}{cccccc} 0&{} \quad 0&{} \quad \phi _0&{} \quad \cdots &{} \quad \phi _{n-4} &{} \quad \phi _{n-3} \\ 0&{} \quad 0&{} \quad 0&{} \quad \cdots &{} \quad \phi _{n-5} &{} \quad \phi _{n-4} \\ \vdots &{} \quad \vdots &{} \quad \ddots &{} \quad \vdots &{} \quad \vdots &{} \quad \vdots \\ 0&{} \quad 0&{} \quad 0&{} \quad \cdots &{} \quad 0 &{} \quad \phi _0 \\ 0&{} \quad 0&{} \quad 0&{} \quad \cdots &{} \quad 0 &{} \quad 0 \\ 0&{} \quad 0&{} \quad 0&{} \quad \cdots &{} \quad 0 &{} \quad 0 \\ \end{array} \right] _{n\times n}. \end{aligned}$$

From the definition of $\{\phi _n\},$ one can easily obtain

$$\begin{aligned} \phi _{n-k}\le \frac{\phi _n}{\left( g^{(\alpha )}_{k-1}-g^{(\alpha )}_{k} \right) } \quad \text{ for } \ \ k=1,2. \end{aligned}$$

Thus, we get

$$\begin{aligned} W_2\varvec{V}\le \frac{1}{\alpha }W_1\varvec{V} \quad \text{ and }\quad W_3\varvec{V}\le \frac{2}{\alpha (1-\alpha )}W_1\varvec{V}. \end{aligned}$$

(64)

Using (64) in (63), we have

$$\begin{aligned} \varvec{V}\le \left( \mu _{1}+\frac{\mu _{2}}{\alpha }+\frac{2\mu _{3}}{\alpha (1-\alpha )}\right) W_1\varvec{V}+2 {\varPsi }_n \varvec{e}=W\varvec{V}+2 {\varPsi }_n \varvec{e}, \end{aligned}$$

where W is defined in (57) with $\mu =\mu _{1}+\frac{\mu _{2}}{\alpha }+\frac{2\mu _{3}}{\alpha (1-\alpha )}.$

Furthermore

$$\begin{aligned} \begin{aligned} \varvec{V}&\le W\varvec{V}+2 {\varPsi }_n \varvec{e}\le W(W\varvec{V}+2 {\varPsi }_n \varvec{e} )+2 {\varPsi }_n \varvec{e}=W^2\varvec{V}+2 {\varPsi }_n \sum _{k=0}^{1}W^{k}\varvec{e}\\&\le \ldots \le W^n \varvec{V}+2 {\varPsi }_n \sum _{k=0}^{n-1}W^{k}\varvec{e}. \end{aligned} \end{aligned}$$

Using the Lemma 4, we obtain (59) and this completes the proof of Lemma 5. $\square$

Theorem 5

Let $(U_h^n,V_h^n)$ be the solution of fully discrete scheme (48)–(49). Then, there exists a positive constant ${{\varDelta } t}^{*}$, such that when ${\varDelta } t\le {{\varDelta } t}^{*},$ the solution $(U_h^n,V_h^n)$ satisfies

$$\begin{aligned} \Vert U_h^n\Vert +\Vert V_h^n\Vert \le C, \end{aligned}$$

(65)

where $n= 1,2,\ldots ,N$ and C is a positive constant independent of h and ${\varDelta } t.$

Proof

First, we consider (49) which represents the case $n=1$ of the linearized scheme. Similar to the proof of Theorem 2, we have the following estimate for the solution $(U_h^1, V_h^1)$:

$$\begin{aligned} {^RD}^{\alpha }_{{\varDelta } t}(\Vert U_h^{1}\Vert ^2+\Vert V_h^{1}\Vert ^2)\le C\big (1+\Vert U_h^1\Vert ^2+\Vert V_h^1\Vert ^2\big ). \end{aligned}$$

(66)

Using the same argument as above, we can further derive the following estimate for the solution $(U_h^n,V_h^n)$ of the linearized scheme (48) which represents the case $n\ge 2$:

$$\begin{aligned} \begin{aligned} {^RD}^{\alpha }_{{\varDelta } t}(\Vert U_h^{n}\Vert ^2+\Vert V_h^{n}\Vert ^2)&\le C\Big (1+(\Vert U_h^n\Vert ^2+\Vert V_h^n\Vert ^2)+(\Vert U_h^{n-1}\Vert ^2+\Vert V_h^{n-1}\Vert ^2)\\&\quad +(\Vert U_h^{n-2}\Vert ^2+\Vert V_h^{n-2}\Vert ^2)\Big ) \quad \text{ for } \ \ \ n\ge 2. \end{aligned} \end{aligned}$$

(67)

With an application of Lemma 5, there exists a positive constant ${{\varDelta } t}^*$, such that when ${\varDelta } t\le {{\varDelta } t}^*$, then

$$\begin{aligned} \begin{aligned} \Vert U_h^{n}\Vert +\Vert V_h^{n}\Vert&\le C \quad \text{ for } \ \ 1\le n\le N. \end{aligned} \end{aligned}$$

This completes the proof. $\square$

Theorem 6

Let $(u^n, v^n)$ be the solution of (1a)–(1d) and $(U_h^n,V_h^n)$ be the solution of fully discrete scheme (48)–(49) Then, there exists a positive constant ${{\varDelta } t}^{*}$, such that when ${\varDelta } t\le {{\varDelta } t}^{*},$ the solution $(U_h^n,V_h^n)$ satisfies

$$\begin{aligned} \Vert u^n-U_h^n\Vert +\Vert v^n-V_h^n\Vert \le C\big ({\varDelta } t^{2}+h^2\big ), \end{aligned}$$

(68)

where $n= 1,2,\ldots ,N$ and C is a positive constant independent of h and ${\varDelta } t.$

Proof

First, we consider (49) which is the case for $n=1$. From (1a)–(1b), we have

$$\begin{aligned} ^RD^{\alpha }_{{\varDelta } t}u^1-{\varDelta } u^{1-\frac{\alpha }{2}}= & {} F_1\left( u^{0},v^{0} \right) +F_{1u}\left( u^{0},v^{0} \right) \left( u^{1,\alpha }-u^0 \right) +F_{1v}\left( u^{0},v^{0}\right) \left( v^{1,\alpha }-v^0 \right) +E_1^1,\\ ^RD^{\alpha }_{{\varDelta } t}v^1-{\varDelta } v^{1-\frac{\alpha }{2}}= & {} F_2 \left( u^{0},v^{0} \right) +F_{2u}\left( u^{0},v^{0}\right) \left( u^{1,\alpha }-u^0 \right) +F_{2v} \left( u^{0},v^{0} \right) \left( v^{1,\alpha }-v^0 \right) +E_2^1, \end{aligned}$$

where errors $E_1^{1}$ and $E_2^1$ are given by

$$\begin{aligned} \begin{aligned} E_1^1&=\, ^RD^{\alpha }_{{\varDelta } t}u^1- \ ^RD^{\alpha }_{{\varDelta } t_{1-\frac{\alpha }{2}}}u+F_1(u^{1-\frac{\alpha }{2}},v^{1-\frac{\alpha }{2}})-\Big (F_1 \left( u^{0},v^{0} \right) +F_{1u} \left( u^{0},v^{0} \right) \left( u^{1-\frac{\alpha }{2} }-u^0 \right) \\&\quad +F_{1v}\left( u^{0},v^{0}\right) (v^{1-\frac{\alpha }{2}}-v^0)\Big )+F_1 \left( u^{0},v^{0} \right) +F_{1u} \left( u^{0},v^{0}\right) \left( u^{1-\frac{\alpha }{2} }-u^0 \right) \\&\quad +F_{1v} \left( u^{0},v^{0} \right) \left( v^{1-\frac{\alpha }{2}}-v^0 \right) -\Big (F_1(u^{0},v^{0})+F_{1u}(u^{0},v^{0})(u^{1,\alpha }-u^0)\\&\quad +F_{1v} \left( u^{0},v^{0} \right) \left( v^{1,\alpha }-v^0 \right) \Big ),\\ E_2^1&=\, ^RD^{\alpha }_{{\varDelta } t}v^1- \ ^RD^{\alpha }_{{\varDelta } t_{1-\frac{\alpha }{2}}}v+F_2 \left( u^{1-\frac{\alpha }{2}},v^{1-\frac{\alpha }{2}} \right) -\Big (F_2(u^{0},v^{0})+F_{2u}(u^{0},v^{0})(u^{1-\frac{\alpha }{2} }-u^0)\\&\quad +F_{2v} \left( u^{0},v^{0} \right) \left( v^{1-\frac{\alpha }{2}}-v^0 \right) \Big )+F_2 \left( u^{0},v^{0} \right) +F_{2u} \left( u^{0},v^{0} \right) \left( u^{1-\frac{\alpha }{2} }-u^0 \right) \\&\quad +F_{2v} \left( u^{0},v^{0} \right) \left( v^{1-\frac{\alpha }{2}}-v^0 \right) -\Big (F_2 \left( u^{0},v^{0} \right) +F_{2u} \left( u^{0},v^{0} \right) \left( u^{1,\alpha }-u^0 \right) \\&\quad +F_{2v} \left( u^{0},v^{0} \right) \left( v^{1,\alpha }-v^0 \right) \Big ).\\ \end{aligned} \end{aligned}$$

(69)

Using (3), hypothesis $H1,\ H2$, and Taylor expansion in (69), errors are bounded by

$$\begin{aligned} \begin{aligned} \Vert E_1^1\Vert \le C \left( {\varDelta } t^2 \right) , \ \ \Vert E_2^1\Vert \le C \left( {\varDelta } t^2 \right) . \end{aligned} \end{aligned}$$

Similar to the proof of Theorem 4, we can get the following estimate for $\theta _{1h}^1,\ \theta _{2h}^1$:

$$\begin{aligned} \begin{aligned} {^RD}^{\alpha }_{{\varDelta } t}\left( \Vert {\theta _{1h}^1}\Vert ^2+\Vert {\theta _{2h}^1}\Vert ^2\right)&\le \left( 1-\frac{\alpha }{2}\right) ^2(3+4C_0^*+4C_0^{**}) (\Vert \theta _{1h}^1\Vert ^2+\Vert \theta _{2h}^1\Vert ^2)\\&\quad +C\big ({\varDelta } t^{2}+h^2\big )^2, \end{aligned} \end{aligned}$$

(70)

where $C_0^*=\max \{|F_{1u}(0,0)|^2,|F_{1v}(0,0)|^2\}$ and $C_0^{**}=\max \{|F_{2u}(0,0)|^2,|F_{2v}(0,0)|^2\}$.

Next, for case $n\ge 2,$ we have

$$\begin{aligned} ^RD^{\alpha }_{{\varDelta } t}u^n-{\varDelta } u^{n-\frac{\alpha }{2}}= & {} F_1(\bar{u}^{n,\alpha },\bar{v}^{n,\alpha })+E_1^n,\\ ^RD^{\alpha }_{{\varDelta } t}v^n-{\varDelta } v^{n-\frac{\alpha }{2}}= & {} F_2(\bar{u}^{n,\alpha },\bar{v}^{n,\alpha })+E_2^n, \end{aligned}$$

where $E_1^{n}$ and $E_2^n$ are given by

$$\begin{aligned} \begin{aligned} E_1^n&=\, ^RD^{\alpha }_{{\varDelta } t}u^n- \ ^RD^{\alpha }_{{\varDelta } t_{n-\frac{\alpha }{2}}}u+F_1(u^{n-\frac{\alpha }{2}},v^{n-\frac{\alpha }{2}})-F_1(\bar{u}^{n,\alpha },\bar{v}^{n,\alpha }),\\ E_2^n&=\, ^RD^{\alpha }_{{\varDelta } t}v^n- \ ^RD^{\alpha }_{{\varDelta } t_{n-\frac{\alpha }{2}}}v+F_2(u^{n-\frac{\alpha }{2}},v^{n-\frac{\alpha }{2}})-F_2(\bar{u}^{n,\alpha },\bar{v}^{n,\alpha }). \end{aligned} \end{aligned}$$

Again, using (3), hypothesis H1, and Taylor expansion to get

$$\begin{aligned} \begin{aligned} \Vert E_1^n\Vert \le C ({\varDelta } t^2), \ \ \Vert E_2^n\Vert \le C ({\varDelta } t^2). \end{aligned} \end{aligned}$$

Similar to the proof of Theorem 4, we can obtain the following estimate for $\theta _{1h}^n,\ \theta _{2h}^n$ for $n\ge 2$:

$$\begin{aligned} \begin{aligned} {^RD}^{\alpha }_{{\varDelta } t}\left( \Vert {\theta _{1h}^n}\Vert ^2+\Vert {\theta _{2h}^n}\Vert ^2\right)&\le \mu _1 (\Vert \theta _{1h}^n\Vert ^2+\Vert \theta _{2h}^n\Vert ^2)+\mu _2(\Vert \theta _{1h}^{n-1}\Vert ^2+\Vert \theta _{2h}^{n-1}\Vert ^2)\\&\quad +\mu _3(\Vert \theta _{1h}^{n-2}\Vert ^2+\Vert \theta _{2h}^{n-2}\Vert ^2) +C\big ({\varDelta } t^{2}+h^2\big )^2, \end{aligned} \end{aligned}$$

(71)

where

Table 1 $L^2({\varOmega })$ errors and convergence rates in the spatial direction for the scheme (6) for Example 1

Table 2 $L^2({\varOmega })$ errors and convergence rates in the spatial direction for the scheme (48)–(49) for Example 1

$$\begin{aligned} \begin{aligned} \mu _1&=2\left( 1-\frac{\alpha }{2}\right) ^2\max \left\{ L_1+2,L_2+2\right\} ,\\ \mu _2&=\max \Big \{2\left( \frac{\alpha }{2}\right) ^2(L_1+2)+8\left( 2-\frac{\alpha }{2}\right) ^2(L_1+L_2),\\&\quad 2\left( \frac{\alpha }{2}\right) ^2(L_2+2)+8\left( 2-\frac{\alpha }{2}\right) ^2(L_1+L_2) \Big \},\\ \mu _3&= 8\left( 1-\frac{\alpha }{2}\right) ^2\left( L_1+L_2\right) . \end{aligned} \end{aligned}$$

Using Lemma 5 in (70) and (71), there exists a positive constant ${{\varDelta } t}^*$, such that when ${\varDelta } t\le {{\varDelta } t}^*$, then

$$\begin{aligned} \Vert {\theta _{1h}^n}\Vert +\Vert {\theta _{2h}^n}\Vert \le C\big ({\varDelta } t^{2}+h^2\big ). \end{aligned}$$

Now, an application of triangular inequality and Theorem 3 completes the proof of Theorem 6. $\square$

Table 3 $L^2({\varOmega })$ errors and convergence rates in the temporal direction for the scheme (6) for Example 1

Table 4 $L^2({\varOmega })$ errors and convergence rates in the temporal direction for the scheme (48)–(49) for Example 1

Table 5 $L^2({\varOmega })$ errors and convergence rates in the spatial direction for the scheme (6) for Example 2

Table 6 $L^2({\varOmega })$ errors and convergence rates in the spatial direction for the scheme (48)–(49) for Example 2

Table 7 $L^2({\varOmega })$ errors and convergence rates in the temporal direction for the scheme (6) for Example 2

Table 8 $L^2$-errors and convergence rates in the temporal direction for the scheme (48)–(49) for Example 2

Table 9 $L^2({\varOmega })$ errors and convergence rates in the spatial direction for the scheme (6) for Example 3

4 Numerical examples

In this section, we test the computational efficiency and numerical accuracy of proposed schemes (6) and (48)–(49) by three numerical examples to verify theoretical estimates. For the one-dimensional problem, we consider the spatial domain ${\varOmega }=(0,1)$ and for the two-dimensional problem, we take ${\varOmega } =(0,1)\times (0,1)$. In Newton’s method, tolerance is taken to be $\epsilon =10^{-7}$. The errors and convergence rates are calculated in $L^2({\varOmega })$ norm at final time level T for different values of $\alpha$. All numerical experiments are performed on a Windows 10, 64-bit operating system with 8 GB RAM and Intel(R) Core 3.41 GHz processor using the software MATLAB.

Table 10 $L^2({\varOmega })$ errors and convergence rates in the spatial direction for the scheme (48)–(49) for Example 3

Table 11 $L^2({\varOmega })$ errors and convergence rates in the temporal direction for the scheme (6) for Example 3

Table 12 $L^2({\varOmega })$ errors and convergence rates in temporal direction for the scheme (48)–(49) for Example 3

Table 13 $L^2({\varOmega })$ errors and convergence rates in the temporal direction for the scheme (75) with L1 approximation for Example 3

Table 14 $L^2({\varOmega })$ errors and convergence rates in the temporal direction for the scheme (75) with GL approximation for Example 3

Example 1

Consider the following one-dimensional problem:

$$\begin{aligned} \begin{aligned} ^C{D}^{\alpha }_{t}u-\frac{\partial ^2 u}{\partial x^2}&= F_1(u,v)+f_1, \quad x\in {\varOmega }, \quad t\in (0,1],\\ ^C{D}^{\alpha }_{t}v-\frac{\partial ^2 v}{\partial x^2}&= F_2(u,v)+f_2, \quad x\in {\varOmega }, \quad t\in (0,1],\\ u(x,t)&= v(x,t)=0, \quad x\in \partial {\varOmega }, \quad t\in (0,1], \\ u(x,0)&= v(x,0)=0,\quad x\in {\varOmega }, \end{aligned} \end{aligned}$$

(72)

where

$$\begin{aligned} \begin{aligned} F_1(u,v)&=5+u^4+v^5,\\ F_2(u,v)&=10+u^5+v^4. \end{aligned} \end{aligned}$$

Source terms $f_1, \ f_2$ are calculated using the exact solution (u, v) which is given by

$$\begin{aligned} u(x,t)=t^{2+\alpha } \sin (2\pi x),\ v(x,t)= t^{3-\alpha } \sin (\pi x), \end{aligned}$$

where $x\in [0,1].$

In this example, we first validate the accuracy of schemes (6) and (48)–(49) in the spatial direction. We take ${\varDelta } t= 10^{-3}$ sufficiently small temporal step size with different values of h. Next, we confirm the accuracy of schemes (6) and (48)–(49) in the temporal direction. We take $h=2\times 10^{-4}$ sufficiently small spatial step size with different values of ${\varDelta } t$.

$L^2({\varOmega })$ errors and convergence rates for schemes (6) and (48)–(49) in the spatial direction are given in Tables 1 and 2, respectively. Similarly, $L^2({\varOmega })$ errors and convergence rates corresponding to schemes (6) and (48)–(49) in the temporal direction are given in Tables 3 and 4, respectively. It can be seen that, for $\alpha =0.4,\ 0.6,$ these estimated convergence rates are tending to limit close to 2 for both schemes, which is in accordance with theoretically derived convergence orders.

Example 2

Consider the following two-dimensional problem:

$$\begin{aligned} \begin{aligned} ^C{D}^{\alpha }_{t}u-{\varDelta }{u}&= F_1(u,v)+f_1, \quad x\in {\varOmega }, \quad t\in (0,1],\\ ^C{D}^{\alpha }_{t}v-{\varDelta }{ v}&= F_2(u,v)+f_2, \quad x\in {\varOmega }, \quad t\in (0,1],\\ u(x,t)&= v(x,t)=0, \quad x\in \partial {\varOmega },\quad t\in (0,1], \\ u(x,0)&= v(x,0)=0,\quad x\in {\varOmega }, \end{aligned} \end{aligned}$$

(73)

where

$$\begin{aligned} \begin{aligned} F_1(u,v)&=\sin (u)+v^2,\\ F_2(u,v)&=u^2+\sin (v),\\ \end{aligned} \end{aligned}$$

and source terms $f_1, \ f_2$ are calculated using the exact solution (u, v) which is given by

$$\begin{aligned} u(x,t)=t^3\sin (2\pi x_1)\sin (2\pi x_2),\ v(x,t)=t^4 \sin (\pi x_1)\sin (\pi x_2), \end{aligned}$$

where $x=(x_1,x_2)\in [0,1]\times [0,1].$

Again for this problem, we first validate the accuracy of schemes (6) and (48)–(49) in the spatial direction. We take ${\varDelta } t= 10^{-3}$ sufficiently small temporal step size with different values of h. Next, we confirm the accuracy of schemes (6) and (48)–(49) in the temporal direction. We take $h=\frac{1}{525}$ sufficiently small spatial step size with different values of ${\varDelta } t$.

In addition, $L^2({\varOmega })$ errors and convergence rates for schemes (6) and (48)–(49) in the spatial direction are given in Tables 5 and 6, respectively. Similarly, $L^2({\varOmega })$ errors and convergence rates corresponding to schemes (6) and (48)–(49) in the temporal direction are given in Tables 7 and 8, respectively. It can be seen that, for $\alpha =0.4,\ 0.6,$ these estimated convergence rates are tending to limit close to 2 for both schemes, which is in accordance with theoretically derived convergence orders.

Example 3

Consider the following one-dimensional problem:

$$\begin{aligned} \begin{aligned} ^C{D}^{\alpha }_{t}u-\frac{\partial ^2 u}{\partial x^2}&= F_1(u,v)+f_1, \quad x\in {\varOmega }, \quad t\in (0,0.5],\\ ^C{D}^{\alpha }_{t}v-\frac{\partial ^2 v}{\partial x^2}&= F_2(u,v)+f_2, \quad x\in {\varOmega }, \quad t\in (0,0.5],\\ u(x,t)&= v(x,t)=0, \quad x\in \partial {\varOmega }, \quad t\in (0,0.5], \\ u(x,0)&= v(x,0)=0,\quad x\in {\varOmega }, \end{aligned} \end{aligned}$$

(74)

where

$$\begin{aligned} \begin{aligned} F_1(u,v)&=u^2+\sin (u)+v^2,\\ F_2(u,v)&=u^2+\cos (v)+v^2. \end{aligned} \end{aligned}$$

Source terms $f_1, \ f_2$ are calculated using the exact solution (u, v) which is given by

$$\begin{aligned} u(x,t)=t^{3+\alpha } x(1-x)\mathrm{e}^x,\ v(x,t)= t^{4-\alpha }x(1-x)\mathrm{e}^x, \end{aligned}$$

where $x\in [0,1]$. In this example, we first verify the spatial accuracy of schemes (6) and (48)–(49) by refining the spatial step size h for fixed ${\varDelta } t= 2\times 10^{-4}$. Next, we validate the temporal accuracy of schemes (6) and (48)–(49) by refining the temporal step size ${\varDelta } t$ for fixed $h= 2\times 10^{-4}$.

We report $L^2({\varOmega })$ errors and convergence rates for schemes (6) and (48)–(49) in the spatial direction in Tables 9 and 10, respectively. Similarly, $L^2({\varOmega })$ errors and convergence rates corresponding to schemes (6) and (48)–(49) in the temporal direction are given in Tables 11 and 12, respectively. We note that, for $\alpha =0.1,\ 0.4,\ 0.6,\ 0.9,$ these estimated convergence rates are in accordance with theoretically derived convergence orders.

To compare our numerical results with the other methods in the literature, we propose another fully discrete Galerkin finite element scheme in a unified way. The scheme is used to approximate the solution $u(t_n),\ v(t_n)$ by $U_h^{n},\ V_h^{n}\in X_h$, such that for each $n=1,2,3,\ldots ,N,$ we have

$$\begin{aligned} \begin{aligned} \langle ^RD^{\alpha }_{N}U_h^{n}, w_{h}\rangle +\langle \nabla U_h^{n}, \nabla w_{h}\rangle&=\langle F_{1}(U_h^{n},V_h^{n}), w_{h}\rangle ,\quad \forall w_{h}\in X_{h},\\ \langle ^RD^{\alpha }_{N}V_h^{n}, \omega _{h}\rangle +\langle \nabla V_h^{n}, \nabla \omega _{h}\rangle&=\langle F_{2}(U_h^{n},V_h^{n}), \omega _{h}\rangle ,\quad \forall \omega _{h}\in X_h,\\ U_h^0=&0,\quad V_h^0=0,\\ \end{aligned} \end{aligned}$$

(75)

where the discrete operator $^RD^{\alpha }_{N}$ denotes either L1 approximation (Lin and Xu 2007) or GL approximation (Podlubny 1999).

The comparison of the scheme (6) with the L1-Galerkin finite element scheme and the GL-Galerkin finite element scheme is illustrated for Example 3. The validation of the accuracy of the scheme (75) is done by selecting the same ${\varDelta } t$ and h as in Example 3. Due to the same convergence order in the spatial direction, we only include the numerical results in temporal direction for the scheme (75) with L1 approximation and GL approximation in Tables 13 and 14, respectively. Theoretically, the L1 approximation has $O({\varDelta } t^{2-\alpha })$ accuracy (Lin and Xu 2007), while GL approximation is $O({\varDelta } t)$ accurate (Podlubny 1999). Tables 13 and 14 report that the temporal convergence rates are in accordance with theoretical convergence order. We conclude that the Galerkin finite element scheme (6) with fractional Crank–Nicolson method provides $O({\varDelta } t^2+h^2)$ accuracy, whereas the scheme (75) with L1 and GL approximation is $O({\varDelta } t^{2-\alpha }+h^2)$ and $O({\varDelta } t+h^2)$ accurate, respectively. Thus, the schemes based on fractional Crank–Nicolson method have superior convergence in the temporal direction as compared to the L1 method as well as GL approximation.

5 Conclusions

In this study, two new fully discrete schemes for solving coupled time-fractional nonlinear diffusion system are proposed. Well-posedness results are discussed at discrete level for both schemes. We established discrete fractional Grönwall-type inequality for GL approximation to the Riemann–Liouville fractional derivative which is useful in the analysis of linearized schemes for TFPDEs. Furthermore, convergence estimates in $L^2({\varOmega })$ norm for proposed schemes are derived. Numerical results are provided in support of our theoretical estimates, thus providing $O({\varDelta } t^2+h^2)$ accuracy. In addition, the proposed fractional Crank–Nicolson method is compared with some existing methods in the literature.