Numerical solution of singular boundary value problems using Green’s function and improved decomposition method

Abstract

In this work, an effective technique for solving a class of singular two point boundary value problems is proposed. This technique is based on the Adomian decomposition method (ADM) and Green’s function. The technique relies on constructing Green’s function before establishing the recursive scheme for the solution components. In contrast to the existing recursive schemes based on ADM, the proposed recursive scheme avoids solving a sequence of nonlinear algebraic or transcendental equations for the undetermined coefficients. The approximate solution is obtained in the form of series with easily calculable components. For the completeness, the convergence and error analysis of the proposed scheme is supplemented. Moreover, the numerical examples are included to demonstrate the accuracy, applicability, and generality of the proposed scheme. The results reveal that the method is very effective, straightforward, and simple.

1 Introduction

The aim of this article is to introduce an improved decomposition method with Green’s function for the approximate solution of the following class of singular two-point boundary value problems [1–3]:

(1.1)

and subject to the following boundary conditions:

(1.2)

where α ₁, β ₁>0, γ ₁, and η ₁ are any finite real constants. We assume that for any $(x,y)\in([0,1]\times\mathbb{R})$, the function f(x,y) and ∂f/∂y are continuous and ∂f/∂y≥0. The problem of type (1.1) arises very frequently in applied sciences and in physiological studies. For example, in the study of distribution of heat sources in the human head [4] and steady-state oxygen diffusion in a spherical cell with Michaelis-Menten uptake kinetics [5]. In particular, when α=0 and f(x,y)=x ^−1/2 y ^3/2, (1.1) is known as Thomas-Fermi equation [6].

Recently, a great deal of interest has been focused in the study of (1.1) and (1.2) (see for example [1–3, 6–12]) and many of the references therein. The main difficulty of the problem (1.1) is that the singularity behavior occurs at x=0. A number of methods has been used to solve such singular boundary value problems. In [7], a standard three-point finite difference scheme was used with uniform mesh for the solution of problem (1.1) for α∈(0,1). In [1, 3], the finite difference methods were considered to obtain the numerical results. The numerical method based on Green’s function was applied to get numerical solutions in [2]. In [11], the novel approach that combines a modified decomposition method with the cubic B-spline collocation technique was presented to obtain approximate solution. Recently, a new modified decomposition method was applied to handle these problems (see [12]). These numerical methods have many advantages, but a huge amount of computational work is needed to obtain accurate numerical solution especially for nonlinear problems.

1.1 Adomian decomposition method (ADM)

In this subsection, we briefly describe standard ADM or MADM for nonlinear singular boundary value problems.

In recent years, many authors [9–28] have shown interest to study of the ADM for different scientific models. Adomian [21] asserted that the ADM provides an efficient and computationally suitable method for generating approximate series solution for a large class of differential equations.

According to Wazwaz [25], (1.1) in the operator form can be written as

(1.3)

where $\mathcal{L}$ is a linear differential operator defined by

$$\mathcal{L}=x^{-\alpha}\frac{d}{dx} \biggl(x^{\alpha} \frac{d}{dx} \biggr). $$

The inverse operator $\mathcal{L}^{-1}$ was proposed as (see [25])

(1.4)

Operating the inverse linear operator $\mathcal{L}^{-1}(\cdot)$ on both sides of (1.3) yields

(1.5)

The solution y and the nonlinear function N(y)≡f(x,y) are decomposed by infinite series as

(1.6)

where A _n are Adomian polynomials that can be constructed for various classes of nonlinear functions with the formula given in [18] as:

(1.7)

Note that Adomian’s polynomial can be generated from Taylor expansion of N(y) about the first component y ₀, i.e., $N(y)=\sum_{k=0}^{\infty}A_{k}=\sum_{k=0}^{\infty}\frac{[y-y_{0}]^{k}}{k!}N^{k}(y_{0})$.

Substituting the series (1.6) into (1.5), we obtain

(1.8)

On comparing both sides of (1.8), the standard ADM is given by

(1.9)

and modified ADM is given by

(1.10)

Thus all components y _n can be calculated recurrently, the series solution of y follows immediately with the undetermined coefficient y′(0), and the unknown constant y′(0) will be determined later using boundary conditions at x=1 (see [11, 22, 23, 28]). The n-term truncated approximate series solution is then given by $\phi_{n}(x)=\sum_{m=0}^{n} y_{m}(x)$.

The ADM has been used for solving nonlinear boundary value problems by several researchers [9–12, 19, 20, 22–24, 26, 27]. Solving such problems using standard ADM or MADM is always a computationally involved task as it requires the computation of undetermined coefficients in a sequence of nonlinear algebraic equations which increases the computational work (see [9, 11, 12, 22–24]). Major disadvantage of the earlier methods for solving nonlinear BVPs is that we need to solve a sequence of growingly higher order polynomials or more difficult transcendental equations [9, 11, 22, 24]. For example, consider nonlinear equation

(1.11)

Applying the standard ADM scheme (1.9) with zeroth component y ₀=ηx, where y′(0)=η to the above problem (1.11), we obtain the components as

and the n-term approximate solutions ϕ _n (x) are given by

One can note that the above calculations become more and more complicated and cannot lead to accurate results for the other approximations. To obtain approximate solution, the other boundary condition at x=1 is imposed on ϕ _n , and solving for η, we obtain the approximate solutions. However, solving such transcendental equation for η require additional computational work, and η may not be uniquely determined (see [9, 12, 22, 24]). In order to avoid solving such transcendental equations for nonlinear boundary value problems, some modification of ADM were proposed in [10, 26, 27].

The main aim of this paper is to introduce a modification of the ADM which combines with Green’s function to overcome the difficulties occurred in the standard ADM or MADM for solving nonlinear singular boundary value problems (1.1). We propose an improved recursion scheme which does not require the computation of unknown constants, that is, without solving a sequence of growingly higher order polynomial or difficult transcendental equations to obtain unknown constant [9, 11, 12, 22, 24, 28]. The main advantage of our proposed method is that it provides a direct recursive scheme for solving the singular boundary value problem.

The rest of paper is organized as follows. In Sect. 2, the description of improved recursive scheme based on Green’s function is presented. In Sect. 3, the convergence of improved recursive scheme is discussed. In Sect. 4, we illustrate our method with numerical results along with the graphical representation. In Sect. 5, conclusion is given.

2 Improved decomposition method

In this section, we propose an improved decomposition method based on Green’s function for solving nonlinear singular two point boundary value problems.

The corresponding homogeneous problem of (1.1) is given by:

and its unique solution is

(2.1)

Let us again consider the problem (1.1) with homogeneousness boundary conditions

(2.2)

The Green’s function of (2.2) can be easily constructed and it is given by

(2.3)

Note that construction of green’s function is presented in the Appendix.

Then the exact solution of (2.2) is given by

(2.4)

Therefore, we obtain the solution of (1.1) as $y(x)=\hat {y}(x)+\tilde{y}(x)$, that is,

(2.5)

Note that the right hand side of (2.5) does not involve any undetermined coefficients.

We now decompose the solution y(x) by a series

(2.6)

and the nonlinear function f(x,y) is decomposed by series

(2.7)

where A _n (y ₀,y ₁,…,y _n ) are Adomian polynomials [18].

Substituting the series (2.6) and (2.7) into (2.5), we obtain

(2.8)

Comparing both sides of (2.8), the improved decomposition method is given by

(2.9)

Note that the improved recursive scheme (2.9) does not require any additional computational work for unknown constants. This modification also avoids solving a sequence of nonlinear algebraic or transcendental equations for the undetermined coefficients with multiple roots, which is required for solution by several earlier modified recursion schemes using the ADM or MADM [9, 11, 23, 24, 28].

The above improved recursive scheme gives the complete determination of solution components y _n and hence, n-term approximate series solution can be obtained as

(2.10)

3 Convergence analysis

In this section, we shall discuss the convergence analysis of improved decomposition method for singular boundary value problem (1.1). To do this, note that (2.5) can be written in the operator equation form as

(3.1)

where g and $\mathcal{N}(y)$ are given by

(3.2)

(3.3)

Note that the maximum value of the Green’s function (2.3) can easily be obtained and it is given by

(3.4)

Lemma 3.1

Let X=C[0,1] be the Banach space with the norm ∥y(x)∥=max _x∈[0,1]|y(x)|. Defining the mapping $\mathcal{N}:X\rightarrow X$, where $\mathcal{N}$ is nonlinear operator defined by (3.3). Assume that the function f(x,y) satisfies the Lipschitz condition |f(x,y ₁)−f(x,y ₂)|≤L|y ₁−y ₂| for all y ₁, y ₂∈X. Then the operator $\mathcal{N}$ satisfies the Lipschitz condition with Lipschitz constant δ=ML, where M is given by (3.4).

Proof

Consider for any y ₁, y ₂∈X, we have

Thus, we have

(3.5)

where δ=ML. Under the condition 0≤δ<1 the mapping $\mathcal{N}$ is contraction therefore, by Banach fixed-point theorem for contraction there exits a unique solution of problem (1.1). □

The improved decomposition method for (3.1) is equivalent to the following recursive scheme

(3.6)

Finding the solution of (3.1) is equivalent to find the sequence {ψ _n } such that ψ _n =y ₀+y ₁+⋯+y _n satisfies the (3.6).

In following theorem, we shall give the convergence of the sequence {ψ _n } to the exact solution y of (3.1).

Theorem 3.1

Let $\mathcal{N}(y)$ be the nonlinear operator defined by (3.3) which satisfies the Lipschitz condition with Lipschitz constant δ<1. If ∥y ₀∥<∞, then there holds ∥y _k+1∥≤δ∥y _k ∥, k=0,1,2,… , and the sequence {ψ _n } defined by (2.10) converges to y.

Proof

Since

we have y _k+1=ψ _k+1−ψ _k , k=1,2,… .

We now show that the sequence {ψ _n } is convergent sequence. To prove this, it is sufficient to show that {ψ _n } is Cauchy sequence in Banach space X=C[0,1]. Using (3.5) and (3.6), we have

Thus we obtain

Now for all $n,m\in\mathbb{N}$, with n≥m, we have

Since 0≤δ<1 so, (1−δ ^n−m)≤1, and ∥y ₀∥<∞, it follows

(3.7)

which converges to zero, that is, ∥ψ _n −ψ _m ∥→0, as m→∞. This implies that there exits ψ such that lim _n→∞ ψ _n =ψ. But, we have $y=\sum_{n=0}^{\infty}y_{n}=\lim_{n\rightarrow\infty} \psi_{n}$, that is, y=ψ which is exact solution of (3.1). This completes the proof. □

Theorem 3.2

The maximum absolute truncation error of the series solution defined by (2.10) to the problem can be estimated by

$$\max_{0\leq x\leq1}\Biggl|y(x)-\sum_{j=0}^{m} y_j\Biggr|\leq\frac{\delta ^{m+1}}{1-\delta}\|y_0\|, $$

where y(x) exact solution and $\psi_{m}=\sum_{j=0}^{m} y_{j}$ approximate series solution.

Proof

From (3.7) we have

Since lim _n→∞ ψ _n =y, fixing m and letting n→∞ in above equation, we obtain

Hence the maximum absolute truncation error is given by

(3.8)

This completes the proof. □

4 Numerical illustrations

In this section, improved scheme (2.9) is implemented for solving singular boundary value problems (1.1). We demonstrate the effectiveness of this scheme with four numerical examples. All the numerical results obtained by proposed method are compared with known results. In addition, the maximum absolute error functions E _n (x) are also plotted.

Example 4.1

Consider the nonlinear singular two point boundary value the problem [29]

(4.1)

where the exact solution is y(x)=ln(1/(4+x ^β)).

We apply the improved scheme (2.9) to (4.1), where 0≤α<1 and α ₁=ln(1/4), β ₁=1, γ ₁=0, η ₁=ln(1/5), and the scheme (2.9) for (4.1) becomes as follow:

(4.2)

The Adomian’s polynomials for f(x,y)=β(βx ^β e ^2y−e ^y(α+β−1)), y ₀=ln(1/4) are obtained using the formula given by (1.7) as:

(4.3)

In particular, for α=0.5, β=1, using (4.2) and (4.3) we obtain the successive solution components:

For α=0.5, β=3.5, using (4.2), (4.3), we obtain the solution components y _n of solution y(x) as:

We now define error function as E _n (x)=|ψ _n (x)−y(x)| and the maximum absolute error is given

$$E^{(n)}=\max_{0<x\leq1}E_n(x). $$

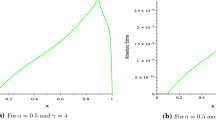
The error functions E _n (x), for n=3,4,5 are plotted in Figs. 1 and 2. In addition, the maximum absolute error E ⁽ⁿ⁾, for n=4,6,8,10 are listed in Tables 1 and 2.

Fig. 1

Error functions E _n , n=3,4,5 of Example 4.1 when α=0.5, β=1

Fig. 2

Error functions E _n , n=3,4,5 of Example 4.1 when α=0.5, β=3.5

Table 1 Maximum error of Example 4.1, when β=1

Table 2 Maximum error of Example 4.1, when β=3.5

Example 4.2

Consider the following nonlinear singular two point boundary value problem

(4.4)

with exact solution $y(x)=\sqrt{{1}/{(1+x^{3/2})}}$.

Applying the scheme (2.9) to (4.4), where α ₁=1, β ₁=1, γ ₁=0, and η ₁=0.7071067812, the scheme (2.9) for (4.4) reads as follow:

(4.5)

where $g(x)=\frac{3}{16} (-4+5 x^{3/2})$.

As given above, the Adomian’s polynomials for f(y)=y ⁵, y ₀=1 are given by:

(4.6)

Using (4.5) and (4.6), we have the successive solution components as

The maximum absolute error functions E _n (x), for n=5,6,7 are plotted in Fig. 3. From the figure we see that when number of iterations increases the error decreases. In addition, the maximum absolute error E ⁽ⁿ⁾, for n=4,6,8,10 are also listed in Table 3.

Fig. 3

Error functions E _n , n=5,6,7 of Example 4.2

Table 3 Maximum error of Example 4.2

Example 4.3

Consider the nonlinear singular two point boundary value problem [12, 24]

(4.7)

with exact solution y(x)=ln[2/(x ²+1)].

Applying the scheme (2.9) to (4.7), where α=0.5 and α ₁=ln(2), β ₁=1, and γ ₁=η ₁=0, and the scheme (2.9) for (4.7) becomes as:

(4.8)

In similar manner, the Adomian’s polynomials for f(y)=(0.5e ^y−e ^2y), y ₀=ln(2) are obtained as:

(4.9)

Making use of (4.8) and (4.9), we have successive solution components y _n as

In Fig. 4, the maximum absolute error functions E _n (x), for n=7,8,9 are plotted. In addition, numerical results for maximum absolute error E ⁽ⁿ⁾, for n=4,6,8,10 are listed in Table 4.

Fig. 4

Error functions E _n , n=7,8,9 of Example 4.3

Table 4 Maximum error of Example 4.3

Example 4.4

Consider the following linear singular two point boundary value problem [29]

(4.10)

with exact solution $y(x)=e^{x^{\beta}}$.

We apply the recursive scheme (2.9) to (4.10), where α ₁=1, β ₁=1, γ ₁=0, and η ₁=e, and the scheme (2.9) for (4.10) can be read as:

(4.11)

where the Adomian polynomials given by A _n =β(βx ^β+α+β−1)y _n .

For α=0.5, β=1: we have the successive solution components y _n , n>0 using (4.11)

The maximum absolute error E ⁽ⁿ⁾, for n=4,6,8,10 are displayed in Table 5. In addition, the error functions E _n (x), for n=5,6,7 are plotted in Fig. 5.

Fig. 5

Error functions E _n , n=5,6,7 of Example 4.4 when α=0.5, β=1

Table 5 Maximum error of Example 4.4, when β=1, α=0.5

5 Conclusion

In this paper, we have demonstrated that improved recursive scheme can be applied to solve a class of nonlinear singular two point boundary value problems efficiently. The accuracy of the numerical results indicates that the proposed method is well suited for the solution of such type of problems. The advantage of current approach is that it provides a direct scheme to obtain approximate solutions and we have also shown graphically that these approximate solutions are almost identical to the exact solution. Another major advantage of proposed method over existing recursive schemes is that it does not require the computation of undetermined coefficients. Moreover, the proposed method provides a reliable technique which requires less work compared to the traditional techniques such as finite difference method, cubic spline method, and standard ADM or MADM. The numerical results of the examples are presented and it has been shown that only a few terms are required to obtain accurate solutions. By comparing the results with other existing methods, it has been proved that proposed method is a powerful method for solving singular two point boundary value problems.

Appendix

Construction of Green’s function of following the problem

Consider the linear differential equation

Integrating the above equation twice first from x to 1 and then from 0 to x, changing the order of integration, and applying the boundary conditions, we obtain

where Green’s function is given by