1 Introduction

In the present study, the following class of two-point nonlinear SBVPs is considered

$$\begin{aligned} y''(x)+\frac{\alpha }{x}y'(x)= f(x, y(x)), \end{aligned}$$
(1)

subject to the following boundary conditions

$$\begin{aligned} y'(0)=0,~~\mu y(1)+\nu y'(1)=\psi ,~~~~~~~~~~~~\alpha \ge 1, \end{aligned}$$
(2)

or,

$$\begin{aligned} y(0)=\omega ,~~\mu y(1)+\nu y'(1)=\psi ,~~~~~~~~~~~~ 0<\alpha < 1, \end{aligned}$$
(3)

where finite constants are \(\mu >0\), \( \nu \ge 0\), \(\psi \), and \(\omega \). We assume that f(x, y) is continuous in \(([0, 1]\times {\mathbb {R}})\) and \(\partial f(x, y)/\partial y\) exists and is continuous.

Although one can consider the problem (1) with the following general nonlinear boundary conditions

$$\begin{aligned}&y'(0)=0~~ or~~ y(0)=\omega ,~~g(y(1), y'(1))=0. \end{aligned}$$
(4)

Problems (1)–(3) frequently occur in different fields of applied science and engineering. Some of these include chemical reactor, control and optimization, boundary layer theory, astrophysics theory, isothermal gas sphere, spherical cloud thermal behavior, nuclear physics, atomic structure, electrohydrodynamics and tumor growth problem (Verma et al. 2020b; Rufai and Ramos 2020, 2021b, a; Ramos and Vigo-Aguiar 2008; Moaaz et al. 2021; Tomar 2021a; Verma et al. 2020a; Van Gorder and Vajravelu 2008; Singh et al. 2016; Verma et al. 2021b; Tomar 2021b; Pandey and Tomar 2021; Verma et al. 2021a; Zhao et al. 2021). Therefore, in physical models, these problems occur naturally, often due to an impulsive sink or source term and having singularity associated with the independent variable. Such problems also arise when generalized ordinary differential equations are obtained with spherical or cylindrical symmetry from partial differential equations. Here, a few special cases of these problems are listed.

  1. 1.

    Michaelis–Menten uptake kinetics in steady-state oxygen diffusion (Lin 1976; McElwain 1978) when \(\alpha =2\) and \(f=-\frac{\eta y(x)}{y(x)+\rho }\), \(\eta ,\rho >0\).

  2. 2.

    The equilibrium of isothermal gas sphere (Keller 1956) when \(\alpha = 2\) and \(f= y(x)^5\).

  3. 3.

    The thermal explosions (Khuri and Sayfy 2010; Chambre 1952) when \(\alpha =1, 2\) and \(f=\rho e^{y(x)}\), where \(\rho \) is a physical parameter.

  4. 4.

    The modeling of the heat source distribution of the human head (Flesch 1975; Duggan and Goodman 1986) when \(\alpha =2\) and \(f=\rho e^{-\eta y(x)}\), \(\eta ,\rho >0\).

For a detailed literature survey one may refer to Verma et al. (2020b) and the references therein. In Ford and Pennline (2009), Pandey (1996), Pandey (1997) and Russell and Shampine (1975) the existence and uniqueness of the problem is studied. Note that the singularity behavior at \(x=0\) is the key difficulty in solving such problems.

As stated, at the initial point \(x=0\), the problem (1) has a singularity, so it adds complexity in terms of obtaining the closed-form solution. Therefore, several researchers have developed various analytical and numerical methods over the past decades to look for the numerical and approximate analytical solution to these problems. Some of the well-known methods in the literature are the Taylor wavelet method (Gümgüm 2020), Cubic splines (Kanth and Bhattacharya 2006; Chawla et al. 1988), B-splines (Çağlar et al. 2009), finite difference method (Chawla and Katti 1985), variational iteration method (VIM) (Kanth and Aruna 2010), Adomian decomposition method (ADM) (Inç and Evans 2003) and its modified versions (Kumar et al. 2020; Wazwaz 2011), a combination of VIM and homotopy perturbation method (VIMHPM) (Singh and Verma 2016), Optimal homotopy analysis method (OHAM) (Singh 2018), a reproducing kernel method (Niu et al. 2018), compact finite difference method (Roul et al. 2019), fixed-point iterative schemes (Tomar 2021a; Assadi et al. 2018) and nonstandard finite difference schemes (Verma and Kayenat 2018). It should be noted that the existing analytical methods require more iterations in order to obtain a relatively good precise solution, resulting in very high x powers and a high number of terms in successive approximate solutions. In addition, a large number of steps are demanded by the numerical technique to get an acceptable numerical solution to the problems. In comparison, to get a highly accurate approximate solution, the proposed methodology needs just a few iterations, resulting in low power of x and fewer terms in the approximate solutions obtained. Unlike the perturbation approaches, the suggested iterative approach does not presume any small parameters in the problems. In addition, to deal with nonlinear terms, the ADM requires the evaluation of Adomian polynomials, which can be time demanding in some cases. At the same time, the OHAM’s convergence depends on the optimal parameter. Therefore, an appropriate methodology must be established that overcomes the limitations mentioned earlier and offers a precise solution to the problems.

The strength of the work presented is two-fold. First, we construct an integral operator and derive the variational iteration (VIM) without using the Lagrange multiplier and restricted variations as required to construct the VIM formula. We then develop an effective algorithm based on domain decomposition by dividing the interval [0, 1] into uniform division subintervals. The approximate solutions are obtained in each subinterval in terms of unknowns constants. Then the values of unknown constants are evaluated by assuming the conditions of continuity of the solution y(x), and its derivative at the end of each subinterval. Then these imposed continuity conditions produce the system of nonlinear equations. To solve the corresponding nonlinear system of equations, the Newton–Raphson method is then implemented. The expansion strategy of the Taylor series is used for computational efficiency and to tackle the strong nonlinear terms such as \(e^{y(x)}\). The key advantages of our approach are that it uses a few iterates to provide a highly precise solution and solves the strong nonlinearity present in the problem very efficiently. Approximate analytical solutions with minimal polynomials are generated by the proposed method. Besides, the suggested approach can be easily applied to large-scale problems as well as parameter-related problems. The method’s convergence is also discussed in the paper. We consider some numerical test examples to support the applicability and robustness of the method. The numerical findings are compared with existing approaches to show the efficacy of the procedure. We also illustrate that the scheme applies to nonlinear singular problems associated with nonlinear boundary conditions.

The draft of this article is structured as follows. The iterative technique for solving the problems (1)–(3) is derived in Sect. 2. We also discussed the convergence analysis of the method in Sect. 3. The numerical simulations are provided to explain the work in Sect. 4 and the comparison of the numerical results is tabulated to show the high performance and superiority of our proposal. Finally, the work is concluded with Sect. 5.

2 The construction of method

In this section, we derive an iterative scheme to solve the considered problem (1) effectively with boundary conditions (2)–(3).

For this purpose and simplicity, problem (1) may be written as follows

$$\begin{aligned} (x^{\alpha }y'(x))'= x^{\alpha }f(x, y(x)). \end{aligned}$$
(5)

Let us define (5) as follows

$$\begin{aligned} \Lambda =(x^{\alpha }y'(x))'- x^{\alpha }f(x, y(x))= 0. \end{aligned}$$
(6)

Now subtracting and adding \((x^{\alpha }y'(x))'\) from (6) leads to

$$\begin{aligned} (x^{\alpha }y'(x))'+ \Lambda -(x^{\alpha }y'(x))' = 0, \end{aligned}$$
(7)

and re-write (7) as follows:

$$\begin{aligned} (x^{\alpha }y'(x))'=- \Lambda +(x^{\alpha }y'(x))'. \end{aligned}$$
(8)

Now transform (8) into an associated integral representation by integrating (8) from 0 to x, then we have

$$\begin{aligned} y' (x) = \frac{1}{x^{\alpha }}\int _{0}^{x}[ - \Lambda +(t^{\alpha }y'(t))' ]{\text {d}}t. \end{aligned}$$
(9)

Integrating (9) from 0 to x again, we get

$$\begin{aligned} y (x)= y (0)+ \int _{0}^{x}\Big ( \frac{1}{t^{\alpha }}\int _{0}^{t}[ - \Lambda +(s^{\alpha }y'(s))' ]{\text {d}}s\Big ) {\text {d}}t. \end{aligned}$$
(10)

Now we get the following integral form after changing the integration order in (10)

$$\begin{aligned} y(x)= y(0)+ \int _{0}^{x}\Big \{K(x,t) \big ( (t^{\alpha }y'(t))' -\Lambda \big )\Big \}{\text {d}}t, \end{aligned}$$
(11)

where K(x, t) is defined as

$$\begin{aligned} K(x, t)= {\left\{ \begin{array}{ll} \frac{x^{1-\alpha }-t^{1-\alpha }}{ 1-\alpha } , &{} \alpha \ne 1, \\ \log (\frac{x}{t}), &{} \alpha = 1. \end{array}\right. } \end{aligned}$$
(12)

Using the following identity

$$\begin{aligned} \int _{0}^{x} K(x,t)(t^{\alpha }y'(t))' {\text {d}}t=y(x)-y(0), \end{aligned}$$

after replacing the value of \(\Lambda \) from (6), Eq. (11) can be written in the following operator form

$$\begin{aligned} y(x)= T[y(x)], \end{aligned}$$
(13)

where

$$\begin{aligned} T[y(x)]=y(x)- \int _{0}^{x}\Big \{K(x,t) \big ( (t^{\alpha }y'(t))'- t^{\alpha }f(t, y(t)) \big )\Big \}{\text {d}}t. \end{aligned}$$

Now Picard’s method for (13) implies

$$\begin{aligned} y_{n+1}(x)= T[y_{n}(x)], \end{aligned}$$

or,

$$\begin{aligned} y_{n+1}(x)&=y_{n}(x)- \int _{0}^{x}\Big \{K(x,t) \big ( (t^{\alpha }y_{n}'(t))'- t^{\alpha }f(t, y_{n}(t)) \big )\Big \}{\text {d}}t, ~~n\ge 0. \end{aligned}$$
(14)

Note that, (14) can be written as follows:

$$\begin{aligned} y_{n+1}(x)&=y_{n}(x)+ \int _{0}^{x}\Big \{{\widetilde{K}}(x,t) \Big ( y_{n}''(t)+\frac{\alpha }{t}y_{n}'(t)- f(t, y_{n}(t)) \Big )\Big \}{\text {d}}t , \end{aligned}$$
(15)

where

$$\begin{aligned} {\widetilde{K}}(x, t)= {\left\{ \begin{array}{ll} \frac{t -t^{\alpha }x^{1-\alpha }}{ 1-\alpha } , &{} \alpha \ne 1, \\ t\log (\frac{t}{x}), &{}\alpha = 1. \end{array}\right. } \end{aligned}$$

Observe that, (15) corresponds to the VIM (Kanth and Aruna 2010; Ramos 2008), which has been developed here without using the Lagrange multipliers and constrained variations that are essential in the usual construction of the standard VIM. Notice that, due to strong nonlinear terms, the successive iterations of (15) lead to the complex integrals, so that the resulting integrals can not be evaluated effectively and require a high number of iterates to get a good accuracy.

To overcome the aforementioned limitations, we introduce an effective algorithm to solve the problem (1) by dividing the interval [0, 1] into N equally spaced subintervals as \(0=x_{0}<x_{1}< \cdots<x_{N-1}<x_{N}=1\), where \(h=1/N\), \(x_{i}=ih,~~0\le i \le N\).

Letting \(y(x_{i})=c_{i}\) and \(y'(x_{i})=c'_{i}\) for \( 0\le i \le (N-1)\). Now according to (14), we can construct the following piecewise scheme on the subintervals \([x_{i}, x_{i+1}]\). Let \(y_{i,n}\) be the nth order approximate solution of (14) on the subinterval \([x_{i}, x_{i+1}]\), \( 0\le i \le (N-1)\).

On the subinterval \([x_{0}, x_{1}]\), the iterative scheme is defined for \(n\ge 0\) as follows:

$$\begin{aligned} y_{0,n+1}(x) =y_{0,n}(x)- \int _{x_{0}}^{x}\Big \{K(x,t) \big ( (t^{\alpha }y'_{0,n}(t))'- t^{\alpha }f(t, y_{0,n}(t)) \big )\Big \}{\text {d}}t, ~~ x_{0}\le x\le x_{1}.\nonumber \\ \end{aligned}$$
(16)

Begin with the initial value \( y_{0,0}(x) =c_{0}\) for boundary conditions (2) and \( y_{0,0}(x) =\omega +c_{0}x\) for boundary conditions (3), we can easily get the nth order approximate solution \(y_{0,n}(x) \) using the iterative formula (16) on the subinterval \([x_{0}, x_{1}]\) in terms of the unknown constant \(c_{0}\) which will be evaluated further.

On the subinterval \([x_{i}, x_{i+1}]\), \( 1 \le i \le (N-1)\), the iterative scheme is defined for \(n\ge 0\) as follows:

$$\begin{aligned} y_{i,n+1}(x) =y_{i,n}(x)- \int _{x_{i}}^{x}\Big \{K(x,t) \big ( (t^{\alpha }y'_{i,n}(t))'- t^{\alpha }f(t, y_{i,n}(t)) \big )\Big \}{\text {d}}t, ~~ x_{i}\le x\le x_{i+1}.\nonumber \\ \end{aligned}$$
(17)

Starting with the initial guess, which is the solution of the corresponding homogenous equation on the subinterval \([x_{i}, x_{i+1}]\),

$$\begin{aligned} y_{i,0}(x)= {\left\{ \begin{array}{ll} c_{i}+\frac{x^{1-\alpha }-x_{i}^{1-\alpha }}{ 1-\alpha }c'_{i} , &{} \alpha \ne 1, \\ c_{i}+ \log (\frac{x}{x_{i}}) c'_{i}, &{} \alpha = 1, \end{array}\right. } \end{aligned}$$

we can easily get the nth order approximate solution \(y_{i,n}(x) \) on the subinterval \([x_{i}, x_{i+1}]\) in terms of unknowns constants \(c_{i}\) and \(c'_{i}\), \( 1\le i \le (N-1)\).

Now, we get the approximate solutions \(y_{i,n}(x) \) on the subintervals \([x_{i}, x_{i+1}]\), \( 0\le i \le N-1\) in terms of \((2N-1)\) unknown constants \(c_{0}, c_{1}, \ldots ,c_{N-1} \) and \(c'_{1}, c'_{2}, \ldots ,c'_{N-1} \). Then all these approximate solutions matched together to obtain a continuous solution on the interval [0, 1] by assuming the continuity of the solution and its derivative at the end points of the subintervals. Hence, we can construct a continuous solution if \(y_{i, n}(x)\) and \(y'_{i, n}(x)\) have same values at the grid points. Therefore, the approximate solution of (1) over [0, 1] leads to the solution of the following nonlinear system of \((2N-1)\) equations

$$\begin{aligned} {\left\{ \begin{array}{ll} y_{i-1, n}(x_{i})= y_{i, n}(x_{i}),~~~~~~~~~~~~~~~1\le i \le N-1,\\ y'_{i-1, n}(x_{i})= y'_{i, n}(x_{i}),~~~~~~~~~~~~~~~1\le i \le N-1,\\ \mu y_{N-1, n}(1)+\nu y'_{N-1, n}(1)= \psi . \end{array}\right. } \end{aligned}$$
(18)

Now solving (18) using the Newton–Raphson method, the \((2N-1)\) unknowns coefficients \(c_{i}\) and \(c'_{i}\) can be evaluated. Therefore, by evaluation of unknowns constants \(c_{0}, c_{1}, \ldots ,c_{N-1} \) and \(c'_{1}, c'_{2}, \ldots ,c'_{N-1} \), an approximate solution to the problem (1) on the entire interval [0, 1] can be achieved using the scheme (17).

Note that, in some cases, the method (17) leads to very complicated integrals because of strong nonlinearity terms which are impossible to evaluate. To overcome this limitation, we use the Taylor series approach around \(t_{i}\) to approximate the integrals as follows:

$$\begin{aligned} y_{i,n+1}(x) =y_{i,n}(x)- \int _{x_{i}}^{x} K(x,t) T_{i,r} {\text {d}}t, ~~~~~~~~~~~~~~~~ x_{i}\le x\le x_{i+1}, \end{aligned}$$
(19)

where

$$\begin{aligned} (t^{\alpha }y'_{i,n}(t))'- t^{\alpha }f(t, y_{i,n}(t))= T_{i,r}+O(t-t_{i})^{r+1}. \end{aligned}$$

The accuracy of the solution, however, depends on the number of terms r, and it is noted that more terms of Taylor series are needed as the iteration proceeds to achieve an expected accuracy.

Algorithm: Now, we summarize the basic structure of the proposed algorithm in the following steps.

  1. 1.

    Discretize the interval [0, 1] into equally spaced subintervals \([x_{i}, x_{i+1}]\), \( 0 \le i \le (N-1)\) with \(x_{0}=0\) and \(x_{N}=1\).

  2. 2.

    On each subinterval, obtain the approximate solutions of problem (1) using the proposed iterative formula (19) in terms of unknowns constants \(c_{0}, c_{1}, \ldots ,c_{N-1} \) and \(c'_{1}, c'_{2}, \ldots ,c'_{N-1} \).

  3. 3.

    The approximate solutions obtained in step 2 matched together to form a continuous solution on the interval [0, 1], which leads to a system of nonlinear equations.

  4. 4.

    Solve the system of nonlinear equation obtained in step 3 using Newton–Raphson method and once the unknowns constants computed, one can get an approximate solution to the considered problem.

3 Convergence of the proposed scheme

Here, the convergence analysis of proposed method with boundary conditions (2)–(3) is addressed.

To demonstrate that the iterative sequence of approximate solutions \(y_{i,n}(x)\) is convergent, assume that f(x, y(x)) satisfies the following Lipschitz condition

$$\begin{aligned} |f(x,y_{i,n})-f(x,y_{i,m})|\le \theta _{i}|y_{i,n}-y_{i,m}|, \end{aligned}$$

and

$$\begin{aligned} |f(x,y_{i}(x))|\le F_{i},~~~(x,y_{i})\in ([x_{i},x_{i+1}]\times {\mathbb {R}}). \end{aligned}$$

Now, consider the partial sum

$$\begin{aligned} y_{i,n}(x)=y_{i,0}(x)+(y_{i,1}(x)-y_{i,0}(x))+(y_{i,2}(x)-y_{i,1}(x))+ \cdots +(y_{i,n}(x)-y_{i,n-1}(x)) \end{aligned}$$
(20)

of the series

$$\begin{aligned} y_{i,0}(x)+\sum \limits _{j=0}^{\infty }(y_{i,j}(x)-y_{i,j-1}(x)). \end{aligned}$$
(21)

3.1 Convergence of the iterative formula (17)

Now, we will show that the partial sum (20) of the series (21) converges a limit \(y_{i}(x)\) as n approaches to infinity, for \(x\in [x_{i}, x_{i+1}]\). After integrating by parts of the first terms in the integrand of (17), we have

$$\begin{aligned} y_{i,n+1}(x) =y_{i,0}(x)+\int _{x_{i}}^{x}\Big \{ t^{\alpha } K(x,t) f(t, y_{i,n}(t)) \Big \}{\text {d}}t, ~~ x_{i}\le x\le x_{i+1}, \end{aligned}$$
(22)

where K(x, t) is given by (12) and letting

$$\begin{aligned} \big | t^{\alpha } K(x,t) \big | \le \kappa _{i}. \end{aligned}$$

For \(n=0\), (22) implies the following inequality

$$\begin{aligned} |y_{i,1}(x) -y_{i,0}(x)|&= \Big |\int _{x_{i}}^{x}\Big \{ t^{\alpha } K(x,t) f(t, y_{i,1}(t)) \Big \}{\text {d}}t\Big |, \nonumber \\&\le \kappa _{i}F_{i}|x-x_{i}|, \end{aligned}$$
(23)

and using the fact that f satisfies Lipschitz condition and (23), we have

$$\begin{aligned} |y_{i,2}(x) -y_{i,1}(x)|&= \Big |\int _{x_{i}}^{x}\Big \{ t^{\alpha } K(x,t) \Big ( f(t, y_{i,1}(t))- f(t, y_{i,0}(t)) \Big ) \Big \}{\text {d}}t\Big |, \nonumber \\&\le \int _{x_{i}}^{x}\Big \{ |t^{\alpha } K(x,t)| \Big ( \theta _{i} |y_{i,1}(x) -y_{i,0}(x)| \Big ) \Big \}{\text {d}}t ,\nonumber \\&\le F_{i} \theta _{i} \kappa _{i}^2\frac{ |x-x_{i}|^2}{2!}, \end{aligned}$$
(24)

and by following the similar process of (24), we can easily get

$$\begin{aligned} |y_{i,3}(x) -y_{i,2}(x)|&\le F_{i} \theta _{i}^{2} \kappa _{i}^3\frac{ |x-x_{i}|^3}{3!}. \end{aligned}$$
(25)

Now, using (23), (24) and (25), we get the following estimate using a simple induction

$$\begin{aligned} |y_{i,j}(x) -y_{i,j-1}(x)|&\le F_{i} \theta _{i}^{j-1} \kappa _{i}^j \frac{ |x-x_{i}|^j}{j!},~~~~~~~~~~x\in [x_{i}, x_{i+1}],\nonumber \\&\le F_{i} \theta _{i}^{j-1} \kappa _{i}^j \frac{ |x_{i+1}-x_{i}|^j}{j!},\nonumber \\&\le F_{i} \theta _{i}^{j-1} \kappa _{i}^j \frac{ N^{-j}}{j!}. \end{aligned}$$
(26)

In view of (26), it is easy to see that the series (21) is absolutely convergent on the each subinterval \([x_{i}, x_{i+1}]\). Hence, the following infinite series

$$\begin{aligned} |y_{i,0}(x)|+\sum \limits _{j=0}^{\infty }|(y_{i,j}(x)-y_{i,j-1}(x))|, \end{aligned}$$

is uniform convergent on each subinterval \([x_{i}, x_{i+1}]\). Consequently, it follows that the nth partial sum of the infinite series (22) tends to \(y_{i}(x)\) as n approaches to infinity, for each \(x\in [x_{i}, x_{i+1}]\). This completes the proof.

3.2 Convergence of the iterative formula (19)

Now, by following the above analysis, we will show that the partial sum (20) of the series (21) converges. In a similar way to (22), we can reduce the iterative formula (19) in the following form

$$\begin{aligned} y_{i,n+1}(x) =y_{i,0}(x)+ \int _{x_{i}}^{x} K(x,t) t^{\alpha } T_{i,r} {\text {d}}t, ~~~~~~~~~~~~~~~~ x_{i}\le x\le x_{i+1}, \end{aligned}$$
(27)

where

$$\begin{aligned} f(t, y_{i,n}(t))= T_{i,r}+O(t-t_{i})^{r+1}. \end{aligned}$$

Let us consider \(r=pn+q\), where p and q are known fixed numbers and using the fact that \(T_{i,r}\) is the approximation of \( f(t, y_{i,n}(t))\), then we have \( T_{i,r} \le f(t, y_{i,n}(t))\) for \(x_{i}\le x\le x_{i+1}\).

For \(n=0\), (27) gives the following estimate

$$\begin{aligned} y_{i, 1}(x) =y_{i,0}(x)+ \int _{x_{i}}^{x} K(x,t) t^{\alpha } T_{i,r} {\text {d}}t \le y_{i,0}(x)+ \int _{x_{i}}^{x} K(x,t) t^{\alpha } f(t, y_{i,0}(t)){\text {d}}t, \end{aligned}$$
(28)

and for \(n=1\), we have

$$\begin{aligned} y_{i, 2}(x) =y_{i,0}(x)+ \int _{x_{i}}^{x} K(x,t) t^{\alpha } T_{i,r} {\text {d}}t \le y_{i,0}(x)+ \int _{x_{i}}^{x} K(x,t) t^{\alpha } f(t, y_{i,1}(t)){\text {d}}t, \end{aligned}$$
(29)

and in a similar way, (27) yields

$$\begin{aligned} y_{i, n}(x) =y_{i,0}(x)+ \int _{x_{i}}^{x} K(x,t) t^{\alpha } T_{i,r} {\text {d}}t \le y_{i,0}(x)+ \int _{x_{i}}^{x} K(x,t) t^{\alpha } f(t, y_{i,n-1}(t)){\text {d}}t.\qquad \end{aligned}$$
(30)

Now, in view of (23)–(26) and by following the above analysis, from (28)–(30) we have

$$\begin{aligned} |y_{i,1}(x) -y_{i,0}(x)|&\le \kappa _{i}F_{i}|x-x_{i}|,\\ |y_{i,2}(x) -y_{i,1}(x)|&F_{i} \theta _{i} \kappa _{i}^2\frac{ |x-x_{i}|^2}{2!}, \end{aligned}$$

and

$$\begin{aligned} |y_{i,j}(x) -y_{i,j-1}(x)|&\le F_{i} \theta _{i}^{j-1} \kappa _{i}^j \frac{ N^{-j}}{j!}. \end{aligned}$$

Consequently, from the above analysis, the series (21) is absolutely convergent.

Next, let us define \( {\widetilde{y}} \) is the solution obtain by the iterative formula (19), then

$$\begin{aligned} {\widetilde{y}}_{i,n+1}(x) =y_{i,0}(x)+ \int _{x_{i}}^{x} K(x,t) t^{\alpha } T_{i,r} {\text {d}}t, ~~~~~~~~~~~~~~~~ x_{i}\le x\le x_{i+1}, \end{aligned}$$
(31)

where

$$\begin{aligned} f(t, {\widetilde{y}}_{i,n}(t))= T_{i,r}+O(t-t_{i})^{r+1}. \end{aligned}$$

Now, from (22) and (31), we have

$$\begin{aligned} y_{i,n+1}(x)-{\widetilde{y}}_{i,n+1}(x) = \int _{x_{i}}^{x}t^{\alpha } K(x,t) (f(t, y_{i,1}(t))-T_{i,r}) {\text {d}}t. \end{aligned}$$
(32)

It is easy to see that, as \(n\rightarrow \infty \), then \(r \rightarrow \infty \) and consequently \(T_{i,r}\approx f(t, y_{i,1}(t))\). Hence, \({\widetilde{y}} \approx y \) and this completes the proof.

3.3 Error analysis

Using (22), we obtain

$$\begin{aligned} y_{i,n+1}(x)-y_{i,n}(x) = \int _{x_{i}}^{x}\Big \{ t^{\alpha } K(x,t) f(t, y_{i,n}(t)) -f(t, y_{i,n-1}(t)) \Big \}{\text {d}}t. \end{aligned}$$
(33)

From the mean-value theorem, we have

$$\begin{aligned} f(t, y_{i,n}(t)) -f(t, y_{i,n-1}(t))=(y_{i,n}-y_{i,n-1})f_{y_{i}}(\xi ), \end{aligned}$$
(34)

where \(\xi \) lies between \( y_{i,n}\) and \(y_{i,n-1}\). Now, letting \( |f_{y_{i}}(y_{i}(x))|\le {\widetilde{F}}_{i}\) and by combining (33) and (34) yields

$$\begin{aligned} |y_{i,n+1}(x)-y_{i,n}(x)|&= \Big | \int _{x_{i}}^{x}\Big \{ t^{\alpha } K(x,t) (y_{i,n}-y_{i,n-1})f_{y_{i}}(\xi ) \Big \}{\text {d}}t\Big |,~~~ x_{i}\le x\le x_{i+1}\\&\le \kappa _{i}{\widetilde{F}}_{i} |x_{i+1}-x_{i}| |y_{i,n}-y_{i,n-1}|, \end{aligned}$$

and hence

$$\begin{aligned} |y_{i,n+1}-y_{i,n}| \le \psi |y_{i,n}-y_{i,n-1}|, \end{aligned}$$
(35)

where \(\psi =\kappa _{i}{\widetilde{F}}_{i} N^{-1} \). This shows that there is a linear convergence and a simple induction yields that

$$\begin{aligned} |y_{i,n+1}(x)-y_{i,n}(x)| \le \psi |y_{i,n}-y_{i,n-1}| \le \psi ^2 |y_{i,n-1}-y_{i,n-2}| \le \cdots \le \psi ^n |y_{i,1}-y_{i,0}|. \end{aligned}$$

4 Numerical results

We consider some numerical test cases in this section to demonstrate the applicability of the proposed methodology. To demonstrate the efficiency of the proposed approach to SBVPs with nonlinear boundary conditions, we present one numerical example. Maple 18 software package is used to evaluate the numerical results in this paper.

We define the absolute error

$$\begin{aligned} e_{i, n+1}(x)=|y_{i,n+1}(x)-y(x)|,~~~~x\in [x_{i}, x_{i+1}], \end{aligned}$$

and the maximum absolute error

$$\begin{aligned} E_{n+1}= \underset{ i}{\text {max}}|y_{i, n+1}(x)-y(x)|,~~x\in [x_{i}, x_{i+1}], \end{aligned}$$

to compare the method’s accuracy, where \(y_{n}\) denotes the nth approximate iterative solution and y is the closed form solution.

Example 1

Consider the linear SBVP Tomar (2021a)

$$\begin{aligned} (xy'(x))' =x\Big (-y(x)+\frac{5}{4}+\frac{x^2}{16}\Big ),~~~y'(0)=0,~~~y(1)=\frac{17}{16}. \end{aligned}$$
(36)

This problem has the true solution \(y(x)=1+\frac{x^2}{16}\). First, we successfully apply the proposed scheme (17) to get the approximate iterative solution of (36) and the maximum absolute errors for different iterations are presented in Table 1. From, Table 1, it is clear that as the number of iterations increases, the absolute error decreases. Also, it is clear that as the value of N increases for an iterative step, the absolute error decreases.

Table 1 Maximum absolute residual errors of Example 1
Full size table

Next, we solve (36) using the present method (19) with two terms of Taylor’s series and get the following successive approximation for \(n=0\) and \(N=5\):

On the interval [0, 0.2],

$$\begin{aligned} y _{0,1}(x)=1.000000000+0.0625000000x^2. \end{aligned}$$

On the interval [0.2, 0.4],

$$\begin{aligned} y _{1,1}(x)=1.000000000+0.0625000000x^2. \end{aligned}$$

On the interval [0.4, 0.6],

$$\begin{aligned} y _{2,1}(x)=1.000000000+0.0625000000x^2. \end{aligned}$$

On the interval [0.6, 0.8],

$$\begin{aligned} y _{3,1}(x)=1.000000000+0.0625000000x^2. \end{aligned}$$

On the interval [0.8, 1.0],

$$\begin{aligned} y _{4,1}(x)=1.000000000+0.0625000000x^2. \end{aligned}$$

Observe that, the approximate solutions \(y _{i,1}(x)\), \(0\le i \le 4\) are the analytical solution \(y(x)=1+0.0625x^2\) of the problem. While the maximum absolute error of the VIM Kanth and Aruna (2010) for \(y_{4}(x)\) is \(2.0 \times 10^{-08}\) with 10th degree polynomial. Clearly, we may say that the present approach is effective. In case, we solve (36) using the present method (19) with three terms of Taylor’s series and then the maximum absolute error is \(4.1 \times 10^{-04}\) for \(n=0\) and \(N=5\), however for the next iteration i.e. \(n=1\) and \(N=5\), we achieved the the analytical solution \(y _{i,2}(x)=1+0.0625x^2\), \(0\le i \le 4\).

Example 2

Consider the following linear problem Tomar (2021a)

$$\begin{aligned} (x^{\alpha }y'(x))'=\gamma x^{\alpha +\gamma -2}y(x)(\gamma x^{\gamma }+\alpha +\gamma -1 ) ,~~~y(0)=1,~~~y(1)=\exp (1). \end{aligned}$$
(37)

The analytical solution of this problem is \(y(x)= \exp (x^{\gamma })\).

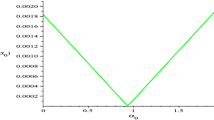
We successfully apply the proposed scheme (17) to get the approximate iterative solution of (37). Comparisons between the maximum absolute error for \( \alpha =0.5\) and \(\gamma =4\) obtained by our method and the existing methods Tomar (2021a); Roul and Warbhe (2016); Chawla and Katti (1982); Kumar and Aziz (2004) are tabulated in Tables 2 and 3. It is clear from tables that the proposed method with a fewer number of iterations and mesh sizes produces a better solution than the existing methods. Moreover, for \( \alpha =2\) and \(\gamma =5\), the maximum absolute error for the proposed method is \(2.3\times 10^{-04}\) for \(n=1\) and \(N=10\) using 20 degree polynomials. Clearly, we may say that the obtained results are sufficiently accurate. Further, we plot absolute errors of (37) obtained using the presented method with various values of \( \alpha \) and \(\gamma \) for \(n=3\) and \(N=10\) in Figs. 1 and 2, which confirm the effectiveness of the method. It is clear that as the number of iterations progresses the absolute error decreases rapidly.

Table 2 Comparison of the maximum absolute errors of Example 2 for proposed method with \(N=10\) for \(\alpha =0.5\) and \(\gamma =4\)
Full size table
Table 3 Comparison of the maximum absolute errors of Example 2 for proposed method with \(n=3\) for \( \alpha =0.5\) and \(\gamma =4\)
Full size table
Fig. 1
figure 1

Graph of absolute error of Example 2 for \(n=3\) and \(N=10\)

Full size image
Fig. 2
figure 2

Graph of the absolute errors of Example 2 for \(n=3\) and \(N=10\)

Full size image

Example 3

Consider the following nonlinear SBVP Gümgüm (2020), which arises in the field of equilibrium of isothermal gas sphere

$$\begin{aligned} (x^{2}y'(x))'+x^{2} y^{5}(x)=0,~~~y'(0)=0,~~~y(1)=\sqrt{\frac{3}{4}}. \end{aligned}$$
(38)

This problem has analytical solution \(y(x)= \sqrt{\frac{3}{3+x^{2}}}\). Using the proposed approach (19) for \(n=3\), \(N=8\) and \(r=(n+6)\) with 11th degree polynomial, we solved the problem (38) and the maximum absolute error obtained by our method is presented in Table 4 along with those obtained by existing methods such as an optimised global hybrid block method Ramos and Singh (2021) with \(M=8\), Taylor wavelet method Gümgüm (2020) using \(M=9\) and 8th order polynomial, VIMHPM Singh and Verma (2016) with 14 iterations and 28th degree polynomial, and 15th degree polynomial, VIM Kanth and Aruna (2010) with 4 iterations and 42nd degree polynomial and the ADM Kumar et al. (2020) with 16 terms. From Table 4, it is clear that the present approach provides far better results than the preexisting methods using a few iterations. Note that, using a lower degree polynomial, the proposed method provides an accurate approximate solution, and hence we may say that the proposed method is an effective and highly promising. In addition, in Fig. 3, the graphs of the absolute error and the obtained solution for \(n=3\) and \(N=10\) are represented. Further, the maximum absolute error and computation run times in seconds are tabulated in Table 5 for the proposed method using \(n=3\) along with other existing methods. Numerical results given in Tables 4 and 5, display a good performance of the proposed scheme.

Table 4 Comparison of absolute maximum errors for example 3
Full size table
Fig. 3
figure 3

Graphs of Example 3 for \(n=3\) and \(N=10\)

Full size image
Table 5 Comparison for Example 3
Full size table

Example 4

Consider the following nonlinear SBVP Tomar (2021a), which arises in the field of thermal explosion in cylindrical vessel

$$\begin{aligned} (xy'(x))'+x e^{y(x)}=0,~~~y'(0)=0,~~~y(1)=0. \end{aligned}$$
(39)

The problem (39) has analytical solution \(y(x)=2\ln \big (\frac{v+1}{vx^{2}+1}\big )\), where \(v=3-2\sqrt{2}\). The maximum absolute error for \(n=2\), \(N=10\) and \(r=2n\) produced by our scheme is tabulated in Table 6 along with the maximum absolute errors obtained by preexisting methods such as B-spline method Çağlar et al. (2009) with \(N=20\) mesh size and VIMHPM Singh and Verma (2016) with 8 iterations, which confirms the accuracy and superiority of the present approach over the existing methods. The absolute error and the obtained solution are also plotted in Fig. 4.

Table 6 Comparison of absolute maximum errors for example 4
Full size table
Fig. 4
figure 4

Graphs of Example 4 for \(n=2\) and \(N=10\)

Full size image
Table 7 Comparison of the approximate solutions of Example 5 for \(\mu =0.1, \nu =1\)
Full size table

Example 5

Consider the following nonlinear SBVP Singh and Verma (2016), which describes the thermal distribution profile in the human head

$$\begin{aligned} (x^{2}y'(x))'+x^{2} \exp ( -y(x)) =0,~~~y'(0)=0,~~~ \mu y(1)+\nu y'(1)=0. \end{aligned}$$
(40)

The analytical solution to this problem is unknown. We successfully solve (40) using the proposed method with \(n=3\), \(N=10\) and \(r=4n\), to obtain the approximate iterative solution of (40) for various values of \(\mu \) and \(\nu \). The numerical results obtained using our method are tabulated in Table 7 for \(\mu =0.1, \nu =1\) along with compact finite difference method (CFDM) Roul et al. (2019) with mesh size 20 and ADM Kumar et al. (2020) with 14 terms. From tables, note that the obtained results of our method are matching with the results of the existing methods. Since the closed-form solution of the problem (40) is not known, then we consider the residual error

$$\begin{aligned} R_{n+1}(x )= (x^{2}y_{n+1}'(x))'+x^{2} \exp (-y_{n+1}(x)), \end{aligned}$$

to reveal the efficiency of the method. In Figs. 5 and 6, we depicted the approximate solutions for different values of \(\mu \) and \(\nu \) to exhibit the accuracy of the method. From these figures, it is clear that for a fixed \(\nu \), the solution profile is decreasing if \(\mu \) is increasing, and for a fixed \(\mu \), the solution profile is increasing if \(\nu \) is increasing. Moreover, the solution profile remains unchanged if \(\mu \) and \(\nu \) simultaneously decreasing or increasing. Therefore, the proposed method is capable of proper study of the behavior of the problem. It is worth to point out that the proposed approach solves the problem efficiently for different values of \(\mu \) and \(\nu \) as the maximum absolute residual error demonstrated in Table 8 while VIMHPM Singh and Verma (2016) failed for \(\mu =0.1\) and \(\nu =1\) because the obtained maximum absolute residual error of Singh and Verma (2016) is \(1.1\times 10^{8}\).

Fig. 5
figure 5

Graph of the approximate solutions of Example 5\(n=3\) and \(N=10\)

Full size image
Fig. 6
figure 6

Graph of the approximate solutions of Example 5\(n=3\) and \(N=10\)

Full size image
Table 8 Maximum absolute residual errors of Example 5\(n=3\) and \(N=10\)
Full size table

Example 6

Consider the following nonlinear SBVP Singh and Verma (2016) that arises from a rotationally symmetrical, shallow membrane cap study

$$\begin{aligned} (x^{3}y'(x))'+x^{3} \Big ( \frac{1}{8 y^{2}(x)}- \frac{1}{2}\Big ) =0,~~~y'(0)=0,~~~y(1)=1. \end{aligned}$$
(41)

The true solution to this problem is unknown. To obtain the approximate solution of (41), we successfully implemented the scheme for \(n=3\), \(N=10\) and \(r=3n\). The numerical results obtained using our scheme are tabulated in Table 9 along with preexisting methods such as VIM Kanth and Aruna (2010) with 3 iterations and VIMHPM Singh and Verma (2016) with 6 iterations. Since the closed-form solution of the problem (41) is not known, then we consider the residual error

$$\begin{aligned} R_{n+1}(x )= (x^{3}y_{n+1}'(x))'+x^{3} \Big ( \frac{1}{8 y_{n+1}^{2}(x)}- \frac{1}{2}\Big ), \end{aligned}$$

to check the efficiency of the method. The approximate solution for \(n=3\) and \(N=10\) is plotted in Fig. 7 and the obtained maximum absolute residual error is \(4.5\times 10^{-16}\), that confirms the method’s effectiveness.

Table 9 Comparison of the approximate solutions for Example 6
Full size table
Fig. 7
figure 7

Graph of the approximate solution for Example 6

Full size image

Example 7

Consider the following singular diffusion problem with nonlinear boundary condition given in Garner and Shivaji (1990)

$$\begin{aligned} (x^2y'(x))'&=\frac{\beta x^2 y(x)}{y(x)+k} ,~~\beta , k>0, \nonumber \\ y'(0)&=0,~~y(1)= 1-\frac{y'(1)}{\beta _{2}}+\frac{\beta _{0}}{\beta _{2}(1+k_{0})}-\frac{\beta _{1}y(1)}{\beta _{2}(y(1)+k_{1})}, \end{aligned}$$
(42)

where \(\beta ,k>0\) and this problem models the oxygen diffusion in a spherical cell with Michaelis–Menten oxygen uptake.

The analytical solution to this problem is unknown. We solve problem (42) using the proposed iterative scheme for \(n=3\), \(N=10\) and \(r=3n\) with \(\beta = \beta _{0}=\beta _{1}=k= k_{0}=k_{1}=\beta _{2}=2\). Since the closed-form solution of the problem (42) is not known, then we consider the residual error

$$\begin{aligned} R_{n+1}(x )= (x^2y_{n+1}'(x))'-\frac{\beta x^2 y_{n+1}(x)}{y_{n+1}(x)+k}. \end{aligned}$$

The graph of the approximate solution is depicted in Fig. 8 and the obtained maximum absolute residual error is \(7.4\times 10^{-15}\), which confirms the efficiency and effectiveness of the method.

Fig. 8
figure 8

Graph of the approximate solution for Example 7

Full size image

5 Conclusion

In this work, we introduced an effective technique for solving linear and nonlinear singular boundary value problems with two types of boundary conditions arising in many scientific phenomena. In the proposed algorithm, we first discretize the domain [0, 1] into a finite number of equally spaced subintervals and then implement the introduced iterative formula to solve the problems in each subinterval. The proposed technique produces a highly accurate and very reliable solution to the problems in a few iterates, as demonstrated by numerical results. The method produces an accurate approximate solution of highly nonlinear problems and the numerical results show a good performance of the proposed method. The effectiveness and robustness have been justified by seven numerical examples, and the obtained results have been compared with the pre-existing methods to demonstrate the superiority of the method. It is clear from numerical simulations that the technique is very useful to study the behavior of problems with parameters and fast convergence of the iterative solutions can be observed as iteration proceeds. Therefore, the present method is a highly promising tool for solving different types of singular problems with strong nonlinearity. Further, the proposed technique has the capability to solve the nonlinear problems with nonlinear boundary conditions which has been illustrated by a numerical example.