Introduction

To design and execute the rock engineering constructions successfully, it is of a high importance to predict the rock mass deformation modulus (Em) since it best represents the pre-failure mechanical behaviors of rock mass (Gholamnejad et al. 2013; Fattahi 2016; Fattahi and Moradi 2018). Literature is consisted of a number of approaches proposed by different researchers to directly predict the Em using in-situ tests; they include plate loading test (PLT), pressure meter (Chun et al. 2009), cable jack, plate jacking, radial jacking, flat jack, and add to the list the geophysical methods. Nowadays, such techniques are the best for this purpose; though they are costly and time-consuming, and only after the excavation operation, they can be done (Gholamnejad et al. 2013). Recently, an increasing number of empirical approaches have been proposed in literature for the prediction of the Em. Bieniawski (1973) pioneered the empirical equations for this purpose; in his model, only rock mass rating (RMR) was considered as the input parameter. The most important drawback of Bieniawski’s approach was that it could be applied to rock masses with RMR > 50. On the other hand, attempting to remove this problem in the Bieniawski’s equation, Serafim and Pereira (1983) introduced an equation for rock masses with RMR < 50. In addition, an empirical equation was introduced by Hoek and Brown (1997) on the basis of the geology strength index (GSI) and the uniaxial compressive strength (UCS) of intact rock. In two other studies, Nicholson and Bieniawski (1990) and Mitri et al. (1994) made the use of two modulus of the intact rock (Ei) in accordance with the value of RMR. Barton (2002) introduced a formula that included both UCS and tunneling quality index (Q) system. In another project, considering three parameters of rock quality designation (RQD), UCS, and weathering degree (WD) of rock, Gokceoglu et al. (2003) offered an empirical equation to literature. Kayabasi et al. (2003) discussed the relation on the basis of WD, Ei, and RQD. The empirical equation of Zhang and Einstein (2004) was based on Ei and RQD. On the other hand, the classification system of rock mass index (RMI) was a basis for Palmström and Singh (2001) to propose relations. In the Hoek and Diederichs’s (2006) study, formulas were offered on the basis of GSI and D (factor of disturbance), while in Sonmez et al.’s (2004) research, they were on the basis of Ei, GSI, and D parameters.

In recent years, the use of computational intelligence methods have been highlighted in different engineering fields (Ray et al 2020; Hasanipanah and Amnieh 2020a, 2020b; Armaghani et al. 2020a, 2020b; Asteris et al. 2020, 2021a, b, 2022a, b; Zhou et al. 2021; Zhu et al. 2021; Du et al. 2022). For instance, Sonmez et al. (2006) utilized the artificial neural networks (ANNs) and Majdi and Beiki (2010) employed a hybrid system of ANNs and genetic algorithms (GA) for the prediction of Em. On the other hand, an adaptive network-based fuzzy inference system (ANFIS) model was introduced by Gokceoglu et al. (2004) to effectively predict the Em of jointed rock masses. Alemdag et al. (2016) predicted the Em using ANN, ANFIS, and genetic programming (GP) models. According to their findings, the performance of GP was better than ANN and ANFIS models. A Monte Carlo simulation (MCS) was employed to predict Em in the study conducted by Fattahi et al. (2019). They demonstrated that the MCS was an acceptable tool in this field. In another study, Majdi and Beiki (2019) used a fuzzy c-means clustering (FCM) method optimized by particle swarm optimization (PSO) and GA for the same purpose. Their results confirmed an acceptable performance of PSO and GA in optimizing the FCM model.

The present study investigates the use of three optimized cascaded forward neural network (CFNN) for predicting the Em. For this work, the Levenberg–Marquardt algorithm (LMA), Bayesian regularization (BR), and scaled conjugate gradient (SCG) procedures are used to optimize CFNN model. In other words, these algorithms were used in the training phase which consisted in the optimization of the weights and bias terms of CFNN. The rest of this paper is organized as follows. Material and Methods are provided in the next section. In the Material section, more explanations about the database is mentioned. Also, in the Methods section, the predictive models are explained. Then, in the next sections, we discussed the performance of the developed models in predicting the Em, and finally the conclusions are stated.

Material and methods

Material

To develop the models proposed in this study, the requirement datasets were borrowed from Chun et al. (2009). In this database, sixty sets of data were prepared using several independent parameters and one dependent parameter (Em).

Data pre-processing one of the most important steps before providing computational intelligence methods which is significantly vital in selecting the properly data-driven model for yielding the favourable accuracy. In this research, eight variables including depth of the measurement of Em, UCS, RQD, discontinuity density (DD), RMR, ground water Condition (GC), discontinuity orientation adjustment (DOA), and discontinuity condition (DC) were used as inputs and Em was used as the output. Table 1 listed the descriptive statistics of all variables. The statistical properties of all the inputs show that the diversity of datasets except depth and DOA parameters are at a suitable level. Of all the input variables, UCS and RMR are the closest to the normal distribution due to having the smallest distance between the mean and median. Figure 1 demonstrates the normalized values probability distribution of all datasets. According to Fig. 1 and results of Table 1, the depth and DOA have the highest skewness (2.333 and -1.664, respectively) and kurtosis (5.127 and 3.481, respectively) among all datasets and consequently both of them deviate more from the normal distribution than the other variables. The statistical analysis of used datasets acknowledges the need for a robust AI model for modelling the Em.

Table 1 Secretive statistics of implemented datasets for the Em prediction
Full size table
Fig. 1
figure 1

Distribution of normalized values of all implemented variables in the modelling

Full size image

Figure 2 demonstrates the correlogram of all utilized variables. Clearly, it can be seen that the DD, UCS, and RMS variables due to having the highest Pearson correlation coefficients (0.727, 0.716, and 0.694, respectively) are identified as the most influential parameters and GC by lowest Pearson correlation coefficient (0.035) has the least impact on the Em modelling.

Fig. 2
figure 2

Correlogram of all variables used in Em prediction

Full size image

Methods

Cascaded forward neural network (CFNN)

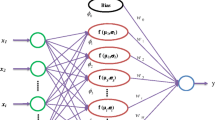
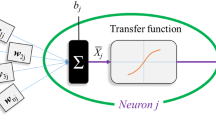
Further rigorous paradigms of ANN called CFNN is largely used as it ensures reliable results when modelling highly complicated systems. The topology of the aforementioned model belongs to the feedforward kind, which is based highly on back-propagation (BP) strategy to refurbish the weights during the learning process (Nait Amar 2020). Three kinds of layers can be considered in a CFNN paradigm, i.e., input, output, and hidden layers. The feature of this model is that the hidden layers are developed in a cascade structure by generating more neurons and interactions along with the whole of inputs and previous hidden neurons (Nait Amar 2020). The CFNN cascade form lets every neuron of the prior layer to be relied upon with the neurons of the next layers (Abujazar et al. 2018). The preferable number of hidden layers, their numbers of neurons and their activation functions in a CFNN model are frequently examined using trial and error method.

The learning phase of CFNN model focuses to achieve suitable values of weights and bias that lead to minimize the quadratic error outlining the gap between the predictions and the true values. To this end, back-propagation (BP) algorithms are the most widespread used thanks to their excellent results provided. In this paper, three alternative approaches namely, Levenberg–Marquardt (LM) algorithm, Bayesian regularization (BR), and scaled conjugate gradient (SCG) are applied, and which will be explained in the next section.

Optimization techniques

Levenberg–Marquardt algorithm (LMA)

The LMA represents one of the most advantageous optimization techniques which are applied to find solutions to the nonlinear least square issues. The stated method has the ability to locate the ultimate solution even from an unsuitable initial hypothesis, but it does not conduct to global minimization. For this technique, the optimization procedure refers to that of Newton’s method, but they differ fairly in their conceptions. In LMA, the Hessian matrix is approximated, in addition to the introduction of a regularization parameter that ameliorates the calculation procedure. The approximations of the Hessian matrix and the gradient are shown in the formulas below (Kişi and Uncuoglu 2005):

$$H={J}^{T}J$$
(1)
$$g={J}^{T}e$$
(2)

with \(J\) and \(e\) denote the Jacobian matrix and the error vector, respectively, whereas \(T\) stands for the transposition operator. The LMA step can be updated as mentioned in Eq. (3) by replacing the approximated Hessian and gradient matrixes and by inserting the regularization parameter in the fundamental formula of Newton’s technique:

$${x}_{i+1}={x}_{i}-{\left(H-\eta I\right)}^{-1}\times g$$
(3)

where \(i\) and \(\eta\) represent the iteration and the regularization parameter, respectively, otherwise, \(x\) denotes the weights.

Bayesian regularization (BR)

The optimization of weights and bias using Bayesian regularization (BR) technique is inspired from LMA approach (MacKay 1992; Foresee and Hagan 1997). Indeed, the concept of BR algorithm is to minimize an objective function, which involves a weighted summation of squared error and squared network weights (Yue et al. 2011). The network weights for the objective function in BR is determined as shown below:

$$F\left(w\right)=\alpha {E}_{w}+\beta {E}_{D}$$
(4)

In the above-equation, \({E}_{w}\) and \({E}_{D}\) indicate the sum of squared network weights and the sum of network errors, correspondingly, however \(\alpha\) and \(\beta\) denote the objective function \(F\left(w\right)\) parameters. The two aforementioned parameters are provided from the theorem of Bayes. To this end, a Gaussian type distribution is relied to choose the training set and determine the weight vector. The training sets selection with some manipulation of algebraic operations lead to the optimum values of \(\alpha\) and \(\beta\). After that, a minimization of \(F\left(w\right)\) and an updating of weights is realized by using the LM algorithm. This calculation steps are repeated until reaching a stopping criterion (Yue et al. 2011).

Scaled conjugate gradient (SCG)

One of most discussed issues of the conventional back-propagation technique that uses the negative descent direction approach to update the weights is the shortage of convergence speed (Yue and Songzheng 2011). The conjugate gradient represents an alternative strategy to remedy this issue, and the error minimization acquired previously is kept as follows:

$${P}_{0}={-g}_{0}$$
(5)

with \({P}_{0}\) represents the conjugate direction and \({-g}_{0}\) means the search direction. In this algorithm, the purpose of the best distance determination is for optimizing the actual search direction. The following equation leads to calculate the proper distance (Kişi and Uncuoglu 2005):

$${x}_{i+1}={x}_{i}+{\alpha }_{i}{g}_{i}$$
(6)

Then, the search direction is determined using the next formula (Kişi and Uncuoglu 2005):

$${P}_{0}={-g}_{0}+{\beta }_{i}{P}_{i-1}$$
(7)

A variety of conjugate algorithm versions can be apprehended according to the \(\beta\) determination steps (Kişi and Uncuoglu 2005). It should be noted that the line search is a computational method but it is expensive, thus, it is preferable to use other cheaper techniques such as the scaled conjugate gradient (SCG). The latter technique incorporates the CG algorithm with trust region technique (Møller 1993).

Development procedure

The database compiled from the published literature was divided into training and testing sets for utilizations in the training and test phases of CFNN model, respectively. The training set involved 80% of the collected measurements, while 20% of the points were devoted for the test set. It is worth mentioning that the different variables of this amassed database were normalized between -1 and 1 using the following formula:

$${Var}_{n}=\frac{2\left({Var}_{i}-{Var}_{min}\right)}{\left({Var}_{max}-{Var}_{min}\right)}-1$$
(8)

where \({Var}_{max}\) and \({Var}_{min}\) represent the maximum and minimum values of a specified variable, respectively, and \({Var}_{n}\) points out its normalized value.

The prediction reliability of CFNN model depends greatly on the appropriate selection of its control parameters, such as its topology, the activation functions of the hidden layers, as well as the techniques applied for optimizing the weights and bias terms of the network. To this end, the trial and error technique was applied for investigating the suitable numbers of hidden layers, their number of neurons, and their activation functions. Besides, and as mentioned in the previous section, three rigorous back-propagation based techniques, including LMA, BR, and SCG were implemented for optimizing the weights and bias of the CFNN model. The gained models were denoted CFNN-LMA, CFNN-BR, and CFNN-SCG, respectively. The workflow of Fig. 3 summarizes the steps of the implementation using these aforesaid algorithms.

Fig. 3
figure 3

Workflow of the implementation procedure

Full size image

Results and discussion

After carrying out the described implementation steps, it was found that the three paradigms, i.e., CFNN-LMA, CFNN-BR, and CFNN-SCG involved two hidden layers with 12 and 9 neurons in each of them, respectively. The most suitable activation function in the hidden layers of these CFNN models was Tansig.

The models were evaluated statistically and graphically using various criteria. The graphical evaluation was carried out through cross plot for examining the integrity of the developed paradigms and histogram of error distribution, which aimed at detecting any likely error trend. Coefficient of determination (R2) and Root mean square error (RMSE) were the main statistical indexes that were used in the assessment of the prediction performance of the gained models. These indexes are expressed as follows (Hasanipanah et al. 2015; Nikafshan Rad et al. 2019; Hasanipanah et al. 2020a, b, c; Armaghani and Asteris 2021; Parsajoo et al. 2021; Li et al. 2021; Ly et al. 2021; Karir et al. 2022):

  1. 1.

    Coefficient of Determination (R2).

    $${R}^{2}=1-\frac{\sum_{j=1}^{N}{\left({{Em}_{j}}_{exp}-{{Em}_{j}}_{pred}\right)}^{2}}{\sum_{j=1}^{N}{\left({{Em}_{j}}_{pred}-\overline{Em }\right)}^{2}}$$
    (9)
  2. 2.

    Root Mean Square Error (RMSE).

    $$RMSE= \sqrt{\frac{1}{N}\sum \nolimits_{j=1}^{N}{\left({{Em}_{j}}_{exp}-{{Em}_{j}}_{pred}\right)}^{2}}$$
    (10)

In the above-equations, the subscripts exp and pred denote the real and estimated values of Em, respectively, \(\overline{Em }\) is the average value of Em, and \(N\) represents the number of samples.

Cross plots of observed Em values and those predicted by the implemented CFNN paradigms are exhibited in Fig. 4. For a given model, it can be said that it generates good prediction performance if a light cloud of its predictions is noticed near the line X = Y (unit-slope line). As shown in the cross plots of Fig. 4, the predictions of the suggested paradigms are well-distributed around the reference line X = Y for both training testing phases. Deviations of the Em values estimated by the newly proposed models from the real data during the training and testing phases are also illustrated in subplots a-c of Fig. 5, for CFNN-LMA, CFNN-BR, and CFNN-SCG, respectively. According to this figure, a satisfactory agreement exists between Em predicted by CFNN-LMA, CFNN-BR, and CFNN-SCG and the real values of the database.

Fig. 4
figure 4

Cross plots of the suggested CFNN models

Full size image
Fig. 5
figure 5

Comparison between the observed Em values and the predictions of the suggested CFNN models versus data index during the training and test phases

Full size image

In another kind of evaluation, the distributions of the noticed errors between the estimations of the three paradigms and actual data are demonstrated in histogram diagrams of Fig. 6. As can be seen, a normal distribution of the associated errors with a centre equal to or very close to zero-error value is achieved in all of the models. This kind of distribution indicates the high reliability of the newly proposed CFNN models.

Fig. 6
figure 6

Histogram diagrams of the errors associated with the predictions of the suggested CFNN models

Full size image

For a detailed assessment of the global integrity of the suggested paradigms, Table 2 states the statistical indexes, namely R2 and RMSE, of these models for training, test, and overall data sets. As indicated in this table, the reliability of CFNN models is clearly deemed for the different data sets as these paradigms achieved high R2 and small RMSE values for these sets. By taking a deeper look to the performance evaluation reported in Table 2 and Figs. 4, 5 and 6, it can be said that although the good prediction performance of the proposed models, CFNN-LMA showed a higher ability and a more reliability compared with CFNN-BR and CFNN-SCG when estimating Em values of the different cases included in the database.

Table 2 Statistical evaluation of the suggested CFNN models
Full size table

Figure 7 illustrates the probability distribution function (PDF) of observed and predicted Em values for better models validation. This Fig demonstrated the PDFs with corresponding each optimized CFNN models for all data sets (training and testing stages). The comparing the PDF of each model demonstrated that the CFNN-LMA yielded better agreement with the observed datasets. Besides, the quartiles values (Q25%, median, and Q75%) of three provided models showed that the CFNN-LMA on account of closest quartile (Q25% = 7.908 and Q75% = 19.75) is more consistent with the observational datasets ((Q25% = 8.085 and Q75% = 19.96) in comparison with CFNN-CG (Q25% = 8.538 and Q75% = 19.35) and CFNN-BR (Q25% = 7.96 and Q75% = 18.53) models. Thus, I can be conclude that the CFNN-LMA yields more promising results than other two models for prediction of Em values.

Fig. 7
figure 7

The probability density function of observed and predicted Em values

Full size image

In the last error validation of model, the cumulative frequency of relative deviation (CFRD) values for three models were examined and depicted in Fig. 8. The results indicated that in the CFNN-LMA, more than 68% of whole datasets have (\(RD \le 10\%\)) and only 7% of all data sets yielded to (\(RD > 30\%\)) whereas in CFNN-SCG model, 51% and 10% of all data sets led to (\(RD \le 10\%\)) and, (\(RD > 30\%\)) respectively. Besides, the CFNN-BR model is introduced as the worst performance among three presented methods because it caused 70% of the data sets to lead to more than 30% relative deviation.

Fig. 8
figure 8

The cumulative frequency of relative deviation (%) for three models

Full size image

In the last step of this work, a sensitivity analysis was carried out on our best paradigm, i.e., CFNN-LMA, to determine the impact of each of the included variables on Em. To gain this, the relevancy factor \((r)\) (Shateri et al. 2015; Nait Amar and Jahanbani Ghahfarokhi 2020; Nait Amar et al. 2021) was computed. It is worth mentioning that the value of this factor demonstrates the impact degree of a given variable, while its sign exhibits the positive or the negative effect of a variable on the output. The relevancy factor is calculated using the following formula:

$$r\left({Inp}_{j},O\right)=\frac{\sum_{i=1}^{N}\left({Inp}_{j,i}-\overline{{Inp }_{j}}\right)\left({O}_{i}-\overline{O }\right)}{\sqrt{\sum_{i=1}^{N}{\left({Inp}_{j,i}-\overline{{Inp }_{j}}\right)}^{2}\sum_{i=1}^{N}{\left({O}_{i}-\overline{O }\right)}^{2}}}$$
(11)

In the above-equation, the data index is specified by the subscript i; \({I}_{j}\) and \(\overline{{I }_{j}}\) point out the jth variable and its average value, respectively, and \(O\) and \(\overline{O }\) refer to the estimated value of the output and its average, respectively.

Figure 9 displays the evaluation of the impact of the variables using the relevancy factor. As can be seen, only discontinuity orientation adjustment has a negative effect on Em values, while the other input parameters have positive impact on Em. From the degree of importance perspective, UCS and discontinuity density are the most impacting parameters on Em with r values of 0.7491 and 0.7437, respectively, while groundwater condition has the weakest effect on Em with an r value of 0.0478.

Fig. 9
figure 9

Evaluation of the importance of the input parameters on Em using the relevancy factor

Full size image

Conclusions

The main purpose of this study is to develop three optimized models, i.e. CFNN-LMA, CFNN-BR and CFNN-SCG to predict Em. When designing surface or underground rock engineering constructions, the prediction of Em is a significant subject, and using the advanced machine learning methods can be useful in this field. Therefore, the authors of this study have tried to propose efficient models to accurately predict Em. To develop the proposed models, we adopted the datasets formerly presented by Chun et al. (2009). Totally, eight effective parameters on Em were used as the input parameters by using sixty sets of data. Then, R2 and RMSE, as two common error indexes, were computed to check the accuracy of the developed models. The following findings can be drawn from the analysis and results:

  • According to the obtained results, the CFNN-LMA model predicted the Em with the RMSE of 1.927 and R2 of 0.984. These values for CFNN-SCG models were 0.945 and 2.717, and also for CFNN-BR model were 0.904 and 3.635. Therefore, the lowest RMSE and the highest R2 were obtained from CFNN-LMA model. This indicates the superiority of the CFNN-LMA model in comparison with CFNN-BR and CFNN-SCG models for predicting Em.

  • Comparing the probability distribution function (PDF) of each developed model showed that the CFNN-LMA yielded better agreement with the observed datasets. Furthermore, based on the cumulative frequency of relative deviation (CFRD), the best results were obtained from CFNN-LMA model. The above results confirm the effectiveness of CFNN-LMA model in this field.

  • In this study, a sensitivity analysis was also performed through the relevancy factor and according to the calculations, only discontinuity orientation adjustment had a negative effect on Em values, and other input parameters had positive impact on Em. Also, it was found that the UCS and discontinuity density were the most impacting parameters on Em.