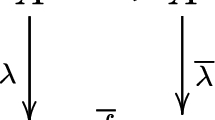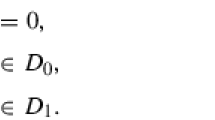1 Introduction

In order to efficiently implement complex S-boxes or permutations in hardware we need first to decompose them into simpler maps.

Definition 1 (Decomposition)

A decomposition of a function \(f: \text {GF}(2^{n}) \rightarrow \text {GF}(2^{n})\) is a finite sequence of functions \(g_{1}, g_{2}, {\dots } g_{t}\) such that

$$f(x) = g_{t} \circ g_{t-1} \circ {\cdots} \circ g_{2} \circ g_{1} (x). $$

This question has been investigated in the context of Threshold Implementation in [12, 16], where the decomposition and factorization of the Present S-box on quadratic S-boxes has been proposed. This research has been extended to all 3 × 3 and 4 × 4 S-boxes in [3, 4]. In the same context it was proven that when n = 4 all S-boxes belonging to the Alternative group have decomposition into quadratic permutations and all S-boxes not belonging to the Alternative group have no such decomposition, the inversion is among the latter [3, 4]. Decompositions of permutations into simpler operations, i.e. with less field multiplications, to enable more efficient side-channel countermeasures have been presented in [7, 8, 11, 17]. The goal of this paper is different - we target a decomposition of permutations into quadratic or cubic permutations.

Let us recall some well known results, which are used in the paper. There is no n-bit permutation with degree n [2], i.e. the maximal algebraic degree of a balanced n-variable Boolean function is n − 1. The inverse of an affine permutation is affine, the (algebraic) degree of a permutation xd is equal to wt(d) (Hamming weight), hence the permutations xd and \(x^{d} \circ x^{2^{i}}\) are affine equivalent since \(x^{2^{i}}\) are linear permutations. It has also been shown that xd is a permutation of GF(2n) if and only if \(\gcd (d,2^{n} - 1) = 1\) [2]. Note that for n = 2m there is no quadratic power function which is a permutation. It can easily be seen that the quadratic function x3 is a permutation whenever n is odd. Indeed, since 2 = − 1 mod 3 it follows that 2n − 1 = 1 mod 3 or in other words \(\gcd (3, 2^{n}-1) = 1\). It can also been seen that x3 is not a permutation when n is even. All involution permutations [15] are a product of disjoint cycles with 1 or 2 elements only.

Recall that a mapping f from GF(2n) into GF(2m) is called differentially δ-uniform (or simply δ-uniform) if for all a ∈GF(2n),a≠ 0, and b ∈GF(2m) we have |{z ∈GF(2n)|f(z + a) − f(z) = b}|≤ δ. It is proven in [14] that the inversion mapping f i.e. \(x^{-1} = x^{2^{n}-2}\) in GF(2n) has \(\deg (f) = n-1\), since wt(2n − 2) = n − 1; it has odd parity; f is differentially 2-uniform if n is odd and it is differentially 4-uniform if n is even. The functions which are 2-uniform are also known as Almost Perfect Nonlinear (APN) functions.

Theorem 1 (5)

There are 5 APN permutations in GF(25) upto affine equivalence, all of those are affine equivalent to powerfunctions \(AP{N^{5}_{1}} = x^{3}\),\(AP{N^{5}_{2}} = x^{5}\), \(AP{N^{5}_{3}} = x^{7}\), \(AP{N^{5}_{4}} = x^{11}\), \(AP{N^{5}_{5}} = x^{15}\).Where \(AP{N^{5}_{5}}\)isequivalent to its inverse, and \(AP{N^{5}_{1}}\)(respectively \(AP{N^{5}_{2}}\))is equivalent to the inverse of \(AP{N^{5}_{4}}\)(respectively \(AP{N^{5}_{3}}\)).Note that \(AP{N^{5}_{1}}\)and \(AP{N^{5}_{2}}\)arequadratic,\(AP{N^{5}_{3}}\)and \(AP{N^{5}_{4}}\)arecubic, and \(AP{N^{5}_{4}}\)hasdegree 4.

There is only one known affine equivalence class of 6-bit APN permutations and it has degree 4. It is known that this permutation can be decomposed into two permutations of degree three and two, namely APN6 = g ∘ f, where f is cubic and g is quadratic.

Carlitz proved the following important theorem [9].

Theorem 2

Given a finite field GF(q) withq > 2 thenall permutation polynomials over it are generated by the special permutationpolynomialsxq− 2(theinversion) andax + b(affinei.e.a,b ∈GF(q) anda≠ 0).

In other words any permutation [10, 18] can be presented as decomposition of affine and inverse permutations. The number of inversions in this decomposition is referred as the Carlitz rank [1].

Our contribution in this paper is twofold - first, we describe a method to decompose any power function as a sequence of power permutations of lower algebraic degree. Using this method we provide decompositions of the inversion in GF(2n) for small n from 3 up to 16, as well as for the APN functions when n = 5. Namely, there exist decompositions into quadratic power permutations for any n not multiple of 4 and decompositions into cubic power permutations for n multiple of 4. The second contribution of this paper is to extend the known, for n = 4, decomposition results to any permutation in GF(2n) with 3 ≤ n ≤ 16. In other words, we show that any permutation can be decomposed in cubic (or quadratic) permutations when n is (or not) multiple of 4. This general result is obtained thanks to the Theorem of Carlitz.

2 Decompositions

We will start with an algorithm which finds decompositions for the inversion into quadratic or cubic power permutations. Note that it is straightforward to apply the same method to other well known power functions as we demonstrate later for the APN functions when n = 5.

Let us recall that for n = 2m there is no quadratic power function which is a permutation, hence there will be no decomposition of the inversion on quadratic power permutations for such n. When n = 12 the only quadratic power permutation is x17, but it has even parity while the inversion has an odd parity, hence no decomposition of the inversion on quadratic power permutations exists when n = 12. Since we consider 3 ≤ n ≤ 16 then when n is multiple of 4 (i.e. n = 4,8,12,16) we will look for decompositions on cubic power permutations, in all the other cases we will search for decompositions on quadratic power permutations. Let us denote by \({\mathcal A}(k)\) the cyclotomic class of a power permutation xk, namely \({\mathcal A}(k) = \{ k2^{i} \mod (2^{n} -1), \ \text {such that} \ \gcd (k2^{i}, 2^{n}-1) = 1 \ \text {for} \ \ i = 0, \ldots , n-1 \}\). Next, we consider the following algorithm (see Fig. 1) in which the first two steps are pre-computations followed by two alternatives for the search loop.

Fig. 1
figure 1

Algorithm for decompositions of power permutations

Full size image

Since we are looking only for decompositions relevant to the S-boxes used in symmetric cryptographic primitives the choice of n between 3 and 16 is entirely justified. We would like to point out as well that the use of cyclotomic classes in the first step of the algorithm is similar to the algorithms in [7, 8, 11, 17], however our goal and the algorithm steps afterwards are different. Thus, the algorithm described above is adapted to serve well our purposes to find all desirable decompositions. Note that the exhaustive search worked out for all n except n = 13,15 and 16.

All decompositions we found for the inversion given in Table 1 are with a minimal length. We applied our algorithm also for \(AP{N^{5}_{3}} = x^{7}\), \(AP{N^{5}_{4}} = x^{11}\) and \(AP{N^{5}_{5}} = x^{15}\) and found that for \(AP{N^{5}_{3}} = x^{4} \circ x^{5} \circ x^{5}\) i.e. decomposition of length 2; for \(AP{N^{5}_{4}} = x^{8} \circ x^{3} \circ x^{5} \circ x^{5}\) i.e. decomposition of length 3; for \(AP{N^{5}_{5}} = x^{5} \circ x^{3}\) i.e. decomposition of length 2; and those are the shortest decompositions.

Table 1 Decompositions of the inversion
Full size table

A confirmation of the above results is given by the decompositions of the inversion in GF(28) i.e. the AES S-box which is of algebraic degree 7, presented in [13]: x− 1 = x32 ∘ x19 ∘ x13 i.e., a composition of 2 permutations of degree 3; x− 1 = x16 ∘ x43 ∘ x53 i.e., a composition of 2 permutations of degree 4; x− 1 = x128 ∘ x23 ∘ x11 i.e., a composition of a permutations of degree 3 with a permutation of degree 4.

To complete our result we use Theorem 2 (Carlitz) and below we state our main Theorem.

Theorem 3

Forn ≤ 16 anypermutation can be decomposed in quadratic permutations, when n is notmultiple of 4 and in cubic permutations, when n is multiple of 4.

Note that Theorem 2 uses a subset of affine transformations of the type ax + b where a,b are field elements. Recall that any affine permutation can be written as \(b + {\sum }_{i = 0}^{n-1} a_{i} x^{2^{i}}\) called also linearized polynomials (plus a constant b) [6], where the coefficients ai are field elements. Since Carlitz considers only a subset of them by using all affine permutations instead we can achieve shorter Carlitz rank. Note that the classes with even/odd Carlitz rank have even/odd parity. We should point out that although the decompositions we have found for the inversion are with minimal length, the decompositions found in Theorem 3 for any S-box might not have minimal length.

Another application of our main Theorem relates to the decompositions of the S-boxes when n = 3 and n = 4. We will use the notations introduced in [3] \({\mathcal A}_{i}^{n}\), \({\mathcal Q}_{j}^{n}\) and \({\mathcal C}_{k}^{n}\) where the upper index n indicates that we consider a permutation with 2n elements, the lower index i,j,k is the number of the considered class among all affine equivalent classes when they are alphabetically ordered and the letter \({\mathcal A}, {\mathcal Q}, {\mathcal C}\) shows whether this is an Affine, Quadratic or Cubic class. All single permutation transpositions (0,j) belong to the class \({Q_{1}^{3}}\) for 3 × 3 permutations. Moreover, all 4 classes for n = 3 can be obtained via Inv ∘ A ∘ Inv ∘ B ∘ Inv, where A, B and C are affine permutations i.e. with Carlitz rank at most 3. Class \({A_{0}^{3}}\) is the affine class, i.e., has rank 0 and the class \({Q_{3}^{3}}\) is the only class with rank 1, since it contains the inversion. Then the class \({Q_{2}^{3}}\) is with rank 2 and the remaining quadratic class \({Q_{1}^{3}}\) is with rank 3. Note that, from the construction used in the proof of the Carlitz Theorem, the single transpositions (i.e. class \({Q_{1}^{3}}\)) are with Carlitz rank 3.

All 302 classes for n = 4 can be obtained as follows: Inv ∘ A ∘ Inv ∘ B ∘ Inv ∘ C ∘ Inv i.e. with Carlitz rank at most 4. Class \({A_{0}^{4}}\) is the affine class and hence with rank 0, the cubic class \(C_{282}^{4}\) is the only class with rank 1 since it contains the inversion. Then there are 59 classes with rank 2: {010,016,024,041,049,050,052, 053,060,061,063,064,066,067,070,071,073,074,076,081,083,089,092,095,096, 099,107,118,126,127,130,131,138,140,142,150,151,164,165,168,171,172,174, 180,192,201,202,211,212,217,236,249,254,262,268,270,273,281,287}. Next there are 150 classes with rank 3 - namely all the classes not belonging to the Alternative group except \(C_{282}^{4}\): {001,003,005,007,009,011,013,015,017,019,021,023,025, 027, 029,030,032,035,037,039,040,042,045,047,048,051,054,056,058,059,062,065, 068,069,072,075,077,079,080,082,084,087,088,090,091,093,094,097,098,100, 102,105,106,108,109,112,113,116,117,119,122,125,128,129,132,133,135,137, 139,141,143,144,146,149,152,153,156,157,160,163,166,167,169,170,173,175, 177,179,181,182,185,186,188,190,191,193,195,197,199,200,203,204,206,207, 209,210,213,216,218,220,222,224,226,227,229,230,232,235,237,239,241,242, 245,246,248,250,251,253,255,256,257,261,263,265,267,269,271,272,274,276, 279,283,284,285,289,290,291,295,298,301}. From the construction used in the proof of the Carlitz Theorem, the single transpositions (0,j) (i.e. class \({C_{1}^{4}}\)) are with Carlitz rank 3. The remaining 91 classes are with rank 4 and among them are all the 6 quadratic classes: {002,004,006,008,012,014,018, 020, 022,026, 028, 031, 033, 034,036,038,043,044,046,055,057,078,085,086,101,103,104,110,111,114,115, 120,121,123,124,134,136,145,147,148,154,155,158,159,161,162,176,178,183, 184,187,189,194,196,198,205,208,214,215,219,221,223,225,228,231,233,234, 238,240,243,244,247,252,258,259,260,264,266,275,277,278,280,286,288,292, 293,294,296,297,299,300}. Five classes {006,136,161,162,278} will have rank 2 instead of rank 4 if all affine transformations are used instead of only the ones of the type ax + b.

3 Conclusions

We have shown that any permutation (for 3 ≤ n ≤ 16 ) can be decomposed in quadratic permutations, when n is not multiple of 4 and in cubic permutations, when n is multiple of 4. There are still two open problems to be solved: Can the inversion be decomposed in quadratic permutations when n is multiple of 4 and n > 4? Can we find decompositions with shorter length?