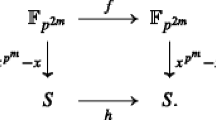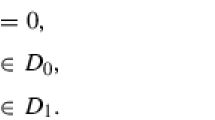Several classes of permutation polynomials with trace functions over $\mathbb {F}_{p^n}$

Abstract

Permutation polynomials over finite fields constitute an active research area and have important applications in many areas of science and engineering. In this paper, several classes of permutation polynomials with trace functions are presented over $\mathbb {F}_{p^{n}} (p=2, 3)$ by investigating the number of solutions to special equations.

1 Introduction

Let q be a power of prime p and $\mathbb {F}_q$ denote the finite field with q elements. Define $\mathbb {F}^{*}_q$ to be the multiplicative group of $\mathbb {F}_q$. A polynomial $f(x)\in \mathbb {F}_q[x]$ is called a permutation polynomial over $\mathbb {F}_q$ if the associated polynomial mapping $f: c \mapsto f(c)$ from $\mathbb {F}_q$ into $\mathbb {F}_q$ is a bijection [8].

Permutation polynomials over finite fields have wide applications in coding theory [6], combinatorial designs [8], and cryptography [10]. Many constructions of permutation polynomials appeared in the recent years, the reader may refer to [4, 8, Chapter 7], [11, Chapter 8], [12] and references therein for more information.

Finding new permutation polynomials, especially, permutation polynomials with good cryptographic properties are of great interest in both theoretical and applied aspects. The trace function has wide application in constructing the sparse permutation polynomials over finite fields. For instance, Charpin, Kyureghyan and Suder [3] studied the permutation properties of the sparse polynomials

$$\begin{aligned} F_{s,t,\gamma }(x)= x^{s} + \gamma \mathrm{Tr}^{n}_{1}\left( x^t\right) \in \mathbb {F}_{2^n}[x], \end{aligned}$$

where s, t are positive integers, and $\gamma \in \mathbb {F}_{2^n}^{*}$. Moreover, they exhibited the differential uniformity of some sparse permutation polynomials in [3]. Based on the trace functions over finite fields, Zeng, Tian and Tu [16] proposed four classes of permutation polynomials with the following form:

$$\begin{aligned} f(x)= \left( \gamma \mathrm{Tr}^{n}_{m}(x)+\delta \right) ^{s} + L(x)\in \mathbb {F}_{2^n}[x], \end{aligned}$$

where $m\mid n$, and s satisfies either $s(2^m+1)\equiv 2^m+1~(\mathrm{mod}\ 2^n-1)$ or $s(2^m-1)\equiv 2^m-1~(\mathrm{mod}\ 2^n-1)$, $\delta$ is an element of $\mathbb {F}_{2^n}$, $L(x)=\mathrm{Tr}^{n}_{m}(x)+x$ or x. By using of Magma, Li, Qu, Chen and Li [7] got all permutation polynomials over $\mathbb {F}_{q^l}$ of the form

$$\begin{aligned} f(x)=cx+\mathrm{Tr}^{kl}_{k}(x^{a}) \end{aligned}$$

with $q=2^k$, $kl<14$, $c\in \mathbb {F}^{*}_{q^l}$ and $a\in [1, q^l-2]$. Kyureghyan and Zieve [5] searched all permutation polynomials of the shape

$$\begin{aligned} f(x)=x+\gamma \mathrm{Tr}^{mn}_{m}(x^k) \end{aligned}$$

(1)

Over $\mathbb {F}_{q^n}$ for odd $q=p^m$, $n>1$ and $q^n\le 5000$, where $\gamma \in \mathbb {F}^{*}_{q^n}$. Following on the research in [5], Ma and Ge [9], Zha et al. [17] further investigated permutation polynomials of the form (1) over $\mathbb {F}_{q^n}$ for some values of p, k and n. The recent progress on permutation polynomials derived from trace functions can be seen in [1, 2, 14, 15, 19] and references therein.

The purpose of this paper is to construct new permutation polynomials with trace functions over finite fields. We obtain five classes of permutation polynomials with trace functions over $\mathbb {F}_{p^{n}}$ by determining the number of solutions of special equations.

The paper is organized as follows. Section 2 gives some preliminaries on necessary concepts and related results. In Sect. 3, three classes of permutation polynomials with trace functions are presented over $\mathbb {F}_{2^{n}}$. In Sect. 4, we introduce two classes of permutation polynomials with trace functions over $\mathbb {F}_{3^n}$. In Sect. 5, the conclusion is given.

2 Preliminaries

In this section, we recall the definitions and some results which will be applied in the sequel.

Definition 1

Let n and m be positive integers with $m\mid n$. The trace function $\mathrm{Tr}^{n}_{m}(x)$ from $\mathbb {F}_{p^n}$ to $\mathbb {F}_{p^m}$ is defined by

$$\begin{aligned} \mathrm{Tr}^{n}_{m}(x)= x+ x^{p^{m}}+ x^{p^{2m}}+ \cdots + x^{p^{(\frac{n}{m}-1)m}}. \end{aligned}$$

If $m=1$, then $\mathrm{Tr}^{n}_{1}(x)$ is called the absolute trace function.

For later usage we need the following results on the number of solutions of linearized equation over finite fields.

Lemma 1

([18, Lemma 3.1]) Let $\alpha \in \mathbb {F}_{2^n}$. For $0\ne r\in \mathbb {Z}_{n}$, the equation

$$\begin{aligned} x^{2^r}+x +\alpha =0 \end{aligned}$$

(2)

has solutions in $\mathbb {F}_{2^n}$ if and only if $\mathrm{Tr}_{e}^{n}(\alpha )=0$, where $e=\gcd (n, r)$. Moreover, if $\mathrm{Tr}_{e}^{n}(\alpha )=0$, then Eq. (2) has $2^e$ solutions in $\mathbb {F}_{2^n}$.

Lemma 2

([13, Theorem 2]) Let $q=3^n$ and n be a positive integer. Let $f(x) = x^3 + ax+b$, where $a,b\in \mathbb {F}_{q}$ and $a\ne 0$. Then the factorizations of f(x) over $\mathbb {F}_{q}$ are characterized as follows:

• (i) f(x) factors over $\mathbb {F}_{q}$ as a product of three linear factors if and only if $-a$ is a square in $\mathbb {F}_{q}$, say $-a=c^2$, and $\mathrm{Tr}_{1}^{n}(\frac{b}{c^3})=0$;

• (ii) f(x) factors over $\mathbb {F}_{q}$ as a product of a linear factor and an irreducible quadratic factor if and only if $-a$ is a nonsquare in $\mathbb {F}_{q}$;

• (iii) f(x) is irreducible if and only if $-a$ is a square in $\mathbb {F}_{q}$, say $-a=c^2$, and $\mathrm{Tr}_{1}^{n}(\frac{b}{c^3})\ne 0$.

Lemma 3

(Hilbert’s Theorem 90) The mapping $\mathrm{Tr}_{1}^{n}: \mathbb {F}_{p^{n}}\rightarrow \mathbb {F}_{p}$ is surjective. For $\alpha \in \mathbb {F}_{p^{n}}$, $\mathrm{Tr}_{1}^{n}(\alpha )=0$ if and only if there exists an element $\beta \in \mathbb {F}_{p^{n}}$ such that $\alpha =\beta -\beta ^p.$

Lemma 4

([1, Lemma 1.2]) Let A, S and $\overline{S}$ be finite sets with $\#S = \#\overline{S}$, and let $f: A \rightarrow A$, $\overline{f}: S \rightarrow \overline{S}$, $\lambda : A \rightarrow S$, and $\overline{\lambda }: A \rightarrow \overline{S}$ be maps such that $\overline{\lambda } \circ f = \overline{f}\circ \lambda$. If both $\lambda$ and $\overline{\lambda }$ are surjective, then the following statements are equivalent:

• (i) f is a bijection (a permutation of A); and

• (ii) $\overline{f}$ is a bijection from S to $\overline{S}$ and f is injective on $\lambda ^{-1}(s)$ for each $s\in S$.

We next recall the quadratic character on $\mathbb {F}_{p^n}$, which is used in Sect. 4. For more information of the quadratic character the reader may refer to [8, Chapter 5].

Let p be an odd prime and n be an integer. The mapping $\chi : x \mapsto x^{\frac{p^n-1}{2}}$ from $\mathbb {F}_{p^n}^{*}$ to $\{-1, 1\}$ is called the quadratic character. It maps the squares in $\mathbb {F}_{p^n}^{*}$ to 1 and the nonsquares to $-1$. It is a homomorphism from the multiplicative group $\mathbb {F}_{p^n}^{*}$ into the group with just two elements $-1, 1$. Sometimes we extend $\chi$ by setting $\chi (0) = 0$ to a mapping $\mathbb {F}_{p^n}^{*} \rightarrow \{-1, 0, 1\}$. In particular, $-1$ is a square element in $\mathbb {F}_{p^n}^{*}$ if and only if $p^n \equiv 1~(\mathrm{mod}\ 4)$, otherwise, $p^n \equiv 3~(\mathrm{mod}\ 4)$.

3 Three classes of permutation polynomials with trace functions over $\mathbb {F}_{2^n}$

In this section, we first introduce two classes of permutation polynomials with trace functions over $\mathbb {F}_{2^{n}}$ for odd n. Then, a class of permutation polynomials with trace functions is proposed over $\mathbb {F}_{2^n}$ for 3 | n.

Theorem 2

Let n, k, i and j be integers with $n=2k-1$ and $\gcd (n, i)=1$. Let u be a nonzero element of $\mathbb {F}_{2^n}$ with $\mathrm{Tr}^{n}_{1}(u^{-1})=1$. Then

$$\begin{aligned} f(x)= x^{2^i} + x + u^{-1}\mathrm{Tr}^{n}_{1}\left( x^{2^j+1}\right) \end{aligned}$$

is a permutation polynomial over $\mathbb {F}_{2^n}$.

Proof

We shall show that for every $a \in \mathbb {F}_{2^n}$, the equation

$$\begin{aligned} f(x) = x^{2^i} + x + u^{-1}\mathrm{Tr}^{n}_{1}\left( x^{2^j+1}\right) = a \end{aligned}$$

has at most one solution in $\mathbb {F}_{2^n}$.

• Case (I) If $\mathrm{Tr}^{n}_{1}(x^{2^j+1}) =0$, then we have

  $$\begin{aligned} x^{2^i} + x = a. \end{aligned}$$

  (3)

Since $\gcd (n, i)=1$, by Lemma 1, Eq. (3) has two solutions $x_{1}$ and $x_{1}+1$ if $\mathrm{Tr}^{n}_{1}(a) =0$, or no solution if $\mathrm{Tr}^{n}_{1}(a) =1$. By Lemma 3, it can be verified that

$$\begin{aligned} \mathrm{Tr}^{n}_{1}\left( \left( x_{1}+1\right) ^{2^j+1}\right) =\mathrm{Tr}^{n}_{1}\left( x_{1}^{2^j+1}+x_{1}^{2^j} + x_{1} + 1\right) =\mathrm{Tr}^{n}_{1}\left( x_{1}^{2^j+1}\right) +1 \end{aligned}$$

for odd n. Thus Eq. (3) has one solution in Case (I) if and only if $\mathrm{Tr}^{n}_{1}(a)=0$.

• Case (II) If $\mathrm{Tr}^{n}_{1}(x^{2^j+1}) =1$, then we obtain

  $$\begin{aligned} x^{2^i} + x + u^{-1} + a =0. \end{aligned}$$

  (4)

Since $\gcd (n, i)=1$, by Lemma 1 again, Eq. (4) has two solutions $x_{2}$ and $x_{2}+1$ if $\mathrm{Tr}^{n}_{1}(u^{-1} + a) =0$, or no solution otherwise. Note that $\mathrm{Tr}^{n}_{1}((x_{2}+1)^{2^j+1}) =\mathrm{Tr}^{n}_{1}(x_{2}^{2^j+1})+1$, it follows from the condition $\mathrm{Tr}^{n}_{1}(u^{-1})=1$ that Eq. (4) has one solution if and only if $\mathrm{Tr}^{n}_{1}(a)=\mathrm{Tr}^{n}_{1}(u^{-1})=1$.

Thus according to the discussion of Cases (I) and (II), f(x) is a permutation polynomial over $\mathbb {F}_{2^n}$. $\square$

Corollary 1

Let n, k, i and j be integers satisfying $n=2k-1$ and $\gcd (n, i)=1$. Let u be a nonzero element of $\mathbb {F}_{2^n}$ with $\mathrm{Tr}^{n}_{1}\left( u^{-1}\right) =1$. Then

$$\begin{aligned} g(x)= ux^{2^{k+i}-2^i} + ux^{2^k-1}+\mathrm{Tr}^{n}_{1}\left( x^{2^{k+j}+2^k-2^j-1}\right) \end{aligned}$$

is a permutation polynomial over $\mathbb {F}_{2^n}$.

Proof

The proof is easy. It can be checked that $(2^k+1)(2^k-1)=2^{2k}-1\equiv 1~(\mathrm{mod}\ 2^n-1)$ and $g(x)= uf(x^{2^k-1})$, where f(x) is defined as in Theorem 2. Therefore, g(x) is a permutation polynomial over $\mathbb {F}_{2^n}$. $\square$

Theorem 3

Let $n=2k-1$ and k be an integer. Then

$$\begin{aligned} f(x)= x^{3\cdot 2^{k-1}-2} + x^{2^k-1}+\mathrm{Tr}^{n}_{1}(x) \end{aligned}$$

is a permutation polynomial over $\mathbb {F}_{2^n}$.

Proof

Since $(3\cdot 2^{k-1}-2)(2^k+1)=3\cdot 2^{2k-1}-2\cdot 2^{k}+3\cdot 2^{k-1}-2\equiv 1-2^{k-1}~(\mathrm{mod}\ 2^n-1)$, we obtain $f(x^{2^k+1})^{2^k}= x^{2^{k}-1} + x^{2^k}+\mathrm{Tr}^{n}_{1}(x^{2^k+1})$. Let $g(x)=f(x^{2^k+1})^{2^k}$. We need to show that $g(x)=a$ has at most one solution for every $a\in \mathbb {F}_{2^n}$.

• Case (I) If $\mathrm{Tr}^{n}_{1}\left( x^{2^k+1}\right) =0$, then

  $$\begin{aligned} x^{2^k-1}+x^{2^k}=a. \end{aligned}$$

  (5)

If $a=0$, then $x=0$ or $x=1$. It is obvious that $x=0$ is a solution of Eq. (5) since $x=1$ does not satisfy $\mathrm{Tr}^{n}_{1}(x^{2^k+1})=0$.

If $a\ne 0$, then from Eq. (5) we have $x^{2^k}(1+x^{-1})=a$, which implies $x\ne 1$, this yields

$$\begin{aligned} x^{2^k}=\frac{ax}{x+1}. \end{aligned}$$

(6)

From Eq. (6) we deduce $x^2=(x^{2^k})^{2^k}=\frac{a^{2^k}x^{2^k}}{x^{2^k}+1}=\frac{a^{2^k+1}x}{(1+a)x+1}$, and then

$$\begin{aligned} (1+a)x^2 + x + a^{2^k+1}=0. \end{aligned}$$

(7)

If $a=1$, then $x=1$, a contradiction.

We next assume that $a\ne 0, 1$. Multiplying both sides of Eq. (7) by $1+a$, we obtain

$$\begin{aligned} (1+a)^2x^2 + (1+a)x + (1+a)a^{2^k+1}=0. \end{aligned}$$

Let $y=(1+a)x$. Then we have

$$\begin{aligned} y^2 + y + a^{2^k+2} +a^{2^k+1}=0. \end{aligned}$$

(8)

Note that Eq. (8) has at most two solutions $y_{1}$ and $y_{1}+1$. Multiplying by x on both sides of Eq. (5) yields $x^{2^k+1}=x^{2^k}+ ax$. By Lemma 3, we have

$$\begin{aligned} \mathrm{Tr}^{n}_{1}\left( x^{2^k+1}\right) =\mathrm{Tr}^{n}_{1}(x^{2^k}+ax)=\mathrm{Tr}^{n}_{1}(x+ax)=\mathrm{Tr}^{n}_{1}(y)=0. \end{aligned}$$

(9)

It is easy to check that only one of $y_{1}$ and $y_{1}+1$ satisfies Eq. (9).

• Case (II) If $\mathrm{Tr}^{n}_{1}\left( x^{2^k+1}\right) =1$, then

  $$\begin{aligned} x^{2^k-1}+x^{2^k}=a+1. \end{aligned}$$

  (10)

If $a=1$, then $x=0$ or $x=1$. It is obvious to see that $x=1$ is the unique solution.

If $a\ne 1$, then $x\ne 0, 1$ and from Eq. (10) we have $x^{2^k}=\frac{(a+1)x}{x+1}$, and so $x^2=(x^{2^k})^{2^k}=\frac{(a+1)^{2^k+1}x}{ax+1}$, which is equivalent to

$$\begin{aligned} ax^2 + x + (a+1)^{2^k+1}=0. \end{aligned}$$

(11)

If $a=0$, then $x=1$. However, $x=1$ is not a solution of Eq. (10). Thus, no solution.

Let $z=ax$. Then Eq. (11) can be written as

$$\begin{aligned} z^2 + z + \left( a^{2^k+2} + a^{2^k+1} + a^2 +a\right) =0. \end{aligned}$$

(12)

It can be checked that Eq. (12) has at most two solutions $z_{1}$ and $z_{1}+1$. From Eq. (10) we have $x^{2^k+1}=x^{2^k}+(a+1)x$. By Lemma 3, we obtain

$$\begin{aligned} \mathrm{Tr}^{n}_{1}\left( x^{2^k+1}\right) =\mathrm{Tr}^{n}_{1}\left( x^{2^k}+(a+1)x\right) =\mathrm{Tr}^{n}_{1}(ax)=\mathrm{Tr}^{n}_{1}(z)=1. \end{aligned}$$

(13)

It is obvious that only one of $z_{1}$ and $z_{1}+1$ satisfies Eq. (13).

Suppose that there exists one solution in Cases (I) and (II) respectively. Combining Eqs. (8) and (12), we obtain

$$\begin{aligned} (y+z)^2 + y+z + a^2 +a =0, \end{aligned}$$

this yields $y+z=a$ or $y+z=a+1$.

For the case $\mathrm{Tr}^{n}_{1}(a)=0$, then $y+z=a+1$, i.e. $z=y+a+1$. Since $y=(1+a)x$, it follows from Eq. (5) that

$$\begin{aligned} \left( \frac{y}{1+a} \right) ^{2^k-1}+ \left( \frac{y}{1+a} \right) ^{2^k}=a, \end{aligned}$$

Which is equivalent to

$$\begin{aligned} y^{2^k+1}+(1+a)y^{2^k}+(a^{2^k+1}+a)y = 0. \end{aligned}$$

(14)

By Eq. (10) we obtain

$$\begin{aligned} \left( \frac{y+a+1}{a} \right) ^{2^k-1}+ \left( \frac{y+a+1}{a} \right) ^{2^k}=a+1. \end{aligned}$$

We further derive

$$\begin{aligned} y^{2^k+1}+y^{2^k}+\left( a^{2^k+1}+1\right) y + a^{2^k+2}+1=0. \end{aligned}$$

(15)

Adding Eqs. (14) and (15) together gives

$$\begin{aligned} y^{2^k}= \frac{1+a}{a}y + \frac{a^{2^k+2}+1}{a}. \end{aligned}$$

(16)

Substituting Eq. (16) into Eq. (14), we derive

$$\begin{aligned} (1+a)y^2 + (1+a)\left( a^{2^k+2}+1\right) =0, \end{aligned}$$

which means

$$\begin{aligned} y=1+a^{2^{k-1}+1}. \end{aligned}$$

(17)

Substituting Eq. (17) into Eq. (16), we obtain

$$\begin{aligned} a^{2^{k-1}+1}(1+a)=0, \end{aligned}$$

which leads to $a=0$ or $a=1$, a contradiction.

For the case $\mathrm{Tr}^{n}_{1}(a)=1$, then $y+z=a$. So from Eq. (10) we deduce

$$\begin{aligned} y^{2^k+1} + a^{2^k+1}y + a^{2^k+2}+a^{2^k+1}=0. \end{aligned}$$

(18)

Adding Eqs. (14) and (18) together, we derive

$$\begin{aligned} y^{2^k} = \frac{a}{1+a}y + a^{2^k+1}. \end{aligned}$$

(19)

Combining Eqs. (19) and (14), we obtain

$$\begin{aligned} y = a^{2^{k-1}} + a^{2^{k-1}+1}, \end{aligned}$$

(20)

and then Eq. (19) becomes

$$\begin{aligned} (1+a)\left( a^{2^{k-1}}+ a^{2^{k-1}+1}\right) ^{2^k} + a\left( a^{2^{k-1}}+ a^{2^{k-1}+1}\right) + a^{2^k+2}+a^{2^k+1} =0, \end{aligned}$$

which can be simplified as

$$\begin{aligned} a(1+a)^{2^{k-1}+1} =0. \end{aligned}$$

Thus we obtain $a=0$ or $a=1$, which is a contradiction. The proof is complete. $\square$

Theorem 4

Let $n=3k$ and k be an integer. Let $u \in \mathbb {F}_{2^{k}}^{*}$. Then

$$\begin{aligned} f(x)= ux^{2^{2k}+2^{k}} + ux^{2^{2k}+1} + \mathrm{Tr}^{3k}_{k}(x) \end{aligned}$$

is a permutation polynomial over $\mathbb {F}_{2^{n}}$.

Proof

Let $\overline{f}(x)=x$. For any $x\in \mathbb {F}_{2^{n}}$, we have

$$\begin{aligned} \mathrm{Tr}^{3k}_{k}(f(x))= & {} u\mathrm{Tr}^{3k}_{k}\left( x^{2^{2k}+2^{k}} + x^{2^{2k}+1}\right) + \mathrm{Tr}^{3k}_{k}(x)\\= & {} \mathrm{Tr}^{3k}_{k}(x) = \overline{f}\left( \mathrm{Tr}^{3k}_{k}(x)\right) . \end{aligned}$$

Therefore, the above diagram commutes. According to the AGW criterion in Lemma 4, f(x) is a permutation polynomial over $\mathbb {F}_{2^{n}}$ if and only if $\overline{f}(x)=x$ is a bijection from $\mathbb {F}_{2^{k}}$ to $\mathbb {F}_{2^{k}}$ and f(x) is an injection on $(\mathrm{Tr}^{3k}_{k})^{-1}(\theta )$ for each $\theta \in \mathbb {F}_{2^{k}}$. Denote $S_{\theta }=\{x\in \mathbb {F}_{2^{n}} ~|~\mathrm{Tr}^{3k}_{k}(x)=\theta \}$. Thus we just need to prove that $f(x)= ux^{2^{2k}+2^{k}} + ux^{2^{2k}+1} + \theta$ is an injection on $S_{\theta }$. For any $a\in S_{\theta }$, we show that $f(x)=a$ has at most one solution. Thus we have

$$\begin{aligned} x^{2^{2k}+2^{k}} + x^{2^{2k}+1} = \frac{a+\theta }{u}. \end{aligned}$$

(21)

Note that $\mathrm{Tr}^{3k}_{k}(x)=\theta$, we obtain

$$\begin{aligned} x^{2^{2k}} = x^{2^{k}} +x + \theta . \end{aligned}$$

(22)

Substituting Eq. (22) into Eq. (21) leads to

$$\begin{aligned} x^{2^{k}}\left( x^{2^{k}} +x + \theta \right) + x(x^{2^{k}} +x + \theta ) = \frac{a+\theta }{u}. \end{aligned}$$

(23)

Let $y=x^{2^{k}} +x$. Then from Eq. (23) we give

$$\begin{aligned} y^2 + \theta y + \frac{a+\theta }{u} =0. \end{aligned}$$

(24)

• Case (I) If $\theta =0$, then $y^{2}=\frac{a}{u}$, this yields $x^{2^{k}} +x =(\frac{a}{u})^{2^{n-1}}$. Plugging it into Eq. (22) gives $x^{2^{2k}}=(\frac{a}{u})^{2^{n-1}}$, so we deduce $x=(\frac{a}{u})^{2^{k-1}}$.

• Case (II) If $\theta \ne 0$, then Eq. (24) has at most two solutions $y_{1}$ and $y_{1}+\theta$. Since $y=x^{2^{k}} +x$, we have $\mathrm{Tr}^{3k}_{k}(y)=0$. However, $\mathrm{Tr}^{3k}_{k}(y_{1}+\theta )=\mathrm{Tr}^{3k}_{k}(y_{1})+\theta \ne \mathrm{Tr}^{3k}_{k}(y_{1})$. Therefore one of $y_{1}$ and $y_{1}+\theta$ satisfies Eq. (24). Without loss of generality, suppose that $y_{1}$ is a solution of Eq. (24), then from Eq. (22) we have $x^{2^{2k}}=y_{1}+\theta$, we further obtain that $x=y_{1}^{2^{k}}+\theta$ satisfies $f(x)=a$. Thus we prove that f(x) is an injection on $S_{\theta }$. Hence we finish the proof. $\square$

4 Two classes of permutation polynomials with trace functions over $\mathbb {F}_{3^n}$

In this section, two classes of permutation polynomials with trace functions are presented over $\mathbb {F}_{3^{n}}$.

Theorem 5

Let $n=2k$ and k be an integer. Let $u, v \in \mathbb {F}_{3^{k}}^{*}$. Then

$$\begin{aligned} f(x)= ux^{3^{2k}-3^{k}+1} + vx^{3^{k}+2} + u\mathrm{Tr}^{2k}_{k}(x) \end{aligned}$$

is a permutation polynomial over $\mathbb {F}_{3^{n}}$ if one of the following two conditions holds:

• (i) k is odd and $u^{-1}v$ is a nonsquare in $\mathbb {F}_{3^k}$;

• (ii) k is even and $u^{-1}v$ is a square in $\mathbb {F}_{3^k}$.

Proof

For every $a\in \mathbb {F}_{3^n}$, we need to prove that the equation

$$\begin{aligned} f(x)=ux^{3^{2k}-3^{k}+1} + vx^{3^{k}+2} + u\mathrm{Tr}^{2k}_{k}(x)=a \end{aligned}$$

(25)

has at most one solution in $\mathbb {F}_{3^n}$.

• Case (I) If $a=0$, then we have

  $$\begin{aligned} x\left( ux^{1-3^{k}} + vx^{3^{k}+1} + ux^{3^{k}-1} + u\right) = 0. \end{aligned}$$

  (26)

It can be checked that $x=0$ is a solution to Eq. (26). Thus we need to prove

$$\begin{aligned} ux^{1-3^{k}} + vx^{3^{k}+1} + ux^{3^{k}-1} + u =0 \end{aligned}$$

(27)

has no solution. Multiplying by $x^{3^{k}+1}$ on both sides of Eq. (27) gives

$$\begin{aligned} ux^2 + vx^{2\cdot 3^{k}+2} + ux^{2\cdot 3^{k}} + ux^{3^{k}+1} =0, \end{aligned}$$

which can be written as

$$\begin{aligned} u\left( x^{3^{k}} - x\right) ^{2} = -vx^{2\cdot 3^{k}+2}. \end{aligned}$$

(28)

If $x\in \mathbb {F}_{3^k}$, then from Eq. (28) we obtain $x=0$ since $v\ne 0$. However, $x=0$ is not a solution of Eq. (27).

If $x\not \in \mathbb {F}_{3^k}$, then $x^{3^{k}} - x\ne 0$. Raising both sides of Eq. (28) to the $\frac{3^k-1}{2}$ power leads to

$$\begin{aligned} \left( x^{3^{k}} - x\right) ^{3^k-1} = \left( -u^{-1}v\right) ^{\frac{3^k-1}{2}}. \end{aligned}$$

(29)

When k is odd, we get $\frac{3^k-1}{2}$ is odd. If $u^{-1}v$ is a nonsquare in $\mathbb {F}_{3^k}$, then from Eq. (29) we derive $(x^{3^{k}} - x)^{3^k-1}=1$.

When k is even, we obtain $\frac{3^k-1}{2}$ is even. If $u^{-1}v$ is a square in $\mathbb {F}_{3^k}$, then from Eq. (29) we deduce $(x^{3^{k}} - x)^{3^k-1}=1$.

However, $(x^{3^{k}} - x)^{3^k-1} =\frac{x-x^{3^{k}}}{x^{3^{k}} - x}=-1$, a contradiction. Therefore $f(x)=a$ has only one solution $x=0$ for $a=0$.

• Case (II) If $a\ne 0$, then we will verify that $f(x) = a$ has at most one nonzero solution. It follows from Eq. (25) that

  $$\begin{aligned} ux^{1-3^{k}} + vx^{3^{k}+1} + ux^{3^{k}-1} + u = \frac{a}{x}. \end{aligned}$$

  (30)

It is easy to see that the left side of Eq. (30) is in $\mathbb {F}_{3^k}$, therefore we obtain $\frac{a}{x}\in \mathbb {F}_{3^k}$, we further have $x^{3^k} = a^{3^k-1}x$. Plugging it into Eq. (25), we obtain

$$\begin{aligned} x^3 + uv^{-1}\left( a^{1-3^k}-1\right) ^2x - v^{-1}a^{2-3^{k}} =0. \end{aligned}$$

(31)

If $a\in \mathbb {F}_{3^k}^{*}$, then from Eq. (31) we derive $x=(v^{-1}a)^{3^{n-1}}$. Thus Eq. (25) has one solution $x=(v^{-1}a)^{3^{n-1}}$.

If $a\not \in \mathbb {F}_{3^k}^{*}$, according to Conditions (i) and (ii) of the theorem, it can be easily check that $-uv^{-1}$ is a square in $\mathbb {F}_{3^k}$. By Lemma 2, Eq. (31) has three solutions and if $x_{1}$ is a solution of Eq. (31), then the other two solutions are $x_{1}+(a^{1-3^k}-1)\sqrt{-uv^{-1}}$ and $x_{1}-(a^{1-3^k}-1)\sqrt{-uv^{-1}}$. Without loss of generality, assume that both $x_{1}$ and $x_{1}+(a^{1-3^k}-1)\sqrt{-uv^{-1}}$ satisfy Eq. (25). Then we have

$$\begin{aligned} x_{1}^{3^k} = a^{3^k-1}x_{1} \end{aligned}$$

and

$$\begin{aligned} \left( x_{1}+\left( a^{1-3^k}-1\right) \sqrt{-uv^{-1}} \right) ^{3^k} = a^{3^k-1}\left( x_{1}+\left( a^{1-3^k}-1\right) \sqrt{-uv^{-1}} \right) . \end{aligned}$$

Combining the above two equations together gives

$$\begin{aligned} 2\left( a^{3^{k}-1}-1\right) \sqrt{-uv^{-1}}=0, \end{aligned}$$

which is not possible since $u\ne 0,v\ne 0$ and $a\not \in \mathbb {F}_{3^k}^{*}$. Similarly, we can prove that any two of these three solutions can not satisfy Eq. (31) simultaneously. Therefore Eq. (25) has at most one solution in $\mathbb {F}_{3^n}$. The proof is complete. $\square$

Theorem 6

Let $n=2k$ and k be an integer. Let $u, v \in \mathbb {F}_{3^{k}}^{*}$. Then

$$\begin{aligned} f(x)= ux^{3^{2k}-3^{k}+1} + vx^{3^{k}+2} + ux + u\mathrm{Tr}^{2k}_{k}(x) \end{aligned}$$

is a permutation polynomial over $\mathbb {F}_{3^{n}}$ if one of the following two conditions holds:

• (i) k is odd and $u^{-1}v$ is a square in $\mathbb {F}_{3^k}$;

• (ii) k is even and $u^{-1}v$ is a nonsquare in $\mathbb {F}_{3^k}$.

Proof

We will show that for every $a\in \mathbb {F}_{3^n}$, the equation

$$\begin{aligned} f(x)= ux^{3^{2k}-3^{k}+1} + vx^{3^{k}+2} + ux^{3^k} - ux = a \end{aligned}$$

(32)

has at most one solution in $\mathbb {F}_{3^n}$.

• Case (I) If $a=0$, then $x=0$ is a solution. Suppose that $x\ne 0$ is another solution. We need to prove that

  $$\begin{aligned} ux^{1-3^{k}} + vx^{3^{k}+1} + ux^{3^{k}-1} - u =0 \end{aligned}$$

  (33)

has no solution. Multiplying by $x^{3^{k}+1}$ on both sides of Eq. (33) gives

$$\begin{aligned} u\left( x^{3^{k}} + x\right) ^{2} = -vx^{2\cdot 3^{k}+2}. \end{aligned}$$

(34)

If $x^{3^{k}}=-x$, then from Eq. (34) we obtain $x=0$ since $v\ne 0$, however, $x=0$ does not satisfy Eq. (33).

If $x^{3^{k}}\ne -x$, then raising both sides of Eq. (34) to the $\frac{3^k-1}{2}$ power derives

$$\begin{aligned} \left( x^{3^{k}} + x\right) ^{3^k-1} = \left( -u^{-1}v\right) ^{\frac{3^k-1}{2}}. \end{aligned}$$

(35)

When k is odd, we obtain $\frac{3^k-1}{2}$ is odd. It follows from Eq. (35) that $(x^{3^{k}} + x)^{3^k-1}=-1$ since $u^{-1}v$ is a square in $\mathbb {F}_{3^k}$.

When k is even, we have $\frac{3^k-1}{2}$ is even. Similarly, we have $(x^{3^{k}} - x)^{3^k-1}=-1$ since $u^{-1}v$ is a nonsquare in $\mathbb {F}_{3^k}$.

However, $(x^{3^{k}} + x)^{3^k-1} =\frac{x+x^{3^{k}}}{x^{3^{k}} + x}=1$, a contradiction with the above two cases. Therefore $f(x)=a$ has only one solution $x=0$ for $a=0$.

• Case (II) If $a\ne 0$, then $x\ne 0$ and it follows from Eq. (32) that

  $$\begin{aligned} ux^{1-3^{k}} + vx^{3^{k}+1} + ux^{3^{k}-1} - u = \frac{a}{x}. \end{aligned}$$

  (36)

It is easy to check that the left side of Eq. (36) is in $\mathbb {F}_{3^k}$, therefore we have $x^{3^k} = a^{3^k-1}x$. Substituting it into Eq. (32), we deduce

$$\begin{aligned} x^3 + uv^{-1}\left( a^{1-3^k}+1\right) ^2x - v^{-1}a^{2-3^{k}} =0. \end{aligned}$$

(37)

If $a^{3^k}=-a$, then Eq. (37) has one solution $x=-(v^{-1}a)^{3^{n-1}}$.

According to Conditions (i) and (ii), we obtain that $-uv^{-1}\in \mathbb {F}_{3^k}^{*}$ is a nonsquare in $\mathbb {F}_{3^k}$, but $-uv^{-1}$ is a square in $\mathbb {F}_{3^{n}}$. Thus we have $(-uv^{-1})^{3^k-1}=1$ and $(\sqrt{-uv^{-1}})^{3^k-1}=-1$, this gives $(\sqrt{-uv^{-1}})^{3^k}=-\sqrt{-uv^{-1}}$.

If $a^{3^k}\ne -a$, according to Lemma 2, then Eq. (37) has three solutions since $-uv^{-1}$ is a square in $\mathbb {F}_{3^{n}}$. If $x_{2}$ is a solution of Eq. (37), then the other two solutions are $x_{2}+(a^{1-3^k}+1)\sqrt{-uv^{-1}}$ and $x_{2}-(a^{1-3^k}+1)\sqrt{-uv^{-1}}$. Without loss of generality, assume that both $x_{2}$ and $x_{2}+(a^{1-3^k}+1)\sqrt{-uv^{-1}}$ are solutions of Eq. (32). Then we have

$$\begin{aligned} x_{2}^{3^k} = a^{3^k-1}x_{2} \end{aligned}$$

and

$$\begin{aligned} \left( x_{2}+\left( a^{1-3^k}+1\right) \sqrt{-uv^{-1}} \right) ^{3^k} = a^{3^k-1}\left( x_{2}+\left( a^{1-3^k}+1\right) \sqrt{-uv^{-1}} \right) , \end{aligned}$$

which is equivalent to

$$\begin{aligned} x_{2}^{3^k}+\left( a^{3^k-1}+1\right) \left( -\sqrt{-uv^{-1}} \right) = a^{3^k-1}x_{2}+\left( 1+a^{3^k-1}\right) \sqrt{-uv^{-1}}. \end{aligned}$$

Combining the above two equations gives

$$\begin{aligned} 2\left( a^{3^{k}-1}+1\right) \sqrt{-uv^{-1}}=0, \end{aligned}$$

which is impossible since $u\ne 0,v\ne 0$ and $a^{3^k}\ne -a$. Similarly, we can show that any two of these three solutions can not satisfy Eq. (37) simultaneously. Therefore Eq. (32) has at most one solution in $\mathbb {F}_{3^n}$. We complete the proof. $\square$

5 Conclusion

In this paper, by determining the solutions of some special equations, three classes of permutation polynomials with trace functions were presented over $\mathbb {F}_{2^{n}}$. Furthermore, two classes of permutation polynomials with trace functions were given over $\mathbb {F}_{3^n}$.