Dealing with stochastic environmental variation in space and time: bet hedging by generalist, specialist, and diversified strategies

Abstract

Building on previous work, we derive an optimization model for a two-state stochastic environment and evaluate the fitnesses of five reproductive strategies across generations. To do this, we characterize spatiotemporal variation and define grain (=patch) size as the scale of fitness autocorrelation. Fitness functions of environmental condition are Gaussian. The strategies include two specialists on each of the environmental conditions; two generalists that each fare equally well under both conditions, but one (a conservative bet hedger) optimizes the shape of the fitness function; and a diversified bet hedger producing an optimal mix of the two specialists within individual broods. When the environment is primarily in one of the two states, the specialist on that state achieves the highest fitness. In the more interesting situation where the two environments are equally prevalent in the long term, with low-moderate environmental variation, a generalist strategy (that copes with both states well) does best. Higher variation favors diversified bet hedgers, or surprisingly, specialists, depending mainly on whether spatial or temporal variation predominates. These strategies reduce variance in fitness and optimize the distribution of offspring among patches differently: specialists by spreading offspring among many independently varying patches, while diversified bet hedgers put all offspring into a few patches or a single patch. We distinguish features consistent with strategies like diversified bet hedgers that spread risk in time from features linked to strategies like specialists that spread risk in space. Finally, we present testable hypotheses arising from this study and suggest directions for future work.

Introduction

Life history strategies in stochastic environments

A key issue in ecology and evolutionary biology is the need to understand how organisms cope with spatial and temporal variation in environmental factors that affect fitness (Starrfelt and Kokko 2012; hereafter S&K). Plasticity within generations can be effective in this context when there are reliable cues predicting the environmental state at later stages of development (Pigliucci 2001; Gabriel et al. 2005). Without reliable cues, however, though the frequency distribution of environmental states may be “known” or genetically encoded, the specific upcoming changes are unpredictable. Under these circumstances, specializing to take advantage of specific conditions when they arise or generalizing to exploit a wide range of conditions are alternative strategies for addressing variable environments. Specialists do well in their favored conditions and may at least get by under other conditions. Generalists manage to do fairly well under many conditions, though not usually as well in any given condition as the relevant specialist (i.e., the specialist-generalist trade-off: Levins 1962, 1968; Futuyma and Moreno 1988; Dall 2010). A key question is then: What patterns of spatial and temporal environmental variation favor specialists versus generalists? Intuition and simple models (e.g., see Dall and Cuthill 1997) indicate that environmental variation tends to favor generalists, but this view requires evaluation within a modeling framework including key features of environmental structure and variation regime that are missing from analyses to date.

To persist in a variable environment, life histories must prove effective across generations that experience different environmental conditions. Successful lineages are those with the highest multiplicative product of lifetime reproductive success across generations (i.e., the highest lineage fitness, the geometric mean per-generation fitness over time; see Levins 1962; Bulmer 1994; Simons 2011). Strategies that specifically maximize lineage fitness by reducing the variance in fitness of the lineage over time at the cost of a reduction in the arithmetic mean fitness are generally known as bet hedging (for recent reviews, see Frank 2011; Starrfelt and Kokko 2012; Wright and Ratikainen 2012). The advantage of this view is most apparent when there is a non-negligible chance of complete reproductive failure in any generation that would potentially extinguish the lineage. In this situation, reducing fitness variation is crucial for persistence, even if this requires greatly shrinking the arithmetic mean fitness.

In reviewing the bet hedging literature and providing a rigorous formulation and analysis of strategic responses to unpredictably varying environments, Starrfelt and Kokko (2012) erected a framework that considerably advances our understanding of bet hedging in natural systems. To do this, they addressed the large and diverse literature from which the bet hedging concept has emerged. Maximizing the geometric mean fitness that we refer to as lineage fitness was emphasized in early work by Dempster (1955), Levins (1962, 1968), and Lewontin and Cohen (1969). The mathematics of bet hedging developed from the work of Gillespie (1974, 1975) on selection for variance in offspring number and population genetics in patchy environments, Seger and Brockmann (1987) and Philippi and Seger (1989) on the distinction between conservative and diversified bet hedging, Seger and Brockmann (1987) and Frank and Slatkin (1990) on the role of Jensen’s inequality, and Frank and Slatkin (1990) on fitness as a random variable and implications for allele frequencies. See S&K for a thorough summary of the theoretical underpinnings of bet hedging.

The two-state stochastic-environment model

To illustrate how spatiotemporal variation can determine the effectiveness of bet hedging strategies in nature, Starrfelt and Kokko (2012) derived and analyzed an optimization model in which the environment experienced by each individual at a given time is in one of two discrete states or conditions. These conditions (e.g., “dry” and “wet”—see Seger and Brockmann 1987) apply to the different locations or patches. Time is assumed to pass in discrete generations (=years here for convenience) that vary between two randomly alternating annual spatial patterns of the environmental conditions (e.g., relatively dry or relatively wet years, based on frequencies of patches in the alternative conditions).

In their analysis of this model, Starrfelt and Kokko (2012) focused on equally frequent alternative spatial patterns between years and on individuals occupying separate patches that vary independently across space and time. They provided a thorough framework for determining the “genotypic variance” and its associated fitness, which is fitness assessed across generations to track the success of each strategy as a genotype through its potential to increase in abundance. Genotypic fitness, expressed as the geometric mean fitness across years, depends on (1) the arithmetic mean and (2) the variance in fitness experienced by individuals and on (3) the correlation in fitness effects of the environment among individuals. In general, bet hedging strategies can prove successful by achieving a fitness-maximizing balance among those three fitness factors.

S&K were primarily concerned with conservative and diversified bet hedging. These two types of bet hedging differ in their influence on the three fitness factors. Conservative bet hedging (CB) reduces the variation in fitness among individuals via the generalist strategy of consistently responding moderately well to a range of different environmental conditions. Diversified bet hedging (DB) is based on risk spreading by specializing on different environmental conditions with certain probabilities (e.g., broods of offspring containing certain frequencies of specialists of different types, an example of phenotypic polymorphism—Frank and Slatkin 1990; Davies et al. 2012). Thus, DB is effective by reducing the environment-based fitness correlation among individuals. Crucially, both CB and DB reduce the genotypic variance in fitness, a general requirement for adaptive bet hedging.

Both strategies are assumed to bear the cost of a reduction in arithmetic mean fitness to achieve variance reduction, but sufficient reduction in variance can in principle more than offset this cost and lead to genotypic geometric-mean fitness maximization. This cost as reduced arithmetic mean fitness is not explicitly incorporated in the S&K analysis, presumably for two reasons: to avoid additional arbitrary assumptions and on the grounds that, in the absence of empirical evidence, the magnitude of such a cost may be considered negligible. But, we suspected that even small bet hedging costs could alter the fitness rankings among strategies across regimes of environmental variation.

In considering variation through space and time, S&K invoke the concept of environmental grain (Levins 1968). For S&K, an environment is coarse-grained if environmental conditions are uniform over space but vary between uniform spatial patterns over time; an environment is fine-grained if environmental conditions vary across space, but the mean condition changes little or not at all through time.

In our analysis, we build on the S&K approach but use the concept of grain differently. To incorporate patchiness arising from spatial autocorrelation of environmental condition into the model (thus connecting with empirically measurable patchiness), we first separate the concepts of spatial and temporal grain. Since time in the S&K model and our extension of it is discrete at the scale of generations (=years), we consider this the (relatively coarse) temporal grain size: in effect, time is perfectly autocorrelated (i.e., fixed and discrete) within years but statistically independent between years. We do not address temporal grain further here but emphasize its independence from spatial grain.

Analogous to variation through time, we consider space to consist of patches within which the environment is completely uniform in condition (i.e., all microhabitats that individuals might occupy within a patch are identical—e.g., either all wet or all dry) and between which environmental conditions are statistically independent (e.g., the probability of being dry or wet in a given year is the same for all patches and does not depend on the state of the neighboring patches). According to this view, spatial grain size is the area of these individual patches. For a given population size and total area occupied, spatially coarse-grained environments consist of relatively few patches among which conditions may differ, and each patch may contain many individuals experiencing identical condition. In contrast, spatially fine-grained environments include many patches that can differ in condition, each containing only a few individuals or perhaps a single individual.

We place special emphasis here on representing constraints on responses that arise from specifying strategy-specific fitness functions of environmental condition, thus allowing the relative success of the strategies under different patterns of spatiotemporal variability to be assessed. This is a particularly important step toward using the analysis presented here to evaluate implications of human-induced rapid environmental change (HIREC) for populations adapted to a given environmental variability regime.

We make the key assumption that adaptation to a particular magnitude of condition (e.g., a moisture level in the environment) implies maximal fitness at that magnitude, with fitness decreasing continuously for increasing differences in conditions. To implement this approach, we represent fitness as a normal or Gaussian function of environmental condition, where the width and height of these functions express constraints to be expected on each strategy. The function then determines fitnesses for the two conditions in the present analysis (and alternative conditions that may arise from HIREC) but also accounts for the relationship between them, depending on the particular strategy.

Our goals in this study are (1) to present a simple framework to characterize physical structure and stochastic variation for evaluating the efficacy of life history strategies, (2) to derive and implement new theory for how strategies can maximize lineage fitness by optimizing features like the spatial distribution of offspring, (3) to show how bet hedging may be explicit or implicit in certain strategies, and (4) to propose new testable hypotheses and identify fruitful future research directions.

Derivation and methods

The modeling framework

Following Starrfelt and Kokko (2012), we assume that each individual in each year experiences one of two discrete states or conditions (see their paper for details of these derivations that can be sketched only briefly here). These conditions (here designated c ₁ and c ₂) apply to the different locations occupied by individuals, with patch conditions assumed to be internally uniform for all intra-patch locations yet statistically independent between patches across space and time. Time is discrete, corresponding to generations (=years here), and each year falls into one of two states (e.g., relatively dry or relatively wet, depending on whether most patches that year are dry or wet). Whether a year is in state 1 (e.g., dry) or state 2 (e.g., wet) randomly alternates, with probabilities in a given year of state 1 or state 2 being P ₁ and P ₂ = 1 − P ₁, respectively. Within any given year, there is a spatial array of patches such that the frequency of patches in year j experiencing condition i is f _ij (e.g., the frequency of wet patches [i = 2] in dry years [j = 1] may be f ₂₁ = 0.25, and thus, f ₁₁ = 0.75 for dry localities in dry years; while the frequency of wet patches in wet years may be f ₂₂ = 0.8, and thus, f ₁₂ = 0.2). Restrictions consistent with these designations are 0.5 ≤ f ₁₁ ≤ 1, 0.5 ≤ f ₂₂ ≤ 1, 0 ≤ f ₁₂ ≤ 0.5, and 0 ≤ f ₂₁ ≤ 0.5. This scheme allows for a full range of environmental variation from purely spatial variation (when f ₁₁ = f ₂₂ = 0.5) to purely temporal variation (when f ₁₁ = f ₂₂ = 1) between the annual patterns. Moreover, the patterns may favor one condition or the other either symmetrically (P ₁ = P ₂ = 0.5) or asymmetrically (P ₁ ≠ P ₂). See Table 1 for a list of symbols, definitions, magnitudes, and units of the variables and parameters used in the model.

Table 1 Variables and parameters of the model

The focus of this study is on reproductive success per generation in sequence across generations. For each generation, reproductive success is assessed as the ratio R of the number of individuals living at the beginning of the next generation that are produced per progenitor at the beginning of the current generation. Because the multiplicative product of these R values indicates the successive numbers of offspring along a lineage, the expected geometric mean of these values over an arbitrarily long sequence expresses long-term evolutionary success as lineage fitness W. The idea is then to evaluate and compare the lineage fitnesses of different strategies over a spatiotemporally varying environment. (Hereafter, fitness = lineage fitness unless otherwise indicated.)

We allow for brood sizes of I individuals (=offspring), taken to consist of genotypes (=strategies) that respond independently, hence the focus on genotypic fitness for each strategy separately. In the present derivation, we ignore density and frequency dependence and explicit interactions among genotypes and address the arithmetic mean reproductive success M and variance V for a single genotype. We then Taylor-expand the per-capita increase rate lnR about the arithmetic mean R value M, ignoring terms beyond second order, and solve for fitness W as the geometric mean e^E(lnR) :

$$ E\left( \ln R\right)=E\left[ \ln M+\frac{R-M}{M}-\frac{{\left(R-M\right)}^2}{2{M}^2}+\cdots \right]\approx \ln M-\frac{V}{2{M}^2}, $$

(1)

where V is the genotypic fitness variance (E[(R-M)²]), and thus

$$ {e}^{E\left( \ln R\right)}=W\approx M{e}^{\frac{V}{2{M}^2}}\ . $$

(2)

Following Bulmer (1994), we use the exponential approximation for W instead of the linear one used by S&K, though results are similar for these alternatives. V expresses temporal variation in expected (mean) fitness over the relevant group of offspring (or genotype, assuming genetic uniformity), hereafter indicated as V _T . (This avoids S&K’s use of V _G , which also refers to a variance in trait values among genotypes in quantitative genetics.) Note that when V _T  = 0, then W = M, but for V _T  > 0, W shrinks from M asymptotically to zero as V _T increases. The logarithmic function associated with the geometric mean fitness incorporates diminishing returns on R: symmetrical variation around R thus reduces the geometric mean as expressed by the mathematical relationship for such concave functions known as Jensen’s inequality (e.g., see Needham (1993)). This effect is captured in Eq. (1), allowing W to be maximized by bet hedging, trading a reduction in arithmetic mean M for a lower variance V _T in Eq. (2).

One of S&K’s most important insights was to consider the implications of expressing genotypic fitness variance V _T as the variance through time of the mean over space of n random variables—the fitnesses of individuals, each assumed to occupy a separate patch of habitat. Thus, V _T corresponds to a standard error based on non-independent sample points. For a given strategy, we let V _P be the fitness variance through time that would be associated with a single patch occupied by a sequence of single individuals of the particular genotype across generations (corresponding to σ ² in S&K). Since the expected magnitudes of these variances and their covariances C _P are all identical, it follows that

$$ {V}_T=\frac{n{V}_P}{n^2}+\frac{n\left(n-1\right){C}_P}{n^2}={V}_P\left(\frac{1}{n}+\frac{\left(n-1\right){\rho}_P}{n}\right)=\frac{1}{n}\left({V}_P+\left(n-1\right){C}_P\right), $$

(3)

where ${\rho}_P=\frac{C_P}{V_P}$ is the correlation coefficient of environmental effects on different individuals within the genotype. Because n is the number of individuals = patches in this fine-grained world, S&K argued that for large groups Eq. (3) becomes simply V _T  = V _P ρ _P . S&K emphasized that the two main types of bet hedging reduce V _T mainly in different ways: conservative bet hedging (CB) by reducing V _P and diversified bet hedging (DB) by reducing the environmental correlation coefficient ρ _P .

We suppose instead that there are I individuals in a brood; each spatial patch contains m individuals, with a total of n patches occupied, making mn = I individuals altogether. By spatial patch, here we mean neighborhoods in which the environment is uniform (i.e., all within-patch locations are perfectly autocorrelated in environmental condition), but between patches, independence in environmental conditions prevails. This mosaic spatial structure is a discrete approximation of continuously shrinking spatial autocorrelation with distance and directly expresses the spatial grain size.

We now let V _P be the variance in mean fitness over the patch by taking account of the m individuals in each patch using

$$ {V}_P={V}_L\left(\frac{1}{m}+\frac{\left(m-1\right){\rho}_L}{m}\right). $$

(4)

This follows the same logic used to generate Eq. (3); here ${\rho}_L=\frac{C_L}{V_L}$ is the fitness correlation coefficient for locations within patches, V _L is the variance in fitness through time at a location within the patch, and C _L is the fitness covariance among locations in the patch. Notice that with only a single individual in each patch (i.e., m = 1, as assumed by S&K) or when all individuals within each patch have identical fitnesses (i.e., ρ _L  = 1), then V _P  = V _L. But in general, substituting (4) into (3),

$$ {V}_T={V}_L\left(\frac{1}{m}+\frac{\left(m-1\right){\rho}_L}{m}\right)\left(\frac{1}{n}+\frac{\left(n-1\right){\rho}_P}{n}\right)=\frac{1}{I}\left({V}_L+\left(m-1\right){C}_L+m\left(n-1\right){C}_P\right). $$

(5)

There are now three components of genotypic temporal variance, perhaps best understood using the middle result in (5) as the multiplicative product of the temporal variance in fitness at any single location (V _L ), a within-patch environmental correlation term, and a between-patch environmental correlation term. Each of these correlation terms is the sum of the magnitude of environmental autocorrelation within location (1/m) or within patch (1/n) and the environmental correlation between locations (ρ _L ) or between patches (ρ _P ), with larger numbers of occupied locations or patches biasing the sum toward ρ _L and ρ _P , respectively. The different strategies influence these multiplicative terms differently, in part via different distributions of offspring within vs. between patches.

The strategies and their fitness distributions

In this study, we focus on five different strategies as alternative means of addressing spatiotemporal variation. We emphasize the role of these strategies as tools in understanding how individuals and lineages with particular environmental tolerances (described by fitness functions) deal with environmental variation. Each strategy is based on normally distributed per-generation fitness functions of the continuous variable environmental condition c, with mean $\overline{c}$ and standard deviation s (see Fig. 1 and Appendix A). Per-generation fitness is the expected lifetime reproductive success R, determined by averaging over R(c ₁) and R(c ₂), weighted by expected frequencies of c ₁ and c ₂, respectively. Preliminary analyses confirmed the intuitively obvious prediction that if one environmental state is much more common than the other, then the specialist on the more common state achieves the highest fitness. Here, we focus on the more interesting scenarios that arise when the long-term expected frequencies of the two environmental states, c ₁ and c ₂, are the same (=0.5).

Fig. 1

Fitness functions of environmental condition for the five strategies (two of which are specialists shown in a. All are Gaussian or combinations of Gaussian functions, and they express fitness as expected lifetime reproductive success R. The alternative environmental conditions in the two-state model are c ₁ and c ₂, and the black dots on the graphs indicate the corresponding fitness values

Of the five strategies, two are specialists, S₁ and S₂, where S₁ has its peak R ₁(c ₁) at c ₁, and S₂ has its peak R ₂(c ₂) at c ₂. The standard deviation s of these fitness functions is assumed to result from an evolutionary trade-off between curve width and height. Here, s is taken to be the largest standard deviation compatible with a maximum possible fitness of 1 (see S&K regarding 1 as an upper fitness limit), under the assumption that the specialist i has been selected to maximize fitness at c _i . The shapes of these and the other functions below indicate the fitness implications of shifts in condition, such as those that might result from long-term shifts in the environment. Though specialist 1 tends to do poorly when the environment is in state 2, and vice versa for specialist 2, in a spatially variable environment, both can reduce variance in annual fitness by spreading offspring across numerous patches, some of which are in the state that they are well adapted to, offsetting low fitness in patches that are in the mismatched environmental state.

There are two types of generalists (G), depending on whether the shape of the fitness function remains fixed (FG) or optimizes a trade-off between height and width of the distribution, a strategy we take to be conservative bet hedging (CB). FG is adapted to the environmental conditions in that it minimizes patch-level variance V _P (=V _L ) by achieving equal fitness in the two conditions, resulting in V _P  = V _L  = 0. Because the fitness functions are symmetrical, this means that the optimal ${\overline{c}}_{{}_G} = \left({c}_1+{c}_2\right)/2$. FG is assumed to have the same standard deviation s and thus the same shape of fitness distribution as the specialists but shifted to the mid-point between c ₁ and c ₂. The CB, however, has the same mid-point but optimizes curve height and width as indicated in Appendix A. This adjustment by CB increases genotypic fitness by maximizing the mean, though as for FG, the peak fitness approaches zero asymptotically in adjusting to increasing environmental variability. A fractional cost of conservative bet hedging δ _C is imposed as a multiplicative factor 1-δ _C on fitness, such that 0 < δ _C  < 1. (Note that we have labeled the flexible generalist strategy “conservative bet hedger” on the assumption that there is an additional cost to pay for this flexibility. We emphasize, however, that FG could itself be considered a conservative bet hedger on the basis that the mean of its Gaussian fitness function is necessarily reduced in exchange for reduced fitness variance.) Though other forms of generalists and conservative bet hedging strategies are certainly possible and can easily be modeled in this framework, FG and CB capture important features that distinguish them from specialist-based strategies and help show how particular regimes of environmental variation make particular strategies successful.

The other strategy is the diversified bet hedger. The DB strategy produces a mix of specialists S₁ and S₂, of which the proportion d ₁ are S₁. Note that this ensures a good match between some subset of the population and the patch it occupies regardless of the variation in conditions, buffering the mean fitness from variation. We assume that the proportion d ₁ is optimized to maximize fitness. With R ₁(c ₁) = R ₂(c ₂) = 1, and the long-term frequencies of c ₁ and c ₂ = 0.5, as assumed here, the optimal value of d ₁ is d ₁ = 0.5. As for the conservative bet hedger, DB strategies may incur a fractional cost δ _D , imposed as a multiplicative cost factor 1-δ _D on fitness, such that 0 < δ _D  < 1.

The way diversified bet hedging addresses the variance in fitness depends on whether it operates between patches (as in the S&K analysis, based on a fine-grained environment) or within patches. Between-patch diversified bet hedging reduces genotypic variance V _T by reducing the environmental correlation ρ _P among the fitnesses of individuals occupying different independently varying patches. When both DB phenotypes S₁ and S₂ (the specialists on conditions c ₁ and c ₂, respectively) jointly occupy individual patches, there is within-patch DB. With m > 1, the optimal d ₁ remains 0.5. The fitness associated with each patch is the mean fitness over each within-patch subset of the brood. This reduces genotypic variance V _T by reducing the within-patch variance, making DB resemble yet another type of generalist.

Fitness distributions, fitnesses at c ₁ and c ₂, and the equations for determining the fitness components of Eq. (5) for the five strategies are presented in Appendix B (supplementary materials).

Obtaining and presenting the numerical results

The results summarized below (1) indicate how fitnesses of the strategies vary with the relative range of environmental variation ε = (c ₂ – c ₁) / s for particular combinations of the frequencies f ₁₁ and f ₁₂ with P ₁ = 0.5 and (2) identify the dominant (highest fitness) strategies across all combinations of P ₁, f ₁₁, and f ₁₂ for particular magnitudes of ε. Bet hedging cost coefficients were set at δ _C  = δ _D  = 0.05. Because P ₂ = 1 − P ₁, f ₂₁ = 1 − f ₁₁, and f ₂₂ = 1 − f ₁₂, we expressed the pattern and frequency combinations simply in terms of the condition 1 magnitudes P ₁, f ₁₁, and f ₁₂. We considered only “unbiased” combinations, meaning that the expected frequencies of patches in environmental conditions 1 and 2 over time were both 0.5. Note that this can come about with say P ₁ more frequent than P ₂, as long as the frequencies compensate by having more localities in environmental condition 2 during pattern−2 years−than are in environmental condition 1 during pattern−1 year. In other words, when one pattern is more frequent, the less frequent pattern is more extreme in frequency for the alternative environmental condition. Figure 2 illustrates example patch distributions for three different combinations of f ₁₁ and f ₁₂ with P ₁ = P ₂ = 0.5, using a grid representation.

Fig. 2

Diagrammatic representation of example patterns and environmental condition frequencies for patches distributed on an 8 × 8 grid. One of the two patterns j specifying the frequency f _ij of each condition i occurs according to the probabilities P _j in each generation; the exact positions of the environmental conditions among patches in a given generation are determined randomly

Results were obtained by calculating the fitnesses for the five strategies at each combination of ε, P ₁, f ₁₁, and f ₁₂. Offspring per patch m and number of occupied patches n for a given total number of offspring I, the curve shape for CB, and the proportion d ₁ of the S₁ phenotype for DB were all optimized. The optimizations on these unimodal fitness landscapes were accomplished by standard numerical hill-climbing techniques. The calculations and graphs were produced in MATLAB 7 (The MathWorks 2012).

Numerical results

Quantitative results of the full analysis are presented in Appendix C (supplementary materials). A summary of the main results follows.

As ε, the relative range of environmental condition, increased, the fitnesses of all types declined: It is inherently more difficult for any strategy to handle a broader range of environments. When ε was relatively small (e.g., ε = 1.5), the fixed generalist FG achieved the highest fitness, regardless of the spatial or temporal pattern of environmental variation. But with larger ε (e.g., ε = 3.0), the fitness of the FG dropped enough that specialists or DB did best. When spatial variation was low (e.g., all or most patches are dry in 1 year but wet in another, and thus, temporal variation between annual patterns is high), diversified bet hedging DB tended to achieve the highest fitness. Generalists CB or FG did poorly in this situation because the two conditions were too different for any generalist to handle well. Specialists also did poorly because they experienced very high temporal variation in fitness; in particular, they had very low fitness in years when their specialized strategy was ill suited for all or almost all patches. This was less of a problem for specialists when extreme years, in which few or no patches fit them optimally, were rare. Thus, with high spatial variation within years (e.g., 50 % of the patches are wet and 50 % are dry, and temporal variation between annual patterns = 0), specialists on one environmental condition or the other had the highest fitness.

For specialists and for DB, there was no effect on fitness of the way offspring were distributed within or among patches in the absence of spatial variation (i.e., when f ₁₁ = 1 and f ₁₂ = 0), since all potential local environments over all space were perfectly correlated. But for specialists with increasing amounts of spatial variation via lower f ₁₁ and higher f ₁₂, placing each offspring in a different patch became increasingly advantageous; this advantage increased for larger brood size I and relative range ε (Fig. 3). Specialists could thus “spread their eggs among many baskets,” some of which will be a good fit for their specialized phenotype. This spatial risk spreading, when coupled with costs of dispersal, is a type of bet hedging that enables specialists to use spatial variation to reduce patch-level correlation as n increases (see Eq. (5)). For DB, there was no effect on fitness of offspring distribution within or among patches when I approached ∞. For finite numbers of offspring with spatial variation (f ₁₁ < 1, f ₁₂ > 0), there was a modest advantage for putting all offspring in a single patch or a small number of patches—an advantage that shrank with I but increased with ε (Fig. 3).

Fig. 3

Results at high levels of environmental variation (ε = 3), depending on whether the variation is predominately temporal or spatial and on brood size (I). Specialists (SP) are optimal when environmental variation is primarily spatial, except when brood size is low. Diversified bet hedgers (DB) are optimal otherwise. With temporal variation predominant, DB does equally well for any distribution of offspring within or between patches; toward increasingly spatial environmental variation and low-to-moderate brood sizes, placing all offspring into a single patch is optimal

Because of these m and n dependencies, the remainder of the results reflect the optima obtained with m = 1 and n = I for specialists and generalists and with m = I and n = 1 for diversified bet hedgers.

When the environment remains constant (i.e., ε = (c ₂ – c ₁)/s = 0), S₁, S₂, and FG have fitnesses of 1, and CB and DB have fitnesses of 0.95, reflecting the costs of bet hedging δ _C and δ _D (see Fig. 4). It is clear from the figure that including these costs qualitatively influences the relationship between strategy dominance and the relative range of environmental variation ε. (Because quantitative effects of modest costs can be visualized from the figure and produce only small shifts in boundaries between dominant strategies, we do not explore these effects further here.) Near and below a relative range of 2, FG dominates by eliminating fitness variation of individuals (V _L  = 0) while achieving a relatively high fitness mean. Above a relative range of 2, mean fitness of FG declines rapidly, as fitness magnitudes are forced out into the tails of the Gaussian curve (see Fig. 1b). The flexibility of CB then provides an advantage over FG, but by this point, other strategies eclipse them both in the Fig. 4 example; only a high δ _D and very low δ _C could produce an interval of CB dominance. With f ₁₁ = f ₁₂ = 0.5 (Fig. 4a), temporal variance in mean environmental conditions across patches is zero. Spreading risk across space by putting only a single individual into each patch then allows specialists to deal effectively with levels of relative range above 2 without paying a cost of diversified bet hedging. But for a sufficiently large difference between f ₁₁ and f ₁₂ (Fig. 4b), DB dominates the specialists by achieving the same mean with lower temporal variance. The greater the relative range and the difference between f ₁₁ and f ₁₂, the more DB dominates the other strategies (Fig. 4c).

Fig. 4

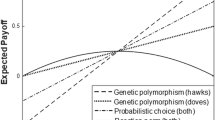
Lineage fitnesses of the strategies as a function of the relative difference in environmental condition ε = (c ₂ – c ₁) / s associated with the alternative states, i.e., the environmental variation, where c ₁ and c ₂ quantify the environmental conditions and s is the standard deviation of Gaussian fitness functions of specialists (SP) and fixed generalists (FG). Three examples of frequency combinations of f ₁₁ and f ₁₂ are illustrated, all with P ₁ = P ₂ = 0.5 and fractional cost factors for conservative and diversified bet hedging δ _C  = δ _D  = 0.05. In all of these cases, we let the number of offspring I = ∞; for the diversified bet hedger DB, all individuals are assumed to occupy a single patch, whereas for all other strategies, there is only one individual in each patch. a For f ₁₁ = f ₁₂ = 0.5, FG has the highest fitness for environmental variation below about 2.2; above this value, SP achieves the highest fitness. b For f ₁₁ = 0.75 and f ₁₂ = 0.25, fg has the highest fitness below about 2.3; above this value, db has the highest fitness. c For f ₁₁ = 1.00 and f ₁₂ = 0.00, the outcome for highest fitnesses is the same as for f ₁₁ = 0.75 and f ₁₂ = 0.25

For a particular value of the relative range of environmental variation ε, we can identify the dominant strategy for all combinations of f ₁₁ and f ₁₂ (Fig. 5). Below a relative range of about 2.2, FG dominated for all possible combinations of f ₁₁ and f ₁₂ in our example (Fig. 5a). Within the small interval 2.2 < ε < 2.3 with large brood sizes, specialists dominated for relatively small differences in the magnitudes of f ₁₁ and f ₁₂, but FG dominated for greater differences (Fig. 5b): The higher temporal variation associated with greater differences between f ₁₁ and f ₁₂ shifted the advantage to FG. This small interval of relative range with a mixture of specialists and FG dominating disappeared for small values of I, replaced by uniform FG dominance, as in Fig. 5a. Relative ranges above about 2.3 consistently produced mixtures of specialists for small differences between f ₁₁ and f ₁₂ and DB for moderate-to-large differences. The region of DB dominance was slightly smaller for large brood sizes, with specialist offspring occupying more patches (Fig. 5c) than for smaller brood sizes (Fig. 5d), though the results remained qualitatively similar.

Fig. 5

Optimal strategies for particular combinations of the condition and frequencies f ₁₁ and f ₁₂ and the pattern frequencies P ₁ and P ₂, under the assumption that the long-term frequencies of patches in the two environmental conditions are the same (i.e., unbiased long-term environmental condition). The main diagonal indicates results for combinations of f ₁₁ and f ₁₂ with P ₁ = P ₂ = 0.5. When P ₁ > P ₂ (e.g., P ₁ = 0.8 and P ₂ = 0.2), pattern 2 will strongly be dominated by condition 2 to compensate for the more modest but frequent domination by environmental condition 1 in pattern 1, thus preserving the long-term unbiased environmental condition. When P ₁ < P ₂ (e.g., P ₁ = 0.2 and P ₂ = 0.8), opposite compensation for the opposite condition frequencies between patterns will likewise preserve the long-term unbiased environmental condition. Recall that ε is the relative range of variation in environmental condition, and I is the total number of offspring in the brood. a ε = 2.00 and I = ∞. b ε = 2.25 and I = ∞. c ε = 2.50 and I = ∞. d ε = 2.50 and I = 16

Discussion

Interpreting the results

A conventional wisdom in evolutionary ecology is that low environmental variability allows organisms to specialize on the usual environmental conditions, whereas higher environmental variability favors flexible generalists. With the two-state model in results not included here, we verified this when low variability meant that one condition was much more common than the other over the long term: greater bias toward one condition made the corresponding specialist increasingly more successful. But in the results presented, we focused on the more informative situations where the two states were equally common in the long term. We quantified variables as the magnitude of differences between the two environmental states (ε) and in the patterns of spatial and temporal variation.

Our analysis introduced four novel features into the two-state stochastic environment model: (1) We let patch area be the scale of spatial autocorrelation (=grain size) and permitted patches to contain the numbers of offspring optimal for any particular strategy. (2) We fleshed out the environmental variation regime to include different magnitudes of the parameters P ₁, f ₁₁, f ₁₂, and ε. (3) We used Gaussian functions to represent how expected lifetime reproductive success R depends on environmental condition c, thus constraining the relationship between the R values under the two different environmental conditions in a reasonable way. And (4), we incorporated bet hedging costs in exchange for the flexibility associated with conservative bet hedging (i.e., optimal shape of the R(c) curve) and with diversified bet hedging (i.e., an optimal combination of the two specialists within each brood). We also incorporated risk spreading in space by specialists; incurring the inevitable dispersal costs made them into bet hedgers as well.

With these modifications of the model, we found that when environmental variation is relatively low (ε ≤ 2), the fixed generalist strategy that does equally well in the two conditions dominates. When environmental variation was relatively high (ε > 2), except for the small range of ε values for large brood sizes producing dominance by specialists and fixed generalists, a mix of specialists and diversified bet hedgers dominated. In this later case, the specialists did best where the temporal variation in the overall spatial mean condition was lowest, and the bet hedgers did best otherwise. The boundary at ε ≈ 2 between regions of dominance by different strategies arises from the shape of the Gaussian functions, which have inflection points one standard deviation from the mean.

Making sense of these generalizations requires understanding for each strategy how the mean (expected) lifetime reproductive success and variance in Eq. (2) and the components of variance V _T in Eq. (5) depend on the features of environmental variation. The characteristics, advantages, and disadvantages in this context of each strategy addressed here are as follows.

Specialists cannot reduce the magnitude of V _L , the variance in fitness through time at any particular location within a patch. They gain no advantage from placing multiple offspring in a single patch, because fitnesses of these offspring will be perfectly correlated. So, specialists distribute offspring among as many patches as possible, spreading risk in space and reducing patch-level correlation. They maintain a relatively high mean fitness and can dominate when temporal variation between mean conditions of the patterns is low, but specialists are vulnerable to high temporal variation, which results in their relatively high V _T . Though we did not explicitly incorporate dispersal costs into the analysis, it is clear that large grain size, large brood size, and high dispersal costs can limit the spreading of the specialists’ offspring across patches, perhaps causing them to put several offspring into each patch (see below). We also note that specialists could spread risk in time instead of (or in addition to) space by using dormancy and other mechanisms to produce cohort splits, with subcohorts completing development in different years (e.g., Cohen 1966). We explore this alternative as a form of bet hedging elsewhere (Crowley and Hopper 2015).

Fixed generalists FG and conservative bet hedgers CB have the major advantage of reducing V _L and thus V _T to zero by achieving equal fitness under the two conditions. FG in particular (which avoids dealing with the cost factor δ _C ) has a high mean lifetime reproductive success for low relative range ε, where FG dominates. But, the straddle between c ₁ and c ₂ pulls the mean down as ε increases beyond 2, and the optimal shape of CB is not enough to compensate. Both FG and CB are best thought of as alternative generalist strategies where CB pays a cost, δ _C , for the flexibility of optimizing the shape of its fitness function. Such a cost in this analysis is minimal, and CB’s failure to dominate over large magnitudes of environmental range, ε, suggest that generalist strategies using a fixed strategy are best suited for the environmental conditions we have imposed when ε is small (e.g., <2).

The diversified bet hedger DB, producing both types of specialists, cannot shrink V _L but can reduce ρ _L to zero by putting equal numbers of both types of specialists into individual patches. This happens when half of the within-patch correlations are between the same types of specialists (ρ _L  = 1), and half are between different types of specialists (ρ _L  = −1), resulting in an average ρ _L  = 0 (but see Appendix B for the case of small brood sizes). Then, by putting all offspring into a single patch, m = I and n = 1, resulting in V _T  = 0. Combining this advantage with the specialists’ mean fitness ≥0.5 even for very high ε makes DB an especially effective strategy for dealing with high temporal variation.

Note that specialists spread risk between patches in a way similar to risk spreading by DB within patches. Thus, because specialists do not pay the cost of bet hedging, when dispersal costs are low, they will always have higher fitness than DB if f ₁₁ and f ₁₂ are similar in magnitude. The advantage is reversed, however, at the higher levels of temporal environmental variation when f ₁₁ and f ₁₂ are sufficiently different. This accounts for the regions of specialist and DB dominance in Figs. 4 and 5.

The two-state model is an important means of addressing spatiotemporal variability in nature (Starrfelt and Kokko (2012) while maintaining tractability. Conceiving of environmental conditions as two discrete alternatives is often a useful simplification or a first-cut approximation of continuous variation (e.g., the El Niño-La Niña dichotomy). The difference in magnitudes of the two conditions (ε) may indicate the expected year-to-year difference in condition and thus provide a solid link to empirical measurements. Moreover, these discrete conditions may influence organisms with discrete life cycles through fitness effects and constraints best represented using continuous fitness functions like those invoked here. The continuous functions allow the fitness implications of shifts in the two conditions or in ε to be immediately recognized. Future work will incorporate annual variation in condition drawn from multinomial or continuous distributions, but most of the same basic principles and dynamics considered here are likely to apply (P.H. Crowley, unpublished analysis).

General issues arising from the analysis

This study addresses particular strategies with continuous fitness functions in the context of various regimes of stochastic spatiotemporal variation, taking bet hedging costs into account. But to keep this analysis tractable, some features known to influence the phenomena of interest here have not been explicitly included. For example, dispersal is obviously required for distributing offspring among patches. How far a female must travel to accomplish this distribution, thus increasing n, depends on the spatial grain size. (Because dispersal is generally costly in energy expenditure and mortality risk, the choice of n may depend in part on this cost that is not included in the model.) Increasing n reduces the genotypic variance V _T for specialists, has no effect on V _T for FG and CB, and increases V _T for DB (see Eq. (5)). Dispersal has been recognized as a type of diversified bet hedging, because it reduces environmental covariance among individuals by spreading risk over more patches, but at some cost (Crowley and Saeki 2009; Wright and Ratikainen 2012; Starrfelt and Kokko 2012; but see also Seger and Brockmann 1987; Hopper 1999; Hopper et al. 2003).

For DB based on producing different types of offspring, the advantages of high numbers of offspring per patch m reduces the value of dispersal, particularly given an associated cost. Our not including the cost of dispersal in the model can mean that the boundary between frequencies in which specialists vs. DB dominate may need to be shifted somewhat more in favor of DB to account for this cost. However, neither have we attempted to account for density dependence, kin competition, or an increase in inbreeding associated with confining much or all of a brood within a single patch. Placing offspring in the parent’s natal patch at each generation potentially insures intense kin competition and possibly inbreeding and overcrowding during intervals of population growth (genotypic expansion). In nature, DB would thus be expected to maintain at least a modest level of offspring dispersal to other patches—though this should be much more spatially restricted than that for specialists.

Our results suggest a strategic continuum from spreading risks over space to spreading risks over time when spatiotemporal variability is high. Specialists can spread risk effectively over space when dispersal to multiple patches that differ in environmental condition is manageable. DB can spread risk over time with minimal dispersal using a combination of specialist strategies, depending on costs of bet hedging, density dependence, kin competition, and inbreeding. Density dependence and kin competition could become costly when enough offspring are added to each patch to increase the intensity of within-patch competition and competitive interactions among brood members. This effect is actually weaker when some number of offspring from a single brood occupies patches already containing many other offspring. This is because the many potential competitors already present must be dealt with regardless, but the increase in competition per offspring added is thereby reduced. Inbreeding becomes an important issue when siblings added to individual patches become likely to mate with each other, and when inbreeding depression is a likely outcome of such matings.

When spatiotemporal environmental variability is moderate or low, generalist strategies are likely to dominate. These deal effectively with variation in both space and time and, by generating equal fitness in the two environments, have no tendency to favor distributing offspring into few vs. many patches—except for the balance of the effects noted above that are not explicitly included in the model. While we found no evidence for the efficacy of conservative bet hedging based on cost-incurring optimal flexibility in the fitness curve shape, this flexibility may prove important in addressing a rapidly changing environment. We note that in our model generalists achieve equal fitness in the two environmental conditions in effect by being specialists on an intermediate condition that never occurs. Future work with continuously distributed environmental conditions (see below) will avoid this by relaxing the two-state assumption altogether.

Our analysis and results have generated hypotheses that should spawn empirical tests. These include

• 1. With high spatiotemporal variability along a gradient from high spatial variation to high temporal variation, offspring within broods should become increasingly variable in traits best suited for different environmental conditions, and offspring dispersal should be reduced.

• 2. For high spatiotemporal variability, low-dispersal strategies and coarse-grained environments should feature high trait variability, and high-dispersal strategies and fine-grained environments should feature low trait variability.

• 3. With moderate-to-low spatiotemporal variability, trait variability among offspring should be low and centered on average environmental conditions.

These hypotheses can be addressed in plant populations that vary in dispersal distances and germination times. For example, the cold desert annual plant Diptychocarpus strictus produces low-dispersal/high-dormancy propagules under stressful conditions but high-dispersal/low-dormancy propagules under non-stressful conditions (Lu et al. 2012), strategies linked by the authors to bet hedging. This environment has high spatiotemporal variability, and the association between dispersal and trait variability (implied by dormancy duration) postulated in hypothesis (2) is found, though environmental grain was not assessed.

Insect populations with flexible generation times and ranges that extend across latitude may be suitable for these studies as well. Multiple mating by insects can produce fitness advantages via bet hedging (Fox and Rauter 2003; Forsman et al. 2007), allowing the possibility of examining these responses and their possible correlations with dispersal at different levels of spatiotemporal variability. Altitudinal gradients along mountainsides may correspond to differences in spatiotemporal variability, for which ecotypes of plants or insects may be compared using common garden experiments. Bet hedging in particular, though extensively supported by observational evidence, requires focused laboratory, greenhouse, and especially field experimentation to achieve broad and definitive empirical support. We add that there may be constraints on the evolution of diversified bet hedging strategies (e.g., polyphenism) that we have neglected such as constraints on developmental plasticity or antagonistic pleiotropic effects (Moran 1992). In many systems, such constraints are seemingly overcome, however, as diversified bet hedging is a taxonomically widespread phenomenon occurring in insects (Hopper 1999), rotifers (García-Roger et al. 2014), fish (Polačik et al. 2014), crustaceans (Hakalahti et al. 2004), and plants (Childs et al. 2010).

Continued theoretical development requires turning to continuous models for a more realistic analysis of reproductive strategies in unpredictable environments. Most of the same concepts will carry over into continuous representations of environmental condition in space and time, though some differences may arise, such as better performance of the conservative bet hedger when the environment varies continuously. This again underscores the importance of connecting with empirical studies to quantify these relationships. A thorough understanding of bet hedging can only be achieved through a close and effective linkage between theoretical and empirical analysis.

Bet hedging may play an important role in understanding the implications of human-induced rapid environmental change (HIREC). Bet hedgers, particularly diversified bet hedgers, may be pre-adapted to respond better to HIREC than are other strategies, a hypothesis currently under study (Sih et al., in preparation). The model presented here can address this question by virtue of its patchiness and grain structure, continuous fitness functions, and means of characterizing environmental variation (f _ij , P _j , c _i , and ε). Strategies adapted to particular patterns of environmental variation can be forced to respond to a new, post-HIREC variation regime, and both the short-term (fitness) and long-term (evolutionary response) can be determined.