1 Introduction

The objective of the clustering method is to classified data into its respective class (Clusters) such that data having similar property falls to the same cluster and different clusters have different properties. The success of any clustering algorithm is purely dependent on how it has been designed, for instance, its encoding scheme, distance measure or objective function, data assignment technique, search strategy, etc. Clustering techniques are broadly defined in two domains Hierarchal and partition clustering [1]. Where former generate a tree-like structure and later divide data such that single data assign to only one cluster. Among them, partition clustering is the first choice for researchers in the past few decades. K means algorithms, which are based on proximity measure as a distance is more preferred as it is easy to implement and flexible for hybridization with other algorithms. But it has limitations with premature convergence and speed as it’s depending on the initial condition of clusters [2].

To find a new pattern in living organisms and frame to mathematical steps is an emerging trend among data researchers. This trend is broadly defined in two subdomain evolutionary and swarm-based algorithms. Evolutionary algorithms are derived from the principle of natural evolution which is existing on this planet for the past millions of years. And follow the interactive pattern of personal growth, collective development, breed selection, and reproduction to survive on the planet. These algorithms are older and more mature. Genetic Algorithm (GA), Differential Evolution (DE), Genetic programming (GP), Genetic Improvement, (GI), Evolution strategy (ES), Linear Genetic Programming (LGP), Gene Expression Programming (GEP), etc. are well known EA algorithms [3].

Swarm-based algorithms are structure with the population having agents interacting local with neighbours and with the global environment, decentralize and self-organized pattern exist in the foraging process. [4]. Examples of SI include Particle swarm optimizer (PSO), artificial bee colony (ABC) algorithm, glow-worm swarm algorithm (GSA), firefly algorithm (FFA), cuckoo search algorithm (CSA), bat algorithm (BA), grey wolf optimizer (GWO), Whale optimization algorithm (WOA), Spider Monkey Optimization (SMO) and so on [5].

In the application of Meta-heuristic algorithms, they have to process a huge amount of data may be neighbour or unknown region. And both should be effectively searched to obtain a true or near optimum solution. In literature, it is known as exploitation and exploration respectively. More weightage to search around local space lead to premature and fast convergence and lessen the effect of global solution on the opposite side more weightage to exploration lead to slow convergence and unpredicted result [5]. Therefore it is an open problem for the researcher to balance between two search spaces. In literature number of researchers tries to solve a said problem with a different approach of initialization, update strategy, proximity measure distance, and many more.

The main contribution of this paper is to improve the search process of the spider monkey optimization algorithm hybridizes with a local neighbour search. This algorithm uses SMO as a global search and to refined search space, the neighbour search is embedded with the local leader phase of SMO. To improve global search a nonlinear property as a chaotic factor is implemented to the global leader phase of the proposed algorithm.

The proposed LNSMO (local neighbour-based spider monkey optimization) algorithm attempts to balance between local and global search space while preserving diversity property. The working of the proposed LNSMO algorithm has been analyzed using the eleven datasets from the UCI repository [6] and is compared with five well-known clustering algorithms like Particle swarm optimization, Genetic Algorithm, Grey wolf optimization, Differential Evolution, and Spider monkey optimization. It is further compared with seven recently developed hybrid clustering algorithms like, VDEO [7], AMADE [8], PSOPC [5], GLPSOK [9], WOAC [10], KMCLUST [11], and TEABC_elite [12]

The performance of the LNSMO algorithm is evaluated based on the sum of within-cluster distance or intra-cluster distance as an objective function and based on convergence speed. Finally to validate the clustering result of the assignment of data to the respective class is correct or not, two quality measures Accuracy and F-measure based on the confusion matrix are calculated. To check the significance of the proposed algorithm with a competent algorithm, statically an unpaired t-test is performed on the clustering result.

The simulation result of the proposed algorithm shows that the LNSMO algorithm performs better than its competitors in terms of SWCD and convergence characteristics. The result of the quality measure indicates that the proposed algorithm is more efficient in terms of the assignment of data to the correct cluster. Analysis of the t-test shows that LNSMO is statically significant compare to a competent algorithm.

The rest of this paper is organized in the following sequence. Section 2 describes the basic definition of the clustering problem and followed by past work done in the field of meta heuristic-based clustering algorithms. Section 3 explains the basic steps of the spider monkey optimization algorithm. Section 4 presents the proposed algorithm with the neighbour search method and chaotic operator. The experimental data set, parameter setting, and results are presented in Sect. 5. Finally, the conclusion and future direction are presented in Sect. 6.

2 Theoretical background

This section first describes the mathematical background and property of the clustering method and thereafter a brief literature review.

2.1 Clustering theory

Data clustering is the method of dividing n number of data points into the finite number of clusters k based on some similarity property having d-dimensional space (attribute). Let the set of n data points with d-dimension be written as \(Y = \{ y_{1} ,y_{2} ,y_{3} ...,y_{n} \}\). The k number of clusters can be written as \(Z = \{ z_{1} ,z_{2} ,z_{3} ...,z_{k} \}\), such that data assign to the same cluster have the same property and different clusters have different properties. And cluster constrained to the following properties [13].

Each cluster should not empty and have at least one member or data point.

$$Z_{i} \ne \phi ,\forall i \in \{ 1,2,...,k\}$$
(1)

Two different clusters should not have a common member or data point

$$Z_{i} \cap Z_{j} = \phi ,\forall i \ne j\,{\text{and}}\,i,j \in \{ 1,2,...,k\}$$
(2)

Each data point should belong to a cluster

$$\bigcup\limits_{i = 1}^{k} {Z_{i} } = Y$$
(3)

The clustering problem with the Meta-heuristic algorithm is an optimization of the data point’s separation such that it creates a well-separated compact cluster and also preserves the above properties. And for better optimization, it required an effective objective or fitness function. The fitness function also accounts for a measure of the partitioning of data points. Mean square error is the most commonly used fitness function in the clustering problem and is defined as [5].

$$f(Y,Z) = \sum\limits_{j = 1}^{n} {\min \{ ||y_{j} - z_{i} ||^{2} \} } ,\{ i = 1,2,3,...k\}$$
(4)

where, min represents the minimum distance between data points \(y_{j}\) and cluster \(z_{i}\) or similarity measure. In this paper well known Euclidean distance is used as a similarity measure.

2.2 Related work

Researchers try to solve the clustering problem either by evolutional or swarm-based algorithms.

Bouyer [14] developed a hybrid clustering method based on improved cuckoo and modified particle swarm optimization with K -Harmonic Means, In this work velocity equation of particle, is updated with global worst and personal worst solutions to balance between local and global search. The advantage of this algorithm is a parameter of the cuckoo search algorithm is updated automatically. Lei Yang [15] presents PSO clustering which is formulated as a tree structure and neighborhood property. In PSO velocity is modified with four components, basic velocity, particle current, and its best position, particle current and population best, particle current, and neighbour best position to refined the search process. PSO is designed as a tree structure in which the tree structure is updated with iteration such that the parent node is better than the child node. Neetu Kushwaha [16] presents teaching–learning-based optimization embedded with PSO and applied to the clustering problem. In which output of TLBO is taken as an input parameter to PSO for fine refinement of clustering results. Yugal Kumar [17] presents cat swarm optimization improve by modification in governing equation and extended with clustering problem. To improve global search global best is embedded in the equation of tracking mode velocity. Acceleration parameters of the algorithm are made dynamic to balance the search process. It is compared with K-Means, genetic algorithm, particle swarm, teaching–learning based optimization, ant colony optimization, and cuckoo search optimization algorithm. And the result shows better performance compare to its competitor. J. Prakash [18] present ABC with the global best property for the clustering problem. In this algorithm to speed up and keep away premature convergence global best and crossover operator is combined with ABC. Results demonstrate that the developed algorithm outperforms ABC and its variants. Ibrahim Aljarah [19] developed Locality informed GWO and applied it to clustering analysis. In this algorithm performance of GWO is improved by the tabu search operator which is acts as a local search near the best solution. The addition of new terms refined search space and perform better than compared algorithms like K-Medoids, K-means, hierarchical clustering and, furthest first techniques. Krishna Gopal Dhal [20] presents a cuckoo search algorithm with modification to balance between local and global search strategy and applied to the clustering method. This exploration is improved by global best and mutation with Levy and Cauchy distribution. A further mutation is controlled by step size derived from fitness. Exploitation is improved by k-neighborhood and previous personal solutions. In the proposed work author tries to improve clustering results by new search strategies and dynamic parameters updating. Yuefeng Tang [21] proposed Glowworm swarm optimization improved by variable step size which is a function of the level of luciferin carried by each glowworm instead of fixes one and initialization method based on iterations. And an improved algorithm was applied to the clustering problem. Yating Li [22] proposed Chaotic starling PSO for clustering. In this algorithm, acceleration coefficients are updated with the logistic map and exponential function is used to update inertial weight. To avoid trapping into local optima, a dynamic disturbance term is added to the velocity equation. Further starling bird's local search capability and neighbours information is used to direct particle search direction. The main drawback algorithm is that it may trap local optima when applied to a problem with multiple local optima. Farzaneh Zabihi [23] present a history driven ABC algorithm to balance local, global search result and extended to data clustering. In this algorithm, a memory archive structure is used to store individual fitness and position which is useful for avoiding fitness calculation. A guided anisotropic search strategy is used to improve local search. Scout bees mutation is improved with the global best component. Ashish Kumar Tripathi [24] proposed grey wolf optimization and enhanced it with new search strategies further applied to data clustering. In this work hunting strategy of a grey wolf is improved with Lévy Flight and Binomial crossover for prey to improve the exploration and exploitation capabilities. It is further parallelized by the map-reduce model in the Hadoop framework for clustering a large number of data sets. Vijay Kumar [25] proposed a clustering approach using a grey wolf algorithm. This algorithm adapts the searchability of GWO to overcome the weakness of local optima in the K-means algorithm. Pranesh Das [11] proposed a modified bee colony optimization for data clustering. To improve clustering and convergence results untrustworthy bees are getting change to participate with some probability. From the second iteration onward center of the previous solution is considered as a center of a present cluster solution. Further to maintain diversity, data that are not assigned in the previous stage are utilized. Hassanzadeh and Meybodi [26] applied the property of the firefly algorithm to K means for improvement in premature convergence of the K- means algorithm. Cluster centers are found by FA and further refined by K- means algorithm. The proposed algorithm is compared with k mean, PSO, KPSO, and proves to be better. Amol kumar [27] proposed a hybrid approach of the exponential grey wolf and whale optimization for clustering. In this approach, the hunting mechanism of the whales is utilized to find a number of clusters, and exploration is improved by exponential grey wolf optimization. Amr Mohamed [28] presents a modified step whale optimization algorithm hybridized with tabu search and applied to the clustering problem. In the proposed work diversification of whale optimization is improved by changing swarm location based on their original position. To preserve the best location from the search space memory element of tabu search is utilized. The further search process is improved by a crossover operator. Yaping Li [29] proposed an improved glow worm algorithm for clustering. For better clustering results good-point set theory is used to distribute the initial population of the K-means algorithm and result further optimized with glow worm optimization. Roselyn Isimeto [30] proposed a glow worm swarm algorithm in which the sensor range parameter of glow warm swarm is found by min, max value of the sensory range, and fitting to quadratic function and solved by a least square method. Further to improve the result, the sum of the mean squared error is made a function of iteration by multiplying the number of clusters that change with iteration dynamically. Manju Sharma [5] proposed polygamous crossover-based PSO for clustering. In the proposed algorithm polygamous crossover operator is embedded with the velocity equation of PSO to refined a search process. The proposed algorithm compared with PSO, GA, DE, FA, GWO, and prove to be better in terms of SWCD. Nehsat et al. [31] presented a hybrid approach of PSO to perform a global search with K- means to perform a local search. Saida et al. [32] applied a cuckoo search capability to the clustering problem. And show better results in terms of distance measure and convergence.

In the proposed work spider monkey optimization improved with neighbour search and a chaotic operator is proposed for data clustering. The next section represents the basic SMO with its limitation, neighbour search method, and chaotic operator to develop the proposed algorithm.

3 SMO and neighbour search method

This section describes the basic theory and limitation of SMO and neighbour search methods which inspired the author to develop a new algorithm.

3.1 Spider monkey optimization algorithm

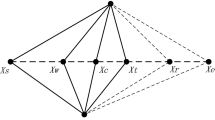
Spider monkey optimization (SMO) algorithm is developed by Jagdish Chand Bansal [33]. It is derived based on the intelligence of spider monkey inspired by the social structure of FFSS (Fission fusion social structure). According to FFSS monkeys distribute them in different size groups for foraging and have the following characteristic. Initially, all spider monkeys were grouped into 40–50 individuals. Each group follows the common leader to find new food source terms as the global leader of that group. In case of lack of required quantity of food, the Global leader divides the main group into smaller groups each having three to eight members for forage. And each group is guided by a local leader. Local leaders decide on searching food sources in each sub-group separately. The member of the group uses unique sound as a communication for social bonding and defining boundaries for defense. The SMO algorithm is structured with six different phases to complete its forage process as discuses in subsequent steps.

In SMO initial population of N spider monkey is generated randomly. Let, D- Dimensional vector space denoted by \(Y_{ij}\) representing spider monkey with \(j{\text{th}}\) dimension and \(i{\text{th}}\) individual. Then \(Y_{ij}\) initialize as,

$$Y_{ij} = Y_{\min j} + U(0,1) \times (Y_{\max j} - Y_{\min j} )$$
(5)

where \(Y_{\min j}\) and \(Y_{\max j}\) represent the lower and upper limit of \(j{\text{th}}\) dimension of \(i{\text{th}}\) individual. U(0,1) is a random number between [0,1]. The subsequent section describes six phases of SMO.

3.1.1 LLP: Local leader phase

In this step new position of the individual is found by information of local leader and individual of the group by Eq. 6. To check the quality of solution fitness measure is used means if current fitness is better than the old solution then the position will be updated with a new value.

$$Ynew_{ij} = Y_{ij} + U(0,1) \times (LL_{kj} - Y_{ij} ) + U( - 1,1) \times (Y_{rj} - Y_{ij} )$$
(6)

where, \(LL_{kj}\) and \(Y_{rj}\) represent \(j{\text{th}}\) dimension of the local group leader and randomly selected \(r{\text{th}}\) spider monkey from \(k{\text{th}}\) group such that \(r \ne i\).

To control the diversity in the current step perturbation rate Pr between [0.1, 0.8] is used, The Pseudocode of the local leader phase is given in Fig. 1.

Fig. 1
figure 1

Pseudocode of local leader phase

Full size image

3.1.2 GLP: Global leader phase

As shown in Eq. 7 position of all individuals is updated based on the position of a global leader and other members of the group.

$$Ynew_{ij} = Y_{ij} + U(0,1) \times (GL_{j} - Y_{ij} ) + U( - 1,1) \times (Y_{rj} - Y_{ij} )$$
(7)

where \(GL_{j}\) show the \(j{\text{th}}\) dimension of the global leader and \(j \in \{ 1,...D\}\) is randomly chosen value. Further, the probability probi which is a function of fitness as depicted in Eq. 8 is used to select a better candidate for the next iteration. Figure 2 Shows the Pseudocode of the global leader phase.

$$prob_{i} = \frac{{fitness_{i} }}{{\sum\limits_{i = 1}^{N} {fitness_{i} } }}$$
Fig. 2
figure 2

Pseudocode of global leader phase

Full size image

3.1.3 GLL: Global leader learning phase

In this step greedy selection based on the best fitness from a population is used to update the global leader position. If the global leader position is not updated then its global limit count is increment by 1.

3.1.4 LLL: Local leader learning phase

In this step greedy selection based on the best fitness from a particular group is used to update the local leader position. If the position of a local leader is not updated then its local limit count is increment by 1.

3.1.5 LLD: Local leader decision phase

This phase helps to decide the position of local leader group members. If any local leader position is not updated up to a predefined number of count (Local Leader Limit) then a member of its group position is generated either by random or by information gained from the local and global leader phase as per Eq. 9 With probability, Pr.

$$Ynew_{ij} = Y_{ij} + U(0,1) \times (GL_{j} - Y_{ij} ) + U(0,1) \times (Y_{ij} - LL_{kj} )$$
(9)

It is revealed from Eq. 9 that the updated position of a spider monkey is repeal from local and attracted to global leader. Finally, the fitness of the updated position is calculated. Figure 3 Shows the Pseudocode of the LLD phase.

Fig. 3
figure 3

Pseudo code of LLD phase

Full size image

3.1.6 GLD: Global leader decision phase

This phase is the same as the previous but applied to the global leader phase. If the position of global leader is not updated for a predefined number of count (Global Leader Limit) then the global leader divides the population into small groups start with two and increment with one till a maximum number of group (MG) forms. Each time in the GLD phase local leader learning phase is repeated to elect a local leader with newly generated group positions. Even after dividing to a maximum number of the group if the position of global leader is not updated then the global leader merges all groups to form a single group.

Figure 4 shows the Pseudocode of the Spider monkey optimization algorithm.

Fig. 4
figure 4

Pseudo code of spider monkey optimization

Full size image

3.2 Neighbour search method

In this method, a neighbour solution is found by moving the present solution by perturbation by some defined strategy. It is also known as neighbour search and result in a Local solution rather than a global solution. This method follows the following basic procedure. [34]. The Pseudocode of Neighbour search method is given in Fig. 5.

Fig. 5
figure 5

Pseudo code of neighbour search method

Full size image

Neighbourhood structure: Neighbour can be defined in many ways. In this work following strategies are applied [35].

Swap neighbourhood: Exchange of ith and jth position.

Insert neighbourhood: Remove the ith position and put it to the jth position.

Reverse neighbourhood: Select two random positions and reverse order of positions between selected positions.

In the SMO algorithm, the position of the spider monkeys is updated based on the positions of other randomly selected monkeys without checking its property. This leads to slow convergence, high breaking, and merging of groups [36]. Further, SMO has not the neighbour search property around the find solution. So to solve the described problem we have proposed, SMO with neighbour search embedded to Local Leader Phase of spider monkey algorithm. Further to improved global search, nonlinear property in terms of a chaotic operator is applied to the global leader phase of SMO.

4 The proposed algorithm (LNSMO)

To balanced exploitation and exploration following modifications are made in a basic variant of the spider monkey optimization algorithm. To improve the local search of an SMO algorithm, a neighbour search is embedded in the LLP phase of the SMO algorithm. In basic SMO, local leader search is influenced by randomly selected spider monkeys without checking its domination in terms of the objective function value. This shows that still there is a possibility of a better neighbour solution near to selected spider monkey. This encourages us to search neighbour solutions for better optimum results. Further to improve global search a chaotic operator derived from a logistic map is introduced in the global leader phase of SMO to overcome premature convergence. The flow chart in Fig. 6 shows the detailed steps of LNSMO and the Pseudocode in Fig. 7 shows the clustering application of the proposed algorithm. The descriptions of other steps of LNSMO are described below.

Fig. 6
figure 6

Flow chart code of LNSMO algorithm

Full size image
Fig. 7
figure 7

Pseudo code of LNSMO clustering algorithm

Full size image

4.1 Neighbour search procedure

To find a better neighbour position in this work we applied swap, insert, and reverse search strategies [35] randomly to the local leader phase of SMO. Following pseudo code in Fig. 8 shows the modification in the Local leader phase with neighbour search procedure.

Fig. 8
figure 8

Pseudo code of modified LLP with Neighbour search algorithm

Full size image
Fig. 9
figure 9

Pseudo code of modified global leader phase

Full size image

4.2 Modified global leader phase

Chaos is a phenomenon of nonlinear dynamics having a property of stochastic randomness, regularity, ergodicity, and sensitivity to an initial condition. This characteristic is helpful to avoid sticking to the local optimum in the search process [37, 38]. The main objective of this section is to improved global search by random and nonlinear property of chaotic factor using a logistic map as shown in Eq. 10

$$w = 0.5 \times rand() + 0.5 \times z$$
(10)

where, rand() is a random number between 0 to 1, And z is a logistic mapping given by Eq. 11

$$z = 4 \times z \times (1 - z)$$
(11)

where z is a random number between 0 to 1.

Finally, the position update equation of global leader phase is modified as,

$$Ynew_{ij} = Y_{ij} + w \times (GL_{j} - Y_{ij} ) + U( - 1,1) \times (Y_{rj} - Y_{ij} )$$
(12)

Figure 9 shows the pseudo-code of the Modified global leader phase.

4.3 Population representation

Every SM position is represented as a search agent having a string of real numbers encoded with K number of cluster centers. The length of each position string is represented as K × D two-dimensional matrixes. Where D represents D dimensional search space. In this representation, each row specifies the cluster center and the column specifies the attribute of the input data set.

For example: Let K = 3 and D = 4, Problem with four attributes and number of cluster three then each position is represented as,

1.2

0.2

1.8

2

Cluster 1

1.3

0.4

2.1

1.9

Cluster 2

0.9

0.2

2

1.7

Cluster 3

4.4 Population initialization

For N number of population, each SM position is initialized with K randomly generated data points based on the minimum and maximum attribute value of the input data set as a cluster center.

4.5 Fitness function

Clustering with a meta-heuristic or swarm algorithm is an optimization problem and to solve the optimization problem we required an objective or fitness function. In this algorithm first Euclidian distance between every data point and cluster centers is calculated, and assign to the nearest cluster. Then after the center of the cluster is refined by the mean value of all data points belongs to that cluster and cluster center. Then fitness function sum of within-cluster distance (SWCD) is calculated as an intra-cluster distance between data points and the cluster center to which they belong. For better clustering results minimum of SWCD is preferred and calculated by Eq. 13.

$$f(C_{1} ,C_{1} ...C_{K} ) = \mathop \sum \limits_{i = 1}^{K} \mathop \sum \limits_{{X_{j} \in C_{i} }}^{{}} ||P_{i} - X_{j} ||$$
(13)

Here, \(P_{i}\) represents cluster center of \(C_{i}\) and \(X_{j}\) represents data belongs to cluster \(C_{i}\).

4.6 Termination criteria

This algorithm runs for a predefined number of iterations and the solution found at the last iteration gives optimum cluster center.

5 Algorithm implementation

The proposed algorithm was implemented with MATLAB and compared with a well-known meta-heuristic algorithm as DE [39], PSO [40], GA [41], GWO [25], and SMO [33].

5.1 Data set

To perform experiments by the proposed algorithm author selects eleven data sets from the UCI repository [6] and the properties of these data sets are given in Table 1. The initial parameters of comparative algorithms are given in Table 2.

Table 1 Properties (Data set)
Full size table
Table 2 Parameter setting
Full size table

5.2 Quality measurements

To analyze the clustering results of the proposed algorithm following quality, measures are calculated [9]. These measurements show that the prediction of assigned data points to a particular cluster is correct as per true class or not. Larger the value better the clustering assignment quality.

Accuracy: It is the fraction of correctly classified to the total number of samples.

$$Accuracy = \frac{TP + TN}{{TP + TN + FP + FN}}$$
(14)

F- measure which account precision and recall written as,

$$F - Measure = \frac{2 \times precision \times recall}{{precision + recall}}$$
(15)

where, TP = True Positive, TN = True negative, FP = False positive and FN = False negative samples.

Further intra-cluster distance in terms of SWCD Eq. 13 is calculated and compared with other algorithms.

5.3 Experiment results

5.3.1 Results and discussion based on SWCD values

Table 3 shows the best, mean, and standard deviation of SWCD values obtain by different algorithms over 20 independent runs. The objective of this experiment is to check whether the proposed algorithm capable of produced compact clustering results or not. To produce stable results each algorithm is repeated with 200 iterations for 20 runs. The SWCD results calculated here are the best, mean, and standard deviation for 20 independent runs calculated for the last or 200th iteration. In Table 3 bold text shows the best results compare to competent algorithm for SWCD value.

Table 3 Best, mean, and standard deviation of SWCD and time value obtained by different algorithms
Full size table

In the Glass dataset proposed algorithm end with a minimum value of SWCD compare to all algorithms, and gives the optimum of mean SWCD, but suffers little with standard deviation. For the cancer dataset LNSMO produced a minimum of SWCD which is comparable with DE, but a significant difference in mean value and standard deviation, which is nearer to zero. This shows the stability of the algorithm compares to others. For the Wine dataset LNSMO end with a more compact result compare to competent algorithms in best, mean, and standard deviation of SWCD. For Seed data output results are comparable with all algorithms, and better than DE. While standard deviation of LNSMO is nearer to zero and shows the higher stability of the proposed algorithm. The results of the Bupa dataset show that the proposed algorithm is comparable with DE but with higher stability and for other algorithms it shows a significant difference. In the CMC dataset LNSMO produced a significant difference in all measures with too small or near to zero variation in SWCD. In the iris dataset, LNSMO is comparable with all the competent algorithms but strong in standard deviation. For the Heart, dataset proposed algorithm produced a significant difference in all measures for all the algorithms, and comparable results with DE but a major difference in standard deviation. The bigger dataset of the Magic, the proposed algorithm produced better results in almost all measures for all the algorithms and comparable with DE. In the HTRU2 dataset, LNSMO produced comparable results with DE but a significant difference in standard deviation. In the Haberman, dataset LNSMO produced comparable results with DE but the more stable result with a minimum of standard deviation. In most cases, LNSMO produced a minimum value of SWCD with a small value of standard deviation which is nearer to zero, which shows the higher stability of the proposed algorithm against others.

5.3.2 Result and discussion based on cluster qualities measures

Table 4 shows the analysis of cluster quality in terms of accuracy and F-measure. The objective of these simulations is to check the assignment of data points to a cluster is as per the actual class or not. The larger value of these measures is preferred for better clustering results. These results are derived from the simulation of 20 independent runs of each algorithm and each algorithm is repeated for 200 iterations. In Table 4 bold text shows the best results compare to competent algorithm for accuracy and F-measure.

Table 4 Mean and standard deviation of cluster quality measure for datasets
Full size table

For the Glass dataset, the accuracy of LNSMO is second best with a small difference to GA which produces the best accuracy among all algorithms. However, the F-Measure value for the proposed algorithm is highest in all comparable algorithms. For the Cancer dataset, LNSMO produced a significant difference in Accuracy which is highest among all comparative algorithms with smaller standard deviation. For F-measure proposed algorithm is comparable with others but smaller standard deviation. For the Wine dataset GA algorithm produced a significant difference in accuracy with LNSMO and other algorithms, but LNSMO dominated in F-measure with GA and other algorithms. Further proposed algorithm shows a smaller standard deviation in accuracy and F-measure compare to all the algorithms. In the Seed dataset, LNSMO output a higher difference in accuracy and F-measure compare to all the algorithms. In the Bupa dataset performance of LNSMO is similar to competitive algorithms accuracy, but the higher difference in F-measure. For the CMC dataset LNSMO produced similar accuracy results with competent algorithms. In F-measure results, LNSMO carries better results than GWO, GA, DE, and similar results with PSO and SMO. For the Iris dataset LNSMO produced better results than PSO, GWO and similar results compare to others in accuracy and F-measure. For the heart dataset proposed algorithm produced similar results compared to all algorithms in accuracy and F-measure. In the Magic dataset, LNSMO produced better results than PSO, GA, DE, and similar to the remaining algorithms for accuracy. In F-measure results, LNSMO produced better results than GA, PSO and similar to remaining algorithms. For the HTRU2 dataset proposed algorithm produced a significant difference in accuracy and F-measure compare to all algorithms. The standard deviation of the F-measure is small and nearer to zero which is best among all the algorithms. In the Haberman dataset, LNSMO produced similar results to all algorithms. Overall results show that the proposed algorithm predicts better or similar results compared to competent algorithms.

5.3.3 Convergence results

Figure 10 depicts the convergence plots for all eleven datasets between iterations and SWCD results. Overall results from Fig. 10 show that DE takes more iteration to converge. SMO algorithm does not trap to local search space but gives sub-optimum results. LNSMO predicts the minimum value of SWCD in less iteration and other algorithms converge prematurely with a higher value of SWCD. Figure 10a for the glass dataset reveals that the proposed algorithm makes a clearer boundary between premature algorithms and DE which take more iterations to converge. SMO does not fall to the local optimum but gives a high value of SWCD. Indirectly it shows that our algorithm is capable to balance between exploration and exploitation characteristics. Figure 10b depicts the convergence results for Cancer clearly shows that LNSMO takes half of the iterations to converge compare to DE. From Fig. 10c of wine, (d) seed, (e) Bupa, and (f) CMC data proposed algorithm converge faster than DE with a smaller value of SWCD, While SMO reveal the same convergence pattern of LNSMO but with higher value of SWCD. From Fig. 10 (g) Iris, (h) Heart, and (i) Magic, It is clear that LNSMO converges faster than DE and other algorithms converge prematurely and SMO follows the same characteristic of LNSMO but the high value of SWCD. From Fig. 10j of the HTRU2 dataset PSO, GWO and GA converge sharply with a higher value of SWCD while DE takes more iterations to compare to LNSMO. From Fig. 10k of the Haberman dataset PSO, GWO and GA converge prematurely with a higher value of SWCD while LNSMO converges faster than DE. Overall results show that LNSMO converges faster than DE and other algorithms stuck to premature convergence, While SMO follows the same characteristic of LNSMO but with a higher value of SWCD.

Fig. 10
figure 10figure 10

Convergence plot for a Glass, b Cancer, c Wine, d Seed, e Bupa, f CMC, g Iris, h Heart, i Magic, j HTRU2, k Haberman

Full size image

5.3.4 Time complexity

Table 3 shows the CPU time in seconds for different algorithms to complete 20 runs. It shows that traditional algorithm like DE, GA, PSO, and GWO takes lesser time compare to the proposed algorithm but they produced suboptimum value in SWCD result. On the other side, SMO does not trap to local optimum but takes more time. The reason behind more time taken by SMO is that it executes six different phases to balance exploration and exploitation. Our proposed algorithm produced better results compare to SMO with the addition of a very small time cost.

5.3.5 Comparison with recently published algorithms

In this comparison following algorithms are selected from the literature. VDEO [7], which is derived from DE involves the calculation of the variance of each feature and optional crossover strategy. AMADE [8] is the hybridization of a memetic algorithm with an adaptive DE mutation operator. PSOPC [5], in which hybridization of PSO is done with crossover operator and polygamous selection. GLPSOK [9], which is the hybridization of PSO-K-means algorithm with Gaussian estimation and Levy flight. WOAC [10], in which recently developed whale optimization is proposed for the clustering problem. KMCLUST [11], In which centroid obtain by a k-means algorithm is feed to the MBCO. TEABC_elite [12], in which K-means and chaotic parameters are combined with the previously proposed EABC_elite algorithm.

Table 5 shows the comparison between LNSMO and the recently published algorithm for best, mean, and standard deviation of SWCD results. In the table, bold values show better results compare to other algorithms. For the Glass dataset, AMADE produced better results in terms of the best and standard deviation of SWCD. TEABC_elite produced a better result in the mean value of SWCD. But our proposed algorithm produced comparable results in all quality measures with AMADE and TEABC_elite. For Cancer dataset proposed and the PSOPC algorithm produced similar results in best and mean values of SWCD with negligible standard deviation. In the Wine dataset, the proposed and the PSOPC algorithm produced similar results in the best value of SWCD while the proposed algorithm produced a better result in the mean value of SWCD. In Bupa dataset, the proposed and PSOPC produced similar results in the mean and best value of SWCD while both produced a negligible standard deviation of SWCD. In CMC dataset proposed and PSOPC algorithm produced a similar value of best SWCD. But proposed algorithm produced better results in the mean and standard deviation of SWCD compare to PSOPC and other algorithms. For the Iris dataset, KMCLUST produced better results of best and mean value of SWCD compare to all algorithms. But results produced by the proposed algorithm are nearer to other and KMCLUST algorithms. For the Haberman dataset, VDEO, PSOPC, and the proposed algorithm produced similar results with negligible standard deviation. From overall observation, it is concluded that the proposed algorithm produced better or similar results with previously published algorithms. In Table 5 bold text shows the best results compare to competent algorithm for SWCD measure.

Table 5 Comparison with recently published algorithms over best, mean, and standard deviation of SWCD
Full size table

Table 6 shows the comparison of LNSMO with a previously published algorithm for accuracy. The proposed algorithm produced better accuracy in Glass, Wine, Bupa, and CMC datasets for all the algorithms, and similar results with the Cancer and Iris dataset. For the Haberman dataset, the accuracy of the proposed algorithm is comparable with published results.In Table 6 bold text shows the best results compare to competent algorithm for accuracy measure.

Table 6 Comparison with recently published algorithms based on Accuracy
Full size table

5.4 Statistical significance analysis

For testing of the best algorithm, an unpaired t-test is performed based on mean SWCD between best and second-best algorithms. Confidence Interval (CI) between the two means is calculated based on data size equal to 20 and 95% of confidence level. In hypothesis testing, a two-tailed P-value of the t-test is the probability of finding extreme results when the null hypothesis for a given test is true. The smaller value of P supports an alternative hypothesis [42].

The confidence interval and P-value of each dataset are used to interpret a significant level of the proposed LNSMO algorithm with the second-best algorithm. The results are highly statically significant (HSS) when P ≤ 0.01. If P ≤ 0.05 statically significant (SS), and when P > 0.10 not statically significant (NSS).

Table 7 shows the result of the unpaired t-test between the best and second-best algorithm based on the mean of SWCD results. For all the dataset two-tailed P-value is less than 0.01 means, LNSMO is highly statically significant compared to all second-best algorithms except Bupa and Magic dataset. In Bupa and Magic dataset, P-value is less than 0.05 means, LNSMO is statically significant compared to the second-best algorithm DE.

Table 7 An unpaired t-test between best and second-best algorithm
Full size table

6 Conclusion and future perspective

In this paper search process of the spider monkey optimization algorithm is improved with a local neighbour search method. To refined search space, the neighbour search is embedded with the local leader phase of SMO. Further global leader phase of the proposed algorithm is improved with a chaotic factor. The proposed LNSMO algorithm is applied to the clustering problem when the number of clusters known before. It is compared with the five traditional algorithms like PSO, GA, SMO, DE, and GWO, and tested on eleven data sets. The simulation results reveal that LNSMO outperforms with comparative algorithms in terms of SWCD, cluster quality measures, and convergence results for all the datasets. Statically unpaired t-test demonstrated that the proposed LNSMO algorithm is statistically significant. Further proposed LNSMO algorithm is compared with seven recently published hybrid meta-heuristic algorithms in which LNSMO produced better or similar results in SWCD and accuracy. Further LNSMO gives optimum results with a reasonable time cost.

In the future proposed LNSMO algorithm can be extended with automatic data clustering when the number of the clusters is not known before. It is also extended with a multi-objective approach and parallel computing. In the future proposed algorithm, LNSMO can be applied to gene expression, image segmentation, etc.