1 Introduction

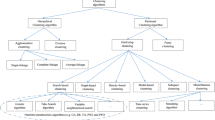
Clustering is an unsupervised learning method that groups data sets items into clusters so that there must be more intra class similarity or more cohesiveness within cluster and low inter class similarity or uniqueness between clusters [1]. Many real world problems can be either declared as of this type or can be transformed to this type of problem. It has been used in various applications like medical and life sciences, data mining, machine learning, artificial intelligence, economics, social sciences and earth sciences [2]. During last few years, a large number of clustering algorithms has been developed which can be roughly categorised into two categories: Partitional and Hierarchal Clustering [3]. Hierarchical clustering build a tree like hierarchical structure for partitioning the data whereas partitional clustering divides the big data into non-overlapping clusters such that each data item belongs to only one cluster. As reported in the literature, partitional clustering is mostly used clustering technique for data partitioning. K mean algorithm [1, 4] is the most influential partitional clustering technique as it is simple and scalable. But, this algorithm can be easily trapped to local minima as its convergence speed depends on the initial clusters state. If the initial states are not chosen appropriately then the K mean algorithm leads to premature convergence. In case of large number of data sets, the searching cost of K-mean algorithm is also large for finding the global optimal solution [5].

During past few decades, enormous metaheuristics and evolutionary approaches have been developed to overcome the above mentioned problem. Evolutionary algorithms are heuristic searches that never promise to give the accurate optimal results, but will definitely generate near optimal solutions in less time. Still, the performance of metaheuristic algorithms requires more refinement for solving the clustering problems [6]. All the metaheuristic techniques based on the concept of randomization and local search. The two main components of metaheuristic algorithms are exploration and exploitation. Exploitation generally searches around the currrent solution and selects the better solution whereas exploration increases the diversity of candidate solutions. A perfect combination of these component is needed for obtaining the best solution. Most popular metaheuristic algorithms are Genetic Algorithm, Differential Evolution, Particle Swarm Optimization, Ant Colony Optimization, Artificial Honey Bee Algorithm [7, 8], Firefly Algorithm, Grey Wolf Optimization [9], Harmony Search [10, 11] etc.

The main contribution of this paper is to provide a hybrid algorithm using Particle Swarm Optimization (PSO), polygamy concept and crossover operator. This approach uses PSO algorithm for global search and a hybrid polygamous approach for crossover so as to refine the search process. The hybridization has been attempted to ensure diversification as well to maintain the balance between exploration and exploitation phase. Two concepts i.e. crossover alpha value updation and inertia updation have been introduced in order to enhance the searching capability. The performance of the proposed PSO polygamous crossover (PSOPC) approach has been evaluated using the datasets from UCI repository [12] and is compared with other clustering approaches like PSO, Genetic Algorithm, Differential Evolution, Grey Wolf Algorithm and Firefly Algorithm.

Firstly, the performance of PSOPC and other algorithms are evaluated based on the intra cluster distance or we can say sum of within cluster distance as an objective function as well as based on their convergence speed. Then in order to evaluate the quality of clustering internally, some quality measurements like Precision, Recall, Accuracy and G measures are used to check whether the prediction of allocating a point to a cluster is correct as per the actual class or not. Simulation results clearly indicate that the proposed PSOPC algorithm outperforms other techniques in terms of generating well compact cluster and as well as solving the problem of premature convergence. Simulation results of quality measurements shows that PSOPC is more efficient as compared to other algorithms in generating efficient clusters that has more similarity with the benchmark results.

1.1 Organization of paper

The rest of the paper is organized in the following sections. Section 2, describes the background details related to clustering problem and the brief literature review of existing work in the area of evolutionary and metaheuristic clustering algorithms. Particle swarm optimization, Genetic algorithm and polygamy concepts are described in Sect. 3 and proposed PSOPC Algorithms is presented in Sect. 4. Real life datasets, parameters initialization and simulation results are given in Sect. 5 and Sect. 6 summarizes the findings of work presented in paper as well as future work.

2 Background

This section firstly describes the basic concepts regarding clustering problem as well as its properties and thereafter gives the brief overview of related work already performed by various researchers in this area.

2.1 The clustering problem

The data clustering in d- dimension Euclidean space is a method of partitioning n data patterns/points/items sets into numerous clusters say (k clusters) depends on some similarity pattern. Let the set of n data patterns be defined as S = {x1, x2, …, xn}. The Cluster set (P) be represented by P = {P1, P2….Pk}, such that the data points belong to same cluster should have more cohesion and data patterns belongs to dissimilar clusters should have more separation and clusters should satisfy the following properties [2, 9, 13].

  1. 1)

    Cluster should not be empty i.e. every cluster should contain at least one data pattern.

    $${\text{i}}.{\text{e}}.,P_{j} \ne \phi ,\quad\forall j \in \left\{ {1,2,3 \ldots k} \right\}$$
    (1)
  2. 2)

    Each data pattern should belong to only one cluster i.e. two different clusters should not contain a common pattern.

    $${\text{i}}.{\text{e}}.,P_{j} \cap P_{i} = \phi ,\quad\forall j \ne i\,and\,j,i \in \{ 1,2,3 \ldots k\}$$
    (2)
  3. 3)

    Each and every pattern must be absolutely attach to a cluster i.e.

    $$\bigcup\limits_{j = 1}^{k} {P_{j} } = S$$
    (3)

If we want to apply a metaheuristic or evolutionary algorithm for clustering, we need to state the problem as an optimization problem. For solving an optima problem, a suitable objective function or fitness function needs to be defined. The partitioning of specified data sets can be done in numerous ways so as to maintain the above mentioned properties. Also suitable fitness or objective function is required to compute the value of partition. The most commonly used fitness function is mean square error and is defined as [14]:

$$f(S,P) = \sum\limits_{j = 1}^{n} {\hbox{min} \{ ||x_{j} } - P_{i} ||^{2} \{ i = 1,2,3 \ldots k\}$$
(4)

where min term represents the similarity between data point xj and cluster center Pi. And a well known similarity measure used in this paper is Euclidean distance, presented as:

$$d(x_{i,} x_{j} ) = \sqrt {\sum\limits_{m = 1}^{d} {|x_{im - } x_{jm} } } |^{2}$$
(5)

where \(x_{im}\) and \(x_{jm}\) represents the value of data points \(x_{i}\) and \(x_{j}\) in mth dimension.

2.2 Related works

K-means (KM) is mainly used conventional clustering algorithm by virtue of its ease and effectiveness. But this algorithm usually converges in a finite number of steps and hence leads to local optima. Hence, a number of evolutionary clustering approaches have been designed by researchers in the past few decades. Shokhri and Alsultan [15] designed a new algorithm using simulated annealing meta-heuristic approach and theoretically proved the efficiency of their algorithm towards convergence to global solution. The main disadvantage of this approach was that no stopping point is computationally available. Maulik and Bandyopadhyay [16] developed a clustering technique based on Genetic Algorithm (GA). GA increased the searching capability by providing a good combination of exploration and exploitation parameters. This approach provided better cluster centers than the existing approaches. Krishna and Murty [17] presented a new hybrid genetic KM algorithm using KM operator instead of crossover in genetic algorithm and a distance based mutation operator. They proved that the proposed algorithm leads to better optimal solution than other evolutionary algorithms. Sung and Jin [18] formulated a heuristic approach for clustering problem, by combining two functions i.e. packing and releasing procedures with the tabu search. This algorithm prevented the searching capability from being stuck to local optima and it outperformed the other heuristic algorithm like simulated annealing (SA), k mean algorithm etc.

Cura [19] developed a novel Particle swarm optimization (PSO) based clustering approach and results revealed that the proposed approach was comparatively more effective and applicable when the number of clusters not known in advance. To decrease the degeneracy arosen by different chromosomes on relating the same cluster center, a new clustering algorithm based on gene rearrangement has been developed by Chang et al. [20]. The proposed algorithm also incorporated a new crossover operator based path that made it more exploratory efficient than KM, GA, KGA algorithm. Shelokar et al. [21] presented an Ant Colony Optimization (ACO) technique for optimal partitioning of different objects into separate clusters. This algorithm mimiced the behaviour of real ants for finding a shortest path from source to destination and then back to source. This approach was compared with other stochastic methods like GA, simulated annealing and tabu search and found more promising in terms of perfect quality solution, processing time and average number of evaluation.

Nehsat et al. [22] presented a hybrid PSO and K mean technique (PSOK) for generating the better cluster centers. PSO provides the global search and then the KM algorithm provides the local search. This algorithm outperformed KM, PSO and other hybrid approaches. [23] simulated the behavior of Artificial bee colony (ABC) with DE, PSO, and other evolutionary algorithms for multimodal problems and found that the ABC is better than the others and this behavior of honey bee can be used for solving the clustering problems. Fathian et al. [24] extended the behavior of Artificial Bee Colony (ABC) for data clustering. They proposed honey bee mating algorithm and compared their results with SA, GA TS and ACO by simulating them on various data sets. The main strength of this technique was its capability of finding better solution, and better processing time. Kwedlo [25] described a hybrid Differential evolution with K mean algorithm (DE-KM) to generate quality clusters in terms of sum of square errors (SSE) criteria. They incorporated the K mean algorithm in the steps of DE algorithm and compared their simulation results with K mean and DE algorithm. The hybrid one was found better than K mean as well as DE.

Another nature inspired recently developed optimization algorithm that simulates the flashing action of fireflies was Firefly Algorithm [26]. Senthilnath [27] used firefly algorithm for data clustering and compared its behavior with ABC and PSO based on classification error percentage performance measure. The results described that the firefly approach used by them is more reliable, efficient and robust in generating the optimal cluster centers. Hassanzadeh and Meybodi [28] also used the concept of firefly algorithm to remove premature convergence of k mean algorithm. They used a hybrid approach by incorporating the FA in K mean algorithm (KFA). Firstly FA was used to find the cluster centers and then the refinement was done by using k mean algorithm for finding the optimal cluster centers. The experimental results revealed that the KFA algorithm improved efficiency than k mean, PAO and KPSO.

Membrane computing is a class of distributed parallel computing motivated by actions of membranes and cells. The objects in cells are evolved by evolution mechanism mainly provided by selection, crossover and mutation operator and they are the candidates of cluster centers and are communicated with each other by two rules—antiport rule and symport rule [29]. Peng et al. [30] used this behavior of tissue like P system to generate better cluster centers and simulation results showed that the P system provides good quality clusters and high robustness. Harmony Search (HS) proposed by Geem et al. [31] is a global optimization approach that is motivated by musician’s harmony improvisation process. Alia et al. [32] proposed a new method using this approach that consists of two stages. Firstly, the HS explored the search space from the given data items in order to discover the better cluster centroid. Then the cluster centroid discovered by HS was evaluated by drafting a c-means function. Their experimental results showed that the proposed approach may decrease the complexity of choosing an initialization population for C mean algorithms. Kumar et al. [9] developed a grey wolf based clustering technique (GWO) and used its search features for finding the better cluster centers. The computational results showed that the developed algorithm provides better values in terms of cluster quality metrics.

Although the above mentioned meta-heuristic evolutionary approaches have been successfully applied on clustering problem, still they are not able to maintain balance between exploration and exploitation. As discussed earlier, a large number of metaheuristic algorithms like GA, DE, PSO, FA, GWO, HS etc. and their hybrid combination with other algorithms have been proposed by different authors. Still, a lot of refinement is required to improve their performance. In this paper we have refined the exploitation behaviour of PSO algorithm with crossover operator of GA and polygamous selection. The shortcomings of GA and PSO algorithms as well as the benefits of polygamous selection have been discussed in next sections that provoke the authors in proposing a new PSOPC hybrid evolutionary algorithm.

3 GA, PSO and polygamy

This section describes the concepts as well as limitation of GA and PSO algorithm that urges the author to describe a new algorithm.

3.1 Genetic algorithm

Genetic algorithm proposed by Holland [33] is a globally optimized search technique based on the mechanism of genetics and natural selection [34]. GA works on the population of fixed length strings and the strings are analogous to chromosomes in genetics. Chromosomes are made up of genes and the values of genes are called alleles. There is a fitness value associated with each chromosome. The sequence of operations in GA include: Initialization, Selection followed by Reproduction and Replacement. Initialization step uses suitable encoding scheme for initialization of population. Then selection operator selects the individual according to specific mating technique. After that reproduction operators are used to preserve trade-off between exploitation and exploration. Thereafter the replacement step replaces the old population with the new one [35]. The execution stops after fixed generations. The Pseudo code of GA is given in Fig. 1.

Fig. 1
figure 1

Pseudo code of GA

Full size image

3.2 PSO

PSO proposed by Eberhart and Kennedy [36] is one of the evolutionary optimization and swarm intelligence based technique. It is a global search approach that searches the search space simultaneously using multiple individual particles that can better investigate the search space for finding the better optimal solution. PSO uses the global best solution, individual particle’s best local solution and its inertia to find out the direction of movement of each particle within the search area [37, 38]. Flow chart showing the sequence of PSO Algorithm is shown in Fig. 2.

Fig. 2
figure 2

Flow chart code of PSO

Full size image

Let p be the number of individuals/Particles in the d-dimensional search space. For each particle i at time period q, the current position is represented as pi(q) and the velocity is Vi(q). The updated position and velocity of every individual during optimization steps is specified by Eqs. 6 and 7

$$V_{i} (q + 1) = wV_{i} (q) + {\text{r1c1(Pbest}}_{\text{i}} ( {\text{q) }} - {\text{ p}}_{\text{i}} ( {\text{q)) + r2c2 (Gbest (q) }} - {\text{ p}}_{\text{i}} ( {\text{q)) }}$$
(6)
$$p_{\text{i}} ( {\text{q + 1) = p}}_{\text{i}} ( {\text{q) + V}}_{\text{i}} ( {\text{q + 1)}}$$
(7)

where Vi(q + 1) is the updated velocity and pi(q + 1) represents ith particle updated position at time period q + 1. pi, is the position of particle i. w is the inertia coefficient (It can be a constant number). r1 and r2 are the two random uniformly distributed numbers in interval (0–1). c1 and c2 are learning coefficients. Pbesti(q) indicates particle i local best position at time (q + 1) and the Gbest (q) is the global best position for all the particles at time q. After each iteration, the local particle best solution is specified by Eq. 8.

$$\begin{aligned} {\text{Pbest}}_{\text{i}} ( {\text{q + 1)}} & {\text{ = Pbest}}_{\text{i}} ( {\text{q), if f(p}}_{\text{i}} ( {\text{q + 1)) > = f(Pbest}}_{\text{i}} ( {\text{q))}} \\ \, & \quad {\text{p}}_{\text{i}} ( {\text{q + 1), if f(p}}_{\text{i}} ( {\text{q + 1)) < f(Pbest}}_{\text{i}} ( {\text{q)) }} \\ \end{aligned}$$
(8)

Here, f(p) represents the fitness function and the global best particle solution is represented by Eq. 9:

$${\text{Gbest(q + 1) = argmin f(Pbest}}_{\text{i}} ( {\text{q + 1), (1}} < {\text{i}} < = {\text{n) )}}$$
(9)

3.3 Polygamy

Polygamy is a crossbreed concept where one individual has multiple mates to generate favourable offspring’s. Polygamy is found to be valuable genetically in a variety of species [39] like Buffalo, Cows, lion, elk, fur seals etc. Polyandry is an additional form of polygamy in which female entity mates with multiple male entity during reproduction season e.g. honey bees are polyandrous as a queen bee usually mates with more than one male that generates diversity in the colony. Similar idea can be used in genetic algorithm, where polygamy is a special case of elitism that selects the best chromosome from each generation and participated in the crossover with all other chromosomes present in the mating pool generated by any of the selection technique [40]. The pseudocode of Polygamous selection for better crossover is shown in Fig. 3:

Fig. 3
figure 3

Pseudo code of polygamy

Full size image

Above sections clearly describe the concept of GA, PSO and Polygamy. Both GA and PSO are the powerful algorithms but they have their own limitations. GA mainly looses the data regarding unselected individuals [41]. So in order to save the data about all individuals PSO has memory component and can solve that problem. But if the value of particle’s position is same as that of local and global best solution, then PSO can also be trapped into local optima. So in order to remove these limitations we have proposed a hybrid algorithm using GA and PSO and also incorporated the concept of polygamous selection before crossover.

The major contributions of the projected algorithm are:

  • A discrete hybrid approach named as PSOPC is formulated as an evolutionary data clustering technique using the concept of PSO, GA and polygamous selection.

  • Due to limited exploitation capability PSO usually stick into local optima. Hence, we incorporate a polygamous selection based crossover operator at updation step of PSO to maintain an efficient stability between exploitation and exploration.

  • In the proposed PSOPC, parameters like inertia weight and alpha values for arithmetic crossover are dynamically updated for further improving the exploration behaviour of PSO.

  • To verify the supremacy of proposed approach, this algorithm is compared with recent well known evolutionary algorithms (like GA, FA, DE, GWO, PSO) on seven real-life data sets. Statistical test over results and graphs clearly reveals that the proposed approach is better than other compared approaches in terms of sum of within cluster distance (SWCD), Precision, Sensitivity, Accuracy, G Measure and convergence speed.

4 Proposed algorithm (PSOPC)

GA is good global optimal technique but it suffers from some difficulties [36] like it sometimes distracts from progress towards better solution due to mutation operators and the change in genetic population leads to the destruction of previous knowledge (except in elitism). The complications of GA can be overwhelmed by PSO as it has memory component. In PSO there is always an interaction within the particles of a group that enhances the progress towards best global solution, and that best global solution is always retained by all the particles [36] but, still PSO algorithm is not capable in preventing from being trapped into local optimal solution and usually converges after a short period of time. So to overcome the above difficulties a novel hybrid algorithm PSOPC is proposed here that uses the concept of PSO along with polygamy and crossover operator. The flowchart of the proposed algorithm is as shown in Figs. 4 and 5 shows the applicability of the proposed approach in clustering problem.

Fig. 4
figure 4

Flow chart of PSOPC approach

Full size image
Fig. 5
figure 5

Pseudocode of PSOPC clustering algorithm

Full size image

The details of all steps of PSOPC are described below:

4.1 Solution space encoding

Every particle is represented as search agent and every agent is represented as a string of real numbers that represents k number of cluster centroid. In case of d-dimensional search space, length of every particle is represented in terms of 2D matrix k × d. Here each row specify the cluster center and the column specify the attributes of data sets from any clustering problem.

Consider the example: Let k = 2 and d = 4, (i.e. problem has four attributes and the number of clusters being considered as two). Then each particle is shown as

figure a

4.2 Population initialization

First of all, each particle is initialized and encoded with k arbitrarily selected data points from data sets as cluster centers. The above initialization step is repeated for each particle of population (npop), where npop is the maximum number of particle’s population.

4.3 Fitness function

Clustering is an unsupervised learning technique. But, if we want to use an evolutionary or metaheuristic algorithm to perform clustering, we should state the problem as an optimization problem. Hence, we need an objective function or fitness function. Fitness computation consists of two tasks:

First of all Euclidean distance of each data points to all clusters centroid is computed. Then, every data point is allotted to corresponding cluster that has minimum Euclidean distance. Subsequently, the centroid of a cluster is replaced with the calculated mean of all data points belong to that cluster.

Then the fitness function is calculated as SWCD that is the most commonly used evaluating criteria for determining the cluster quality. Lower the value of the SWCD, better will be the cluster quality. The objective function is given in equation

$${\text{F(}}P_{ 1 ,} P_{2} \ldots {\text{P}}_{\text{k}} ) =\sum\limits_{\text{i = 1}}^{\text{k}} {\sum\limits_{{{\text{x}}_{\text{j}} \in P_{i} }} {||z_{i} } } - {\text{ x}}_{\text{j}} { || }$$
(10)

Here Zi represents cluster centroid of cluster Pi.

4.4 Inertia coefficient, particle position and velocity updation

The inertia coefficient w is fixed in the beginning of PSOPC. This inertia value plays a crucial role in updating the velocity and selection of a good particle position; hence as the search proceeds, PSOPC gradually changes the alpha value. Initially the value of w is set to 2, and then it iteratively decreases to 0.1, till it reaches a threshold of 0.4. Thereafter, it will remain same for remaining iterations.

Then, velocity and position of each particle is updated using Eqs. 6 and 7.

4.5 Apply polygamy and perform crossover

Polygamous selection selects the best particle from each generation and this particle will participate in the crossover with all other chromosomes present in the mating pool generated by any of the selection technique. In PSOPC we perform the arithmetic crossover [42] by passing two parents, one is the best particle (Pbest) of the iteration generated by Eq. 8 and other is randomly generated (Prand). Pseudocode of the arithmetic crossover is given as:

Arithmetic Crossover (x1, x2)

    Input:

    Define alpha coefficient

    Output:

    Child particles: PChild1, Pchild2

  Begin

  PChild1 = alpha.*x1 + (1-alpha).*x2;

  PChild2 = alpha.*x2 + (1-alpha).*x1

  End

The value of alpha is gradually decreased by some constant factor until it reaches the threshold. In proposed approach the value of alpha is primarily set to 0.8, and for every iteration it gradually decreased with 0.01 values, till it reaches a threshold of 0.3. After that, its value will remain unchanged for the remaining generations. Then the existing particles are replaced with the generated offspring’s as well as the value of particle local best and global iteration best is also updated.

4.6 Termination condition

In this algorithm the computation is performed for the predetermined number of iterations. The best cluster centroid or particle generated after last iteration gives the solution of the clustering problem.

5 Implementation and observations

The proposed algorithm has been implemented in MATLAB and compared with the recent well known algorithms reported in literature, like GA [16], PSO [19, 43], DE [25], FA [28] GWO [9, 43] using standard benchmark datasets.

5.1 Data set used

To analyse the efficiency of PSOPC, the author has performed experiments on seven benchmark datasets obtained from UCI repository [12]. Table 1 shows the properties of datasets used for simulation.

Table 1 Data set properties
Full size table

5.2 Parameter setting

GA parameters

∙ Population size: 30

∙ Number of Generation: 200

∙ Crossover: PMX crossover

∙ Probability of Crossover: 0.8

∙ Probability of Mutation: 0.01

PSO parameters

∙ No of particles: 30

∙ Number of Generation: 200

∙ Inertia Weight (w) = 1 with gradual decrease by 0.01 and Velocity max = 255;

∙ Personal and Global Learning Coefficient 2.0;

DE parameters

∙ Population size: 30

∙ Number of Generation: 200

∙ Scaling Factor Lower Bound: 0.2

∙ Scaling Factor Upper Bound: 0.8

∙ Probability of Crossover: 0.2

FA parameters

∙ No of Fireflies: 30

∙ Number of Generation: 200

∙ Light Absorption Coefficient gamma = 1

∙ Attraction Coefficient beta = 2

∙ Mutation Coefficient alpha = 0.1

PSOPC parameters

∙ No of particles: 30

∙ Number of Generation: 200

∙ Initial Inertia Weight (w): 2

∙ Global Learning Coefficient: 2.0

∙ Personal Learning Coefficient: 2.0

∙ Gradually decreasing Crossover Probability pcmin = 0.2, pcmax = 1, Pdec = 0.02

GWO parameters

∙ Population size: 30

∙ No of Generation: 200

∙ Alpha linearly decreasing from 2 to 0

5.3 Cluster quality metrics

To analyse the effectiveness of the proposed algorithm, the simulation results are compared using some extensively used cluster quality measurements [44, 45] i.e. Precision, Senstivity, Accuracy and G-Measure (Fowlkes–Mallows index) by comparing each point’s obtained cluster with the corresponding actual cluster. For each such pair, these metrics indicate whether the prediction of allocating a point to a cluster is correct as per the actual class. Larger values of these measures are indicators of improved clustering. These metrics are mathematically defined as follows [9, 45]:

Precision Represents the fraction of relevant datapoints among the retrieved datapoints.

$${\text{Prec(i,j) = M}}_{\text{ij}} {\text{ / M}}_{\text{i}} \,$$
(11)

where \({\text{M}}_{\text{ij}}\) is the number of data sets of class j belongs to ith cluster. \({\text{M}}_{\text{i}}\) is the total number of data sets of cluster i.

Sensitivity/Recall: represents the fraction of retrieved relevant datapoints over the total number of relevant datapoints.

$${\text{Senstivity(i,j) = M}}_{\text{ij}} {\text{ / M}}_{\text{j}} \,$$
(12)

where \({\text{M}}_{\text{j}}\) is the total number of data sets of Class j.

Accuracy: represents the fraction of retrieved relevant datapoints over the total number of cases.

$${\text{Accuracy(i,j) = M}}_{\text{ij}} {\text{ / M}}_{\text{T}} \,$$
(13)

where \({\text{M}}_{\text{j}}\) is the total number of cases.

Fowlkes–Mallows (FM) index Also known as G Measure.

$$\begin{aligned} \sqrt {\Pr ec(i,j) \times Senstivity} (i,j) \hfill \\ \hfill \\ \end{aligned}$$
(14)

Also the results are compared with other metaheuristic algorithms in terms of intra cluster distance as shown in Eq. 10. Lower the value of the SWCD, better will be the cluster quality.

5.4 Simulation results

Table 2 indicates the mean and standard deviation computational results of different stochastic approaches for 20 independent runs. The main aim of this simulation is to check whether the proposed algorithm is able to generate compact clusters or not. As shown in Table 2, values attained by PSOPC outperform the other algorithms. For wine dataset, the SWCD optimal value obtained from proposed approach is 16,292.184 with very small standard deviation and for glass dataset optimal value obtained from PSOPC is 210.433 which is better than the other approaches. For IRIS dataset, the optimal value obtained from PSOPC is 96.5403 which is comparable with that of PSO and FA but convergence speed of PSOPC is better as compared to PSO and FA as shown in Fig. 16. For Haberman dataset, the optimal value obtained from PSOPC is 2566.9889 which is same as that of PSO, FA and GA. But, in context of mean and standard deviation results, PSOPC is much better than other ones. For Bupa and CMC dataset, the optimal value obtained from PSOPC is 9851.721 and 5532.1847 respectively which is comparable with other algorithms but PSOPC is faster in terms of convergence towards optimal solution as shown in Fig. 17. For Cancer dataset, the mean value of SWCD in PSOPC is 2964.387 with 4.67e−13 standard deviation which is much better than other algorithms. As discussed in Sect. 4.2, lower the value of SWCD better will be the clustering. Simulation results in Table 2 clearly show the value of SWCD for PSOPC is lower in most of the cases. In some cases, mean SWCD value of PSOPC is similar to other algorithm but PSOPC is found to be better in these cases with zero or negligible standard deviation. For PSOPC, best and mean value are exactly same for Haberman, Bupa, Iris, Cancer. In order to test the robustness of these clustering algorithms, we repeated the experiments 20 times for each data set. In each run we have performed 200 iterations, The Best value taken here is value corresponding to 200th iteration of each run. Consider the case for IRIS dataset, value of SWCD at 200th iteration is 96.6555 for each 20 runs. But if we consider the values for all iterations of each run and then calculate its mean, then it comes out to be different. Mean value of simulation result for 4000 iterations (200 × 20) is 99.370, but best value is 96.655 in case of Iris. Similar is the case with Haberman, Bupa and Cancer datasets also.

Table 2 Best, (mean) and [SD] values of SWCD obtained by simulation of algorithms
Full size table

The analysis of the clusters quality in terms of precision, sensitivity, accuracy and FM index is provided in Tables 3, 4, 5, 6, 7, 8 and 9 and Figs. 6, 7, 8 and 9. The main aim of these simulations is to check whether the prediction of allocating a point to a cluster is correct as per the actual class. Larger values of these measures are the indicators of improved clustering. Results have been simulated for 20 independent runs for PSOPC and other corresponding algorithms for iris, Bupa, Haberman, Breast Cancer, CMC, Wine, and Glass datasets respectively. Simulation results indicate that the PSOPC performs better in most of the cases than other algorithms in terms of precision, sensitivity, accuracy and FM index. The Proposed algorithm PSOPC is found to be better in almost all the cases with zero or negligible standard deviation

Table 3 Mean [SD] of IRIS cluster quality metrics
Full size table
Table 4 Mean [SD] of Bupa cluster quality metrics
Full size table
Table 5 Mean [SD] of Haberman cluster quality metrics
Full size table
Table 6 Mean [SD] of Breast Cancer cluster quality metrics
Full size table
Table 7 Mean [SD] of CMC cluster quality metrics
Full size table
Table 8 Mean [SD] of Wine cluster quality metrics
Full size table
Table 9 Statistical unpaired t test based on mean of SWCD between best and second best algorithm
Full size table
Fig. 6
figure 6

Comparison of precision quality for glass dataset

Full size image
Fig. 7
figure 7

Comparison of senstivity quality for glass dataset

Full size image
Fig. 8
figure 8

Comparison of accuracy quality for glass dataset

Full size image
Fig. 9
figure 9

Comparison of G measure quality for glass dataset

Full size image

Table 3 shows the values of cluster quality metrics for Iris datasets. Precision values for different algorithms indicate the probability of correct assignment of data points in the same clusters. Sensitivity is the probability that specifies that we have predicted correctly. The G measure is the geometric mean of both Precision and Sensitivity. It is the single term used to measure the clustering quality. Accuracy is the closeness of the result to the actual result. The values of Precision, Sensitivity, Accuracy and G Measure for PSOPC are 0.9119, 0.9, 0.9 and 0.9059 respectively, which are better than the corresponding values of other algorithms. Table 4 shows the values of cluster quality metrics for Bupa datasets. The values of all the quality measures for PSOPC are more than other algorithms. The values of FA are approximately similar to PSOPC algorithm but PSOPC is better in terms of negligible standard deviation. For Haeberman, the values of Precision, Sensitivity and G Measure for PSOPC are 0.515, 0.5192 and 0.5171 respectively with almost zero standard deviation. Overall performance of PSOPC is better that others, although accuracy of FA is also same as PSOPC, as shown in Table 5. Similarly Table 6 indicates that the precision and Accuracy value for both PSOPC and FA are 0.9640, 0.9640 and 0.9648, 0.9648 respectively. But PSOPC is better in terms of Sensitivity and G Measure.

Tables 7 and 8 show the Precision, Sensitivity, Accuracy and G Measure value for CMC and Wine datasets. Values clearly indicate that the value of all the cluster quality measures is better for PSOPC as compared to other algorithms. For example as shown in Table 7, Precision value for PSOPC is 0.3196 with 5.85e−17 deviation which is far much better than other algorithm.

Figures 6, 7, 8 and 9 show the graphical representation of cluster quality metrics for glass dataset. As shown in Fig. 6, Precision value for glass dataset for PSOPC is highest and GWO, and DE are next. This simulation result clearly indicates that the probability of correct assignment of data points in the same clusters by PSOPC is more than that of the other algorithms. Sensitivity is the fraction of actual pairs that has been identified. Figure 7 shows that the value of sensitivity for PSOPC, GWO, FA, DE, GA and PSO. It can be observed from Fig. 7 that PSOPC predicted the pairing of data points more correctly than the other algorithms. The values of accuracy of various algorithms are represented in Fig. 8, indicates that the clustering performed by PSOPC is more close to actual dataset than the other clustering techniques. One common term used to describe all the above measurements is G measure that is the geometric mean of both precision and recall. Figure 9 clearly indicates that PSOPC is more favourable to determine the similarity between the actual and the clustered datasets. Value of G measure for PSOPC is much higher than the other compared algorithms. Higher value of G measure indicates the more similarity between the benchmark and clustered classification.

Overall it can be analysed from various tables shown above that corresponding to most of the datasets the performance of PSOPC in terms of accuracy and G measure is better than other algorithms. In some cases, the performance of PSOPC has not improved, but is comparable with other algorithms. For example in Tables 2, 3, 4, 5, 6, 7 and 8, the performance of PSOPC is comparable to FA but is better than other algorithms. But since, in this work we are working on improving the convergence speed. So, it will be interesting to note, whether PSOPC can perform better than FA algorithm in terms of Convergence speed. In the next section we will study the performance of various algorithms in terms of convergence speed.

5.5 Best cluster centers

The best cluster centroids generated by PSOPC algorithm are shown in Figs. 10, 11, 12, 13, 14, 15 and 16. Values of cluster centers are plotted by taking d = 2 (attributes) for all the datasets. Dark Black circle is representing the centre of Cluster and the data point in one specific colour indicates one cluster. Data sets taken for simulation are having different number of instances, attributes and classes. Figures 10, 11, 12, 13, 14, 15 and 16 clearly show that the proposed PSOPC is able to perform clustering on different types of datasets.

Fig. 10
figure 10

IRIS best cluster center

Full size image
Fig. 11
figure 11

Bupa best cluster center

Full size image
Fig. 12
figure 12

Glass best cluster center

Full size image
Fig. 13
figure 13

Wine best cluster center

Full size image
Fig. 14
figure 14

Haberman best cluster center

Full size image
Fig. 15
figure 15

CMC best cluster center

Full size image
Fig. 16
figure 16

Cancer best cluster center

Full size image

Figures 17, 18 and 19 show the convergence graph between PSOPC, GA, FA, DE, GWO and PSO for some datasets. Algorithms are simulated for 200 iterations. For Iris and glass datasets, PSOPC converges at faster rate as well as providing the better results for SWCD than the other algorithms. As shown in Fig. 17 for CMC dataset, FA converges earlier than the PSOPC but it leads to premature convergence, Hence PSOPC is providing more optimal solution and converges faster than other algorithms.

Fig. 17
figure 17

Convergence result for iris

Full size image
Fig. 18
figure 18

Convergence result for CMC

Full size image
Fig. 19
figure 19

Convergence result for glass

Full size image

Figures and tables demonstrate that the PSOPC performs better than other metaheuristic approaches in context of proper combination of exploration and exploitation for almost all the datasets. The results obtained by this algorithm may not be the globally best, but the proposed algorithm has been found to perform better in most of the data sets. Performance of our designed approach is better in one or more ways such as optimality, convergence speed, standard deviation and cluster quality metrics.

Although the experimental results given in various tables clearly indicate that the PSOPC is optimal than the other simulated approaches, but statistical evaluation of the results can be quite useful to validate the supremacy of this approach. The section below reports about the statistical tests and their interpretation details.

5.6 Statistical significance test

For statistical testing of best algorithm, an unpaired t test has been performed between the mean SWCD results of best algorithm over other contender algorithm. Size of data taken for this statistical test is 20 and Confidence Interval (CI) between the two mean is calculated by taking 95% of confidence level (0.05% significance level). The two paired P value [46] of the t test represents the probability of supporting the alternate hypothesis, when the null hypothesis is true -type I error. For each data set, P value and confidence interval is interpreting the significance level of PSOPC compared to the second best contender algorithm.

If P ≤ 0.01 then results are Highly Statically Significant (HSS), else if P ≤ 0.05, then results are Statically Significant (SS), if P > 0.10 then results are Not Statically Significant (NSS). Unpaired T test is performed between the best and the second best algorithm for all the datasets. In case of Wine as well as Cancer datasets, proposed PSOPC is highly statically significant than the FA as its P value is less than 0.0001. In case of Glass dataset, the two tailed P value is 0.0140 that indicates that the PSOPC is statically significant than PSO algorithm. For Haberman dataset, P value Between PSOPC and DE is 0.0162 that indicates that PSOPC is statically significant than DE. In case of Bupa and CMC datasets, two tailed P value is less than 0.0001 that indicates that the PSOPC is highly statistically significant than the FA and DE respectively. For Iris dataset, PSOPC is not statistically significant than PSO. So results of Table 9 clearly signify that the proposed approach has been found to be statistically significant on most of the data sets except for IRIS data set.

6 Conclusion and future scope

Over the last decades, many metaheuristic algorithms are widely used in unsupervised data clustering problems. Two most powerful techniques are GA and PSO. But they have their own limitations. GA mainly looses the data regarding unselected individuals and PSO gets easily trapped into local optima, if the value of particle’s position is same as that of local and global best solution. This paper presented a hybrid metaheuristic approach PSOPC that depends on the integrated concept of PSO, genetic algorithm and the polygamous concept for mating. Polygamy is a special case of elitism where the best individual is used for mating with other individual for the refinement of population. The proposed algorithm was applied on seven real clustering datasets and was analysed with other metaheuristic approaches like Particle Swarm optimization, Genetic Algorithm, Differential Evolution, Firefly Algorithm, Grey Wolf Optimization. The simulation results revealed that PSOPC outperforms other approaches in context of convergence speed, as well as optimality of the solution. Further the proposed approach is more efficient in generating well separated clusters. Simulation results of cluster quality measures like Precision, Senstivity, G measure and Accuracy clearly reveal that the proposed algorithm is better in performing data clustering than the other compared algorithms. Statistical upaired t test demonstrated that PSOPC is statistically more significant in most of the cases. The present paper focused on clustering by knowing number of clusters in advance, future work will aim to do the clustering over dynamic data for which the number of clusters cannot be predetermined. The work can also be extended for automatic clustering in various applications like image segmentation, protein synthesis etc. There is also a possibility of designing the multiobjective version of this proposed approach for solving the suitable problems having multiple objectives of optimization.