1 Introduction

The flow problem in porous tubes or channels received much attention in recent years because of its various applications in biomedical engineering, for example in the dialysis of blood in artificial kidney, in the flow of blood in the capillaries, in the flow in blood oxygenators, as well as in many other engineering areas such as the design of filters, in transpiration cooling boundary layer control and gaseous diffusion. Because of its relevance to a wide variety of situations, convection in porous media is a well-developed field of investigation. Over recent decades, it has generally been recognized that some rheological complex fluids such as polymer solutions, blood, paints, butter, synovial fluid, salvia, soups, jams, ice-creams and certain oils cannot be adequately described by the Navier–Stokes theory. Because of this, several constitutive equations and flows for non-Newtonian fluids have been developed [1]. Undoubtedly, the equations of motion of these fluids are highly nonlinear and with higher order than the Navier–Stokes equations. One important and simple model that has been used to describe the rheological characteristics exhibited by certain fluids is the second-grade fluid. However, the second-grade fluid model [2] does not give reasonable results for flows of highly elastic fluids (polymer melts) that occur at high Deborah number [3]. For such situations the upper-convected Maxwell (UCM) model is quite appropriate. The suction flow in a channel for a UCM fluid was examined by Choi et al. [4]. More recently, Sadeghy et al. [5] examined the hydrodynamic flow of the UCM model over a steadily moving plate. Recently, the subject of hydromagnetics has attracted the attention of many authors, due not only to its inherent interest, but also to its many applications to problems of geophysical and astrophysical significance. The solution of the problem of magneto-hydrodynamic (MHD) flow of a Newtonian fluid through a flat channel is known and is usually given in textbooks on fluid dynamics. For large values of the Hartman number, the flow exhibits the characters of boundary layer, namely the Hartman layers. These also manifest themselves in ducts with other shapes. A particularly large literature exists on the solution of MHD flows through rectangular ducts [6–13]. These scientific problems and phenomena are modeled by ordinary or partial differential equations. In most cases, these problems do not admit analytical solution, so these equations should be solved using special techniques. In recent years, much attention has been devoted to the newly developed methods to construct an analytic solution of equation; such methods include the Adomian decomposition method [14] and Perturbation techniques. Perturbation techniques are too strongly dependent upon the so-called ‘‘small parameters’’ [15]. Thus, it is worthwhile to develop some new analytic techniques independent of small parameters. One of these techniques is Homotopy Analysis Method (HAM), which was introduced by Liao [16–21]. This method has been successfully applied to solve many types of nonlinear problems [22–26].

In this Letter, the equations of the two-dimensional MHD of an upper-convected Maxwell fluid in a permeable channel with slip at the boundaries are solved through HAM. The effects of Reynolds number Rew, slip condition k, Hartman number M and Deborah number De on velocity distributions are examined in detail. The convergence of the series solution is also explicitly discussed. The auxiliary parameter validity is different for each Reynolds number Rew, slip condition k, Hartman number M and Deborah number De. The afore-mentioned method gives rapidly convergent series with specific significant features for each scheme. Most authors studied permeable channel at various situations with no-slip boundary condition. The main objective of the present paper is to study a steady incompressible laminar UCM fluid flow through a porous channel with slip condition on walls.

2 Problem statement and mathematical formulation

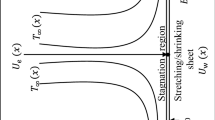
Let us consider the steady laminar flow of an incompressible and electrically conducting fluid in a channel with slip at the permeable walls as shown in Fig. 1. The slip boundary conditions are exerted on walls. The uniform magnetic field B 0 is imposed along the y-axis. It is assumed that the magnetic Reynolds Number is small and the induced magnetic field due to the motion of the electrically conducting fluid is negligible. It is also assumed that the electrical conductivity of fluid σ is constant and the external electric field is zero.

Fig. 1
figure 1

Schematic diagram of the permeable channel

Full size image

The constitutive equation for a Maxwell fluid is [27].

$$T\, = \, - pI + S,$$
(1)

where T is the Cauchy stress tensor and the extra-stress tensor S satisfies.

$$S + \lambda \left( {\frac{{{\text{d}}S}}{{{\text{d}}t}} - LS - SL^{T} } \right)\, = \,\mu A_{1}$$
(2)

In which μ is the viscosity, λ is the relaxation time and the Rivlin-Ericksen tensor A 1 is defined through

$$A_{1} \, = \,\nabla V + \left( {\nabla V} \right)^{T}$$
(3)

For the steady two-dimensional flow, the equations of continuity and momentum for the magneto-hydrodynamic flow are [28, 29].

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}\, = \,0,$$
(4)
$$\rho \left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right)\, = \, - \frac{\partial p}{\partial x} + \frac{{\partial S_{xx} }}{\partial x} + \frac{{\partial S_{xy} }}{\partial y} - \sigma \,B_{0}^{2} \,u,$$
(5)
$$\rho \left( {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}} \right)\, = \, - \frac{\partial p}{\partial x} + \frac{{\partial S_{yx} }}{\partial x} + \frac{{\partial S_{yy} }}{\partial y},$$
(6)

where ρ is the fluid density and S xx , S xy , S yx and S yy are the components of the extra-stress tensor. After some modification, the governing continuity and momentum equations for the motion can be written as follows [30, 31]

$$\frac{{\partial u^{ * } }}{{\partial x^{ * } }} + \frac{{\partial \nu^{ * } }}{{\partial y^{ * } }}\, = \,0$$
(7)
$$u^{*} \frac{{\partial u^{*} }}{{\partial x^{*} }} + v^{*} \frac{{\partial u^{*} }}{{\partial y^{*} }} + \lambda \left[ {u^{*2} \frac{{\partial^{2} u^{*} }}{{\partial x^{*2} }} + v^{ * 2} \frac{{\partial^{2} u^{ * } }}{{\partial y^{*2} }} + 2\,u^{ * } \,v^{ * } \frac{{\partial^{2} u^{ * } }}{{\partial x^{*} \partial y^{*} }}} \right]\, = \,\upsilon \frac{{\partial^{2} u^{ * } }}{{\partial y^{*2} }}\, - \frac{{\sigma B_{0}^{2} }}{\rho }u^{ * } ,$$
(8)

where (u *, v *) are the fluid velocity components along x *- and y *-directions, respectively. The flow is symmetric about the center line of the channel, y * = 0 and we only focus our attention on the flow in the region 0 < y * < H. The boundary conditions for this problem can be written as follows [32]:

$$y^{*} \, = \,0\!:\frac{{\partial u^{ * } }}{{\partial y^{*} }} = 0,\,\quad v^{ * } = 0,$$
(9)
$$y^{*} \, = \,H\!\!: - \beta u^{ * } = \frac{{\partial u^{ * } }}{{\partial y^{ * } }},\,\quad v^{ * } = V_{\rm{w}} ,$$
(10)

where β and V w are the coefficients of sliding friction and characteristic wall suction velocity, respectively. The following dimensionless variables are introduced.

$$x\,\, = \,\,\frac{{x^{*} }}{H}\,;\,\quad y\, = \,\frac{{y^{*} }}{H};\quad u^{ * } \, = \, - \,V_{\rm{w}} \,x\,f^{{\prime }} \left( y \right);\quad v^{ * } \, = \,V_{\rm{w}} \,\,f\left( y \right);\quad k\, = \,\frac{\mu }{H\,\beta }.$$
(11)

Equation (1) is automatically satisfied. And Eqs. (2)–(4) may be written as:

$$f^{{{\prime \prime \prime }}} - M^{2} f^{{\prime }} + \text{Re}_{\text{w}} \,\left( {f^{{{\prime }2}} - f\,f^{{\prime \prime }} } \right) + {\text{De}}\,\left( {2f\,f^{{\prime }} \,f^{{\prime \prime }} - f^{2} \,f^{{{\prime \prime \prime }}} } \right)\, = \,0$$
(12)

The boundary conditions become

$$\begin{gathered} y\, = \,0\!:{\quad} f^{{\prime \prime }} \, = \,0;\quad f = 0. \hfill \\ y\, = \,1\!: {\quad}f^{{\prime }} = - \,k\,f^{{\prime \prime }} ;\quad f\, = \,1. \hfill \\ \end{gathered}$$
(13)

Against the differential equation of the model which is in third order, there are four boundary conditions for this problem. Some authors satisfy boundary conditions in the initial guess function. In the present study, creatively with derivation of Eq. (12) and introduce fourth-order differential equation we can satisfy all of boundary conditions in main equation. Then we have,

$$f^{{{\prime \prime \prime }}} - M^{2} f^{{\prime \prime }} + \text{Re}_{\rm{w}} \,\left( {f^{{\prime }} \,f^{{\prime \prime }} - f\,f^{{{\prime \prime \prime }}} } \right) + {\text{De}}\,\left( {2\,f^{{{\prime }2}} f^{{\prime \prime }} \, - 2\,f\,f^{{{\prime \prime }2}} \, + f^{2} \,f^{{{\prime \prime \prime }}} } \right)\, = \,0$$
(14)

Here, \(\text{Re}_{\text{w}} \, = \,\frac{{V_{\text{w}} \,H}}{\upsilon }\) is the Reynolds number, \(\,{\text{De}} = \frac{{\lambda \,V_{\rm{w}}^{2} }}{\upsilon }\) is the Deborah number, and \(M^{2} \, = \,\frac{{\sigma \,B_{0}^{2} \,H}}{\mu }\) is the Hartman number, where Rew > 0 corresponds to suction and Rew < 0 is for injection.

3 Application of homotopy analysis method

For HAM solutions, we choose the initial guess and auxiliary linear operator in the following form:

$$f_{0} \left( {\it{y}} \right)\, = \, - \frac{1}{{2\left( {3\,k + 1} \right)}}y^{3} + \frac{{3\left( {2k + 1} \right)}}{{2\left( {3\,k + 1} \right)}}\,y,$$
(15)
$$L\left( f \right) \, = \, f^{{{\prime \prime\, \prime \prime }}} ,$$
(16)
$$L\,\left( {\frac{1}{6}c_{1} \,y^{3} + \frac{1}{2}c_{2} \,y^{2} + c_{3} \,y + c_{4} } \right)\, = \,0,$$
(17)

where c i (i = 1, 2, 3, 4) are constants. Let \(P \in \left[ {0,1} \right]\) denotes the embedding parameter and ħ indicates non-zero auxiliary parameters. We then construct the following equations:

3.1 Zeroth-order deformation equations

$$\left( { 1 - P} \right)L\left[ {F\left( {y; p} \right) - f_{0} \left( y \right)} \right] \, = \, p\hbar H\left( y \right)N\left[ {F\left( {y; p} \right)} \right]$$
(18)
$$F\left( {0; p} \right) = 0; {\quad}F^{{\prime \prime }} \left( {0; p} \right)\, = \,0,{\quad} F\left( { 1; p} \right) = 1,{\quad}kF^{{\prime \prime }} \left( { 1; p} \right) + F^{{\prime }} \left( { 1; p} \right) = 0$$
(19)
$$\begin{aligned} N[F(y\,;p)] & = \,\frac{{{\text{d}}^{4} F(y\,;p)}}{{{\text{d}}y^{4} }} + \,\text{Re} \left[ {\frac{{{\text{d}}F(y\,;p)}}{{{\text{d}}y}}\frac{{{\text{d}}^{2} F(y\,;p)}}{{{\text{d}}y^{2} }} - F(y\,;p)\frac{{{\text{d}}^{3} F(y\,;p)}}{{{\text{d}}y^{3} }}} \right] - M^{2} \frac{{{\text{d}}^{2} F(y\,;p)}}{{{\text{d}}y^{2} }} \\ & \quad + {\text{De}}\left[ {2\left( {\frac{{{\text{d}}F(y\,;p)}}{{{\text{d}}y}}} \right)^{2} \,\frac{{{\text{d}}^{2} F(y\,;p)}}{{{\text{d}}y^{2} }} - 2F(y\,;p)\left( {\frac{{{\text{d}}^{2} F(y\,;p)}}{{{\text{d}}y^{2} }}} \right)^{2} + \left( {F(y\,;p)} \right)^{2} \,\frac{{{\text{d}}^{4} F(y\,;p)}}{{{{\rm d}}y^{4} }}} \right]. \\ \end{aligned}$$
(20)

For p = 0 and p = 1 we have

$$\begin{array}{*{20}c} {F(y;0)\, = \,\,f_{0} (y)} {\quad} {F(y;1)\, = \,f(y)} \\ \end{array}$$
(21)

When p increases from 0 to 1 then F(y; p) varies from f 0(y) to f(y). By Taylor’s theorem and using Eq. (20), F(y; p) can be expanded in a power series of p as follows:

$$\begin{array}{*{20}c} {F(y;p) = f_{0} (y) + \sum\limits_{m - 1}^{\infty } {f_{m} (y)p^{m} ,} } {\quad} {f_{m} (y) = \left. {\frac{1}{m!}\frac{{\partial^{m} (F(y;p))}}{{\partial p^{m} }}} \right|_{p = 0} \,} \\ \end{array}$$
(22)

In which ħ is chosen in such a way that this series is convergent at p = 1; therefore, we have through Eq. (21) that

$$f(y)\, = \,f_{0} (y) + \sum\limits_{m - 1}^{\infty } {f_{m} (y),} \,$$
(23)

3.2 mth-order deformation equations

$$L\left[ {f_{m} \left( y \right) - \chi_{m} f_{m - 1} \left( y \right)} \right] \, = \, \hbar H\left( y \right)R_{m} \left( y \right)$$
(24)
$$F_{m} \left( {0; p} \right) \, = \, 0;{\quad} F^{{\prime \prime }}_{m} \left( {0; p} \right) = 0,{\quad} F_{m} \left( { 1; p} \right) = 0,{\quad} kF^{{\prime \prime }}_{m} \left( { 1; p} \right) + F^{{\prime }}_{m} \left( { 1; p} \right)\, = 0$$
(25)
$$\begin{aligned}R_{m} \left( y \right) & = f_{{m - 1}}^{{\prime \prime\, \prime \prime }} + \sum\limits_{{k = 0}}^{{m - 1}} \left[\text{Re} \left( {\mkern 1mu} f_{{m - 1 - k}}^{\prime } {\mkern 1mu} f_{k}^{{\prime \prime }} - f_{{m - 1 - k}} {\mkern 1mu} {\mkern 1mu} f_{k}^{{\prime \prime \prime }}\right) + {\text{De}}\,f_{{m - 1 - k}}^{\prime } \left( \sum\limits_{{l = 0}}^{k} \left( 2\,{\mkern 1mu} f_{{k - l}}^{\prime } \,f_{l}^{{\prime \prime }} \right) \right)\right.\\&\quad-\left. {\text{De}}{\mkern 1mu} f_{{m - 1 - k}} \left( \sum\limits_{{l = 0}}^{k} \;\left( {{\mkern 1mu} 2{\mkern 1mu} {\mkern 1mu} f_{{k - l}}^{{\prime \prime }} {\mkern 1mu} f_{l}^{{\prime \prime }} {\mkern 1mu} - f_{{k - l}} {\mkern 1mu} {\mkern 1mu} f_{l}^{{\prime \prime \prime \prime }} } \right) \right)\right] - M^{2} {\mkern 1mu} f_{{m - 1}}^{{\prime \prime }} \end{aligned}$$
(26)

Now we determine the convergency of the result, the differential equation and the auxiliary function according to the solution expression. So let us assume:

$$H(y)\, = \,1$$
(27)

We have found the answer by maple analytic solution device. The first deformation of the solution is presented below

$$\begin{aligned} f_{1} \left( {\text{y}} \right) & = - \frac{5\hbar }{672}\frac{{\,{\text{De}}\,y^{9} }}{{\left( {3k + 1} \right)^{3} }} - \frac{3\hbar }{2}\frac{{\left( { - 0.0071429\text{Re}_{\text{w}} k - 0.042857{\text{De}} - 0.0023810\text{Re}_{\text{w}} - 0.085714{\text{De}}\,k} \right){\text{y}}^{7} }}{{27k^{3} + 27k^{2} + 9k + 1}} \\ - \frac{3\hbar }{2}\frac{{\left( { - 0.15000M^{2} k^{2} - 0.10000M^{2} k - 0.016667M^{2} + 0.30000{\text{De}}\,k^{2} + 0.30000{\text{De}}\,k + 0.075000{\text{De}}} \right){\text{y}}^{5} }}{{27k^{3} + 27k^{2} + 9k + 1}} \\ + \frac{\hbar }{840}\left[ {\frac{{\left( {3780{\text{De}}\,k^{3} - 1890M^{2} k^{3} - 189\text{Re}_{\text{w}} k^{2} + 2268{\text{De}}\,k^{2} - 1638M^{2} k^{2} - 90\text{Re}_{\text{w}} k - 462M^{2} k + 468{\text{De}}\,k} \right){\text{y}}^{3} }}{{1 + 54k^{2} + 12k + 108k^{3} + 81k^{4} }}} \right. \\ + \left. {\frac{{\left( { - 9\text{Re}_{\text{w}} + 52{\text{De}} - 42M^{2} } \right){\text{y}}^{3} }}{{1 + 54k^{2} + 12k + 108k^{3} + 81k^{4} }}} \right] - \frac{\hbar }{1120}\left[ {\frac{{\left( { - 8\text{Re}_{\text{w}} - 96\text{Re}_{\text{w}} k - 1764M^{2} k^{3} 1440{\text{De}}\,k^{2} + 77{\text{De}}\,k - 364M^{2} k} \right){\text{y}}}}{{1 + 54k^{2} + 12k + 108k^{3} + 81k^{4} }}} \right. \\ + \left. {\frac{{\left( { - 1428M^{2} k^{2} + 3528{\text{De}}\,k^{3} - 216\text{Re}_{\text{w}} k^{2} - 28M^{2} + 7{\text{De}}} \right){\text{y}}}}{{1 + 54k^{2} + 12k + 108k^{3} + 81k^{4} }}} \right] \\ \end{aligned}$$
(28)

The solutions f(y) were too long to be mentioned here; therefore, they are shown graphically

4 Convergence of the HAM solution

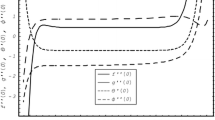
As pointed out by Liao [12], the convergence and rate of approximation for the HAM solution strongly depend on the value of auxiliary parameter ħ. The appropriate region for ħ is a horizontal line segment, which indicates a numerical range for having a convergent series solution. As mentioned we can adjust ħ to get most accurate solution, but in this problem we have a wide acceptable range values of ħ; therefore, we can take ħ from this region, as you can see in Table 1. In the following, to investigate the range of admissible values of the auxiliary parameter ħ, take the case of \(f^{{\prime \prime \prime}}\, (0)\) at M = 2, De = 0.1, Rew = 1 and different value of slip number as shown in Fig. 2. As can be seen, the range of admissible values of the auxiliary parameter ħ equals −1.5 < ħ < 0.0. In the same manner, the admissible values of ħ at k = 0.2, Rew = 1, M = 2 and different values of Deborah number are shown in Fig. 3.

Table 1 The results of ħ-validity for different value of De, k, M and Rew
Full size table
Fig. 2
figure 2

The ħ-validity for M = 2, De = 0.1, Rew = 1 and different value of k

Full size image
Fig. 3
figure 3

The ħ-validity for M = 2, K = 0.2, Rew = 1 and different value of De

Full size image

5 Results and discussion

In the present study, HAM method is applied to obtain an explicit analytic solution of an upper-convected maxwell fluid in a permeable channel with slip at the boundaries in the presence of uniform magnetic field (Fig. 1). HAM is used for this aim due to many advantages which some of them are described by Liao [12, 34] as follows,

  1. a.

    Unlike all other analytic techniques, HAM provides us with great freedom to express solutions of a given nonlinear problem by means of different base functions.

  2. b.

    HAM always provides us with a family of solution expressions in the auxiliary parameter ħ, even if a nonlinear problem has a unique solution, so the auxiliary parameter ħ provides us with an additional way to conveniently adjust and control the convergence region and rate of solution series.

  3. c.

    Unlike perturbation techniques, the Homotopy Analysis Method is independent of any small or large quantities. So, the Homotopy Analysis Method can be applied no matter if governing equations and boundary/initial conditions of a given nonlinear problem contain small or large quantities or not.

First, the present code is validated by comparing the obtained results with the numerical method for different values of active parameters. shown in Figs. 4, 5, 6, 7 and Table 2. The numerical solution is performed using the algebra package Maple 16.0, to solve the present problem. The package uses a second-order difference scheme combined with an order bootstrap technique with mesh-refinement strategies: the difference scheme is based on either the trapezoid or midpoint rules; the order improvement/accuracy enhancement is either Richardson extrapolation or a method of deferred corrections. The midpoint method, also known as the fourth-order Runge–Kutta–Fehlberg method, improves the Euler method by adding a midpoint in the step which increases the accuracy by one order. Thus, the midpoint method is used as a suitable numerical technique [35, 36]. By observing the overall pattern, it is noticed that this comparison shows an excellent agreement, so that we are confident that the present results are accurate.

Fig. 4
figure 4

The comparison between the numerical, HAM solution for f(y) and f ′(y) when Rew = 4, K = 0.9, M = 4, ħ = −0.8 and different values of De

Full size image
Fig. 5
figure 5

The comparison between the numerical, HAM solution for f(y) and f ′(y) when Rew = 8, K = 0.1, De = 0.1, ħ = −0.8 and different values of M

Full size image
Fig. 6
figure 6

The comparison between the numerical, HAM solution for f(y) and f ′(y) when Rew = 8, De = 0.1, M = 2, ħ = −0.8 and different values of K

Full size image
Fig. 7
figure 7

The comparison between the numerical, HAM solution for f(y) and f ′(y) when De = 0.1, K = 0.1, M = 2, ħ = −0.8 and different values of Rew

Full size image
Table 2 The results of HAM and numerical methods for f(y) and f′(y) for De = 0.1, k = 0.1, M = 0 and Rew = 4
Full size table

This investigation is completed by depicting the effects of some important parameters Reynolds number Rew, Deborah number De, Hartman number M and slip condition k to determine how these parameters affect the velocity components. Effect of Reynolds number (Rew) on velocities contours at k = 0.1, M = 2, De = 0.1 is shown in Fig. 8. As can been seen, increasing the Re number makes a decrease in velocity profiles also it is worth to mention that the Reynolds number indicates the relative significance of the inertia effect compared to the viscous effect.

Fig. 8
figure 8

Effects of Rew on the velocity components u * and v * contours and vector V, when a Rew = 1 and b Rew = 10 at (k = 0.1, M = 2, De = 0.1, ħ = −0.8)

Full size image

On the other hand, Fig. 9 shows the effect of viscoelastic material parameter, i.e. Deborah number on the velocity components when M = 4, Rew = 4, k = 0.9. The Deborah number (De) represents the ratio of a relaxation time, and the characteristic time scale of an experiment or a computer simulation probing the response of the material [31, 33]. As can be seen, an increase in the elastic parameter is noticed to decrease both u- and v-velocity components at any given point. It means that the smaller the Deborah number, the more fluid the material appears. Higher Devalues imply a strongly elastic behavior. Figure 10 shows the effect of Hartman number M on the velocity components for k = 0.1, De = 0.1, Rew = 8. Increase in the magnetic parameter leads to decrease in the velocity components and contours at given point. This is due to the fact that applied transverse magnetic field produces a damping in the form of Lorentz force thereby decreasing the magnitude of velocity. The drop in velocity as a consequence of increase in the strength of magnetic field is observed.

Fig. 9
figure 9

Effects of De on the velocity components u * and v * contours and vector V, when a De = 0.0 and b De = 0.9 at k = 0.9, M = 4, Rew = 4, ħ = −0.8

Full size image
Fig. 10
figure 10

Effects of M on the velocity components u * and v * contours and vector V, when a M = 0 and b M = 5 at k = 0.1, De = 0.1, Rew = 8, ħ = −0.8

Full size image

Finally, Fig. 11 shows the effect of slip condition on the velocity contours when De = 0.1, M = 2, Rew = 8. As seen in these figures, by decreasing slip condition, the slip coefficient β increases and the flow over the border desires to no-slip condition.

Fig. 11
figure 11

Effects of k on the velocity components u * and v * contours and vector V, when a k = 0.0 and b k = 0.9 at De = 0.1, M = 2, Rew = 8, ħ = −0.8

Full size image

6 Conclusion

In the present paper, the problem of a MHD flow of an upper-convected Maxwell viscoelastic fluid in a permeable channel with slip at the boundaries has been studied for the analytical solution using homotopy analysis method (HAM). The effects of physical flow parameters such as the Reynolds number, Deborah number, Hartman number and slip condition on the flow characteristics have been examined. As a main outcome from the present study:

  • It is observed that the results of HAM are in excellent agreement with numerical ones, so HAM can be used for finding analytical solutions of equations in science and engineering problems simplicity. Also, in HAM, we can choose ħ in such a way that we get most accurate solution and this is the most important feature of this technique.

  • The results show that increase in the M Hartman number associates with the reduction in velocity profile. Moreover, it is worth to mention that the velocity patterns are minimally influenced by the changes in De Deborah number parameter.

  • In addition, the flow over the border desires to no-slip condition by increasing in the values of slip parameter k.