Soret and Dufour effects in the flow of viscous fluid by a curved stretching surface

Abstract

The main focus in this study is to study the flow of a viscous fluid through a curved stretched surface. Soret and Dufour effects along with Joule heating are incorporated. Appropriate transformations yield the nonlinear ordinary differential system. Convergent series solutions of velocity, temperature and concentration are constructed. Graphical illustrations thoroughly demonstrate the features of the involved pertinent parameters. Skin friction coefficient, Nusselt and Sherwood numbers are also obtained and discussed graphically. Current computations reveal that the radial velocity experience decline with the increase of Hartman number. Further, fluid temperature declines for higher Prandtl and Soret numbers.

1 Introduction

The study of Newtonian fluids has received special attention of the scientists and engineers due to abundant applications of these fluids in industry and technology. Some of the common examples of Newtonian fluids are oil, water, ethylene glycol etc. The well-known Navier–Stokes equation describes the flow of Newtonian fluid. Sizeable literature on this topic exists in the literature. Ellahi et al [1] described slip flow of the viscous fluid with heat and mass transfer. Sweet et al [2] developed analytic solution for the unsteady magnetohydrodynamic (MHD) flow of a viscous fluid between moving parallel plates. Abbas et al [3] discussed MHD stagnation point flow subject to homogeneous–heterogeneous reactions and slip velocity. Turkyilmazoglu [4] developed exact solutions for the incompressible viscous fluid of a porous rotating disk flow. Lin and Zheng [5] demonstrated Marangoni boundary layer flow and heat transfer of copper–water nanofluid over a porous medium disk. Zeeshan et al [6] manifested magnetic dipole influences in viscous flows of a ferrofluid past a radiative stretching surface.

Magnetic field in fluid flow has many applications in engineering, polymer industry, physics, metallurgy and chemistry. In such applications, the desired characteristics of the end product mainly depend on the rate of heat cooling. The intensity and orientation of the applied magnetic field control the fluid behaviour. Magnetic field has a tendency to change heat transfer characteristics by rearranging fluid concentration. MHD flow has an important role in problems related to physiological fluids, for instance, blood plasma and blood pump machines, in sink float separation and in the construction of loud speakers as sealing materials. Keeping these features in mind, different flow configurations of MHD are examined by numerous researchers. Kumari et al [7] examined transient MHD stagnation flow of a non-Newtonian fluid due to impulsive motion from rest. Exact analytical solutions for heat and mass transfer of MHD slip flow in nanofluids have been studied by Turkyilmazoglu [8]. Hayat et al [9] analysed convective bidirectional flow of a nanofluid with MHD. Lin et al [10] presented MHD pseudoplastic nanofluid unsteady flow and heat transfer in a finite thin film over a stretching surface with internal heat generation. Numerical investigation of the effect of magnetic field on mixed convection heat transfer of the nanofluid in a channel with sinusoidal walls has been carried out by Rashidi et al [11]. Sheikholeslami and Rokni [12] examined nanofluid two-phase model under the influence of induced magnetic field.

In industrial and technological processes, stretched flow of flat surface has significant applications. Glass fibre making, extrusion of plastic sheet, crystal growing, hot rolling, wire drawing etc. are examples of stretching surface. Stretched flow caused by a sheet has been studied by Crane [13]. After that, several researchers examined flow problems with different stretching configurations. Cortell [14] studied stretched flow of the viscous fluid with thermal radiation. Mabood and Das [15] examined melting heat transfer on the hydromagnetic flow of a nanofluid over a stretching sheet with radiation and second-order slip. Chemical reaction and radiation effects on non-Newtonian fluid flow over a stretching sheet with non-uniform thickness and heat source have been studied by Ibrahim et al [16]. In all the abovementioned studies, mathematical modelling is done using Cartesian coordinate system and flat sheet is stretched. Stretched flow due to curved surface is studied by Sajid et al [17]. Governing equations are obtained through curvilinear coordinate system. For stretched flows, pressure is negligible whereas for curved stretching surface inside the boundary layer pressure is not negligible. Flow by curved stretched surface is a hot topic due to its inevitable applications in polymer industry, in contemporary technology and engineering processes. Examples of such applications are: melt-spinning, polymer extrusion from a dye, the cooling of huge metallic plate in a cooling bath, may be an electrolyte, manufacture of rubber and plastic sheets, wire drawing, production of paper and polymer sheet, thinning, annealing of copper wires, filaments, glass fibres, roll-paper production, liquid crystals in condensation processes etc. Rosca and Pop [18] presented stretched/shrinked flow over a curved sheet. Imtiaz et al [19] examined convective flow of Jeffrey liquid due to a curved stretching surface with chemical reaction and MHD. Convective flow of ferrofluid due to a curved stretching surface with homogeneous–heterogeneous reactions has been analysed by Imtiaz et al [20].

Heat and mass transfer with Soret and Dufour effects is an important subject due to a wide range of applications such as in the solidification of binary alloys, groundwater pollutant migration, chemical reactors, geosciences multicomponent melts, oil reservoirs, isotope separation and in mixture of gases. Generally, the effects of diffusion of matter caused by temperature gradients (Soret effect) and diffusion of heat caused by concentration gradients (Dufour effect) can be influential when the temperature and concentration gradients are very large. Hayat et al [21] examined heat and mass transfer under Soret and Dufour’s effect on mixed convection boundary layer flow over a stretching vertical surface in a porous medium filled with a viscoelastic fluid. Turkyilmazoglu and Pop [22] studied Soret and heat source effects on the unsteady radiative MHD free convection flow from an impulsively started infinite vertical plate. Soret and Dufour effects on free convection heat and mass transfer from an arbitrarily inclined plate in a porous medium with constant wall temperature and concentration have been analysed by Cheng [23]. Pal and Mondal [24] presented the influence of chemical reaction and thermal radiation on mixed convection heat and mass transfer over a stretching sheet in Darcian porous medium with Soret and Dufour effects. Altawallbeh et al [25] studied linear and nonlinear double-diffusive convection in a saturated anisotropic porous layer with Soret effect and internal heat source. Soret and Dufour effects on unsteady double diffusive natural convection in porous trapezoidal enclosures have been analysed by Al-Mudhaf et al [26].

The phenomenon of heat transfer has numerous applications in industry and engineering processes, e.g. nuclear reactor cooling, energy production, cooling of electronic devices, transportations, microelectronics, fuel cells etc. Flow due to curved stretching surfaces has promising applications in engineering and industrial sectors such as paper production, polymer sheet, thinning, annealing of copper wires, filaments, glass fibre, a wind up rollpaper production, polymer sheet, thinning, annealing of copper wires, filaments, glass fibre, etc. Major objective of the recent attempt is to examine Soret and Dufour effects on MHD flow past a curved stretching sheet. Joule heating is also considered and convergence results for approximate solutions are developed by employing homotopy analysis method (HAM) [27,28,29,30,31,32]. Impact of different parameters on velocity, temperature and concentration is discussed. Moreover, local skin friction coefficient, Nusselt and Sherwood numbers are analysed.

2 Model development

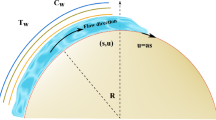
We consider the two-dimensional flow of incompressible viscous fluid coiled in the form of a circle with radius (R). The sheet is stretched in s direction and r is taken perpendicular to s. Magnetic effects with constant intensity $(B_{0})$ is exerted in radial direction. Joule heating is present. Under the assumption of low magnetic Reynolds number the induced magnetic field is neglected (see figure 1 [17]).

Fig. 1

Geometry of the problem.

Equations representing the flow of fluid [17, 21] are

$$\begin{aligned}&\frac{\partial }{\partial r}\{(r+R)v\}+R\frac{\partial u}{\partial s}=0, \end{aligned}$$

(1)

$$\begin{aligned}&\frac{u^{2}}{r+R}=\frac{1}{\rho }\frac{\partial p}{\partial r}, \end{aligned}$$

(2)

$$\begin{aligned}&v\frac{\partial u}{\partial r}+\frac{Ru}{r+R}\frac{\partial u}{\partial s}+ \frac{uv}{r+R} \nonumber \\&\quad =-\frac{1}{\rho }\frac{R}{r+R}\frac{\partial p}{\partial s} \nonumber \\&\quad \quad + \frac{\mu }{\rho }\left( \frac{\partial ^{2}u}{\partial r^{2}}+\frac{1}{r+R} \frac{\partial u}{\partial r}-\frac{u}{(r+R)^{2}}\right) \nonumber \\&\quad \quad -\frac{\sigma B_{0}^{2}u}{\rho }, \end{aligned}$$

(3)

$$\begin{aligned}&\rho C_{p}\left( v\frac{\partial T}{\partial r}+\frac{uR}{r+R}\frac{\partial T}{\partial s}\right) \nonumber \\&\quad =K\left( \frac{1}{r+R}\frac{\partial T}{\partial r}+ \frac{\partial ^{2}T}{\partial r^{2}}\right) \nonumber \\&\quad \quad +\frac{DK_{T}}{C_{s}}\left( \frac{1}{r+R}\frac{\partial C}{\partial r}+\frac{\partial ^{2}C}{\partial r^{2}}\right) +\sigma B_{0}^{2}u^{2}, \end{aligned}$$

(4)

$$\begin{aligned}&\left( v\frac{\partial C}{\partial r}+\frac{uR}{r+R}\frac{\partial C}{ \partial s}\right) \nonumber \\&\quad =D\left( \frac{1}{r+R}\frac{\partial C}{\partial r}+\frac{ \partial ^{2}C}{\partial r^{2}}\right) \nonumber \\&\quad \quad +\frac{DK_{T}}{T_{m}}\left( \frac{1}{ r+R}\frac{\partial T}{\partial r}+\frac{\partial ^{2}T}{\partial r^{2}} \right) . \end{aligned}$$

(5)

Here u and v represent components of velocity in s and r directions. Further p, $\mu$, $\rho$, $\sigma$, $C_{p}$, T, K, D, C, $K_{T}$, $T_{m}$ and $C_{s}$ are respectively the pressure, dynamic viscosity, density, electrical conductivity, specific heat, temperature, thermal conductivity, mass diffusion coefficient, fluid concentration, ratio of thermal diffusion, mean temperature and concentration susceptibility.

The boundary conditions in the considered problem are

$$\begin{aligned}&u=as,\quad v=0,\quad T=T_{w},\quad C=C_{w}\quad \mathrm {at}\quad r=0, \nonumber \\&u\rightarrow 0,\quad \frac{\partial u}{\partial r}\rightarrow 0,\quad T\rightarrow T_{\infty },\nonumber \\&C\rightarrow C_{\infty }\,\quad \mathrm {as}\ r\rightarrow \infty .\end{aligned}$$

(6)

We consider

$$\begin{aligned}&u=asf^{\prime }(\eta ), \quad v=\frac{-R\sqrt{a\nu }f(\eta )}{r+R}, \nonumber \\&\eta =\sqrt{\frac{a}{\nu }}r, \quad p=\rho a^{2}s^{2}P(\eta ), \nonumber \\&\theta =\frac{T-T_{\infty }}{T_{w}-T_{\infty }}, \quad \phi =\frac{ C-C_{\infty }}{C_{w}-C_{\infty }}, \end{aligned}$$

(7)

in which $T_{w}$, $C_{w}$, $T_{\infty }$ and $C_{\infty }$ respectively represent constant sheet temperature, constant sheet concentration, ambient fluid temperature and ambient fluid concentration, $a>0$ is the stretching constant and $\nu$ is the kinematic viscosity.

Now continuity equation is identically satisfied and other expressions are

$$\begin{aligned}&\frac{\partial P}{\partial \eta }=\frac{f^{\prime {2}}}{\eta +k}, \end{aligned}$$

(8)

$$\begin{aligned}&\frac{2kP}{\eta +k}=f^{\prime \prime \prime }+\frac{f^{\prime \prime }}{\eta +k}-\frac{f^{\prime }}{(\eta +k)^{2}}-\frac{kf^{\prime ^{2}}}{\eta +k} \nonumber \\&~~~~~~~~~~~\quad +\frac{ kff^{\prime \prime }}{\eta +k}+\frac{kff^{\prime }}{(\eta +k)^{2}} -M^{2}f^{\prime }, \end{aligned}$$

(9)

$$\begin{aligned}&\theta ^{\prime \prime }+\frac{\theta ^{\prime }}{\eta +k}+\mathrm {Du}\Pr \left( \phi ^{\prime \prime }+\frac{\phi ^{\prime }}{\eta +k}\right) \nonumber \\&\quad ~~+\mathrm {Br}M^{2}f^{\prime {2}}+\Pr \left( \frac{k}{\eta +k}\right) f\theta ^{\prime }=0, \end{aligned}$$

(10)

$$\begin{aligned}&\phi ^{\prime \prime }+\frac{\phi ^{\prime }}{\eta +k}+\mathrm {Sr}\,\mathrm {Sc}\left( \theta ^{\prime \prime }+\frac{\theta ^{\prime }}{\eta +k}\right) \nonumber \\&~~ \quad +\mathrm {Sc}\left( \frac{k }{\eta +k}\right) f\phi ^{\prime }=0, \end{aligned}$$

(11)

$$\begin{aligned}&f(0) =0,\quad f^{\prime }(0)=1,\quad \theta (0)=1,\quad \phi (0)=1, \nonumber \\&f^{\prime }(\infty ) =0,\quad f^{\prime \prime }(\infty )=0,\quad \theta (\infty )=0, \nonumber \\&\phi (\infty )=0, \end{aligned}$$

(12)

with

$$\begin{aligned}&k =R\sqrt{\frac{a}{\nu }},\quad \mathrm {Du}=\frac{DK_{T}(C_{w}-C_{\infty })}{\mu C_{s}C_{p}(T_{w}-T_{\infty })}, \nonumber \\&\mathrm {Sr}=\frac{DK_{T}(T_{w}-T_{\infty })}{ \nu T_{m}(C_{w}-C_{\infty })}, \nonumber \\&\mathrm {Sc} =\frac{\nu }{D},\quad \mathrm {Pr} =\frac{\nu }{\alpha },\quad \mathrm {Br}=\frac{\mu a^{2}s^{2}}{K(T_{w}-T_{\infty })}, \nonumber \\&M^{2}=\frac{\sigma B_{0}^{2}}{\rho a}. \end{aligned}$$

(13)

Here k, Du, Sr, Sc, Pr, Br and M are respectively the curvature parameter, Dufour number, Soret number, Schmidt number, Prandtl number, Brinkman number and Hartman number.

Eliminating pressure in eqs (8) and (9), we get

$$\begin{aligned}&f^{iv}+\frac{2f^{\prime \prime \prime }}{\eta +k}-\frac{f^{\prime \prime } }{(\eta +k)^{2}}+\frac{f^{\prime }}{\left( \eta +k\right) ^{3}} \nonumber \\&\quad +\frac{k}{ \eta +k}\left( ff^{\prime \prime \prime }-f^{\prime }f^{\prime \prime }\right) -\frac{k}{(\eta +k)^{2}}\big ( f^{\prime ^{2}}-ff^{\prime \prime }\big ) \nonumber \\&\quad - \frac{kff^{\prime }}{\left( \eta +k\right) ^{3}}-M^{2}\left( f^{\prime \prime }+\frac{f^{\prime }}{\eta +k}\right) =0. \end{aligned}$$

(14)

Mathematical expressions for skin friction coefficient, local Nusselt and Sherwood numbers are

$$\begin{aligned}&C_{\mathrm {f}}=\frac{\tau _{w}}{\rho U_{w}^{2}},\quad \mathrm {Nu}=\frac{sq_{w}}{K\left( T_{w}-T_{\infty }\right) }, \nonumber \\&\mathrm {Sh}=\frac{sh_{m}}{D(C_{w}-C_{\infty })}, \end{aligned}$$

(15)

where $\tau _{w}$, $q_{w}$ and $h_{m}$ denote the shear stress on the surface and fluxes due to temperature and concentration

$$\begin{aligned}&\tau _{w}=\left. \mu \left( -\frac{u}{r+R}+\frac{\partial u}{\partial r} \right) \right| _{r=0},\quad q_{w}=-\left. K\frac{\partial T}{\partial r}\right| _{r=0}, \nonumber \\&h_{m}=-\left. D\frac{\partial C}{\partial r} \right| _{r=0}. \end{aligned}$$

(16)

We can write

$$\begin{aligned}&C_{\mathrm {f}}({\text {Re}}_{s})^{1/2}=\left( f^{\prime \prime } (0)-\frac{f^{\prime }(0) }{k}\right) , \nonumber \\&\mathrm {Nu}({\text {Re}}_{s})^{-1/2}=-\theta ^{\prime }(0),\quad \mathrm {Sh}({\text {Re}}_{s})^{-1/2}=-\phi ^{\prime }(0),\nonumber \\ \end{aligned}$$

(17)

where ${\text {Re}}_{s}=U_{w}s/\nu$ is the local Reynolds number.

3 Solutions procedure

Parameters ${\mathcal {H}}_{f}$, ${\mathcal {H}}_{\theta }$ and ${\mathcal {H}}_{\phi }$, linear operators ${\mathcal {L}}_{f}$, ${\mathcal {L}}_{\theta }$ and ${\mathcal {L}}_{\phi }$ along with initial guesses $f_{0}(\eta )$, $\theta _{0}(\eta )$ and $\phi _{0}(\eta )$ are

$$\begin{aligned}&{\mathcal {H}}_{f}=\mathrm {e}^{-\eta },\quad {\mathcal {H}}_{\theta }=\mathrm {e}^{-2\eta },\quad {\mathcal {H}}_{\phi }=\mathrm {e}^{-2\eta }, \end{aligned}$$

(18)

$$\begin{aligned}&{\mathcal {L}}_{f}=f^{iv}-5f^{\prime \prime }+4f,\quad {\mathcal {L}}_{\theta }=\theta ^{\prime \prime }-\theta , \nonumber \\&{\mathcal {L}}_{\phi }=\phi ^{\prime \prime }-\phi , \end{aligned}$$

(19)

$$\begin{aligned}&f_{0}(\eta )=\mathrm {e}^{-\eta }-\mathrm {e}^{-2\eta },\quad \theta _{0}(\eta )=\mathrm {e}^{-\eta }, \quad \phi _{0}(\eta ) =\mathrm {e}^{-\eta },\nonumber \\ \end{aligned}$$

(20)

with properties

$$\begin{aligned}&{\mathcal {L}}_{f}[ c_{1}\mathrm {e}^{-\eta }+c_{2}\mathrm {e}^{\eta }+c_{3}\mathrm {e}^{-2\eta }+c_{4}\mathrm {e}^{2\eta }] =0, \nonumber \\&{\mathcal {L}}_{\theta }[ c_{5}\mathrm {e}^{\eta }+c_{6}\mathrm {e}^{-\eta }] =0, \nonumber \\&{\mathcal {L}}_{\phi }[ c_{7}\mathrm {e}^{\eta }+c_{8}\mathrm {e}^{-\eta }] =0, \end{aligned}$$

(21)

where $c_{i} (i= 1{-}7)$ are the unknowns to be determined.

3.1 Zeroth-order deformation problems

Let $p\in [0,1]$ be the embedding parameter. Then deformation equations of zero order are written as

$$\begin{aligned}&(1-q){\mathcal {L}}_{f}[ {\hat{f}}(\eta ;q)-f_{0}(\eta )] \nonumber \\&\quad =q\hbar _{f} {\mathcal {N}}_{f}[ {\hat{f}}(\eta ;q)] , \end{aligned}$$

(22)

$$\begin{aligned}&(1-q){\mathcal {L}}_{\theta }[ {\hat{\theta }}(\eta ;q)-\theta _{0}(\eta )] \nonumber \\&\quad =q\hbar _{\theta }{\mathcal {N}}_{\theta }[ {\hat{\theta }}(\eta ;q), {\hat{f}}(\eta ;q)] , \end{aligned}$$

(23)

$$\begin{aligned}&{\hat{f}}(0;q)=0, \ {\hat{f}}^{\prime }(0;q)=1, \ {\hat{f}}^{\prime }(\infty ;q)=0, \nonumber \\&{\hat{f}}^{\prime \prime }(\infty ;q)=0, \end{aligned}$$

(24)

$$\begin{aligned}&{\hat{\theta }}(0;q)=1, \quad {\hat{\theta }}(\infty ;q)=0, \end{aligned}$$

(25)

where $\hbar _{\theta }$ and $\hbar _{f}$ are auxiliary parameters and $q\in [0,1]$ depicts the embedding parameter. When value of q changes from zero to one, then both ${\hat{\theta }}(\eta ;q)$ and ${\hat{f}}(\eta ;q)$ change from initial guesses $\theta _{0}(\eta )$ and $f_{0}(\eta )$ to solutions $\theta (\eta )$ and $f(\eta )$. ${\mathcal {N}}_{f}$ and ${\mathcal {N}}_{\theta }$ are nonlinear operators and written as

$$\begin{aligned}&{\mathcal {N}}_{f}[ {\hat{f}}(\eta ;p)] =\frac{\partial ^{4}f}{ \partial \eta ^{4}}+\frac{2}{\eta +k}\frac{\partial ^{3}f}{\partial \eta ^{3} }-\frac{1}{(\eta +k)^{2}}\frac{\partial ^{2}f}{\partial \eta ^{2}} \nonumber \\&\quad +\frac{1}{ \left( \eta +k\right) ^{3}}\frac{\partial f}{\partial \eta }+\frac{k}{\eta +k }\left( \frac{\partial f}{\partial \eta }\frac{\partial ^{3}f}{\partial \eta ^{3}}-\frac{\partial f}{\partial \eta }\frac{\partial ^{2}f}{\partial \eta ^{2}}\right) \nonumber \\&\quad -\frac{k}{(\eta +k)^{2}}\left( \left( \frac{\partial f}{\partial \eta } \right) ^{2}-f\frac{\partial ^{2}f}{\partial \eta ^{2}}\right) -\frac{kf}{ \left( \eta +k\right) ^{3}}\frac{\partial f}{\partial \eta } \nonumber \\&\quad -M^{2}\left( \frac{\partial ^{2}f}{\partial \eta ^{2}}+\frac{1}{\eta +k}\frac{\partial f}{ \partial \eta }\right) , \end{aligned}$$

(26)

$$\begin{aligned}&{\mathcal {N}}_{\theta }[ {\hat{\theta }}(\eta ;p),{\hat{f}}(\eta ;p),{\hat{\phi }} (\eta ;p)] \nonumber \\&\quad =\frac{\partial ^{2}\theta }{\partial \eta ^{2}}+\frac{1}{ \eta +k}\frac{\partial \theta }{\partial \eta }+\mathrm {Du}\,\Pr \left( \frac{\partial ^{2}\phi }{\partial \eta ^{2}}+\frac{1}{\eta +k}\frac{\partial \phi }{\partial \eta }\right) \nonumber \\&\quad \quad +\mathrm {Br}\,M^{2}\left( \frac{\partial f}{\partial \eta } \right) ^{2}+\Pr \left( \frac{k}{\eta +k}\right) f\frac{\partial \theta }{\partial \eta }, \end{aligned}$$

(27)

$$\begin{aligned}&{\mathcal {N}}_{\phi }[ {\hat{\phi }}(\eta ;p),{\hat{f}}(\eta ;p),{\hat{\theta }} (\eta ;p)] \nonumber \\&\quad =\frac{\partial ^{2}\phi }{\partial \eta ^{2}}+\frac{1}{ \eta +k}\frac{\partial \phi }{\partial \eta }+\mathrm {Sr\,Sc}\left( \frac{\partial ^{2}\theta }{\partial \eta ^{2}}+\frac{1}{\eta +k}\frac{\partial \theta }{\partial \eta }\right) \nonumber \\&\quad \quad +\mathrm {Sc}\left( \frac{k}{\eta +k}\right) f\frac{\partial \phi }{\partial \eta }. \end{aligned}$$

(28)

3.2 mth-Order deformation problems

Deformation problems showing order m are listed below:

$$\begin{aligned}&{\mathcal {L}}_{f}\left[ f_{m}(\eta )-\chi _{m}f_{m-1}(\eta )\right] =\hbar _{f} {\mathcal {R}}_{f,m}(\eta ), \end{aligned}$$

(29)

$$\begin{aligned}&{\mathcal {L}}_{\theta }\left[ \theta _{m}(\eta )-\chi _{m}\theta _{m-1}(\eta ) \right] =\hbar _{\theta }{\mathcal {R}}_{\theta ,m}(\eta ), \end{aligned}$$

(30)

$$\begin{aligned}&{\mathcal {L}}_{\phi }\left[ \phi _{m}(\eta )-\chi _{m}\phi _{m-1}(\eta )\right] =\hbar _{\phi }{\mathcal {R}}_{\phi ,m}(\eta ), \end{aligned}$$

(31)

$$\begin{aligned}&f_{m}(0)=f_{m}^{\prime }(0)=f_{m}^{\prime }(\infty )=f^{\prime \prime }(\infty )=\theta _{m}(0) \nonumber \\&\quad =\theta _{m}(\infty )=\phi _{m}(0)=\phi _{m}(\infty )=0, \end{aligned}$$

(32)

$$\begin{aligned}&{\mathcal {R}}_{f,\,m}\left( \eta \right) =f_{m-1}^{iv}+\frac{2f_{m-1}^{\prime \prime \prime }}{\eta +k}-\frac{f_{m-1}^{\prime \prime }}{(\eta +k)^{2}} \nonumber \\&~~~~~~~~~~~~~~~~~ -M^{2}\left( f_{m-1}^{\prime \prime }+\frac{f_{m-1}^{\prime }}{\eta +k} \right) \nonumber \\&~~~~~~~~~~~~~~~~~+\frac{k}{\eta +k}\sum \limits _{k=0}^{m-1} \left( \left( f_{m-1-k}f_{k}^{\prime \prime \prime }-f_{m-1-k}^{\prime }f_{k}^{\prime \prime }\right) \right. \nonumber \\&~~~~~~~~~~~~~~~~~-\frac{k}{(\eta +k)^{2}}\left( f_{m-1-k}^{\prime }f_{k}^{\prime }-f_{m-1-k}f_{k}^{\prime \prime }\right) \nonumber \\&~~~~~~~~~~~~~~~~~\left. -\,\frac{kf_{m-1-k}f_{k}^{\prime }}{ \left( \eta +k\right) ^{3}}\right) +\frac{f_{m-1}^{\prime }}{\left( \eta +k\right) ^{3}}, \end{aligned}$$

(33)

$$\begin{aligned}&{\mathcal {R}}_{\theta ,m}(\eta )=\theta _{m-1}^{\prime \prime }+\frac{\theta _{m-1}^{\prime }}{\eta +k} \nonumber \\&~~~~~~~~~~~~~~~~~ +\mathrm {Du}\,\Pr \left( \phi _{m-1}^{\prime \prime }+\frac{ \phi _{m-1}^{\prime }}{\eta +k}\right) \nonumber \\&~~~~~~~~~~~~~~~~~ +\mathrm {Br}\,M^{2}\sum \limits _{k=0}^{m-1}\left( f_{m-1-k}^{\prime }f_{k}^{\prime }\right. \nonumber \\&~~~~~~~~~~~~~~~~~\left. +\Pr \left( \frac{k}{\eta +k}\right) f_{m-1-k}\theta _{k}^{\prime }\right) ,\end{aligned}$$

(34)

$$\begin{aligned}&{\mathcal {R}}_{\phi ,m}(\eta )=\phi _{m-1}^{\prime \prime }+\frac{\phi _{m-1}^{\prime }}{\eta +k} \nonumber \\&~~~~~~~~~~~~~~~~ +\mathrm {Sr\,Sc}\left( \theta _{m-1}^{\prime \prime }+\frac{ \theta _{m-1}^{\prime }}{\eta +k}\right) \nonumber \\&~~~~~~~~~~~~~~~~ +\mathrm {Sc}\left( \frac{k}{\eta +k}\right) f_{m-1-k}\phi _{k}^{\prime }, \end{aligned}$$

(35)

$$\begin{aligned}&\chi _{m} = \left\{ \begin{array}{c} 0, \ \ m\le 1 \\ 1, \ \ m>1 \end{array} \right. . \end{aligned}$$

(36)

The general solutions $(f_{m}$, $\theta _{m}$, $\phi _{m})$ comprising some particular solutions $(f_{m}^{*}$, $\theta _{m}^{*}$, $\phi _{m}^{*})$ are

$$\begin{aligned} f_{m}(\eta )= & {} f_{m}^{*}(\eta )+c_{1}\mathrm {e}^{-\eta }+c_{2}\mathrm {e}^{\eta }+c_{3}\mathrm {e}^{-2\eta }+c_{4}\mathrm {e}^{2\eta }, \nonumber \\ \theta _{m}(\eta )= & {} \theta _{m}^{*}(\eta )+c_{5}\mathrm {e}^{\eta }+c_{6}\mathrm {e}^{-\eta }, \nonumber \\ \phi _{m}(\eta )= & {} \phi _{m}^{*}(\eta )+c_{7}\mathrm {e}^{\eta }+c_{8}\mathrm {e}^{-\eta }. \end{aligned}$$

(37)

4 Analysis of the results

4.1 Results for convergent series solutions

HAM introduces auxiliary parameters $\hbar _{f}$, $\hbar _{\theta }$ and $\hbar _{\phi }$. Auxiliary parameters are important for developing convergence results for series solutions. Thus, appropriate range of values of the parameters are obtained by plotting $\hbar$-curves at 11th-order of approximation that can be seen in figures 2–4. Specific range of values for series solutions are found in the ranges $-0.3\le \hbar _{f}\le -0.05$, $-1.0<\hbar _{\theta }\le -0.75$ and $-1.1<\hbar _{\phi }\le -0.75$. Further, the convergence results are obtained at $\hbar _{f}=-0.11$, $\hbar _{\theta }=-0.75$ and $\hbar _{\phi }=-0.75$ (see table 1).

Fig. 2

$\hbar _{f}$-curve of velocity.

Fig. 3

$\hbar _{\theta }$-curve of temperature.

Fig. 4

$\hbar _{\phi }$-curve of concentration.

Table 1 Convergence results for HAM-based solutions with $k=0.4$, $\hbox {Du}=0.11$, $\hbox {Sr}=0.11$, $\hbox {Sc}=1$, $\hbox {Br}=0.1$, $\Pr =1$ and $M=0.3$.

Fig. 5

Influence of k on $f^{\prime }(\eta )$.

Fig. 6

Influence of M on $f^\prime (\eta )$.

4.2 Discussions and results

This section illustrates graphical description for velocity, temperature, concentration, surface drag force and heat and mass transfer rates corresponding to certain parameters appearing in the definition of the given problem.

4.2.1 Dimensionless velocity profiles

Figures 5 and 6 represent graphs of velocity along radial direction, i.e. $f^{\prime }(\eta )$ that are reversely effected by both k and M. In figure 5, larger k comprises increasing radius of the sheet that causes $f^{\prime }(\eta )$ to increase. Figure 6 indicates reduction in $f^{\prime }(\eta )$ with respect to M. It is due to the fact that larger M offers more resistive force which decreases $f^{\prime }(\eta )$.

Fig. 7

Influence of k on $\theta (\eta )$.

Fig. 8

Influence of M on $\theta (\eta )$.

4.2.2 Dimensionless temperature profiles

Figures 7–13 show the behaviour of different parameters on temperature $\theta (\eta )$. Figure 7 displays the effect of k on $\theta (\eta )$. An increasing trend of $\theta (\eta )$ is seen for increasing k. It is due to the fact that radius of the sheet rises via ascending k. Resistance to the flow of fluid enhances and $\theta (\eta )$ increases. Figure 8 shows that $\theta (\eta )$ is directly related to M. Increment in M rises the resistive forces. Thus, more heat is produced within the system and so $\theta (\eta )$ increases. Increasing behaviour of $\theta (\eta )$ is shown in figure 9. Depending on larger Du the thermal diffusion increases and thus temperature increases. In figure 10 decreasing graph of Sr is shown. In fact, larger Sr reduces the viscosity which provides less resistance and consequently temperature reduces. Figure 11 shows that $\theta (\eta )$ rises for larger values of Sc. Larger Sc increases the viscosity of the fluid and thus more resistance is offered that adds up more heat energy to the fluid. This leads to an enhancement in $\theta (\eta )$. Figure 12 shows the impact of Br upon $\theta (\eta )$. Ascending values of Br increases the fluid viscosity that provides more heat energy due to more collisions between the fluid particles and so $\theta (\eta )$ rises. Effects of Pr on $\theta (\eta )$ in a decreasing manner can be seen in figure 13. As $\Pr$ depicts fraction of diffusivity in momentum to thermal diffusivity, larger $\Pr$ causes reduction in the coefficient of thermal diffusion and as a consequence $\theta (\eta )$ decreases.

Fig. 9

Influence of Du on $\theta (\eta )$.

Fig. 10

Influence of Sr on $\theta (\eta )$.

Fig. 11

Influence of Sc on $\theta (\eta )$.

Fig. 12

Influence of Br on $\theta (\eta )$.

Fig. 13

Influence of $\Pr$ on $\theta (\eta )$.

Fig. 14

Influence of k on $\phi (\eta )$.

Fig. 15

Influence of M on $\phi (\eta )$.

Fig. 16

Influence of Du on $\phi (\eta )$.

Fig. 17

Influence of Sr on $\phi (\eta )$.

4.2.3 Dimensionless concentration profiles

Graphical results of concentration profile are depicted in figures 14–18. Figure 14 shows the impact of curvature parameter k on concentration profile $\phi ( \eta )$. As viscosity is inversely related to k, concentration rises with the increase in curvature parameter. Concentration profiles $\phi ( \eta )$ are presented for various values of M in figure 15. As M is increased it causes retardation to the fluid flow which enhances the fluid concentration. Figure 16 illustrates the fluctuation in concentration profile for varying values of Du. Larger values of Du causes low friction which in turn enhances the concentration. Contrary to the effect of Du, Sr increases $\phi (\eta )$ (see figure 17). An impact of Sc on $\phi (\eta )$ is shown in figure 18. Larger value of Sc indicates that the momentum diffusivity dominates the mass diffusivity, which causes enhancement in the fluid concentration.

Fig. 18

Influence of Sc on $\phi (\eta )$.

Fig. 19

Influence of k on ${\text {Re}}^{1/2}C_{\mathrm {f}}$.

Fig. 20

Influence of M on (${\text {Re}}_{s})^{-1/2}$Nu.

4.2.4 Skin friction coefficient, Nusselt number and Sherwoood number

Impact of curvature parameter (k) on skin friction coefficient $(C_{\mathrm {f}}( {\text {Re}})^{1/2})$ via Hartman number (M) is illustrated in figure 19. Here $C_{\mathrm {f}}( {\text {Re}})^{1/2}$ decreases by increasing the values of k. Figure 20 portrays the variation of M with Nusselt number Nu$\left( {\text {Re}}_{s}\right) ^{-1/2}$ against k. Here, it is seen that surface heat flux enhances for larger values of M and it decreases with the enhancement in k. Influence of Du on Sherwood number Sh$\left( {\text {Re}}_{s}\right) ^{-1/2}$ via $\Pr$ is illustrated in figure 21. Here surface mass flux increases by increasing the values of Du.

Fig. 21

Influence of Du on $(\hbox {Re}_{s})^{-1/2} \hbox {Sh}$.

Fig. 22

Influence of k on $P(\eta )$.

Fig. 23

Influence of M on $\ P(\eta )$.

Table 2 Comparison of surface drag force with values from Mabood and Das [15] and Imtiaz et al [19] at $k=\infty$.

4.2.5 Dimensionless pressure

Graphical results of dimensionless pressure ($P(\eta ))$ are sketched in figures 22 and 23. $P(\eta )$ shows dual behaviour in both these figures. Influences of M and k on $P(\eta )$ are reverse. Hence $P(\eta )$ vanishes far away from the sheet.

Comparison of skin friction coefficient for various values of M in limiting cases is presented in table 2. Here it is seen that the obtained solutions agree well with the results of Mabood and Das [15] and Imtiaz et al [19].

5 Concluding remarks

Here the effects of Soret and Dufour numbers on MHD viscous fluid flow induced by curved stretching sheet is analysed. Further, inclusion of Joule heating modifies the heat characteristics. The following results are outlined:

• Curvature number contributes to an enhancement in velocity profiles.

• Fluid temperature rises with an increase in Du while it reduces when Sr is increased.

• Temperature and concentration increase with an increment in M.

• Influence of Du on concentration is qualitatively opposite to that of Sr.

• Surface drag force is found to decline upon increasing k.

• Sh shows increasing trend for larger Pr.