1 Introduction

In recent years, the behaviours of dynamical systems with different time-scales have attracted much attention by researchers. Bursting phenomenon represents mixed-mode oscillations which appear in the combination of nearly harmonic small-amplitude oscillations, described by quiescent states (QSs) and relatively large-amplitude oscillations, defined as spiking states (SPs), which have been explored in systems of diverse disciplines, for instance, describing bursting phenomenon in neuroscience [1,2,3], biologic systems [4,5,6], chemical systems [7, 8], physic systems [9,10,11], etc.

To study the mechanism of transition between the SPs and QSs, Rinzel [12] first put forward a classical analysis method. He presented an analysis and qualitative viewpoint of bursting for Chay–Keizer theoretical model by dividing the dynamical system into two subsystems, denoted by the fast subsystem and the slow subsystem. This method is also known as fast–slow analysis method. In accordance with this work, Izhikevich [13] showed how the type of bifurcation determines the neuron-computational properties of the cells, and how the phenomenon of neural bursting is depicted. The main idea is that judging by the analysis of the equilibrium states and bifurcation in fast subsystem, the slow subsystem can be applied to regulate the dynamical behaviours of the whole system in any period. Therefore, the corresponding bifurcation mechanism of mixed-mode oscillations is revealed.

Up to now, the dynamical systems with vector fields, which have been considered comprehensively, are almost continuous [14,15,16,17]. In fact, there exist many non-smooth factors. For example, friction may evolve in mechanical problems [18, 19], threshold strategy in ecological economic dynamics [20, 21], the discontinuous functional response in a ratio-dependent predator–prey model [22], etc. The influence of these factors may show more complicated and richer dynamics in related systems [23, 24], which remains a challenge for future researchers.

Table 1 Eigenvalues of different equilibrium points.
Full size table

In this paper, based on these considerations, and taking the well-known three-dimensional Chua’s system as an example, we try to explore the related dynamics of the system with discontinuous vector fields by adding a voltage-based steering switch and a periodically changed electrical source, which can also be called Filippov-type system.

This paper is structured as follows: In §2, a general description for the Chua’s system is presented. In §3, the conventional bifurcations and the non-conventional bifurcations are discussed by analysing different distributions of equilibrium branches and the corresponding bifurcations. Two different mixed-mode oscillations are shown which reveal the associated dynamical mechanisms, and the related numerical simulations are provided to verify the theoretical findings in §4. Finally, in §5, we give a concise conclusion.

2 Mathematical model

To explore the mixed-mode oscillations in a set of Fillippov-type systems with two time-scales which is based on the typical three-dimensional Chua’s system [25], the mathematical model, by adding a voltage-based steering switch and a periodically changed electrical source, can be expressed by the following non-dimensional form:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}=\alpha (y-x-f(x))+w+\delta \,{\mathop {\mathrm{sign}}}(x),\\ {\dot{y}}=x-y+z,\\ {\dot{z}}=-\beta y,\\ \end{array} \right. \end{aligned}$$
(1)

with \(w\,{=}\,F\cos ({\Omega }\tau )\), where F and \(\Omega \) represent the amplitude and the frequency of the external periodic excitation, respectively. The term \(f(x)\,{=}\,mx+n{{x}^{3}}\) describes the nonlinear property of resistance. When an order gap exists between the exciting frequency \(\Omega \) and the natural one, denoted by \({\Omega _N}\), such as \({\Omega \ll {\Omega _N}}\), the influence of two time-scales may emerge, which often behaves in mixed-mode oscillations.

Because of the term \(\delta \,{\mathop {\mathrm{sign}}}(x)\), the non-smooth boundary \(\Sigma \), denoted by \( H \,{=}\, \{ ({x},{y},{z})\left| {{x}} \right. \,{=}\, 0\} \), can be obtained, which divides the phase space into two smooth regions, described by \( D_{+} \,{=}\, \{ ({x},{y},{z})\left| {{x}} \,{>}\, 0\right. \} \) and \( D_{-} \,{=}\, \{ ({x},{y},{z})\left| {{x}} \,{<}\, 0\}\right. \) corresponding to the two different smooth subsystems \(A_{+}\) and \(A_{-}\), respectively. By changing the parameters, bifurcations may happen not only in the two regions but also on the non-smooth boundary, resulting in intricate behaviours of the systems.

3 Bifurcation analysis

For a nonlinear system, its natural frequency will alter along with the dynamical behaviours. For example, when the trajectory of the system tends to a stable focus, the natural frequency is approximately the imaginary part of the eigenvalue of the conjugate complex numbers, and when the trajectory tends to a limit cycle, the natural frequency is calculated by the frequency of periodic oscillation. For non-smooth systems, the natural frequencies are relatively complex. For instance, the non-smooth interface \(H \,{=}\, \{ ({x},{y},{z})\left| {{x}} \right. \,{=}\, 0\}\) of System (1) separates the phase space into two smooth regions, shown by \( D_{+} \,{=}\, \{ ({x},{y},{z})\left| {{x}} \,{>}\, 0\}\right. \) and \( D_{-} \,{=}\, \{ ({x},{y},{z})\left| {{x}} \,{<}\, 0\}\right. \). For obtaining the value about its natural frequency, we set the system without external periodic excitation, that is, \(F\,{=}\,0\). By computation, the equilibrium point can be uniformly expressed by \( (x_{E},0,-x_{E})\), where \(x_{E}\) satisfies

$$\begin{aligned} -\alpha [(m+1){{x}_{E}}+nx_{E}^{3}]+\delta \, \mathrm {sign}({{x}_{E}})\,{=}\,0.\ \end{aligned}$$

Obviously, there are different numbers of equilibrium points for different parameters. When \(m\,{=}\,-1.25, n\,{=}\,0.25 \hbox { and } \delta \,{=}\,-1.0\), the non-smooth system has three different equilibrium points. These points present the structure of characteristic subspace corresponding to different eigenvalues in the two regions and on the interface (see table 1).

When the trajectory oscillates near the equilibrium point \(x_{E}^{0}(0,0,0)\), the natural frequency is \(\Omega _{N0}\,{=}\,3.2409\), and when the trajectory oscillates around the equilibrium point \(x_{E}^{0\pm }(\mp 1.3978,0,\pm 1.3978)\), the same natural frequency is \(\Omega _{N0\pm }\,{=}\,3.4483\) in the region \(D_{\pm }\).

Here, taking the exciting frequency \(\Omega \,{=}\,0.1\), the other parameters are constants. It is evident that there is an order gap between the excitation frequency and the natural one of the system. Therefore, note that when \({\Omega \ll {\Omega _N}}\), in any intrinsic period \(t\in [{{t}_{0}},{{t}_{0}}+{2\text { }\!\!\pi \!\!\text { }}/{{{\Omega }_{N}}}]\), the external excitation w may change from \({{W}_{A}}\,{=}\,A\sin (\Omega {{t}_{0}})\) to \({{W}_{B}}\,{=}\,A\sin (\Omega {{t}_{0}}+2\text { }\!\!\pi \!\!\text { }{\Omega }/{{{\Omega }_{\text {N}}}})\,{\approx }\,{{W}_{A}}\), which indicates that w is almost a constant. Correspondingly, the system is divided into two smooth subsystems, expressed as:

For \(x>0\),

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}=\alpha (y-x-f(x))+w+\delta ,\\ {\dot{y}}=x-y+z,\\ {\dot{z}}=-\beta y\\ \end{array} \right. \end{aligned}$$
(2)

and for \(x<0\),

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}=\alpha (y-x-f(x))+w-\delta ,\\ {\dot{y}}=x-y+z,\\ {\dot{z}}=-\beta y\\ \end{array} \right. \end{aligned}$$
(3)

3.1 Conventional bifurcation analysis of the two subsystems

Note that the whole excitation term w is seen as a parameter, resulting in two generalised autonomous subsystems. Now, we concentrate on the equilibria of two subsystems. By calculation, the equilibrium point can be written in the form \(E^{*}(x_{0},0,-x_{0})\), where \(x_{0}\) satisfies

$$\begin{aligned} -\alpha [(m+1){{x}_{0}}+nx_{0}^{3}]+w+\delta \ \hbox {sign}({{x}_{0}})=0. \end{aligned}$$
(4)

The stability of the equilibrium point \(E^{*}\) can be determined by the following characteristic equation:

$$\begin{aligned} f(\lambda )={{\lambda }^{3}}+(1+\alpha +\eta ){{\lambda }^{2}}+(\beta +\eta )\lambda +\beta (\alpha +\eta ),\nonumber \\ \end{aligned}$$
(5)

where \(\eta =3\alpha nx_{0}^{2}+\alpha m\).

Here, in accordance with the Routh–Hurwitz criteria, all roots of eq. (5) possess negative real parts only when the following conditions hold:

$$\begin{aligned}&1+\alpha +\eta>0,\ \beta (\alpha +\eta )>0,\ \\&(1+\alpha +\eta )(\beta +\eta )-\beta (\alpha +\eta )>0. \end{aligned}$$

Hence, the equilibrium point is locally asymptotically stable.

Next, we obtain two types of co-dimension one bifurcations.

1. Fold bifurcation (FB)

When the following conditions hold:

$$\begin{aligned} \mathrm {FB}:\ \ \alpha =-\eta ,\quad (1+\alpha +\eta>0,\ (\beta +\eta )>0). \end{aligned}$$
(6)

In that way, FB may emerge, causing jumping phenomenon among different equilibria.

2. Hopf bifurcation (HB)

According to the HB theorem [26, 27], HB can occur, which should satisfy the following two conditions:

(i) Bifurcation condition:

$$\begin{aligned}&\mathrm {HB}:\ \ (1+\alpha +\eta )(\beta +\eta )-\beta (\alpha +\eta )=0,\nonumber \\&\qquad \quad (1+\alpha +\eta>0,\ \beta +\eta >0). \end{aligned}$$
(7)

(ii) Transversality condition:

The corresponding characteristic equation (5) is

$$\begin{aligned} f(\lambda )={{\lambda }^{3}}+(1+\alpha +\eta ){{\lambda }^{2}}+(\beta +\eta )\lambda +\beta (\alpha +\eta ), \end{aligned}$$

where \(\eta =3\alpha nx_{0}^{2}+\alpha m\).

Differentiating eq. (5) with respect to w, noticing that \(\lambda \) is a function of w, and applying the derivative of the composite function, we obtain

$$\begin{aligned} 3{{\lambda }^{2}}\frac{\mathrm {d}\lambda }{\mathrm {d}w}&+(1+\alpha +\eta )\cdot 2\lambda \frac{\mathrm {d}\lambda }{\mathrm {d}w}+{{\lambda }^{2}}\frac{\mathrm {d}\eta }{\mathrm {d}x}\cdot \frac{\mathrm {d}x}{\mathrm {d}w}\nonumber \\&+(\beta +\eta )\frac{\mathrm {d}\lambda }{\mathrm {d}w} +\lambda \frac{\mathrm {d}\eta }{\mathrm {d}x}\cdot \frac{\mathrm {d}x}{\mathrm {d}w}+\beta \frac{\mathrm {d}\eta }{\mathrm {d}x}\cdot \frac{\mathrm {d}x}{\mathrm {d}w}=0, \end{aligned}$$
(8)

which leads to

$$\begin{aligned}&{{\left( \frac{\mathrm {d}\lambda }{\mathrm {d}w}\right) }^{-1}}\nonumber \\&=\frac{[(m+1)+3nx_{0}^{2}][3{{\lambda }^{2}}+2\lambda (1+\alpha +\eta )+\beta +\eta ]}{-6nx_{0}^{2}({{\lambda }^{2}}+\lambda +\beta )}.\nonumber \\ \end{aligned}$$
(9)

Substituting \(\lambda =i\omega _{0}\) into eq. (9), separating the real part, and we have

$$\begin{aligned} \mathrm {Re}\left( \frac{\mathrm {d}\lambda }{\mathrm {d}w }\right) ^{-1}&= \mathrm {Re}\frac{[(m+1)+3nx_{0}^{2}][3{{(i{{\omega }_{0}})}^{2}}+2i{{\omega }_{0}}(1+\alpha +\eta )+\beta +\eta ]}{-6nx_{0}^{2}({{(i{{\omega }_{0}})}^{2}}+i{{\omega }_{0}}+\beta )} \\&=\frac{[(m+1)+3nx_{0}^{2}][3\omega _{0}^{4}+(2+2\alpha -4\beta +\eta )\omega _{0}^{2}+\beta (\beta +\eta )]}{-6nx_{0}^{2}[\omega _{0}^{4}+(1-2\beta )\omega _{0}^{2}+{{\beta }^{2}}]}. \end{aligned}$$

\(\left\{ {\mathrm {d}({\text {Re}}\lambda )}/{\mathrm {d}w} \right\} {{|}_{\lambda =i{{\omega }_{0}}}}\) and \( \{ {{\text {Re}}}{{({\mathrm {d}\lambda }/{\mathrm {d}w})}^{-1}} \}{{|}_{\lambda = i{{\omega }_{0}}}}\) have identical signs, implying that

$$\begin{aligned}&\mathrm {sign}\left\{ \frac{\mathrm {d}({\text {Re}}\lambda )}{\mathrm {d}w} \right\} {{\bigg |}_{\lambda =i{{\omega }_{0}}}}\\&=\mathrm {sign}\left\{ {\text {Re}}{{\left( \frac{\mathrm {d}\lambda }{\mathrm {d}w}\right) }^{-1}} \right\} {{\bigg |}_{\lambda =i{{\omega }_{0}}}} =\frac{[(m+1)+3nx_{0}^{2}][3\omega _{0}^{4}+(2+2\alpha -4\beta +\eta )\omega _{0}^{2}+\beta (\beta +\eta )]}{-6nx_{0}^{2}[\omega _{0}^{4}+(1-2\beta )\omega _{0}^{2}+{{\beta }^{2}}]}. \end{aligned}$$

Thus, the transversality condition

$$\begin{aligned} \left\{ \frac{\mathrm {d}({\text {Re}}\lambda )}{\mathrm {d}w} \right\} {{\bigg |}_{\lambda =i{{\omega }_{0}}}}\ne 0 \end{aligned}$$

if the following condition is satisfied:

$$\begin{aligned}&{[}(m+1)+3nx_{0}^{2}][3\omega _{0}^{4}+(2+2\alpha -4\beta +\eta )\omega _{0}^{2}\\&\quad +\beta (\beta +\eta )]\ne 0. \end{aligned}$$

After setting the parameters, it can be determined.

Therefore, the HB appears, resulting in the instability of the equilibrium point to limit cycle, and the related frequency

$$\begin{aligned} {{\Omega }_{\mathrm {H}}}=\sqrt{\beta +\eta }. \end{aligned}$$
(10)

3.2 Non-smooth bifurcation analysis on the boundary

When the trajectory touches the boundary \(\Sigma \), unconventional bifurcation may occur. As system (1) is of Filippov-type, we can use differential inclusions theory [28] and introduce the auxiliary parameter q restricted in the continuously closed interval [0,1], then system (1) can be further expressed by

$$\begin{aligned} A:=\left\{ \begin{aligned}&A_{-} ,&q=0, \\&q{{A}_{+}}+(1-q){{A}_{-}} ,&0<q<1,\\&A_{-} ,&q=1. \end{aligned} \right. \end{aligned}$$
(11)

When the trajectory is situated in the region \(D_{-}\), \(q\,{=}\,0\), while its dynamic evolution entirely depends on the smooth subsystem \(A_{-}\). When the trajectory is situated in the region \(D_{+}\), \(q=1\), while its dynamic evolution entirely hinges on the smooth subsystem \(A_{+}\). When \(0<q<1\), by simple calculation, the auxiliary parameter q is shown as

$$\begin{aligned} q=\frac{-\alpha {{y}_{s}}-{{w}_{s}}+\delta }{2\delta }, \end{aligned}$$
(12)

where \(y_{s}\) and \(w_{s}\) are values of state variable y and the slow-changing parameter w when the trajectory begins to touch the non-smooth boundary \(\Sigma \).

Meanwhile, the sliding region can be calculated as

$$\begin{aligned} {{\Sigma }_{s}}:=\bigg \{(y,z)\left| y=\frac{-w-(2q-1)\delta }{\alpha } \right. \bigg \},\quad q\in (0,1). \end{aligned}$$

Additionally, the boundaries of the sliding motion are

$$\begin{aligned} \partial {{\Sigma }_{s+}}:=\bigg \{(y,z)\left| y=\frac{-w-\delta }{\alpha } \right. \bigg \},\quad q=1 \end{aligned}$$

and

$$\begin{aligned} \partial {{\Sigma }_{s-}}:=\bigg \{(y,z)\left| y=\frac{-w+\delta }{\alpha } \right. \bigg \},\quad q=0. \end{aligned}$$

The following definitions [29] of the corresponding equilibrium of Filippov-type system (1) are given which are essential in this work.

DEFINITION 3.1

A point X is defined as in pseudo-equilibrium if it is an equilibrium of the sliding motion for system (1), i.e.,

$$\begin{aligned} q{{A}_{+}}(X,w)+(1-q){{A}_{-}}(X,w)=0,\ H(X,w)=0 \end{aligned}$$

and

$$\begin{aligned} 0<q<1. \end{aligned}$$

DEFINITION 3.2

A point X is known as a boundary-equilibrium point if

$$\begin{aligned} {{A}_{+}}(X,w)=0\quad \hbox {or}\quad {{A}_{-}}(X,w)=0 \end{aligned}$$

and

$$\begin{aligned} H(X,w)=0. \end{aligned}$$

Then, two special types equilibrium points can be obtained, one is restricted in the sliding region, i.e., pseudo-equilibrium point, expressed by

$$\begin{aligned} {{E}_{s0}}:=\{(0,0,0)| q\in (0,1),\ -\left| \delta \right|<w<\left| \delta \right| \}, \end{aligned}$$

while the other is situated on the boundary of the sliding region \(\partial {{E}_{s\pm }}\), i.e., the boundary equilibrium points, shown as

$$\begin{aligned}&{{E}_{s+}}:=\{(0,0,0)|q=1,\ w=\left| \delta \right| \},\\&{{E}_{s-}}:=\{(0,0,0)|q=0,\ w=-\left| \delta \right| \}. \end{aligned}$$

By choosing w as the bifurcation parameter, system (1) may undergo boundary equilibrium bifurcation at \(w=w^{*}\), if there is a point \(X=X^{*}\) located in the smooth region \(D_{+}\) such that

  1. (1)

    \({{A}_{+}}({{X}^{*}},{{w}^{*}})=0\), but \({{A}_{-}}({{X}^{*}},{{w}^{*}})=0\);

  2. (2)

    \(H({{X}^{*}},{{w}^{*}})=0\);

  3. (3)

    A non-degeneracy condition which guarantees that X is an isolated equilibrium to vector field \(A_{+}\):

    \(\det ({{A}_{+,X}})=-\alpha \beta \ne 0;\)

  4. (4)

    The equilibrium branch to either of the smooth subsystem must border-collide with the non-smooth boundary at \(E_{s\pm }\), i.e., transversality condition:

    $$\begin{aligned}&{{H}_{w}}({{X}^{*}},{{w}^{*}})-{{H}_{X}}({{X}^{*}},{{w}^{*}})A_{+,X}^{-1}({{X}^{*}},{{w}^{*}})\\&\quad {{A}_{+,w}}({{X}^{*}},{{w}^{*}}) =1/\alpha \ne 0, \end{aligned}$$

    where \( {{H}_{w}}({{X}^{*}},{{w}^{*}})\) represents the gradient of \( {H}({{X}^{*}},{{w}^{*}})\).

In order to obtain more details about the boundary equilibrium bifurcation, the boundary equilibrium points will be discussed. Firstly, for a sufficiently small neighbourhood near the boundary equilibrium point \(E_{s+},\) let X also be an equilibrium point located in the smooth region \(D_{+}\). Then

$$\begin{aligned} {{A}_{+}}(X,w)=0,\quad H(X,w):={{h}_{1}}>0. \end{aligned}$$
(13)

Let \(X_{s}\) be a pseudo-equilibrium point to system (1), which means

$$\begin{aligned}&{{A}_{+}}({{X}_{s}},w)+(q-1)({{A}_{+}}-{{A}_{-}})=0,\ \nonumber \\&0<q<1,\quad H({{X}_{s}},w):=0. \end{aligned}$$
(14)

Linearising eqs (13) and (14) at \(E_{s+}\), we obtain

$$\begin{aligned}&{{A}_{+,X}}X+{{A}_{+,w}}(w-\left| \delta \right| )=0,\nonumber \\&{{H}_{X}}X+{{H}_{w}}(w-\left| \delta \right| )={{h}_{1}}>0 \end{aligned}$$
(15)

and

$$\begin{aligned}&{{A}_{+,X}}{{X}_{s}}+{{A}_{+,w}}(w-\left| \delta \right| )+(q-1)({{A}_{+}}-{{A}_{-}})=0,\nonumber \\&0<q<1, \qquad {{H}_{X}}{{X}_{s}}+{{H}_{w}}(w-\left| \delta \right| )=0. \end{aligned}$$
(16)

From eqs (15) and (16), we have

$$\begin{aligned}&{{h}_{1}}=({{H}_{w}}-{{H}_{X}}A_{+,X}^{-1}{{A}_{+,w}})(w-\left| \delta \right| ),\\&q-1=({{H}_{w}}-{{H}_{X}}A_{+,X}^{-1}{{A}_{+,w}})(w-\left| \delta \right| )/\nonumber \\&\quad ({{H}_{X}} A_{+,X}^{-1}({{A}_{+}}-{{A}_{-}})), \end{aligned}$$

or, equivalently

$$\begin{aligned} q-1={{h}_{1}}/({{H}_{X}}A_{+,X}^{-1}({{A}_{+}}-{{A}_{-}}))={{h}_{1}}/(-2\delta /\alpha ).\nonumber \\ \end{aligned}$$
(17)

Therefore, with the help of ref. [29] and using eq. (17), we can state the following theorem.

Theorem 3.1

For system (1), assuming \({{H}_{X}}A_{+,X}^{-1}({{A}_{+}}-{{A}_{-}})\,{=}\,-2\delta /\alpha \,{\ne }\, 0,\) persistence can be obtained at the boundary equilibrium bifurcation point when \(-2\delta /\alpha <0\). Instead, a non-smooth FB can be obtained if \(-2\delta /\alpha >0\).

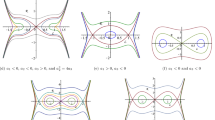
For example, for the parameters fixed at \( m\,{=}\,-1.25, n=0.25, F=3.0, \delta =-1.0\) and \(\beta =13.5\), figure 1 shows the typical equilibrium branches as well as the bifurcations of the two generalised autonomous subsystems and non-smooth boundary as the change about the parameter w. The solid lines denote the stable equilibrium branches, and the red dotted lines correspond to the unstable equilibrium branches.

Fig. 1
figure 1

Equilibrium branches and the related bifurcations of the two generalised autonomous subsystems and non-smooth boundary: (a) \(\alpha =3.0\) and (b) \(\alpha =7.0\).

Full size image

As shown in figure 1, EB\(i (i\,{=}\,1,2)\) represent the typical equilibrium branches of the two subsystems \(A_{\pm }\), while \(\Sigma \) denotes the non-smooth boundary. The EB\(i(i\,{=}\,1,2)\) exist practically, while black dotted lines exist theoretically in accordance with the related subsystems’ conditions. They cannot be actually obtained because of the non-smooth boundary. We calculate the corresponding conventional bifurcation and non-smooth bifurcation points by the theoretical analysis above. We can observe the FB \(\hbox {LP}1,2(w,x)=(\mp 0.7113,\ \mp 0.5774)\) and non-smooth FB points \(\hbox {A}3,6(w,\, x)\,{=}\,(\pm 1,\ 0)\) on the boundary \(\Sigma \) in figure 1a, and FB \(\hbox {LP}1,2(w,x)=(\mp 0.3264,\ \mp 0.5774)\), supercritical HB points \(\hbox {H}1,2(w,x)\,{=}\,(\mp 0.4610,\ \mp 0.7769)\), subcritical HB points \(\hbox {SH}1,2(w,x)=(\mp 1.3958, \mp 1.0981)\) as well as non-smooth FB points \(\hbox {A}3,6(w,x)=(\pm 1,0)\) in figure 1b. As \(\alpha \) increases, the dynamical behaviours of system (1) may change.

4 Bursting phenomena

As two scales are involved in the system, diverse forms of mixed-mode oscillations may appear. For discussing the mechanism of dynamical behaviours, we provide here the concept of transformed phase portrait.

The traditional phase portraits of a dynamical system can be acquired on the phase space of state variables. For example, the portrait on the plane (x, y, z) indicates the relationship between different state variables with the variation of time t. To describe the relationship between state variables and the slow-varying parameter w, we give the transformed phase portrait, denoted by \( {{\Pi }_{T}} \,{:}\, \{[x(t),y(t),z(t),w(t)],\ t\,{\in }\, R\}\) with \(w(t)\,{=}\,F\cos (\Omega t)\), to study the effect of bifurcations in the wake of the change of the slow-varying parameter on the dynamical behaviours of the system.

In this section, we take \(\alpha \) as a regulating parameter, exploring the evolution laws of dynamical behaviours for the system about \(\alpha \) with different values. Two representative cases will be analysed in the following sections.

4.1 Symmetric point-point type fold / fold-sliding bursting

Now, we choose \(\alpha =3.0\). The phase portraits on the (x, y), (x, y, z) planes and the time history diagram about the state variable y are presented in figure 2. The red arrows on the trajectory express the direction of the flow.

Fig. 2
figure 2

Movement for \(\alpha =3.0\). (a) Phase portrait on the (x, y) plane, (b) time history and (c) phase portrait on the (x, y, z) plane.

Full size image

To consider the mechanism of the mixed-mode oscillations, the superposition of the associated bifurcation figure (see figure 1a) and the transformed phase portrait is plotted in figure 3b.

Fig. 3
figure 3

(a) Transformed phase portrait of system (1) on the (w, x) plane and (b) superposition of the bifurcation figure and the transformed phase portrait.

Full size image

Remarks

Red arrows on the trajectory show the direction of the flow, and the lines and dots are shown as in §3.2.

As shown in figure 3b, without loss of generality, we assume that the trajectory starts at the point A1 with minimum value of w, i.e., \(w=-3.0\). The movement of trajectory is governed by the subsystem \(A_{-}\), and so the trajectory moves nearly along the stable equilibrium branch EB1 with the increase of time t, signifying that the system stays in the quiescent state (QS). Till the value of external excitation increases through the FB point LP1\((w,x)=(-{0}{.7113, -0.5774})\), jumping phenomenon appears, leading to a fast transition towards the upper branch in an S-shaped curve.

When the trajectory arrives at A2\(({{w}_{2}},{{x}_{2}})\,{=}\,(-0.1 207,0)\) on the boundary \(\Sigma \), shown in figure 3b, corresponding to the point \({\mathrm{A}_{s2}}({{x}_{s2}},{{y}_{s2}})=(0,0.0380)\), the transition is finished. According to eq. (12), we obtain \(q\,{=}\,(-{{y}_{s2}}-{{w}_{2}}+\delta )/2\delta \,{\approx }\, 0.4966\,{\in }\, (0,1)\), implying that the trajectory may tend to pseudo-equilibrium and show sliding motion on the boundary, and indicating the QS for the system. When it reaches the boundary equilibrium point \( {\mathrm{A}{3}}({{w}_{3}},{{x}_{3}})=(1,0)\), and the corresponding point \( {\mathrm{A}_{s3}}({{x}_{s3}},{{y}_{s3}})\,{=}\,(0,0)\) is obtained, the parameter q may pass through the maximum value of the interval [0, 1] as there is a further increase in the slow-varying parameter w. At the same time, non-smooth FB A3 occurs as per Theorem 3.1, so that the trajectory deviates from boundary \(\Sigma \) to enter into the smooth region \(D_{+}\), as there exists a stable equilibrium branch \(\hbox {EB}2\) in \(D_{+}\).

After that, the behaviours of the system are governed by subsystem \(A_{+}\), the trajectory jumps to the stable attractor which is laid on \(\hbox {EB}2\). With the evolution of time, the amplitude of the oscillation gradually decreases, and then the trajectory tends to the stable branch \(\hbox {EB}2\). The trajectory moves almost strict along \(\hbox {EB}2\), till it gets to the point \(\hbox {A}4\), implying that w arrives at its maximum value, i.e., \(w=3.0\). The first half period of the movement is completed.

According to the symmetry of system (1), the remaining evolution process of the trajectory \(\hbox {A}4\rightarrow \hbox {A}5\rightarrow \hbox {A}6\rightarrow \hbox {A}1\) is similar to the mechanism from \(\hbox {A}1\rightarrow \hbox {A}2\rightarrow \hbox {A}3\rightarrow \hbox {A}4\). When the trajectory goes back to the starting point A1 at last, then one period mixed-mode oscillation is finished.

It is noted that the bifurcation which involves the generation of limit cycle is not presented in the above analysis, which means that in this case these is no oscillation related to the cycle. Since the lower QS in region \(D_{-}\) switches to the upper QS in region \(D_{+}\) via FB, non-smooth FB and slide motion, the mixed-mode oscillations can be called symmetric point-point type fold / fold-sliding bursting.

4.2 Symmetric point-cycle-cycle type Hopf / Hopf / fold-sliding bursting

When we increase the parameter to \(\alpha \,{=}\,7.0\), the FB points, the HB points and non-smooth FB can be observed, corresponding to figure 1b. Figure 4 shows the phase portrait on the (x, y) plane and the corresponding time history of state variable y, respectively. The three-dimensional phase portrait on the (x, y, z) phase space is given also in figure 4c, for demonstrating the relationship between the x, y, z state variables. The red arrows on the trajectory indicates the direction of the flow.

By comparing with the case \(\alpha \,{=}\,3.0\), the distinct difference about the structure of bursting oscillation is found.

Fig. 4
figure 4

Movement for \(\alpha =7.0\). (a) Phase portrait on the (x, y) plane, (b) time history and (c) phase portrait on the (x, y, z) plane.

Full size image

To reveal the mechanism of the periodic mixed-mode oscillations, the superposition of the transformed phase portrait and the bifurcation figure (see figure 1b) is described in one period, in figure 5b.

Fig. 5
figure 5

(a) Transformed phase portrait of system (1) on the (w, x) plane and (b) superposition of the bifurcation figure and the transformed phase portrait.

Full size image

Remarks

Red arrows indicate the direction of the flow, the green solid dots denote the stable limit cycle, which is labelled by \(\hbox {LC}_{s}^{\pm }\) and caused by the supercritical HB. The green hollow dots represent unstable limit cycle, which is labelled by \(\hbox {LC}_{s}^{\pm }\) and caused by the subcritical HB. The \(\hbox {LPC}i~(i=1,2,3,4)\) can be interpreted as the FB points of limit cycles, the lines and other dots are as described in §3.2.

One revolution of the oscillation is represented in details and it can be noted that w is a slow-varying parameter in this paper. The trajectory starts from the point \(\hbox {A}1\) corresponding to the minimum value \(w\,{=}\,-3.0\). Thus, it is governed by the subsystem \(A_{-}\). As w increases, the trajectory turns to the right till it gets to the point \(\hbox {SH}1(w,x)\,{=}\,(-1.3958,-1.0981)\), subcritical HB occurs, leading to the equilibrium losing its stability. Owing to the slow passage effect [13, 30], the trajectory still moves along the equilibrium branch \(\hbox {EB}1\), until the trajectory arrives at the point \(\mathrm{H}1(w,x)=(-0.4610,-0.7769)\), supercritical HB can be found, and thus the stable limit cycle disappears, causing the branch EB1 to be stable which means the delay phenomenon is over.

With the value of w increasing to \({{w}_{\mathrm{{LP}}1}}=-0.3264\), FB appears, causing the trajectory to reach the point \(\hbox {A}2({{w}_{2}},{{x}_{2}})\,{=}\,(0.1357,0)\) which is located on the boundary via jumping phenomenon. The corresponding point \( {{\hbox {A}}_{s2}}({{x}_{s2}},{{y}_{s2}})\,{=}\,(0,-0.0209)\) is observed in figure 4. From eq. (12), we obtain the auxiliary parameter \(q=(-{{y}_{s2}}-{{w}_{2}}+\delta )/2\delta \approx 0.5365\in (0,1)\), which is located in the closed interval [0,1], signifying that the trajectory may tend to pseudo-equilibrium and keep on sliding on the non-smooth boundary \(\Sigma \) indicating that the trajectory may exist in the QS. When it arrives at the boundary equilibrium point \({{\hbox {A}}{3}}({{w}_{3}},{{x}_{3}})\,{=}\,(1,0)\), the corresponding point \( {{\hbox {A}}_{s3}}({{x}_{s3}},{{y}_{s3}})\,{=}\,(0,0)\) is derived. By calculation, the parameter \(q\,{=}\,1\), and the non-smooth FB A3 occurs, resulting in the trajectory deviating from the boundary \(\Sigma \) to enter into the region \(D_{+}\). This implies that the behaviours of the system are governed by subsystem \(A_{+}\).

Due to the existence of stable limit cycle \(\hbox {LC}_{s}^{+}\) caused by supercritical HB H2, the trajectory starts to converge to the stable limit cycle \(\hbox {LC}_{s}^{+}\), while before this process is done, the FB of limit cycles \(\hbox {LPC}1\) leads to the disappearance of \(\hbox {LC}_{s}^{+}\) , and so the trajectory has no choice but to converge to the stable branches EB2. When the trajectory gets to the point A4, at which w arrives at its maximum value \(w\,{=}\,3.0\), the first half period of the movement is finished.

Then, as t increases, the slow-varying parameter decreases, leading the trajectory to return to the other half period of the motion. Because of the symmetrical property of the system, here we omit the process in the second half period of the movement.

Comparing to the case \(\alpha \,{=}\,3.0\), the SP can be described with the parameter \(\alpha \,{=}\,7.0\). From the above analysis, the HB causes the alternation between QS and SP in the mixed-mode oscillations in figure 5b, while the FB and non-smooth FB connect the QS along the stable branches and it shows sliding motion on the boundary. Thus, this mixed-mode oscillation can be known as symmetric Hopf / Hopf / fold-silding bursting.

5 Conclusion

In this paper, we have studied the mixed-mode oscillations for the modified Chua’s system with two scales. When the excitation frequency is much less than the natural one of the system, the whole external excitation term can be considered as a slow-varying parameter, and by taking a suitable value for parameter \(\alpha \), two different types of bursting are obtained. By combining the transformed phase portraits and the corresponding bifurcation analysis, the mechanism of bursting oscillations can be derived. One type is the symmetric point-point type fold / fold-sliding bursting and the other is the symmetric point-cycle-cycle type Hopf / Hopf / fold-sliding bursting. As discussed already, two different QSs can be observed in this paper, one is the QS induced by the trajectory almost moving along with the stable equilibrium branches and the other is the QS caused by the trajectory showing sliding movement on the boundary.

In addition, the non-smooth factor for a voltage-based steering switch is considered in this paper. By analysing the unconventional bifurcation when the trajectory touches the non-smooth boundary, we find that the trajectory shows sliding movement on the boundary and non-smooth FB at the boundary equilibrium occurs. The numerical results are consistent with theoretical analysis. If the system is a Filippov-type system possessing two or more parallel non-smooth boundaries, what will be the dynamical behaviour of the system? We shall leave it for the future.