1 Introduction

Heat transfer plays a key role in physics and engineering problems. Highest heat transfer rate can improve the efficiency of many processes in electronic cooling and heat exchangers. The commonly used base fluids are oil, water and ethylene glycol mixture, which have very low thermal conductivity and, therefore, known as poor heat transfer fluids. On the other hand, many solids, particularly, metals have higher thermal conductivities compared to base fluids. For the enhancement of thermal conductivity of base fluids, nanosized solid particles with sizes up to 100 nm are suspended in the base fluids and the resulting mixture is known as the nanofluid. The term nanofluid was introduced by Choi [1]. Buongiorno [2] was the first one to study comprehensively the convective transport in nanofluids and considered seven mechanisms such as inertia, thermophoresis, Brownian diffusion, gravity settling, fluid draining, diffusiophoresis and Magnus effect [3]. He observed that the absolute velocity of the nanoparticle can be considered as the sum of the velocity of the base fluid and a relative velocity. Among these mechanisms, he found that only two mechanisms were very important, namely, Brownian diffusion and thermophoresis. Detailed studies on nanofluids have been done by Daungthongsuk and Wongwises [4] and Wang and Mujumdar [5, 6]. Mustafa et al [7] investigated the boundary layer stagnation point flow of an incompressible nanofluid towards a stretching sheet. Kameswaran et al [8] computed the dual solutions of the stagnation point flow of a nanofluid towards a stretching surface. Bachok et al [9] investigated the boundary layer stagnation point flow of a nanofluid towards a stretching / shrinking sheet and calculated a dual solution up to a certain value of the velocity ratio parameter. Mansur et al [10] considered the stagnation point flow of a nanofluid towards a stretching / shrinking sheet and used Buongiorno’s model. They found that the skin friction coefficient decreases due to the stretching of the sheet but increases by increasing the suction parameter. Pal et al [11] investigated the buoyancy effects on the stagnation point flow of nanofluids towards a stretching / shrinking sheet in a porous medium in the presence of internal heat generation / absorption. Abbas et al [12] considered the hydromagnetic stagnation point flow of a viscous fluid over a stretching / shrinking sheet in the presence of homogeneous / heterogeneous reactions with slip condition. Pal and Mandal [13] analysed buoyancy effects on the stagnation point flow of nanofluids towards a stretching / shrinking sheet in a porous medium by considering heat generation, viscous dissipation and radiation effects. Naramgari and Sulochana [14] investigated magnetohydrodynamics (MHD) effects on the boundary layer flow of nanofluid towards a permeable stretching / shrinking sheet with suction and injection. They found that nanoparticle concentration decreases and mass transfer rate increases due to the enhancement in Brownian motion and thermophoresis. Mustafa et al [15] considered three different magnetic nanoparticles in the study of stagnation point flow over a stretchable rotating disk in the presence of an external applied magnetic field. Nandy and Pop [16] investigated the two-dimensional MHD stagnation point flow of a nanofluid towards a shrinking sheet in the presence of thermal radiation. Studies on nanofluid flow towards a nonlinear stretching / shrinking sheet have been made by many researchers [17,18,19,20,21,22,23,24,25,26,27,28,29].

Boundary conditions play a vital role in material processing technologies and significantly modify the characteristics of manufactured products. In the above studies, two types of boundary conditions were considered, namely, prescribed surface heat flux (PHF) and prescribed surface temperature (PST). There is another type of boundary condition called Newtonian heating which is also known as conjugate convective flow [30] in which, heat is transported to the convective fluid passing through a boundary surface having finite heat capacity. Newtonian heating occurs in different engineering devices such as heat exchangers in which the conduction in the solid wall is affected by the convection in the fluid [31]. Salleh et al [32] studied the effect of Newtonian heating on the laminar boundary layer flow over a stretching sheet. They found numerical solutions to the problem of using the finite difference scheme along with two cases ‘constant wall temperature (CWT)’ and ‘constant heat flux (CHF)’. Mohamed et al [33] investigated the boundary layer stagnation point flow of an incompressible fluid towards a stretching sheet with Newtonian heating. A number of studies with Newtonian and convective boundary conditions have been considered by many researchers [34,35,36,37,38,39,40,41,42,43].

The aim of this study is to investigate the effect of Newtonian heating on the stagnation point flow over a nonlinear permeable stretching / shrinking sheet in a nanofluid. The governing partial differential equations of this analysis are converted into nonlinear ordinary differential equations by using suitable similarity transformation and the solution is obtained numerically by using the spectral collocation method. The effects of pertinent parameters on temperature and concentration profiles, skin friction coefficient, local Nusselt number and local Sherwood number are discussed and shown graphically. The dual solutions are reported for specific values of suction parameter in a certain range of the velocity ratio parameter.

Fig. 1
figure 1

Schematic diagram near the stagnation region.

Full size image

2 Formulation of the flow problem

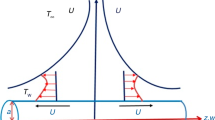
A steady boundary layer flow in the region of the stagnation point of a viscous incompressible nanofluid towards a nonlinear stretching / shrinking horizontal permeable sheet is discussed. The sheet is stretched or shrunk nonlinearly along the x-axis, keeping O fixed as the stagnation point and the y-axis is perpendicular to the sheet as shown in figure 1. The nonlinear stretching / shrinking velocity and the straining velocity in potential flow are assumed as \(u_{\mathrm{w}}(x) = cx^{m}\) and \(u_{\mathrm{e}}(x) = {ax}^{m}\), respectively, where a is a positive constant and c is the constant in wall velocity, which is considered less than zero (\(c < 0\)) in the shrinking case and greater than zero (\(c > 0\)) in the stretching case. Using the mathematical model reported by Buongiorno [2], the governing equations of the problem under the boundary layer approximation can be written in the simplified form as (see Rana and Bhargava [18])

$$\begin{aligned}& \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, \end{aligned}$$
(1)
$$\begin{aligned}& u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=u_\text {e} (x)\frac{\hbox {d}u_\text {e} (x)}{\hbox {d}x}+\nu \frac{\partial ^{2}u}{\partial y^{2}}, \end{aligned}$$
(2)
$$\begin{aligned}& u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \frac{\partial ^{2}T}{\partial y^{2}}+\tau \left[ D_\text {B} \frac{\partial C}{\partial y}\frac{\partial T}{\partial y} \right. \nonumber \\&\, \left. +\frac{D_\text {T} }{T_\infty }\left( {\frac{\partial T}{\partial y}} \right) ^{2} \right] , \end{aligned}$$
(3)
$$\begin{aligned}& u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_\text {B} \frac{\partial ^{2}C}{\partial y^{2}}+\frac{D_\text {T} }{T_\infty }\frac{\partial ^{2}T}{\partial y^{2}}, \end{aligned}$$
(4)

with boundary conditions

$$\begin{aligned}&u=u_\text {w} (x)=cx^{m},\quad v=v_\text {w} (x),\quad -k\frac{\partial T}{\partial y}=h_s T, \nonumber \\&C=C_\text {w} \quad \hbox {at}\quad y=0, \nonumber \\&u = u_\text {e} (x)=ax^{m},\quad T\rightarrow T_\infty ,\quad \nonumber \\&C\rightarrow C_\infty \;\hbox {as}\quad y\rightarrow \infty . \end{aligned}$$
(5)

The components of velocity along and normal to the surface are u and v, respectively, and T is the temperature, C is the concentration of the nanoparticle, \(\nu \) is the kinematic viscosity, \(\alpha \) is the thermal diffusivity, \(\tau ={(\rho c_{p} )_\text {p}}/{(\rho c_{p} )}_{\text {f}}\), where \((\rho c_{p} )_\text {p}\) and \({(\rho c_{p} )}_{\text {f}}\) are the heat capacity of the nanoparticle and base fluid, \(D_{\mathrm{B}}\) and \(D_{\mathrm{T}}\) are the Brownian and thermophoretic diffusion coefficients, \(T_{\infty }\) is the ambient temperature of the fluid, \(v_{\mathrm{w}}\) is the suction / injection velocity at the wall along the y-axis which exhibits suction when \(v_{\mathrm{w}} < 0\) or injection when \(v_{\mathrm{w}} > 0\), \(h_{s}\) is the heat transfer coefficient, \(m \ne 1\) is a nonlinear parameter, \(C_{\mathrm{w}}\) and \(C_{\infty }\) are the nanoparticle concentrations at the wall and far away from the wall. Now, introduce the following similarity transformation (see Rana and Bhargava [18]), which converts the governing partial differential equations into ordinary differential equations:

$$\begin{aligned} u= & {} ax^{m}{f}'(\eta ), \nonumber \\ v= & {} -\sqrt{\frac{a\nu (m+1)}{2}}x^{{(m-1)}/2}\left[ {f(\eta )+\frac{m-1}{m+1}\eta {f}'(\eta )} \right] , \nonumber \\ \eta= & {} y\sqrt{\frac{a(m+1)}{2\nu }}x^{{(m-1)}/2}, \nonumber \\ \theta= & {} \frac{T-T_\infty }{T_\infty },\quad \varphi =\frac{C-C_\infty }{C_\text {w} -C_\infty }. \end{aligned}$$
(6)

The differentiation with respect to \(\eta \) is denoted by prime. For similarity solution of the governing equations, a suction or injection velocity \(v_{\mathrm{w}}\) is assumed as (see Zaimi et al [19])

$$\begin{aligned} v_\text {w} =-\sqrt{\frac{a\nu (m+1)}{2}}x^{(m-1)/2}\gamma , \end{aligned}$$

where \(\gamma \) is a constant which stands for suction when \(\gamma \) is greater than zero, i.e. (\(\gamma > 0\)) and injection when \(\gamma \) is less than zero, i.e. (\(\gamma < 0\)). Using similarity transformation (6) into eqs (2)–(4), the dimensionless form of the ordinary differential equations are obtained as

$$\begin{aligned}& {f}'''+f{f}''+\frac{2m}{m+1}(1-{f}'^{2})=0, \end{aligned}$$
(7)
$$\begin{aligned}& {\theta }''+\Pr (f{\theta }'+N{b}\, {\theta }'{\varphi }'+N{t} {\theta }'^{2})=0, \end{aligned}$$
(8)
$$\begin{aligned}& {\varphi }''+\hbox {Sc}f{\varphi }'+\frac{N{t} }{N{b} }{\theta }''=0. \end{aligned}$$
(9)

Boundary conditions (5) reduce to

$$\begin{aligned}& f(0)=\gamma ,\quad {f}'(0)=\frac{c}{a},\quad \nonumber \\& {\theta }'(0)=-\gamma _s (1+\theta (0)),\quad \varphi (0)=1, \nonumber \\& {f}'(\infty )=1,\quad \theta (\infty )=0,\quad \varphi (\infty )=0, \end{aligned}$$
(10)

where the Prandtl number \(\Pr =\nu /\alpha _{,}\) Schmidt number \(\hbox {Sc}=\nu /D_\text {B}\), Brownian and thermophoresis parameters are \(N{b} =\tau D_\text {B} (C_\text {w} -C_\infty )/\nu \) and \(N{t} =\tau D_\text {T} /\nu \) respectively, the conjugate parameter for Newtonian heating is \(\gamma _s =h_s \sqrt{2\nu /a(m+1)}x^{(1-m)/2}\) and the ratio of the constant of the stretching / shrinking velocity with the straining velocity is c / a which corresponds to stretching when \(c/a > 0\) and shrinking when \(c/a < 0\). The relations of the skin friction coefficient, local Nusselt and Sherwood numbers are shown as

$$\begin{aligned}&C_{f} =\frac{\tau _\text {w} }{\rho u_\text {e}^2 },\quad \hbox {Nu}_x =\frac{xq_\text {w} }{k(T_\text {w} -T_\infty )},\;\nonumber \\&\hbox {Sh}_x=\frac{xq_\text {m} }{D_\text {B} (C_\text {w} -C_\infty )}, \end{aligned}$$
(11)

where \(\tau _\text {w} \) is the shear stress at the wall, \(q_\text {w} \) and \(q_\text {m} \) are the heat and mass fluxes from the wall, respectively, which are written as

$$\begin{aligned}& \tau _\text {w} =\mu \left( {\frac{\partial u}{\partial y}} \right) _{y=0} ,\quad q_\text {w} =-k\left( {\frac{\partial T}{\partial y}} \right) _{y=0} , \nonumber \\& q_\text {m} =-D_\text {B} \left( {\frac{\partial C}{\partial y}} \right) _{y=0} . \end{aligned}$$
(12)

Substituting eq. (12) into eq. (11), the skin friction coefficient, local Nusselt number and local Sherwood number take the new form as follows:

$$\begin{aligned}& C_{f}\hbox {Re}_x^{1/2} =\sqrt{\frac{m+1}{2}}{f}''(0),\\& \hbox {Nu}_{x}\hbox {Re}_x^{-1/2} =-\sqrt{\frac{m+1}{2}}\frac{{\theta }'(0)}{\theta (0)}, \\& \hbox {Sh}_{x}\hbox {Re}_x^{-1/2} =-\sqrt{\frac{m+1}{2}}{\varphi }'(0). \end{aligned}$$

3 Flow stability

In the present study, dual solutions are found against the velocity ratio parameter, namely, c / a for the shrinking sheet case. In these solutions, one solution is physically realisable, i.e. stable and second solution is unstable. To check which solution is physically realisable, Weidman et al [44], Najib et al [45], Rosca and Pop [46], Postelnicu and Pop [47], Awaludin et al [48], Ismail et al [49] and Fauzi et al [50] performed stability analysis. Before examining the analysis first, the governing eqs (2)–(4) are converted into an unsteady problem by introducing the time variable in dimensionless form as \(\tau =ax^{m-1}t\) and the dimensionless functions \(f(\eta ),\theta (\eta )\;\hbox {and}\;\varphi (\eta )\) are replaced by \(f(\eta ,\tau ),\theta (\eta ,\tau )\;\hbox {and}\;\varphi (\eta ,\tau )\). The resulting governing equations for the unsteady flow are given as

$$\begin{aligned}& \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=u_\text {e} (x)\frac{\hbox {d}u_\text {e} (x)}{\hbox {d}x}+\nu \frac{\partial ^{2}u}{\partial y^{2}}, \end{aligned}$$
(13)
$$\begin{aligned}& \frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \frac{\partial ^{2}T}{\partial y^{2}}+\tau \left[ D_\text {B} \frac{\partial C}{\partial y}\frac{\partial T}{\partial y}\right. \nonumber \\& \left. \quad \,\, +\frac{D_\text {T} }{T_\infty }\left( {\frac{\partial T}{\partial y}} \right) ^{2} \right] , \end{aligned}$$
(14)
$$\begin{aligned}& \frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_\text {B} \frac{\partial ^{2}C}{\partial y^{2}}+\frac{D_\text {T} }{T_\infty }\frac{\partial ^{2}T}{\partial y^{2}}. \end{aligned}$$
(15)

Using the time variable, the similarity transformation given in eq. (6) takes a new form and is written as

$$\begin{aligned} u= & {} ax^{m}\frac{\partial f}{\partial \eta } \nonumber \\ v= & {} -\sqrt{\frac{a\nu (m+1)}{2}}\left[ {f+\frac{m-1}{m+1}\eta \frac{\partial f}{\partial \eta }} \right] x^{{(m-1)}/2}, \nonumber \\ \eta= & {} y\sqrt{\frac{a(m+1)}{2\nu }}x^{{(m-1)}/2}, \nonumber \\ \theta= & {} \frac{T-T_\infty }{T_\infty },\quad \varphi =\frac{C-C_\infty }{C_\text {w} -C_\infty },\quad \tau =ax^{m-1}t. \end{aligned}$$
(16)

Governing eqs (13)–(15) are written in the dimensionless form after using the transformation given in eq. (16), and we have

$$\begin{aligned}& \frac{\partial ^{3}f}{\partial \eta ^{3}}+f\frac{\partial ^{2}f}{\partial \eta ^{2}}+\frac{2m}{m+1}\left( {1-\left( {\frac{\partial f}{\partial \eta }} \right) ^{2}} \right) \nonumber \\&\quad -\frac{2}{m+1}\frac{\partial ^{2}f}{\partial \eta ~\partial \tau }\left( {1+\left( {m-1} \right) \tau \frac{\partial f}{\partial \eta }} \right) =0, \end{aligned}$$
(17)
$$\begin{aligned}& \frac{\partial ^{2}\theta }{\partial \eta ^{2}}+\Pr \left( {f\frac{\partial \theta }{\partial \eta }+N{b} \frac{\partial \theta }{\partial \eta } \frac{\partial \varphi }{\partial \eta }+N{t} \left( {\frac{\partial \theta }{\partial \eta }} \right) ^{2}} \right) \nonumber \\&\quad -\frac{2\Pr }{m+1}\frac{\partial \theta }{\partial \tau }\left( {1+\left( {m-1} \right) \tau \frac{\partial f}{\partial \eta }} \right) =0, \end{aligned}$$
(18)
$$\begin{aligned}& \frac{\partial ^{2}\varphi }{\partial \eta ^{2}}+\hbox {Sc}f\frac{\partial \varphi }{\partial \eta }-\frac{2\hbox {Sc}}{m+1}\frac{\partial \varphi }{\partial \tau }\left( {1+\left( {m-1} \right) \tau \frac{\partial f}{\partial \eta }} \right) \nonumber \\&\quad +\frac{N{t} }{N{b} }\frac{\partial ^{2}\theta }{\partial \eta ^{2}}=0. \end{aligned}$$
(19)

The boundary condition given in eq. (5) takes the following form:

$$\begin{aligned}& f(0,\tau )=\gamma ,\quad \frac{\partial f}{\partial \eta }(0,\tau )=\frac{c}{a}, \nonumber \\& \frac{\partial \theta }{\partial \eta }(0,\tau )=-\gamma _s \left( {1+\theta (0,\tau )} \right) , \nonumber \\& \varphi (0,\tau )=1,\quad \frac{\partial f}{\partial \eta }(\infty ,\tau )=1,\nonumber \\& \theta (\infty ,\tau )=0,\quad \varphi (\infty ,\tau )=0. \end{aligned}$$
(20)

To perform the stability analysis for the solution \(f=f_0 (\eta ),\theta =\theta _0 (\eta )\;\hbox {and}\;\varphi =\varphi _0 (\eta )\) which represents the steady solution and satisfying the BVP given in eqs (7)–(9), we write the functions \(f(\eta ,\tau ),\theta (\eta ,\tau ) \hbox { and } \varphi (\eta ,\tau )\) in the following form (see Weidman et al [44], Najib et al [45] and Rosca and Pop [46]):

$$\begin{aligned} f(\eta ,\tau )= & {} f_0 \left( \eta \right) +\hbox {e}^{-\gamma \tau }F(\eta ,\tau ), \nonumber \\ \theta (\eta ,\tau )= & {} \theta _0 \left( \eta \right) +\hbox {e}^{-\gamma \tau }H(\eta ,\tau ), \nonumber \\ \varphi (\eta ,\tau )= & {} \varphi _0 \left( \eta \right) +\hbox {e}^{-\gamma \tau }P(\eta ,\tau ). \end{aligned}$$
(21)

In eq. (21), the functions \(f(\eta ,\tau ),\theta (\eta ,\tau )\;\hbox {and}\;\varphi (\eta ,\tau )\) are small, relative to \(f_0 (\eta ),\theta _0 (\eta )\;\hbox {and}\;\varphi _0 (\eta )\) and \( \gamma \) is an unknown eigenvalue. On substituting eq. (21) into eqs (17)–(19), the following linearised problems are obtained:

$$\begin{aligned}& \frac{\partial ^{3}F}{\partial \eta ^{3}}+f_0 \frac{\partial ^{2}F}{\partial \eta ^{2}}+{f}''_0 F \nonumber \\&\quad +\frac{2}{m+1}\frac{\partial F}{\partial \eta }\left[ {\left( {1+\left( {m-1} \right) \tau {f}'_0 } \right) \gamma -2m{f}'_0 } \right] \nonumber \\&\quad -\frac{2}{m+1}\frac{\partial ^{2}F}{\partial \eta \partial \tau }\left( {1+\left( {m-1} \right) \tau {f}'_0 } \right) =0, \end{aligned}$$
(22)
$$\begin{aligned}& \frac{\partial ^{2}H}{\partial \eta ^{2}}+\Pr \left[ {f_0 \frac{\partial H}{\partial \eta }+F{\theta }'_0 +N{b} \left( {{\theta }'_0 \frac{\partial P}{\partial \eta }+{\varphi }'_0 \frac{\partial H}{\partial \eta }} \right) } \right. \nonumber \\&\left. {\quad +N{t} \left( {2{\theta }'_0 \frac{\partial H}{\partial \eta }} \right) } \right] +\frac{2\Pr }{m+1}(1+(m-1)\tau {f}'_0 )\gamma H \nonumber \\&\quad -\frac{2\Pr }{m+1}(1+(m-1)\tau {f}'_0 )\frac{\partial H}{\partial \tau }=0, \end{aligned}$$
(23)
$$\begin{aligned}& \frac{\partial ^{2}P}{\partial \eta ^{2}}+\hbox {Sc}\left( {f_0 \frac{\partial P}{\partial \eta }+F{\varphi }'_0 } \right) \nonumber \\&\quad +\frac{2\hbox {Sc}}{m+1}(1+(m-1)\tau {f}'_0 )\gamma P \nonumber \\&\quad -\frac{2\hbox {Sc}}{m+1}\left( {1+\left( {m-1} \right) \tau {f}'_0 } \right) \frac{\partial P}{\partial \tau }+\frac{N{t} }{N{b} }\frac{\partial ^{2}H}{\partial \eta ^{2}}=0\nonumber \\ \end{aligned}$$
(24)

subject to the boundary conditions

$$\begin{aligned}& F(0,\tau )=0,\quad \frac{\partial F}{\partial \eta }(0,\tau )=0,\nonumber \\& \frac{\partial H}{\partial \eta }(0,\tau )=-\gamma _s H(0,\tau ),\quad P(0,\tau )=0, \nonumber \\& \frac{\partial F}{\partial \eta }(\infty ,\tau )=0,\quad H(\infty ,\tau )=0,\quad P(\infty ,\tau )=0.\nonumber \\ \end{aligned}$$
(25)

For the stability of the solutions, i.e. \(f_0 (\eta ), \theta _0 (\eta )\) and \(\varphi _0 (\eta )\) of the steady boundary value problem given in eqs (7)–(9), subject to the boundary conditions given in eq. (10), put \(\tau =0\) suggested by Weidman et al [44] and the solutions given in eqs (22)–(24), i.e. \(F=F_0 (\eta ),\;H=H_0 (\eta )\;\hbox {and}\;P=P_0 (\eta )\) cause the initial growth or decay of the solution given in eq. (21):

$$\begin{aligned} {F}'''_0&+f_0 {F}''_0 +{f}''_0 F_0 +\frac{2}{m+1}\left[ {\gamma -2m{f}'_0 } \right] {F}'_0 =0, \end{aligned}$$
(26)
$$\begin{aligned} {H}''_0&+\Pr \left[ f_0 {H}'_0 +F_0 {\theta }'_0 \right. \nonumber \\&+\left. Nb \left( {{\theta }'_0 {P}'_0 +{\varphi }'_0 {H}'_0 } \right) +Nt \left( {2{\theta }'_0 {H}'_0 } \right) \right] \nonumber \\&+\frac{2\Pr }{m+1}\gamma H_0 =0, \end{aligned}$$
(27)
$$\begin{aligned} {P}''_0&+\hbox {Sc}\left( {f_0 {P}'_0 +F_0 {\varphi }'_0 } \right) +\frac{2\hbox {Sc}}{m+1}\gamma P_0 +\frac{Nt}{Nb}{H}''_0 =0,\nonumber \\ \end{aligned}$$
(28)

and the boundary conditions given in eq. (25) take the following form:

$$\begin{aligned}& F_0 (0)=0,\;{F}'_0 (0)=0,\nonumber \\& {H}'_0 (0)=-\gamma _s H_0 (0),\;P_0 (0)=0, \nonumber \\& {F}'_0 (\infty )=0,\;H_0 (\infty )=0,\;P_0 (\infty )=0. \end{aligned}$$
(29)

To solve an eigenvalue problem given in eqs (26)–(28) subject to the boundary condition given in eq. (29), an infinite set of eigenvalues \(\gamma _1<\gamma _2 <\gamma _3 \cdots \) are obtained by adding an extra boundary condition \({F}''_0 (0)=1\) according to the study of Harris et al [51]. The smallest negative eigenvalue corresponds to the unstable solution due to initial growth or disturbance in the solution and the smallest positive eigenvalue corresponds to the stable solution due to the initial decay in the solution according to Fauzi et al [50] and Harris et al [51].

4 Numerical solution

To obtain the numerical solution of the nonlinear ordinary differential equations given in eqs (7)–(9) with respect to the boundary conditions given in eq. (10), a numerical scheme, known as the spectral collocation scheme, is applied. In this scheme, the unknown \(f(\xi ), \theta (\xi )\;\hbox {and}\;\varphi (\xi )\) are expressed in terms of the truncated series of \(N + 1\) basis functions \( T_n \), and we get

$$\begin{aligned} f(\xi )\approx f_N (\xi )= & {} \sum _{n=0}^N {a_n (\xi )T_n (\xi )} , \end{aligned}$$
(30)
$$\begin{aligned} \theta (\xi )\approx \theta _N (\xi )= & {} \sum _{n=0}^N {b_n (\xi )T_n (\xi )} , \end{aligned}$$
(31)
$$\begin{aligned} \varphi (\xi )\approx \varphi _N (\xi )= & {} \sum _{n=0}^N {c_n (\xi )T_n (\xi )} . \end{aligned}$$
(32)

The Chebyshev polynomials of degree n which is defined in the interval form [\(-1, 1\)] are considered as the basis functions (see Boyd [52]):

$$\begin{aligned} T_n (\xi )=\cos (n\cos ^{-1}\xi ). \end{aligned}$$

The \(N + 1\) unknowns \(a_{n}\), \(b_{n}\) and \(c_{n}\) are determined to get the solution. The physical domain is truncated from [0, \(\eta _{\infty }\)] to [\(-1, 1\)] using the following transformation:

$$\begin{aligned} \xi =2\frac{\eta }{\eta _\infty }-1, \end{aligned}$$
(33)

where \(\eta _{\infty }\) is the physical infinity at the edge of the boundary layer. By using the above-mentioned transformation in eq. (33), eqs (7)–(9) are converted into a new form as

$$\begin{aligned}& 8\frac{\hbox {d}^{3}f}{\hbox {d}\xi ^{3}}+4\eta _\infty f\frac{\hbox {d}^{2}f}{\hbox {d}\xi ^{2}}\nonumber \\&\quad +\frac{2m}{m+1}\left( {\eta _\infty ^3 -4\eta _\infty \left( {\frac{\hbox {d}f}{\hbox {d}\xi }} \right) ^{2}} \right) =0, \end{aligned}$$
(34)
$$\begin{aligned}& \frac{4}{\Pr }\frac{\hbox {d}^{2}\theta }{\hbox {d}\xi ^{2}}+2\eta _\infty f\frac{\hbox {d}\theta }{\hbox {d}\xi }+4Nb \frac{\hbox {d}\theta }{\hbox {d}\xi }\frac{\hbox {d}\varphi }{\hbox {d}\xi }+4Nt \left( {\frac{\hbox {d}\theta }{\hbox {d}\xi }} \right) ^{2}=0,\nonumber \\ \end{aligned}$$
(35)
$$\begin{aligned}& 4\frac{\hbox {d}^{2}\varphi }{\hbox {d}\xi ^{2}}+2\hbox {Sc}\eta _\infty f\frac{\hbox {d}\varphi }{\hbox {d}\xi }+4\frac{Nt}{Nb}\frac{\hbox {d}^{2}\theta }{\hbox {d}\xi ^{2}}=0 \end{aligned}$$
(36)

with boundary conditions eq. (10) becomes

$$\begin{aligned}&f(-1)= \gamma ,\quad \frac{\hbox {d}f(-1)}{\hbox {d}\xi }=\frac{c\eta _\infty }{2a}, \nonumber \\&\frac{\hbox {d}\theta (-1)}{\hbox {d}\xi }= -\frac{\gamma _s \eta _\infty }{2}(1+\theta (-1)),\nonumber \\&\varphi (-1) = 1,\quad \frac{\hbox {d}f(1)}{\hbox {d}\xi }=\frac{\eta _\infty }{2},\nonumber \\&\theta (1)=0,\quad \varphi (1)=0. \end{aligned}$$
(37)

After substituting the truncating series form solutions (30)–(32) into eqs (34)–(36), the non-zero residues \(R_{1}\), \(R_{2}\) and \(R_{3}\) are obtained as

$$\begin{aligned}&R_1 = \frac{8}{(1-\xi ^{2})^{5/2}}\mathop \sum \limits _{n=0}^N na_n \nonumber \\&\quad \times \left( {-3n\xi \sqrt{1-\xi ^{2}}\cos (n\cos ^{-1}\xi )} \right. \nonumber \\&\quad +\sin (n\cos ^{-1}\xi )-n^{2}\sin (n\cos ^{-1}\xi )\nonumber \\&\quad +2\xi ^{2}\sin (n\cos ^{-1}\xi ) +n^{2}\xi ^{2}\sin (n\cos ^{-1}\xi ) \nonumber \\&\quad \left. +\frac{2m}{1+m}\left( {\eta _\infty ^{3}-4\eta _\infty \left( {\mathop \sum \limits _{n=0}^N \frac{na_n \sin (n\cos ^{-1}\xi )}{\sqrt{1-\xi ^{2}}}} \right) ^{2}} \right) \right) \nonumber \\&\quad +4\frac{\eta _\infty }{(1-\xi ^{2})}\mathop \sum \limits _{n=0}^N a_n \cos (n\cos ^{-1}\xi )\mathop \sum \limits _{n=0}^N na_n \nonumber \\&\quad \times \left( {-n\cos (n\cos ^{-1}\xi )+\xi \frac{\sin (n\cos ^{-1}\xi )}{\sqrt{1-\xi ^{2}}}} \right) , \end{aligned}$$
(38)
$$\begin{aligned} R_2= & {} \left( 2\eta _\infty \mathop \sum \limits _{n=0}^N a_n \cos (n\cos ^{-1}\xi )\right. \nonumber \\&\left. +4Nb \mathop \sum \limits _{n=0}^N \frac{nc_n \sin (n\cos ^{-1}\xi )}{\sqrt{1-\xi ^{2}}} \right) \nonumber \\&\times \mathop \sum \limits _{n=0}^N \frac{nb_n \sin (n\cos ^{-1}\xi )}{\sqrt{1-\xi ^{2}}}\nonumber \\&+4Nt \left( {\mathop \sum \limits _{n=0}^N \frac{nb_n \sin (n\cos ^{-1}\xi )}{\sqrt{1-\xi ^{2}}}} \right) ^{2} \nonumber \\&+\frac{4}{\Pr }\frac{1}{(1-\xi ^{2})}\mathop \sum \limits _{n=0}^N nb_n \nonumber \\&\times \left( {-n\cos (n\cos ^{-1}\xi )+\xi \frac{\sin (n\cos ^{-1}\xi )}{\sqrt{1-\xi ^{2}}}} \right) , \end{aligned}$$
(39)
$$\begin{aligned} R_3= & {} 2\hbox {Sc}\mathop \sum \limits _{n=0}^N a_n \cos (n\cos ^{-1}\xi )\mathop \sum \limits _{n=0}^N \frac{nc_n \sin (n\cos ^{-1}\xi )}{\sqrt{1-\xi ^{2}}} \nonumber \\&+4\frac{Nt}{Nb}\frac{1}{(1-\xi ^{2})}\mathop \sum \limits _{n=0}^N nb_n \nonumber \\&\times \left( {-n\cos (n\cos ^{-1}\xi )+\xi \frac{\sin (n\cos ^{-1}\xi )}{\sqrt{1-\xi ^{2}}}} \right) \nonumber \\&+4\frac{1}{(1-\xi ^{2})}\mathop \sum \limits _{n=0}^N nc_n \nonumber \\&\times \left( {-n\cos (n\cos ^{-1}\xi )+\xi \frac{\sin (n\cos ^{-1}\xi )}{\sqrt{1-\xi ^{2}}}} \right) . \nonumber \\ \end{aligned}$$
(40)

The problem is to find the unknown coefficients \(a_{n}\), \(b_{n}\) and \(c_{n}\) such that the residues are minimised throughout the domain of the solution. The unknown coefficients \(a_{n}\), \(b_{n}\) and \(c_{n}\) are chosen such that the residues are minimised in the problem domain. In this study, the collocation scheme is used at the set of \(N + 1\) collocation point which is known as the Gauss–Lobatto collocation point (see Canuto et al [53], Javed and Mustafa [54]) and the residues \(R_{1}\), \(R_{2}\) and \(R_{3}\) become exactly equal to zero. Newton’s iteration method (see Jaluria [55]) is used to achieve three systems of \(N + 1\) linear algebraic equations. For \(N = 54\) the grid independent is achieved for all parameters involved in this study.

5 Results and discussion

The numerical technique known as the Chebyshev spectral collocation point method is used to solve the nonlinear system of ordinary differential equations given in eqs (7)–(9) with boundary conditions given in eq. (10) and the effects of pertinent parameters, namely, suction, velocity ratio, Prandtl number, thermophoresis and Brownian motion, Newtonian heating and Schmidt number on the \({f}'\) (velocity), \(\theta \) (temperature), \(\varphi \) (nanoparticle concentration) profiles, \(C_{\mathrm{f}}\hbox {Re}_{{x}}^{1/2}\) (skin friction coefficient), \(\hbox {Nu}_{{x}}\hbox {Re}_{{x}}^{-1/2}\) (local Nusselt number) and \(\hbox {Sh}_{{x}}\hbox {Re}_{{x}}^{-1/2 }\) (Sherwood number) are shown using graphs. The dual solution of the problem for some values of the suction parameter \(\gamma \) are found by considering different \(\eta _{\infty }\), the initial guess and two distinct structures of boundary layer thicknesses are observed. The solid line represents the first solution and the dotted line represents the second solution. For the validity of the applied spectral collocation scheme, a comparison of the values of \({f}''(0)\), \(\theta (0)\;\hbox {and}\;-{\theta }'(0)\) with the previous studies considered by Wang [56], Bachok et al [9] and Mohamed et al [33] was made and shown in tables 1 and 2.

Table 1 Numerical results of \({f}''(0)\) for some values of c / a with \(m = 1\) and \(\gamma = 0\).
Full size table
Table 2 Numerical results of \( -{\theta }'(0) \hbox { and } \theta (0) \) for some values of Pr when \(m = \gamma _{s} = 1\) and \(\gamma = c/a = 0\).
Full size table
Table 3 Smallest eigenvalues for different values of c / a when \(\gamma =2.5\).
Full size table
Fig. 2
figure 2

Skin friction coefficient against c / a for distinct values of suction parameter \(\gamma \).

Full size image
Fig. 3
figure 3

Local Nusselt number against c / a for distinct values of suction parameter \(\gamma \).

Full size image
Fig. 4
figure 4

Sherwood number against c / a for distinct values of suction parameter \(\gamma \).

Full size image

This shows that our computed solutions are in good agreement and hence our solution scheme and code are highly accurate. A number of researchers like Weidman et al [44] and Rosca and Pop [46] have discussed the stability analysis of multiple solutions. They have proved that the first solution is a stable solution due to the positive eigenvalue and the second solution is an unstable solution due to the negative eigenvalue. In this study, the stability analysis is also performed, and the eigenvalues are calculated for both the first and the second solutions. The smallest positive and negative eigenvalues for different values of m are shown in table 3. Figures 2–4 show the variation of \(C_{\mathrm{f}}\hbox {Re}_{{x}}^{1/2}\), \(\hbox {Nu}_{{x}}\hbox {Re}_{{x}}^{-1/2}\) and \(\hbox {Sh}_{{x}}\hbox {Re}_{{x}}^{-1/2}\) against the velocity ratio parameter c / a for some values of the suction parameter \(\gamma \) with fixed values of the remaining parameters \(m = 2\), \(\hbox {Sc} = 1.5\), \(\hbox {Pr} = 7\), \(\gamma _{s} = 1\) and \(Nt=Nb = 0.3\). From these figures, it is seen that dual solutions exist for each positive value of c / a under different values of suction parameter \(\gamma \) (\(=\) 2.5, 3 and 3.5) but for negative values of c / a, there exist critical values \(t_{1}\) for which dual solution exists, i.e. \(c/a > t_{1}\) and no solution for \(c/a < t_{1}\), which are presented in table 4. It is also seen that the region of c / a for which the dual solution exists increases with the increase in suction parameter \(\gamma \). Zaimi et al [19] found dual solutions for the same values of suction parameter \(\gamma \) (\(=\) 2.5, 3 and 3.5) without considering the stagnation point flow and they calculated the critical values which are shown in table 3 and from this table, it is seen that the ranges of the dual solutions in the present study are increased compared to a previous study due to the presence of stagnation point in the flow field. This finding shows that the stagnation point flow widens the ranges of dual solutions. Figure 2 depicts that the values of \(C_{\mathrm{f}}\hbox {Re}_{{x}}^{1/2}\) increase in the stable solution (first solution) and decrease in the unstable solution (second solution) by increasing the values of the suction parameter \(\gamma \). The values of \(C_{\mathrm{f}}\hbox {Re}_{{x}}^{1/2}\) in the first solution become higher than the values of the second solution. In figures 3 and 4, \(\hbox {Nu}_{{x}}\hbox {Re}_{{x}}^{-1/2}\)  and \(\hbox {Sh}_{{x}}\hbox {Re}_{{x}}^{-1/2}\) are plotted against the velocity ratio parameter c / a for some values of the suction parameter \(\gamma \) (\(=\) 2.5, 3.0 and 3.5). From these figures, it is noted that both \(\hbox {Nu}_{{x}}\hbox {Re}_{{x}}^{-1/2}\) and \(\hbox {Sh}_{{x}}\hbox {Re}_{{x}}^{-1/2}\) increase with the increase of suction parameter \(\gamma \). In the case of the first solution, \(\hbox {Nu}_{{x}}\hbox {Re}_{{x}}^{-1/2}\) (Nusselt number) decreases up to a certain value of c / a and after that value, it becomes an increasing function but the values of \(\hbox {Sh}_{{x}}\hbox {Re}_{{x}}^{-1/2}\) (Sherwood number) decrease by decreasing the values of c / a. The values of \(\hbox {Nu}_{{x}}\hbox {Re}_{{x}}^{-1/2}\) in the first solution become smaller than the values of the second solution and an opposite behaviour is noticed for the values of \(\hbox {Sh}_{{x}}\hbox {Re}_{{x}}^{-1/2}\). Figure 5 illustrates the variation of \(\hbox {Nu}_{{x}}\hbox {Re}_{{x}}^{-1/2}\) against c / a for some values of Pr. It is seen that for large values of Prandtl number Pr, i.e. 5 and 7, the values of \(\hbox {Nu}_{{x}}\hbox {Re}_{{x}}^{-1/2}\) decrease up to a certain value of c / a, and after that value, it becomes an increasing function but for \(\hbox {Pr} = 3\), the values of \(\hbox {Nu}_{{x}}\hbox {Re}_{{x}}^{-1/2}\) increase against the velocity ratio parameter c / a. It is also seen that \(\hbox {Nu}_{{x}}\hbox {Re}_{{x}}^{-1/2}\) increases by increasing the values of Pr because Prandtl number is the ratio of momentum diffusivity and thermal diffusivity.

Table 4 Critical values \(t_{1}\) of c / a for some values of \(\gamma \) when \(m = 2\).
Full size table
Fig. 5
figure 5

Local Nusselt number against c / a for distinct values of Prandtl number Pr.

Full size image
Fig. 6
figure 6

Velocity profile for distinct values of \(\gamma \) when \(m = 2\), \(\hbox {Sc} = 1.5\), \(\hbox {Pr} = 7\), \(\gamma _{s} = 1\), \(Nt=Nb = 0.3\): (a) shrinking sheet \((c/a =-3)\) and (b) stretching sheet \((c/a = 2)\).

Full size image
Fig. 7
figure 7

Temperature profile for distinct values of Nt when \(m = 2\), \(\hbox {Sc} = 1.5\), \(\hbox {Pr} = 7\), \(\gamma _{s}= 1\), \(Nb = 0.3\), \(\gamma = 2.5\): (a) shrinking sheet \((c/a = -3)\) and (b) stretching sheet \((c/a = 2)\).

Full size image
Fig. 8
figure 8

Nanoparticle concentration profile for distinct values of Nt when \(m = 2\), \(\hbox {Sc} = 1.5\), \(\hbox {Pr} = 7\), \(\gamma _{s} = 1\), \(Nb = 0.3\) \(\gamma = 2.5\): (a) shrinking sheet \((c/a = -3)\) and (b) stretching sheet \((c/a = 2)\).

Full size image
Fig. 9
figure 9

Temperature profile for distinct values of Nb when \(m = 2\), \(\hbox {Sc} = 1.5\), \(\hbox {Pr} = 7\), \(\gamma _{s} = 1\), \(Nt = 0.3\), \(\gamma = 2.5\): (a) shrinking sheet \((c/a = -3)\) and (b) stretching sheet \((c/a = 2)\).

Full size image
Fig. 10
figure 10

Nanoparticle concentration profile for distinct values of Nb when \(m = 2\), \(\hbox {Sc} = 1.5\), \(\hbox {Pr} = 7\), \(\gamma _{s} = 1\), \(Nt = 0.3\), \(\gamma = 2.5\): (a) shrinking sheet \((c/a = -3)\) and (b) stretching sheet \((c/a = 2)\).

Full size image
Fig. 11
figure 11

Temperature profile for distinct values of Sc when \(m = 2\), \(\hbox {Pr} = 7\), \(\gamma _{s} = 1\), \(Nt=Nb = 0.3\), \(\gamma = 2.5\): (a) shrinking sheet \((c/a = -3)\) and (b) stretching sheet \((c/a = 2)\).

Full size image
Fig. 12
figure 12

Nanoparticle concentration profile for distinct values of Sc when \(m = 2\), \(\hbox {Pr} = 7\), \(\gamma _{s} = 1\), \(Nt=Nb = 0.3\) and \(\gamma = 2.5\): (a) shrinking sheet \((c/a = -3)\) and (b) stretching sheet \((c/a = 2)\).

Full size image
Fig. 13
figure 13

Temperature profile for distinct values of \(\gamma _{s}\) when \(m = 2\), \(\hbox {Sc} = 1.5\), \(\hbox {Pr} = 7\), \(Nt=Nb= 0.3\), \(\gamma = 2.5\): (a) shrinking sheet \((c/a = -3)\) and (b) stretching sheet \((c/a = 2)\).

Full size image
Fig. 14
figure 14

Nanoparticle concentration profile for distinct values of \(\gamma _{s}\) when \(m = 2\), \(\hbox {Sc} = 1.5\), \(\hbox {Pr} = 7\), \(Nt=Nb = 0.3\), \(\gamma = 2.5\): (a) shrinking sheet \((c/a = -3)\) and (b) stretching sheet \((c/a = 2)\).

Full size image

For the small value of Prandtl number, i.e. \(\hbox {Pr} = 3\), the first solution maintains a higher value of \(\hbox {Nu}_{{x}}\hbox {Re}_{{x}}^{-1/2}\) for \(-3.565< c/a < -0.15\), and after that, the second solution crosses the first solution. For large values of Pr other than 3, the first solution has smaller values of \(\hbox {Nu}_{{x}}\hbox {Re}_{{x}}^{-1/2}\) than the second solution. Figures 6a and 6b demonstrate the effects of \(\gamma \) (suction) on velocity profiles for shrinking and stretching cases, respectively, and other parameters are considered fixed. For the first solution in figure 6a, the velocity increases and the momentum boundary layer thickness reduces by increasing the values of \(\gamma \) (suction) because suction enhances the flow near the surface and reduces the momentum boundary layer thickness in the case of shrinking sheet. Also, for the second solution, a negative velocity gradient is found at the edge of the sheet and becomes positive away from the sheet. In figure 6b, velocity reduces for the first solution with the increase of suction parameter \(\gamma \) because suction is responsible for the delay in fluid motion over a stretching sheet. In the case of the second solution, velocity reduces by increasing the suction parameter \(\gamma \) for the initial values of \(\eta \) and becomes an increasing function for large \(\eta \). Figures 7a, 7b and 8a, 8b illustrate the temperature and nanoparticle concentration profiles for some values of the thermophoresis parameter Nt. Figures 7a and 7b reveal that a variation of Nt from 0.1 to 0.7 enhances both temperature and thermal boundary layer thickness for the first and the second solutions, respectively. This is because the strength of thermophoresis parameter Nt generates a force known as the thermophoretic force due to which a rapid flow is observed away from the surface. Therefore, the hot fluid moves away from the sheet. But it is noticed that the magnitude of temperature difference and the increase in boundary layer is almost negligible. It is further noticed that the thermal boundary layer thickness is higher in the case of shrinking sheet than in the case of stretching sheet. Figures 8a and 8b show that the nanoparticle concentration increases with the increase of Nt for both the first and second solutions, and this is because thermophoresis increases the mass transfer of nanofluids, i.e. nanoparticles disperse from a hot surface to the ambient fluid. The nanoparticles face resistance from the hot surface and, therefore, nanoparticles import heat from the heated sheet to the moving fluids, and thus, the concentration boundary layer thickness increases. In figure 8a, a positive concentration gradient \({\varphi }'(0)\) is obtained at the surface of the plate for the second solution when the thermophoresis parameter \(Nt = 0.7\) and becomes negative for other values of Nt ( \(=\) 0.4 and 0.1). Also in figures 8a and 8b, the concentration boundary layer thickness is higher in the second solution than in the first solution. Figures 9a, 9b and 10a, 10b are plotted to show the effect of Nb (Brownian motion) on temperature and nanoparticle concentration profiles. Figure 9a and 9b demonstrate that the variation of Nb from 0.1 to 0.3 enhances temperature and thermal boundary layer thickness for both the first and the second solutions. This is because the collision between nanoparticles and molecules of a base fluid like water generates additional energy and warms the boundary layer, and consequently, thermal conductivity increases. Figures 10a and 10b illustrate that the nanoparticle concentration decreases with the increase of the Brownian motion parameter Nb for both solutions. Also, for the second solution, the concentration boundary layer thickness in both shrinking and stretching cases is greater than that of the first solution. This is because Brownian motion generates due to the interaction of the base fluid and the nanoparticles which warms the fluid within the boundary layer. The nanoparticles deposit on the heated sheet and enhance the surface area of the sheet and, consequently, the concentration of nanoparticles in the base fluid decreases. In figure 10a, a positive concentration gradient \({\varphi }'(0)\) is obtained for \(Nb = 0.1\) and negative concentration gradient \({\varphi }'(0)\) is obtained for \(Nb = 0.2\) and 0.3. The influence of Schmidt number on the temperature profile and nanoparticle concentration profile are presented in figures 11a, 11b and 12a, 12b for both shrinking and stretching cases, respectively. In figures 11a and 11b, it is seen that the temperature and thermal boundary layer thickness increase with the increasing values of Sc for both solutions. On the other hand, the nanoparticle concentration profile shows an opposite behaviour by increasing Sc for both the first and second solutions. From both figures 12a and 12b, it is observed that the concentration boundary layer thickness for \(\hbox {Sc} = 2\) for the second solution is larger than that for the first solution in the shrinking and stretching cases, which is responsible for the instability of the second solution. The temperature and nanoparticle concentration profiles for different values of conjugate parameter \(\gamma _{s}\) are presented in figures 13a, 13b and 14a, 14b. The effect of conjugate parameter \(\gamma _{s}\) on the temperature profile for both the first and second solutions shows that the temperature and thermal boundary layer thickness increase with the increase of \(\gamma _{s}\) in both the shrinking and stretching cases, respectively. It is noted that when the conjugate parameter \(\gamma _{s}\) is zero, the temperature at the wall becomes zero, i.e. there is no heat transfer and when \(\gamma _{s} \rightarrow \infty \), the Newtonian heating condition becomes the condition of constant wall temperature. Physically, it is observed that the temperature becomes zero when the conjugate parameter \(\gamma _{s}\) is zero. Therefore, by increasing the conjugate parameter \(\gamma _{s}\), the temperature enhances within the boundary layer. The same behaviour is observed in the nanoparticle concentration profile but in the second solution, the boundary layer thickness is greater than that for the first solution.

6 Conclusion

In this study, we have theoretically investigated the effect of Newtonian heating on the flow of a nanofluid over a nonlinear permeable stretching / shrinking sheet near the region of stagnation point. The governing equations of the flow problem are solved numerically by using the spectral collocation method and dual solutions are found for specific values of suction parameter \(\gamma \). The effects of pertinent parameters, namely suction, velocity ratio, Prandtl number, thermophoresis and Brownian motion parameters, Schmidt number and Newtonian heating parameter \(\gamma _{s}\) on the velocity, temperature, nanoparticle concentration profiles, skin friction coefficient, local Nusselt number and local Sherwood number are examined using graphs. The key findings in this study are:

  1. 1.

    Temperature and concentration increase with increasing values of \({ Nt}\) for both stretching and shrinking sheets. Also, the thermal and concentration boundary layer thicknesses are higher in the shrinking case than in the stretching case.

  2. 2.

    Temperature increases and concentration decreases with increasing values of \({ Nb}\) and Schmidt number Sc for both stretching and shrinking sheets. Also, the thermal and concentration boundary layer thicknesses are higher in the shrinking case than in the stretching case.

  3. 3.

    Skin friction coefficient increases in the first solution and decreases in the second solution with the increase of suction parameter \(\gamma \). The values of the first solution are higher than that of the second solution. The suction parameter \(\gamma \) widens the ranges of dual solutions.

  4. 4.

    Local Nusselt number and local Sherwood number increase with the increase of suction parameter \(\gamma \). The values of the local Nusselt number and local Sherwood number in the first solution are smaller in magnitude than in the second solution.

  5. 5.

    Local Nusselt number increases with the increase of Prandtl number Pr.

  6. 6.

    Temperature and concentration profiles increase with the increase of the Newtonian heating parameter \(\gamma _{s}\) for both stretching and shrinking sheets.