Theoretical investigation of chemically reactive flow of water-based carbon nanotubes (single-walled and multiple walled) with melting heat transfer

Abstract

This study reports the chemically reacting flow of carbon nanotubes (CNTs) over a stretchable curved sheet. The flow is initialised due to a stretched surface. A heat source is present. Water is considered as the base liquid. The vital interest of this work is that heat phenomenon is studied via melting heat transfer. Xue relation of nanoliquid is implemented to explain the properties of both single- and multiwall CNTs. Mathematical systems (partial differential equations) for the flow field are obtained. Appropriate transformations are utilised in order to transform partial differential systems into nonlinear ordinary differential systems. Further, these systems are solved numerically. Variations in flow, temperature, concentration, skin friction coefficient and Nusselt number via the involved influential variables are illustrated graphically.

1 Introduction

The development in industrial and thermal engineering directly depends on the requirement of processing more compact and efficient heat transfer equipment. In order to fulfil such requirements, scientists and engineers have made many attempts to design various equipment and fluids for the higher heat transfer rate. The consequence of such attempts is that solid materials are better thermal conductors than liquids. Nowadays, various liquids are used as cooling agents. In order to improve the thermal conductance of such liquids, scientists and engineers add some small (nano-) sized particles into it. Such nanosized materials are referred to as nanomaterials or nanoparticles. Nanoparticles are made of metal carbides (copper, gold, etc.), oxides (alumina, titania), copper oxides, etc. Kerosene oil, ethylene glycol, bioliquids, water and some lubricants are utilised as traditional liquids. The suspension of such nanosized materials and the base material is known by nanofluids. Enhancing the thermal conductance of the base liquid by adding nanosized materials into it was initially done by Choi [1]. Nanomaterials appear as cylinders, spheres, blades, bricks, etc. It has been observed that the thermal conductance of the base liquid depends highly on the shape of the nanomaterials. Better performance in terms of enhancing the thermal conductance of the base liquid is observed for cylindrical-shaped nanomaterials (nanotubes) [2]. Carbon nanotubes (CNTs) are seamless cylindrical materials with one (single-wall) or more (multiwall) layers of graphene. There is an extensive range of applications of CNTs, like in energy storages, microelectronics, coating and films, purification of drinking water, defense, sports materials, etc. [3]. Time-independent squeezed flow of CNTs with heat transfer via convection is analysed by Hayat et al [4]. Turkyilmazoglu [5] explored the nanofluid flow and heat transfer with single- and multiphase models. Qayyum et al [6] examined the chemical reacting flow of Jeffrey fluid by a stretchable sheet of variable thickness. Hayat et al [7] explored the stagnation flow with melting effect in the flow of single- and multiwall carbon nanomaterials towards a stretched surface. Shiekholeslami and Ellahi [8] inspected the convective heat transfer in the flow of nanofluid with magnetic effects. Hayat et al [9] studied the Marangoni convection flow CNTs in the presence of radiation effects. Qayyum et al [10] explored the chemically reacting flow of water-based nanomaterials with thermal radiations. An experimental study on the hybrid photovoltaic / thermoelectric system in the flow of nanofluid is performed by Soltani et al [11]. Irreversibility in the flow of viscous fluid with Ag and Cu nanoparticles subject to the stretchable surface is examined by Hayat et al [12].

Due to a vast range of applications, the flow by a stretchable sheet is extensively discussed. The stretchable sheet has a vital impact on finished produced materials in the manufacturing processes. Applications of the stretchable sheet include fibre spinning, glass blowing, generation of flow in hot rolling, polymer sheet extrusion, paper production and many more. Flow over a stretchable surface was initially analysed by Crane et al [13]. Hayat et al [14] scrutinised the revised Fourier model in the flow of Jeffrey material with variable thickness and temperature-dependent thermal conductivity. Heat transport in the flow of nanofluid by a permeable stretched sheet was explored by Shekholeslami et al [15]. The squeezed flow of Jeffrey fluid in a rotating frame with non-Fourier heat flux was presented by Hayat et al [16]. Khan et al [17] presented the Casson liquid flow subject to the stretchable surface near a stagnation point. The flow of a viscous fluid over a curved stretchable surface was presented by Sajid et al [18]. Hayat et al [19] studied magnetohydrodynamics flow of viscous materials with Soret and Dufour effect subject to curved stretching. Imtiaz et al [20] worked on the curved stretching flow with convective conditions and homogeneous–heterogeneous reactions. Naveed et al [21] examined the time-independent flows by a curved stretched sheet with magnetic effect. Khan et al [22] examined the radiative nanomaterial stagnation flow of cross fluid with activation energy. Okechi et al [23] explored the flow of viscous fluid by an exponential curved stretchable sheet.

In chemical processes, such as assembling of ceramics, catalysis, handling crop from harm by solidification, processing of food, production of polymers etc. both chemical reactions (homogeneous and heterogeneous) have a vital role. In the boundary layer flow, isothermal chemical reactions were examined by Merkin [24]. Chemically reacting Darcy–Forchheimer flow was analysed by Khan et al [25]. Stagnation point flow with chemical reactions and non-Fourier heat flux is presented by Hayat et al [26]. Flow on a non-Newtonian fluid with chemical reactions and magnetic effect by a variable thickness stretchable sheet was examined by Qayyum et al [27]. Khan et al [28] considered the homogeneous–heterogeneous reactions in flow rate type fluid with variable thicknesses. Khan et al [29] explored the chemical reacting flow of ferrofluid by a curved stretchable surface with convective heat transfer. The Darcy–Forchheimer flow a Newtonian fluid subject to homogeneous–heterogeneous reactions was explored by Khan et al [25]. Khan et al [30] studied the viscous dissipation and Joule heating in MHD flow with chemical reactions. Some investigations regarding the fluid model are presented in [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49].

Scientists and engineers had paid their attention only towards the dispersion of nanomaterials of $\hbox {Cu},\hbox {Al}_2 \hbox {O}_3,\hbox {Ag}$ in the traditional liquids. The focus of this work is to analyse and model high rate of heating or cooling by dispersing single- and multiwall CNTs in the base liquid known as water. Flow and heat transport characteristics are explored with melting heat transfer and heat source. Flow is addressed by a curved stretchable sheet. The governing expressions for the flow field are solved through bvp4c. Flow, temperature, skin friction and local Nusselt number are examined graphically for both single- and multiwall CNTs.

2 Mathematical modelling

The flow of CNTs over a stretchable curved surface is discussed. The homogeneous–heterogeneous reactions are taken into account. Transfer of heat is studied via melting heat transfer and heat source. Curvilinear coordinates are adopted in such a manner that the x-axis is chosen along the curved stretchable surface while the r-axis is considered perpendicular to it. According to Khan et al [48], the simple homogeneous and heterogeneous reactions are addressed as

$$\begin{aligned} A_1 +B_1 \rightarrow 3B_1 ,\quad \hbox {rate} = k_1 a_1 b_1^2 \end{aligned}$$

(1)

and

$$\begin{aligned} A_1 \rightarrow B_1 ,\quad \hbox {rate} = k_2 a_1 . \end{aligned}$$

(2)

Here $A_1$ and $B_1$ are chemical species, $k_1$ and $k_2$ are rate constants while $a_1$ and $b_1$ are concentrations of chemical species.

The considered flow expressions are

$$\begin{aligned}&(r+R)\frac{\partial v}{\partial r} +v+R\frac{\partial u}{\partial s}=0, \end{aligned}$$

(3)

$$\begin{aligned}&\frac{u^{2}}{r+R}=\frac{1}{\rho _{nf} }\frac{\partial p}{\partial r},\end{aligned}$$

(4)

$$\begin{aligned}&v \frac{\partial u}{\partial r}+\frac{Ru}{r+R}\frac{\partial u}{\partial s}+\frac{uv}{r+R} =-\frac{1}{\rho _{nf} }\frac{R}{r+R}\frac{\partial p}{\partial s}\nonumber \\&\qquad +\nu _{nf} \left( {\frac{\partial ^{2}u}{\partial r^{2}}+\frac{1}{r+R}\frac{\partial u}{\partial r}-\frac{u}{\left( {r+R} \right) ^{2}}} \right) , \end{aligned}$$

(5)

$$\begin{aligned}&v \frac{\partial T}{\partial r}+\frac{Ru}{r+R}\frac{\partial T}{\partial s}=\frac{k_{nf} }{\left( {\rho c_p } \right) _{nf} }\left( {\frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r+R}\frac{\partial T}{\partial r}} \right) \nonumber \\&\quad +\frac{Q^{{*}}}{\left( {\rho c_p } \right) _{nf} }(T-T_m ), \end{aligned}$$

(6)

$$\begin{aligned}&v\frac{\partial a_1 }{\partial r}+\frac{R}{r+R}u\frac{\partial a_1 }{\partial s}\nonumber \\&\quad =D_{A_1} \left( {\frac{\partial ^{2}a_1 }{\partial r^{2}}+\frac{1}{r+R}\frac{\partial a_1 }{\partial r}} \right) -k_1 a_1 b_1^2 , \end{aligned}$$

(7)

$$\begin{aligned}&v\frac{\partial b_1 }{\partial r}+\frac{R}{r+R}u\frac{\partial b_1 }{\partial s}\nonumber \\&\quad =D_{B_1} \left( {\frac{\partial ^{2}b_1 }{\partial r^{2}}+\frac{1}{r+R}\frac{\partial b_1 }{\partial r}} \right) +k_1 a_1 b_1^2, \end{aligned}$$

(8)

with

$$\begin{aligned}&\left. \begin{aligned}&u=U_w =as,\quad T=T_m \\&D_{A_1 } \frac{\partial a_1 }{\partial r}=k_2 a_1 ,\quad D_{B_1 } \frac{\partial b_1 }{\partial r}=-k_2 a_{1\,} \hbox {at }r=0\\&u\rightarrow 0,\quad \frac{\partial u}{\partial r}\rightarrow 0,\quad T\rightarrow T_\infty ,\quad a_1 \rightarrow a_0\\&b_1 \rightarrow 0 \quad \hbox { when }r\rightarrow \infty \end{aligned}\right\} . \end{aligned}$$

(9)

Melting heat transfer condition is given by [7]

$$\begin{aligned} k_{nf} \left( {\frac{\partial T}{\partial r}} \right) _{r=0} =\rho _{nf} \left[ {\lambda +C_s (T_m -T_0 )} \right] v(r,s)_{r=0} . \end{aligned}$$

(10)

In the above expressions u and v are velocity components, p is the pressure, $k_{nf}$, $\upsilon _{nf}$ and $\rho _{nf}$ are thermal conductivity, kinematic viscosity and density of the nanomaterial, T and $T_m$ are the temperature of the fluid and the melting surface, $Q^{*}$ is the heat source coefficient, $D_{A_1}$ and $D_{B_1}$ are diffusion coefficients of the chemical species, $U_w$ is the stretching velocity and $\lambda$ is the latent heat of the fluid.

Xue [49] found that the earlier models of nanofluid are only valuable for rotational or spherical elliptical materials having a very small axial ratio. By utilising such models, space distribution properties of CNTs cannot be described by means of thermal conductivity. To fulfil this void, a model on the base of Maxwell theory was presented by Xue [49]. This model is valid for elliptically rotational nanotubes having a larger axial ratio and also balancing impact of space distribution on CNTs. Thus, according to Xue [49] relation for the CNTs, we have

$$\begin{aligned} \left. \begin{aligned}&\mu _{nf} = \frac{\mu _f }{\left( {1-\phi } \right) ^{2.5}},\quad \nu _{nf} =\frac{\mu _{nf} }{\rho _{nf} }\\&\rho _{nf} =\left( {1-\phi } \right) \rho _f +\phi \rho _\mathrm{CNT} \\&\alpha _{nf} = \frac{k_{nf} }{\rho _{nf} \left( {c_p } \right) _{nf} }\\&\frac{k_{nf} }{k_{f} }=\frac{\left( {1-\phi } \right) +2\phi \frac{k_\mathrm{CNT} }{k_\mathrm{CNT} -k_f }\ln \frac{k_\mathrm{CNT} +k_f }{2k_f }}{\left( {1-\phi } \right) +2\phi \frac{k_f }{k_\mathrm{CNT} -k_f }\ln \frac{k_\mathrm{CNT} +k_f }{2k_f }} \end{aligned}\right\} . \end{aligned}$$

(11)

Here $\mu _{f}$, $\mu _{nf}$ respectively are dynamic fluid and nanofluid viscosities, $\phi$ is the nanoparticle volume fraction, $k_{f}$ and $k_\mathrm{CNT}$ respectively are the thermal conductivity of the base fluid and carbon nanotubes, $(c_p )_{nf}$ is the specific heat of the nanofluid and $C_s$ is the heat capacity of the solid surface.

Appropriate transformations are defined by

$$\begin{aligned} \left. \begin{aligned}&u=as{f}'(\eta ),\quad v=-\frac{R}{\left( {r+R} \right) }\sqrt{\frac{a\nu _f }{2l}}f\left( \eta \right) \\&\eta =\sqrt{\frac{a}{\nu _f }}r,\quad T=T_m +(T_\infty -T_m )\theta (\eta )\\&p=\rho _f a^{2}s^{2}P\left( \eta \right) , \quad a_1 =a_0 g(\eta ),\quad b_1 =b_0 h(\eta )\end{aligned}\right\} .\nonumber \\ \end{aligned}$$

(12)

Incompressibility condition (3) is satisfied and eqs (4)–(8) give

$$\begin{aligned}&{P}'(\eta )=\left( {1-\phi +\phi \frac{\rho _\mathrm{CNT} }{\rho _{f} }} \right) \frac{f^{\prime 2}}{\eta +\gamma }, \end{aligned}$$

(13)

$$\begin{aligned}&\left. \begin{aligned}&\frac{2\gamma }{(\eta +\gamma )}P\left( \eta \right) = (1-\phi )^{2.5}\left( {1-\phi +\phi \frac{\rho _\mathrm{CNT} }{\rho _{f} }} \right) \\&\quad \times \left( {\frac{\gamma }{\eta +\gamma }f{f}''-\frac{\gamma }{\eta +\gamma }{f}'^{2}+\frac{\gamma }{\eta +\gamma }f{f}'} \right) \\&\quad -\frac{{f}'}{(\eta +\gamma )^{2}}+\frac{1}{\eta +\gamma }{f}''+{f}'''\end{aligned}\right\} \nonumber \\\end{aligned}$$

(14)

$$\begin{aligned}&\frac{k_{nf}/ {k_f }}{\left( {1-\phi +\phi \frac{\left( {\rho c_p } \right) _\mathrm{CNT} }{\left( {\rho c_p } \right) _{f} }} \right) }\left( {{\theta }''+\frac{\theta ^{\prime } }{\eta +\gamma }} \right) \nonumber \\&\quad +\frac{\gamma }{\eta +\gamma }\Pr \, f{\theta }'+\delta \Pr \, \theta =0, \end{aligned}$$

(15)

Here $\gamma$ is the curvature parameter, Pr is the Prandtl number and $\delta$ is the heat source parameter.

$$\begin{aligned}&\frac{1}{\hbox {Sc}}{g}''+\frac{{g}'}{\hbox {Sc}(\eta +\gamma )}-K_1 gh^{2}+\frac{\gamma }{\eta +\gamma }f{g}'=0, \end{aligned}$$

(16)

$$\begin{aligned}&\frac{\varepsilon }{\hbox {Sc}}{h}''+\frac{{h}'}{\hbox {Sc}(\eta +\gamma )}+K_1 gh^{2}+\frac{\gamma }{\eta +\gamma }f{h}'=0, \end{aligned}$$

(17)

and the related flow field boundary conditions are

$$\begin{aligned} \left. \begin{aligned}&f'\left( 0 \right) =1,\quad \theta \left( 0 \right) =0,\quad g'(0)=K_{2} g(0) \\&\delta {h}'(0)=-K_{2} h(0) \\&\frac{k_{nf} }{k_f }M{\theta }'\left( 0 \right) +\left( {1-\phi +\phi \frac{\rho _\mathrm{CNT} }{\rho _f}} \right) \Pr \,f(0)=0 \\&f'\left( \infty \right) \rightarrow 0,\quad \,{f}''\left( \infty \right) \rightarrow 0,\quad \theta \left( \infty \right) \rightarrow 1 \\&{g}'(\infty )\rightarrow 0,\quad h(\infty )\rightarrow 0 \end{aligned}\right\} .\nonumber \\ \end{aligned}$$

(18)

For comparable size $D_{A_1 }$ and $D_{B_1 }$ are equal, i.e. for $\varepsilon =1$, we have

$$\begin{aligned} g\left( \eta \right) +h\left( \eta \right) =1. \end{aligned}$$

(19)

Equations (16) and (17) yield

$$\begin{aligned} \frac{1}{\hbox {Sc}}{g}''+\frac{{g}'}{\hbox {Sc}(\eta +\gamma )}-K_1 g(1-g)^{2}+\frac{\gamma }{\eta +\gamma }f{g}'= & {} 0\nonumber \\ \end{aligned}$$

(20)

with

$$\begin{aligned} {g}'(0)=K_2 g(0),\quad {g}'(\infty )\rightarrow 0, \end{aligned}$$

(21)

where Sc is the Schmidt number, $K_1$, $K_2$ are homogeneous and heterogeneous reaction parameters, M is the melting parameter while $f,\theta$ and g are dimensionless velocities, $\varepsilon$ is the ratio of diffusion coefficients, temperature and concentration profile.

The involved physical variables are defined by

$$\begin{aligned} \left. \begin{aligned}&\gamma = \sqrt{\frac{a}{\nu _f }}R,\quad M=\frac{C_{pf} \left( {T_\infty -T_m } \right) }{\lambda +C_s\left( {T_m -T_0 } \right) },\quad \varepsilon =\frac{D_{B_1 } }{D_{A_1 } } \\&\Pr = \frac{\mu _{f} (\rho c_p )_{f} }{k_{f} },\quad \delta =\frac{Q^{{*}}}{a(\rho c_p )_{f} },\quad K_1 =\frac{2a_0^2 k_1 }{a}\\&K_2 =\frac{k_2 }{D_{A_1 } }\sqrt{\frac{\nu _f }{a}},\quad \hbox {Sc}= \frac{\nu _f }{D_{A_1 } }\end{aligned}\right\} . \nonumber \\ \end{aligned}$$

(22)

Now eliminating P from eqs (13) and (14), we get

$$\begin{aligned}&\frac{1}{\left( {1-\phi } \right) ^{2.5}(1-\phi +\phi \frac{\rho _\mathrm{CNT} }{\rho _f })}\left[ f^{(iv)}+\frac{2}{\eta +\gamma }{f}'''\right. \nonumber \\&\quad \left. +\frac{{f}'}{(\eta +\gamma )^{3}}-\frac{1}{(\eta +\gamma )^{2}}{f}'' \right] \end{aligned}$$

(23)

$$\begin{aligned}&\quad +\frac{\gamma }{\eta +\gamma }f{f}'''-\frac{\gamma }{\eta +\gamma }{f}'{f}''+\frac{\gamma }{(\eta +\gamma )^{2}}f{f}''\nonumber \\&\quad -\frac{\gamma }{(\eta +\gamma )^{2}}{f}'^{2}-\frac{\gamma }{(\eta +\gamma )^{3}}f{f}'=0. \end{aligned}$$

(24)

The skin friction coefficient and local Nusselt number in dimensionless variables become

$$\begin{aligned} C_{{} { fs}} =\frac{\tau _{{w}} }{\rho _{{f}} U_{{w}}^2 },\quad \hbox {Nu}_{{s}} =\frac{sq_{{w}} }{k_{{f}} (T_{{f}} -T_\infty )}, \end{aligned}$$

(25)

where

$$\begin{aligned}&\tau _w =\mu _{nf}\left( {\frac{\partial u}{\partial r}-\frac{u}{r+R}} \right) _{r=0} ,\nonumber \\&q_{\mathrm{w}} =-\kappa _{nf} \left( {\frac{\partial T}{\partial r}} \right) _{r=0} . \end{aligned}$$

(26)

$$\begin{aligned}&\hbox {Re}_s^{1/2} C_{fs} =\frac{1}{\left( {1-\phi } \right) ^{2.5}}({f}''\left( 0 \right) -\frac{1}{\gamma }{f}'(0)),\nonumber \\&\hbox {Nu}_s\hbox { Re}_s^{-1/2} =-\frac{k_{nf} }{k_{{f}} }{\theta }'(0), \end{aligned}$$

(27)

where $\hbox {Re}_s =U_w s/\nu _f$ represents the local Reynolds number.

3 Solution methodology

We have solved the nonlinear ODEs numerically by means of bvp4c technique. This method solves the first-order ODEs. That is why we have transferred these higher-order ODEs along with boundary conditions into first-order ODEs. Thus, we adopt the following procedure:

$$\begin{aligned}&f=z_0 , \quad {f}'=z_{01}, \quad {f}''=z_{02} , \quad {f}'''=z_{03} , \nonumber \\&\theta =z_1 ,\quad {\theta }'=z_{11} ,\quad g=z_2 ,\quad {g}'=z_{21} , \end{aligned}$$

(28)

where

$$\begin{aligned}&{z}'_0 =z_{01} ,\quad {z}'_{01} =z_{02} ,\quad {z}'_{02} =z_{03} ,\quad {z}'_1 =z_{11} ,\nonumber \\&{z}'_2 =z_{21} , \end{aligned}$$

(29)

$$\begin{aligned}&{z}'_{03} =-\frac{2}{\eta +\gamma }z_{03} -\frac{z_{01} }{(\eta +\gamma )^{3}}+\frac{1}{(\eta +\gamma )^{2}}z_{02} , \end{aligned}$$

(30)

$$\begin{aligned}&-\left( {1-\phi } \right) ^{2.5}\left( {1-\phi +\phi \frac{\rho _\mathrm{CNT} }{\rho _{{f}} }} \right) \nonumber \\&\quad \times \left( {{\begin{array}{l} {\dfrac{\gamma }{\eta +\gamma }z_0 z_{03} -\dfrac{\gamma }{\eta +\gamma }z_{01} z_{02} } \\[2mm] {+\dfrac{\gamma }{(\eta +\gamma )^{2}}z_0 z_{02} -\dfrac{\gamma }{(\eta +\gamma )^{2}}z_{01}^2 } \\[2mm] {-\dfrac{\gamma }{(\eta +\gamma )^{3}}z_0 z_{01} } \\ \end{array} }} \right) , \end{aligned}$$

(31)

$$\begin{aligned}&{z}'_{11} =\frac{-\left( {1-\phi +\phi \frac{\left( {\rho c_p } \right) _\mathrm{CNT} }{\left( {\rho c_p } \right) _f }} \right) }{{k_{nf} }/{k_f }}\nonumber \\&\quad \qquad \times \left( {\frac{\gamma }{\eta +\gamma }\Pr \, z_0 z_{11} +\delta \Pr \, z_1 } \right) -\frac{z_1 }{\eta +\gamma }, \end{aligned}$$

(32)

$$\begin{aligned}&{z}'_{21} =-\hbox {Sc}\left( \frac{z_{21} }{\hbox {Sc}(\eta +\gamma )}-K_1 z_2 (1-z_2 )^{2}\right. \nonumber \\&\qquad \quad \left. +\frac{\gamma }{\eta +\gamma }z_0 z_{21} \right) , \end{aligned}$$

(33)

while the boundary conditions are

$$\begin{aligned} \left. \begin{aligned}&z_{01} (0)=1,\quad \,z_1 (0)=0,\quad z_{21} (0)=K_2 z_2 (0), \\&\frac{k_{nf} }{k_f }M\,z_{11} (0)+\left( {1-\phi +\phi \frac{\rho _\mathrm{CNT} }{\rho _f }} \right) \\&\quad \times \frac{\gamma }{\eta +\gamma } \Pr \, z_0 (0)=0 \\&z_{02} \rightarrow 0, \,z_{01} \rightarrow 0, \,z_1 \rightarrow 1, \,z_{21} \rightarrow 1\hbox { when }\;\eta \rightarrow \infty \end{aligned}\right\} .\nonumber \\ \end{aligned}$$

(34)

The above system of first-order ODEs is further solved by finite difference scheme which follows the three-stage Lobatto IIIa formula in MATLAB software.

Fig. 1

Behaviour of ${f}'$ vs. $\phi$.

Fig. 2

Behaviour of ${f}'$ vs. $\gamma$.

Fig. 3

Behaviour of ${f}'$ vs. M.

Fig. 4

Behaviour of $\theta$ vs. $\phi$.

Fig. 5

Behaviour of $\theta$ vs. $\gamma$.

4 Analysis

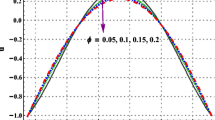
This section reports the variations of influential parameters on flow, temperature, concentration, skin friction and local Nusselt number. Variations in velocity through $\phi , \gamma$ and M are shown in figures 1–3 for both single- and multiwall CNTs. Intensification in the velocity of the fluid is observed with increase in $\phi , \gamma$ and M. It is also elaborated that the impact of multiwall CNTs dominates the single-wall CNTs because of low density. Increase in $\gamma$ corresponds to an enhancement in the curved surface radius. A large number of particles gain the velocity of the surface due to the increase in the contact area of the fluid particles and the surface, and as a result, the fluid velocity increases. For higher M, rapid movement of the fluid particle occurs towards the melting surface leading to an increase in velocity. An improvement in the momentum layer thickness is also observed with increase in $\phi , \gamma$ and M. Figures 4, 5, 6 and 7 are plotted for variations in temperature through $\phi , \gamma , M$ and $\delta$, respectively. Increase in $\phi$ and M leads to a decay in the temperature of the fluid while the opposite trend is observed for higher $\delta$ and $\gamma$. Rise in fluid temperature is more efficient for multiwall CNTs when compared with single-wall CNTs. Increase in M leads to higher convective flow from heat fluid towards the melting stretchable surface. Thus, the temperature of the fluid decays. Figures 8, 9 and 10 show the variation in concentration with higher $K_1$, $K_2$ and $\hbox {Sc}$. It is noticed that the concentration is higher for larger $\hbox {Sc}$ while the opposite trend is observed for increase in $K_1$ and $K_2$. Skin friction under the influence of $\phi , \gamma$ and M is shown in figures 11, 12 and 13. It is observed that the skin friction is larger for higher $\phi$ and $\gamma$ while it decays with increase in M. Figures 14, 15 and 16 show the variation of local Nusselt number through $\phi$, $\gamma$ and M. The rate of heat transfer (Nusselt number) intensifies with higher $\phi$ while the opposite behaviour has been observed for larger $\gamma$ and M. This dominating trend has been observed for multiwall CNTs when compared with single-wall CNTs. The characteristics of base liquid and nanotubes are shown in table 1.

Fig. 6

Behaviour of $\theta$ vs. M.

Fig. 7

Behaviour of $\theta$ vs. $\delta$.

Fig. 8

Behaviour of g vs. $K_1$.

Fig. 9

Behaviour of g vs. $K_2$.

Fig. 10

Behaviour of g vs. Sc.

Fig. 11

Behaviour of $C_f \sqrt{\mathrm{Re}}_s$ vs. $\phi$.

Fig. 12

Behaviour of $C_f \sqrt{\mathrm{Re}_{s}}$ vs. $\gamma$.

Fig. 13

Behaviour of $C_f \sqrt{\text {Re}}_s$ vs. M.

Fig. 14

Behaviour of $\frac{\text {Nu}_s}{\sqrt{\text {Re}_s}}$ vs. $\phi$.

Fig. 15

Behavior of $\frac{\text {Nu}_s}{\sqrt{\mathrm{Re}_{{s}}}}$ via $\gamma$.

Fig. 16

Behaviour of $\frac{{\text {Nu}_s} }{\sqrt{\text {Re}}_s}$ vs. M.

Table 1 Heat transport features of CNTs and water [9].

5 Consequences

In the present investigation, we have illustrated chemically reacting flow of water-based CNTs by a stretchable curved sheet. The vital results are

• the flow is higher for larger $\phi , \gamma$ and M. Impact of multiwall CNTs on the flow field is higher when compared with single-wall CNTs;

• the temperature of the fluid is enhanced for $\gamma$ while the opposite behaviour is examined for increase in $\phi$, M and $\delta$. Here also multiwall CNTs show dominating features when compared with single-wall CNTs;

• larger $K_1$ enhances the concentration while it reduces with an increase in $K_2$ and $\hbox {Sc}$;

• large $\phi$ and $\gamma$ cause increase in skin friction coefficient while it reduces for larger M;

• heat transfer rate enhances with increase in $\phi$ while it decays for larger $\gamma$ and M;

• impact of multiwall CNTs on skin friction coefficient and local Nusselt number is more than that of single-wall CNTs.