Temperature and concentration gradient effects on heat and mass transfer in micropolar fluid

Abstract

This study investigates the temperature and concentration gradients on the transfer of heat and mass in the presence of Joule heating, viscous dissipation and time-dependent first-order chemical reaction in the flow of micropolar fluid. Governing boundary value problems are solved analytically and the effects of parameters involved are studied. The behaviour of the Nusselt number (at both disks) is noted and recorded in a tabular form. The present results have an excellent agreement with the already published results for a special case. The rate of transport of heat by concentration gradient and the diffusion of solute molecules by temperature gradient are increased. The concentration field is increased by constructive chemical reaction and it decreases when the rate of destructive chemical reaction is increased.

1 Introduction

The study of non-Newtonian fluids is very important as many fluids in industry are of non-Newtonian nature. Moreover, many fluids used in the engineering processes are non-Newtonian. Due to the diversity in the non-Newtonian fluids, several constitutive equations for non-Newtonian fluids have been proposed. The micropolar fluid model is one of them. This model predicts microstructure which experiences rotation when the fluid deforms. Blood, certain biological fluids and liquid crystals with rigid molecules are well-known examples of micropolar fluids. Due to the immersion of microstructures in fluids, the microrotation, spin inertia, couple stresses, etc. are significant. Therefore, the usual conservation laws are not sufficient to describe the motion of micropolar fluid, i.e. one additional conservation law, the law of conservation of angular momentum, is used to model the flow of micropolar fluids. Mathematically speaking, addition of one more law to the usual conservation laws makes the problem more complex. Despite this fact, several researchers have studied the flow of micropolar fluid over different geometries. Some latest studies are mentioned in [1,2,3,4,5,6,7]. Squeezing flows occur at industry in the transport processes. Owing to this, the squeezing flows are studied immensely. For example, Kuzma [8] studied the effects of inertia on squeezing film flow. Theoretical analysis for the flow induced by the sinusoidal variation of gap between two disks was performed by Ishizawa and Takahashi [9]. Ishizawa et al [10] studied the unsteady flow between the parallel disks moving towards each other with time-dependent velocity. Hamza [11] considered the effects of magnetic field on the squeezing flow of viscous fluid between the two parallel plates and solved the problem by regular perturbation method. Usha and Sridharan [12] investigated the effects of time-dependent variation of gap (between two parallel elliptic gap) on the flow and concluded that external periodic force causes distortion in the waveform. Debaut [13] simulated the heat transfer effects in the squeezing flow of viscoelastic fluid using finite-element method. Khaled and Vafai [14] examined the effects of magnetic field on heat transfer in the flow over sensor surface. Duwairi et al [15] conducted the study for heat transfer in the squeezing flow between the parallel plates. Mahmood et al [16] studied the heat transfer effects on the flow over a porous surface. Theoretical investigations of unsteady squeezing flow of viscous fluid were carried out by Rashidi et al [17]. Domairy and Aziz [18] studied the effects of magnetic fluid and variation of distance between the porous disks analytically and compared the results obtained by direct numerical simulations. The squeezing effects of two parallel disks on the flow of micropolar fluid were studied by Hayat et al [19]. The effects of magnetic field on the squeezing flow of second grade fluid were analysed by Hayat et al [20]. The analytical treatment of the squeezing flow of Jeffrey fluid was done by Qayyum et al [21]. The analytical and numerical solutions for the problem describing the heat transfer in viscous fluid squeezed between two parallel disks were computed by Tashtoush et al [22]. Bahadir and Abbasov [23] considered the effects of Ohmic’s heating on the squeezing flow of an electrically conducting fluid in the presence of magnetic field and solved the resulting problems both analytically and numerically.

The transport of heat due to density differences caused by solute is significant in many industrial and natural processes. The effect of diffusion of heat due to concentration gradient is called diffusion thermo / Dufour effect. Soret also observed that temperature gradient enhances the process of diffusion of solute molecules. This process of transportation of solute molecules by temperature gradient is called thermal diffusion / Soret effect. Many studies on temperature and concentration gradient effects on transport of heat and mass are available. However, some recent studies are mentioned here. For example, Srinivasacharya et al [24] theoretically studied the effects of transport of heat and mass in mixed convection flow in a porous medium and concluded that the transport of heat and mass can be enhanced by temperature and concentration gradients. Osalusi et al [25] studied thermal diffusion and diffusion thermoeffects on magnetohydrodynamic flow over a rotating disk in the presence of viscous dissipation and Joule heating. The effects of temperature and concentration differences on the magnetohydrodynamic boundary layer flow over a porous surface were investigated by Hamid et al [26]. Beg et al [27] explored the effects of thermal diffusion and diffusion thermo on transfer of heat and mass in an electrically conducting fluid between parallel plates in the presence of sink / source. Simultaneous effects including thermal diffusion, diffusion thermo and chemical reaction on the flow of dusty viscoelastic fluid in the presence of magnetic field are studied theoretically by Prakash et al [28]. Thermal diffusion and diffusion thermo effects on the transfer of heat and mass in the Heimenz flow in a porous medium are discussed by Tsai and Huang [29]. Similarity solutions for the problems describing the heat and mass transfer in free convective flow over a porous stretchable surface are derived by Afify [30]. Awais et al [31] analysed the effect of temperature and concentration gradients on the flow of Jeffery fluid over a radially stretching surface. The thermal diffusion and diffusion thermoeffects on the flow of partially ionised fluid are examined by Hayat and Nawaz [32]. Seadawy and El-Rashidy [33] investigated nonlinear Rayleigh–Taylor instability in the heat and mass transfer in the flow in a cylinder.

The review of literature reveals that no study on Soret and Dufour effects on the transport of heat and mass in an axisymmetric squeezing flow of micropolar fluid between disks is available yet. The present investigation fills this gap. Such flows are significant as they occur in industry and engineering. Besides this, the transport of heat and mass due to concentration and temperature gradients, respectively, is encountered in compression and moulding processes. Due to this reason, the transport of heat and mass in the presence of temperature and concentration gradients is considered. This paper is organised as follows. Mathematical modelling is done in §2. The boundary value problems are solved by homotopy analysis method (HAM). This method is a powerful technique and has been employed by many researchers [19,20,21, 34]. A brief solution procedure is given in §3. The boundary conditions are verified in §4. Validation of results are recorded in §5 and results are discussed in §6.

2 Modelling and conservation laws

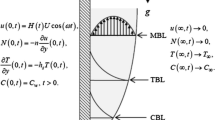
Let us consider the effects of temperature and concentration gradient on heat and mass transfer in the flow induced by the disk moving towards the lower disk subjected to the pores. The Joule heating, viscous dissipation and first-order chemical reaction are considered. Time-dependent magnetic field is applied and the induced magnetic field is neglected under the assumption of small magnetic Reynolds number [18,19,20]. The disks have constant temperatures and concentrations at the surface of disks are also constant. Physical model is given in figure 1.

Conservation equations for the two-dimensional axisymmetric flow [1,2,3,4,5,6,7, 35, 36] are as follows:

$$\begin{aligned}&\frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial w}{\partial z}=0, \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z} \nonumber \\&\quad =-\frac{1}{\rho }\frac{\partial p}{\partial r}+\frac{1}{\rho }( \mu +k) \left[ \frac{\partial ^{2}u}{\partial r^{2}}+ \frac{1}{r}\frac{\partial u}{\partial r}+\frac{\partial ^{2}u}{\partial z^{2} }-\frac{u}{r^{2}}\right] \nonumber \\&\qquad -\frac{k}{\rho }\frac{{\partial }N_{2}}{\partial z}-\frac{\sigma B_{0}^{2}}{ \rho (1-at)}u, \end{aligned}$$

(2)

$$\begin{aligned}&\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}\nonumber \\&\quad =-\frac{1}{\rho }\frac{\partial p}{\partial z}+\frac{1}{\rho } ( \mu +k) \left[ \frac{\partial ^{2}w}{\partial r^{2}}+\frac{1}{r} \frac{\partial w}{\partial r}+\frac{\partial ^{2}w}{\partial z^{2}}\right] \nonumber \\&\qquad -\frac{k}{\rho }\left[ \frac{\partial N_{2}}{\partial r}+\frac{N_{2}}{r} \right] , \end{aligned}$$

(3)

$$\begin{aligned}&\frac{\partial N_{2}}{\partial t}+u\frac{\partial N_{2}}{\partial r}+w\frac{ \partial N_{2}}{\partial z}\nonumber \\&\quad =\frac{\gamma _{1}}{\rho j}\left[ \frac{\partial ^{2}N_{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial N_{2}}{\partial r}+ \frac{\partial ^{2}N_{2}}{\partial z^{2}}-\frac{N_{2}}{r^{2}}\right] \nonumber \\&\qquad -\frac{k }{\rho j}\left[ 2N_{2}+\frac{\partial w}{\partial r}-\frac{\partial u}{ \partial z}\right] , \end{aligned}$$

(4)

$$\begin{aligned}&\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z} =\frac{K_{c}}{\rho C_{p}}\left( \frac{\partial ^{2}T}{ \partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{\partial ^{2}T }{\partial z^{2}}\right) \nonumber \\&\quad +\frac{( 2\mu +k) }{\rho C_{p}}\left\{ \left( \frac{\partial u}{\partial r}\right) ^{2}+\frac{u^{2}}{r^{2}}+\left( \frac{\partial w}{\partial z}\right) ^{2}\right. \nonumber \\&\quad \left. +\frac{1}{2}\left( \frac{\partial u}{\partial z}+\frac{\partial w}{ \partial r}\right) ^{2}\right\} +\frac{k}{2\rho C_{p}}\left( \frac{\partial u }{\partial z}-\frac{\partial w}{\partial r}-2N_{2}\right) ^{2}\nonumber \\&\quad -\frac{2\beta }{\rho C_{p}}\frac{N_{2}}{r}\frac{\partial N_{2}}{\partial r} \nonumber \\&\quad +\frac{\gamma _{1}}{\rho C_{p}}\left\{ \left( \frac{\partial N_{2}}{ \partial r}\right) ^{2}+\frac{N_{2}^{2}}{r^{2}}+\left( \frac{\partial N_{2}}{ \partial z}\right) ^{2}\right\} \nonumber \\&\quad +\frac{\alpha ^{*}}{\rho C_{p}}\left\{ \frac{\partial T}{\partial z} \left( \frac{\partial N_{2}}{\partial r}+\frac{N_{2}}{r}\right) -\frac{ \partial N_{2}}{\partial z}\frac{\partial T}{\partial r}\right\} \nonumber \\&\quad +\frac{ \sigma B_{0}^{2}}{\rho C_{p}(1-at)}u^{2} \nonumber \\&\quad +\frac{DK_{T}}{C_{p}C_{s}}\left( \frac{\partial ^{2}C}{\partial r^{2}}+ \frac{1}{r}\frac{\partial C}{\partial r}+\frac{\partial ^{2}C}{\partial z^{2} }\right) , \end{aligned}$$

(5)

$$\begin{aligned}&\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial r}+w\frac{\partial C}{\partial z} =D\left( \frac{\partial ^{2}C}{\partial r^{2}}+\frac{1}{r} \frac{\partial C}{\partial r}+\frac{\partial ^{2}C}{\partial z^{2}}\right) \nonumber \\&\quad +\frac{DK_{T}}{T_{\mathrm {m}}}\left( \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r} \frac{\partial T}{\partial r}+\frac{\partial ^{2}T}{\partial z^{2}}\right) \nonumber \\&\quad -\frac{K_{1}}{(1-at)}( C-C_{h}). \end{aligned}$$

(6)

In the above equations, $\mathrm {d}/\mathrm {d}t$ is the material derivative; u and w are the components of velocity field V along the radial (r) and axial (z) directions, respectively; T and C signify the temperature and concentration fields, respectively; j denotes the microinertia per unit mass; $N_{2}$ is the azimuthal component of microrotation field ${{\Omega }}$; $\mu$ and k are the viscosity coefficients; $\rho$ and $C_{p}$ represent the fluid density and specific heat of fluid, respectively; $B_{0}$ is the magnetic field strength; $K_{c}$ and $\sigma$ signify the thermal and electrical conductivities, respectively; $\alpha ^{*}$ denotes the micropolar heat conduction coefficient; D symbolises the Brownian motion coefficient; $K_{T}$ denotes the thermophoretic diffusion coefficient; $C_{s}$ signifies the concentration susceptibility; $T_{\mathrm {m}}$ denotes the mean fluid temperature; $K_{1}$ represents the chemical reaction constant; $C_{h}$ is the constant concentration at the upper disk; a is the constant having dimension 1 / t; and $\alpha ,$ $\beta ,$ $\gamma _{1}$ are the gyroviscosity coefficients. Further, $\mu ,$k,  $\alpha ,$ $\beta$ and $\gamma _{1}$ fulfill the following conditions:

$$\begin{aligned} \lambda +2\mu +k\ge 0,\quad k\ge 0,\quad 3\alpha +\beta +\gamma _{1}\ge 0,\quad \gamma _{1}\ge \vert \beta \vert . \end{aligned}$$

(7)

The velocity boundary conditions are developed through no slip assumption whereas rotation vector at the surface of disks is proportional to the vorticity. Thus, the boundary conditions for velocity, rotation vector, temperature and concentration fields are

$$\begin{aligned} \left. \begin{array}{l} u=0,\quad w=W_{w}=\dfrac{\mathrm {d}h_{w}}{\mathrm {d}t}=-\dfrac{a}{2}H( 1-at) ^{-1/2} ,\\ N_{2}=-n\dfrac{\partial u}{\partial z},\quad T=T_{h}, C=C_{h}\ \mathrm {at} \ z=H\sqrt{1-at}, \\ u=0,w=-W_{0},\quad N_{2}=-n\dfrac{\partial u}{\partial z},\\ T=T_{w},\quad C=C_{w}\ \mathrm {at} \ z=0. \end{array} \right\} \nonumber \\ \end{aligned}$$

(8)

Using the transformations

$$\begin{aligned}&u=\frac{ar}{2( 1-at) }f^{\prime }( \eta ) ,\quad w=-\frac{aH}{2\sqrt{1-at}}f( \eta ) ,\nonumber \\&N_{2}=\frac{ar}{ 2H( 1-at) ^{3/2}}h( \eta ) , \quad \theta ( \eta ) =\frac{T-T_{h}}{T_{w}-T_{h}},\nonumber \\&\phi ( \eta )=\frac{C-C_{h}}{C_{w}-C_{h}},\quad \eta =\frac{z}{ H\sqrt{1-at}}, \end{aligned}$$

(9)

in eqs (1)–(8), one obtains

$$\begin{aligned}&( 1+K) f^{\prime \prime \prime \prime }-\frac{\hbox {Re }}{2}(\eta f^{\prime \prime \prime }+3f^{\prime \prime }-2ff^{\prime \prime \prime })\nonumber \\&\quad -Kh^{\prime \prime }-\hbox {Re }Mf^{\prime \prime }=0, \end{aligned}$$

(10)

$$\begin{aligned}&f( 0) =S,\quad f( 1) =\frac{1}{2},\quad f^{\prime }( 0) =0,\quad f^{\prime }( 1) =0,\nonumber \\ \end{aligned}$$

(11)

$$\begin{aligned}&\left( 1+\frac{K}{2}\right) h^{\prime \prime }-\hbox {Re }K( 2h-f^{\prime \prime }) \nonumber \\&\quad -\frac{\hbox {Re }}{2}( 3h+\eta h^{\prime }+f^{\prime }h-2fh^{\prime }) =0, \end{aligned}$$

(12)

$$\begin{aligned}&h( 1) =-nf^{\prime \prime }( 1) ,\quad h( 0) =-nf^{\prime \prime }( 0) , \end{aligned}$$

(13)

$$\begin{aligned}&\theta ^{\prime \prime }+\frac{1}{2}\Pr \hbox {Re }( f\theta ^{\prime }-\eta \theta ^{\prime }) \nonumber \\&\quad +\frac{1}{2}\left( 1+\frac{K}{2}\right) \Pr \mathrm {Ec }\left( \frac{3}{\delta ^{2}}f^{\prime 2}+\frac{1}{2}f^{\prime \prime 2}\right) \nonumber \\&\quad +\frac{K}{8}\Pr \mathrm { Ec }(f^{\prime \prime 2}+4h^{2}-4f^{\prime \prime }h)-\frac{B}{2}\frac{\Pr \mathrm { Ec }}{\delta ^{2}}h^{2}\nonumber \\&\quad +\frac{1}{4}\left( 1+\frac{K}{2}\right) \frac{\Pr \mathrm { Ec }}{\hbox {Re }}\left( \frac{2 }{\delta ^{2}}h^{2}+h^{\prime 2}\right) \nonumber \\&\quad +A\hbox {Re }\Pr h\theta ^{\prime }+ \frac{1}{4}\hbox {Re }\Pr \mathrm { Ec}\,Mf^{\prime 2}\nonumber \\&\quad +\mathrm { Du }\Pr \phi ^{\prime \prime }=0, \end{aligned}$$

(14)

$$\begin{aligned}&\theta (0)=1,\quad \theta (1)=0, \end{aligned}$$

(15)

$$\begin{aligned}&\phi ^{\prime \prime }+\frac{1}{2}\hbox {Re }\mathrm { Sc }( f\phi ^{\prime }-\eta \phi ^{\prime }) +\mathrm { Sr}\,\mathrm {Sc}\,\theta ^{\prime \prime }\nonumber \\&\quad -\hbox {Re }\mathrm { Sc}\,\gamma \phi =0, \end{aligned}$$

(16)

$$\begin{aligned}&\phi (0)=1,\quad \phi (1)=0. \end{aligned}$$

(17)

Fig. 1

Schematic diagram.

Table 1 Verification of the boundary conditions for the suction case $(S>0)$ when $M=2$, Re $=$ 2.0, $K=0.5$ and

Table 2 Verification of the boundary conditions for the blowing case $(S<0)$ when $M=2$, Re$=$2.0, $K=0.5$ and

Table 3 The convergence of temperature and concentration fields for suction when $S=1=\hbox {Re }=\gamma ,$ $M=1.5=A=B,$ $K=0.5=\Pr =\mathrm {Ec}=\mathrm {Du}=\mathrm {Sr}=\mathrm {Sc},$

In the above derivation, we have taken $\gamma _{1}=(\mu +k/2)j,$ $j=\nu (1-at)/a$ [19, 20]. The dimensionless parameters in eqs (9)–(15) are the micropolar parameter $K=k/\mu$, the Reynolds number $\hbox {Re }=aH^{2}/\nu$, the Hartmann number $M=\sigma B_{0}^{2}/\rho a$, the suction / injection parameter $S=W_{0}\sqrt{1-at}/aH$ (it is worth mentioning that $S>0$ corresponds to suction, $S<0$ corresponds to injection, $S=0$ is the case when there is no suction / injection at the lower disk), the Prandtl number $\Pr =\mu C_{p}/K_{c}$, the Eckert number $\mathrm { Ec}=(ar)^{2}/C_{p}(T_{w}-T_{h})(1-at)^{2}$, the dimensionless radial length $\delta =r/H\sqrt{(1-at)}$, the dimensionless material parameters $A=\alpha ^{*}/\rho C_{p}H^{2}(1-at)$ and $B=\beta /\mu H^{2}(1-at)$, the Dufour number $\mathrm {Du}=DK_{T}(C_{w}-C_{h})/\nu C_{p}C_{s}(T_{w}-T_{h})$, the Schmidt number $\mathrm {Sc}=\nu /D$, the chemical reaction parameter $\gamma =K_{1}/a$ and the Soret number $\mathrm {Sr}=DK_{T}(T_{w}-T_{h})/\nu T_{\mathrm {m}}(C_{w}-C_{h})$.

The Nusselt number Nu and the Sherwood number Sh at both the disks are

$$\begin{aligned}&\mathrm {Nu}_{1,2} =\frac{ -K_{c}h_{w}(t)\frac{\partial T}{\partial Z} \vert _{z=0,h_{w}}}{K_{c}(T_{w}-T_{h})}\nonumber \\&\qquad \quad \,\,=\mathrm {Nu}_{1}=-\theta ^{\prime }(1),\nonumber \\&\mathrm {Nu}_{2}=-\theta ^{\prime }(0),\quad \nonumber \\&\mathrm {Sh}_{1,2} =\frac{ -h_{w}(t)D\frac{\partial C}{\partial Z}\vert _{z=0,h_{w}}}{D(C_{w}-C_{h})}\nonumber \\&\qquad \quad \,\,=\mathrm {Sh}_{1}=-\phi ^{\prime }(1),\nonumber \\&\mathrm {Sh}_{2}=-\phi ^{\prime }(0). \end{aligned}$$

(18)

3 Analytical solutions

The boundary value problems given by eqs (10)–(17) are solved analytically using the linear operators

$$\begin{aligned}&\pounds _{f}f( \eta ) =\frac{\mathrm{d}^{4}f}{\mathrm{d}\eta ^{4}},\quad \pounds _{h}h( \eta ) =\frac{\mathrm{d}^{2}h}{\mathrm{d}\eta ^{2}}, \nonumber \\&\pounds _{\theta }( \theta ( \eta ) ) =\frac{ \mathrm {d}^{2}\theta }{\mathrm{d}\eta ^{2}},\quad \pounds _{\phi }( \phi ( \eta ) ) =\frac{\mathrm{d}^{2}\phi }{\mathrm{d}\eta ^{2}} \end{aligned}$$

(19)

and the initial guesses

$$\begin{aligned}&f_{0}( \eta )=S-\frac{3}{2}(2S-1)\eta ^{2}+(2S-1)\eta ^{3}, \nonumber \\&h_{0}( \eta ) =-nf^{\prime \prime }( 0) -n [ f^{\prime \prime }( 1) -f^{\prime \prime }( 0) ] \eta , \nonumber \\&\theta _{0}( \eta ) =1-\eta ,\quad \phi _{0}(\eta )=1-\eta . \end{aligned}$$

(20)

4 Verification of boundary conditions

The boundary conditions for the microrotation are $h(0)=-nf^{\prime \prime }( 0)$ and $h(1)=-nf^{\prime \prime }( 1)$ at lower and upper disks, respectively. Here we take $n=1/2$, the case when microrotation at the solid surface is equal to vorticity. So, boundary conditions for $n=1/2$ are: $h(0)=-f^{\prime \prime }( 0) /2$ and $h(1)=-f^{\prime \prime }( 0) /2$. Numerical values of $f^{\prime \prime }( 0)$, h(0), $f^{\prime \prime }( 1)$ and h(1) both for suction and injection are given in tables 1 and 2, respectively. These tables show that boundary conditions are satisfied at each iteration. These tables also show that approximate series solutions converge at 10th order of approximations for $S>0$ and 15th order of approximations for $S<0$ (see tables 1 and 2). Table 3 shows that the Nusselt and Sherwood numbers at upper and lower disks converge at 21th order of approximations.

Table 4 Comparison of the present results with the published work [18] for the suction case when $S=0.3,$ $K=0$ and $\hbox {Re }=1.$

5 Validation of the study

Present results are verified by comparing with the already published work by Domairy and Aziz [18]. This comparison is represented in tables 4 and 5. Table 4 gives the comparison of the present results with the results obtained by homotopy perturbation method (HPM) [18] for different values of Reynolds and Hartmann numbers when $S=0.3$. This table reflects an excellent agreement between the HAM (present) and HPM [18] solutions. Table 5 also compares the values of f and $f^{\prime }$ for the present case with the values of f and $f^{\prime }$ obtained by HPM [18] for different values of independent variable $\eta$. An excellent agreement is observed. Moreover, the present results and already published work are also compared graphically as shown in figure 2. This figure shows that there is an excellent agreement between the results.

Table 5 Comparison of the present results with the published work [18] for the suction case when $S=0.1,$ $K=0$ and $\hbox {Re }=1$.

Fig. 2

Comparison between the HAM solution (solid lines) and HPM solution [18] (filled circles) when $\hbox {Re }=0.5,K=0$ and $S=0.1.$

Fig. 3

The effect of Prandtl number $\Pr$ on the dimensionless temperature $\theta (\eta )$.

Fig. 4

The effect of Eckert number Ec on the dimensionless temperature $\theta (\eta )$.

Fig. 5

The effect of Dufour number Du and Soret number Sr on the dimensionless temperature $\theta (\eta ).$

6 Results and discussion

Transport of heat and mass caused by convection, diffusion, temperature and concentration differences in the flow of micropolar fluid are modelled. The governing problems are solved analytically. The behaviour of emerging parameters on the transport of heat and mass is studied graphically. The behaviour of temperature and concentration field under the variation of physical parameters is studied. Moreover, the Nusselt numbers and Sherwood numbers (at both the disks) are noted and tabulated. The effects of dimensionless parameters on the dimensionless temperature $\theta (\eta )$ are noted in figures 3–8. The effect of the Prandtl number on dimensionless temperature $\theta (\eta )$ is displayed in figure 3. There is an increase in temperature when $\Pr$ is increased. Ec appears as a coefficient of viscous dissipation and Joule heating terms (see eq. (14)). An increase in the Eckert number corresponds to an increase in the dissipated heat. Therefore, the temperature rises. Moreover, an increase in the Eckert number enhances the effect of Joule heating and the temperature is expected to increase. This fact is well exhibited by the present theoretical results (see figure 4). The effect of temperature and concentration gradients on the dimensionless temperature is shown in figure 5. An increase in Du causes more concentration gradient and more heat transfer from disks into the fluid and the temperature of the fluid increases. This is what the present results exhibit. The behaviour of temperature by varying Sc is given in figure 6. This figure indicates that the temperature increases as Sc is increased. An increase in M corresponds to an increase in magnetic intensity and dissipated heat due to increase in Joule heating and adds to the fluid. Consequently, the temperature of fluid rises. This behaviour is well supported by the present theoretical results as shown in figure 7. The effect of K is illustrated in figure 8. This figure reveals that the temperature has an increasing trend when the micropolar parameter is increased because K appears as a coefficient of some of the viscous dissipation terms in the energy equation (see eq. (14)) and an increase in it causes an increase in the heat dissipated due to friction force, and so the temperature increases.

Fig. 6

The effect of Schmidt number Sc on the dimensionless temperature $\theta (\eta ).$

Fig. 7

The effect of Hartmann number M on the dimensionless temperature $\theta (\eta ).$

Fig. 8

The effect of micropolar parameter K on the dimensionless temperature $\theta (\eta ).$

Fig. 9

The effect of Eckert number Ec on the dimensionless concentration $\phi (\eta ).$

Fig. 10

The effect of Soret number Sr and Dufour number Du on the dimensionless concentration $\phi (\eta ).$

Fig. 11

The effect of Schmidt number Sc on the dimensionless concentration $\phi (\eta ).$

Fig. 12

The effect of chemical reaction parameter $\gamma$ on the dimensionless concentration $\phi (\eta ).$

Fig. 13

The effect of Hartmann number M on the dimensionless concentration $\phi (\eta ).$

The effects of dimensionless parameters on the dimensionless concentration $\phi (\eta )$ are shown in figures 9–13. The effect of Ec on the concentration field is given in figure 9. An increase in Ec forces the concentration field to decrease. The effects of Sr and Du numbers on the dimensionless concentration $\phi (\eta )$ are given in figure 10. This figure illustrates that the concentration increases when Du is increased but it decreases when Sr is increased. The dimensionless concentration $\phi (\eta )$ is a decreasing function of Sc (see figure 11). The phenomenon of diffusion of solution is greatly affected by the chemical reaction. The chemical reaction parameter $\gamma >0$ when the reaction is a destructive chemical reaction, whereas $\gamma <0$ when the chemical reaction is constructive. When there is no chemical reaction, $\gamma =0.$ The behaviour of concentration field under the variation of chemical reaction parameter $\gamma$ is shown in figure 12. For constructive chemical reaction, the concentration increases but for destructive chemical reaction, the concentration is decreased. The effect of magnetic field on the dimensionless concentration field is shown in figure 13. This figure shows that the concentration field is a decreasing function of M because the Lorentz force is an opposing force and the motion of the fluid slows down as magnetic intensity is increased. The transport of solute particles due to convection becomes slow and hence the concentration decreases.

Table 6 Numerical values of Nusselt numbers Nu$_{1}$ and Nu$_{2}$ and Sherwood numbers Sh$_{1}$ and Sh$_{2}$ for different values of dimensionless parameters.

The numerical values of the Nusselt Nu$_{1,2}$ and Sherwood Sh$_{1,2}$ numbers at lower and upper disks are computed and are recorded in table 6. The Nusselt number at the upper disk Nu$_{1}$ increases with an increase in $\hbox {Re},$ M, K, suction parameter $(S>0),$ injection parameter $(S<0),$ Ec, $\Pr ,$ Du, Sr, Sc and destructive chemical reaction parameter $(\gamma >0),$ whereas it decreases by increasing the constructive chemical reaction parameter $(\gamma <0).$ Similarly, the Nusselt number at the lower disk Nu$_{2}$ is a decreasing function of M, $K,$ suction parameter ($S>0),$ injection parameter $(S<0),$ Ec, $\Pr ,$ Du, Sr, Sc and destructive chemical reaction parameter $(\gamma >0)$. However, Nu$_{2}$ is an increasing function of $\hbox {Re}$ and the constructive chemical reaction parameter $(\gamma <0).$ The Sherwood number at the upper disk Sh$_{1}$ decreases with an increase in $\hbox {Re},$ M,  K, suction parameter $(S>0),$ injection parameter $(S<0),$ Ec, $\Pr ,$ Du, Sr, Sc and destructive chemical reaction parameter $(\gamma$ $>0),$ whereas it increases by increasing the constructive chemical reaction parameter $(\gamma <0)$. Similarly, the Sherwood number at the lower disk Sh$_{2}$ is an increasing function of $\hbox {Re},$ M, $K,$ suction parameter ($S>0),$ injection parameter $(S<0),$ Ec, Pr, Du, Sr, Sc and destructive chemical reaction parameter $(\gamma >0)$. However, Sh$_{2}$ is a decreasing function of the constructive chemical reaction $(\gamma <0).$

7 Final remarks

The Dufour and Soret effects on heat and mass transfer in micropolar fluid in the presence of Joule heating and first-order chemical reaction are investigated. Some of the observations are recorded below.

• 1. Joule heating causes an increase in temperature by increasing the magnetic field intensity because more heat dissipates due to Ohmic dissipation. This heat adds to the fluid and so its temperature increases, but the Joule heating causes a decrease in concentration by increasing the magnetic field intensity.

• 2. Viscous dissipation (the rate at which work is done by the viscous force) is the heat that dissipates because of friction, the friction due to the viscous nature of fluid which adds to the fluid and hence its temperature increases. Further, Ec appears as a coefficient of viscous dissipation term. Thus, an increase in Ec corresponds to the generation of more heat due to viscous dissipation. This is a quite adherence with the physically realistic case.

• 3. The diffusion of molecules of solute is greatly affected by both constructive and destructive chemical reactions.

• 4. The Nusselt number at both the disks increases when the chemical reaction is increased.

• 5. The heat transfer rate (at the upper disk) Nu$_{1}$ is increased when $\hbox {Re},$ $M,$ $K,$ $\mathrm{suction\, parameter}\, (S>0),$ injection parameter ($S<0),$ Ec, Pr, Du, Sr, constructive chemical reaction parameter ($\gamma <0)$ and Sc are increased. However, it decreases when $\gamma <0.$ Heat transfer rate (at the lower disk) Nu$_{2}$ is increased when $\hbox {Re }$ and$\ \gamma$ $<0$ are increased but it is decreased by increasing $M,$ $K,$ suction parameter (S${>}0),$ injection parameter (S${<}0),$ Ec, Pr, Du, Sr, Sc and destructive chemical reaction parameter ($\gamma {>}0).$

• 6. Diffusion rate of solute molecules from the upper disk Sh$_{1}$ into the flow regime is decreased by increasing $\hbox {Re},$ $M,$ $K,$ suction parameter (S > 0), injection parameter (S < 0), Ec, Pr, Du, Sr, Sc and destructive chemical reaction parameter ($\gamma>0).$ However, it increases when $\gamma <0$. Diffusion rate of the solute molecules from the lower disk Sh$_{2}$ is decreased when $\gamma$ $<0$ is increased but it increases by increasing $\hbox {Re},$ $M,$ $K,$ suction parameter ($S>$ 0), injection parameter ($S<$ 0), Ec, Pr, Du, Sr, Sc and destructive chemical reaction parameter ($\gamma >0).$