Introduction

Nanofluids are a type of fluid that have been infused with tiny nanoparticles. These nanoparticles can be made up of a variety of materials, including metals, oxides and other materials. When these nanoparticles are mixed into a fluid, they can dramatically change its properties. Nanofluids have been shown to have enhanced thermal conductivity, improved lubrication and increased stability. They also have the potential to improve a wide range of medical and industrial processes from cooling systems to energy production. Nanofluids can be used in medical imaging, drug delivery, tissue engineering and cancer treatment. Choi [1] was the explorer who laid the groundwork for the evolution of nanofluids as a new category of thermal transmitted fluids. He proposed the idea that adding small amounts of nanoparticles to a fluid could dramatically enhance its thermal conductivity. Soon after this, Kim et al. [2] investigated the convective instability and heat transmission properties of nanofluids. Buongiorno [3] documented a study to explain the convective heat transmission in nanofluids. Tiwari and Das [4] examined the heat transfer performance of a square cavity filled with nanofluid under differentially heated conditions. The study also investigates the influence of the lid-driven motion on the heat transfer performance of the nanofluid. Buongiorno’s work [3] was extended by Khan and Pop [5] in regard to boundary layer nano-liquid flow over a stretchable sheet. The examination explored the effects of various parameters such as the stretching rate, nanoparticle volume fraction, thermal conductivity and heat transfer characteristics of the nanofluid. The heat and mass transmission phenomenon of nanofluid flow past a vertical plate under natural convection conditions were elaborated by Kuznetsov et al. [6]. Cu–H\(_{2}\)O-based nanofluid was evaluated and documented by Raza et al. [7], by taking into account the impact of Brownian motion and thermophoresis, which are two unique properties of nanofluids. Further literature can be seen [8,9,10].

Fig. 1
figure 1

Geometrical perspective of problem

Full size image
Fig. 2
figure 2

Action of \((\kappa )\) over \(f^{\prime }(\zeta )\)

Full size image
Fig. 3
figure 3

Action of \((\phi )\) over \(f^{\prime }(\zeta )\)

Full size image
Fig. 4
figure 4

Action of \((\alpha _{1})\) over \(f^{\prime }(\zeta )\)

Full size image

Carbon nanotubes (both single and multiple-walled) are one of the most fascinating and promising materials of our time. These incredibly small tubes are made up of carbon atoms, arranged in a unique way that creates a strong, flexible and highly conductive structure. They are so small that they are measured in nanometers or billionths of a meter. Carbon nanotubes have the strength to revolutionize a broader aspect of industries from electronics to medicine to energy. They are already being used in everything from super-strong materials to ultrafast computer chips, and scientists are constantly discovering new ways to harness their unique properties. Maxwell [11] conducted a formal investigation on carbon nanotubes, exploring their effects on electricity and magnetism. Later on, Xue [12] developed a model to predict the thermal conductivity of CNT-based composites. The model takes into account the microstructure of the composites, including the orientation, length and concentration of the CNTs as well as the thermal conductivity of the surrounding matrix material. Khan et al. [13] investigated the dynamics of Stoke’s first problem for CNTs suspended nanofluids in the presence of slip boundary condition. The results of the study show that the inclusion of CNTs enhances the heat transmission rate and the skin friction coefficient, while slip boundary condition has a prominent impact on the fluid flow and heat transfer performance of the nanofluid. Hayat et al. [14] investigated the radiation effects for nanofluid flow over a rotating disk in the presence of carbon nanotubes (CNTs) and partial slip. Wakif et al. [15] performed a semi-analytical analysis of electro-thermo-hydrodynamic stability in dielectric nanofluids using Buongiorno’s mathematical model. A mathematical model to analyze the behavior of CNT-based nanomaterial flow in the presence of two coaxially circulating disks was unveiled by Khan et al. [16]. The results of the study show that the existence of CNTs enhances the heat transmission rate and reduces the occurrence of entropy, while affecting the flow and temperature fields of the nanomaterial. Acharya et al. [17] scrutinized the mixed convective flow of carbon nanotubes (CNTs) over a convectively heated curved surface. Due to the prominent applications of carbon nanotubes, many researchers tried to harness the properties of CNTs [18,19,20,21,22].

Fig. 5
figure 5

Action of \((\kappa )\) over \(\theta (\zeta )\)

Full size image
Fig. 6
figure 6

Action of \((\phi )\) over \(\theta (\zeta )\)

Full size image
Fig. 7
figure 7

Action of \((\lambda _{1})\) over \(\theta (\zeta )\)

Full size image
Fig. 8
figure 8

Action of \((R_{\text{D}})\) over \(\theta (\zeta )\)

Full size image

Nowadays scrutinization of non-Newtonian fluids has become the central hotspot for engineers and scientists owing to its bright and encouraging applications in industry. Non-Newtonian fluids are fluids which disobey law of viscosity unveiled by Newton. Salient utilization of non-Newtonian liquids incorporates; drag reducing agents (heavy oils and greases), printing technology, biological systems and strategies, food processing, fluorescent lamps, electric devices and many others. One of many proposed non-Newtonian liquids is second-grade fluid, which possesses stress tensor relationship with dual derivatives. In recent times, Hayat and Sajid [23] amplified second-grade axisymmetric fluid flow past an elastic sheet. Saif et al. [24] given thought to a stagnation point stream of a second-grade nano-material in the vicinity of nonlinear extending surface with a fluctuating thickness. Abderrahim [25] documented a numerical procedure in order to simulate steady MHD flows of radiative Casson fluids over a horizontal stretching sheet. Hayat et al. [26] given an explanation of second-grade fluid flow across a porous surface. Radiative stream of a second-grade nanofluid overtop an extending surface was illustrated by Jamshed et al. [27]. The Stefan blowing impact was incorporated by Gowda et al. [28] to investigate the second-grade fluid flow overtop a curved elastic surface. Further literature can be found at [29,30,31,32].

Fig. 9
figure 9

Action of \((\kappa )\) over \(P(\zeta )\)

Full size image
Fig. 10
figure 10

Action of \((\kappa )\) over \(P^{\prime }(\zeta )\)

Full size image
Fig. 11
figure 11

Action of \((\kappa )\) over (Cf)

Full size image
Fig. 12
figure 12

Action of \((\kappa )\) over (Nu)

Full size image

The study of fluid flow over a stretchable boundary is essential in the manufacturing of polymer films, sheets and fibers. Stretching of polymer materials is a critical step in the formation of these materials and proper understanding of the boundary layer flow is essential for achieving the desired properties. Moreover in the production of textiles, boundary layer flow over a stretching surface plays a crucial role in the spinning and weaving of fibers. Aerodynamics, bio-inspired robotics, wind and water turbines are some crucial practical applications of boundary layer flow across a flexible surface. Sakiadis [33] initiated the investigations of streams in regard with boundary layer description across a stretchable surface and unveiled its numerical findings. The 2-D laminar flow of viscous fluid across a stretchable sheet was investigated by Crane [34]. Most of the previous studies incorporated boundary layer flow due to stretching surface, either linear or nonlinear; however, scrutinization of fluid flows through curved extending surfaces has not been studied much. Sajid et al. [35] were the pioneers who initiated the study of fluid flow in regard with boundary layer description across a curved elongating surface. Hayat et al. [36] illustrated the effects of Darcy–Forchheimer flow, Cattaneo–Christov heat flux as well as heterogeneous-homogeneous reactions on the behavior of viscous fluid flow over a curved stretching surface. Hayat et al. [37] unveiled a numerical model to analyze the influences of convective heat and mass transfer via nonlinear curved stretching sheet. Sugunamma et al. [38] documented the impact of frictional heated radiative ferrofluid flow over a slandering stretchable surface. Further work can be seen at [39,40,41,42].

We conducted this investigation because CNTs are widely used in the engineering and healthcare sectors. Over a curved stretched sheet, we investigated the heat transfer through a radiative flow of a boundary layer description and internal heat generation of a second-grade nanofluid made of carbon nanotubes (SWCNTs and MWCNTs). In-depth literary analysis revealed that a combination of such effects had never before been investigated. As a result, the inquiry is divided into several sections. Following a review of the literature, the first section elaborates the mathematical formulation, while the second section includes the mathematical solution obtained numerically by deploying NDSolve technique using software Mathematica along with significant discoveries via graphical representation. The final portion is set up to draw conclusions from the entire investigation.

Mathematical analysis

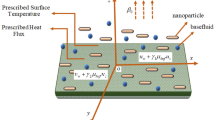
The flow under inspection is 2D-steady incompressible flow overtop a curved extending sheet at \(\grave{r}=\grave{R}_{\text{c}}^{*}.\) Geometrical vision of problem is described by Fig. 1. Curvilinear coordinates have been engaged to model the governing equations. Nanofluid being studied is composed by introducing nano-sized particles of carbon nanotubes (SWCNTs and MWCNTs) to second-grade fluid (base fluid). Moreover, effects of internal heat generation and thermal radiation have also been utilized to inspect the process of thermal transmission. The curved sheet is being stretched linearly in \(\grave{s}\) direction with velocity \(\grave{u}=a\grave{s},\) where \(a>0\) is the stretching constant. The free stream temperature and sheet’s temperature are represented as \(\grave{T}_{\infty }\) and \(\grave{T} _{\text{w}}\), respectively.

The second-grade fluid possess an extra stress tensor [27] defined as

$$\begin{aligned}{} & {} \mathbf {\tau }=-p\mathbf {I+}\grave{\mu }\textbf{A}_{1} +\grave{\alpha }_{1} \textbf{A}_{2}+\grave{\alpha }_{2}\textbf{A}_{1}^{2}, \end{aligned}$$
(1)

where p denotes pressure, \(\textbf{I}\) indicates identity tensor, \(\grave{ \mu }\) is dynamic viscosity, \(\alpha _{\text{j}}(j=1,2)\) are second-grade material constants and the first two Rivlin–Ericksen tensors \(\textbf{A}_{1}\) and \(\textbf{A}_{2}\) are described as

$$\begin{aligned} \left. \begin{array}{c} \textbf{A}_{1}=(\hbox {grad}\textbf{V})^\text{t}+(\hbox {grad}\textbf{V}), \\ \textbf{A}_{2}=\textbf{A}_{1}(\hbox {grad}\textbf{V})+\frac{\text{d}\textbf{A}_{1}}{ \text{d}t}+(\hbox {grad}\textbf{V})^\text{t}\textbf{A}_{1}, \end{array} \right\} \end{aligned}$$
(2)

in which d/dt is material time derivative, and \(\textbf{V}\) is the velocity vector. This fact should be noticed that when \(\alpha _{1}=\alpha _{2}=0,\) the fundamental equation for second-grade fluid reduces to that of viscous fluid. Employing the above assumption under boundary layer approximation, the equations that govern the flow are expressed as [27, 39]:

$$\begin{aligned}{} & {} \frac{\partial }{\partial \grave{r}}\left( (\grave{r}+\grave{R}_{\text{c}}^{*}) \grave{v}\right) +\grave{R}_{\text{c}}^{*}\frac{\partial \grave{u}}{\partial \grave{s}}=0\textbf{,} \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \frac{\grave{u}^{2}}{\grave{r}+\grave{R}_{\text{c}}^{*}} =\frac{1}{\grave{\rho } _{\text{nf}}}\frac{\partial P}{\partial \grave{r}}, \grave{v}\frac{\partial \grave{u}}{\partial \grave{r}}+\frac{\grave{R} _{\text{c}}^{*}\grave{u}}{\grave{r}+\grave{R}_{\text{c}}^{*}} \frac{\partial \grave{ u}}{\partial \grave{s}}+\frac{\grave{u}\grave{v}}{\grave{r}+\grave{R} _{\text{c}}^{*}}\nonumber \\{} & {} \qquad\quad =-\frac{1}{\grave{\rho }_{\text{nf}}}\frac{\grave{R}_{\text{c}}^{*}}{ \grave{r}+\grave{R}_{\text{c}}^{*}}\frac{\partial P}{\partial \grave{s}} +\nu _{\text{nf}}\left( \frac{\partial ^{2}\grave{u}}{\partial \grave{r}^{2}} +\frac{1}{ \grave{r}+\grave{R}_{\text{c}}^{*}}\frac{\partial \grave{u}}{\partial \grave{r}} -\frac{\grave{u}}{(\grave{r}+\grave{R}_{\text{c}}^{*})^{2}}\right) \end{aligned}$$
(4)
$$\begin{aligned}{} & {} +\frac{\alpha _{1}}{\grave{\rho }_{\text{nf}}}\left( \begin{array}{c} \frac{2\grave{R}_{\text{c}}^{*}}{\grave{r}+\grave{R}_{\text{c}}^{*}}\frac{\partial ^{2}\grave{u}}{\partial r^{2}}\frac{\partial \grave{u}}{\partial \grave{s}}- \frac{2\grave{R}_{\text{c}}^{*}}{(\grave{r}+\grave{R}_{\text{c}}^{*})^{2}}\frac{ \partial \grave{u}}{\partial \grave{r}}\frac{\partial \grave{u}}{\partial \grave{s}}+\frac{2}{\grave{r}+\grave{R}_{\text{c}}^{*}}\grave{v}\frac{\partial ^{2}\grave{u}}{\partial \grave{r}^{2}} \\ -\frac{2}{(\grave{r}+\grave{R}_{\text{c}}^{*})^{2}}\grave{v}\frac{\partial \grave{u}}{\partial r}-\frac{4\grave{R}_{\text{c}}^{*}}{(\grave{r}+\grave{R} _{\text{c}}^{*})^{2}}\grave{u}\frac{\partial ^{2}\grave{u}}{\partial \grave{r} \partial \grave{s}}-\frac{4\grave{u}}{(\grave{r}+\grave{R}_{\text{c}}^{*})^{2}} \frac{\partial \grave{v}}{\partial \grave{r}}+\frac{2\grave{R}_{\text{c}}^{*}}{( \grave{r}+\grave{R}_{\text{c}}^{*})^{3}}\grave{u}\frac{\partial \grave{u}}{ \partial \grave{s}} \end{array} \right) , \end{aligned}$$
(5)
$$\begin{aligned}{} & {} \grave{v}\frac{\partial \grave{T}}{\partial \grave{r}}+\frac{R_{\text{c}}^{*} \grave{u}}{\grave{r}+\grave{R}_{\text{c}}^{*}}\frac{\partial \grave{T}}{ \partial \grave{s}} =\alpha _{\text{nf}}\left( \frac{\partial ^{2}\grave{T}}{ \partial \grave{r}^{2}}+\frac{1}{\grave{r}+\grave{R}_{\text{c}}^{*}}\frac{ \partial \grave{T}}{\partial \grave{r}}\right) \nonumber \\{} & {} \quad -\frac{1}{\grave{\rho }_{\text{nf}}( \grave{r}+\grave{R}_{\text{c}}^{*})}\frac{\partial }{\partial \grave{r}}(\grave{ r}+\grave{R}_{\text{c}}^{*})\grave{q}_{\text{r}} +\frac{\grave{\gamma }}{(\grave{\rho } C_{\text{p}})_{\text{nf}}}(\grave{T}-\grave{T}_{\infty }). \end{aligned}$$
(6)

The associated constraints are as follows:

$$\begin{aligned} \left. \begin{array}{c} \grave{u}=a\grave{s},\grave{v}=0,\grave{T}=\grave{T}_{\text{w}}\text { \ \ \ \ \ at } \grave{r}=0, \\ \grave{u}\rightarrow 0,\frac{\partial \grave{u}}{\partial \grave{r}} \rightarrow 0,\grave{T}\rightarrow \grave{T}_{\infty }\text { \ \ \ \ \ as } \grave{r}\rightarrow \infty . \end{array} \right\} \end{aligned}$$
(7)

where \(\grave{v}\) and \(\grave{u}\) are velocities along \(\grave{r}\) and \(\grave{s}\) directions, respectively, for the curved sheet \(\grave{R} _{\text{c}}^{*}\) indicates its radius of curvature, \(\grave{T}\) stands for base fluid’s (second grade fluid) temperature, P for dimensionless pressure, \(\grave{q}_{\text{r}}\) for radiative heat flux, \(\grave{\gamma }\) for rate of volumetric heat generation caused by heat source. Furthermore, \((\rho C_\text{p})_{\text{nf}}\) stands for volumetric heat capacity of nanofluid \(\grave{\mu } _{\text{nf}}\) for dynamic viscosity of nanofluid \(\grave{k}_{\text{nf}}\) for thermal conductivity and \(\alpha _{\text{nf}}\) for thermal diffusivity and their mathematical expressions [12] are stated as

$$\begin{aligned}{} & {} \left. \begin{array}{c} \mu _{\text{nf}}=\frac{\mu _{\text{f}}}{(1-\phi )^{2.5}}\text {, }\alpha _{\text{nf}}=\frac{k_{\text{nf}} }{(\rho C_{\text{p}})_{\text{nf}}}, \\ (\rho C_{\text{p}})_{\text{nf}}=(1-\phi )(\rho C_{\text{p}})_{\text{f}}+\phi (\rho C_{\text{p}})_{\text{CNT}}, \end{array} \right\} \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \left. \begin{array}{c} \frac{(\rho C_{\text{p}})_{\text{nf}}}{(\rho C_{\text{p}})_{\text{f}}}=1-\left( 1-\frac{(\rho C_{\text{p}})_{\text{CNT}}}{(\rho C_{\text{p}})_{f}}\right) \phi , \\ \rho _{\text{nf}}=(1-\phi )\rho _{\text{f}}+\phi \rho _{\text{CNT}}, \end{array} \right\} \end{aligned}$$
(9)
$$\begin{aligned}{} & {} \frac{k_{\text{nf}}}{k_{\text{f}}}=\frac{(1-\phi )(k_{\text{CNT}}-k_{\text{f}}) +2\phi k_{\text{CNT}}\ln \left( \frac{k_{\text{CNT}}+k_{\text{f}}}{2k_{\text{f}}}\right) }{(1-\phi )(k_{\text{CNT}}-k_{\text{f}})+2\phi k_{\text{f}}\ln \left( \frac{k_{\text{CNT}}+k_{\text{f}}}{2k_{\text{f}}}\right) }, \end{aligned}$$
(10)

where \(\grave{\mu }_{\text{f}}\) stands for base fluid’s viscosity, \(\phi\) for concentration of nanoparticles, \(\alpha _{\text{nf}}\) for thermal diffusivity of nanofluid and \((\rho _{\text{f}},\rho _{\text{CNT}})\) and \((k_{\text{f}},k_{\text{CNT}})\) stands for density and thermal conductivity of base fluid (second grade fluid) and carbon nanotubes, respectively.

The term for radiative heat flux is estimated by Rooseland’s approximation [43] as:

$$\begin{aligned}{} & {} \grave{q}_{\text{r}}=-\frac{4\grave{\sigma }^{*}}{3\grave{a}_{\text{R}}} \frac{\partial \grave{T}^{4}}{\partial \grave{r}}, \end{aligned}$$
(11)

where \(\grave{a}_{\text{R}}\) denotes the coefficient for Rooseland mean approximation and \(\grave{\sigma }\) is Stefan–Boltzmann constant. Temperature variation is taken into account in such fashion that \(\ \grave{T}^{4}\) can be expanded about \(\grave{T}_{\infty }\) using Taylor series expansion while omitting terms of higher order:

$$\begin{aligned} \grave{T}^{4}\approx 4\grave{T}_{\infty }^{3}\grave{T}-3\grave{T}_{\infty }^{4}. \end{aligned}$$
(12)

Now using Eq. (11) and Eq. (12) in Eq. (6) we get:

$$\begin{aligned}{} & {} \grave{v}\frac{\partial \grave{T}}{\partial \grave{r}}+\frac{\grave{R} _{\text{c}}^{*}\grave{u}}{\grave{r} +\grave{R}_{\text{c}}^{*}} \frac{\partial \grave{ T}}{\partial \grave{s}} \nonumber \\{} & {} \quad =\frac{\grave{k}_{\text{nf}}}{(\rho C_{\text{p}})_{\text{nf}}}\left( 1+ \frac{16\grave{\sigma }^{*}\grave{T}_{\infty }^{3}}{3\grave{a}_{\text{R}}\grave{k }_{\text{f}}(\grave{k}_{\text{nf}}/\grave{k}_{\text{f}})}\right) \nonumber \\{} & {} \quad \left( \frac{\partial ^{2}\grave{ T}}{\partial \grave{r}^{2}}+\frac{1}{\grave{r}+\grave{R}_{\text{c}}^{*}}\frac{ \partial \grave{T}}{\partial \grave{r}}\right) +\frac{\grave{\gamma }}{(\rho C_{\text{p}})_{\text{nf}}}(\grave{T}-\grave{T}_{\infty }). \end{aligned}$$
(13)

Taking \(R_{\text{D}}=\frac{16\grave{\sigma }^{*}\grave{T}_{\infty }^{3}}{3\grave{ a}_{\text{R}}\grave{k}_{\text{f}}}\) as radiation parameter [44], Eq. (13) takes the form:

$$\begin{aligned}{} & {} \grave{v}\frac{\partial \grave{T}}{\partial \grave{r}}+\frac{\grave{R} _{\text{c}}^{*}\grave{u}}{\grave{r}+\grave{R}_{\text{c}}^{*}}\frac{\partial \grave{ T}}{\partial \grave{s}} =\frac{\nu _{\text{f}}}{\curlywedge _{3}}\frac{1}{\Pr } \frac{\grave{k}_{\text{nf}}}{\grave{k}_{\text{f}}}\left( 1+\frac{R_{\text{D}}}{(\grave{k}_{\text{nf}}/ \grave{k}_{\text{f}})}\right) \nonumber \\{} & {} \quad \left( \frac{\partial ^{2}\grave{T}}{\partial \grave{r }^{2}}+\frac{1}{\grave{r}+\grave{R}_{\text{c}}^{*}}\frac{\partial \grave{T}}{ \partial \grave{r}}\right) +\frac{\grave{\gamma }}{(\grave{\rho }C_{\text{p}})_{\text{nf}}}(\grave{T}-\grave{T} _{\infty }), \end{aligned}$$
(14)

where Pr \(=\frac{\nu _{\text{f}}}{\grave{\alpha }_{\text{f}}}\), symbolizes Prandtl number. To simplify the governing equations, we engage the following similarity variables:

$$\begin{aligned} \left. \begin{array}{c} \grave{u}=\grave{a}\grave{s}f^{\prime }(\varsigma ),\grave{v}=-\frac{\grave{R }_{\text{c}}^{*}}{\grave{r}_{\text{d}}+\grave{R}_{\text{c}}^{*}}\sqrt{\grave{a}\nu _{\text{f}}} f(\varsigma ),\varsigma =\sqrt{\frac{\grave{a}}{\nu _{\text{f}}}}\grave{r}, \\ P=\rho \grave{a}^{2}\grave{s}^{2}P(\varsigma ),\grave{T}=\grave{T}_{\infty }+ \frac{A\grave{s}}{l}\theta (\varsigma ),\theta (\varsigma )=\frac{\grave{T}- \grave{T}_{\infty }}{\grave{T}_{\text{w}}-\grave{T}_{\infty }}. \end{array} \right\} \end{aligned}$$
(15)

With the help of Eq. (15), Eq. (3) is trivially satisfied and Eq. (4), Eq. (5) and Eq. (14) can be written as:

$$\begin{aligned}{} & {} \frac{\partial P}{\partial \varsigma }\frac{1}{\curlywedge _{1}} =\frac{ f^{\prime 2}}{\varsigma +\kappa }, \nonumber \\{} & {} \frac{2\kappa }{\varsigma +\kappa }\frac{P}{\curlywedge _{1}}-\frac{\kappa }{ \varsigma +\kappa }ff^{\prime \prime } +\frac{\kappa }{\varsigma +\kappa } f^{\prime ^{2}}-\frac{\kappa }{(\varsigma +\kappa )^{2}}ff^{\prime }-\curlywedge _{2}\left( f^{\prime \prime \prime }+\frac{1}{\varsigma +\kappa }f^{\prime \prime }-\frac{1}{(\varsigma +\kappa )^{2}}f^{\prime }\right) \end{aligned}$$
(16)
$$\begin{aligned}{} & {} -\frac{\alpha _{1}}{\curlywedge _{1}}\left( \begin{array}{c} -\frac{2\kappa }{(\varsigma +\kappa )^{2}}\left( ff^{\prime \prime \prime }+4f^{\prime }f^{\prime \prime }\right) +\frac{2\kappa }{\varsigma +\kappa } f^{\prime }f^{\prime \prime \prime } \\ +\frac{2\kappa }{(\varsigma +\kappa )^{3}}(2f^{\prime \prime }+3f^{\prime 2})-\frac{4\kappa }{(\varsigma +\kappa )^{4}}ff^{\prime } \end{array} \right) =0, \end{aligned}$$
(17)
$$\begin{aligned}{} & {} \left( 1+\frac{R_{\text{D}}}{(\grave{k}_{\text{nf}}/\grave{k}_{\text{f}})}\right) \left( \theta ^{\prime \prime }+\frac{\theta ^{\prime }}{\varsigma +\kappa }\right) -\frac{ \Pr }{(\grave{k}_{\text{nf}}/\grave{k}_{\text{f}})}\left( \curlywedge _{3}\frac{\kappa }{ \varsigma +\kappa }(f^{\prime }\theta -f\theta ^{\prime })\right. \left. -\lambda _{1}\theta \right) =0, \end{aligned}$$
(18)

where \(\kappa =\sqrt{\frac{\grave{a}}{\nu _{\text{f}}}}\grave{R}_{\text{c}}^{*}\) symbolizes dimensionless radius of curvature \(\alpha _{1}=\frac{\grave{\alpha }_{1}a}{\mu _{\text{f}}}\)and \(\lambda _{1}=\frac{\grave{\gamma }}{\grave{a}(\rho C_{\text{p}})_{\text{f}}}\) stands for heat generation parameter. If we set second-grade parameter \(\alpha _{1}=0\) then the modeled governing equations will govern the rheological properties of Newtonian nanofluids (a limiting case). Further parameters \(\curlywedge _{1},\curlywedge _{2}\) and \(\curlywedge _{3}\) are formulated as:

$$\begin{aligned} \left. \begin{array}{c} \curlywedge _{1}=1-\phi +\phi \frac{\rho _{\text{CNT}}}{\rho _{\text{f}}}, \\ \curlywedge _{2}=\frac{1}{(1-\phi )^{2.5}\left( 1-\phi +\phi \frac{\rho _{\text{CNT}}}{\rho _{\text{f}}}\right) }, \\ \curlywedge _{3}=1-\left( 1-\frac{(\rho C_{\text{p}})_{\text{CNT}}}{(\rho C_{\text{p}})_{\text{f}}} \right) \phi . \end{array} \right\} \end{aligned}$$
(19)

The utilization of Eq. (15) transforms Eq. (7) into dimensionless form as:

$$\begin{aligned} \left. \begin{array}{c} f(0)=0,f^{\prime }(0)=1,\theta (0)=1, \\ f^{\prime }(\infty )=0,f^{\prime \prime }(\infty )=0,\theta (\infty )=0. \end{array} \right\} \end{aligned}$$
(20)

Getting rid of pressure from Eq. (16) and Eq. (17) we get:

$$\begin{aligned}{} & {} \curlywedge _{2}\left( f^{\text{iv}}+\frac{1}{(\zeta +\kappa )^{3}}f^{\prime }\right. \left. - \frac{1}{(\zeta +\kappa )^{2}}f^{\prime \prime }+\frac{2}{\zeta +\kappa } f^{\prime \prime \prime }\right) \nonumber \\{} & {} \qquad +\frac{\kappa }{\zeta +\kappa }\left( ff^{\prime \prime \prime }-f^{\prime }f^{\prime \prime }\right) \nonumber \\{} & {} \qquad +\frac{\kappa }{(\zeta +\kappa )^{2}}\left( ff^{\prime \prime }-f^{\prime ^{2}}\right) -\frac{\kappa }{(\zeta +\kappa )^{3}}ff^{\prime } \nonumber \\{} & {} \qquad +\frac{\alpha _{1}}{\curlywedge _{1}}\left( \begin{array}{c} \frac{2\kappa }{\zeta +\kappa }\left( f^{\prime }f^{\text{iv}}+f^{\prime \prime }f^{\prime \prime \prime }\right) -\frac{10\kappa }{(\zeta +\kappa )^{2}} f^{\prime }f^{\prime \prime \prime }-\frac{2\kappa }{(\zeta +\kappa )^{2}} ff^{\text{iv}}-\frac{8\kappa }{(\zeta +\kappa )^{2}}f^{\prime \prime 2} \\ +\frac{6\kappa }{(\zeta +\kappa )^{3}}ff^{\prime \prime \prime }+\frac{ 24\kappa }{(\zeta +\kappa )^{3}}f^{\prime }f^{\prime \prime }-\frac{16\kappa }{(\zeta +\kappa )^{4}}f^{\prime 2}-\frac{12\kappa }{(\zeta +\kappa )^{4}} ff^{\prime \prime }+\frac{12\kappa }{(\zeta +\kappa )^{5}}ff^{\prime } \end{array} \right) =0. \end{aligned}$$
(21)

Ultimately, pressure P can be obtained as follows:

$$\begin{aligned}{} & {} P=\curlywedge _{1}\frac{\varsigma +\kappa }{2\kappa }\left( \begin{array}{c} \frac{\kappa }{\varsigma +\kappa }ff^{\prime \prime }-\frac{\kappa }{ \varsigma +\kappa }f^{\prime ^{2}}+\frac{\kappa }{(\varsigma +\kappa )^{2}} ff^{\prime }+\curlywedge _{2}\left( f^{\prime \prime \prime }+\frac{1}{ \varsigma +\kappa }f^{\prime \prime }-\frac{1}{(\varsigma +\kappa )^{2}} f^{\prime }\right) \\ -\frac{\grave{\alpha }_{1}}{\curlywedge _{1}}\frac{\grave{a}}{\grave{\mu }_{f}} \left( \begin{array}{c} -\frac{2\kappa }{(\varsigma +\kappa )^{2}}\left( ff^{\prime \prime \prime }+4f^{\prime }f^{\prime \prime }\right) +\frac{2\kappa }{\varsigma +\kappa } f^{\prime }f^{\prime \prime \prime } \\ +\frac{2\kappa }{(\varsigma +\kappa )^{3}}(2f^{\prime \prime }+3f^{\prime 2})-\frac{4\kappa }{(\varsigma +\kappa )^{4}}ff^{\prime } \end{array} \right) \end{array} \right) . \end{aligned}$$
(22)
Table 1 Thermophysical characteristics of carbon nanotubes (SWCNTs and MWCNTs) are tabulated as:
Full size table

In \(\grave{s}\)-direction, the skin-friction coefficient \((C_{\text{f}})\) as well as local Nusselt number \((Nu_{\grave{s}})\) are defined as:

$$\begin{aligned}{} {} C_{\text{f}}=\frac{\tau _{\grave{\text{r}}\grave{\text{s}}}}{\rho _{\text{f}}u_{\text{w}}^{2}},\text { \ }Nu_{ \grave{s}}=\frac{(s_{\text{d}}\grave{q}_{\text{w}})/k_{\text{f}}}{(\grave{T}_{\text{w}}-\grave{T} _{\infty })}, \end{aligned}$$
(23)

where \(u_{\text{w}}\) is velocity in \(\grave{s}\)-direction, \(\tau _{\grave{\text{r}}\grave{\text{s} }}\) and \(\grave{q}_{\text{w}}\) describes shear stress as well as heat flux at curved stretchable surface in \(\grave{s}\)-direction respectively as follows:

$$\begin{aligned}{} & {} \left. \begin{array}{c} \tau _{\grave{\text{r}}\grave{\text{s}}}=\left. \frac{1}{(1-\phi )^{2.5}}\mu _{\text{nf}}\left( \frac{\partial \grave{u}}{\partial \grave{r}}-\frac{\grave{u}}{\grave{r}+ \grave{R}}+\frac{2\alpha _{1}}{\mu _{\text{nf}}}\left( \frac{\grave{v}}{\grave{r}+ \grave{R}}\frac{\partial \grave{u}}{\partial \grave{r}}+\frac{\grave{R}}{ \grave{r}+\grave{R}}\frac{\partial \grave{u}}{\partial \grave{r}}\frac{ \partial \grave{u}}{\partial \grave{s}}-\frac{2\grave{u}\grave{v}}{\left( \grave{r}+\grave{R}\right) ^{2}}-\frac{2\grave{R}\grave{u}}{\left( \grave{r}+ \grave{R}\right) ^{2}}\frac{\partial \grave{u}}{\partial \grave{r}}\right) \right) \right| _{\grave{r}=0}, \\ \grave{q}_{\text{w}}=\left. -k_{\text{nf}}\left( 1+\frac{16\sigma ^{*}\grave{T} _{\infty }^{3}}{3a_{\text{R}}k_{\text{f}}(k_{\text{nf}}/k_{\text{f}})}\right) \frac{\partial \grave{T}}{ \partial \grave{r}}\right| _{\grave{r}=0}. \end{array} \right\} \end{aligned}$$
(24)

Employing Eq. (15) in Eq. (23) and Eq. (24), we get expressions for skin-friction coefficient as well as local Nusselt number as:

$$\begin{aligned} \left. \begin{array}{c} \hbox {Re}_{\grave{\text{s}}}^{1/2}C_{\text{f}}=\frac{1}{(1-\phi )^{2.5}}2\left( f^{\prime \prime }(0)-\frac{f^{\prime }(0)}{\kappa }+\alpha _{1}\left( -2\frac{ f^{\prime }(0)^{2}}{\kappa }+f^{\prime }(0)f^{^{\prime \prime }}(0)\right) \right) , \\ \hbox {Re}_{\grave{\text{s}}}^{-1/2}Nu_{\grave{\text{s}}}=-\frac{k_{\text{nf}}}{k_{\text{f}}}\left( 1+ \frac{R_{\text{D}}}{(k_{\text{nf}}/k_{\text{f}})}\right) \theta ^{\prime }(0), \end{array} \right\} \end{aligned}$$
(25)

where \(\hbox {Re}_{\grave{\text{s}}}=\frac{a\grave{s}^{2}}{\nu _{\text{f}}}\) expresses local Reynolds number.

Numerical solution and discussion

The assessment of exact solution for the resultant system of nonlinear Eqs. (16), (18) and (21) together with boundary conditions (20) is a tedious task. A well systematic technique, namely shooting method is engaged using software MATHEMATICA to get the numerical solution. Under the aegis of this approach, a boundary value problem (BVP) is transformed into an initial value problem (IVP) with first-order differential equations with a minimal number of lacking initial constraints. These lacking initial constraints are selected in such a way that they must satisfy the asymptotic boundary constraints. Table 1 along with Eqs. \((8-10)\) is utilized to calculate numerical values of parameters formulated in Eq. (19), which are involved in evaluating the exact solution for derived nonlinear system of equations. The pressure effects can be calculated using Eq. (22). Table 2 is generated to assess the effectiveness and accuracy of the numerical technique employed in this study. This table guarantees the validity of employed numerical technique by showcasing that our outcomes using shooting method aligns closely with results in existing literature obtained by Runge–Kutta–Fehlberg fourth–fifth-order method. Table 3 serves to present a comprehensive comparison between our results and the findings in existing literature, which shows an excellent agreement. After achieving the solution, this section is compiled to explore the effects of numerous parameters including dimensionless curvature \((\kappa )\), solid volume fraction of CNTs \((\phi )\), heat generation parameter \((\lambda _{1})\), radiation parameter \((R_{\text{D}})\) and Prandtl number \((\Pr )\) on focused physical quantities, i.e., velocity \(f^{\prime }(\zeta )\) and temperature \(\theta (\zeta )\) of fluid. The effect of dimensionless curvature \((\kappa )\) on fluid’s velocity \(f^{\prime }(\zeta )\) is unveiled in Fig. 2. It can be seen that an upsurge in values of dimensionless curvature \((\kappa )\) causes a decline in fluid’s velocity \(f^{\prime }(\zeta )\). This is due to the fact that value of \(\kappa\) determines the flow regime in curved surface. For low values of \(\kappa\) \((\kappa<<1)\), the flow is considered to be in the "low-curvature" regime, where the effects of curvature are negligible. However, for high values of \(\kappa\) \((\kappa>>1)\), the flow is in the "high-curvature" regime, where curvature has a significant influence on the flow behavior. The influence of solid volume fraction \((\phi )\) of CNTs on velocity profile \(f^{\prime }(\zeta )\) of nanofluid is unveiled in Fig. 3. A certain inflation has been noticed as the solid volume fraction \((\phi )\) of CNTs is increased. As the solid volume fraction \((\phi )\) of CNTs in the fluid increases, the number of collisions between the nanotubes and the fluid molecules also increases. These collisions cause the nanoparticles to move around in a random manner, which is known as the Brownian motion effect. This random movement of the nanoparticles creates a more chaotic environment for the fluid molecules, thereby enhancing their velocity. Moreover it has been noted that SWCNTs have slightly less velocity as compared to MWCNTs due to greater density values of MWCNTs. Figure 4 portrays the influence of second-grade fluid parameter \((\alpha _{1})\) over fluid’s velocity \(f^{\prime }(\zeta )\). As the second-grade fluid parameter gets amplified, the velocity rises. This is because the added elasticity of the fluid can enhance its ability to resist deformation under shear. The fluid’s higher elasticity allows it to absorb and store more energy, resulting in greater momentum transfer and increased velocity. Figure 5 elucidates the impact of dimensionless curvature \((\kappa )\) on temperature profile \(\theta (\zeta )\). Physically larger values of \((\kappa )\) corresponds to reduction in viscous force (i.e., decay in kinematic velocity of fluid). Decay in kinematic viscosity of fluid corresponds to lower heat transfer. Hence, a declination in temperature profile \(\theta (\zeta )\) is certain. Figure 6 unveils the action of solid volume fraction \((\phi )\) of CNTs on temperature profile \(\theta (\zeta )\). Carbon nanotubes (both single and multiple-walled) have relatively greater thermal conductivity and lesser specific heat then base fluid (second grade fluid). So increasing their volume \((\phi )\) in nanofluid will cause a rise in \(\theta (\zeta )\). Moreover as the volume fraction \((\phi )\) of carbon nanotubes in the fluid increases, the movement of fluid molecules becomes more restricted and the frictional forces between the fluid and the solid particles increase. This increase in frictional forces results in an increase in heat generation, which raises the temperature of the fluid. Additionally, carbon nanotubes themselves can absorb heat and transfer it to the surrounding fluid, which can further increase the temperature. Action on temperature profile \(\theta (\zeta )\) by heat generation parameter \((\lambda _{1})\) elucidates Fig. 7. The heat generation parameter \((\lambda _{1})\) is a measure of the amount of energy being generated per unit volume of the fluid. As the heat generation parameter \((\lambda _{1})\) increases, the amount of energy being generated per unit volume of the fluid also increases. This leads to an increase in the amount of heat energy transferred to the fluid, causing the temperature \(\theta (\zeta )\) of the fluid to rise. Figure 8 depicts the sway of radiation parameter \((R_{\text{D}})\) on temperature of fluid \(\theta (\zeta )\). As predicted, the fluid’s temperature amplifies quite significantly as an upsurge in \(\left( R_{\text{D}}\right)\). The radiation parameter \((R_{\text{D}})\) comprises mean absorption coefficient which reduces as increase in \(\left( R_{\text{D}}\right)\) consequently the heat transfer rate seems increases at every point away from sheet. Hence, an increase in fluid’s temperature is certain. When using slurry mixtures as base fluid, it is worth noting that these are examined by taking the value of Prandtl number as 5.83, which is lower as compared to water and other common base fluids. Prandtl number is the ratio of momentum dfusivity to thermal diffusivity that’s why its larger values decline the temperature distribution. The effect of dimensionless curvature \((\kappa )\) on pressure profile \(P(\zeta )\) is explained in Fig. 9. One can notice that an increment in value of \((\kappa )\) causes an upsurge in pressure inside the boundary layer. However, pressure approaches to zero far away from the boundary. This is because as we move far from boundary the stream lines of fluid flow conduct the same manner as for the case of flat stretching surface. Moreover, Fig 10 guarantees that pressure variations can be neglected throughout the flow for the case \((\kappa =1000)\), i.e., a flat stretching sheet, while it cannot be neglected for curved surfaces.

Table 2 Error analysis of the values of \(-\hbox {Re}_{\grave{\text{s}} }^{1/2}C_{\text{f}}\) to address the validity of numerical method with \(R_{\text{D}}=\lambda _{1}=\alpha _{1}=0\)
Full size table
Table 3 Comparative analysis of the values of \(-\hbox {Re}_{\grave{\text{s}} }^{1/2}C_{\text{f}}\) for distinct numerics of \(\kappa\) and \(\phi\), with \(R_{\text{D}}=\lambda _{1}=\alpha _{1}=0\)
Full size table

Figure 11 shows the impact of dimensionless curvature over skin friction coefficient \((C_{\text{f}})\). An amplification in dimensionless curvature \((\kappa )\) leads to a rise in skin friction coefficient \((C_{\text{f}})\) in a flow over a curved stretching surface due to the increased surface area of the curved surface. As the dimensionless curvature \((\kappa )\) of the surface rises, the surface area also gets broadened, which can lead to a higher skin friction coefficient \((C_{\text{f}})\). This is due to the fact that the fluid molecules in contact with the surface experience a higher shear stress as the dimensionless curvature \((\kappa )\) rises, resulting in a boost in skin friction coefficient \((C_{\text{f}})\). Figure 12 portrays the influence of dimensionless curvature \((\kappa )\) over local Nusselt number \((Nu_{\grave{\text{s}} })\). As the dimensionless curvature of the surface rises \((\kappa )\), the surface area also expands, which can lead to a rise in the convective heat transfer coefficient and, subsequently, an increment in the local Nusselt number \(\left( Nu_{\text{s}}\right)\). Additionally, the boundary layer thickness drops as the dimensionless curvature \((\kappa )\) of the surface rises, resulting in an increment in heat transfer rate at the surface, which can also contribute to a rise in the local Nusselt number \(\left( Nu_{\text{s}}\right)\). Table 4 displays how several factors such as solid volume fraction of carbon nanotubes \(\left( \phi \right)\), radiation parameter \(\left( R_{\text{D}}\right)\) and internal heat generation parameter \((\lambda _{1})\) affects skin-friction coefficient \(\left( C_{\text{f}}\right)\) and local Nusselt number \(\left( Nu_{\grave{\text{s}}}\right)\) defined in Eq. (25). An increment in solid volume fraction of carbon nanotubes \(\left( \phi \right)\) reduces the skin friction coefficient \((C_{\text{f}})\) due to the unique properties of carbon nanotubes. These properties, such as their high aspect ratio and excellent thermal conductivity enhances the transfer of heat and momentum in the fluid, which leads to a reduction in skin friction coefficient \((C_{\text{f}})\). When the second-grade fluid parameter \((\alpha _{1})\) is higher, fluid’s viscosity tends to decrease with increasing shear rate. This decrease in viscosity with shear rate is known as shear-thinning behavior. The shear-thinning behavior of the second-grade fluid leads to the reduction in the effective viscosity near the surface, resulting in decline of skin friction coefficient \((C_{\text{f}})\). Furthermore thermal radiation \((R_{\text{D}})\) and internal heat generation \((\lambda _{1})\) do not change the value of the local skin friction coefficient \((C_{\text{f}})\) because they do not directly affect the shear stress at the surface. Skin friction coefficient is the ratio of shear stress to the dynamic pressure of the fluid and is based solely on the fluid properties and flow conditions at the surface. Thermal radiation \((R_{\text{D}})\) and internal heat generation \((\lambda _{1})\) are related to the energy balance of the fluid, but they do not directly influence the fluid flow behavior at the surface. Therefore, they do not affect the skin friction coefficient \((C_{\text{f}})\).

Table 4 Numerical data for local Nusselt number and skin friction coefficient for various parameters
Full size table

Carbon nanotubes have enhanced thermal conductivity, which can amplify the transfer of heat between the fluid and the surface. As the solid volume fraction of carbon nanotubes \(\left( \phi \right)\) strengthens, so does the thermal conductivity of the nanofluid, which leads to an advancement in the local Nusselt number \(\left( Nu_{\text{s}}\right)\). Increment in second-grade fluid parameter \((\alpha _{1})\) leads to formation of thicker boundary layer near the solid surface. The thicker boundary layer acts as a barrier to heat transfer, reducing the convective heat transfer coefficient. As a result, the convective heat transfer decreases, resulting in lower local Nusselt number \(\left( Nu_{\text{s}}\right)\). The Nusselt number \(\left( Nu_{\text{s}}\right)\) is a dimensionless parameter that relates the convective heat transfer coefficient to the thermal conductivity of the fluid and the characteristic length of the surface. It has been perceived that rate of heat flux raises as an upsurge in radiation parameter \((R_{\text{D}})\) contains mean absorption coefficient which generates as rise in (\(R_{\text{D}})\)). For this reason, the heat transfer rate seems maximizing at every point away from sheet. So, the local Nusselt number gets amplified as a rise in radiation parameter \((R_{\text{D}})\). Moreover, an increment in heat generation parameter \((\lambda _{1})\) causes a reduction in local Nusselt number (Nu).

Conclusions

This investigation scrutinizes heat transmission through a radiative flow of boundary layer nature incorporating heat generation of second-grade nanofluid (slurry mixture) containing carbon nanotubes (SWCNTs and MWCNTs) overtop a curved extending surface. Main highlights are:

  • The velocity profile \(f^{\prime }(\zeta )\) gets amplified as an upsurge in solid volume fraction \(\left( \phi \right)\) and second-grade parameter \((\alpha _{1})\) and reduces as an increment in dimensionless curvature \((\kappa )\).

  • The temperature \(\theta (\zeta )\) of the fluid rises due to amplification of heat generation parameter \((\lambda _{1})\), radiation parameter \((R_{\text{D}})\) and solid volume fraction \(\left( \phi \right)\) of carbon nanotubes, while an opposite trend is noticed for the upsurge in dimensionless curvature \((\kappa )\).

  • The skin friction coefficient \((C_{\text{f}})\) drops due to an increment in solid volume fraction \(\left( \phi \right)\) and it gets amplified due to a rise in dimensionless curvature \((\kappa )\) and it remains invariant for upsurge in radiation parameter \((R_{\text{D}})\) and internal heat generation \((\lambda _{1})\).

  • Local Nusselt \((Nu_{\text{s}})\) number rises as an upsurge in values of solid volume fraction \(\left( \phi \right)\), dimensionless curvature \((\kappa )\) and internal heat generation \((\lambda _{1})\), while it diminishes as a rise in radiation parameter \((R_{\text{D}})\).