1 Introduction

Riemann–Hilbert (RH) problem is the 21st question that Hilbert mentioned at the International Congress of Mathematicians in Paris [1]. It belongs to the scope of boundary value problem of matrix-valued functions on the complex plane. Usually, the RH problem is defined as follows [2]. Assume that \(\Sigma \) is a directed path on the complex plane \(\mathcal {C}\), \(\Sigma ^{0}\)=\(\Sigma \setminus \){self-intersection of \(\Sigma \)}. Suppose that there is a smooth map on \(\Sigma ^{0}\)

$$\begin{aligned} G(z):\Sigma ^{0}\rightarrow ML(n,\mathcal {C}). \end{aligned}$$

Then, \((\Sigma , G)\) determines a RH problem, i.e., looking for a \(n\times n\) matrix P(z), which satisfies

  • P(z) is analytical in \(\mathcal {C}\setminus \Sigma \);

  • P(z) satisfies the following jump condition

    $$\begin{aligned} P_{+}(z)=P_{-}(z)G(z), z\in \Sigma ; \end{aligned}$$

  • \(P(z)\rightarrow I, z\rightarrow \infty \).

In fact, the RH problem is a boundary value problem of matrix value function on complex plane, and we can convert it into integral equations. Because RH problem is a problem on complex plane, the biggest advantage of RH approach is to transform the problem solvable on complex plane. For example, some definite integrals are difficult to integrate in the real domain, but can be solved when treated as complex integrals.

It is known that the methods by which the solutions of the integral equations can be obtained include inverse scattering transformation [3], Darboux transformation [4], symmetry reduction method [5], Hirota bilinear method [6], Lax pair nonlinear method [7], Wronskian technique [8], and so on. RH approach is a direct and simple method to solve the soliton equations. The problem can be solved by Lax pair of integrable systems and analysis of the spectral function. One can construct the RH problem similar to the above description, and then get the soliton solutions of the original equations.

Now RH approach has been developed into a powerful analytical tool to solve problems in a large class of pure and applied mathematics, which can be widely applied to initial boundary value problem [9,10,11,12,13,14,15,16], asymptotic of orthogonal polynomials [17], Bäcklund transformation [18, 19], and long-time asymptotics [20,21,22]. Afterward, It is found that the RH approach can be used to obtain the solutions of integral equations by inverse scattering theory [23,24,25,26,27,28,29,30]. In recent years, Wazwaz solved multiple soliton solutions of the equations [31,32,33,34]. Then, RH approach has been widely used to get multi-soliton solutions of multi-dimensional equations [35,36,37,38,39].

In this paper, we mainly discuss multi-soliton solutions of the N-component nonlinear Schrödinger (NLS) equations by RH approach. The N-component NLS equations [40] take the form

$$\begin{aligned} iq_{lt}+\frac{1}{2}q_{lxx}+\sum _{l=1}^{N}|q_{l}|^{2}q_{l}=0,~~l=1,\ldots ,N, \end{aligned}$$
(1.1)

where \(q_{l}=q_{l}(t,x)\) \((l=1,\ldots ,N)\) are functions and the subscripts mean the partial derivatives.

The organization of this paper is given as follows. In Sect. 2, we transform Lax pair to construct the RH problem for the N-component NLS equations. In Sect. 3, the multi-soliton solutions for the N-component NLS equations are obtained, which are relevant to the spectral parameter. Then, the 2-soliton solutions of the three-component NLS equations are given and the corresponding 2-soliton graphs are drawn. In Sect. 4, we give the conclusion.

2 Riemann–Hilbert problem

Based on Eq. (1.1), we have the Lax pair

$$\begin{aligned} {\left\{ \begin{array}{ll} \Phi _{x}+i\eta \sigma \Phi =iQ\Phi , \\ \Phi _{t}+i\eta ^{2}\sigma \Phi =[i\eta Q+\frac{1}{2}(i\sigma Q^{2}-\sigma Q_{x})]\Phi , \end{array}\right. } \end{aligned}$$
(2.1)

where

$$\begin{aligned} \begin{aligned} Q&=\left( \begin{array}{ccccc} 0 &{} q_{1}^{*} &{} q_{2}^{*}&{} \cdots &{} q_{N}^{*}\\ q_{1} &{} 0 &{} 0 &{} \cdots &{} 0\\ q_{2} &{} 0 &{} 0 &{} \cdots &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ q_{N} &{} 0 &{} 0 &{} \cdots &{} 0 \end{array}\right) ,\\ \sigma&=\left( \begin{array}{ccccc} -1 &{} 0 &{} 0 &{} \cdots &{} 0\\ 0 &{} 1 &{} 0 &{} \cdots &{} 0\\ 0 &{} 0 &{} 1 &{} \cdots &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} 1 \end{array}\right) , \end{aligned} \end{aligned}$$
(2.2)

\(\eta \) is the spectral parameter. Then, we get the Jost solution of Lax pair (2.1) with asymptotic form by

$$\begin{aligned} \Phi \sim e^{-i\eta \sigma x-i\eta ^{2}\sigma t}, ~~~~|x|\rightarrow \infty . \end{aligned}$$
(2.3)

In order to facilitate calculation, we define a matrix function \(\Psi =\Psi (x,t;\eta )\). Letting

$$\begin{aligned} \begin{aligned} \Phi =\Psi e^{-i\eta \sigma x-i\eta ^{2}\sigma t}, \end{aligned} \end{aligned}$$
(2.4)

then we have

$$\begin{aligned} \begin{aligned} \Psi \rightarrow I, ~~~~|x|\rightarrow \infty . \end{aligned} \end{aligned}$$
(2.5)

The Lax pair (2.1) can be rewritten as

$$\begin{aligned} {\left\{ \begin{array}{ll} \Psi _{x}+i\eta [\sigma ,\Psi ]=U_{1}\Psi ,\\ \Psi _{t}+i\eta ^{2}[\sigma ,\Psi ]=U_{2}\Psi , \end{array}\right. } \end{aligned}$$
(2.6)

where \(U_{1}=iQ\) and \(U_{2}=i\eta Q+\frac{1}{2}(i\sigma Q^{2}-\sigma Q_{x})\). Then, the Volterra integral equations can be expressed as

$$\begin{aligned} \begin{aligned}&\Psi _{1}(t,x;\eta )\\&\quad =I+\int _{-\infty }^{x}e^{-i\eta (x-x')\sigma }U_{1}\Psi _{1}e^{i\eta (x-x')\sigma }\mathrm{d}x',\\&\Psi _{2}(t,x;\eta )\\&\quad =I-\int _{x}^{+\infty }e^{-i\eta (x-x')\sigma }U_{1}\Psi _{2}e^{i\eta (x-x')\sigma }\mathrm{d}x'. \end{aligned} \end{aligned}$$
(2.7)

By calculation, we can know

$$\begin{aligned} \begin{aligned}&e^{-i\eta (x-x')\sigma }U_{1}e^{i\eta (x-x')\sigma }=\\&\quad \left( \begin{array}{cccc} 0 &{} iq_{1}^{*}e^{2i\eta (x-x')}&{} \cdots &{} iq_{N}^{*}e^{2i\eta (x-x')} \\ iq_{1}e^{-2i\eta (x-x')} &{} 0 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ iq_{N}e^{-2i\eta (x-x')} &{} 0 &{} \cdots &{} 0 \end{array}\right) . \end{aligned} \end{aligned}$$
(2.8)

Let \(\Psi _{1}=([\Psi _{1}]_{1}, [\Psi _{1}]_{2},\ldots , [\Psi _{1}]_{N+1})\) and \(\Psi _{2}=([\Psi _{2}]_{1}, [\Psi _{2}]_{2},\ldots [\Psi _{2}]_{N+1}))\). Then, it can be obtained that \([\Psi _{1}]_{1}\) is analytic in \(\mathcal {C}^{-}\), \([\Psi _{1}]_{2},\ldots ,[\Psi _{1}]_{N+1}\) are analytic in \(\mathcal {C}^{+}\). \([\Psi _{2}]_{1}\) is analytic in \(\mathcal {C}^{+}\), \([\Psi _{2}]_{2},\ldots ,[\Psi _{2}]_{N+1}\) are analytic in \(\mathcal {C}^{-}\). We can rewrite \(\Psi _{1,2}\) as follows

$$\begin{aligned} \Psi _{1}= & {} ([\Psi _{1}]_{1}, [\Psi _{1}]_{2},\ldots , [\Psi _{1}]_{N+1})\nonumber \\= & {} (\Psi _{1}^{-}, \Psi _{1}^{+},\ldots , \Psi _{1}^{+}), \end{aligned}$$
(2.9)
$$\begin{aligned} \Psi _{2}= & {} ([\Psi _{2}]_{1}, [\Psi _{2}]_{2},\ldots , [\Psi _{2}]_{N+1})\nonumber \\= & {} (\Psi _{2}^{+}, \Psi _{2}^{-},\ldots , \Psi _{2}^{-}). \end{aligned}$$
(2.10)

Based on the properties of \(\Psi _{1,2}\) and tr Q=0, we can know that \(\det \Psi _{1,2}\) are independent for all x. By the asymptotic conditions \(\Psi _{1,2}\rightarrow I\) as \(|x|\rightarrow \infty \), we know that

$$\begin{aligned} \begin{aligned} \det \Psi _{1,2}=1. \end{aligned} \end{aligned}$$
(2.11)

Therefore, \(\Psi _{1,2}\) are linearly related by a spectral matrix \(S(\eta )=(s_{kj}(\eta ))_{(N+1)\times (N+1)}\), which can be expressed as

$$\begin{aligned} \begin{aligned} \Psi _{1}E=\Psi _{2}ES(\eta ), ~~~~E=e^{-i\eta \sigma x}. \end{aligned} \end{aligned}$$
(2.12)

Then, we have

$$\begin{aligned} \begin{aligned} \det S(\eta )=1. \end{aligned} \end{aligned}$$
(2.13)

Taking the inverse of both sides of Eq. (2.12), we can obtain

$$\begin{aligned} \begin{aligned} \Psi _{1}^{-1}=ES(\eta )^{-1}E^{-1}\Psi _{2}^{-1}. \end{aligned} \end{aligned}$$
(2.14)

Applying Eq. (2.14) and the analytic properties of column vectors of \(\Psi _{1,2}\), we can get the analytic properties of \(\Psi _{1,2}^{-1}\), that is

$$\begin{aligned} \begin{aligned} \Psi _{1}^{-1}&=\left( \begin{array}{l} (\Psi _{1}^{-1})^{1}\\ (\Psi _{1}^{-1})^{2}\\ \vdots \\ (\Psi _{1}^{-1})^{N+1} \end{array}\right) =\left( \begin{array}{l} \hat{\Psi }_{1}^{+}\\ \hat{\Psi }_{1}^{-}\\ \vdots \\ \hat{\Psi }_{1}^{-} \end{array}\right) ,\\ \Psi _{2}^{-1}&=\left( \begin{array}{l} (\Psi _{2}^{-1})^{1}\\ (\Psi _{2}^{-1})^{2}\\ \vdots \\ (\Psi _{2}^{-1})^{N+1} \end{array}\right) =\left( \begin{array}{l} \hat{\Psi }_{2}^{-}\\ \hat{\Psi }_{2}^{+}\\ \vdots \\ \hat{\Psi }_{2}^{+} \end{array}\right) . \end{aligned} \end{aligned}$$
(2.15)

In order to construct a matrix RH problem, we need to determine two matrix functions

$$\begin{aligned} {\left\{ \begin{array}{ll} P_{1}=([\Psi _{2}]_{1},[\Psi _{1}]_{2},\ldots ,[\Psi _{1}]_{N+1})\\ \qquad =(\Psi _{2}^{+},\Psi _{1}^{+},\ldots ,\Psi _{1}^{+}), ~~\eta \in \mathcal {C}^{+},\\ P_{2}=\left( \begin{array}{l} (\Psi _{2}^{-1})^{1}\\ (\Psi _{1}^{-1})^{2}\\ \vdots \\ (\Psi _{1}^{-1})^{N+1} \end{array}\right) =\left( \begin{array}{l} \hat{\Psi }_{2}^{-}\\ \hat{\Psi }_{1}^{-}\\ \vdots \\ \hat{\Psi }_{1}^{-} \end{array}\right) , ~~\eta \in \mathcal {C}^{-}. \end{array}\right. } \end{aligned}$$
(2.16)

Let

$$\begin{aligned} \begin{aligned} B_{1}=\left( \begin{array}{llll} 0 &{} 0 &{} \cdots &{} 0 \\ 0 &{} 1 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} 1 \end{array}\right) , \ \ \ B_{2}=\left( \begin{array}{llll} 1 &{} 0 &{} \cdots &{} 0 \\ 0 &{} 0 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} 0 \end{array}\right) . \end{aligned} \end{aligned}$$
(2.17)

Then, \(P_{1,2}\) can be rewritten as

$$\begin{aligned}&P_{1}=\Psi _{1}B_{1}+\Psi _{2}B_{2}\nonumber \\&\quad =\Psi _{1}\left( \begin{array}{lllll} r_{11} &{} 0 &{} \cdots &{} 0 \\ e^{-2i\eta x}r_{21} &{} 1&{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ e^{-2i\eta x}r_{N+1,1} &{} 0 &{} \cdots &{} 1 \end{array}\right) , \end{aligned}$$
(2.18)
$$\begin{aligned}&P_{2}=B_{1}\Psi _{1}^{-1}+B_{2}\Psi _{2}^{-1}\nonumber \\&\quad =\left( \begin{array}{lllll} s_{11} &{} e^{2i\eta x}s_{12}&{} \cdots &{} e^{2i\eta x}s_{1,N+1} \\ 0 &{} 1 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} 1 \end{array}\right) \Psi _{1}^{-1}, \end{aligned}$$
(2.19)

where \(R(\eta )=S^{-1}(\eta )=(r_{kj}(\eta ))_{(N+1)\times (N+1)}\). We can study the asymptotic expansion of \(P_{1}\)

$$\begin{aligned} \begin{aligned} P_{1}=P_{1}^{(0)}+\frac{P_{1}^{(1)}}{\eta }+\frac{P_{1}^{(2)}}{\eta ^{2}}+o(\eta ^{-3}). \end{aligned} \end{aligned}$$
(2.20)

Submitting (2.20) into the first equation of (2.6) and comparing the corresponding coefficients of \(\eta \), we obtain

$$\begin{aligned} \begin{aligned}&O(\eta ^{1}): \ i[\sigma ,P_{1}^{(0)}]=0,\\&O(\eta ^{0}): \ P_{1,x}^{(0)}+i[\sigma ,P_{1}^{(1)}]=U_{1}P_{1}^{(0)}. \end{aligned} \end{aligned}$$
(2.21)

We can get

$$\begin{aligned} \begin{aligned} P_{1}\rightarrow I, ~~\eta \in \mathcal {C}^{+}\rightarrow \infty . \end{aligned} \end{aligned}$$
(2.22)

Similarly,

$$\begin{aligned} \begin{aligned} P_{2}\rightarrow I, ~~\eta \in \mathcal {C}^{-}\rightarrow \infty . \end{aligned} \end{aligned}$$
(2.23)

By the above calculation, we propose the RH problem of the N-component NLS equations

  • \(P_{1}(t,x;\eta )\) is analytic in \(\mathcal {C}^{+}\), \(P_{2}(t,x;\eta )\) is analytic in \(\mathcal {C}^{-}.\)

  • \(P_{2}(t,x;\eta )P_{1}(t,x;\eta )=G(t,x;\eta ), ~~\eta \in \mathcal {R}\),

  • \(P_{1,2}(t,x;\eta )\rightarrow I, ~~~as ~\eta \rightarrow \infty ,\)

where the jump matrix takes the form

$$\begin{aligned} \begin{aligned}&G(t,x;\eta )\\&\quad =\left( \begin{array}{lllll} 1 &{} e^{2i\eta x}s_{12} &{}\cdots &{}e^{2i\eta x}s_{1,N+1} \\ e^{-2i\eta x}r_{21} &{} 1 &{}\cdots &{} 0 \\ \vdots &{} \vdots &{}\ddots &{} \vdots \\ e^{-2i\eta x}r_{N+1,1} &{} 0 &{}\cdots &{} 1 \\ \end{array}\right) . \end{aligned} \end{aligned}$$
(2.24)
Fig. 1
figure 1

Evolution plot of the 2-soliton \(|q_{1}|\), Re\(q_{1}\), and Im\(q_{1}\)

Full size image
Fig. 2
figure 2

The soliton along the x-axis with different t

Full size image

3 Multi-soliton solutions of the N-component NLS equations

3.1 Multi-soliton solutions

In this section, we can get the multi-soliton solutions of Eq. (1.1). Firstly, we should derive the properties of the zeros of \(\det P_{1,2}(\eta )\). On the basis of Eqs. (2.18) and (2.19), we can get

$$\begin{aligned} \begin{aligned} \det P_{1}(\eta )=r_{11}(\eta ), ~~\eta \in \mathcal {C}^{+},\\ \det P_{2}(\eta )=s_{11}(\eta ), ~~\eta \in \mathcal {C}^{-}. \end{aligned} \end{aligned}$$
(3.1)

In other words, zeros of \(\det P_{1}(\eta )\) are zeros of \(r_{11}(\eta )\) and zeros of \(\det P_{2}(\eta )\) are zeros of \(s_{11}(\eta )\). Obviously, Q defined by (2.2) is a Hermite matrix, that is

$$\begin{aligned} \begin{aligned} Q^{\dag }=Q, \end{aligned} \end{aligned}$$
(3.2)

where \(\dag \) means conjugate transpose. Using Eqs. (2.18)-(2.19) and \(\Psi _{1,2}^{\dag }(\eta ^{*})=\Psi _{1,2}^{-1}(\eta )\), we can get the following relationship

$$\begin{aligned} \begin{aligned} P_{2}^{\dag }(\eta ^{*})=P_{1}(\eta ). \end{aligned} \end{aligned}$$
(3.3)

Then, it follows from the scattering relation (2.12) that

$$\begin{aligned} \begin{aligned} S^{\dag }(\eta ^{*})=S^{-1}(\eta ), ~~s_{11}^{*}(\eta ^{*})=r_{11}(\eta ). \end{aligned} \end{aligned}$$
(3.4)
Fig. 3
figure 3

Evolution plot of the 2-soliton \(|q_{2}|\), Re\(q_{2}\), and Im\(q_{2}\)

Full size image

The points \(\eta _{j}\) \((j=1,2,\ldots ,N)\) are zeros of \(\det P_{1}(\eta )\) in \(\mathcal {C}^{+}\), and \(\eta _{j}^{*}(j=1,2,\ldots ,N)\) are zeros of \(\det P_{2}(\eta )\) in \(\mathcal {C}^{-}.\) According to \(\det P_{1}(\eta _{j})=\det P_{2}^{*}(\eta ^{*}_{j})\), we suppose that nonzero column vectors \(\nu _{j}\) and nonzero row vectors \(\nu _{j}^{*}\) are the solutions of the following linear equations, respectively,

$$\begin{aligned} \begin{aligned} P_{1}(\eta _{j})\nu _{j}(\eta _{j})=0,\\ \nu _{j}^{*}(\eta _{j}^{*})P_{2}(\eta _{j}^{*})=0. \end{aligned} \end{aligned}$$
(3.5)

In fact, the scattering data for solving the RH problem (2.24) is composed of the discrete scattering data \(\{\eta _{j},\eta _{j}^{*},\nu _{j},\nu _{j}^{*}\}\) and the continuous scattering data \(\{s_{21}, s_{31},\ldots ,s_{N+1,1}\}\). From Eqs. (3.3) to (3.5), we get

$$\begin{aligned} \begin{aligned} \nu _{j}^{*}=\nu _{j}^{\dag }. \end{aligned} \end{aligned}$$
(3.6)

Differentiating Eq. (3.5) with respect to x and considering Lax pair (2.6) and Eq. (3.6), we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \nu _{j}=e^{-i\eta _{j}\sigma x-i\eta _{j}^{2}\sigma t}\nu _{j,0},\\ \nu _{j}^{*}=\nu _{j,0}^{\dag }e^{i\eta _{j}^{*}\sigma x+i{\eta _{j}^{*}}^{2}\sigma t}, \end{array}\right. } \end{aligned}$$
(3.7)

where \(\nu _{j0}\) are the \((N+1)\)-dimensional constant column vectors. Then, we can get multi-soliton solutions for Eq. (1.1) in the reflectionless case. Define the matrix \(M=(M_{kj})_{(N+1)\times (N+1)}\)

$$\begin{aligned} \begin{aligned} M_{kj}=\frac{\nu _{k}^{*}\nu _{j}}{\eta _{j}-\eta _{k}^{*}}. \end{aligned} \end{aligned}$$
(3.8)
Fig. 4
figure 4

The soliton along the x-axis with different t

Full size image

Based on the canonical normalization condition (2.16), the RH problem has the unique solution

$$\begin{aligned} \begin{aligned} P_{1}(\eta )=I-\sum _{k,j=1}^{N}\frac{\nu _{k}\nu _{j}^{*}(M^{-1})_{kj}}{\eta -\eta _{j}^{*}},\\ P_{2}(\eta )=I+\sum _{k,j=1}^{N}\frac{\nu _{k}\nu _{j}^{*}(M^{-1})_{kj}}{\eta -\eta _{k}}. \end{aligned} \end{aligned}$$
(3.9)

Then, we can expand \(P_{1}\) as follows

$$\begin{aligned} \begin{aligned} P_{1}=P_{1}^{(0)}+\frac{P_{1}^{(1)}}{\eta }+\frac{P_{1}^{(2)}}{\eta ^{2}}+o(\eta ^{-3}). \end{aligned} \end{aligned}$$
(3.10)

Putting the asymptotic expansion (3.10) into Eq. (2.6), we have

$$\begin{aligned} \begin{aligned} i[\sigma , P_{1}^{(1)}]=iQ. \end{aligned} \end{aligned}$$
(3.11)

Hence, the potential functions \(q_{l}\) \((l=1,2,\ldots ,N)\) can be expressed as

$$\begin{aligned} q_{l}=2(P_{1}^{(1)})_{l+1,1},~~l=1,2,\ldots ,N, \end{aligned}$$
(3.12)

where \(({P_{1}^{(1)}})_{l+1,1}\) \((l=1,2,\ldots ,N\)) are the (\(l+1\),1) entry of matrix \(P_{1}^{(1)}\), which can be obtained from Eq. (3.9), that is

$$\begin{aligned} \begin{aligned} P_{1}^{(1)}=-\sum _{k,j=1}^{N}\nu _{k}\nu _{j}^{*}(M^{-1})_{kj}. \end{aligned} \end{aligned}$$
(3.13)

Substituting Eq. (3.7) into Eq. (3.13), a general multi-soliton solutions for the N-component NLS equations can be shown as

$$\begin{aligned} q_{l}=-2\sum ^{N}_{k,j=1}\nu _{k,l+1}\nu _{j,1}^{*}(M^{-1})_{kj},~~l=1,2,\ldots ,N, \end{aligned}$$
(3.14)

where \(\nu _{k}=(\nu _{k1}, \nu _{k2},\ldots ,\nu _{k,N+1})^{T}\) and \(\nu _{j}^{*}=(\nu _{j1}^{*}, \nu _{j2}^{*},\ldots ,\nu _{j,N+1}^{*})\) \((k,j=1,2,\ldots ,N)\) are defined by Eq. (3.7).

Fig. 5
figure 5

Evolution plot of the 2-soliton \(|q_{3}|\), Re\(q_{3}\), and Im\(q_{3}\)

Full size image

3.2 2-soliton solutions

Particularly, we can study the case of \(N=3\). The three-component NLS equations can be written as

$$\begin{aligned} \begin{aligned} iq_{lt}+\frac{1}{2}q_{lxx}+\sum _{l=1}^{3}|q_{l}|^{2}q_{l}=0,~~l=1,2,3. \end{aligned} \end{aligned}$$
(3.15)

We can obtain the soliton solutions for this particular case. Assuming \(\nu _{1,0}=(\alpha _{1},\beta _{1},\gamma _{1},\epsilon _{1})^{T}\), \(\nu _{2,0}=(\alpha _{2},\beta _{2},\gamma _{2},\epsilon _{2})^{T}\), and letting \(\xi _{1}=-i\eta _{1}x-i\eta _{1}^{2}t\), \(\xi _{2}=-i\eta _{2}x-i\eta _{2}^{2}t\), \(\eta _{1}=a_{1}+ib_{1}\), \(\eta _{2}=a_{2}+ib_{2}\). We can get 2-soliton solutions as follows

$$\begin{aligned} q_{1}= & {} \frac{-2(\beta _{1}\alpha _{1}^{*}e^{\xi _{1}-\xi _{1}^{*}}m_{22}-\beta _{1}\alpha _{2}^{*}e^{\xi _{1}-\xi _{2}^{*}}m_{12} -\beta _{2}\alpha _{1}^{*}e^{\xi _{2}-\xi _{1}^{*}}m_{21}+\beta _{2}\alpha _{2}^{*}e^{\xi _{2}-\xi _{2}^{*}}m_{11})}{m_{11}m_{22}-m_{12}m_{21}}, \end{aligned}$$
(3.16)
$$\begin{aligned} q_{2}= & {} \frac{-2(\gamma _{1}\alpha _{1}^{*}e^{\xi _{1}-\xi _{1}^{*}}m_{22}-\gamma _{1}\alpha _{2}^{*}e^{\xi _{1}-\xi _{2}^{*}}m_{12} -\gamma _{2}\alpha _{1}^{*}e^{\xi _{2}-\xi _{1}^{*}}m_{21}+\gamma _{2}\alpha _{2}^{*}e^{\xi _{2}-\xi _{2}^{*}}m_{11})}{m_{11}m_{22}-m_{12}m_{21}}, \end{aligned}$$
(3.17)
$$\begin{aligned} q_{3}= & {} \frac{-2(\epsilon _{1}\alpha _{1}^{*}e^{\xi _{1}-\xi _{1}^{*}}m_{22}-\epsilon _{1}\alpha _{2}^{*}e^{\xi _{1}-\xi _{2}^{*}}m_{12} -\epsilon _{2}\alpha _{1}^{*}e^{\xi _{2}-\xi _{1}^{*}}m_{21}+\epsilon _{2}\alpha _{2}^{*}e^{\xi _{2}-\xi _{2}^{*}}m_{11})}{m_{11}m_{22}-m_{12}m_{21}}, \end{aligned}$$
(3.18)

where

$$\begin{aligned} m_{11}= & {} \frac{\alpha _{1}^{*}\alpha _{1}e^{-\xi _{1}^{*}-\xi _{1}}+\beta _{1}^{*}\beta _{1}e^{\xi _{1}^{*}+\xi _{1}} +\gamma _{1}^{*}\gamma _{1}e^{\xi _{1}^{*}+\xi _{1}}+\epsilon _{1}^{*}\epsilon _{1}e^{\xi _{1}^{*}+\xi _{1}}}{\eta _{1}-\eta _{1}^{*}}, \end{aligned}$$
(3.19)
$$\begin{aligned} m_{12}= & {} \frac{\alpha _{1}^{*}\alpha _{2}e^{-\xi _{1}^{*}-\xi _{2}}+\beta _{1}^{*}\beta _{2}e^{\xi _{1}^{*}+\xi _{2}} +\gamma _{1}^{*}\gamma _{2}e^{\xi _{1}^{*}+\xi _{2}}+\epsilon _{1}^{*}\epsilon _{2}e^{\xi _{1}^{*}+\xi _{2}}}{\eta _{2}-\eta _{1}^{*}}, \end{aligned}$$
(3.20)
$$\begin{aligned} m_{21}= & {} \frac{\alpha _{2}^{*}\alpha _{1}e^{-\xi _{2}^{*}-\xi _{1}}+\beta _{2}^{*}\beta _{1}e^{\xi _{2}^{*}+\xi _{1}} +\gamma _{2}^{*}\gamma _{1}e^{\xi _{2}^{*}+\xi _{1}}+\epsilon _{2}^{*}\epsilon _{1}e^{\xi _{2}^{*}+\xi _{1}}}{\eta _{1}-\eta _{2}^{*}}, \end{aligned}$$
(3.21)
$$\begin{aligned} m_{22}= & {} \frac{\alpha _{2}^{*}\alpha _{2}e^{-\xi _{2}^{*}-\xi _{2}}+\beta _{2}^{*}\beta _{2}e^{\xi _{2}^{*}+\xi _{2}} +\gamma _{2}^{*}\gamma _{2}e^{\xi _{2}^{*}+\xi _{2}}+\epsilon _{2}^{*}\epsilon _{2}e^{\xi _{2}^{*}+\xi _{2}}}{\eta _{2}-\eta _{2}^{*}}. \end{aligned}$$
(3.22)

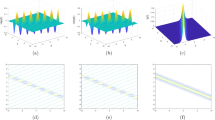
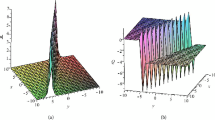
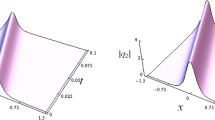
By selecting appropriate parameter values \(\alpha _{1}=\alpha _{2}=1\), \(\beta _{1}=\beta _{2}=\frac{1}{4}\), \(\gamma _{1}=\gamma _{2}=\frac{\sqrt{59}}{8}\), \(\epsilon _{1}=\epsilon _{2}=\frac{1}{8}\), \(a_{1}=-0.1\), \(b_{1}=0.2\), \(a_{2}=0.2\), and \(b_{2}=0.3\), three-dimensional plots and x-curves of solutions are shown in Figs. 1, 2, 3, 4, 5, and 6.

4 Conclusion

In general, we investigate the multi-soliton solutions of the N-component NLS equations via RH approach.

By the Volterra equations, the corresponding analytical properties can be obtained. Then, we define \(P_{1}\) and \(P_{2}\) to construct the RH problem. In reflectionless case, making full use of the symmetric relation of the potential matrix and giving the zero point relation of the determinant of two analytic matrix functions in the problem, one can construct the multi-soliton solutions. For the multi-component NLS equations, it is more complicated than standard NLS equations. The multi-soliton solutions of N-dimensional NLS equations via the RH approach have not been well studied before, and therefore we take the factor of multi-component into consideration.

Fig. 6
figure 6

The soliton along the x-axis with different t

Full size image

RH approach can be used not only to solve the initial boundary value problem of integrable systems, but also to analyze the solution of long-time behavior, quantum field theory and statistical model, orthogonal polynomial theory, and random matrix theory. In addition, it can be used in plasma physics, ocean engineering, atmospheric sciences, Bose–Einstein condensate, nonlinear optics and so on. The Riemann–Hilbert approach can be applied to many equations of similar types. In future, we can innovate and improve the method and apply it to many more complex equations.