The phenomenon of tristable stochastic resonance driven by $\alpha$-noise

Abstract

In this paper, the tristable stochastic resonance (SR) phenomenon induced by $\alpha$-stable noise is analysed. The mechanism for realizing resonance is explored based on research concerning the potential function and resonant output of a system. The rules for resonance system parameters q, p, skewness parameter r and intensity amplification factor Q of $\alpha$-stable noise to act on the resonant output are explored under different values of stability index $\alpha$ and asymmetric skewness $\beta$ of $\alpha$-stable noise. The results will contribute to a reasonable selection of parameter-induced tristable SR system parameters under $\alpha$-stable noise, and lay the foundation for a practical engineering application of weak signal detection based on the SR.

1 Introduction

Signal detection is designed to obtain useful information from noisy observations. However, it is difficult to detect signals effectively because of strong noise in the real environment and weak signal amplitude. At present, signal detection methods can be divided into three major categories: matched filtering, energy detection, and feature extraction. All these methods focus mainly on removing and suppressing noise to detect a useful signal, but the useful signal itself may be suppressed in the process of dealing with the noise. Compared with traditional methods, application of strong noise in stochastic resonance (SR) for the purpose of detecting a weak signal does not mask the useful signal, but instead strengthens weak signals, promoting the detection and extraction of useful information [1, 2]. This concept was put forward by Benzi and other people in 1981 to explain some problems of the quaternary glacier. Then it was used to describe a phenomenon in which the output response is increased by the effect of internal and external noise in a nonlinear system [3, 4]. Subsequently, SR was widely applied in areas such as physics, biology, chemistry, and electronics [5,6,7,8,9,10,11].

Classical SR was put forward on the basis of bistable system. The bistable system became the main direction of SR research because it is easy to construct and analyse the bistable system [3, 4, 7, 8]. However, with the advancement of research, besides the bistable system, SR could also be realized by other kinds of system, such as monostable system [12], linear oscillator [13], chaotic system [14], delay system [15], bidimensional Duffing system [16], fractional linear oscillator [17] and so on. SR theory is significantly enriched by these models which expand the application of SR to some degree. In recent years, a kind of tristable system is put forward which attracts lots of attention from many scholars. The utility of tristable system in mechanical failure detection is studied in [18]. The principles and parameters of tristable system are analysed in [19]. In [20], the SR phenomenon is studied in a triple-well system by varying the depth of the wells. In [21], the steady-state problems of the tristable system are studied under the action of colour-correlated multiplicative and additive coloured noise. The logic SR phenomenon in triple-well potential systems driven by Gaussian coloured noise is analysed in [22].

The theory of SR investigated in the above references is based on Gaussian noise. Actually, Gaussian noise is the ideal state of random noise which can only simulate the noise vibrating in a small interval. As to the signal which has great amplitude fluctuation, it is obviously not applicable. In fact, non-Gaussian noise with significant pulse peaking and trailing frequently disturbs our daily life. This kind of noise can be described by $\alpha$-stable distribution which can reflect really, accurately and objectively the phenomenon of stochastic disturbance. Nowadays, many scholars shift their research to analyse the phenomenon of SR under $\alpha$-stable noisy environment.

The phenomenon of logical SR in a trip-well potential system driven by a coloured non-Gaussian noise is investigated in [23]. The parameter-induced SR in an overdamped system with $\alpha$-stable noise is studied in [24]. The signal detection based on symmetric bistable system under $\alpha$-stable noisy background is discussed in [25]. SR of asymmetric bistable system with $\alpha$-stable noise is analysed in [26]. The characteristic of a power function type monostable SR system inspired by $\alpha$-stable noise is explored in [27]. So far, there is no published study of the phenomenon of SR induced by parameters of tristable system under $\alpha$ stable noisy environment. In order to ensure the credibility of the experimental results, it is necessary to accurately select the appropriate parameters which can produce the phenomenon of SR. Meanwhile, the effects of each parameter need to be analysed from the perspective of physics and mathematics. In this paper, based on [19], the induction effect of every parameter to SR under $\alpha$-stable noisy environment is studied. On this basis, the SR caused by noise is also analysed and investigated. The influence on resonance output from noise intensity amplification coefficient Q, skewness r, system structural parameters q and p under the $\alpha$-stable noisy environment with different characteristic parameter $\alpha$ and symmetry parameter $\beta$ is studied in this paper. These results will contribute to reasonably choose the system parameters and intensity amplification factor of tristable SR system under the $\alpha$-stable noise, and provide a reliable basis for practical engineering application of weak signal detection by SR.

2 Tristable system

2.1 System model

The first-order nonlinear Langevin equation is the most widely used system model in SR research. Like the bistable system model, a tristable SR system driven by weak signals and $\alpha$-noise also has the following expression:

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}=-\frac{\mathrm{d}U(x)}{\mathrm{d}x}+s(t)+Q\eta (t), \end{aligned}$$

(1)

where U(x) is the tristable system potential function, $s(t)=A\sin (2\pi ft)$ is the input weak signal to be detected, $\eta (t)$ is the input $\alpha$-noise, Q is the amplification coefficient of $\alpha$-noise.

The potential function of the classic tristable system is

$$\begin{aligned} U(x)=\frac{a}{6}x^6 -\frac{b}{4}x^4 +\frac{c}{2}x^2 -rx. \end{aligned}$$

(2)

In order to simplify the analysis, let $a=1$, then

$$\begin{aligned} U_1 (x)=\frac{1}{6}x^6 -\frac{b}{4}x^4 +\frac{c}{2}x^2 -rx. \end{aligned}$$

(3)

It is a tristable potential function, b and c are system structural parameters, and $b, c>0, b^{2}-4c>0$. r is the skewness of potential function which shows the asymmetry of the tristable system. When $r=0$, the potential function is symmetric along y-axis, and the system is called the symmetric tristable system. The minimal value of the potential function is the stable equilibrium point, and the maximum value is the unstable equilibrium point. In order to simplify the analysis, we assume two parameters p and $q\, (p<q)$ both of which are greater than 0. Then the tristable potential function should meet the condition

$$\begin{aligned} \left\{ {{\begin{array}{l} {{U}'_1 (x)=x(x+p)(x-p)(x+q)(x-q)-r} \\ {{U}'_1 (p)-r<0} \\ {{U}'_1 (q)-r<0} \\ \end{array} }} \right. \end{aligned}$$

(4)

where

$$\begin{aligned} p= & {} \sqrt{(b-\sqrt{b^{2}-4c})/2},\\ q= & {} \sqrt{(b+\sqrt{b^{2}-4c})/2}. \end{aligned}$$

The features of tristable system are analysed in detail on the basis of equilibrium point p and q in [19].

Symmetric tristable system function under $\alpha$-noise is

$$\begin{aligned} V(x)=\frac{1}{6}x^6 -\frac{b}{4}x^4 +\frac{c}{2}x^2 -rx+Q\eta (t)x. \end{aligned}$$

(5)

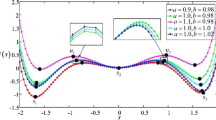
In order to make it easy to understand, let $r=0, p=1, q=2, Q\eta (t)=0.3$. Figure 1a shows the curve of $U_1 (x)$ and V(x) which are the potential functions before and after the $\alpha$-stable noise is added, respectively. The minimal points of $U_1 (x)$ are $x_{s1,s2} =\pm m, x_{s3} =0$, the maximum points are $x_{u1,u2} =\pm n$. Because of the introduction of $\alpha$-noise, the extreme points of V(x) are changed. Under this condition, V(x) also has three minimal points ${x}^{\prime }_{s1}, {x}^{\prime }_{s2},{x}^{\prime }_{s3}$ and two maximum points ${x}'_{u1} ,{x}'_{u2}$. Obviously, the horizontal ordinates of these extreme points are the solution of equation ${\mathrm{d}V(x)}/{\mathrm{d}x}=0$.

Fig. 1

The potential function and its solution of the tristable system: (a) The potential function before and after modulated by noise and (b) the solution of the tristable system.

It is hard to get the closed-form expression of ${\mathrm{d}V(x)}/{\mathrm{d}x}=0$ because it contains the high order terms. Let

$$\begin{aligned} f_1 (x)=x^5 -bx^3 +cx -r \end{aligned}$$

and

$$\begin{aligned} f_2 (x)=Q\eta (t), \end{aligned}$$

where $f_1$ is the derivative of equivalent potential function without noise and $f_2$ is the additive $\alpha$-stable noise. Under the same parameters in figure 1a, two curves are shown in figure 1b. Then the value of horizontal ordinate for intersection points of $f_1$ and $f_2$ are the solutions of ${\mathrm{d}V(x)}/{\mathrm{d}x}=0$, corresponding to the extreme points of V(x) in figure 1a, and they perhaps are the solutions of eq. (5). Under the same parameters in figure 1a, two curves are shown as in figure 1b.

Among the five intersections of $f_{1}$ and $f_{2}, {x}'_{u1}$ and ${x}'_{u2}$ are the maximum values of potential function V(x) which are also the unstable equilibrium points. With a slight disturbance, the particle would depart these equilibrium points which actually are the unstable results of tristable system eq. (1). Among the five points of intersection, only ${x}'_{s1} , {x}'_{s2}$ and ${x}'_{s3}$ are the stable results for eq. (1). They are also the stable equilibrium points of V(x), the adjusted location of the potential well. The middle barrier height is

$$\begin{aligned} \Delta U_m =\frac{2bc-(b^{2}-4c)(b-\sqrt{b^{2}-4c})}{24} \end{aligned}$$

and the side barrier height is

$$\begin{aligned} \Delta U_s =\frac{(b^{2}-4c)\sqrt{b^{2}-4c}}{12}. \end{aligned}$$

Actually, after a short-term evolution of transient process, tristable system eq. (1) perhaps only has one stable result which has three forms: ${x}'_{s1}, {x}'_{s2}$ and ${x}'_{s3}$, and the specific stable output of eq. (1) is decided by the original environment.

2.2 Characterization of tristable SR

According to Kramer’s rate theory and adiabatic approximation, the transition rate of the particle in the middle potential well is

$$\begin{aligned} r_{K,m\rightarrow s} =\frac{w_u w_0 }{2\pi }\exp \left( -\frac{\Delta U_m }{Q}\right) . \end{aligned}$$

(6)

The transition rate of the particle in the side potential well is

$$\begin{aligned} r_{K,s\rightarrow m} =\frac{w_u w_s }{2\pi }\exp \left( -\frac{\Delta U_s }{Q}\right) , \end{aligned}$$

(7)

where $w_u ,w_s$ are the frequencies corresponding to the potential minimum $x_{s1} ,x_{s2}$ and barrier top $x_{u1} ,x_{u2}$, respectively. $w_0$ is the frequency corresponding to the potential minimum $x_{s3}$. Before the transition from one stable state to another, the particle needs to get past certain potential barriers, which means the amplitude of the input signal should be larger than a specific threshold that can be obtained through a potential function with the input signal being constant.

When the input signal is a constant A, the potential function without noise is

$$\begin{aligned} V_1 (x)=\frac{1}{6}x^6 -\frac{b}{4}x^4 +\frac{c}{2}x^2 +A. \end{aligned}$$

(8)

When the potential function meets the conditions where the limit point coincides with the inflection point, then

$$\begin{aligned} \left\{ {{\begin{array}{l} {\dfrac{\partial V_1 (x)}{\partial x}=x^5 -bx^3 +cx +A=0} \\ {\dfrac{\partial ^{2}V_1 (x)}{\partial ^{2}x}=5x^4 -3bx^2 +c=0} \\ \end{array} }} \right. . \end{aligned}$$

(9)

The value of A can be calculated by solving eq. (9). Then we can obtain the input threshold of the system

$$\begin{aligned} \left\{ {{\begin{array}{l} {A_{c,m\rightarrow s} =\eta _1 (p,q)} \\ {A_{c,s\rightarrow m} =\eta _2 (p,q)} \\ \end{array} }} \right. . \end{aligned}$$

(10)

When $A<A_{c,m\rightarrow s}$, the particle cannot overcome the potential barrier in either the middle potential well or the side wells. When $A>\max (A_{c,m\rightarrow s} ,A_{c,s\rightarrow m} )$, the particle can overcome the potential barrier in all potential wells and maintain periodic motion. Despite $A<\max (A_{c,m\rightarrow s} ,A_{c,s\rightarrow m} )$, with the influence of noise and the periodic signal, the system’s output can conduct periodic motion between the potential wells after overcoming the barriers. This phenomenon is called tristable SR.

Therefore, two conditions need to be met to achieve tristable SR: (1) the noise-driven transition between stable states should be consistent with the cycle of the input signal, which means $f<{\min (r_{K,m\rightarrow s} ,r_{K,s\rightarrow m} )}/2$; (2) the amplitude A of the weak signal should be slightly smaller than the critical value $\max (A_{c,m\rightarrow s} ,A_{c,s\rightarrow m} )$. Otherwise, although with the help of noise, the particle still cannot overcome the barrier to achieve SR.

Then, we report the effect of different SR stages on the mean residence time $(T_{\mathrm{MR}})$ on three wells. Before the resonance, the system switches rarely from one well to an adjacent well and the residence time in each well is random. The mean residence time in a higher depth well is longer than in a lower depth well. As the state gets closer to resonance, mean residence times in the wells vary. When the state reaches resonance, there is almost periodic switching between the wells. The system enters the middle well twice, once from the right well and once from the left well, during one drive cycle of the periodic input signal f sin $\omega t$. And the sum of the mean residence times $T_{\mathrm{MR}}^{\mathrm{L}}+T_{\mathrm{MR}}^{\mathrm{R}} + 2T_{\mathrm{MR}}^{\mathrm{M}}$ is T, where $T(= 2\pi /\omega$) is the period of the external periodic force. Periodic switching is lost when the state surpasses resonance. After the resonance, erratic switching occurs among the wells.

In this paper, fourth-order Runge–Kutta algorithm is utilized to solve eq. (1) (more details could be seen in [25, 27]). If the characteristic index $\alpha$-becomes bigger, the intensity of the pulse of $\alpha$-stable noise will become weaker, which would result in the fast change of route in long-term transition. Thus, artificial block should be executed on the output signal x(t) during the simulation [28], so as to prevent the infinite jump of particle. The block function is selected as: when $\left| {x(t)} \right| >2, x(t)=\mathrm{sign}(x(t))\times 2$.

3 $\alpha$-Stable distribution

3.1 Characteristic function of $\alpha$-stable distribution

When Levy studied the centre limit theory in 1952, he published $\alpha$-stable distribution whose probability density function and distribution function have no explicit expression except for some special situations, such as the Levy distribution, Cauchy distribution and normal distribution. Thus, characteristic function is used to describe $\alpha$-stable distribution. If the random variable x obeys $\alpha$-stable distribution, its characteristic function can be expressed as [29, 30]

$$\begin{aligned}&\varphi (t)\nonumber \\&\quad \!\! {=}\left\{ {{\begin{array}{l} {\exp \left[ {-\gamma |t|\left( {1{+}i\beta \frac{2}{\pi }\hbox {sign}(t)\log |t|} \right) +i\delta t} \right] ,\alpha {=}1} \\ {\exp \left[ {{-}\gamma ^\alpha |t|^\alpha \left( {1{-}i\beta \hbox {sign}(t)\tan \frac{\pi \alpha }{2}} \right) +i\delta t} \right] ,\alpha {\ne }1} \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$

(11)

where $\alpha \in (0,2]$ is the characteristic exponent which decides the impulse and trailing; $\beta \in [-1,1]$ is the skewness which is used to clarify the symmetric degree; $\gamma \in [0,+\infty )$ is the scale parameter to measure the distribution degree of sample and average value; $\delta \in (-\infty ,+\infty )$ is the location parameter to decide the distribution centre. $\alpha$-stable distribution is expressed by $S_\alpha (\gamma ,\beta ,\delta )$ with three special examples: (1) when $\alpha =2$, the normal distribution is showed in figure 2a where the average value is $\delta$ and the variance is $2\gamma ^2$, (2) when $\alpha =1,\beta =0$, Cauchy distribution is showed in figure 2b with the location parameter of $\delta$ and scale parameter of $\gamma$, (3) when $\alpha =0.5,\beta =1$, the Levy distribution is showed in figure 2c with the location parameter of $\delta$ and scale parameter of $\gamma$.

Fig. 2

The probability density function (PDF) of $\alpha$ distribution $S_\alpha (\gamma ,\beta ,\delta )$: (a) the PDF of $\alpha$ distribution $S_2 (\gamma ,0,\delta )$, where $(\gamma ,\delta )\in \{(1,0),(1,1),(1,-1),(2,0),(1,1),(1,-1)\}$; (b) the PDF of $\alpha$ distribution $S_1 ({\gamma },0,\delta )$, where $(\gamma ,\delta )\in \{(0,0),(0,1),(0,-1),(0,0),(0,2),(0,-2)\}$; (c) the PDF of $\alpha$ distribution $S_{0.5}(\gamma ,1,\delta )$, where $(\gamma ,\delta )\in \{(1,0),(1,1),(1,-1),(2,0),(3,2),(3,-2)\}$.

3.2 The generation of $\alpha$-stable distribution

It is supposed that there are two independent random variables V, W, where V is the uniform distribution of $(-\pi /{2,\pi /2})$ and W is the exponential distribution with the average value of 1. Then the variable X which obeys $\alpha$-stable distribution can be obtained by the method of Janicki–Weron [24, 26].

When $\alpha \ne 1$,

$$\begin{aligned} X= & {} N_{\alpha ,\beta ,\sigma } \frac{\sin (\alpha (V+M_{\alpha ,\beta } ))}{(\cos (V))^{1/\alpha } }\nonumber \\&\times \left[ {\frac{\cos (V-\alpha (V+M_{\alpha ,\beta } ))}{W}} \right] ^{(1-\alpha )\alpha } +\mu \end{aligned}$$

(12)

where

$$\begin{aligned}&M_{\alpha ,\beta }=\frac{\arctan (\beta \tan ({\pi \alpha }/2))}{\alpha },\\&N_{\alpha ,\beta ,\sigma }=\sigma [\cos (\arctan (\beta \tan ({\pi \alpha }/2)))]^{-1/\alpha }. \end{aligned}$$

When $\alpha =1$,

$$\begin{aligned} X= & {} \frac{2\sigma }{\pi }\left[ (\pi /2+\beta V)\tan (V)\right. \nonumber \\&\left. -\beta \ln \left( {\frac{(\pi /2)W\cos (V)}{\pi /2+\beta V}} \right) \right] +\mu . \end{aligned}$$

(13)

4 The mean of SNRI

Signal-noise ratio (SNR), signal-noise ratio increase (SNRI) and the degree of multifactuality (DM) [31] are the indexes to evaluate the influence on input signal of system, which are widely used in SR system. Sure, we can use SNR for evaluating, but for the strength and improvement effect on input signal from SR system, SNRI is still better. And compared with DM, SNRI is easier to calculate. Thus, SNRI is chosen as the indicator to measure SR system. SNRI is defined as

$$\begin{aligned} \hbox {SNRI}=\frac{S_{\mathrm{out}} (f_0 )/n_{\mathrm{out}} (f_0 )}{S_{\mathrm{in}} (f_0 )/n_{\mathrm{in}} (f_0)}, \end{aligned}$$

(14)

where $S_{\mathrm{out}} (f_0 )$ and $S_{\mathrm{in}} (f_0 )$ are the input and the output power of the signal respectively. $n_{\mathrm{out}} (f_0 )$ and $n_{\mathrm{in}} (f_0 )$ are the input and the output power of the $\alpha$-stable noise respectively.

From eq. (14), if the signal of SR system is required to strengthen and improve, let $\mathrm{SNRI}>1$, and as SNRI is increasing, the performance of SR would be improved.

In order to avoid accidental situation and increase the reliability of data, all the simulation experiments in this paper use the mean of K times SNRI (MSNRI) to measure the improved performance of tristable system which is defined as

$$\begin{aligned} \hbox {MSNRI}=\frac{1}{K}\sum _{k=1}^K {\hbox {SNRI}_k } , \end{aligned}$$

(15)

where K is the time of simulation experiments and $\hbox {SNRI}_{k}$ is the SNRI of the kth simulation experiment.

5 The SR of tristable system driven by $\alpha$-stable noise

In the study of SR phenomenon, the simulation system chooses the signal

$$\begin{aligned} s(t)=A\sin (2\pi f_0 t) \end{aligned}$$

submerged in $\alpha$-stable noise, where

$$\begin{aligned} A=0.1,\,f_0 =0.01\,\hbox {Hz}. \end{aligned}$$

The sample frequency $f_s =5\,\hbox {Hz}$, characteristic indexes are $\alpha =1,\beta =0,\delta =1,\gamma =0$ ($\alpha$-noise) and $\alpha =2,\beta =0,\delta =1,\gamma =0$ (Gaussian noise) respectively, and the system parameters are $p=0.5, q=1.2$. The noise intensity is in the interval of [0, 1], and the simulation number of times K is 100. As figure 3 shows, the curve of MSNRI and $A_{m}$, the mean of K times spectrum peaks, changes with noise intensity Q when $f=f_0$.

$A_{m}$ indicates the absolute intensity of the output characteristic signal. The MSNRI reflects the identification ability of the output signal relative to the input signals. Both $A_{m}$ and MSNRI increased first and then decreased with the increase of Q. What is more, they hit the peak value under the optimal noisy intensity $Q_\mathrm{op}$, which are the classical features of SR. As a result, SR can be realized by the tristable system described in eq. (1) under noisy environment.

Fig. 3

The curves of output signal vs. noise intensity Q: (a) MSNRI–Q curves and (b) $A_{m}$–Q curves.

Fig. 4

The SR of the tristable system: (a) waveform, (b) spectrum of the input signal and (c) spectrum of the output signal.

If the parameters in figure 3 remain unchanged, when $Q=0.09$, the phenomenon of SR can be realized by the tristable system. Figure 4 shows a part of the low-frequency wave (0–0.25 Hz) of the input and output signal respectively. From it we can see that the normalized peak of the output spectrum reached the maximum value at $f=f_0$, and much larger than that of the input spectrum. Meanwhile, the noise power of high-frequency transfer to the region of low frequency and the spectrum of output signal nearly obeys Lorentz distribution. As a result, noise plays an active role in tristable SR system. The SR phenomenon can be achieved either under Gaussian noise or $\alpha$-stable noise. The main difference is that the intervals of system parameters which could induce SR effect are distinct. From figure 3, we can see that the parameter region of Q that can realize robust SR under $\alpha$-stable noise would move to the left and become larger compared to the case of Gaussian white noise.

5.1 The SR under different characteristic indexes $\alpha$

When $\alpha = 0.2$, 0.6, 1, 1.4 and 1.8 respectively, other parameters of noise distribution: $\beta =0, \delta =1, \gamma =0$, both signals to be detected and sampling frequency remain unchanged. According to the related parameters, when $Q=0.09, p=0.5$, the curve of MSNRI vs. system parameter q is shown in figure 5.

Fig. 5

MSNRI vs. q curves under different $\alpha$ values.

Figure 6 shows the curve of MSNRI vs. p when $q=1.2, Q=0.09$. Figure 7 shows the curve of MSNRI vs. r when $p=0.5, q=1.2, Q=0.09$.

Figure 5 shows the curves of MSNRI changing with q under different $\alpha$. Thus, SR can be realized by changing q. When $q\in [0.5,2.25]$, it can be seen that MSNRI first increased and then decreased. It means that the particle jumps out of the potential barrier under the combined action of noise and input signal, then the SR appears when the particle jumps in different potential wells. When q is increased from 0.5 to 1.05, the most suitable match between noise, non-linear system and input signals would be gradually realized. When $q=1.05$, MSNRI would hit the peak in this interval. When q is increased from 1.05 to 2.25, the potential barrier would continue to increase, and the most suitable match would disappear, leading to the decrease of MSNRI.

From figure 6, there is a peak when MSNR changes with p. And when $p\in [0.08,0.92]$, the curves in figure 6 show an uptrend at first and then a downtrend which is the typical phenomenon of SR. Figure 7 shows the curves when MSNRI changes with symmetric parameter r under different $\alpha$ with many wave peaks. When $r=0$, MSNRI is the highest and the curve is symmetric, which means the effect of SR is the best when the tristable system is symmetric.

Fig. 6

MSNRI vs. p curves under different $\alpha$ values.

Fig. 7

MSNRI vs. r curves under different $\alpha$ values.

For certain values of q (p or r), there is the interval of p (q or r) in which the resonance is better. Meanwhile, the resonance interval of q (p or r) basically remains unchanged when $\alpha$ changes. In q interval (p or r), when $\alpha =1$, MSNRI is the highest which is the best output effect of SR. When $\alpha$ diverges from 1, the output effect of SR system becomes weaker.

Fig. 8

MSNRI vs. Q curves under different $\alpha$ values.

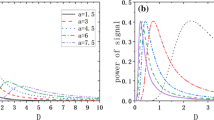
Similarly, if q, p are fixed, the curves of MSNRI changing with Q are shown in figure 8 under different $\alpha$. As noise intensity Q increases, all the MSNRI hit the peak value under every $\alpha$ showing an uptrend and then a downtrend, indicating that an optimum value is reached to achieve the best SR effect. Most intervals of Q with better resonance effect lie in [0, 0.4]. When $\alpha =1$, the MSNRI hits the highest value. As characteristic index of $\alpha$ deviates from 1, MSNRI decreases.

5.2 SR under different values symmetric parameter $\beta$

The symmetric parameter $\beta$ is −1, 0 and 1 respectively, other noise parameters have corresponding values such as $\alpha =1,\delta =1,\gamma =0$, signal to be detected and sampling frequency remains unchanged. It is assumed that when $Q =0.09, p = 0.5$, then a simulated curve of MSNRI is depicted with different values of q (figure 9). And when $q =1.2$, the MSNRI curve by varying p is shown in figure 10. When the systematic structure parameter $p = 0.5, q = 1.2$, the MSNRI curve is shown in figure 11 with skewness parameter r changing.

Fig. 9

MSNRI vs. q curves under different $\beta$ values.

Fig. 10

MSNRI vs. p curves under different $\beta$ values.

Fig. 11

MSNRI vs. r curves under different $\beta$ values.

Just like the change of MSNRI under different $\alpha$, the curve of MSNRI also has peak value with the change of system parameters under different $\beta$. And with the change in $\beta$ and system parameters, similar things have happened to MSNRI. From figure 9, we can see that the MSNRI graph fluctuates with different q under different $\beta$. When $q\in [0.65,2.25]$, potential barrier height has been affected leading to particle jump and SR.

From the MSNRI curves by varying q, p and r respectively, it can be seen that good resonance effect can be established in fixed $q \,(p$ or r) with relevant $p\, (q$ or r). And after further and careful observation in every interval, it can be seen that the interval of q, p and r with better resonance effect does not change with $\beta$. By vertical contrast, we also realize that when $\beta =0$, MSNRI is higher than that when $\beta \ne 0$.

Fig. 12

MSNRI vs. Q curves under different $\beta$ values.

When the symmetric parameter $\beta$ differs, the trend of MSNRI changing with Q is shown in figure 12. It shows that there is a better resonance effect in the Q interval converging in the same area. And when $\beta =0$, MSNRI is higher than that when $\beta \ne 0$.

6 Conclusion

In this paper, the SR under $\alpha$-stable noise environment centring on tristable system is investigated. The laws for the resonant output of tristable system, governed by parameters q and p, the intensity amplification factor Q of $\alpha$-noise, the skewness r, are explored under different values of characteristic index $\alpha$ and symmetry parameter $\beta$ of $\alpha$-noise. Results show that no matter whether it is under any different characteristic index $\alpha$ or symmetric parameter $\beta$ of the $\alpha$-noise, the weak signal can be detected by adjusting the system parameters q (p or r). The intervals of q (p or r) which can induce SR are certain, and do not change with $\alpha$ or $\beta$. Moreover, the same rule is found, which by adjusting the intensity amplification factor Q of $\alpha$-noise, can also realize the synergistic effect when studying the noise-induced SR, and the interval of Q does not change with $\alpha$ nor $\beta$; the best value of characteristic index is $\alpha = 1$ under any system parameters, and the best value of symmetry parameter is $\beta = 0$ under any system parameters. So, the system performance is best when $\alpha = 1$ and $\beta = 0$, and the more deflective with 1 the $\alpha$ is, the weaker the SR effect is. Finally, the function of skewness r is investigated, and it is found that the system performance is better when $r = 0$ and $r =\pm 20$. The SR effect is best when $r =$ 0. Meanwhile, $r=0$ is the symmetry axis of the MSNRI curve, and does not change with $\alpha$ nor $\beta$. Put it another way, the SR becomes strongest in a symmetric tristable system. These results will contribute to reasonably choosing the system parameters and intensity amplification factor of power function type tristable SR system under $\alpha$-noise, and provide a reliable basis for practical engineering application of weak signal detection by SR.