1 Introduction

Over the past few decades, significant advancements have been made by scholars in the research of stochastic resonance (SR) [1], which has found widespread applications in various fields such as biological [2, 3], physical [4, 5], and neural networks [6, 7]. Initially, the focus of scholars was on SR in bistable systems that were driven by Gaussian white noise and periodic force. In Ref. [8], a second-order underdamped bistable system was proposed, which was driven by additive noise in the form of Gaussian white noise. Ref. [9] and Ref. [10] focused on investigating different asymmetric bistable systems that were driven by multiplicative and additive Gaussian white noise. In Ref. [11], the authors presented a time-delayed bistable system and analyzed the phenomenon of SR using statistical complexity measure and normalized Shannon entropy. Although Gaussian noise is widely used and easy to analyze, the probability density distribution of noise in real applications is often more complex. To apply SR in practical engineering, scholars have turned to research on nonlinear systems driven by non-Gaussian noise [12,13,14,15,16,17,18]. Fuentes et al. [13] observed the SR phenomenon in bistable systems driven by non-Gaussian noise and found that the resonance effect was enhanced when the noise deviated from the Gaussian distribution. Jin and Li [14] proposed a piecewise bistable system induced by correlated multiplicative and additive color noise and derived the expression of output signal-to-noise ratio (SNR) using two-state theory. They also investigated the effects of color noise on SNR. Guo et al. [15] studied and analyzed SR in piecewise bistable systems under multiplicative non-Gaussian noise and additive Gaussian white noise. The results showed that the effects of non-Gaussian noise and Gaussian white noise on SNR are different. In Ref. [16], a coupled bistable SR system driven by levy noise was proposed, and the effects of system parameters on the mean signal-to-noise gain were studied. Additionally, scholars have researched SR driven by non-Gaussian noise in neural networks. In Ref. [17], a simplified one-dimensional F-N neural network driven by correlated multiplicative non-Gaussian noise and additive Gaussian white noise was studied. In Ref. [18], SR phenomenon in time-delayed F-N neural networks driven by non-Gaussian noise was studied, and the effects of time delay and non-Gaussian noise strength on SNR were discussed.

Recent studies have shown that the dynamics of tri-stable systems are more complex and exhibit better performance than bistable systems, leading to extensive research on tri-stable systems [19,20,21,22,23]. In Ref. [19], a standard underdamped tri-stable SR system was proposed through parameter transformation based on the classical tri-stable system. In Ref. [20], a piecewise tri-stable SR system was proposed and applied in bearing fault detection. The SR phenomenon in a tri-stable system with time-delayed feedback was studied, and the effects of time delay strength and length on SNR were explored in Ref. [21]. However, these studies on tri-stable SR systems are all based on Gaussian white noise, and very few papers have investigated tri-stable SR systems driven by non-Gaussian noise, which exhibits properties more consistent with real noise. Additionally, the analysis of the resonance behavior of an asymmetric tri-stable system is more complex than that of a symmetric tri-stable SR system. Moreover, the derivation of the spectrum amplification becomes further complicated when the system is driven by multiplicative non-Gaussian noise and additive Gaussian white noise. Hence, based on the above discussions, this paper proposes an ATSSR system driven by correlated multiplicative non-Gaussian noise and additive Gaussian white noise.

The contents of this paper are organized as follows: In Sect. 1, the potential structure of ATSSR system is analyzed. In Sect. 2, the specific expressions of SPD, MFPT, and SA are derived under the limit of adiabatic approximation, and the effects of each parameter on them are analyzed. In Sect. 3, a periodic attenuated pulse signal and a harmonic vibration signal are constructed, and simulated fault signal detection experiments are performed using the ATSSR system. Finally, the conclusions and outlook are provided for future research in Sect. 4.

2 ATSSR system

2.1 System model

Driven by a periodic forcing and correlated multiplicative non-Gaussian noise and additive Gaussian white noise, ATSSR system can be described as the Langevin equation of Eq. (1):

$$ \dot{x} = - \dot{U}\left( x \right) + A_{0} \cos \left( {2\pi f_{0} t} \right) + x\varsigma \left( t \right) + \varepsilon \left( t \right) $$
(1)

where \(A_{0}\) and \(f_{0}\) are the amplitude and frequency of the external periodic forcing, respectively.

\(U\left( x \right) = x^{2} \left( {a - bx} \right)\left( {a + x} \right) + cx^{6}\) is the asymmetric tri-stable potential function, and a, b, and c are positive real numbers. Since the symmetry of the potential function is not related to the parameter c, without loss of generality, c is fixed as c = 0.2 in Fig. 1. As can be shown, ATSSR system has three stable points s1, s2, and s3, and two unstable points u1 and u2. For convenience, s1, s2, and s3 are called the potential well on the left, middle, and right, respectively. It can be seen that the depth and width of the left and right potential wells become shallower and narrower, respectively, while the depth of the middle potential well increases as a increases. Nevertheless, the height of the middle barrier decreases as b increases.

Fig. 1
figure 1

Potential structure

Full size image

In Eq. (1), \(\varepsilon \left( t \right)\) is a Gaussian white noise with the statistical characteristic: \(\left\langle {\varepsilon \left( t \right)} \right\rangle = 0\), \(\left\langle {\varepsilon \left( t \right)\varepsilon \left( {t_{1} } \right)} \right\rangle = 2Q\delta \left( {t - t_{1} } \right)\). \(\varsigma \left( t \right)\) can be generated by the following equation:

$$ \frac{d\varsigma \left( t \right)}{{dt}} = - \frac{1}{{\tau_{1} }}\frac{d}{d\varsigma }V_{q} \left( \varsigma \right) + \frac{1}{{\tau_{1} }}\xi \left( t \right) $$
(2a)
$$ V_{q} \left( \varsigma \right) = \frac{D}{{\tau_{1} \left( {q - 1} \right)}}\ln \left( {1 + \frac{{\tau_{1} \left( {q - 1} \right)}}{D}\frac{{\varsigma^{2} }}{2}} \right) $$
(2b)

The process \(\varsigma \left( t \right)\) is consistent with the Ornstein–Uhlenbeck process when q = 1, while it is a non-Gaussian process when q ≠ 1. And the first-order and second-order moments of \(\varsigma \left( t \right)\) satisfy:

$$ \left\langle {\varsigma \left( t \right)} \right\rangle = 0 $$
(3a)
$$ \left\langle {\varsigma^{2} \left( t \right)} \right\rangle = \left\{ {\begin{array}{*{20}c} {\frac{2D}{{\tau_{1} \left( {5 - 3q} \right)}},\;q \in \left( { - \infty ,\frac{5}{3}} \right)} \\ {\infty ,\quad \quad \quad q \in \left( {\frac{5}{3},3} \right)} \\ \end{array} } \right. $$
(3b)

D and \(\tau_{1}\) are noise intensity and correlation time, respectively, and q represents the degree of deviation of \(\varsigma \left( t \right)\) from the Gaussian distribution. \(\xi \left( t \right)\) is a Gaussian white noise with mean value 0 and intensity D, and its correlation intensity and correlation time with \(\varepsilon \left( t \right)\) are \(\lambda\) and \(\tau_{2}\), respectively, that is: \(\left\langle {\xi \left( t \right)\varepsilon \left( {t_{1} } \right)} \right\rangle = \left\langle {\xi \left( {t_{1} } \right)\varepsilon \left( t \right)} \right\rangle = 2\lambda \frac{{\sqrt {DQ} }}{{\tau_{2} }}\delta \left( {t - t_{1} } \right)\).

According to Ref. [24], when \(\left| {q - 1} \right| < < 1\), i.e., \(\varsigma \left( t \right)\) slightly deviates from the Gaussian distribution, it can be obtained:

$$ \frac{1}{{\tau_{1} }}\frac{d}{d\varsigma }V_{q} \left( \varsigma \right) = \frac{\varsigma }{{\tau_{1} }}\left[ {1 + \frac{{\tau_{1} }}{D}\left( {q - 1} \right)\frac{{\varsigma^{2} }}{2}} \right]^{ - 1} \approx \frac{\varsigma }{{\tau_{1} }}\left[ {1 + \frac{{\tau_{1} }}{D}\left( {q - 1} \right)\frac{{\left\langle {\varsigma^{2} } \right\rangle }}{2}} \right]^{ - 1} $$
(4)

for \(q < \frac{5}{3}\), \(\left\langle {\varsigma^{2} \left( t \right)} \right\rangle = \frac{2D}{{\tau_{1} \left( {5 - 3q} \right)}}\). Therefore, Eq. (4) can be simplified as follows:

$$ \frac{1}{{\tau_{1} }}\frac{d}{d\varsigma }V_{q} \left( \varsigma \right) = \frac{1}{{\tau_{1} }}\frac{5 - 3q}{{2\left( {2 - q} \right)}}\varsigma \left( t \right) = \frac{1}{{\tau_{{{\text{eff}}}} }}\varsigma \left( t \right) $$
(5)

where \(\tau_{{{\text{eff}}}}\) is the effective correlation time and \(\tau_{{{\text{eff}}}} = \frac{{2\left( {2 - q} \right)}}{5 - 3q}\tau_{1}\).

Taking Eq. (4) into Eq. (2a), it is obtained:

$$ \frac{d\varsigma \left( t \right)}{{dt}} = - \frac{1}{{\tau_{{{\text{eff}}}} }}\varsigma \left( t \right) + \frac{1}{{\tau_{{{\text{eff}}}} }}\xi_{1} \left( t \right) $$
(6)

where \(\xi_{1} \left( t \right)\) is a Gaussian white noise, which satisfies: \(\left\langle {\xi_{1} \left( t \right)} \right\rangle = 0\), \(\left\langle {\xi_{1} \left( t \right)\xi_{1} \left( {t_{1} } \right)} \right\rangle = 2D_{{{\text{eff}}}} \delta \left( {t - t_{1} } \right)\). \(D_{{{\text{eff}}}}\) is the effective noise intensity and \(D_{{{\text{eff}}}} = \left[ {\frac{{2\left( {2 - q} \right)}}{5 - 3q}} \right]^{2} D\).

\(\xi_{1} \left( t \right)\) and \(\varepsilon \left( t \right)\) are cross-correlated noise with correlation strength \(\lambda\) and correlation time \(\tau_{2}\):

$$ \left\langle {\xi_{1} \left( t \right)\varepsilon \left( {t_{1} } \right)} \right\rangle = \left\langle {\xi_{1} \left( {t_{1} } \right)\varepsilon \left( t \right)} \right\rangle = 2\lambda \frac{{\sqrt {D_{{{\text{eff}}}} Q} }}{{\tau_{2} }}\delta \left( {t - t_{1} } \right) $$
(7)

Applying the unified color noise approximation, the Markov process of Eq. (1) is:

$$ \dot{x} = \frac{1}{{A_{h} \left( {x,\tau_{1} } \right)}}\left[ {h\left( {x,t} \right) + x\xi_{1} \left( t \right) + \varepsilon \left( t \right)} \right] $$
(8)

where \(h\left( {x,t} \right) = - \dot{U}\left( x \right) + A_{0} \cos \left( {2\uppi f_{0} t} \right)\), \(A_{h} \left( {x,\tau_{{{\text{eff}}}} } \right) = 1 - \tau_{{{\text{eff}}}} \left[ {\frac{d}{dx}h\left( {x,t} \right) - \frac{1}{x}h\left( {x,t} \right)} \right]\), and \(A_{h} \left( {x,\tau_{{{\text{eff}}}} } \right) > 0\).

Equation (8) can be rewritten as the differential form of Eq. (9):

$$ \dot{x} = \alpha \left( x \right) + \beta \left( x \right)\Gamma \left( t \right) $$
(9)

where \(\alpha \left( x \right){ = }\frac{{h\left( {x,t} \right)}}{{A_{h} \left( {x,\tau_{1} } \right)}}\), \(\beta \left( x \right) = \frac{{\left( {D_{{{\text{eff}}}} x^{2} + {{2\lambda \sqrt {D_{{{\text{eff}}}} Q} x} \mathord{\left/ {\vphantom {{2\lambda \sqrt {D_{{{\text{eff}}}} Q} x} {\left( {1 + 2\tau_{2} } \right)}}} \right. \kern-0pt} {\left( {1 + 2\tau_{2} } \right)}} + Q} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}{{A_{h} \left( {x,\tau_{1} } \right)}}\), and the statistical properties of \(\Gamma \left( x \right)\) are: \(\left\langle {\Gamma \left( t \right)} \right\rangle = 0\), \(\left\langle {\Gamma \left( t \right)\Gamma \left( {t - t_{1} } \right)} \right\rangle = 2\delta \left( {t - t_{1} } \right)\).

2.2 Steady-state probability density of ATSSR system

The Fokker–Planck equation of Eq. (10) can be approximated as follows:

$$ \frac{{\partial \rho \left( {x,t} \right)}}{\partial t} = - \frac{\partial }{\partial x}\left[ {\alpha \left( {x,t} \right) + \beta \left( x \right)\beta^{\prime}\left( x \right)} \right]\rho \left( {x,t} \right) + \frac{{\partial^{2} }}{{\partial x^{2} }}\beta^{2} \left( x \right)\rho \left( {x,t} \right) $$
(10)

The steady-state probability density (SPD) function is:

$$ \rho_{{{\text{st}}}} \left( x \right) = \frac{N}{\beta \left( x \right)}\exp \left[ { - \frac{{\tilde{U}\left( {x,t} \right)}}{{D_{{{\text{eff}}}} }}} \right] $$
(11)

where \(N = \left[ {\int {\frac{{\exp \left[ { - {{\tilde{U}\left( {x,t} \right)} \mathord{\left/ {\vphantom {{\tilde{U}\left( {x,t} \right)} {D_{{{\text{eff}}}} }}} \right. \kern-0pt} {D_{{{\text{eff}}}} }}} \right]}}{\beta \left( x \right)}} } \right]^{ - 1}\) is the normalization constant, and \(\tilde{U}\left( {x,t} \right)\) is the generalized potential function whose expression is:

$$ \tilde{U}\left( {x,t} \right) = D_{{{\text{eff}}}} \int {\frac{{U^{\prime}\left( x \right) - A_{0} \cos \left( {2\pi f_{0} t} \right)}}{{x^{2} + {{2\lambda \sqrt {D_{{{\text{eff}}}} Q} x} \mathord{\left/ {\vphantom {{2\lambda \sqrt {D_{{{\text{eff}}}} Q} x} {\left( {1 + 2\tau_{2} } \right)}}} \right. \kern-0pt} {\left( {1 + 2\tau_{2} } \right)}} + Q}}A_{h} \left( {x,\tau_{1} } \right)dx} $$
(12)

By neglecting the second-order term of \(A_{0}\) in \(\tilde{U}\left( {x,t} \right)\), we can obtain:

$$ \tilde{U}\left( {x,t} \right) = U_{0} \left( x \right) - A_{0} g\left( x \right)\cos \left( {2\uppi f_{0} t} \right) + o\left( {A_{0}^{2} } \right) $$
(13)
$$ U_{0} \left( x \right) = D_{{{\text{eff}}}} \int {\frac{{\left[ {6cx^{5} - 4bx^{3} + 3a\left( {1 - b} \right)x^{2} + 2ax} \right]\left\{ {1 - \tau_{{{\text{eff}}}} \left[ { - 24cx^{4} + 8bx^{2} - 3a\left( {1 - b} \right)x} \right]} \right\}}}{{x^{2} + 2\lambda \left( {1 + 2\tau_{2} } \right)^{ - 1} \sqrt {D_{{{\text{eff}}}} Q} x + Q}}} dx $$
(14)
$$ g\left( x \right) = D_{{{\text{eff}}}} \int {\frac{{\left\{ {1 - \tau_{{{\text{eff}}}} \left[ { - 24cx^{4} + 8bx^{2} - 3a\left( {1 - b} \right)x} \right]} \right\} - \tau_{{{\text{eff}}}} \left[ {6cx^{4} - 4bx^{2} + 3a\left( {1 - b} \right)x + 2a} \right]}}{{x^{2} + 2\lambda \left( {1 + 2\tau_{2} } \right)^{ - 1} \sqrt {D_{{{\text{eff}}}} Q} x + Q}}} dx $$
(15)

Setting a = 1.5, c = 0.1, \(\tau_{1} = 0.1\), \(\tau_{2} = 0.1\), Fig. 2 shows the effects of certain parameters of the two noises and the asymmetric intensity on the particle motion states. In Fig. 2(a), SPD on the left and right potential wells decreases, while SPD on the middle potential well increases when D increases, which indicates that particles are more prone to transit from the outermost potential wells to the middle potential well. In Fig. 2(b), the effect of Q on SPD is opposite to D, the probability of particles transition from the middle to the outermost potential wells increases as Q increases. In Fig. 2(c), SPD on the left and the middle potential well decreases, while SPD on the right potential well increases when q increases. In Fig. 2(d), with the increase in \(\lambda\), SPD increases on the left potential well and decreases on both right and middle potential wells. In Fig. 2(e), SPD on the right potential well is greater than the left one when b > 1, since the depth of the right potential well is larger and particles are less likely to transit. In addition, SPD rises on right potential well and falls on middle and left potential wells when b > 1, and vice versa when b < 1.

Fig. 2
figure 2figure 2

Curves of steady-state probability density under different parameters. (a) Steady-state probability density as a function of D (b = 0.98, \(\lambda = 0.1\), q = 1, Q = 0.5). (b) Steady-state probability density as a function of Q (b = 0.98, \(\lambda = 0.1\), q = 1, D = 0.5). (c) Steady-state probability density as a function of q (b = 0.98, \(\lambda = 0.1\), D = 0.5, Q = 0.5). (d) Steady-state probability density as a function of \(\lambda\) (b = 0.98, q = 1, D = 0.5, Q = 0.5). (e) Steady-state probability density as a function of b (\(\lambda = 0.1\), q = 1, D = 0.5, Q = 0.5)

Full size image

2.3 Mean First-Pass Time of ATSSR system

In this section, the escape of particles through Mean First-Pass Time (MFPT) is analyzed. By defining \(T_{{s_{1} \to s_{2} }}\) as the MFPT of the particles from s1 to s2, according to the definition of MFPT, it can be obtained that:

$$ T_{{s_{1} \to s_{2} }} = \int_{{s_{1} }}^{{s_{2} }} {\frac{dx}{{\sqrt {\beta \left( x \right)} \rho_{{{\text{st}}}} \left( x \right)}}\int_{ - \infty }^{x} {dy} } \rho_{{{\text{st}}}} \left( y \right) = \frac{2\pi }{{\sqrt {U^{\prime \prime } \left( {s_{1} } \right)U^{\prime \prime } \left( {u_{1} } \right)} }}\exp \left[ {\frac{{\tilde{U}\left( {u_{1} ,t} \right) - \tilde{U}\left( {s_{1} ,t} \right)}}{{D_{{{\text{eff}}}} }}} \right] $$
(16)

Similarly:

$$ T_{{s_{2} \to s_{3} }} = \int_{{s_{2} }}^{{s_{3} }} {\frac{dx}{{\sqrt {\beta \left( x \right)} \rho_{st} \left( x \right)}}\int_{ - \infty }^{x} {dy} } \rho_{st} \left( y \right) = \frac{2\pi }{{\sqrt {U^{\prime \prime } \left( {s_{2} } \right)U^{\prime \prime } \left( {u_{2} } \right)} }}\exp \left[ {\frac{{\tilde{U}\left( {u_{2} ,t} \right) - \tilde{U}\left( {s_{2} ,t} \right)}}{{D_{{{\text{eff}}}} }}} \right] $$
(17)

Figure 3 demonstrates the variation of \(\ln \left( {T_{{s_{1} \to s_{2} }} } \right)\) with D which shows a decreasing trend as D increases, indicating that the time for the particles to transit from s1 to s2 decreases. This is because as the multiplicative noise intensity increases, the more energy is available to facilitate particles transit and the shorter the time required for the transition. In Fig. 3(a), \(\ln \left( {T_{{s_{1} \to s_{2} }} } \right)\) decreases when q increases, which indicates that less time is needed for particles to transit from s1 to s2 as the deviation of \(\varsigma \left( t \right)\) from the Gaussian distribution increases. In Fig. 3(b), \(\ln \left( {T_{{s_{1} \to s_{2} }} } \right)\) is smaller when the two noises are not correlated and the time for particles to transit from s1 to s2 increases as \(\lambda\) increases. The power of two uncorrelated noises can be superimposed, while the power of the correlated noise cannot be superimposed; thus, the particles can get more energy to transit when additive noise and multiplicative noise are correlated. However, as \(\lambda\) increases, the correlated intensity of the two noises increases, which leads to an increase in the transit time.

Fig. 3
figure 3

Mean First-Pass Time of particles from s1 to s2 as a function of D (a = 1, b = 0.8, c = 0.1, \(\tau_{1} = 0.1\), \(\tau_{2} = 0.1\), Q = 0.5)

Full size image

Similarly, Fig. 4 shows the variation of \(\ln \left( {T_{{s_{1} \to s_{2} }} } \right)\) with Q, which can be seen that \(\ln \left( {T_{{s_{1} \to s_{2} }} } \right)\) decreases as Q increases. Since the increase in additive noise intensity also provides more energy for the particles to transit and facilitates the transition. But the effects of q and \(\lambda\) on \(\ln \left( {T_{{s_{1} \to s_{2} }} } \right)\) are different, \(\ln \left( {T_{{s_{1} \to s_{2} }} } \right)\) decreases when q increases, while \(\ln \left( {T_{{s_{1} \to s_{2} }} } \right)\) increases as \(\lambda\) increases. Figure 5 shows the effects of D and Q on \(\ln \left( {T_{{s_{1} \to s_{2} }} } \right)\) for both symmetric and asymmetric potential functions, which can be seen that \(\ln \left( {T_{{s_{1} \to s_{2} }} } \right)\) decreases with increasing D or Q. But when the potential function is symmetrically distributed, the particles take more time to transit from s1 to s2. This is because the potential well on the left side is deeper, and it is more difficult for particles to transit from the left side potential well to the middle potential well when b = 1, which is consistent with the previous theoretical results.

Fig. 4
figure 4

Mean First-Pass Time of particles from s1 to s2 as a function of Q (a = 1, b = 0.8, c = 0.1, \(\tau_{1} = 0.1\), \(\tau_{2} = 0.1\), D = 0.5)

Full size image
Fig. 5
figure 5

Mean First-Pass Time of particles from s1 to s2 as a function of D and Q under different b (a = 1, c = 0.1, \(\tau_{1} = 0.1\), \(\tau_{2} = 0.1\), \(\lambda = 0.1\), q = 1)

Full size image

Figures 6 and 7 describe the variation of \(\ln \left( {T_{{s_{2} \to s_{3} }} } \right)\) with D and Q, respectively. \(\ln \left( {T_{{s_{2} \to s_{3} }} } \right)\) decreases with the increases in D or Q, indicating that when the external energy increases, less time is needed for particles to transit. Whether \(\ln \left( {T_{{s_{2} \to s_{3} }} } \right)\) as a function of D or Q, \(\ln \left( {T_{{s_{2} \to s_{3} }} } \right)\) decreases as q or \(\lambda\) increases.

Fig. 6
figure 6

Mean First-Pass Time of particles from s2 to s3 as a function of D (a = 1, b = 0.8, c = 0.1, \(\tau_{1} = 0.1\), \(\tau_{2} = 0.1\), Q = 0.5)

Full size image
Fig. 7
figure 7

Mean First-Pass Time of particles from s2 to s3 as a function of Q (a = 1, b = 0.8, c = 0.1, \(\tau_{1} = 0.1\), \(\tau_{2} = 0.1\), D = 0.5)

Full size image

Figure 8 indicates the variation of \(\ln \left( {T_{{s_{2} \to s_{3} }} } \right)\) with D and Q under different b. Similarly, \(\ln \left( {T_{{s_{2} \to s_{3} }} } \right)\) decreases in both cases as D or Q increases. However, different from Fig. 5, the transit time of the particles from s2 to s3 is shorter because the depth of the middle potential well is significantly less than the depth of the potential wells on either side when the potential function is symmetric.

Fig. 8
figure 8

Mean First-Pass Time of particles from s2 to s3 as a function of D and Q under different b (a = 1, c = 0.1, \(\tau_{1} = 0.1\), \(\tau_{2} = 0.1\), \(\lambda = 0.1\), q = 1)

Full size image

2.4 Spectrum amplification

To further analyze the SR behavior of particles, this section examines the spectral amplification factor of ATSSR system. Assume that \(p_{i} \left( {i = 1,2,3} \right)\) is the probability of a Brownian particle at the steady-state point \(s_{i} \left( {i = 1,2,3} \right)\) and \(\sum {p_{i} } = 1\). The master equation for \(p_{i}\) can be obtained as follows:

$$ \frac{{dp_{i} }}{dt} = \sum\nolimits_{j = 1}^{3} {R_{i,j} } p_{j} $$
(18)

where R is the transition matrix, and its specific expression is shown in Appendix A.

The probability flow equation of Eq. (18) can be decomposed as follows:

$$ p_{i} = p_{i}^{\left( 0 \right)} + A_{0} \Delta p_{i} $$
(19)

Substituting Eq. (19) into Eq. (18), it is obtained as follows:

$$ \frac{{d\Delta p_{i} }}{dt} = \sum\nolimits_{j = 1}^{3} {R_{i,j}^{\left( 0 \right)} } \Delta p_{j} + \phi_{i} \cos \left( {2\pi f_{0} t} \right) $$
(20)

Among them, \(R^{\left( 0 \right)}\) represents the undisturbed transition matrix, and \(\phi\) can be expressed as follows:

$$ \phi = \frac{1}{{D_{{{\text{eff}}}} }}\left( {\begin{array}{*{20}c} { - r_{1,2}^{\left( 0 \right)} \Delta g_{1,2} p_{1}^{\left( 0 \right)} + r_{2,1}^{\left( 0 \right)} \Delta g_{2,1} p_{2}^{\left( 0 \right)} } \\ {r_{1,2}^{\left( 0 \right)} \Delta g_{1,2} p_{1}^{\left( 0 \right)} - \left( {r_{2,1}^{\left( 0 \right)} \Delta g_{2,1} + r_{2,3}^{\left( 0 \right)} \Delta g_{2,3} } \right)p_{2}^{\left( 0 \right)} + r_{3,2}^{\left( 0 \right)} \Delta g_{3,2} p_{3}^{\left( 0 \right)} } \\ {r_{2,3}^{\left( 0 \right)} \Delta g_{2,3} p_{2}^{\left( 0 \right)} - r_{3,2}^{\left( 0 \right)} \Delta g_{3,2} p_{3}^{\left( 0 \right)} } \\ \end{array} } \right) $$
(21)

Under the limit of long time, the simplified Eq. (21) is:

$$ \Delta p_{i} = \lambda_{i} \sin \left( {2\pi f_{0} t} \right) + \sigma_{i} \cos \left( {2\pi f_{0} t} \right) $$
(22)

Combining Eqs. (20) and (22), the specific expressions of \(\lambda_{i}\) and \(\sigma_{i}\) are:

$$ \begin{aligned} \lambda _{i} & = \sum\nolimits_{{j = 1}}^{3} {2\pi f_{0} \left[ {\mu _{j}^{2} + \left( {2\pi f_{0} } \right)^{2} } \right]^{{ - 1}} } a_{j} \nu _{{j,i}} , \\ \sigma _{i} & = \sum\nolimits_{{j = 1}}^{3} {\mu _{j} \left[ {\mu _{j}^{2} + \left( {2\pi f_{0} } \right)^{2} } \right]^{{ - 1}} } a_{j} \nu _{{j,i}} \\ \end{aligned} $$
(23)

where \(\mu_{j}\) and \(\nu_{j}\) are the eigenvalues and corresponding eigenvectors of \(R^{\left( 0 \right)}\), respectively, and \(a_{j}\) is the expansion coefficients of \(\phi\), satisfying \(\phi = \sum\nolimits_{j = 1}^{3} {a_{j} v_{j} }\).

The mean time response of the system by a periodic signal is:

$$ \begin{gathered} \left\langle {x\left( t \right)|x_{0} ,t_{0} } \right\rangle = \int {xP\left( {x,t|x_{0} ,t_{0} } \right)dx} \\ = \int {x\sum\nolimits_{i = 1}^{3} {p_{i} \left( t \right)\delta \left( {x - s_{i} } \right)} dx} \\ \end{gathered} $$
(24)

When \(t_{0} \to - \infty\), Eq. (24) can be expressed as follows:

$$ \left\langle {x\left( t \right)} \right\rangle_{{{\text{as}}}} = A\sin \left( {2\pi f_{0} t + \psi } \right) $$
(25)

where A and \(\psi\) are the amplitude and phase of the asymptotic average response, respectively:

$$ A = A_{0} \sqrt {\left[ {\sqrt {\left( {s_{1} A_{1} } \right)^{2} + 2s_{1} s_{2} A_{1} A_{2} \cos \left( {\Gamma_{1} } \right) + \left( {s_{2} A_{2} } \right)^{2} } + s_{3} A_{3} \cos \left( {\Gamma_{2} } \right)} \right]^{2} + \left[ {s_{3} A_{3} \sin \left( {\Gamma_{2} } \right)} \right]^{2} } $$
(26)

With \(A_{i} = \sqrt {\lambda_{i}^{2} + \sigma_{i}^{2} }\), \(\psi_{i} = \arctan \left( {{{\sigma_{i} } \mathord{\left/ {\vphantom {{\sigma_{i} } {\lambda_{i} }}} \right. \kern-0pt} {\lambda_{i} }}} \right)\), \(\Gamma_{1} = \psi_{2} - \psi_{1}\), \(\Gamma_{2} = \psi_{3} - \psi_{1} - \Lambda_{1}\), \(\Lambda_{1} = \arctan \left\{ {{{s_{2} A_{2} \sin \left( {\Gamma_{1} } \right)} \mathord{\left/ {\vphantom {{s_{2} A_{2} \sin \left( {\Gamma_{1} } \right)} {\left[ {s_{1} A_{1} + s_{2} A_{2} \cos \left( {\Gamma_{1} } \right)} \right]}}} \right. \kern-0pt} {\left[ {s_{1} A_{1} + s_{2} A_{2} \cos \left( {\Gamma_{1} } \right)} \right]}}} \right\}\).

Therefore, the SA of ATSSR system is:

$$ \eta = \frac{{A^{2} }}{{A_{0}^{2} }} = \sum\nolimits_{i = 1}^{3} {\left( {s_{i} A_{i} } \right)^{2} } + 2s_{1} s_{2} A_{1} A_{2} \cos \left( {\Gamma_{1} } \right) + 2s_{3} A_{3} \cos \left( {\Gamma_{2} } \right)\sqrt {\sum\nolimits_{i = 1}^{2} {\left( {s_{i} A_{i} } \right)^{2} + 2s_{1} s_{2} A_{1} A_{2} \cos \left( {\Gamma_{1} } \right)} } $$
(27)

Since \(s_{2} = 0\), \(\eta\) is simplified as follows:

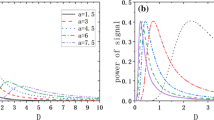
$$ \eta = \left( {s_{1} A_{1} } \right)^{2} + \left( {s_{3} A_{3} } \right)^{2} + 2\left| {s_{1} A_{1} } \right|s_{3} A_{3} \cos \left( {\Gamma_{2} } \right) $$
(28)

Setting a = 1, c = 0.1, \(\tau_{1} = 0.1\), \(\tau_{2} = 0.1\), Fig. 9 and Fig. 10 describe the variation of \(\eta\) with D, where \(\eta\) first increases and then decreases as D increases, indicating that the system occurs in stochastic resonance and that D corresponding to the peak is the noise energy required for the system to achieve optimal synergy. In Fig. 9, the peak of \(\eta\) corresponds to a smaller D as q increases. The difference is that when the potential function is symmetric, \(\eta\) is greater, but the system requires more energy for the occurrence of SR. In Fig. 10, \(\eta\) as a function of D varies with \(\lambda\) changes under different b. When b = 0.8, the peak of \(\eta\) increases and the corresponding D decreases with the increase in \(\lambda\), while the peak value of \(\eta\) decreases and the corresponding D increases when b = 1.

Fig. 9
figure 9

Spectrum amplification (\(\eta\)) as a function of D and q under different b (\(\lambda = 0.1\), Q = 0.2)

Full size image
Fig. 10
figure 10

Spectrum amplification (\(\eta\)) as a function of D and \(\lambda\) under different b (q = 1, Q = 0.2)

Full size image

Figures 11 and 12 show the variation of \(\eta\) with Q. Similarly, as Q increases, there is a single peak, indicating the occurrence of SR. In Fig. 11, the peak of \(\eta\) increases as q increases and its position shifts to the right, but the peak is higher when b = 1. In Fig. 12, the peak of \(\eta\) decreases with increasing \(\lambda\), at the same time, the peak is higher for b = 1.

Fig. 11
figure 11

Spectrum amplification (\(\eta\)) as a function of Q and q under different b (\(\lambda = 0.1\), D = 0.2)

Full size image
Fig. 12
figure 12

Spectrum amplification (\(\eta\)) as a function of Q and \(\lambda\) under different b (q = 1, D = 0.2)

Full size image

Figure 13 discusses the influence of D and Q on \(\eta\). In Fig. 13(a), when the potential structure is asymmetric, \(\eta\) as a function of D, the peak value increases and the corresponding position of the peak shifts to the left with the increase in Q. But when Q > 0.3, SR phenomenon disappears. In Fig. 13(b), when the potential structure is symmetrical, the peak value decreases and the corresponding D decreases with the increase in Q. And \(\eta\) always decreases with the increase in D when Q > 0.2, then no sign of the SR phenomenon can be observed.

Fig. 13
figure 13

Spectrum amplification (\(\eta\)) as a function of D and Q under different b (\(\lambda = 0.1\), q = 1)

Full size image

3 Numerical simulations

To verify the feasibility of the proposed ATSSR system in weak signal detection, a periodic attenuated pulse signal and a harmonic vibration signal are constructed for simulation experiments.

3.1 A periodically attenuated pulse signal detection

Bearings are commonly found in a variety of machinery and their fault signals can take many forms, some of which are in the form of shocks in order to effectively detect faulty bearings at an early stage and reduce losses. Therefore, periodically attenuated pulse signal is constructed to simulate the signal collected when an actual bearing fault occurs, and the ATSSR system is used for bearing fault signal detection to verify the practicality of the system.

$$ s(t) = A\exp \left[ { - 100\left( {{{t - \left\lfloor {t/T} \right\rfloor } \mathord{\left/ {\vphantom {{t - \left\lfloor {t/T} \right\rfloor } T}} \right. \kern-0pt} T}} \right)} \right] \times \sin \left[ {100\pi \left( {{{t - \left\lfloor {t/T} \right\rfloor } \mathord{\left/ {\vphantom {{t - \left\lfloor {t/T} \right\rfloor } T}} \right. \kern-0pt} T}} \right)} \right] $$
(32)

where sampling frequency \(f_{s} = 2000{\text{Hz}}\), sampling points \(N = 2000\), amplitude \(A = 0.2\), period \(T = 0.2\), and characteristic signal frequency \(f = {1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T} = 5{\text{Hz}}\). Figure 14(a) shows the time–frequency spectrum diagram of the original periodically attenuated pulse signal. Figure 14(b) shows the time–frequency diagram of the signal after adding Gaussian white noise with an intensity of 1.5. It shows that the signal is submerged in noise, and the fault characteristic signal frequency cannot be observed in the spectrogram under the background of strong noise. Since the characteristic signal frequency does not meet the requirement of small parameter, the secondary sampling is performed first and sampling frequency \(f_{sr} = 5{\text{Hz}}\), and then, the fault signal is processed through ATSSR system. Figure 14(c) shows the time–frequency diagram of the output signal. A large amount of noise in the time-domain signal is filtered out, and the amplitude of the signal is amplified by nearly 5 times. In the frequency domain, a peak occurs at f = 4.998 Hz, with a difference of 15.9 from the sub-peak. In addition, the peak at the characteristic frequency is more prominent than the surrounding noise components, which proves the feasibility of the system in signal detection.

Fig. 14
figure 14

Periodically attenuated pulse signal detection based on ATSSR system. (a) A periodically attenuated pulse signal. (b) The signal after adding Gaussian white noise. (c) ATSSR system output signal

Full size image

3.2 A harmonic vibration signal detection

Rotating machines are widely used in systems such as generators, transportation, and medical equipment. It is a prerequisite to ensure their operational safety for reducing losses and avoiding personal injuries; thus, early fault prediction of rotating machines is very important. Generally, the operating status of the machine can be observed through the generated harmonic vibration signals of the rotating machinery system. The harmonic vibration signals are mostly multi-frequency signals, so a vibration signal with three frequencies is constructed to verify its practicality:

$$ s\left( t \right) = 0.1\sin \left( {2\pi ft} \right) + 0.1\sin \left( {2\pi \times 2ft} \right) + 0.1\sin \left( {2\pi \times 3ft} \right) $$
(33)

where the fundamental frequency \(f = 15\;{\text{Hz}}\), sampling frequency \(f_{s} = 5000\;{\text{Hz}}\), and sampling points \(N = 4096\). Figure 15(a) shows the time domain and frequency spectrum of the original multi-frequency harmonic vibration signal. After adding Gaussian white noise with an intensity of 1.2, the time–frequency diagram of the signal is shown in Fig. 15(b). The signal is submerged in strong noise in the time domain and the frequency domain, and the periodicity and characteristic frequency of the signal cannot be observed. Since the three harmonic frequencies do not meet the small parameters, similarly, the secondary sampling is performed first and sampling frequency \(f_{sr} = 5\;{\text{Hz}}\), and then, the fault signal is processed through ATSSR system. Figure 15(c) shows the time–frequency diagram of output signal from ATSSR system. The time-domain signal is significantly less interfered by noise, and the signal waveform shows periodicity, and its amplitude is about twice that of the original signal. In addition, high-frequency noise is almost filtered out, and the amplitudes at the three harmonic frequencies are all higher than the surrounding noise components. The results indicate that the system can detect the characteristic frequency of the harmonic vibration fault signal.

Fig. 15
figure 15

Harmonic vibration signal detection based on ATSSR system. (a) A harmonic vibration signal. (b) The signal after adding Gaussian white noise. (c) ATSSR system output signal

Full size image

4 Conclusions

In this paper, an asymmetric tri-stable potential function is proposed and its resonant behaviors driven by the periodic forces, and the correlated multiplicative non-Gaussian noise and additive Gaussian white noise are investigated. Firstly, the effects of D, Q, q, \(\lambda\), and b on SPD and MFPT are analyzed. The main conclusions are as follows: (i) The effects of D and Q on SPD are opposite. (ii) Whether increasing D or Q, MFPT for particles to transit between wells is reduced. Then, the effects of D and Q on SA are analyzed for different q, \(\lambda\), and b. The results show that \(\eta\) has single peak with the increasing in D or Q, indicating that parameter-induced SR appears. Besides, the asymmetric intensity has a significant effect on \(\eta\). Finally, a periodic attenuated pulse signal and a harmonic vibration signal are constructed, and ATSSR system is used for simulated fault signal detection experiments. The experimental results exhibit good performances and prove the feasibility of ATSSR system in fault signal detection.

In this paper, we have only considered two typical correlation noises for fault detection analysis. However, practical applications involve various types of noise. Therefore, in further research, we plan to analyze the detection performance of this system under different combinations of noise sources. Moreover, to further improve the detection performance, we intend to search and construct new potential functions that can enhance the output signal-to-noise ratio.