Heat transfer with thermal radiation on MHD particle–fluid suspension induced by metachronal wave

Abstract

In this article, effects of heat transfer on particle–fluid suspension induced by metachronal wave have been examined. The influence of magnetohydrodynamics (MHD) and thermal radiation are also taken into account with the help of Ohm’s law and Roseland’s approximation. The governing flow problem for Casson fluid model is based on continuity, momentum and thermal energy equation for fluid phase and particle phase. Taking the approximation of long wavelength and zero Reynolds number, the governing equations are simplified. Exact solutions are obtained for the coupled partial differential equations. The impact of all the embedding parameters is discussed with the help of graphs. In particular, velocity profile, pressure rise, temperature profile and trapping phenomena are discussed for all the emerging parameters. It is observed that while fluid parameter enhances the velocity profile, Hartmann number and particle volume fraction oppose the flow.

1 Introduction

Flagella and cilia are two names that are simultaneously used for similar structures of eukaryotic cells. In Latin language cilia means eyelashes and the term cilia is often used when the cellular appendages are very small and bound in one cell. Their inner arrangement is formed by a cylindrical core known as ‘axoneme’. Axoneme is the cylindrical arrangement of microtubules (elastic elements) and dynein (molecular motors). It is well known that motion of cilia is similar to an active sliding which is the same as the well-known phenomenon in muscle. The diameter of cilia is about $0.2 \, \mu \hbox {m}$ and the length of cilia ranges from $2 \, \mu \hbox {m}$ to many millimeters [1]. When many cilia are adjoined together, they exhibit waves known as ‘metachronal waves’ on a very large scale. Cilia are basically organized in rows along and across the surface of the cell and respiratory tract epithelia. The motion of closed cilia interacting with hydrodynamics process form a metachronal wave [2, 3]. The propulsion of different fluids through ciliated surfaces have better efficiency compared to the random transport of cilia. The motion of cilia induced by a metachronal wave enhances the fluid propulsion and control the continuity of the flow.

Individually, ciliary motion takes various shapes, depending on the structure of ciliary system [4,5,6]. Examples include oscillatory, excitable beating, planar, helical etc. When a metachronal wave propagates along the same direction as the effective stroke, then this phenomenon is known as metachronism. When an effective stroke and a metachronal wave point in reverse direction then this coordination is known as antiplectic. When a viewer observes in the direction of a metachronal wave, he observes an effective stroke which is perpendicular to the direction of a wave. This mechanism is known as dexioplectic, and the mirror image of this composition is known as laeoplectic. For the past few years, the motion of cilia attracted the attention of many researchers. For instance, Nadeem et al [7] considered ciliary motion of non-Newtonian Carreau fluid through the asymmetric channel. He obtained perturbation solution for the nonlinear differential equation. Bhatti et al [8] studied the influence of magnetohydrodynamics on the metachronal wave of particle–fluid suspension due to the motion of cilia through a planar channel and presented the exact solution for the fluid and particle phases. Siddiqui et al [9] explored the Newtonian effects on hydromagnetic flow induced by the motion of cilia through a channel. Later, Siddiqui et al [10] considered the effects of non-Newtonian fluid induced by metachronal wave through a tube. Akbar et al [11] examined the influence of magnetic field for a metachronal beating of cilia for nanofluid with Newtonian heating. Haroon et al [12] analysed the ciliary motion of power-law fluid through an axisymmetric tube.

The heat transfer and magnetohydrodynamics (MHD) on metachronal wave due to cilia motion have been studied by many researchers using different media. Akbar and Butt [13] considered the effects of Hartmann number and heat transfer on the metachronal beating of cilia motion. Nadeem and Sadaf [14] studied theoretically and mathematically the Cu–blood nanofluid for metachronal wave induced by cilia motion through a curved channel. Akbar and Butt [15] analysed the impact of heat transfer on the metachronal wave of copper nanofluids and obtained the exact solutions. Siddiqui et al [16] investigated the influence of magnetic field on ciliary motion of Newtonian fluid through a cylindrical tube. Akbar and Butt [17] studied the heat transfer effects on Newtonian fluid flow due to the metachronal wave of cilia. Akram et al [18] explored the influence of inclined magnetic field on Jeffrey fluid flow due to metachronal wave. Akbar [19] presented the biomathematical analysis of carbon nanotubes due to cilia motion. Bhatti et al [20] examined the simultaneous effects of slip and endoscopy on blood flow of particle–fluid suspension induced by a peristaltic wave. Akbar and Khan [21] examined the cilia motion of biviscosity fluid through a symmetric channel. A few recent studies on the said topic can be seen in refs [22,23,24,25].

Motivated by the above studies, in this paper, we aim to analyse the heat transfer effects on MHD particle–fluid suspension induced by the metachronal wave. An approximation of creeping flow and long wavelength has been used to model the governing flow problem for fluid phase and particle phase. The resulting coupled linear partial differential equation for the fluid phase and the particle phase are solved analytically and exact solution is obtained. The impact of all emerging parameters is discussed with the help of graphs and streamlines. This paper is designed in the following way: Section 1 deals with the Introduction, §2 describes the mathematical formulation of the governing flow problem, §3 deals with the solution methodology and finally, §4 is devoted to graphical and numerical results of different emerging parameters.

2 Mathematical formulation

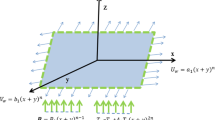
Let us consider the unsteady irrotational, hydromagnetic and sinusoidal motion of Casson particle–fluid which is incompressible and electrically conducting when an external magnetic field is applied through a two-dimensional channel. Let a metachronal wave travels with a constant velocity ${\tilde{{c}}}$ that is generated by a collective beating of cilia along the walls of the channel whose inner surfaces are ciliated. We have selected a Cartesian coordinate system for the channel in such a way that ${\tilde{{X}}}$-axis is taken along the axial direction and ${\tilde{{Y}}}$-axis is taken along the transverse direction.

The envelope for the cilia tips is assumed to be written as [22]

$$\begin{aligned} {\bar{Y}}= & {} {\bar{F}} ( {{\tilde{X}} ,{\tilde{t}} } )={\tilde{a}} + {\tilde{a}} \epsilon \cos \frac{2\pi }{\lambda }( {{\tilde{X}} -{\tilde{c}} {\tilde{t}} } ), \end{aligned}$$

(1)

$$\begin{aligned} {\bar{X}}= & {} {\bar{G}} ( {{\tilde{X}} ,{\tilde{t}} } )={\tilde{X}}_0 +{\tilde{a}} \epsilon \alpha \cos \frac{2\pi }{\lambda }( {{\tilde{X}} -{\tilde{c}} {\tilde{t}} } ). \end{aligned}$$

(2)

${\tilde{X}}, {\tilde{Y}}$ are the Cartesian coordinates, ${\tilde{t}}$ is the time, ${\tilde{a}}$ is the mean radius of the channel, ${\tilde{c}}$ is the wave velocity, $\uplambda$ is the wavelength. The vertical and horizontal velocities for cilia motion can be written as [22]

$$\begin{aligned} {\tilde{U}}_{f,p} =\frac{-\frac{2\pi }{\lambda }{\tilde{a}} \epsilon \alpha {\tilde{c}} \cos \frac{2\pi }{\lambda }( {{\tilde{X}} -{\tilde{c}} {\tilde{t}} } )}{1-\frac{2\pi }{\lambda }{\tilde{a}} \epsilon \alpha {\tilde{c}} \cos \frac{2\pi }{\lambda }( {{\tilde{X}} -{\tilde{c}} {\tilde{t}} } )}, \end{aligned}$$

(3)

$$\begin{aligned} {\tilde{V}}_{f,p} =\frac{-\frac{2\pi }{\lambda }{\tilde{a}} \epsilon \alpha {\tilde{c}} \sin \frac{2\pi }{\lambda }( {{\tilde{X}} -{\tilde{c}} {\tilde{t}} } )}{1-\frac{2\pi }{\lambda }{\tilde{a}} \epsilon \alpha {\tilde{c}} \sin \frac{2\pi }{\lambda }( {{\tilde{X}} -{\tilde{c}} {\tilde{t}} } )}, \end{aligned}$$

(4)

where the subscripts f and p stand for the fluid phase and the particulate phase.

The governing equation of continuity, momentum, and thermal energy equation for the fluid and particulate phases can be stated as [25, 26]

Fluid phase:

$$\begin{aligned} \frac{\partial {\tilde{U}}_f }{\partial {\tilde{X}} }+\frac{\partial {\tilde{V}}_f }{\partial {\tilde{Y}} }=0, \end{aligned}$$

(5)

(6)

(7)

(8)

where C is the volume fraction density, $\rho$ is the fluid density, k is the thermal conductivity, S is the drag force, $\mu _s$ is the viscosity of the fluid, $\sigma$ is the electrical conductivity, $B_0$ is the applied magnetic field, c is the specific heat.

Particulate phase:

$$\begin{aligned} \frac{\partial {\tilde{U}}_p }{\partial {\tilde{X}} }+\frac{\partial {\tilde{V}}_p }{\partial {\tilde{Y}} }= & {} 0, \end{aligned}$$

(9)

$$\begin{aligned}&C\rho _p \left( {\frac{\partial {\tilde{U}}_p }{\partial {\tilde{t}} }+{\tilde{U}}_p \frac{\partial {\tilde{U}}_p }{\partial {\tilde{X}} }+{\tilde{V}}_p \frac{\partial {\tilde{U}}_p }{\partial {\tilde{Y}} }} \right) \nonumber \\&\quad =-C\frac{\partial {\tilde{P}} }{\partial {\tilde{X}} }+\frac{CS}{\varpi _v }( {{\tilde{U}}_f -{\tilde{U}}_p } ), \end{aligned}$$

(10)

$$\begin{aligned}&C\rho _p \left( {\frac{\partial {\tilde{V}}_p }{\partial {\tilde{t}} }+{\tilde{U}}_p \frac{\partial {\tilde{V}}_p }{\partial {\tilde{X}} }+{\tilde{V}}_p \frac{\partial {\tilde{V}}_p }{\partial {\tilde{Y}} }} \right) \nonumber \\&\quad = -C\frac{\partial {\tilde{P}} }{\partial {\tilde{Y}} }+\frac{CS}{\varpi _v }( {{\tilde{V}}_f -{\tilde{V}}_p } ), \end{aligned}$$

(11)

$$\begin{aligned}&\rho _p Cc_p \left( {\frac{\partial {\bar{T}}_p }{\partial {\tilde{t}} }+{\tilde{U}}_p \frac{\partial {\bar{T}}_p }{\partial {\tilde{X}} }+{\tilde{V}}_p \frac{\partial {\bar{T}}_p }{\partial {\tilde{Y}} }} \right) \nonumber \\&\quad = \frac{\rho _p Cc_p }{\varpi _T }( {{\bar{T}}_f -{\bar{T}}_p } ), \end{aligned}$$

(12)

where $\varpi _T$ is the temperature relaxation time and $\varpi _v$ is a velocity relaxation time.

The mathematical expression for the drag coefficient and the empirical relation for the viscosity of the suspension can be defined as

$$\begin{aligned}&S=\frac{9\mu _0 }{2 {\check{a}}^{2}}{\tilde{\lambda }} ( C), \nonumber \\&{\tilde{\lambda }} ( C ) = \frac{4+3\sqrt{8C-3C^{2}}+3C}{({2-3C})^{2}},\nonumber \\&\mu _s =\frac{\mu _0 }{1-\chi C},\; \chi =0.07\mathrm{e}^{[ {2.49C+\frac{1107}{T}\mathrm{e}^{-1.69C}} ]}. \end{aligned}$$

(13)

The nonlinear radiative heat flux with the help of Roseland’s approximation can be written as

$$\begin{aligned} Q_r =-\frac{16{\bar{\sigma }} {\bar{T}}^{3}}{3{\bar{k}}} \frac{\partial {\bar{T}} }{\partial {\tilde{Y}} }. \end{aligned}$$

(14)

The rheological equation of state for an isotropic and incompressible Casson fluid is

(15)

where $\varepsilon _{ij}$ is the component of the deformation rate, ${\Pi }$ is the product of the deformation rate, ${\Pi }_c$ is the critical value of the product based and ${\mu }_b$ is the plastic viscosity. Let us define the transformation variable from fixed frame to wave frame. We have

$$\begin{aligned}&{\tilde{x}} ={\tilde{X}} -{\tilde{c}} {\tilde{t}} , \quad {\tilde{y}} ={\tilde{Y}}, \quad {\tilde{u}}_{f,p} ={\tilde{U}}_{f,p} -{\tilde{c}} ,\nonumber \\&{\tilde{v}}_{f,p} ={\tilde{V}}_{f,p} ,\quad {\tilde{p}} ={\tilde{P}}. \end{aligned}$$

(16)

Introduce the following non-dimensional quantities

$$\begin{aligned}&\tilde{x}=\frac{x}{\lambda },\quad {\tilde{y}} =\frac{y}{{\tilde{a}} },\quad {\tilde{u}}_{f,p} =\frac{u_{f,p} }{{\tilde{c}} },\quad P_r =\frac{\mu _s c}{{k}}, \nonumber \\&{\tilde{v}}_{f,p} =\frac{v_{f,p} }{{\tilde{c}} \delta },\quad {\phi }=\frac{{\tilde{b}} }{{\tilde{a}} },\quad p=\frac{{\tilde{a}}^{2}}{\lambda {\tilde{c}} \mu _s }{\tilde{p}} ,\quad \hbox {Re}=\frac{\rho {\tilde{a}} {\tilde{c}} }{\mu _s }, \nonumber \\&N_1 =\frac{S{\tilde{a}}^{2}}{\varpi _v\mu _s },\quad M=\sqrt{\frac{B_0^2 {\tilde{a}}^{2}\sigma }{\mu _s }},\quad \theta _{f,p} =\frac{{\bar{T}}_{f,p} -{\bar{T}}_0 }{{\bar{T}}_1 -{\bar{T}}_0 }, \nonumber \\&E_c =\frac{{\tilde{c}}^{2}}{c( {{\bar{T}}_1 -{\bar{T}}_0 } )},\quad R_d =\frac{4{\bar{\sigma }} {\bar{T}}^{3}}{\mu _s c{\bar{k}}}, \end{aligned}$$

(17)

where M is the Hartmann number, $P_{r}$ is the Prandl number, $\phi$ is the amplitude ratio, Re is the Reynolds number, $\theta$ is the dimensionless temperature, $E_{c}$ is the Eckert number and $\bar{\sigma }$ is the Stefan–Boltzmann constant. Using eqs (16) and (17) in eqs (1)–(15), and considering the approximation of long wavelength and zero Reynolds number approximation, the resulting equations after some simplification for the fluid phase can be written as

$$\begin{aligned} \left( {1+\frac{1}{{\Lambda }}} \right) \frac{\partial ^{2}u_f }{\partial y^{2}}-M^{2} ({u_f +1}) -\frac{1}{1-C}\frac{\hbox {d}p}{\hbox {d}x}=0,\nonumber \\ \end{aligned}$$

(18)

$$\begin{aligned}&\left( {\frac{1}{P_{r} }+\frac{4}{3}R_d } \right) \frac{\partial ^{2}\theta _f }{\partial y^{2}}+E_c \left( {1+\frac{1}{{\Lambda }}} \right) \left( {\frac{\partial u_f }{\partial y}} \right) ^{2} \nonumber \\&\quad +\,\frac{E_c }{N_1 ( {1-C} )}\left( {\frac{\hbox {d}p}{\hbox {d}x}} \right) ^{2}=0, \end{aligned}$$

(19)

where ${\Lambda }$ is the dimensionless fluid parameter and $R_{d}$ is the radiation parameter.

For the particulate phase, it can be written as

$$\begin{aligned}&\frac{1}{N_1 }\frac{\hbox {d}p}{\hbox {d}x}= ({u_f -u_p}), \end{aligned}$$

(20)

$$\begin{aligned}&\theta _f =\theta _p . \end{aligned}$$

(21)

Their corresponding boundary conditions are

$$\begin{aligned} u_f^{\prime } ( 0 )=0,\quad \theta _f ( 0 )= 0 \end{aligned}$$

and

$$\begin{aligned}&u_f (h)=-1-\frac{2\pi {\phi }\alpha \beta \cos 2\pi (x)}{1-2\pi {\phi }\alpha \beta \cos 2\pi (x)},\nonumber \\&\theta _f (h)=1. \end{aligned}$$

(22)

$\alpha$ is the eccentricity of the elliptic path and $\epsilon$ is the ratio of the cilia length.

3 Solution of the problem: Exact solutions

After integrating eqs (18) and (19) twice, the solution of velocity profile $({u_f ,u_p})$ and temperature profile $({\theta _f, \theta _p})$ can be written in simplified form as

$$\begin{aligned}&u_f (y)=\frac{M^{2}( {1-C} )+ {\frac{\mathrm{d}p}{\mathrm{d}x}}-\left( {( {-1+C} )M^{2} {\mathbb {N}}+\frac{\mathrm{d}p}{\mathrm{d}x}} \right) \cosh My\sqrt{\frac{{\Lambda }}{1+ {\Lambda }}}}{\left( {-1+c} \right) M^{2}\cosh Mh\sqrt{\frac{ {\Lambda }}{1+ {\Lambda }}}}, \end{aligned}$$

(23)

$$\begin{aligned}&u_p (y)=-\frac{1}{N_1 }\frac{\mathrm{d}p}{\mathrm{d}x} +\frac{M^{2}( {1-C} )+\frac{\mathrm{d}p}{\mathrm{d}x} -\left( {( {-1+C} )M^{2}{\mathbb {N}}+\frac{\mathrm{d}p}{\mathrm{d}x}} \right) \cosh My\sqrt{\frac{ {\Lambda }}{1+ {\Lambda }}}}{( {-1+c})M^{2}\cosh Mh\sqrt{\frac{ {\Lambda }}{1+ {\Lambda }}}}, \end{aligned}$$

(24)

$$\begin{aligned}&\theta _{f,p} (y)=\frac{4M^{2}y\left( {2( {-1+C} )N_1 ({3+4P_r R_d})+3E_c h\left( {\frac{\mathrm{d}p}{\mathrm{d}x}} \right) ^{2}P_r ( {-h+y} )} \right) }{8( {-1+C} )hM^{2}N_1 ({3+4P_r R_d } )}\nonumber \\&-\frac{3( {-1+C} ){\mathbb {C}}^{2}E_c N_1 P_r ( {h-y}) ( {1+ {\Lambda }} )( {-1+ ( {-1+2hM^{2}y} ) {\Lambda }} )}{8( {-1+C} )hM^{2}N_1 ( {3+4P_r R_d } ) {\Lambda }^{2}}\nonumber \\&+\frac{3( {-1+c} ){\mathbb {C}}^{2}E_c N_1 P_r ( {1+ {\Lambda }} )^{2}\left( {y\cosh 2Mh\sqrt{\frac{ {\Lambda }}{1+ {\Lambda }}}-h\cosh 2My\sqrt{\frac{ {\Lambda }}{1+ {\Lambda }}}} \right) }{8( {-1+C} )hM^{2}N_1 ({3+4P_r R_d }) {\Lambda }^{2}}. \end{aligned}$$

(25)

The volume flow rate for the fluid phase and the particulate phase is given by

$$\begin{aligned} Q=Q_f +Q_p , \end{aligned}$$

(26)

where

$$\begin{aligned} Q_f= & {} ( {1-C} ) \int _0^h u_f \hbox {d}y, \end{aligned}$$

(27)

$$\begin{aligned} Q_p= & {} C \int _0^h u_p \hbox {d}y. \end{aligned}$$

(28)

The pressure gradient $\hbox {d}p\slash \hbox {d}x$ is obtained after solving eqs (27) and (28). The non-dimensional pressure rise $({\Delta p})$ is evaluated numerically by using the following expression:

$$\begin{aligned} \Delta p= \int _0^1 \frac{\hbox {d}p}{\hbox {d}x}\hbox {d}x. \end{aligned}$$

(29)

The expression for stream function is defined as

$$\begin{aligned} {\tilde{U}}_{f,p } =\frac{\partial {\Phi }}{\partial y},\quad {\tilde{V}}_{f,p} =-\frac{\partial {\Phi }}{\partial x}, \end{aligned}$$

(30)

where

$$\begin{aligned} h= & {} 1+{\phi }\sin 2\pi x, \nonumber \\ {\mathbb {C}}= & {} \frac{\left( {( {-1+C} )M^{2}{\mathbb {N}}+\frac{\mathrm{d}p}{\mathrm{d}x}} \right) \sqrt{\frac{ {\Lambda }}{1+ {\Lambda }}}}{( {1-C} )M^{2}\cosh Mh\sqrt{\frac{ {\Lambda }}{1+ {\Lambda }}}},\nonumber \\ \mathbb {N}= & {} \frac{2\pi \phi \alpha \beta {\text { cos }}2\pi (x)}{1 - 2\pi \phi \alpha \beta {\text { cos }}2\pi (x)}. \end{aligned}$$

(31)

4 Results and discussion

This section describes the graphical results for all the parameters that arise in the governing flow problem. To analyse the novelties of all the pertinent parameters, computational software Mathematica has been used to bring out the inclusion of wavenumber ${{\beta }}$, measure of the eccentricity ${{\alpha }}$, particle volume fraction C, Hartmann number M, Casson fluid parameter ${{\Lambda }}$, Eckert number ${{E}}_{{c}}$, Prandtl number ${{P}}_{{r}}$ and radiation parameter ${{R}}_{{d}}$ on velocity profile ${{u}}_{{f}}$, temperature profile ${{\theta }}_{{{f}},{{p}}}$, pressure rise ${{\Delta }} {{p}}$ and trapping phenomena. The expression for pressure rise ${{\Delta }} {{p}}$ in eq. (29) is evaluated numerically with the help of computer-generated codes. For this purpose, figures 2–13 are sketched, whereas figure 1 represents the geometry of the governing flow problem.

Fig. 1

Geometry of the problem.

Fig. 2

Velocity profile for various values of ${{\alpha }}$ and ${{\Lambda }}$ when ${{R}}_{{d}} ={{3}}, {{P}}_{{r}} = {{6}}, {{E}}_{{c}} = {{0.5}}, {{\beta }} = {{0.2}}, {{C}}= {{0.2}}, {{M}}={{1}}$.

Fig. 3

Velocity profile for various values of ${{\beta }}$ and C when ${{\alpha }} = {{0.5}}, {{\Lambda }}={{1}}, {{R}}_{{d}} ={{3}}, {{P}}_{{r}} ={{6}}, {{E}}_{{c}} ={{0.5}}, {{M}}={{1}}$.

Figures 2–4 represent the velocity profile against Casson fluid parameter ${{\Lambda }}$, wavenumber ${{\beta }}$, a measure of the eccentricity ${{\alpha }}$, Hartmann number M and particle volume fraction C. Figure 2a shows that when the eccentricity parameter ${{\alpha }}$ increases, then the velocity profile increases when ${{y}}<0.6$. However, when ${{y}}>0.6$ the velocity profile shows opposite behaviour and decreases with the increment in ${{\alpha }}$. From figure 2b we can see that the Casson fluid parameter ${{\Lambda }}$ enhances the velocity profile. In eq. (16) the results for Newtonian fluid can be obtained by taking ${{\Lambda }}\rightarrow \infty$. It can be observed from figure 3a that when the wavenumber ${{\beta }}$ increases then it causes a reduction in the velocity profile when ${{y}}>0.6$ but for ${{y}}<0.6$ it enhances the velocity profile. It can be noticed from figure 3b that large values of particle volume fraction C causes a reduction in the velocity profile. When the magnetic field is applied to any electrically conducting fluid, then it produces a Lorentz force which tends to oppose the flow. It can be seen from figure 4 that magnetic field opposes the flow due to the influence of Lorentz force.

Fig. 4

Velocity profile for various values of M when ${{\alpha }} ={{0.5}}, {{\Lambda }} ={{1}}, {{R}}_{{d}} ={{3}}, {{P}}_{{r}} ={{6}}, {{E}}_{{c}} ={{0.5}}, {{\beta }} = {{0.2}}, {{C}}= {{0.2}}$.

Fig. 5

Temperature profile for various values of ${{P}}_{{{r}}}$ and ${{R}}_{{d}}$ when ${{\alpha }} ={{0.5}}, {{\Lambda }} = {{1}}, {{E}}_{{c}} ={{0.5}}, {{\beta }} ={{0.2}}, {{C}}={{0.2}}, {{M}}={{1}}$.

Fig. 6

Temperature profile for various values of $\Lambda$ and ${{E}}_{{c}}$ when ${{\alpha }} ={{0.5}}, {{\Lambda }} ={{1}}, {{R}}_{{d}} ={{3}}, {{P}}_{{r}} ={{6}}, {{C}}={{0.2}}, {{M}}={{1}}$.

Fig. 7

Pressure rise vs. volume flow rate for various values of ${{\Lambda }}$ and ${{\beta }}$ when ${{\alpha }} ={{0.5}}, {{R}}_{{d}} ={{3}}, {{P}}_{{r}} = {{6}}, {{E}}_{{c}} = {{0.5}}, {{C}}={{0.2}}, {{M}}={{1}}$.

Figures 5 shows the behaviour of temperature profile against Prandtl number ${{P}}_{{r}}$ and radiation parameter ${{R}}_{{d}}$, and figure 6 shows the behaviour of temperature profile against fluid parameter ${{\Lambda }}$ and Eckert number. Figure 5a shows that Prandtl number ${{P}}_{{r}}$ enhances the temperature profile. In fact, here we can also see that when the Prandtl number ${{P}}_{{r}} >1$ then the momentum diffusivity becomes more significant as compared to thermal diffusivity. From figure 5b, we can see that radiation parameter ${{R}}_{{d}}$ causes a reduction in the temperature profile. Hence, similar behaviour on temperature profile has been observed for Casson fluid parameter ${{\Lambda }}$ as shown in figure 6a. Figure 6b shows that Eckert number ${{E}}_{{c}}$ enhances the temperature profile.

Fig. 8

Pressure rise vs. volume flow rate for various values of C and M when ${{\alpha }} ={{0.5}}, {{\Lambda }}={{1}}, {{R}}_{{d}} ={{3}}, {{P}}_{{r}} ={{6}}, {{E}}_{{c}} ={{0.5}}, {{\beta }} ={{0.2}}$.

Fig. 9

Streamlines for various values of ${{\alpha }}$, $(\mathbf{a}) \,{{0.1}}, (\mathbf{b}) \,{{0.5}}, (\mathbf{c}) \,{{0.8}}$ when ${{\Lambda }}={{1}}, {{\beta }} ={{0.2}},{{C}}={{0.2}}, {{M}}= {{1}}$.

Fig. 10

Streamlines for various values of ${{\Lambda }}$, $(\mathbf{a}) \,{{0.5}}, (\mathbf{b}) \,{{2}}, (\mathbf{c}) \,\infty$ when ${{\alpha }} ={{0.5}},{{\beta }} ={{0.2}},{{C}}={{0.2}}, {{M}}= {{1}}$.

Fig. 11

Streamlines for various values of ${{\beta }}$, $(\mathbf{a}) \,{{0.1}}, (\mathbf{b}) \,{{0.3}}, (\mathbf{c}) \,{{0.4}}$ when ${{\alpha }} ={{0.5}}, {{\Lambda }}={1},{{C}}={{0.2}}, {{M}}={{1}}$.

Fig. 12

Streamlines for various values of C, $(\mathbf{a}) \,{{0.1}}, (\mathbf{b}) \,{{0.3}}, (\mathbf{c}) \,{{0.6}}$ when ${{\alpha }} ={{0.5}}, {{\Lambda }}={1},{{\beta }} ={{0.2}}, {{M}}= {{1}}$.

Fig. 13

Streamlines for various values of M, $(\mathbf{a}) \,{{1}}, (\mathbf{b}) \,{{2}}, (\mathbf{c}) \,{{3}}$ when ${{\alpha }} ={{0.5}}, {{\Lambda }}={{1}}, {{\beta }} ={{0.2}}, {{C}}={{0.2}}$.

To analyse the pumping characteristics, figures 7 and 8 are sketched for pressure rise against Casson fluid parameter ${{\Lambda }}$, Hartmann number M, wavenumber ${{\beta }}$ and particle volume fraction C. Furthermore, these figures are divided into four regions, i.e. retrograde pumping region $({{{\Delta }} {{p}}>0, Q<0})$, peristaltic pumping region $({{{\Delta }} {{p}}>0, Q>0} )$, free pumping region $({{{\Delta }} {{p}}<0, Q<0} )$ and co-pumping region $({{\Delta }} {{p}} < 0, Q > 0)$. Figure 7a shows that when the Casson fluid parameter ${{\Lambda }}$ increases, then the pumping rate increases in the free pumping region and co-pumping region. However, it shows opposite behaviour in retrograde pumping region. From figure 7b, we can see that the influence of wavenumber ${{\beta }}$ shows similar behaviour in all the regions and diminish with the increment in wavenumber ${{\beta }}$. Figure 8a is plotted against particle volume fraction C. It can be observed from this figure that particle volume fraction C has a very significant effect on pressure rise and decreases in retrograde pumping region. It can be seen from figure 8b that due to the influence of Hartmann number M the pressure rise shows dual behaviour in retrograde pumping region. When ${{Q}}<-1$, then the pressure rise increases with the increment in Hartmann number M but its behaviour is opposite when ${{Q}}>-1$.

The next most interesting and engrossing part of this section is the trapping phenomena which can be analysed with the help of streamlines. It is originated due to the formation of internally circulating bolus in the fluid that is enclosed by streamlines known as trapping. The physical mechanism is also applicable to the formulation of thrombus in blood and the transport of food bolus (gastrointestinal tract). Figures 9–13 are prepared for particle volume fraction C, Hartmann number M, measure of eccentricity ${{\alpha }}$, wavenumber ${{\beta }}$, and Casson fluid parameter ${{\Lambda }}$ respectively. It can be observed from figure 9 that when the eccentricity parameter ${{\alpha }}$ increases then it does not cause any greater impact on the magnitude of the bolus. We can see that the magnitude of the bolus is reduced very slowly. However, the number of bolus remains constant. It can be seen from figure 10 that when the Casson fluid parameter ${{\Lambda }}$ increases then the magnitude of the bolus decreases very gradually. From figure 11, we can see that when the wavenumber ${{\beta }}$ increases then the number of boluses reduces and the size of the bolus also decreases. Figure 12 shows that with the increment in particle volume fraction C, the magnitude of bolus decreases very moderately. In figure 13, we can see that when the Hartmann number M increases then the size and the number of bolus decrease very rapidly.

5 Conclusion

In this article, effects of heat transfer and MHD on particle–fluid induced by metachronal wave has been studied. The governing equations for the flow problem are modelled with the help of long wavelength and zero Reynolds number approximation. The resulting coupled partial differential equations are solved analytically and exact solutions are presented. Major outcomes of the present study are summarized below:

• Velocity profile shows similar behaviour due to the increment in eccentricity parameter ${{\alpha }}$ and wavenumber ${{\beta }}$.

• Velocity profile decreases due to the increment in particle volume fraction C and Hartmann number M.

• Prandtl number ${{P}}_{{r}}$ and Eckert number ${{E}}_{{c}}$ enhance the temperature profile.

• An increment in thermal radiation ${{R}}_{{d}}$ and Casson fluid parameter ${{\Lambda }}$ causes a reduction in the temperature profile.

• Pressure rise behaves in the same way in all the regions for wavenumber ${{\beta }}$.

• The behaviour of particle volume fraction C and Casson fluid parameter ${{\Lambda }}$ on pressure rise is the same.

• The present results for Newtonian fluid can also be obtained by taking ${{\Lambda }}\rightarrow \infty$.

• The present results reveal various interesting behaviours that warrant further study on a particle–fluid and metachronal wave.