Finite Element Study of Flow of Partially Ionized Fluid Containing Nanoparticles

Abstract

This article investigates the impact of nanosized particles (Cu and Ag) on the thermal performance of partially ionized non-Newtonion liquid (Casson fluid) exposed to non-uniform magnetic field in the presence of thermal radiations. Mathematical models based on basic governing laws are complex, nonlinear and coupled which are solved by finite element method in order to investigate the underlying physics. The results are validated by comparing with already published benchmarks. Convergence, error and mesh-free analysis are done. The CPU times of present method and method used in published benchmark are noted. The present method has less CPU time than CPU time required by method used in published benchmark. The wall shear stress increases, whereas wall heat flux decreases as the intensity of the magnetic field is increased. This observation is noted for the both cases of Cu and Ag nanoparticles. However, the wall shear stress for the case of Ag nanoparticles is greater than the wall shear stress for the case of Cu nanofluid. The usage of Ag nanoparticles is recommended as their dispersion in the base fluid increases the effective thermal conductivity in comparison of Cu nanofluid. Hall and ion-slip currents have shown remarkable increase in velocity and a significant reduction.

1 Introduction

Mixture of nanoparticles (in size 1–100 nm) and traditional liquid is known as nanofluid. The study of dispersion of nanoparticles in fluid has significant role in the improvement of thermal conductivity of nanofluids. Nanoparticles have various applications in heat transfer including a nuclear reactor, microchannel and thermal fluid and cooling system. Heat transfer in the presence of nanoparticles is examined by many researchers. However, here we describe the most relevant. Awais et al. [1] investigated heat and mass transport of Oldroyd-Beta fluid containing nanoparticles over the bidirectional moving surface. Awais et al. [2] also examined heat transportation in MHD flow of nanofluid with slip constraint. Bilal et al. [3] numerically studied the impact of nanoparticles on double diffusion in hydromagnetic flow over a stretching surface. Hassan et al. [4] simultaneously considered the influence of shape of nanoparticles and oscillating magnetic on the flow of ferrofluid. Zeeshan et al. [5] examined the impact of nanoparticles including entropy generation in flow due to rotation of disk. The role of hybrid nanoparticles on an enhancement transport of heat in hydromagnetic flow during the peristaltic mechanism of micropolar fluid was investigated by Ahmad and Nadeem [6]. An enhancement of biofluid during peristaltic movement of the fluid subject to Cu nanoparticles is also analyzed by Ahmad and Nadeem [7]. Awais et al. [8] discussed an enhancement in thermal conductivity of couple stress fluid when nanosize particles are dispersed. Hayat et al. [9] considered the effects of nanoparticles and thermal radiation on peristaltic transportation of biofluid in a channel with pores. They noted a remarkable impact of nanoparticles on the pumping phenomenon.

Newtonian and non-Newtonian fluids may have the property of emitting thermal radiations during thermal changes in the fluid. The effects of such radiations can be incorporated in extensive work on the thermal radiations are available, but we describe the most relevant. For instance, Mehmood et al. [10] considered thermal radiation in the hydromagnetic flow of dusty liquid by an inclined plane with dissipation. Khan et al. [11] modeled the simultaneous effects including thermal radiations and thermal slip on the transport of heat in magnetohydrodynamic flow past a cylinder having pores. Abbasi et al. [12] developed mathematical models for transport of heat in Jeffery liquid subjected thermal radiations and double stratification and derived their solutions in order to examine the role of thermal radiations on mixed convection in the flow. Awais et al. [13] discussed the thermal performance of nanofluid in the presence of thermal radiations emitted by the fluid. Hayat et al. [14] used the correlations for thermal properties of the base fluid and nanosized properties to investigate the thermal performance of working fluid in the presence of Marangoni effects.

The dynamics of ionized exposed to magnetic field have totally distinct dynamics of non-ionized fluid as ionized fluids experienced three forces namely the Lorentz force, the Hall force and force due to ion collision (ion-slip force). Existing literature reports for flows under the action of Lorentz force. Some developments are also made for flow in the presence of Hall currents. However, literature is scant for flows including Hall and ion-slip impacts. Motsa and Shateyi [15] derived the set of partial differential equations by considering the effects of Hall currents on the transport of mass subjected to chemical reactions and solved them numerically in order to examine the behavior of associated parameters. Hayat et al. [16] developed the mathematical models by considering the effects of Hall currents and Ohmic dissipation on the transport of heat in mixed convective flow generated peristaltic mechanism. Hayat and Nawaz [17] modeled three-dimensional flow of magnetohydrodynamic liquid composed of charged particles exposed to the magnetic field. They noted remarkable impact of Hall currents on momentum diffusion. Results of Hall effects of convection flow in appearance of magnetohydrodynamic channel incorporated viscous fluid past a channel is examined by Hayat et al. [18]. Hayat et al. [19] considered Hall and ion-slip influences in peristaltic flow of Jeffery nanofluid. Jha et al. [20] did mathematical modeling for flow experiencing Hall and ion Buoyancy forces and derived the solution of resulting models in order to examine the role of Hall and Buoyancy forces on mixed convection flow. Hayat et al. [21] used the governing laws and Maxwell’s equations to investigate peristaltic phenomenon under the Hall and ion slip currents. Recently, Nawaz et al. [22] studied the three-dimensional heat transfers in polymeric material containing nanoparticles in the presence of Hall and slip currents.

For the simulations of hydromagnetic flow situations, numerous numerical schemes have been employed by the researchers working in the fluid of computational fluid dynamics (CFD). The most liberal method is Galerkin finite element method (GFEM). The method process is efficacious concerning the solution of coupled nonlinear problems with complicated boundary conditions. Implementation of Galerkin finite element method (GFEM) as the simulations of fluid flow problems can be seen through Refs. [25, 26].

To the best of author’s knowledge, the finite element study on thermal performance of Casson fluid subjected to the dispersion of Cu and Ag nanoparticles is not conducted so far. The present investigation is advancement in this direction. A comparative study on the impact of copper and silver nanoparticles on thermal performance is also carried out. The finite element method is to implement to the modeled the problems, and parametric analysis is done in order to analyze the dynamics of associated parameters. Extensive numerical experiments are performed and obtained observations are displayed. Eventually, the whole work is summarized.

2 Problem Development

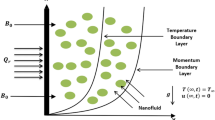
Consider 3D flow as a mixture of viscous fluid with copper and silver as nanoparticles. Flow is by nonlinear velocity of surface. Radiation effects are present. Non-uniform magnetic field $\varvec{B} = B_{0} \left( {x + y} \right) ^{n - 1}$ is applied in z-direction. Surface has velocity as $V_{\text{w}} = [a_{1} (x + y)^{n} ,b_{1} (x + y)^{n} ]$ where $a_{1} ,\,\;b_{1} ,\,\;n > 0$ are constant, and the wall temperature is defined as $T_{\text{w}} = T_{\infty } + A_{0} T_{0} (x + y)^{2n}$ Further Joule heating and viscous dissipation are present. Physical configuration is shown in Fig. 1.

Fig. 1

Physical configuration

Conservation laws of mass, momentum and energy for an incompressible flow of Casson fluid are

$$\nabla \cdot {\mathbf{V}} = 0,$$

(1)

$$\rho_{\text{nf}} \frac{{{\text{d}}{\mathbf{V}}}}{{{\text{d}}t}} = - \nabla P + \mu_{\text{nf}} \left( {1 + \frac{1}{\beta }} \right)\nabla^{2} {\mathbf{V}} + {\mathbf{J}} \times {\mathbf{B}},$$

(2)

$$(\rho c_{\text{p}} )_{\text{nf}} \frac{{{\text{d}}T}}{{{\text{d}}t}} = k_{\text{nf}} \nabla^{2} {\mathbf{T}} + tr({\varvec{\uptau}}{\mathbf{L}}) + \frac{1}{{\sigma_{\text{nf}} }}{\mathbf{J}} \cdot {\mathbf{J}} - \nabla \cdot {\mathbf{q}}_{\text{r}} ,$$

(3)

$$\nabla \cdot {\mathbf{B = 0}},\quad \nabla \times {\mathbf{B = }}{\varvec{\upmu}}_{0} {\mathbf{J}},\quad \nabla \times {\mathbf{E = }}\frac{{\partial {\mathbf{B}}}}{\partial t},$$

(4)

$${\mathbf{J = }}{\varvec{\upsigma}}_{\text{nf}} [{\mathbf{E + V}} \times {\mathbf{B}}]{\mathbf{ - }}\frac{{\beta_{\text{e}} }}{{|{\mathbf{B}}|}}({\mathbf{J}} \times {\mathbf{B}}){\mathbf{ + }}\frac{{\beta_{\text{e}} \beta_{\text{i}} }}{{|{\mathbf{B}}|^{2} }}({\mathbf{J}} \times {\mathbf{B}}) \times {\mathbf{B}}$$

(5)

where $P$ is the pressure, $\frac{\text{d}}{{{\text{d}}t}}$ is the material derivative, $\mu_{\text{nf}}$ is the dynamic viscosity of the nanofluid, $\varvec{V}$ is the velocity field, $J$ is the current density, $\rho_{\text{f}}$ is the fluid density, $\rho_{nf}$ is the density of the nanofluid, $\varvec{B}$ is the magnetic induction, $k_{nf}$ is the thermal conductivity of the nanofluid, $\sigma_{\text{nf}}$ is the electrical conductivity of the nanofluid and $\beta$ is the Casson fluid yield stress parameter and $\left( {c_{\text{p}} } \right)_{\text{nf}}$ is the specific heat of the nanofluid, $\beta_{\text{i}} \left( { = \omega_{\text{i}} \tau_{\text{i}} } \right)$ is the ion-slip parameter which is the product of cyclotron frequency $\left( {\omega_{\text{i}} } \right)$ of ions and ion collision time $(\tau_{\text{i}} ),\beta_{\text{e}} ( = \omega_{\text{e}} \tau_{\text{e}} )$ is the product of cyclotron frequency of electrons $\left( {\omega_{\text{i}} } \right)$ and electrons collision time $\left( {\tau_{\text{e}} } \right)$ and $\varvec{q}_{\text{r}}$ is the radiative heat flux vector which can be calculated by the Stefan–Boltzmann law [9] for the thermal radiations.

The use of boundary-layer approximations $O\left( x \right) = O\left( y \right) = O\left( {u_{1} } \right), O\left( {u_{2} } \right) = O\left( T \right) = 1, O\left( z \right) = \delta , O\left( {\nu_{\text{nf}} } \right) = \delta^{2}$ in Eqs. (1)–(5) gives

$$\frac{{\partial u_{1} }}{\partial x} + \frac{{\partial u_{2} }}{\partial y} + \frac{{\partial u_{3} }}{\partial z} = 0,$$

(6)

$$\begin{aligned} & u_{1} \frac{{\partial u_{1} }}{\partial x} + u_{2} \frac{{\partial u_{1} }}{\partial y} + u_{3} \frac{{\partial u_{1} }}{\partial z} \\ & \quad = \nu_{\text{nf}} \left( {1 + \frac{1}{\beta }} \right)\frac{{\partial^{2} u_{1} }}{{\partial z^{2} }} + \frac{{\sigma_{\text{nf}} B_{0}^{2} (x + y)^{n - 1} }}{{\rho_{\text{nf}} [(1 + \beta_{\text{e}} \beta_{\text{i}} )^{2} + \beta_{\text{e}}^{2} ]}}\\&\quad\qquad[u_{2} \beta_{\text{e}} - (1 + \beta_{\text{e}} \beta_{\text{i}} )u_{1} ], \end{aligned}$$

(7)

$$\begin{aligned}&u_{1} \frac{{\partial u_{2} }}{\partial x} + u_{2} \frac{{\partial u_{2} }}{\partial y} + u_{3} \frac{{\partial u_{2} }}{\partial z} \\& \quad = \nu_{\text{nf}} \left( {1 + \frac{1}{\beta }} \right)\frac{{\partial^{2} u_{2} }}{{\partial z^{2} }} - \frac{{\sigma_{\text{nf}} B_{0}^{2} (x + y)^{n - 1} }}{{\rho_{\text{nf}} [(1 + \beta_{\text{e}} \beta_{\text{i}} )^{2} + \beta_{\text{e}}^{2} ]}}\\& \quad \qquad[u_{1} \beta_{\text{e}} + (1 + \beta_{\text{e}} \beta_{\text{i}} )u_{2} ], \end{aligned}$$

(8)

$$\begin{aligned} u_{1} \frac{\partial T}{\partial x} + u_{2} \frac{\partial T}{\partial y} + u_{3} \frac{\partial T}{\partial z} & = \left( {\frac{{k_{\text{nf}} }}{{(\rho c_{\text{p}} )_{\text{nf}} }} + \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{(\rho c_{\text{p}} )_{\text{nf}} 3k^{ * } }}} \right)\frac{{\partial^{2} T}}{{\partial z^{2} }} \\ & \quad+ \frac{{\sigma_{\text{nf}} B_{0}^{2} (x + y)^{n - 1} }}{{(\rho c_{\text{p}} )_{\text{nf}} [(1 + \beta_{\text{e}} \beta_{\text{i}} )^{2} + \beta_{\text{e}}^{2} ]}}(u_{1}^{2} + u_{2}^{2} ) \\ & \quad + \,\frac{{\mu_{\text{nf}} }}{{(\rho c_{\text{p}} )_{\text{nf}} }}\left(1 + \frac{1}{\beta }\right)[\left(\frac{{\partial u_{1} }}{\partial z}\right)^{2} + \left(\frac{{\partial u_{2} }}{\partial z}\right)^{2} ], \\ \end{aligned}$$

(9)

where $u_{1} ,u_{2}$ and $u_{3} ,$ locate the velocities components on space coordinates, subscript $f$ is the base fluid, $nf$ is the thermo-physical properties of nanofluid, $B_{0}$ is magnitude of the constant magnetic field and intends its magnitude. Several models for thermo-physical properties of base fluid, solid nanosized particles and nanofluid are in practice. The numerical values of thermal properties used in this study are recorded in Table 1. Here, we have used the models due to Tiwari and Das [27]. This model is given by

$$\left. {\begin{array}{*{20}l} \begin{gathered} \rho _{{{\text{nf}}}} = (1 - \phi )\rho _{{\text{f}}} + \phi \rho _{{\text{s}}} ,\mu _{{{\text{nf}}}} = \frac{{\mu _{{\text{f}}} }}{{(1 - \phi )^{{\frac{5}{2}}} }}, \hfill \\ \sigma = \frac{{\sigma _{{\text{s}}} }}{{\sigma _{{\text{f}}} }},k_{{{\text{nf}}}} = \left\{ {\frac{{k_{{\text{s}}} + 2k_{{\text{f}}} - 2\phi (k_{{\text{f}}} - k_{{\text{s}}} )}}{{k_{{\text{s}}} + 2k_{{\text{f}}} + \phi (k_{{\text{f}}} - k_{{\text{s}}} )}}} \right\} \hfill \\ \end{gathered} \hfill \\ \begin{gathered} (\rho c)_{{{\text{nf}}}} = (1 - \phi )(\rho c)_{{\text{f}}} + \phi (\rho c)_{{\text{s}}} , \hfill \\ \sigma _{{{\text{nf}}}} = \sigma _{{\text{f}}} \left( {1 + \frac{{3(\sigma - 1)\phi }}{{\sigma + 2 - (\sigma - 1)\phi }}} \right),\nu _{{{\text{nf}}}} = \frac{{\mu _{{{\text{nf}}}} }}{{\rho _{{{\text{nf}}}} }} \hfill \\ \end{gathered} \hfill \\ \end{array} } \right\},$$

(10)

where $\phi$ is the solid volume fraction of nanoparticles.

Table 1 Thermo-physical properties of fluid and nanoparticles

The boundary conditions concerning the existing flow investigation are

$$\left. {\begin{array}{*{20}l} {u_{1} = a_{1} (x + y)^{n} ,u_{2} = b_{1} (x + y)^{n} ,w = 0,T = T_{\text{w}} \,{\text{at}}\,z = 0} \hfill \\ {u_{1} = 0,u_{2} = 0,T \to T_{\infty } \;{\text{as}}\;z \to \infty .} \hfill \\ \end{array} } \right\},$$

(11)

The change of variables

$$\left. {\begin{array}{*{20}l} {u_{1} = a_{1} (x + y)^{n} f^{\prime } ,u_{2} = a_{1} (x + y)^{n} g^{\prime } ,\eta = \sqrt {\frac{{a_{1} }}{v}} (x + y)^{{\frac{n - 1}{2}}} z,} \hfill \\ {u_{3} = - \sqrt {a_{1} v} (x + y)^{{\frac{n - 1}{2}}} \{ \frac{n + 1}{2}(f + g) + \frac{n - 1}{2}\eta (f^{\prime } + g^{\prime } )\} ,} \hfill \\ {\theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }},} \hfill \\ \end{array} } \right\}$$

(12)

transforms Eqs. (6)–(9) into the following set of boundary value problems

$$\left. {\begin{array}{*{20}l} \begin{gathered} \left(1 + \frac{1}{\beta }\right)f^{{\prime \prime \prime }} - \phi _{1} [nf^{\prime } (f^{\prime } + g^{\prime } ) - \frac{{n + 1}}{2}(f + g)f^{{\prime \prime }} ] \hfill \\ \quad + \frac{{\phi _{2} M^{2} }}{{(1 + \beta _{{\text{e}}} \beta _{{\text{i}}} )^{2} + \beta _{{\text{e}}}^{2} }}[\beta _{{\text{e}}} g^{\prime } - (1 + \beta _{{\text{e}}} \beta _{{\text{i}}} )f^{\prime } ] = 0 \hfill \\ \end{gathered} \hfill \\ {\quad \quad f(0) = 0,f^{\prime } (0) = 1,f^{\prime } (\infty ) = 0,} \hfill \\ \end{array} } \right\},$$

(13)

$$\left. {\begin{array}{*{20}l} \begin{gathered} \left(1 + \frac{1}{\beta }\right)g^{{\prime \prime \prime }} - \phi _{1} [ng^{\prime } (f^{\prime } + g^{\prime } ) - \frac{{n + 1}}{2}(f + g)g^{{\prime \prime }} ] \hfill \\ \quad - \frac{{\phi _{2} M^{2} }}{{(1 + \beta _{{\text{e}}} \beta _{{\text{i}}} )^{2} + \beta _{{\text{e}}}^{2} }}[\beta _{{\text{e}}} f^{\prime } + (1 + \beta _{{\text{e}}} \beta _{{\text{i}}} )g^{\prime } ] = 0 \hfill \\ \end{gathered} \hfill \\ {\quad \quad g(0) = 0,g^{\prime } (0) = \lambda ,g^{\prime } (\infty ) = 0,} \hfill \\ \end{array} } \right\},$$

(14)

$$\left. {\begin{array}{*{20}l} \begin{gathered} \left(1 + \frac{4}{{3N_{{\text{R}}} }}\right)\theta ^{{\prime \prime }} + \frac{{k_{{\text{f}}} }}{{k_{{{\text{nf}}}} }}\phi _{3} \frac{{n + 1}}{2}\Pr \theta ^{\prime } (f + g) - n\Pr \theta (f^{\prime } + g^{\prime } ) \hfill \\ \quad + \frac{{k_{{\text{f}}} }}{{k_{{{\text{nf}}}} }}\frac{{\mu _{{\text{f}}} }}{{\mu _{{{\text{nf}}}} }}\frac{{\phi _{2} }}{{(1 - \phi )^{{2.5}} }}\frac{1}{{(1 + \beta _{{\text{e}}} \beta _{{\text{i}}} )^{2} + \beta _{{\text{e}}}^{2} }}\Pr {\mkern 1mu} {\text{Ec}}M^{2} [(f^{\prime } )^{2} + (g^{\prime } )^{2} ] \hfill \\ \end{gathered} \hfill \\ {\quad + (1 + \frac{1}{\beta })\frac{{k_{{{\text{nf}}}} }}{{k_{{\text{f}}} }}\frac{{\mu _{{{\text{nf}}}} }}{{\mu _{{\text{f}}} }}\Pr {\mkern 1mu} {\text{Ec}}[(f^{{\prime \prime }} )^{2} + (g^{{\prime \prime }} )^{2} ] = 0,} \hfill \\ {\quad \quad \theta (0) = 1,{\mkern 1mu} \;\theta (\infty ) = 0,} \hfill \\ \end{array} } \right\},$$

(15)

where

$$\begin{aligned} \phi_{1} & = (1 - \phi )^{{\frac{5}{2}}} ((1 - \phi ) - \phi \frac{{\rho_{\text{s}} }}{{\rho_{\text{f}} }}),\\ \phi_{2} & = (1 - \phi )^{{\frac{5}{2}}} ((1 + \frac{3(\sigma - 1)\phi }{\sigma + 2 - (\sigma - 1)\phi })), \\ \phi_{3} & = 1 - \phi + \frac{{\phi (\rho c)_{\text{s}} }}{{(\rho c)_{\text{f}} }}, \\ \end{aligned}$$

and $N_{\text{R}}$ denotes radiation parameter, $\Pr$ terms Prandtl number, ${\text{Ec}}$ is the Eckert number, $M$ represents Hartmann number. These dimensionless parameters are defined by

$$\begin{aligned}&N_{\text{R}} = \frac{{k_{\text{nf}} k^{ * } }}{{4\sigma^{ * } T_{\infty }^{3} }},\quad {\text{Ec}} = \frac{{a^{2} }}{{(c_{\text{p}} )_{\text{f}} A_{0} T_{0} }},\quad \mathop {\Pr }\limits = \frac{{\mu_{\text{f}} (c_{\text{p}} )_{\text{f}} }}{{k_{\text{f}} }},\\ &M^{2} = \frac{{\sigma_{\text{f}} B_{0}^{2} }}{{\rho_{\text{f}} a}},\quad \lambda = \frac{{b_{1} }}{{a_{1} }}. \end{aligned}$$

The dimensionless shear stresses at the elastic sheet are

$$\begin{aligned} & C_{{f_{x} }} = \frac{{\tau_{zx} \;|_{z = 0} }}{{\frac{1}{2}\rho_{\text{f}} a^{2} (x + y)^{2n} }},\quad C_{{g_{y} }} = \frac{{\tau_{zy} \;|_{z = 0} }}{{\frac{1}{2}\rho_{\text{f}} a^{2} (x + y)^{2n} }},\, \\ & C_{{f_{x} }} (Re)^{{\frac{1}{2}}} = \frac{{2\sqrt {n + 1} }}{{(1 - \phi )^{2.5} }}\left( {1 + \frac{1}{\beta }} \right)f^{\prime \prime } (0),\\ & C_{{g_{y} }} (Re)^{{\frac{1}{2}}} = \frac{{2\sqrt {n + 1} }}{{(1 - \phi )^{2.5} }}\left( {1 + \frac{1}{\beta }} \right)g^{\prime \prime } (0). \\ \end{aligned}$$

(16)

The dimensionless rate of heat transfer at the sheet is

$${\text{Nu}} = - \frac{{k_{\text{nf}} (x + y)\frac{\partial T}{\partial y}\;|_{z = 0} }}{{k_{\text{f}} (T - T_{\infty } )}},\quad (Re)^{{ - \frac{1}{2}}} {\text{Nu}} = - \frac{{k_{\text{nf}} \sqrt {n + 1} }}{{k_{\text{f}} }}\theta^{\prime } (0),$$

(17)

3 Numerical Scheme

Several techniques for solutions of governing problems modeled in fluid dynamics have been in practices. For example, the studies [1, 2, 17] apply homotopy analysis method to find analytic series solutions of modeled similarity boundary value problems. Spectral method is also powerful technique which has been applied to the fluid problems by several researchers. For instance, a comprehensive literature review on Tau method is given in by Ortiz [28]. Scheffel [29] has given detailed analysis for the implementation of spectral method to magnetohydrodynamic problems. However, this text is limited to initial value problems. Patera [30] proposed spectral element method, which is combination of spectral method and finite element method, for the numerical solutions of incompressible Navier–Stokes equations. He validated his proposed technique by comparing the results with numerical and experimental data. Mercader et al. [31] implemented spectral methods for high-order equations. Canuto et al. [32] has discussed spectral methods for fluid dynamics in his book. Ehrenstein and Peyret [33] presented Chebyshev collocation method of unsteady Navier–Stokes equations based on vorticity-stream functions formulation. Smith et al. [34] has implemented spectral collocation to the flow past a circular cylinder. The spectral method has been successfully implemented with Newtonian fluid flows (see Refs. [28,29,30,31,32,33,34]), and available literature on spectral method may provide a foundation to extend them to the problems associated with non-Newtonian fluid flows. Implementation of Spectral method to no-Newtonian fluid problems needs lot of development. But it is not a matter to worry, as there is another powerful technique called Galerikin finite element method which has been successfully implemented on heat and mass transfer problems associated with the flows of non-Newtonian fluid [22,23,24,25,26]. The studies mentioned in Refs. [22,23,24,25,26] have shown an excellent agree with published benchmarks. Therefore, the present complex, coupled and nonlinear problems (13)–(15) are solved by the finite element method (FEM). Some details about FEM related to the problems (13)–(15) are given in “Appendix A”. Further, the mesh-free analysis is given in Table 2.

Table 2 Numerical values of $f^{\prime}\left( {\frac{{\eta_{\rm{max} } }}{2}} \right), g^{\prime}\left( {\frac{{\eta_{\rm{max} } }}{2}} \right)$ and $\theta \left( {\frac{{\eta_{\rm{max} } }}{2}} \right)$ at the mid of computational domain [0, 7] for different elements when $N_{\text{R}} = 0.1, {\text{Ec}} = 1.9, \Pr = 0.5, \lambda = 0.5, \mu_{\text{f}} = 6.9 \times 10^{ - 3} , \beta = 0.5, \beta_{\text{e}} = 0.5, \beta_{\text{i}} = 0.3, \phi = 0.1$

The results obtained from any numerical method are physically realistic only when they are mesh free. In present work, the mesh-free analysis is also shown in Table 2. It is depicted in Table 2 that calculated results are meshfree when the domain [0, 7] is breakdown into 330 elements. Hence, the upcoming analysis is carried out with 330 elements (Table 2).

Errors and error estimates There are several methods [36] for defining errors and their estimates. The well-known method is residual-based estimates which works on the total energy norm defined by

$$\left| {\left| {\mathbf{e}} \right|} \right| = \left( {\mathop \sum \limits_{K = 1}^{m} \left( {\left| {|{\mathbf{e}}|} \right|_{K}^{2} } \right)} \right)^{{\frac{1}{2}}}$$

where

$$\left| {\left| {\mathbf{e}} \right|} \right|_{K} = \mathop \int \limits_{\sigma } (\pounds\,e)^{T} (\nabla e){\text{d}}\varOmega \quad {\text{where }}{\mathbf{e}} = f - \hat{f}.$$

The details about residual-based estimators in term of total energy norm can found in “Appendix B”.

Tolerance and stopping criterion The skin friction coefficients and Nusselt number versus indicated values of parameters are computed by running the indigenous computer which solves the problem in an iterative manner order. Since exact solutions of problems under the consideration are not available. Therefore, the stopping criterion is defined by the error $|\omega^{i + 1} - \omega^{i} | < \varepsilon$ where $\varepsilon$ is very small and in the present case it is equal to $10^{ - 8}$ such that $\omega^{i + 1} \simeq \omega^{i}$. Thus, $\left( {\text{Re} } \right)^{{\frac{1}{2}}} C_{{f_{x} }} , \left( {\text{Re} } \right)^{{\frac{1}{2}}} C_{{g_{y} }}$ and $\left( {\text{Re} } \right)^{{ - \frac{1}{2}}} {\text{Nu}}$ are noted when above given criterion is satisfied. Errors for each parametric value are also displayed in Tables 6 and 7.

Validation of study The Galerkin finite element method (GFEM) formulation is used to develop a computer program to simulate the velocity and temperature. The results are validated when $M = {\text{Ec}} = \phi = 0, \beta \to \infty$ and $N_{\text{R}} \to \infty$ to published results [35]. The validation of results is displayed in Tables 3, 4 and 5 below.

Table 3 Comparison of present results with published work with their CPU times when $n = 3,\,\lambda = 1,\,\beta_{\text{i}} = 0.3,\,\beta_{\text{i}} = M = 0,\,N_{\text{R}} \to \infty ,\,{\text{Ec}} = 0,\;\phi = 0,\,\Pr = 0.5,\,\beta \to \infty$

Table 4 Comparison of the present results of $\left( {1 + \frac{1}{\beta }} \right)f^{\prime\prime}\left( 0 \right)$ and $\left( {1 + \frac{1}{\beta }} \right)f^{\prime\prime}\left( 0 \right)$ with the published work of Khan et al. [35] when $\beta_{\text{i}} = \beta_{\text{e}} = M = 0, N_{\text{R}} \to \infty , {\text{Ec}} = 0, \phi = 0, { \Pr } = 0.5, \beta \to \infty , { \Pr } = 0.5$

Table 5 Comparison of the present results of $- \theta^{\prime}\left( 0 \right)$ with the published work of Khan et al. [35] when $M = 0, N_{\text{R}} \to \infty , {\text{Ec}} = 0, \phi = 0, \beta_{\text{i}} = 0.3, \beta_{\text{e}} = 0.3$

4 Results and Discussion

Modeled problems (13)–(15) are solved numerically by FEM in order to investigate the dynamics of parameters on velocities and temperature. Numerical experiments versus parametric variation are conducted to explore the underlying physics. Dotted curves represent the flow fluids associated with Cu nanofluids, whereas flow field associated Ag nanofluid are shown by solid curves.

4.1 Observations Regarding Velocity

Effects of Hall and ion-slip currents The impact of parameter $\left( {\beta_{\text{i}} } \right)$ on the velocity of Cu nanofluid and Ag nanofluid is investigated in Figs. 2 and 3. Figures 2 and 3 declare that the velocity has an increasing trend when ion-slip parameter $\beta_{\text{i}}$ is enhanced. This increasing trend is noted for the both cases of Cu and Ag nanofluid. However, the influence of $\beta_{\text{i}}$ on flow of Cu nanoparticles is more significant than Ag nanoparticles. This increasing trend is based on the fact that ion-slip current is responsible for its influence on the flow of a force called ion-slip force which is opposite to the opposing magnetic force. Also from mathematical point of view, the parametric $\beta_{\text{i}}$ appears (with its square power) in the denominator of Lorentz force (which is opposing force), so an increase in $\beta_{\text{i}}$ results a remarkable decrease in the Lorentz force. Eventually, the flow slows down (see Figs. 2 and 3). The similar observations are noted for the parameter $\beta_{\text{e}}$ (see Figs. 4 and 5). Hall force is also an opposite force to the retarding magnetic force, and an increase in $\beta_{\text{e}}$ corresponds to an increase in Hall force which results a significant reduction in the Lorenz force. Consequently, a remarkable increase in the velocity of Cu nanofluid and Ag nanofluid is noted. It is also noted from numerical experiments that Cu nanofluid experiences less Lorentz force than the Lorentz force experienced by the Ag nanofluid. Further, Hall and ion-slip forces in case of flow of Cu nanofluid are stronger than those in case of flow Ag nanofluid. Momentum boundary-layer thickness is enhanced when $\beta_{\text{e}}$ and $\beta_{\text{i}}$ are enhanced; alternatively, an increase in $\beta_{\text{i}}$ and $\beta_{\text{i}}$ corresponds ion collision and electrons collisions, respectively. These collision rates are proportional to ion and Hall currents, and therefore, ion-slip and Hall forces are increased which results a remarkable reduction in magnetic force.

Fig. 2

Variation of velocity $f^{\prime}\left( \eta \right)$ of Cu/Ag nanofluid for different values of ion-slip parameter $\beta_{i}$ when $\beta = 1,\,n = 4,\,M^{2} = 0.1,\,\Pr = 3,\,N_{R} = 0.3,\,{\text{Ec}} = 0.1,\,\beta_{e} = 0.5,\,\phi = 0.1$

Fig. 3

Variation of velocity $g^{\prime}\left( \eta \right)$ of Cu/Ag nanofluid for different values of ion-slip parameter $\beta_{\text{i}}$ when $\beta = 1,\,n = 4,\,M^{2} = 0.1,\;\Pr = 3,\,N_{\text{R}} = 0.3,\;{\text{Ec}} = 0.1,\,\beta_{\text{e}} = 0.5,\,\phi = 0.1$

Fig. 4

Variation of velocity $f^{\prime}\left( \eta \right)$ of Cu/Ag nanofluid for different values of Hall parameter $\beta_{\text{e}}$ when $\beta = 1,\,n = 4,\,M^{2} = 0.1,\;\Pr = 3,\;N_{R} = 0.3,\;{\text{Ec}} = 0.1,\;\beta_{e} = 0.5,\;\phi = 0.1$

Fig. 5

Variation of velocity $g^{\prime}\left( \eta \right)$ of Cu/Ag nanofluid for different values of Hall parameter $\beta_{\text{e}}$ when $\beta = 1,\,n = 4,\,M^{2} = 0.3,\,\Pr = 3,\,N_{\text{R}} = 0.5,\,{\text{Ec}} = 0.1,\,\beta_{i} = 0.1,\,\phi = 0.1$

Impact of variation of intensity of magnetic field on fluid flow Figures 6 and 7 depict that an increase in the intensity of applied magnetic field enhances the magnitude of the Lorentz force which retards the flow. Therefore, velocity and associated layer thickness are reduced. Hence, it is concluded that momentum layer thickness may be controlled by the applied magnetic field.

Fig. 6

Variation of velocity $f^{\prime}\left( \eta \right)$ of Cu/Ag nanofluid for different values of Hartmann number $M$ when $\beta = 2,\,\Pr = 3,\,n = 4,\,\beta_{\text{e}} = 0.5,\,N_{\text{R}} = 0.3,\,{\text{Ec}} = 0.1,\,\beta_{i} = 0.3,\,\phi = 0.1$

Fig. 7

Variation of velocity $g^{\prime}\left( \eta \right)$ of Cu/Ag nanofluid for different values of Hartmann number $M$ when $\beta = 2,\,\Pr = 3,\,n = 4,\,\beta_{\text{e}} = 0.5,\,N_{\text{R}} = 0.3,\,{\text{Ec}} = 0.1,\,\beta_{\text{i}} = 0.3,\,\phi = 0.1$

4.2 Parametric Study Regarding Temperature

The dynamics of parameters $N_{\text{R}} , M, {\text{Ec}}, M, \beta_{\text{e}}$ and $\beta_{i}$ on the temperature of mixtures of copper and Casson fluid and Aluminum-Casson fluid are simulated in Figs. 8, 9, 10, 11 and 12.

Fig. 8

Variation of temperature $\theta \left( \eta \right)$ of Cu/Ag nanofluid for different values of radiation parameter $N_{\text{R}}$ where $\beta = 2, \,\Pr = 12, \,M^{2} = 0.1,\, n = 4, \,{\text{Ec}} = 0.3,\, \beta_{\text{e}} = 0.3, \,\beta_{\text{i}} = 0.3, \,\phi = 0.1$

Fig. 9

Variation of temperature $\theta \left( \eta \right)$ of Cu/Ag nanofluid for different values of Eckert number ${\text{Ec}}$ when $\beta = 2,\,\Pr = 12,\,M^{2} = 0.1,\,N_{\text{R}} = 0.3,\,\beta_{\text{e}} = 0.5,\,\beta_{\text{i}} = 0.3,\,n = 4,\,\phi = 0.1$

Fig. 10

Variation of temperature $\theta \left( \eta \right)$ of Cu/Ag -nanofluid for different values of Hartmann number $M$ when $\beta = 2, \,\Pr = 3.5,\, {\text{Ec}} = 0.1, \,N_{\text{R}} = 0.3, \,\beta_{\text{e}} = 0.5,\, \beta_{\text{i}} = 0.3,\, n = 4,\, \phi = 0.1$

Fig. 11

Variation of temperature $\theta \left( \eta \right)$ of Cu/Ag nanofluid for different values of ion-slip parameter $\beta_{i}$ when $\beta = 2, \,\Pr = 1.5,\, {\text{Ec}} = 0.1, \,N_{\text{R}} = 0.5,\, \beta_{\text{e}} = 0.5,\, M^{2} = 0.1,\, n = 4, \,\phi = 0.1$

Fig. 12

Variation of temperature $\theta \left( \eta \right)$ of Cu/Ag nanofluid for different values of Hall parameter $\beta_{\text{e}}$ when $\beta = 2,\, \Pr = 3.5,{\kern 1pt} \, {\text{Ec}} = 0.3,\, N_{\text{R}} = 0.5,\, \beta_{i} = 0.3,\, M^{2} = 0.5, \,n = 4, \,\phi = 0.1$

Impact of thermal radiation parameters The mixtures of Casson and nanoparticles are assumed to emit thermal radiations when mixture deform under thermal changes during the flow. This emission of electromagnetic waves radiation takes heat energy away from the liquid regime. Eventually, the temperature of nanofluid decreases. This phenomenon is simulated through various numerical experiments. The obtained results are given in Fig. 8. A significant reduction in thermal boundary-layer thickness is observed while increasing thermal radiation parameter. It is also noted that the emission of thermal radiation for Ag nanofluid is stronger than emission of thermal radiation in the case of Cu nanofluid.

Influence of viscous dissipation Due to viscous nature of nanofluid, heat dissipates and diffuses in the fluid regime. This additional friction heat causes a rise in temperature (see Fig. 9).

Impact of Ohmic dissipation The intensity of magnetic field is proportional to electric current produced as a result of change in magnetic flux and electric current is proportional to the Ohmic dissipation. The impact of magnetic field on the temperature is shown in Fig. 10. This graphical display of temperature contours reflects that the process of passage of electric current in Cu nanofluid produces heat greater than the heat produced in Ag nanofluid. By virtue of this, thermal boundary-layer thickness in Ag nanofluid is greater than thermal boundary-layer thickness.

Impact of Hall and ion-slip current on temperature Hall and ion-slip parameters appear as denominator in Joule heating in energy Eq. (15). Joule heating term reflects that rate at which heat is produced by passage of an electric current is inversely proportional to the sum of the squares of $\beta_{\text{e}}$ and $\beta_{\text{i}}$. Therefore, the production of Joule heating is reduced for an increase $\beta_{\text{e}}$ and $\beta_{\text{i}}$. Thus, Hall and ion-slip currents may play a significant in controlling the thermal boundary-layer thickness (see Figs. 11 and 12).

4.3 Rate of Heat Transfer and Skin Friction

The wall stresses versus different values of power-law index (n) and Hartmann number are examined for Cu and Ag nanosized particles in Tables 6 and 7. Both tables show that the shear stresses have increasing trend when power-law index and Hartmann number are increased. It is also observed that wall shear stress in case of Cu nanofluid is less than the shear stress for Ag nanofluid. Tables 6 and 7 also depict that heat transfer rate in Ag nanofluid is greater than the heat transfer rate in Cu nanofluid. Therefore, usage of Ag nanosized particles as thermal performance increasing agent is recommended due to two reasons: (1) Ag nanofluid enhances the effective thermal conductivity of working fluid than the enhancement in thermal conductivity by Cu nanosized particles, (2) Ag nanofluid exerts less shear stress at the surface of sheet than the shear stress exerted by Cu nanosized particles.

Table 6 Numerical values of $\left( {\text{Re} } \right)^{{\frac{1}{2}}} C_{{f_{x} }} , \left( {\text{Re} } \right)^{{\frac{1}{2}}} C_{{g_{y} }}$ and $\left( {\text{Re} } \right)^{{ - \frac{1}{2}}} {\text{Nu}}$ with errors for different values of n and $M$ for silver $\left( {\text{Ag}} \right)$ nanoparticles when $N_{R} = 0.1,\, {\text{Ec}} = 1.9,\,\Pr = 1.02,\, \lambda = 0.5,\, \mu_{\text{f}} = 6.9 \times 10^{ - 3} , \,\beta = 3, \,\beta_{\text{e}} = 0.5,\, \beta_{\text{i}} = 0.3,\, \phi = 0.1$

Table 7 Numerical values of $\left( {\text{Re} } \right)^{{\frac{1}{2}}} C_{{f_{x} }} , \left( {\text{Re} } \right)^{{\frac{1}{2}}} C_{{g_{y} }}$ and $\left( {\text{Re} } \right)^{{ - \frac{1}{2}}} Nu$ with errors for different values of n and $M$ for Copper (Cu) nanoparticles when $N_{\text{R}} = 0.1, {\text{Ec}} = 1.9, \Pr = 1.02, \lambda = 0.5, \mu_{\text{f}} = 6.9 \times 10^{ - 3} , \beta = 3, \beta_{\text{e}} = 0.5, \beta_{i} = 0.3, \phi = 0.1$

5 Concluding Remarks

Three-dimensional simulations for Casson plasma (which radiates thermal radiations and exhibits yield stress) in the presence of dissipation effects are carried out by Galerikin finite element method (GFEM). The weak form of the residual equations is used to derive the elements of stiffness matrix. The following observations are noted.

• The wall shear stress increases with the decrease in wall heat flux as the intensity of the magnetic field is increased. The observation is noted for the both cases of Cu and Ag nanoparticles. However, the wall shear stress for the case of Ag nanofluid is greater than the wall shear stress for the case of Cu nanofluid

• The usage of Ag nanoparticles is recommended as their dispersion in the base fluid increases the effective thermal conductivity in comparison with the effective thermal conductivity of Cu nanofluid

• The velocity of the nanoplasma increases when $\beta_{\text{i}}$ is increased as the force due to ion-slip current opposite to force due to magnetic force. Furthermore, a rise in $\beta_{\text{i}}$ causes an increase in the force due to ion collisions. As this force is opposite to the force due to applied magnetic field; therefore, the force due to applied magnetic field is reduced. Hence, the velocity of the plasma increases. An increase in the boundary-layer thickness is also noted when ion-slip parameter is increased

• The velocity of the Casson plasma decreases when the power-law index associated with wall velocity is increased. Likewise, boundary-layer thickness increases when power-law index is increased. This behavior of the velocity is noted for both the cases of Ag and Cu nanoparticles

• The temperature of the plasma decreases when the intensity of thermal radiation is increased. Consequently, a reduction in thermal boundary layer is observed. The Casson fluid cools down.

Appendices

Appendix A

Key calculations for finite element method The integral residual statements are given by

$$\begin{aligned} &{\mathop \int \nolimits_{{\eta _{e} }}^{{\eta _{{e + 1}} }} w_{p} [f^{\prime } - h]{\text{d}}\eta = 0,} \hfill \\ &{\mathop \int \nolimits_{{\eta _{e} }}^{{\eta _{{e + 1}} }} w_{p} [g^{\prime } - K]{\text{d}}\eta = 0,} \hfill \\& {\mathop \int \nolimits_{{\eta _{e} }}^{{\eta _{{e + 1}} }} w_{p} [\left( {\tfrac{{1 + \beta }}{\beta }} \right)h^{{\prime \prime }} - nh^{2} \varphi _{1} - nhK\varphi _{1} + \tfrac{{n + 1}}{2}fh^{\prime } \varphi _{1} } \hfill \\& \quad + \tfrac{{n + 1}}{2}g\varphi _{1} h^{\prime } + \,\tfrac{{\beta _{e} \varphi _{2} }}{{(\{ 1 + \beta _{{\text{e}}} \beta _{{\text{i}}} \} ^{2} + \beta _{{\text{e}}}^{2} )}}KM^{2} \hfill \\& \quad - \tfrac{{\varphi _{2} }}{{(\{ 1 + \beta _{{\text{e}}} \beta _{{\text{i}}} \} ^{2} + \beta _{{\text{e}}}^{2} )}}(1 + \beta _{{\text{e}}} \beta _{{\text{i}}} )hM^{2} ]{\text{d}}\eta = 0, \hfill \\& {\mathop \int \nolimits_{{\eta _{e} }}^{{\eta _{{e + 1}} }} w_{p} [K^{{\prime \prime }} \left( {\tfrac{{1 + \beta }}{\beta }} \right) - nK^{2} \varphi _{1} - nhK\varphi _{1} + \tfrac{{n + 1}}{2}fK^{\prime } \varphi _{1} } \hfill \\& {\quad + \,\tfrac{{n + 1}}{2}gK^{\prime } \varphi _{1} - \tfrac{{\varphi _{2} \beta _{{\text{e}}} }}{{(\{ 1 + \beta _{{\text{e}}} \beta _{{\text{i}}} \} ^{2} + \beta _{{\text{e}}}^{2} )}}hM^{2} } \hfill \\& {\quad - \tfrac{{\varphi _{2} (1 + \beta _{{\text{e}}} \beta _{{\text{i}}} )}}{{(\{ 1 + \beta _{{\text{e}}} \beta _{{\text{i}}} \} ^{2} + \beta _{{\text{e}}}^{2} )}}KM^{2} ]{\text{d}}\eta = 0,} \hfill \\& \mathop \int \nolimits_{{\eta _{e} }}^{{\eta _{{e + 1}} }} w_{p} [\theta ^{{^{{\prime \prime }} }} (\tfrac{{3N_{R} + 4}}{{3N_{R} }}) + \tfrac{{n + 1}}{2}\tfrac{{k_{f} }}{{k_{{nf}} }}\varphi _{3} \Pr \theta ^{{^{\prime } }} f \hfill \\& \quad - \tfrac{{n + 1}}{2}\tfrac{{k_{f} }}{{k_{{nf}} }}\varphi _{3} \Pr \theta ^{{^{\prime } }} g - n\Pr h\theta - n\Pr K\theta \hfill \\& \quad + \,\tfrac{{k_{f} }}{{k_{{nf}} }}\tfrac{{\mu _{f} }}{{\mu _{{nf}} }}\tfrac{1}{{(\{ 1 + \beta _{e} \beta _{i} \} ^{2} + \beta _{e}^{2} )}}\varphi _{2} M^{2} \Pr \,{\text{Ec}}K^{2} \hfill \\& \quad + \tfrac{{\mu _{{\text{f}}} }}{{\mu _{{{\text{nf}}}} }}\tfrac{{{\text{Ec}}}}{{(\{ 1 + \beta _{{\text{e}}} \beta _{{\text{i}}} \} ^{2} + \beta _{{\text{e}}}^{2} )}}\varphi _{2} \tfrac{{k_{{\text{f}}} }}{{k_{{{\text{nf}}}} }}M^{2} \Pr h^{2} \hfill \\& \quad + \left( {\tfrac{{1 + \beta }}{\beta }} \right){\text{Ec}}\tfrac{{k_{{nf}} }}{{k_{f} }}\tfrac{{\mu _{{nf}} }}{{\mu _{f} }}\Pr h^{{\prime 2}} + \left( {\tfrac{{1 + \beta }}{\beta }} \right)Ec\tfrac{{k_{{nf}} }}{{k_{f} }}\tfrac{{\mu _{{nf}} }}{{\mu _{f} }}\Pr K^{{\prime 2}} ]{\text{d}}\eta = 0, \hfill \end{aligned}$$

where $w_{p} ,(p = 1,2,3,4,5)$ are the weight functions. The unknown are approximated by Galerkin approximations which are selected in following forms

$$\left. {\begin{array}{*{20}l} {g = \sum\nolimits_{j = 1}^{2} {\psi_{j} } g_{j} ,\quad f = \sum\nolimits_{j = 1}^{2} {\psi_{j} } f_{j} ,\quad h = \sum\nolimits_{j = 1}^{2} {\psi_{j} } h_{j} ,} \hfill \\ {K = \sum\nolimits_{j = 1}^{2} {\psi_{j} } K_{j} ,\quad \theta = \sum\nolimits_{j = 1}^{2} {\psi_{j} } \theta_{j} ,\quad j = 1,2,} \hfill \\ \end{array} } \right\},$$

where $f_{j} ,h_{j} ,K_{j}$ and $\theta_{j}$ are the unknown nodal values and $\psi_{j}$ are linear shape functions which are defined by

$$\psi_{j} = ( - 1)^{j - 1} \left( {\frac{{1 - \frac{{\eta_{j + 1} }}{\eta }}}{{1 - \frac{{\eta_{j - 1} }}{\eta }}}} \right),\quad j = 1,2.$$

Using above defined approximations in weak form of residual statements, one gets the following elements

$$\begin{aligned} K_{{ij}}^{{14}} & = 0,K_{{ij}}^{{15}} = 0,b_{i}^{1} = 0,K_{{ij}}^{{21}} = 0, \\ K_{{ij}}^{{22}} & = \mathop \int \nolimits_{{\eta _{e} }}^{{\eta _{{e + 1}} }} \left( {\tfrac{{d\psi _{j} }}{{d\xi }}} \right)\psi _{i} {\text{d}}\eta ,K_{{ij}}^{{23}} = 0,K_{{ij}}^{{24}} = - \mathop \int \nolimits_{{\eta _{e} }}^{{\eta _{{e + 1}} }} (\psi _{j} )\psi _{i} , \\ K_{{ij}}^{{25}} & = 0,b_{i}^{2} = 0,K_{{ij}}^{{31}} = 0,K_{{ij}}^{{32}} = 0, \\ K_{{ij}}^{{33}} & = \mathop \int \nolimits_{{\eta _{e} }}^{{\eta _{{e + 1}} }} [ - \tfrac{{{\text{d}}\psi _{i} }}{{{\text{d}}\xi }}\left( {\tfrac{{1 + \beta }}{\beta }} \right)\left( {\tfrac{{{\text{d}}\psi _{j} }}{{{\text{d}}\xi }}} \right) - \varphi _{1} (\psi _{j} )n\psi _{i} \overline{h} \\ & \quad - n\varphi _{1} (\psi _{j} )\psi _{i} \overline{K} + \tfrac{{n + 1}}{2}\psi _{i} \varphi _{1} \left( {\tfrac{{{\text{d}}\psi _{i} }}{{{\text{d}}\xi }}} \right)\overline{f} \\ & \quad + \tfrac{{n + 1}}{2}\psi _{i} \varphi _{1} \left( {\tfrac{{{\text{d}}\psi _{j} }}{{{\text{d}}\xi }}} \right)\overline{g} - \tfrac{{\varphi _{2} }}{{(1 + \beta _{e} \beta i)^{2} + \beta _{e}^{2} }} \\ & \quad \quad M^{2} (1 + \beta _{e} \beta i)(\psi _{j} )\psi _{i} ]{\text{d}}\eta , \\ \end{aligned}$$

$$\begin{aligned} K_{{ij}}^{{34}} & = \mathop \int \nolimits_{{\eta _{e} }}^{{\eta _{{e + 1}} }} \tfrac{{\varphi _{2} }}{{(1 + \beta _{{\text{e}}} \beta _{{\text{i}}} )^{2} + \beta _{e}^{2} }}\beta _{{\text{e}}} M^{2} \psi _{i} (\psi _{j} ), \\ K_{{ij}}^{{35}} & = 0,\,\;b_{i}^{3} = 0,\,\;K_{{ij}}^{{41}} = 0,\,\;K_{{ij}}^{{42}} = 0, \\ K_{{ij}}^{{43}} & = \mathop \int \nolimits_{{\eta _{e} }}^{{\eta _{{e + 1}} }} - \tfrac{{M^{2} \varphi _{2} }}{{(1 + \beta _{{\text{e}}} \beta _{{\text{i}}} )^{2} + \beta _{e}^{2} }}\beta _{{\text{e}}} \psi _{i} (\psi _{j} ), \\ K_{{ij}}^{{44}} & = \mathop \int \nolimits_{{\eta _{e} }}^{{\eta _{{e + 1}} }} \left[ { - \tfrac{{{\text{d}}\psi _{i} }}{{{\text{d}}\xi }}\left( {\tfrac{{{\text{d}}\psi _{j} }}{{{\text{d}}\xi }}} \right)\left( {\tfrac{{1 + \beta }}{\beta }} \right) - n\varphi _{1} \psi _{i} (\psi _{i} )\overline{h} } \right. \\ & \quad - n\varphi _{1} \psi _{i} (\psi _{j} )\overline{K} + \tfrac{{n + 1}}{2}\varphi _{1} \psi _{i} (\tfrac{{{\text{d}}\psi _{j} }}{{{\text{d}}\xi }})\overline{f} \\ & \quad + \tfrac{{n + 1}}{2}\varphi _{1} \psi _{i} \left( {\tfrac{{{\text{d}}\psi _{j} }}{{{\text{d}}\xi }}} \right)\overline{g} - \tfrac{{M^{2} \varphi _{2} }}{{(1 + \beta _{{\text{e}}} \beta _{{\text{i}}} )^{2} + \beta _{{\text{e}}}^{2} }} \\ & \quad \quad \left. {(1 + \beta _{{\text{e}}} \beta _{{\text{i}}} )\psi _{i} (\psi _{j} )} \right]{\text{d}}\eta , \\ K_{{ij}}^{{45}} & = 0,\,\;\;b_{i}^{4} = 0,\,\;K_{{ij}}^{{51}} = 0,\,\;\;K_{{ij}}^{{52}} = 0, \\ \end{aligned}$$

$$\begin{aligned} K_{{ij}}^{{53}} & = \mathop \int \nolimits_{{\eta _{e} }}^{{\eta _{{e + 1}} }} \left[ {\tfrac{{k_{{\text{f}}} }}{{k_{{{\text{nf}}}} }}\tfrac{{\Pr \,{\text{Ec}}}}{{(1 + \beta _{{\text{e}}} \beta _{{\text{i}}} )^{2} + \beta _{{\text{e}}}^{2} }}\varphi _{2} \tfrac{{\mu _{{\text{f}}} }}{{\mu _{{{\text{nf}}}} }}(\psi _{i} )M^{2} (\psi _{j} )\overline{h} } \right. \\ & \quad \left. { + \tfrac{{k_{{{\text{nf}}}} }}{{k_{{\text{f}}} }}\left( {\tfrac{{1 + \beta }}{\beta }} \right)\tfrac{{\mu _{{{\text{nf}}}} }}{{\mu _{{\text{f}}} }}\Pr \left( {\tfrac{{{\text{d}}\psi _{j} }}{{{\text{d}}\xi }}} \right)\overline{{h^{{^{\prime } }} }} {\text{Ec}}} \right]{\text{d}}\eta , \\ K_{{ij}}^{{54}} & = \mathop \int \nolimits_{{\eta _{e} }}^{{\eta _{{e + 1}} }} \left[ {\tfrac{{M^{2} }}{{(1 + \beta _{{\text{e}}} \beta _{{\text{i}}} )^{2} + \beta _{{\text{e}}}^{2} }}\tfrac{{\mu _{{\text{f}}} }}{{\mu _{{{\text{nf}}}} }}\varphi _{2} \tfrac{{k_{{\text{f}}} }}{{k_{{{\text{nf}}}} }}{\text{Ec}}(\psi _{i} )(\psi _{j} )\overline{K} } \right. \\ & \quad \left. { + \tfrac{{k_{{{\text{nf}}}} }}{{k_{{\text{f}}} }}\Pr \tfrac{{\mu _{{{\text{nf}}}} }}{{\mu _{{\text{f}}} }}\left( {\tfrac{{1 + \beta }}{\beta }} \right){\text{Ec}}(\psi _{i} )\tfrac{{{\text{d}}\psi _{j} }}{{{\text{d}}\xi }}\overline{{K^{{^{\prime } }} }} } \right]{\text{d}}\eta , \\ K_{{ij}}^{{55}} & = \left[ { - \left( {\tfrac{{3N_{{\text{R}}} + 4}}{{3N_{{\text{R}}} }}} \right)\left( {\tfrac{{{\text{d}}\psi _{i} }}{{{\text{d}}\xi }}} \right)\tfrac{{{\text{d}}\psi _{j} }}{{{\text{d}}\xi }} + \tfrac{{n + 1}}{2}\tfrac{{k_{{\text{f}}} }}{{k_{{{\text{nf}}}} }}\varphi _{3} \psi _{i} } \right. \\ & \quad \quad \left( {\tfrac{{{\text{d}}\psi _{j} }}{{{\text{d}}\xi }}} \right)\overline{f} \Pr + \tfrac{{k_{{\text{f}}} }}{{k_{{{\text{nf}}}} }}\psi _{i} \left( {\tfrac{{{\text{d}}\psi _{j} }}{{{\text{d}}\xi }}} \right)\overline{g} \\ & \quad \left. { - \Pr (\psi _{j} )\overline{h} n\psi _{i} - n\psi _{i} (\psi _{j} )\overline{h} \Pr } \right]{\text{d}}\eta ,\,\;\;b_{i}^{5} = 0. \\ \end{aligned}$$

where

$$\overline{f} = \mathop \sum \limits_{i = 1}^{2} \psi_{i} \overline{f}_{i} ,\quad \overline{h} = \mathop \sum \limits_{i = 1}^{2} \psi_{i} \overline{h}_{i} ,\quad \overline{K} = \mathop \sum \limits_{i = 1}^{2} \psi_{i} \overline{K}_{i} ,$$

in which $\overline{f}_{i} ,\,\overline{h}_{i}$ and $\overline{K}_{i}$ are nodal values at the previous iteration.

Appendix B

Error and error estimates There are several methods for defining the errors and estimation of errors. The most common method for finding the error is

$$e = f - \hat{f},$$

where $f$ is the exact solution and $\hat{f}$ is the approximate finite element solution. For more elaboration, consider differential equation.

$$\pounds\,f + b = 0.$$

The energy norm can be written as

$$\left| {\left| {\mathbf{e}} \right|} \right| = |\mathop \int \limits_{\sigma } (e^{T} \pounds\,e{\text{d}}\varOmega )|^{{\frac{1}{2}}} \approx |\mathop \int \limits_{\sigma } |f - \hat{f}|\pounds[f - \hat{f}]{\text{d}}\varOmega |^{{\frac{1}{2}}}$$

Now the error in field $f$ is denoted by $|\Delta f| = \left( {\frac{{\left| {\left| {\mathbf{e}} \right|} \right|_{{L_{2} }}^{2} }}{\varOmega }} \right)^{{\frac{1}{2}}}$ where $\varOmega \;$ is the physical/computational domain. The above given absolute error for the computational domain in term of elements of domain.

$$\left| {\left| {\mathbf{e}} \right|} \right| = \left(\mathop \sum \limits_{k = 1}^{m} (\left| {|e|} \right|_{K}^{2} )\right)^{1/2}$$

where $K$ refers to individual elements $\varOmega_{K}$. The relative energy norm error is defined as

$$E_{K} = \frac{||e||}{||f||} \times 100\% .$$

The more details about the errors and error estimates can be found in Ref. [34]. However, this method of error estimation can be used as if exact solution is available but in most of the cases, as in present case, the exact solutions are not available. For this case, there is another way called residual-based estimators. To explain the concept of residual-based error, let us consider diffusion equation with source term.

$$- \nabla^{T} (k\nabla \phi ) + Q = 0,\,\;\;{\mathbf{X}} \in \varOmega ,$$

with the boundary conditions

$$\begin{aligned} & \phi = \hat{\phi }\;{\text{on}}\;\varGamma_{\phi } \\ & {\mathbf{q}}^{T} \hat{n} = q_{n} \;\;{\text{on}}\;\;\varGamma_{q} , \\ \end{aligned}$$

where

$${\mathbf{q}}^{T} = - k\nabla \phi = [q_{x} ,\,\;q_{y} ]^{T}$$

The error in the finite element solution can be written as

$$e = \phi - \hat{\phi }$$

The total energy norm is

$$\left| {\left| {\mathbf{e}} \right|} \right| = \left( {\mathop \sum \limits_{k = 1}^{m} \left( {\left| {|e|} \right|_{k}^{2} } \right)^{{\frac{1}{2}}} } \right)$$

$$||{\mathbf{e}}||_{K}^{2} = \mathop \int \limits_{{\sigma_{K} }} (\nabla e)^{T} k\nabla e{\text{d}}\varOmega = \mathop \int \limits_{{\sigma_{K} }} \frac{1}{k}[(q_{x} - \hat{q}_{x} )^{2} + (q_{y} - \hat{q}_{y} )^{2} ]{\text{d}}\varOmega.$$