1 Introduction

Negative ion plasma is the plasma which contains both negative and positive ion species in addition to electrons. This type of plasma has great importance in various fields of plasma science and technology. The existence of a considerable number of negative ions in the Earth’s ionosphere [1] and cometary comae [2] is well known. Positive–negative ion plasmas are found in plasma processing reactors [3,4], neutral beam sources [5], and low-temperature laboratory experiments [6,7]. Furthermore, negative ions are found in the upper region of Titan atmosphere [8,9]. These particles may act as organic building blocks for even more complicated molecules. In this kind of plasma, the electron number density decreases according to the charge neutrality, i.e., n e=n +−n −, where n e, n +, and n − are the electron, positive and negative ion densities, respectively. This results in a decrease in the shielding effect of the electrons. So, most of the phenomena are actually affected by the negative ions themselves, as well as by the lack of electrons [7]. Under specific laboratory conditions, the presence of nanodust clusters could change the plasma behaviour. These clusters could be considered as immobile or mobile charged nanodust grains. The presence of immobile nanodust grains changes the general properties of the propagated linear and nonlinear waves that are produced by the positive ions [10].

It is well known that different nonlinear equations are widely employed to describe many complex phenomena in science, e.g., fluid mechanics, plasma physics, optical fibres, solid-state physics, geophysics, etc. Various techniques such as inverse scattering method [11], bilinear transformation [12], tanh-function method [13], extended tanh method [14], sine–cosine method [15], F-expansion method [16], general expansion method [17], \(G^{\prime }/G\) method [18,19], homogeneous balance (HB) [20], etc. were used to obtain the solutions of these nonlinear equations. The HB method is a direct and an effective algebraic method to determine the exact travelling wave solutions. Interestingly, the homogeneous balance (HB) method was extended to investigate other kinds of exact solutions [21,22] in addition to solitary solutions. Fan [23] described two new applications of the homogeneous balance method and explored for Backlund transformation and similarity reduction of nonlinear partial differential equations. Fan showed that there is a definite correlation among the HB, the Weiss–Tabor–Carnevale (WTC), and the Clarkson–Kruskal (CK) methods. The aim of this work is to use the HB method to solve the evolution equation describing the present model namely, the extended Korteweg–de Vries (EKdV) equation, and obtain a class of appropriate solutions to describe the possible nonlinear waves in negative ion plasma.

This paper is organized as follows: In §2, we present the governing equations for the positive–negative ion plasmas. In §3, the reductive perturbation method is employed to derive the EKdV equation describing the system. The HB method is applied to obtain possible solutions of the EKdV equation. Discussion and numerical results are presented in §4. Finally, the results are summarized in §5.

2 Basic equations and formulation of the problem

We consider a one-dimensional, collisionless, unmagnetized plasma consisting of positive ions, negative ions, electrons, and stationary (positive /negative) charged dust impurities. The description of such plasma is governed by the fluid equations

$$ \frac{\partial n_{+}}{\partial t}+\frac{\partial}{\partial x}(n_{+} u_{+})=0, $$
(1)
$$ m_{+}n_{+}\left(\frac{\partial}{\partial t}+u_{+}\frac{\partial}{\partial x}\right) u_{+}+\frac{\partial P_{+}}{\partial x}+eZ_{+}n_{+}\frac {\partial\phi}{\partial x}=0, $$
(2)

for positive ions,

$$ \frac{\partial n_{-}}{\partial t}+\frac{\partial}{\partial x}(n_{-} u_{-})=0, $$
(3)
$$ m_{-}n_{-}\left(\frac{\partial}{\partial t}+u_{-}\frac{\partial}{\partial x}\right) u_{-}+\frac{\partial P_{-}}{\partial x}-eZ_{-}n_{-}\frac {\partial\phi}{\partial x}=0, $$
(4)

for negative ions, and

$$ n_{\mathrm{e}}=n_{\mathrm{e}}^{(0)}\left[ 1+(q-1)\frac{e\phi}{k_{\mathrm{B}}T_{\mathrm{e}}}\right] ^{({q+1})/{2(q-1)}}, $$
(5)

for electrons.

Here n +,−,e is the positive ion /negative ion /electron number density, u +,− is the positive /negative ion fluid velocity, m +,− is the positive /negative ion mass, ϕ is the electrostatic wave potential and e is the magnitude of the electron charge. The ion pressure is assumed to be adiabatic and is expressed by \(P_{s}=n_{s}^{(0)}k_{\mathrm {B}}T_{s}{n_{s}^{3}} (s=+,-)\), k B is the Boltzmann constant, T s and T e are the positive (negative) ions, and electron temperatures, \(n_{\mathrm {e},+,-}^{(0)}\) is the equilibrium density for the electrons, positive ions, and negative ions.

The system of equations is closed with the Poisson equation

$$ \frac{\partial^{2}\phi}{\partial x^{2}}=4\pi e(Z_{+}n_{+}-Z_{-}n_{-} -n_{\mathrm{e}}+\rho Z_{\mathrm{d}}n_{\mathrm{d}}), $$
(6)

where n d is the dust number density, Z d is the dust charge number, and the symbol ρ=± is used for positively or negatively charged dust impurities. In equilibrium, the neutrality condition of the plasma is satisfied, viz., \(Z_{+}n_{+}^{(0)}-Z_{-}n_{-}^{(0)}-n_{\mathrm {e}}^{(0)}+\rho Z_{\mathrm {d}}n_{\mathrm {d}}=0\).

The normalized set of the above dynamic equations can be written as

$$ \frac{\partial\bar{n}_{+}}{\partial\bar{t}}+\frac{\partial (\bar{n}_{+}\bar{u}_{+})}{\partial\bar{x}}=0\,, $$
(7)
$$ \frac{\partial\bar{u}_{+}}{\partial\bar{t}}+\bar{u}_{+} \frac{\partial\bar{u}_{+}}{\partial\bar{x}}+\sigma_{+}\bar {n}_{+}\frac{\partial\bar{n}_{+}}{\partial\bar{x}}+\frac {\partial\bar{\phi}}{\partial\bar{x}}=0, $$
(8)

for the positive ions,

$$ \frac{\partial\bar{n}_{-}}{\partial\bar{t}}+\frac{\partial (\bar{n}_{-}\bar{u}_{-})}{\partial\bar{x}}=0, $$
(9)
$$ \frac{\partial\bar{u}_{-}}{\partial\bar{t}}+\bar{u}_{-} \frac{\partial\bar{u}_{-}}{\partial\bar{x}}+\sigma_{-}Q_{-} \bar{n}_{-}\frac{\partial\bar{n}_{-}}{\partial\bar{x}} -Q_{-}{\Delta}_{-}\frac{\partial\bar{\phi}}{\partial\bar{x}}=0, $$
(10)

for the negative ions, and

$$ n_{\mathrm{e}}=\left[ 1+(q-1)\bar{\phi}\right]^{({q+1})/{2(q-1)}}, $$
(11)

for electrons, and finally the Poisson’s equation

$$ \frac{\partial^{2}\bar{\phi}}{\partial\bar{x}^{2}}=\bar{n} _{+}-\alpha{\Delta}_{-}\bar{n}_{-}-\gamma{\Delta}_{+}\bar{n}_{\mathrm{e}} +\rho\beta. $$
(12)

Here, Q −=m +/m − is the mass ratio, σ +,−=3T +,−/T e, Δ−=Z −/Z +, and Δ+=1/Z +.

Now, the neutrality condition is given by

$$ 1=\alpha{\Delta}_{-}+\gamma{\Delta}_{+}-\rho\beta, $$
(13)

where \(\alpha =n_{-}^{(0)}/n_{+}^{(0)},\gamma =n_{\mathrm {e}}^{(0)}/n_{+}^{(0)}\), and \(\beta =Z_{\mathrm {d}}n_{\mathrm {d}}/Z_{+}n_{+}^{(0)}\).

In eqs (7)–(12), the densities for the positive ions, negative ions, and electrons are normalized with their equilibrium densities. The velocities of the positive ions and negative ions are normalized by the ion-acoustic speed of the positive ions, C si=(k B T e/m +)1/2 and the potential ϕ is normalized by k B T e/e. The space and time are normalized by the positive ion Debye length \(\lambda _{\text {Di}}=(k_{\mathrm {B}}T_{\mathrm {e}}/4\pi n_{+}^{(0)} e^{2}Z_{+}^{2})^{1/2} \) and the positive ion plasma period \(\omega _{\text {pi}}^{-1}=(4\pi n_{+}^{(0)}e^{2}Z_{+}^{2}/m_{+})^{-1/2}\), respectively. The upper bar in eqs (7)–(12) will be omitted henceforth.

3 Derivation of the evolution equation

Now, we derive a dynamical equation for the nonlinear propagation of the dust ion-acoustic waves (DIAWs) using eqs (7)–(12). We employ the reductive perturbation technique, and accordingly we introduce the stretching space-time coordinates

$$ \xi=\epsilon(x-\lambda t)\,\quad\text{and} \quad\tau=\epsilon^{3}t, $$
(14)

where 𝜖 is a smallness parameter (0<𝜖≪1) measuring the strength of nonlinearity and λ is the wave propagation speed. Furthermore, the dependent variables are expanded as a power series in 𝜖 around their corresponding equilibrium values as

$$ {\Psi}={\Psi}^{(0)}+{\sum}_{n=1}^{\infty}\epsilon^{n}{\Psi}^{(n)}, $$
(15)

where

$$ {\Psi}=\{n_{+},n_{-},n_{\mathrm{e}},u_{+},u_{-},\phi\}^{T} $$
(16)

and

$$ {\Psi}^{(0)}=\{1,1,1,0,0,0\}^{T}. $$
(17)

Substituting eqs (14)–(17) in eqs (7)–(12) allows us to develop equations in various powers of 𝜖. The lowest-order equations of 𝜖 read as

$$ n_{\mathrm{e}}^{(1)}=\frac{q+1}{2}\phi^{(1)},\quad n_{-}^{(1)}=\frac{-Q_{-}{\Delta}_{-}} {(\lambda^{2}-\sigma_{-}Q_{-})}\phi^{(1)},\quad u_{-}^{(1)}=\frac{-\lambda Q_{-}{\Delta}_{-}}{(\lambda^{2}-\sigma_{-}Q_{-})}\phi^{(1)} $$
(18)

and

$$ n_{+}^{(1)}=\frac{1}{(\lambda^{2}-\sigma_{+})}\phi^{(1)},\quad u_{+}^{(1)} =\frac{\lambda}{(\lambda^{2}-\sigma_{+})}\phi^{(1)}\,. $$
(19)

The Poisson equation then provides the compatibility condition

$$ \frac{1}{(\lambda^{2}-\sigma_{+})}+\frac{\alpha Q_{-}{\Delta}_{-}^{2}} {(\lambda^{2}-\sigma_{-}Q_{-})}-\gamma{\Delta}_{+}\frac{q+1}{2}=0. $$
(20)

To the next order in 𝜖, we obtain a set of equations in the second-order perturbed quantities which can be solved using eqs (18) and (19) to give the second-order perturbed quantities as follows:

$$ n_{+}^{(2)}=\frac{1}{(\lambda^{2}-\sigma_{+})}\left[ \phi^{(2)} +\frac{(3\lambda^{2}+\sigma_{+})}{2(\lambda^{2}-\sigma_{+})^{2}}\phi^{(1)2}\right] , $$
(21)
$$ u_{+}^{(2)}=\frac{\lambda}{(\lambda^{2}-\sigma_{+})}\left[ \phi^{(2)} +\frac{1}{2}\left(\frac{(3\lambda^{2}+\sigma_{+})}{(\lambda^{2}-\sigma_{+})^{2}}-\frac{2}{(\lambda^{2}-\sigma_{+})}\right) \phi^{(1)2}\right], $$
(22)
$$ n_{-}^{(2)}=\frac{Q_{-}{\Delta}_{-}}{(\lambda^{2}-\sigma_{-}Q_{-})}\left[ -\phi^{(2)}+\frac{Q_{-}{\Delta}_{-}(3\lambda^{2}+\sigma_{-}Q_{-})}{2(\lambda ^{2}-\sigma_{-}Q_{-})^{2}}\phi^{(1)2}\right], $$
(23)
$$ u_{-}^{(2)}=\frac{\lambda Q_{-}{\Delta}_{-}}{(\lambda^{2}-\sigma_{-}Q_{-} )}\left[ -\phi^{(2)}+\frac{Q_{-}{\Delta}_{-}}{2}\left(\frac{(3\lambda ^{2}+\sigma_{-}Q_{-})}{(\lambda^{2}-\sigma_{-}Q_{-})^{2}}-\frac{2} {(\lambda^{2}-\sigma_{-}Q_{-})}\right) \phi^{(1)2}\right], $$
(24)
$$ n_{\mathrm{e}}^{(2)}=\frac{q+1}{2}\phi^{(2)}+\frac{(3+2q-q^{2})}{8}\phi^{(1)2} \,, $$
(25)

while Poisson equation gives

$$ \left[ \frac{1}{(\lambda^{2}-\sigma_{+})}+\frac{\alpha Q_{-}{\Delta}_{-}^{2}} {(\lambda^{2}-\sigma_{-}Q_{-})}-\gamma{\Delta}_{+}\frac{q+1}{2}\right] \phi^{(2)}+B\phi^{(1)2}=0, $$
(26)

where

$$ B=\frac{1}{2}\left[ \frac{(3\lambda^{2}+\sigma_{+})}{(\lambda^{2}-\sigma_{+})^{3}}-\frac{\alpha Q_{-}^{2}{\Delta}_{-}^{3}(3\lambda^{2}+\sigma_{-}Q_{-} )}{(\lambda^{2}-\sigma_{-}Q_{-})^{3}}-\frac{\gamma{\Delta}_{+}(3+2q-q^{2})} {8}\right] . $$
(27)

The coefficient of ϕ (2) is zero due to the condition (20) and ϕ (1)≠0, and therefore, B should be at least of the order of 𝜖 and now B ϕ (1)2 becomes of the order of 𝜖 3; so it should be included in the next order of Poisson equation. If we consider the next order in 𝜖, we obtain a set of equations in the third-order perturbed quantities, which can be solved with the help of eqs (18)–(25) to give

$$\begin{array}{@{}rcl@{}} \frac{\partial n_{+}^{(3)}}{\partial\xi}&= & \frac{2\lambda}{(\lambda ^{2}-\sigma_{+})^{2}}\frac{\partial\phi^{(1)}}{\partial\tau}+\frac {(3\lambda^{2}+\sigma_{+})}{(\lambda^{2}-\sigma_{+})^{3}}\frac{\partial (\phi^{(1)}\phi^{(2)})}{\partial\xi}\\ && +\frac{3}{(\lambda^{2}-\sigma_{+})^{5}}\left[ \lambda^{2}(\lambda ^{2}+3\sigma_{+})+\frac{1}{2}(\lambda^{2}+\sigma_{+})(3\lambda^{2}+\sigma_{+})\right] \phi^{(1)2}\frac{\partial\phi^{(1)}}{\partial\xi}\\ && +\frac{1}{(\lambda^{2}-\sigma_{+})}\frac{\partial\phi^{(3)}}{\partial\xi} \,, \end{array} $$
(28)
$$\begin{array}{@{}rcl@{}} \frac{\partial n_{-}^{(3)}}{\partial\xi}&=& \frac{-2\lambda Q_{-}{\Delta}_{-}} {(\lambda^{2}-\sigma_{-}Q_{-})^{2}}\frac{\partial\phi^{(1)}}{\partial\tau} +Q_{-}^{2}{\Delta}_{-}^{2}\frac{(3\lambda^{2}+\sigma_{-}Q_{-})}{(\lambda ^{2}-\sigma_{-}Q_{-})^{3}}\frac{\partial(\phi^{(1)}\phi^{(2)})}{\partial\xi} \\ &&- \frac{3Q_{-}^{3}{\Delta}_{-}^{3}}{(\lambda^{2}\,-\,\sigma_{-}Q_{-})^{5}}\!\left[ \lambda^{2}(\lambda^{2}\,+\,3\sigma_{-}Q_{-})\,+\,\frac{1}{2}(\lambda^{2}\,+\,\sigma _{-}Q_{-})(3\lambda^{2}\,+\,\sigma_{-}Q_{-})\right] \\&&\times \phi^{(1)2}\frac{\partial \phi^{(1)}}{\partial\xi} -\frac{Q_{-}{\Delta}_{-}}{(\lambda^{2}-\sigma_{-}Q_{-})}\frac{\partial \phi^{(3)}}{\partial\xi}\,, \end{array} $$
(29)
$$\begin{array}{@{}rcl@{}} \frac{\partial n_{\mathrm{e}}^{(3)}}{\partial\xi} & =&\frac{q+1}{2}\frac{\partial \phi^{(3)}}{\partial\xi}+\frac{(3+2q-q^{2})}{4}\frac{\partial(\phi^{(1)} \phi^{(2)})}{\partial\xi}\\ && +\frac{1}{16}(q-3)(q+1)(3q-5)\phi^{(1)2}\frac{\partial\phi^{(1)}} {\partial\xi}. \end{array} $$
(30)

The Poisson equation of this order yields

$$ \frac{\partial^{2}\phi^{(1)}}{\partial\xi^{2}}=\left(n_{+}^{(3)}-n_{+}^{(2)}\right) -\alpha{\Delta}_{-}\left(n_{-}^{(3)}-n_{-}^{(2)}\right) -\gamma{\Delta}_{+}\left(n_{\mathrm{e}}^{(3)}-n_{\mathrm{e}}^{(2)}\right) . $$
(31)

Differentiating eq. (31) and using eqs (21), (23), (25), (28)–(30), we obtain the EKdV equation

$$ \frac{\partial u}{\partial\tau}+ABu\frac{\partial u}{\partial\xi}+ACu^{^{2}} \frac{\partial u}{\partial\xi}+\frac{1}{2}A\frac{\partial^{3}u}{\partial \xi^{3}}=0, $$
(32)

where ϕ (1) is replaced by u for simplicity. The coefficients A and C are given as

$$ A=-\frac{1}{\lambda}\left[ \frac{1}{(\lambda^{2}-\sigma_{+})^{2}} +\frac{\alpha Q_{-}{\Delta}_{-}^{2}}{(\lambda^{2}-\sigma_{-}Q_{-})^{2}}\right]^{-1}, $$
(33)
$$\begin{array}{@{}rcl@{}} C & =&-\frac{3}{2(\lambda^{2}-\sigma_{+})^{5}}\left[ \lambda^{2}(\lambda ^{2}+3\sigma_{+})+\frac{1}{2}(\lambda^{2}+\sigma_{+})(3\lambda^{2}+\sigma_{+})\right] \\ && -\frac{3\alpha Q_{-}^{3}{\Delta}_{-}^{4}}{2(\lambda^{2}-\sigma_{-}Q_{-})^{5}} \left[ \lambda^{2}(\lambda^{2}+3\sigma_{-}Q_{-})+\frac{1}{2}(\lambda^{2}+\sigma_{-}Q_{-})(3\lambda^{2}+\sigma_{-}Q_{-})\right] \\ &&+ \frac{\gamma{\Delta}_{+}}{16}(q-3)(q+1)(3q-5). \end{array} $$
(34)

It is known that if one solves the basic set of fluid eqs (7)–(12) exactly to obtain the energy equation including the Sagdeev potential, then the obtained evolution equation describes the large /finite amplitude wave. When the Sagdeev potential is expanded for small but finite amplitude limit, we obtain the same result as predicted by the reductive perturbation theory. The tricky point here is to make the expansion carefully to obtain the same coefficients. So, considering B has small value is just a bridge to maintain the large-amplitude limit with the small-amplitude limit that is covered by the perturbation theory. There are many papers to prove this point (e.g., [24] and [25]).

4 Use the HB method to solve the EKdV equation

Consider the EKdV eq. (32) in the form

$$ \frac{\partial u}{\partial\tau}+{\Gamma} u\frac{\partial u}{\partial\xi}+{\Lambda} u^{^{2}}\frac{\partial u}{\partial\xi}+{\Omega}\frac{\partial^{3}u}{\partial \xi^{3}}=0, $$
(35)

where Γ=A B, Λ=A C, and Ω=A/2. We seek for the special solution of eq. (35), the travelling wave solution, in the form

$$ u(\xi,\tau)=u(\zeta),\quad \zeta= \xi-\vartheta\,\tau, $$
(36)

where 𝜗 is a constant to be determined later. Using the transformation (36) in eq. (35), eq. (35) reduces to a nonlinear ordinary differential equation (ODE) which will be solved later. The next crucial step is to express the solution of eq. (35) in the form

$$ u(\zeta)=\underset{i=0}{\overset{n}{ {\displaystyle\sum}} } a_{i} \omega^{i}+\underset{i=1}{\overset{n}{ {\displaystyle\sum}} }b_{i}\left[ 1+\omega\right]^{-i} $$
(37)

and

$$ \omega^{\prime}=k+M\omega+P\omega^{2}, $$
(38)

where a i and b i are constants, while k, M, and P are parameters to be determined later, ω=ω(ζ) and \(\omega ^{\prime } =\mathrm {d}\omega /\mathrm {d}\zeta \). To determine the parameter n, it is necessary to create a balance between the highest-order linear term and the nonlinear terms. Substituting (37) and (38) in the relevant ODE form of eq. (35) yields a system of ODEs with respect to a 0, a i , b i , k, M, P, and 𝜗 (where i=1,...,m), because all the coefficients of ω j (where j=0,1,...) have to vanish. Using Mathematica, one can determine a 0, a i , b i , k, M, P, and 𝜗.

It is noted that eq. (38) has a form of Riccati equation, which can be solved using the HB method as follows:

Case I.

When P=1 and M=0, the Riccati eq. (38) has the following solutions:

$$ \omega=\left\{ \begin{array}{ll} -\sqrt{-k}\, \tanh[\sqrt{-k}\zeta], & \quad \text{with}~k<0,\\ -\sqrt{-k}\, \coth[\sqrt{-k}\zeta], & \quad \text{with}~k<0, \end{array} \right. $$
(39)
$$ \omega=-\frac{1}{\zeta},\quad \text{with}~k=0, $$
(40)

and

$$ \omega=\left\{ \begin{array}{ll} \sqrt{k}\,\tan[\sqrt{k}\zeta], & \quad\text{with}~k>0,\\ -\sqrt{k}\,\cot[\sqrt{k}\zeta], & \quad\text{with}~k>0. \end{array} \right. $$
(41)

As coth- and cot-type solutions appear in pairs with tanh- and tan-type solutions, respectively, they are omitted in this paper.

Case II.

Let \(\omega ={\sum }_{i=0}^{m}A_{i}\tanh ^{i}\left (p_{1}\zeta \right ) \). Balancing \(\omega ^{\prime }\) with ω 2 leads to

$$ \omega=A_{0}+A_{1}\tanh\!\left(p_{1}\zeta\right)\!. $$
(42)

Substituting eq. (42) in (38), we have the following solution of eq. (38):

$$ \omega=-\frac{p_{1}}{2P}\tanh\!\left(\frac{p_{1}}{2}\zeta\right)-\frac{M}{2P} ,\quad \text{with}\quad Pk=\frac{M^{2}-{p_{1}^{2}}}{4}. $$
(43)

Similarly, let \(\omega ={\sum }_{i=0}^{m}A_{i}\coth ^{i}\left (p_{1}\zeta \right ) \), then we obtain the following solution:

$$\omega=-\frac{p_{1}}{2P}\coth\left(\frac{p_{1}}{2}\zeta\right)-\frac{M}{2P}, $$

with \(Pk=({M^{2}-{p_{1}^{2}}})/{4}\), where k, M, p 1, and P are constants.

Case III.

We suppose that the Riccati eq. (38) has the following solutions of the form

$$ \omega=A_{0}+{\sum}_{i=0}^{m}(A_{i}f^{i}+B_{i}f^{i-1}g), $$
(44)

with

$$ f=\frac{1}{\cosh\zeta+r} \quad\text{and}\quad g=\frac{\sinh\zeta}{\cosh\zeta+r}. $$
(45)

Substituting eqs (44) and (45) in (38), we have the following solution of eq. (38):

$$ \omega=-\frac{1}{2P}\left(M+\frac{\sinh\left(\zeta\right) +\sqrt{r^{2} -1}}{\cosh\left(\zeta\right) +r}\right), \quad \text{with}\ Pk=\frac{M^{2} -1}{4}, $$
(46)

where r is the arbitrary constant. It should be noticed that solution (46), as r=1, degenerates to

$$ \omega=-\frac{1}{2P}\left[ M+\tanh\!\left(\frac{\zeta}{2}\right) \right] . $$
(47)

Case IV.

We suppose that the Riccati eq. (38) has the following solutions of the form

$$ \omega=A_{0}+{\sum}_{i=0}^{m}\sinh^{i-1}(A_{i}\sinh\varrho+B_{i}\cosh\varrho), $$
(48)

where \(\mathrm {d}\varrho /\mathrm {d}\zeta =\sinh \varrho \) or \(\mathrm {d}\varrho /\mathrm {d}\zeta =\cosh \varrho \). Balancing \(\omega ^{\prime }\) with ω 2 leads to m=1

$$ \omega=A_{0}+A_{1}\sinh\varrho+B_{1}\cosh\varrho, $$
(49)

when \(\mathrm {d}\varrho /\mathrm {d}\zeta =\sinh \varrho \), we substitute (49) and \(\mathrm {d}\varrho /\mathrm {d}\zeta =\sinh \varrho \) into (38) and set the coefficient of \(\sinh ^{i} \varrho \cosh ^{j}\varrho \), i=0,1,2, j=0,1 to zero and on solving the obtained set of algebraic equations we get

$$ A_{0}=\frac{-M}{2P},\quad A_{1}=0,\quad B_{1}=\frac{1}{P}, $$
(50)

where k=(M 2−4)/4P and

$$ A_{0}=\frac{-M}{2P},\quad A_{1}=\pm\sqrt{\frac{1}{2P}},\quad B_{1}=\frac{1}{P}, $$
(51)

where k=(M 2−1)/4P. When \(\mathrm {d}\varrho /\mathrm {d}\zeta =\sinh \varrho \) we have

$$ \sinh\varrho=-\text{cosech}\zeta,\quad \cosh\varrho=-\coth\zeta. $$
(52)

From (50)–(52), we obtain

$$ \omega=-\frac{M+2\coth\zeta}{2P}, $$
(53)

for k=(M 2−4)/4P and

$$ \omega=-\frac{M\pm\text{cosech}\zeta+\coth\zeta}{2P}, $$
(54)

for k=(M 2−1)/4P.

On introducing different classes of solutions of the EKdV eq. (35), we determine the direct solutions of eq. (35) with clear details of the used methodology. We shall use the transformation u(x,t)=U(ζ), ζ=x−𝜗 t in eq. (35). Therefore, eq. (35) reduces to the following ODE:

$$ -\vartheta U^{\prime}+{\Gamma} UU^{\prime}+{\Lambda} U^{2}U^{\prime}+{\Omega} U^{\prime\prime\prime}=0. $$
(55)

Integrating eq. (55) twice with respect to ζ, we get

$$ -\lambda U+\frac{\Gamma}{2}U^{2}+\frac{\Lambda}{3}U^{3}+{\Omega} U^{\prime \prime}=0. $$
(56)

Using eq. (37) and balancing \(U^{\prime \prime }\) with U 3 yields n=1. Therefore, we are looking for the solution of the form

$$ U=a_{0}+b_{0}+a_{1}\omega+b_{1}(1+\omega)^{-1}. $$
(57)

Substituting eqs (57) and (38) in eq. (56), we get a polynomial equation ω. Hence, equating the coefficient of ω j (j=0,1,2,...) to zero and solving the obtained system of overdetermined algebraic equation using the symbolic manipulation package Mathematica, results in three sets of equations:

The first set is represented by

$$\begin{array}{@{}rcl@{}} M & =&0,\quad {\Lambda}\neq0,\quad ~~~~~a_{0}=-\frac{\Gamma}{2{\Lambda}},\quad a_{1}=\frac{i\sqrt{6}P\sqrt{\Omega}}{\sqrt{\Lambda}},\quad b_{1} =0,\\ {\Gamma} & \neq&0,\quad \vartheta=\frac{\Gamma a_{0}}{3},\quad P{\Omega} \neq0,\quad ~~~~~~k=\frac{2\vartheta-{\Gamma} a_{0}}{4P{\Omega}}, \end{array} $$
(58)

the second set is represented by

$$\begin{array}{@{}rcl@{}} a_{0} & =&\frac{\sqrt{\frac{3}{2}}M\sqrt{\Omega}}{\sqrt{\Lambda}},\quad M\neq0,\quad a_{1}=\frac{2Pa_{0}}{M},\\ b_{1} & =&0,\quad P{\Omega}\neq0,\quad k=\frac{\Omega M^{2}+2\vartheta} {4P{\Omega}}, \end{array} $$
(59)

and the third set is represented by

$$\begin{array}{@{}rcl@{}} M & =&2P,\quad a_{0}=\frac{\sqrt{6}P\sqrt{\Omega}}{\sqrt{\Lambda}},\quad k\neq0,\quad a_{1}=a_{0},\\ b_{1} & =&\frac{\sqrt{6}\sqrt{-{\Omega} k^{2}+2P{\Omega} k-P^{2}{\Omega}}} {\sqrt{\Lambda}}, \\ \vartheta & =&-2{\Omega} P^{2}+2k{\Omega} P+{\Lambda} a_{0}b_{1}. \end{array} $$
(60)

For the first set (58), when P=1 we get the solutions satisfying Case I. Therefore, for k>0 the solution of the EKdV eq. (35) will be

$$ u_{1}(x,t)=\frac{i\sqrt{\Omega}\sqrt{\frac{{\Gamma}^{2}}{\Omega{\Lambda}}} \tan\left(\frac{\zeta\sqrt{\frac{{\Gamma}^{2}}{\Omega{\Lambda}}}}{2\sqrt{6}} \right)} {2\sqrt{\Lambda}}-\frac{\Gamma}{2{\Lambda}} $$
(61)

and

$$ u_{2}(x,t)=\frac{i\sqrt{\Omega}\sqrt{\frac{{\Gamma}^{2}}{\Omega{\Lambda}}} \cot\left(\frac{\zeta\sqrt{\frac{{\Gamma}^{2}}{\Omega{\Lambda}}}}{2\sqrt{6}} \right)} {2\sqrt{\Lambda}}-\frac{\Gamma}{2{\Lambda}}, $$
(62)

while for k<0

$$ u_{3}(x,t)=-\frac{\Gamma}{2{\Lambda}}-\frac{i\sqrt{\Omega}\sqrt{-\frac {{\Gamma}^{2}}{\Omega{\Lambda}}}\tanh\!\left(\frac{\zeta\sqrt{-\frac{{\Gamma}^{2}} {\Omega{\Lambda}}}}{2\sqrt{6}}\right)} {2\sqrt{\Lambda}}, $$
(63)
$$ u_{4}(x,t)=-\frac{\Gamma}{2{\Lambda}}-\frac{i\sqrt{\Omega}\sqrt{\frac{{\Gamma}^{2}}{\Omega{\Lambda}}}\coth\left(\frac{\zeta\sqrt{-\frac{{\Gamma}^{2}} {\Omega{\Lambda}}}}{2\sqrt{6}}\right)} {2\sqrt{\Lambda}}, $$
(64)

and for k=0

$$ u_{5}(x,t)=\frac{\Gamma\zeta+2i\sqrt{6{\Omega}{\Lambda}}}{2\zeta{\Lambda}}. $$
(65)

For the second set (59), we apply the compatibility condition for the solutions satisfying Cases II, III, and IV as

$$ Pk=\frac{M^{2}-{p_{1}^{2}}}{4}. $$
(66)

Substituting P and k from (59), in eq. (66) and solving for p 1, we obtain

$$ p_{1}=\frac{i\sqrt{-\frac{{\Gamma}^{2}}{\Lambda}}}{\sqrt{3{\Omega}}}\quad \text{or}\quad p_{1}=\frac{-i\sqrt{-\frac{{\Gamma}^{2}}{\Lambda}}}{\sqrt{3{\Omega}}} . $$
(67)

Therefore, the solution of eq. (35) will be

$$ u_{6}(x,t)=-\frac{i\sqrt{6{\Omega}}p_{1}\tanh\!\left(\zeta p_{1}\right)} {\sqrt{\Lambda}} $$
(68)

and

$$ u_{7}(x,t)=-\frac{i\sqrt{6{\Omega}}p_{1}\coth\left(\zeta p_{1}\right)} {\sqrt{\Lambda}}. $$
(69)

In the same manner, Case III gives the solution

$$ u_{8}(x,t)=-\frac{i\sqrt{\frac{3}{2}{\Omega}}\left(\sinh(\zeta)+\sqrt{r^{2} -1}\right)} {\sqrt{\Lambda}(r+\cosh(\zeta))}, $$
(70)

with the condition p 1=1.

For Case IV, the solution form is

$$ u_{9}(x,t)=\frac{i\sqrt{\frac{3}{2}}\sqrt{\Omega}\text{cosech}\left(\frac{\zeta}{2}\right) \left(\cosh\left(\frac{\zeta}{2}\right) +2M\sinh\left(\frac{\zeta}{2}\right) \right)} {\sqrt{\Lambda}}, $$
(71)

with the same condition p 1=1, and

$$ u_{10}(x,t)=-\frac{i \sqrt{6} \sqrt{\Omega} \coth(\zeta)}{\sqrt{\Lambda}}, $$
(72)

with the condition p 1=2.

Hence, for the solutions satisfying Cases II–IV, we have the compatibility condition

$$Pk=\frac{M^{2}-{p_{1}^{2}}}{4}. $$

Therefore, substituting for P and k, from (60) and solving for p 1, it is found that

$$ p_{1}=\sqrt{2} \sqrt{\frac{2 P^{2} {\Omega}-2 k P {\Omega}}{\Omega}} \quad \text{or}\quad p_{1}= -\sqrt{2} \sqrt{\frac{2 P^{2} {\Omega}-2 k P {\Omega}} {\Omega}}. $$
(73)

The solution of eq. (55) will be

$$ u_{11}(x,t)=\frac{-\sqrt{6}\sqrt{-(k-P)^{2}{\Omega}}P^{2}-\sqrt{\Lambda} a_{0}\left(P-p_{1}\left(P+\tanh\!\left(\zeta p_{1}\right) \right) \right) {}^{2}}{P\sqrt{\Lambda}\left(p_{1}\left(P+\tanh\!\left(\zeta p_{1}\right) \right) -P\right)} $$
(74)

and

$$ u_{12}(x,t)=\frac{-\sqrt{6}\sqrt{-(k-P)^{2}{\Omega}}P^{2}-\sqrt{\Lambda} a_{0}\left(P-\left(P+\coth\left(\zeta p_{1}\right) \right) p_{1}\right) {}^{2}}{P\sqrt{\Lambda}\left(\left(P+\coth\left(\zeta p_{1}\right) \right) p_{1}-P\right)} , $$
(75)

where a 0 is given by eq. (60), with the relative conditions. Similarly, Case III results in the solution

$$\begin{array}{@{}rcl@{}} &&u_{13}(x,t)\\ &&\,=\,\!\frac{-8\sqrt{6}P^{2}\sqrt{\!-(k\,-\,P)^{2}{\Omega}}(r\,+\,\cosh(\zeta ))^{2}\!\,-\,\sqrt{\Lambda}\!\left(2r^{2}\,+\,\cosh(2\zeta)\!+4\sqrt{r^{2}\,-\,1}\sinh (\zeta)\,-\,3\!\right)\! a_{0}}{4P\sqrt{\Lambda}(r+\cosh(\zeta))\left(\sinh (\zeta)+\sqrt{r^{2}-1}\right)} ,\\ \end{array} $$
(76)

with the condition p 1=1.

For Case IV, the solution can be written in the form

$$ u_{14}(x,t)=\frac{4\sqrt{6}\sqrt{-(k-P)^{2}{\Omega}}P^{2}+a_{0}\sqrt{\Lambda} \left[ 4P+\coth\left(\frac{\zeta}{2}\right) \right]^{2}}{2P\sqrt {\Lambda}\left[ 4P+\coth(\zeta)+\text{cosech}(\zeta)\right]} , $$
(77)

with the same condition p 1=1, and

$$ u_{15}(x,t)=\frac{-\sqrt{6}\sqrt{-(k-P)^{2}{\Omega}}\tanh(\zeta)P^{2}-a_{0} \sqrt{\Lambda}\coth(\zeta)}{P\sqrt{\Lambda}}, $$
(78)

with the condition p 1=2.

4.1 Numerical analysis and discussion

We have considered a collisionless, unmagnetized plasma consisting of q-nonextensive electrons, positive ions, negative ions, as well as charged immobile dust grains. To investigate the nonlinear dynamics of the DIAWs, the reductive perturbation technique is employed to obtain an EKdV equation. The latter is solved using an extended homogeneous balance method. The extended homogeneous balance method gives different classes of solutions of the EKdV equation. These solutions include many types like rational, periodical, shock solutions, etc. For example, solution (65) represents the rational-type solutions, which may be helpful to explain the creation of very high energy in the plasma system. Because the rational solution is a discrete joint union of manifolds, particle systems describe the motion of a pole of the evolution equation. Solutions (61) and (62) are examples exhibiting the sinusoidal-type periodical solutions, which develop a singularity at a finite point, i.e., for any fixed t=t 0 there exists a value of ζ 0 at which these solutions blow up (see figure 1). Note that these excitations never reach zero, except in a very specific combination of parameter values. The prediction for a potential excitation blow-up indicates that an instability in the system may occur due to the effect of nonlinearity. In simple terms, the balance between dispersion and nonlinearity may be disturbed by variations of plasma quantities (e.g., temperature, pressure, density, etc.). This might locally destroy the localized excitation stability leading to an amplitude increase to very high values; as this represents an increase in the electric potential, it might lead to an acceleration of the moving particles. It is important to note that eq. (69) is a form of explosive /blow-up solutions as depicted in figure 2.

Figure 1
figure 1

Three-dimensional profile of the periodic solution (eq. (61)) for α=0.6, β=0.1, and q=0.7.

Full size image
Figure 2
figure 2

Three-dimensional profile of the explosive /blow-up pulse (eq. (69)) for the same parameters as in figure 1.

Full size image

Another different nonlinear wave that could be of interest is represented by solution (63), which represent the shock waves. Equation (63) can be written as

$$ u(\zeta)=\frac{1}{2}\phi_{m}\left[ 1-\tanh\!\left(\frac{2\zeta}{W}\right) \right] , $$
(79)

where ϕ m and W are the amplitude and width of the shocks, respectively, and are given by

$$ \phi_{m}=-\frac{B}{C}\quad \text{and} \quad W=2\frac {\sqrt{-12/C}}{\left\vert \phi_{m}\right\vert} . $$
(80)

It is clear from eq. (80) that to have shock waves, C should acquire negative values; i.e., C<0. The Earth’s ionosphere plasma (H +, H −) will be used as an example to numerically investigate the nonlinear coefficient C and negative dust grains are considered. The numerical analysis in figure 3 defines the possible regions of negative C that is represented by green zone, while for white zone, C is greater than zero. Hence, our numerical analysis of the shock wave profile is limited within the blue region.

Figure 3
figure 3

The contour plot of the coefficient C with α and β for negative dust particles, where q=0.6, σ +=σ −=0.5, and Q=0.03.

Full size image

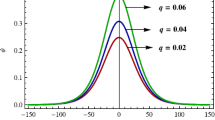
Now, we shall study the variation of the shock wave profile against q, σ 1,σ 2,α, and β as depicted in figures 4–6. Figure 4 shows that the increase of the nonextensive parameter q would lead to an enhancement in the shock amplitude. Actually, increasing the shock amplitude increases the potential difference and accelerates the particles to high velocity. However, for higher q values near to unity the system behaves like Maxwellian. Therefore, when the system nears either the Maxwellian state or the equilibrium state, the particles accelerates more.

Figure 4
figure 4

The shock wave profile for different values of q where q=0.6 (——), 0.8 (⋯⋅), 0.97 (- - - - -). Here, α=0.5, β=0.1, σ +=σ −=0.5, and Q=0.03.

Full size image

Figure 5 clearly shows that the increase in positive ion-to-electron temperature ratio would make the shock amplitude taller but the negative ion-to-electron temperature ratio makes the shock amplitude shorter. On the other hand, the ion temperature accelerates the particles due to the generation of high potential shock waves.

Figure 5
figure 5

The shock wave profile for different values of σ + and σ − where σ +=σ −=0.5 (—–), σ +=0.6, =0.5 (⋯⋅), σ +=0.5, =0.6 (- - - - -). Here, α=0.5, β=0.1, q=0.6, and Q=0.03.

Full size image

It is obvious from figure 6 that the excess of negative-to-positive ion density ratio and the negative dust-to-positive ion density ratio would lead to an increase in the shock amplitude, but the former is more effective than the latter. In other words, the increase of negative ions in the plasma system creates high potential difference due to their dynamics, while the negative stationary dust has less influence. Of course, the dynamics of the charged particles has a significant effect even if it has less mass than the stationary dust. The latter usually plays a role in neutralizing the background but does not play an effective role in wave dynamics.

Figure 6
figure 6

The shock wave profile for different values of α and β where α=0.5, β=0.1 (—–), α=0.6, β=0.1 (⋯⋅), α=0.5, β=0.2 (- - - - -). Here, σ +=σ −=0.5, q=0.6, and Q=0.03.

Full size image

5 Summary

In this paper, we have studied the nonlinear propagation of dust ion-acoustic waves in dusty plasmas, where a background of stationary dust was considered. We have derived the EKdV equation describing the system. Using homogeneous balance method we obtained a new class of solutions of the EKdV equation. These solutions include different rational solutions and shock wave solution. We have used the present model to investigate the behaviour of nonlinear structures in the Earth’s ionosphere plasma environment. Numerical analysis of the solutions revealed that the profile of the nonlinear pulses suffer amplitude and width modifications due to the enhancement of the dust particle density, negative ion density, and nonextensive electron parameter. Furthermore, the necessary condition for the propagation of shock waves is examined.