1 Introduction

The cross-axis flexural pivot is a compliant mechanism which allows the controlled relative rotation between two attached bodies. Figure 1 shows an example of the device in its basic and preferred embodiment. As a compliant mechanism, it gains mobility thanks to the deformation of its links and flexible components rather than through the use of specific kinematic pairs [1]. For this reason, the cross-axis flexural pivot does not have any degree of freedom in the strict sense, but however preserves the mobility thanks to the specific shape of its parts which produces controlled deformation of the entire structure. In particular, the relative movement of the two attached bulky parts is based on the presence of two flexible beams that deform and store energy during movement. This energy can be used for driving the relative motion back to the original undeformed configuration. Thanks to this characteristic, the cross-axis flexural pivot is used in automatic deployment system, controlled devices and similar applications, without necessarily having to insert specific components such as torsional springs [2, 3].

Fig. 1
figure 1

An example of cross-axis flexural pivot

Full size image

The cross-axis flexural pivots are easy to manufacture and easy to assemble. They can be produced by means of common moulding of plastic material or by cutting of metal sheets. Moreover, they allow high performances in terms of accuracy, reliability, low wear, low weight, low noise and low maintenance.

The main challenge in the design of compliant mechanisms and in particular in the design of flexural pivots concerns with the careful definition of morphological and structural properties of components in order to achieve the desired articulation and required functionality [4, 5]. The mobility of compliant mechanisms is allowed thanks to the deformations of its members which however must be limited by mechanical resistance considerations.

According to the scientific literature, the design methodologies of compliant mechanisms (analysis and synthesis) are often addressed using the pseudo-rigid-body approach [6–10]. Following this methodology, the compliant mechanism is associated to a system with all rigid bodies, kinematic pairs and concentrated elastic elements that reproduces the global behaviour of the device in an satisfactory manner. The pseudo-rigid-body model allows the application of the common design techniques for rigid-body mechanisms both for synthesis and analysis purposes.

The definition of a pseudo-rigid-body mechanism is a good compromise between simplicity in modelling and accuracy in the estimation of functional behaviour. The equivalent rigid body has to be implemented taking into account all the possible deformation modes.

In 2002, Jensen and Howell [11] approached the modelling of cross-axis flexural pivot. They proposed two methodologies for addressing the implementation of surrogate pseudo-rigid-body mechanism. The first one is based on the use of a single central pivot with a torsional spring and the second one is based on the implementation of a four-bar mechanism with four torsional springs.

For the specific application to the cross-axis flexural pivot, the pseudo-rigid-body approach has two main drawbacks. First of all, it is not suitable for very large deformation configurations (pseudo-hinges rotation of more than \(50^{\circ }\div 60^{\circ }\)), since the approximation using concentrated articulations leads to unacceptable errors due to linear stiffness approximations [1, 12]. Secondly, the approach is suitable for static and quasi-static assessment, but gives too inaccurate results in dynamic simulations because the inertia distribution of the moving parts is badly approximated as well [13].

Another possible approach in the design of this type of mechanisms makes use of finite element modelling [3, 14]. This methodology allows a precise and accurate description of the shape and the elastic behaviour of each link of the device but requires considerable computational resources. This limitation is mainly due to the need for complex formulations for taking into account the highly nonlinear effects of large displacements. Finite elements can be suitable for refinement analyses but are often too computational onerous for preliminary design and optimization and for interactive assessment and simulation.

The objective of the paper is to present an innovative methodology for approaching the design of compliant mechanism having a computational efficient formulation (faster than finite elements), but able to achieve more precise results with respect to the pseudo-rigid-body model in the whole range of displacement. The proposed methodology makes use of the dynamic splines that are suitable for the simulation of very flexible slander links.

Dynamic splines have been introduced in computer-aided design simulation by Quin and Terzopoulus [15], optimized by Theetten et al. [16] and specialized in multibody dynamics simulation by Valentini et al. [17]. They combine physics-based constraining equations with spline geometry representation. Their main advantage is that even a complex and large displacement of a beam-shaped element can be expressed in terms of a polynomial closed form expression using common spline description, deducing geometrically exact expressions of kinetic and elastic energies.

In comparison to classical finite element approaches, the dynamic splines allow the use of the same representation for drawing and simulating without requiring the meshing of flexible parts. Moreover, they allow accurate modelling requiring a reduced number of variables (degrees of freedom) [17, 18]. This characteristic is very suitable for implementing interactive design methodologies based on real-time or very fast simulations [19].

The paper is organized as follow. In a first part, the mathematical modelling of the cross-axis flexural pivot using dynamic splines is presented. In a second part, the results of simulations are presented together with a comparison using nonlinear finite element approach. In the last part, details of the integration of the proposed methodology into an interactive design environment based on augmented reality are discussed.

 

2 Modelling the cross-axis flexural pivot using dynamic splines

2.1 General equations of motion

The cross-axis flexural pivot is a mechanical system which can be modelled using two rigid bodies and two flexible splines (see Fig. 2). The rigid bodies represent the attachment parts and the splines represent the compliant beam-shaped elements which allow the articulation. Since the motion of the system is expected in a plane, a 2D simplification can be used.

Fig. 2
figure 2

Nomenclature of cross-axis flexural pivot model using dynamic splines

Full size image

Each beam can be described with a cubic Bézier spline using four control points and can be expressed in the polynomial parametric form as:

$$\begin{aligned} \text{ beam}\,\,1 \rightarrow \mathbf{C}_1 \left( u \right)&= \sum _{i=0}^3 {b_i \left( u \right)\mathbf{P}_i}\end{aligned}$$
(1)
$$\begin{aligned} \text{ beam}\,\,2 \rightarrow \mathbf{C}_2 \left( v \right)&= \sum _{i=0}^3 {b_i \left( v \right)\mathbf{Q}_i} \end{aligned}$$
(2)

where \(\mathbf{P}_i\) are the control points of the curve \(\mathbf{C}_1 \) that passes through the centre of each cross-section of beam 1; \(\mathbf{Q}_i\) are the control points of the curve \(\mathbf{C}_2 \) that passes through the centre of every cross-section of beam 2; \(b_i (x)\) are the blending functions that for a cubic 4-point B-spline can be assumed as:

$$\begin{aligned} \begin{array}{l} b_0 (x)=(1-x)^{3} \\ b_1 (x)=3\cdot x\cdot (1-x)^{2} \\ b_2 (x)=3\cdot x^{2}\cdot (1-x) \\ b_3 (x)=x^{3} \\ \end{array} \end{aligned}$$
(3)

Considering one of the rigid bodies as the ground, the entire system possesses 19 degrees of freedom (8 for the description of each spline and 3 for the description of the other rigid body).

The equations of motion of whole system can be written in terms of generalized coordinates and deduced using Lagrange equations:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{d}{dt}\frac{\partial T}{\partial \dot{q}_i}-\frac{\partial T}{\partial q_i}-\left[{\frac{\partial \varvec{\uppsi }}{\partial q_i}} \right]^{T}\cdot \varvec{\lambda }=Q_i\quad i=1\ldots 19 \\ {\varvec{\uppsi }=\mathbf{0}} \\ \end{array}\right. \end{aligned}$$
(4)

where \(q_i\) is the \(i\)-th generalized coordinate—for the spline they are the coordinates \(x\) and \(y\) of the control points; for the rigid body they are the kinematic descriptors (\(x\) and \(y\) coordinates of the centre of mass and the attitude angle \(\theta )\); \(\dot{q}_i =\frac{dq_i}{dt}\) is the time derivative of the \(i\)-th generalized coordinate; \(T\) is the kinetic energy of the whole system; \(\varvec{\uppsi }\) is the vector containing the constraint equations; \(\varvec{\lambda }\) is the vector of Lagrange multipliers associated to the constraint equations; \(F_i\) is the component of all generalized forces acting on the \(i\)-th coordinate \(q_i\).

2.2 Definition of constraints

The investigated system includes four constraints describing the connection between the beams and the two rigid bodies. All these connections can be modelled using 2 degrees of freedom constraints applied to both ends of the beams.

Four constraints (8 scalar equations) are needed to express the coincidence of the first and last control points of the splines to the corresponding points on the ground and the moving rigid body:

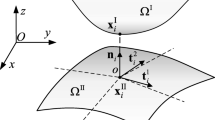
$$\begin{aligned} \begin{array}{l} \psi _{1,2} =\mathbf{C}_1 (0)-\mathbf{A1}=\mathbf{P}_0 -\mathbf{A1} \\ \psi _{3,4} =\mathbf{C}_1 (1)-\mathbf{B1}=\mathbf{P}_3 -\mathbf{B1} \\ \psi _{5,6} =\mathbf{C}_2 (0)-\mathbf{A2}=\mathbf{Q}_0 -\mathbf{A2} \\ \psi _{7,8} =\mathbf{C}_2 (1)-\mathbf{B2}=\mathbf{Q}_3 -\mathbf{B2} \\ \end{array} \end{aligned}$$
(5)

Four other constraints have to be introduced in order to ensure that the relative angles between the rigid body 1 and the first point of both beams and the rigid body 2 and the last control points are constant. Since the control points do not possess rotational degrees of freedom, these conditions have to be written using Frenet frame components [17]. For the particular case, with reference to Fig. 3, we have:

$$\begin{aligned} \begin{array}{l} \psi _9 =\left.{\frac{d\mathbf{C}_\mathbf{1}}{du}} \right|_{u=0} \times \mathbf{m}_{\mathbf{A1}} \\ \psi _{10} =\left.{\frac{d\mathbf{C}_\mathbf{1}}{du}} \right|_{u=1} \times \mathbf{m}_{\mathbf{B1}} \\ \psi _{11} =\left.{\frac{d\mathbf{C}_\mathbf{2}}{dv}} \right|_{v=0} \times \mathbf{m}_{\mathbf{A2}} \\ \psi _{12} =\left.{\frac{d\mathbf{C}_\mathbf{2}}{dv}} \right|_{v=1} \times \mathbf{m}_{\mathbf{B2}} \\ \end{array} \end{aligned}$$
(6)

where \(\times \) denotes the cross product, \(\mathbf{t}=\frac{d\mathbf{C}}{dx}\) is the generic tangent unit vector and the unit vectors \(\mathbf{m}\) are fixed to the corresponding rigid bodies.

In order to produce the initial deformation of the flexural pivot the rotational motion of the rigid body has to be prescribed using a driving constraint:

$$\begin{aligned} \psi _{13} =\vartheta _2 -\vartheta _2^0 \end{aligned}$$
(7)

For deployment simulation (i.e. free motion of the cross-axis flexural pivot), the constraint in Eq. (7) has to be removed.

Fig. 3
figure 3

Cross-axis flexural pivot articulation for a prescribed rotation of the upper rigid body

Full size image

 

2.3 Computation of forces

Each generalized force acting on the flexible beam have two contributions:

$$\begin{aligned} F_i =F_{i,elastic} +F_{i,external} \end{aligned}$$
(8)

The first one, \(F_{i,elastic}\), is due to the elastic forces generated by the deformation of the beams. It can be computed from the derivative of the overall elastic energy \(U_{elastic}\) with respect to the generalized coordinates as:

$$\begin{aligned} F_{i,elastic} =-\frac{\partial U_{elastic}}{\partial q_i} \end{aligned}$$
(9)

The second contribution to the generalized forces, \(F_{i,external}\), depends on the external forces and torques acting on the structure. In the simulated scenario this contribution has been neglected.

For the 2D (planar) case, the overall elastic energy \(U_{elastic}\), required to compute the elastic forces in Eq. (8) is composed of two terms. The first one is due to bending, the second one is due to stretching.

The bending elastic energy is proportional to the square of the variation of the bending strain:

$$\begin{aligned} U_{bending}&= \frac{1}{2}\int \limits _{spline} {EI\left( {\varepsilon _{b} -\varepsilon _{b}^{0}} \right)^{2}ds} \nonumber \\&= \frac{1}{2}\int \limits _{0}^{1} {EI\left( {\varepsilon _{b} -\varepsilon _{b}^{0}} \right)^{2} \left\Vert{\frac{dC}{dx}} \right\Vert{dx}} \end{aligned}$$
(10)

where \(\varepsilon _b^0 \) is the bending strain of the free form spline (undeformed condition); \(\varepsilon _b\) is the bending strain of the deformed spline; \(E\) is the Young modulus of the material of the beam; \(I\) is the moment of inertia of the cross section of the beam with respect to the bending axis (section is considered symmetrical and untwisted).

\(\left\Vert {\frac{d\mathbf{C}}{dx}} \right\Vert\) is the generic derivative of the two parametric expressions in Eqs. (1) and (2) with respect to the corresponding variable \(x\).

The bending strain can be expressed with the scalar Frenet curvature \(\kappa (x)\):

$$\begin{aligned} \varepsilon _b (x)=\kappa (x) \end{aligned}$$
(11)

The generalized elastic forces due to bending can be evaluated as:

$$\begin{aligned} Q_{i,bending}&= -\frac{\partial U_{bending}}{\partial q_{i}}\nonumber \\&= -\frac{1}{2}\int \limits _{spline} {EI\frac{\partial \left( {\varepsilon _{b} -\varepsilon _{b}^{0}} \right)^{2}}{\partial q_{i}}ds}\nonumber \\&= -\frac{1}{2}\int \limits _0^1 {EI\frac{\partial \left( {\kappa -\kappa _0} \right)^{2}}{\partial q_i}\left\Vert {\frac{d\mathbf{C}}{dx}} \right\Vert{dx}} \end{aligned}$$
(12)

It is important to underline that Eq. (12) takes into account the influence of the actual beam length in the computation of the bending strain. Since the evaluation of the integral in Eq. (12) has to be performed over the entire length of the spline (over \(ds)\), the effects of beam lengthening can be taken into account, obtaining accurate results for large displacement analysis [17].

The stretching elastic energy is proportional to the square of the variation of the stretching strain:

$$\begin{aligned} U_{stretching}&= \frac{1}{2}\int \limits _{spline} {EA\left( {\varepsilon _s -\varepsilon _s^0} \right)^{2}ds}\nonumber \\&= \frac{1}{2}\int \limits _0^1 {EA\left( {\varepsilon _s -\varepsilon _s^0} \right)^{2}\left\Vert {\frac{d\mathbf{C}}{dx}} \right\Vert} dx \end{aligned}$$
(13)

where \(A\) is the cross section area of the beam; \(\varepsilon _s^0 \) is the stretching strain of the free form spline (undeformed configuration); \(\varepsilon _s\) is the stretching strain of the deformed spline.

The stretching strain can be evaluated as:

$$\begin{aligned} \varepsilon _s -\varepsilon _s^0 =\frac{\left\Vert {\frac{d\mathbf{C}}{dx}} \right\Vert-\left\Vert {\frac{d\mathbf{C}_0}{dx}} \right\Vert}{\left\Vert {\frac{d\mathbf{C}_0}{dx}} \right\Vert} \end{aligned}$$
(14)

where \(\left\Vert {\frac{d\mathbf{C}_0}{dx}} \right\Vert\) is the derivative of the curve of the free form spline (undeformed configuration).

The generalized elastic forces due to stretching can be evaluated as:

$$\begin{aligned} Q_{i,stretching}&= -\frac{\partial U_{stretching}}{\partial q_i}\nonumber \\&= -\frac{1}{2}\int \limits _{spline} {EA\frac{\partial \left( {\varepsilon _s -\varepsilon _s^0} \right)^{2}}{\partial q_i}}ds\nonumber MYAMP]=&-\frac{1}{2}\int \limits _{0}^{1} {EA\frac{\partial \left( {\varepsilon _s -\varepsilon _s^0} \right)^{2}}{\partial q_i}\left\Vert {\frac{d\mathbf{C}}{dx}} \right\Vert} dx \end{aligned}$$
(15)

The kinetic energy \(T\) has three contributions:

$$\begin{aligned} T=T_{rigid\_body 1} +T_{rigid\_body 2} +T_{beam1} +T_{beam 2} \end{aligned}$$
(16)

where \(T_{rigid\_body1}\) and \(T_{rigid\_body2}\) are the kinetic energies of the two rigid bodies; \(T_{beam1}\) and \(T_{beam2}\) are the kinetic energies of the two flexible beams.

The kinetic energy of the \(i\)-th rigid bodies can be computed as:

$$\begin{aligned} T_{rigid\_body(i)} =\frac{1}{2}\text{ mass}_i \left\Vert {\mathbf{VG}_i} \right\Vert^{2}+\frac{1}{2}J_i \vartheta _i^2 \end{aligned}$$
(17)

where \(\text{ mass}_i\) is the mass of the \(i\)-th rigid body; \(\mathbf{VG}_i\) is the velocity vector of the centre of mass of the \(i\)-th rigid body; \(J_i\) is the moment of inertia of the \(i\)-th rigid body with respect to the centre of mass along a direction normal to the plane of movement; \(\vartheta _i\) is the angle describing the attitude of the the \(i\)-th rigid body.

For the two elastic beams we have:

$$\begin{aligned} T_{beam} =\frac{1}{2}\int \limits _{spline} {\left( {{\dot{\mathbf{C}}}^{T}\cdot \mathbf{M}\cdot {\dot{\mathbf{C}}}} \right)ds} \end{aligned}$$
(18)

where \({\dot{\mathbf{C}}}=\frac{d\mathbf{C}}{dt}\) is the time derivative of the spline parametric expression [Eqs. (1) and (2)]; \(\mathbf{M}=\left[ \begin{array}{llll} \mu&0&\ldots&0 \\ 0&\mu&\ldots&0 \\ \ldots&\ldots&\ldots&\ldots \\ 0&0&\ldots&\mu \\ \end{array} \right]_{8\times 8}\) is the inertia matrix and \(\mu \) is the linear density depending on the shape and the material of the beam.

3 Numerical simulations and validation

In order to validate the numerical model described in the previous section, two simulation scenarios have been implemented and solved. In general, all the simulations concerned with one of the rigid body kept fixed (as ground) and the beams and the other rigid body movable.

3.1 Static behaviour

The first simulation concerned with the verification of the static elastic behavior of the flexural hinge when one of the rigid bodies is rotated with respect to the other one. Inertia effects have been neglected. For this type of simulation, the equations to be solved are:

$$\begin{aligned} \left\{ \begin{array}{l} {\left[ {\frac{\partial \varvec{\uppsi }}{\partial q_i}} \right]^{T}\cdot \varvec{\lambda }+Q_i =0\,\,i=1\ldots 19} \\ {\varvec{\uppsi }=\mathbf{0}} \\ \end{array} \right. \end{aligned}$$
(19)

The prescribed rotation of the upper rigid body can be expressed by the specific constraint in Eq. (7) assuming \(\vartheta _{2}^{0} =90^{\circ }\) which is a very large rotation.

Table 1 includes other numerical input data used in the model definition.

Table 1 Parameters definition for the implemented cross-axis flexural pivot model
Full size table

Figure 3 shows a sequence of snapshots of the rotation increments during the simulation.

The same scenario has been implemented using finite elements, describing each flexible elements with 20 beam elements and performing a nonlinear static solution by 20 displacement increments.

The two models have been compared with respect to the position of the center of mass of the movable rigid body and the overall rotational stiffness.

The comparison between the trajectories of the upper body center of mass is depicted in Fig. 4.

Fig. 4
figure 4

Comparison between the trajectories of the rigid body centre of mass

Full size image

It can be observed that the two trajectories are very close. The maximum difference at the end of the movement is below 1 %.

The rotational stiffness \(K_\vartheta \) of the compliant mechanism can be computed from the reaction force \(\lambda _{13}\) of the driving constraint in Eq. (7) which represents the torque to be applied to the rigid body in order to produce the required rotation \(\vartheta _2^0\) as:

$$\begin{aligned} K_\vartheta \left( {\vartheta _2} \right)=-\frac{\partial \lambda _{13} \left( {\vartheta _2} \right)}{\partial \vartheta _2} \end{aligned}$$
(20)

The comparison between the global stiffness values from the two models is plotted in Fig. 5.

Fig. 5
figure 5

Comparison between the rotational stiffness values of the pivot

Full size image

Again, the differences of the results obtained from the two approaches are negligible. The dynamic spline model tends to overestimate the overall stiffness. This behavior is due to the limited number of the control points (four) chosen in the description of the deformed shape.

3.2 Dynamic behaviour

The second set of simulations concerned with the verification of the dynamic behavior of the flexural hinge when one of the rigid bodies (the upper one) is free to move after the hinge has been displaced.

In this case, the equations to be solved are included in the whole system of Eq. (4) and the driving constraint in Eq. (7) has to be disabled. The initial conditions about the positions of each part are taken from the end of the static simulation.

The same scenario has been implemented using finite elements, describing each flexible elements using 20 beam elements and performing a nonlinear dynamic solution by means of an explicit solver.

The two models have been compared with respect to the time history of the position of the centre of mass of the movable rigid body.

The comparison between the two models is presented in Fig. 6.

Fig. 6
figure 6

Comparison between upper body’s centre of mass trajectories during the dynamic simulation

Full size image

It can be observed that the two time histories are slightly different and this behavior can be explained considering the differences of the computed stiffness (see Fig. 5) which slightly alter the modal behavior of the system. In particular, the dynamic spline model presents an higher free vibration frequency (due to the higher global stiffness) due to the limited number of control points used in the description of its deformation.

4 Implementation into an interactive environment

In order to verify the suitability of the proposed modelling approach for an implementation into an interactive scenario, the discussed model has been integrated into an marker-based augmented reality environment. In the proposed scenario, the two rigid bodies are attached to two patterned markers (see Fig. 7) which can be moved on a plane by the user. By this way, the user can interactively change the relative position between them and the spline flexes accordingly.

Fig. 7
figure 7

Snapshots of the cross-axis flexural pivot interactive simulation in augmented reality

Full size image

The relative rotation between the two markers is used to update the constraint equations by changing the parameter \(\vartheta _2^0\) in Eq. (7). A possible translational displacement between the two bodies has been also taken into account including two other driving constraints on the moving body.

During the simulation, the user can decide to release the connection between the second marker and the corresponding rigid body, performing a subsequent dynamic simulation.

For the static simulation the equations to be solved are those in Eq. (19). Their real-time solution is possible since the updating of the relative position is performed synchronously with respect to the acquisition frame rate (25 Hz). It means that the value of the driving constraints changes very slowly each solution step and the equations are solved starting from an initial point which is very close to the correct one.

The dynamic equations are implemented and solved using the sequential impulse solver strategy which is very suitable for accurate and real-time simulations [20–22].

4.1 Sequential impulse solver

The sequential impulse formulation can be split into two main steps. The first one is about the solution of the equations of motion in (4) neglecting the constraint equations:

$$\begin{aligned} \mathbf{M}\ddot{\mathbf{q}}_{\mathbf{approx}} =\mathbf{F}_\mathbf{e} \end{aligned}$$
(21)

By this way, Eq. (21) can be solved for \({\ddot{\mathbf{q}}}_{\mathbf{approx}}\) that represent the vector of approximated generalized coordinates.

The values of the corresponding approximated generalized velocities and positions can be computed by linear approximation:

$$\begin{aligned} {\dot{\mathbf{q}}}_{\mathbf{approx}} =h{\ddot{\mathbf{q}}}_{\mathbf{approx}}\end{aligned}$$
(22)
$$\begin{aligned} \mathbf{q}_{\mathbf{approx}} =h{\dot{\mathbf{q}}}_{\mathbf{approx}} \end{aligned}$$
(23)

where \(h\) is the fixed integration time step which is set 1/4 of the video stream acquisition frame rate (1/100 s).

In order to correct the \({\dot{\mathbf{q}}}_{\mathbf{approx}}\) and fulfill the constraint equations, a series of impulses \(\mathbf{P}_{\mathbf{constraint}}\) has to be applied to the bodies. Each impulse is computed imposing the fulfillment of the constraint equations written in terms of generalized coordinates. The application of these impulses causes a variation of momentum:

$$\begin{aligned} \mathbf{M}\left({{\dot{\mathbf{q}}}_{\mathbf{corrected}} -{\dot{\mathbf{q}}}_{\mathbf{approx}}}\right)=\mathbf{P}_{\mathbf{constraint}} \end{aligned}$$
(24)

where \({\dot{\mathbf{q}}}_{\mathbf{corrected}}\)is the vector of generalized velocities after the application of impulses \(\mathbf{P}_{\mathbf{constraint}}\).

The corrected velocities can be computed from Eq. (24) as:

$$\begin{aligned} {\dot{\mathbf{q}}}_{\mathbf{corrected}} ={\dot{\mathbf{q}}}_{\mathbf{approx}} +\mathbf{M}^{-1}\mathbf{P}_{\mathbf{constraint}} \end{aligned}$$
(25)

Considering that the impulses are related to the constraint equations, they can be computed as

$$\begin{aligned} \mathbf{P}_{\mathbf{constraint}} =\varvec{\uppsi }_\mathbf{q} \varvec{\lambda } \end{aligned}$$
(26)

where \(\varvec{\lambda }\) is the vector of Lagrange multipliers associated to the impulses.

Since the effect of the impulses is to correct the generalized velocities and fulfill the kinematic constraints, the \({\dot{\mathbf{q}}}_{\mathbf{corrected}}\) has to satisfy the constraint equations written in terms of velocities (according to the index 2 DAE system):

$$\begin{aligned}&\varvec{\uppsi }=\mathbf{0}\Rightarrow \frac{\partial \varvec{\uppsi }}{\partial t}=\varvec{\uppsi }_\mathbf{q} {\dot{\mathbf{q}}}+\varvec{\uppsi }_\mathbf{t} =\mathbf{0}\end{aligned}$$
(27)
$$\begin{aligned}&\varvec{\uppsi }_\mathbf{q} {\dot{\mathbf{q}}}_{\mathbf{corrected}} +\varvec{\uppsi }_\mathbf{t} =\mathbf{0} \end{aligned}$$
(28)

Inserting Eq. (26) into Eq. (25) and substituting \({\dot{\mathbf{q}}}_{\mathbf{corrected}}\) into Eq. (8) we can obtain:

$$\begin{aligned} \varvec{\uppsi }_\mathbf{q} \left( {{\dot{\mathbf{q}}}_{\mathbf{approx}} +\mathbf{M}^{-1}\varvec{\uppsi }_\mathbf{q} ^{T}\varvec{\lambda }} \right)+\varvec{\uppsi }_\mathbf{t} =\mathbf{0} \end{aligned}$$
(29)

Equation (9) can be solved for \(\varvec{\lambda }\) obtaining:

$$\begin{aligned} \varvec{\lambda }=\left( {\varvec{\uppsi }_\mathbf{q} \mathbf{M}^{-1}\varvec{\uppsi }_\mathbf{q} ^{T}} \right)^{-1}\left( {\varvec{\uppsi }_\mathbf{q} {\dot{\mathbf{q}}}_{\mathbf{approx}} +\varvec{\uppsi }_\mathbf{t}} \right) \end{aligned}$$
(30)

Then, the impulses can be computed using Eq. (6) and the corrected values of generalized velocities using Eq. (25).

Since the impulses are computed sequentially, the global fulfillment of the constraint equations cannot be directly achieved. Some iterations are required.

A thorough description about the sequential impulse solver strategy goes beyond the scope of the paper and the interesting reader can find other implementation details in [23].

4.2 Augmented reality implementation

The tracking and recognition of markers have been implemented using ARToolkit libraries (freely downloadable at the internet site http://sourceforge.net/project/showfiles.php?group_id=116280). Graphical interfaces has been implemented using standard OpenGL libraries.

The computational strategy has been implemented as follows:

  • Equations of motion are solved using a fixed time step (1/100 s) with the sequential impulse solver;

  • Each image frame acquisition, four integration steps are performed in order to improve the stability of the solution;

  • During the simulation, the user can interactively switch from an elasto-kinematic simulation (enforcing constraints) to a fully dynamic simulation;

  • The intent of the user is recorded using two patterned markers;

  • Each frame, after the computation of the simulation steps, output results are retrieved and augmented scene is rendered and projected back to the user.

Figure 7 shows three snapshots taken during the interactive simulation.

5 Conclusion

An innovative method for addressing the simulation of cross-axis flexural pivot has been presented. The method is based on the use of the dynamic spline formulation.

The methodology allows a more detailed description of both elastic and inertia contributions of the flexible parts with respect to the commonly used pseudo-rigid body approach. On the other side, modelling beams using dynamic spline allows a computationally more efficient and compact formulation with respect to finite elements. The methodology is able to simulate the high geometrical non-linearity of the model and to reproduce in an accurate way both static and dynamic behaviour.

Actually, the spline description using only four control points each flexible beam leads to negligible approximations in comparison to finite element model. This simplification seems to be an adequate compromise for having a reduced computational complexity and accurate results.

The formulation has been successfully integrated into an high interactive design environment based on the use of marker-based augmented reality and demonstrated to be suitable for real-time processing and event-based simulation.

The efficient formulation and the ability to be integrated into an interactive environment make the proposed methodology very suitable for conceptual design, preliminary reviews and simulation of deployment systems or similar devices based on the use of compliant assemblies.

Concerning with the qualification of the proposed model, according to [24] the proposed approach has strong levels of parsimony, exactness, precision and a medium level of specialization. For all these reasons, the methodology can be extended to other compliant structures, based on beam schemes.