1 Introduction

In the last several decades, the tools for computer aided engineering (CAE) have offered invaluable assistance to engineers. Their continuous development aims at providing the maximum in terms of performance and reliability in a variety of engineering tasks. An important ingredient of those tools is the simulation of physical processes and phenomena. The conventional approach implies off-line simulations followed by the assessment and analysis of the obtained results in postprocessors in order to gain an insight into the physical quantities of interest that characterize the processes. However, the strong development of advanced visualization systems, followed by further development of already existing software components and necessary hardware, have enabled the integration of a novel concept into many areas of engineering and other fields of application. The concept is based on the Virtual Reality (VR) or Augmented Reality (AR) technology and real-time simulations, thus offering the possibility of manipulating and analyzing a 3D virtual world.

The finite element method (FEM), as an established numerical method in the field of structural analysis, is typically addressed to compute the behavior of deformable structures. Although numerically demanding, with the increasing computational power of modern hardware it is also the method of choice for interactive and real-time simulations, either used directly for the computation or as a part of particularly developed techniques. The possibility of FEM-based real-time simulations has been a subject of interest in a number of fields.

With the purpose of enhancing structural analysis with AR technologies, Huang et al. [17] proposed a system that integrates sensor measurement and real-time FEA simulation into an AR-based environment and superimposes the FEA results directly onto real-world objects. In order to speed up the computation, the authors introduce the assumption of linear and quasi-static behavior, while the real-time solver is based on the concept of pre-computing the inverse of the stiffness matrix. Similarly, Fiorentino et al. [15] presented an AR-based application that visualizes the linear FEM results overlaid over the real model for interactive teaching of dynamic stress/strain distribution in engineering education. Cerracchio et al. [6] implemented the linear inverse FEM for real-time reconstruction of the deformed structural shape using in situ strain measuremenets. Adopting linear behavior in the aforementioned applications allowed significant numerical savings and therewith acceleration of computational processes. If, however, the consideration of nonlinear behavior is a necessity for reasonable simulation accuracy, the numerical effort and the complexity of simulation increase notably.

A number of authors have addressed the difficulty of performing real-time FEM computations of nonlinear structural deformations by suggesting approaches based on neural-networks to obtain highly efficient, real-time solutions. Such approach consists in using the nonlinear FEM computations to provide a set of results for the training phase and can thus be classified as model reduction technique. It was applied to a number of problems such as real-time simulation of impact [16], geometrically nonlinear deformation of a cantilever beam [38] and a shell structure [8], etc. Dulong et al. [12] proposed a similar approach for real-time interaction between a designer and a virtual prototype as a support to design optimization. They also used a set of nonlinear FEM computations in what they refer to as training phase, while the actual deformation for a specific load case is determined by an interpolation method proposed by the authors. Furthermore, a real-time control system can also benefit from reduced but sufficiently accurate models of the system being controlled to improve the predictor part of the controller. Kalkkuhl et al. [20] applied the nonlinear FEM-based neural-network approach to a longitudinal vehicle dynamics control. Generally speaking, the approach based on a pre-computed set of deformed configurations is promising but the validity of the resulting model is strongly dependent on the deformation set density and range of deformation covered in the training phase.

In the field of multi-body system (MBS) dynamics with flexible bodies, real-time simulation is not a strict requirement, but high simulation efficiency belongs to the priorities. Though apparent savings are made by considering parts mainly as rigid-bodies, accounting for deformational behavior of some parts becomes crucial in certain simulations. In such a case, model reduction is one of the basic ideas on how to cope with the computational burden. On the contrary to the above mentioned technique of model reduction (training of neural-networks), a kind of direct FE-model reduction is introduced here based on modal coordinates. It implies that orthogonal mode shapes, calculated in a step prior to simulation, represent the degrees of freedom, in terms of which the elastic behavior of the body is described. The solution used by commercial MBS software packages is the Component Mode Synthesis (CMS) technique, particularly the Craig–Bampton method [9]. The flexible behavior remains linear with respect to the floating reference frame attached to the body. Some modal-based solutions are proposed to account for moderate geometric nonlinearities by means of the geometric stiffness matrix [41, 26, 27] or modal warping [27, 7, 29]. It is also possible to divide a model into a linear part that is further reduced and a part that considers the geometrically nonlinear effects in order to efficiently account for local nonlinearities [29]. The success of these solutions is strongly dependant on the character and range of deformation and modes provided, so they need to be used with special care.

Many solutions for interactive VR-simulations have been developed and most advances have been motivated by the demand for providing real-time deformation of human tissue in surgical simulations. Pioneer works in the 90s were based on linear FE models. Bro-Nielsen and Cotin [4] used simple tetrahedral elements in the framework of linear elasticity. In order to further reduce the numerical effort during simulation, the stiffness matrix was condensed so that only the surface nodes were involved and the so-obtained stiffness matrix was additionally inverted prior to simulation. All these steps done to produce high numerical efficiency reflect the limitations of available hardware at that time. Model reduction techniques were also exploited in this field, combined with nonlinear visco-elastic material models [11, 35] or with the extended finite element method (XFEM) [36]. Certain developments rely on use of modern hardware tools to provide the necessary computational power for the demanding real-time simulations [18]. Cueto and Chinesta [10] gave a survey of developed solutions for real-time simulation in surgery including techniques that involve supercomputing facilities, parallel implementations on GPUs (graphics processor units), model order reduction, etc.

2 Setting objectives and the choice of method

Strictly speaking, real-time simulation could be understood as a simulation, in which the computer model runs at the same rate, or even faster, than the actual physical system. The standard DIN ISO/IEC 2382 [40] defines real-time simulation in a somewhat looser manner, by essentially stating that it refers to the operation of a computing system, whereby the programs process data in such a manner that the processing results are available within a predetermined period of time. According to the standard, the processing time is not necessarily the same or faster than the real-time. Indeed, in certain fields of application, a simulation would still do what it is meant for, even if it performed somewhat slower than the real time, but the resulting simulation could be played at an interactive frame rates.

One can easily identify the means that can be addressed to achieve the objective of real time simulation:

  • Powerful hardware components,

  • Optimization and parallelization of computer programs,

  • Appropriate formalisms and algorithms for the computation of physical processes.

In the recent years, hardware components have seen a rapid pace of development offering ever increasing computational power. This refers to both the central processing units (CPU) and graphics processing units (GPU). Particularly modern GPUs can be used as a modified form of stream processors providing a massive computational power [18, 37].

Program optimization with respect to the requirements of real time simulation implies modifications in the program so that it executes more rapidly. Modern compilers offer significant assistance in this aspect. As modern processors contain multiple cores, the possibility of parallelization is another important aspect. This may also affect the choices made in the third group, because different solver types possess different parallelization potential. By the choice of adapted formalisms to describe and compute deformational behavior of structures, one can significantly affect the numerical efficiency and possibly make a trade-off between the efficiency and accuracy. Certain solutions even allow to perform this trade-off dynamically, i.e. during the simulation, based on immediate requirements.

This paper is focused on the third aspect. It aims at a FEM-based solution that keeps full fidelity FE models (no model reduction is performed), covers geometric nonlinearities to a large extent, performs fast even on conventional hardware tools and offers acceptable accuracy, the definition of which depends on specific application. Keeping the focus on developments with similar objectives, available literature offers several approaches. The simplest one would be a model based on mass-spring system, which substitutes a continuum with a collection of point masses connected by a network of massless springs, which are reminiscent of early days of discretization methods. The main advantages are the simplicity and ability to cope with geometric nonlinearities with a relatively small numerical effort and hence the interest in the approach for the purpose of real-time simulation in various simulators [30, 22]. But it also brings serious drawbacks related to achievable accuracy and ambiguity of model building [32]. Due to rapid hardware development the attention was turned to more demanding FE models. The rigorous geometrically nonlinear FEM is computationally very demanding and, hence, carefully chosen simplifications of the rigorous geometrically nonlinear FEM are required in order to meet the aforementioned objectives. The potential of the co-rotational approach was recognized in a number of works, particularly in the field of computer graphics. Capell et al. [5] proposed division of objects into sub-domains, while their local rigid-body rotations were considered by means of local coordinate frames. A similar but extended idea was proposed by Müller et al. [31] who implemented local coordinate frames at nodes. The idea was modified by Etzmuß et al. [13] by using local coordinate frames attached to triangular elements in order to model cloth behavior. The authors of the present work consider the possibility of using a simplified co-rotational FEM formulation with element-based rotation in combination with shell and solid elements to meet the above set objectives.

3 A simplified co-rotational FEM formulation

The total and updated Lagrangian formulations [2] are known as classical FE formulations for geometrically nonlinear analysis used in most commercially available FE software packages. The only difference between the two formulations lies in the choice of different reference configurations and, provided the appropriate constitutive tensors are employed, they yield identical results [2]. They provide the accuracy necessary for engineering tasks, but are also numerically quite demanding and may also exhibit convergence issues.

A high-quality overview of different co-rotational formulations including a detailed analysis of their properties is given by Felippa and Haugen [14]. Having in mind the set objectives, the authors of the present work propose a rather simplified co-rotational FE formulation that combines the advantages of the linear and geometrically nonlinear FE analysis. The idea of the approach is to cover geometric nonlinearities to a significant extent through the consideration of the element-based rigid-body rotation and to neglect further effects such as the geometric stiffness and the dependence of the element stiffness matrix on the deformational displacements. These simplifications mean that the formulation is not suitable for certain types of analyses, such as buckling analysis, which is primarily due to the lack of the geometric stiffness matrix. The idea can be seen as a refinement of the approach used in MBS programs. Within MBS the overall flexible body motion is decomposed into a rigid-body motion and (typically small, linear) deformable motion. The same idea is used in this work, but it is applied on the element level. Hence, in the present approach the elastic behavior of each element is considered to be linear with respect to the local element frame that is attached to the element and follows its rigid-body motion. In what follows, the computation of internal forces and tangential stiffness matrix together with some details of handling translational and rotational degrees of freedom within the framework of the applied co-rotational formulation will be addressed. Given the rotation matrix at time t, \(^t{{\mathbf {R_e}}}\), which describes the rigid-body rotation of an element between its initial configuration, \(^0{{\mathbf {x_e}}}\), and its current configuration, \(^t{{\mathbf {x_e}}}\), the rotation-free translations between the two configurations, read (see Fig. 1):

$$\begin{aligned} _0^t{\mathbf {u_R}}={^t{{\mathbf {R_e}}}^T}{^t{{\mathbf {x_e}}}}-{^0{{\mathbf {x_e}}}} \end{aligned}$$
(1)

where the left superscript denotes the time at which the quantity of interest is given, while the left subscript (where applicable) refers to the element orientation with respect to which the quantity is given. The left subscript is omitted with the rotation matrix as it is always given with respect to the initial element configuration (at time \(t=0\)).

Fig. 1
figure 1

Co-rotational concept rotation-free translations in the original element orientation

Full size image

As already mentioned, the element behavior is considered to be linear with respect to the local reference frame and, hence, the element internal forces with respect to the initial configuration can be simply computed by means of a pre-computed element stiffness matrix, \({^0{{\mathbf {K_e}}}}\):

$$\begin{aligned} {_0^t{\mathbf {F_e}}}={^0{{\mathbf {K_e}}}}\left( {^t{{\mathbf {R_e}}}^T} \; {^t{{\mathbf {x_e}}}}-{^0{{\mathbf {x_e}}}}\right) \end{aligned}$$
(2)

To proceed with the solution, the internal forces are rotated by means of \(^t{{\mathbf {R_e}}}\) to the current element orientation:

$$\begin{aligned} {_t^t{\mathbf {F_e}}}={^t{{\mathbf {R_e}}}} \; {_0^t{\mathbf {F_e}}}={^t{{\mathbf {R_e}}}}{^0{{\mathbf {K_e}}}}{^t{{\mathbf {R_e}}}^T}\;{^t{{\mathbf {x_e}}}}-{^t{{\mathbf {R_e}}}}{^0{{\mathbf {K_e}}}{^0{{\mathbf {x_e}}}}} \end{aligned}$$
(3)

It should be noticed that the term \({^0{\mathbf {K_e}}{^0{\mathbf {x_e}}}}\) can be computed in a pre-step, i.e. prior to simulation and further used during the simulation. Also, Eq. (3) reveals the updated element stiffness matrix, which is simply given by rotating the initial, linear element stiffness matrix, \({^0{\mathbf {K_e}}}\), through \({^t{\mathbf {R_e}}}\):

$$\begin{aligned} {^t{\mathbf {K_e}}}={^t{\mathbf {R_e}}}{^0{\mathbf {K_e}}}{^t{\mathbf {R_e}}^T} \end{aligned}$$
(4)

As solids have only translational degrees of freedom and nodal forces as loads, Eqs. (1–4) give the essence of the co-rotational FEM formulation for this type of finite elements. Typically, shell elements also employ rotations as degrees of freedom and the procedure needs to be adequately extended. The rotations and translations do not share the same properties and the update of rotational degrees of freedom is more demanding. The incremental nodal rotations computed in each time-step are used to update the shell normals at each node starting from normals in the previously determined configuration. This is done by computing the incremental rotation matrix of a shell normal as [1]:

$$\begin{aligned}&{^{t-\varDelta {t}}{\mathbf {Q_i}}}\nonumber \\&={\mathbf {I}}+\frac{\sin {^{t-\varDelta {t}}}\gamma _i}{^{t-\varDelta {t}}\gamma _i}{^{t-\varDelta {t}}{{\mathbf {S_i}}}}+\frac{1}{2}\left( \frac{\sin \left( {^{t-\varDelta {t}}}\gamma _i/2\right) }{\left( ^{t-\varDelta {t}}\gamma _i/2\right) }\right) ^2{^{t-\varDelta {t}}{{\mathbf {S_i}}}}^2 \end{aligned}$$
(5)

where

$$\begin{aligned} {^{t-\varDelta {t}}\gamma _i}=\sqrt{{^{t-\varDelta {t}}\varDelta {}\theta ^2_{i1}}+{^{t-\varDelta {t}}\varDelta {}\theta ^2_{i2}}+{^{t-\varDelta {t}}\varDelta {}\theta ^2_{i3}}} \end{aligned}$$
(6)

and

$$\begin{aligned} {^{t-\varDelta {t}}{\mathbf {S_i}}}= \begin{bmatrix} 0&-{^{t-\varDelta {t}}\varDelta \theta _{i3}}&{^{t-\varDelta {t}}\varDelta \theta _{i2}}\\ {^{t-\varDelta {t}}\varDelta \theta _{i3}}&0&-{^{t-\varDelta {t}}\varDelta \theta _{i1}}\\ -{^{t-\varDelta {t}}\varDelta \theta ^2_{i2}}&{^{t-\varDelta {t}}\varDelta \theta _{i1}}&0 \end{bmatrix} \end{aligned}$$
(7)

with \({^{t-\varDelta {t}}\varDelta \theta _{i1}},{^{t-\varDelta {t}}\varDelta \theta _{i2}}\) and \({^{t-\varDelta {t}}\varDelta \theta _{i1}}\) denoting the 3 incremental global nodal rotations between the configurations at times \(t-\varDelta {t}\) and t, while the index i refers to node i. The rotation matrix \({^{t-\varDelta {t}}{\mathbf {Q_i}}}\) is further used to update the orientation of the shell normal at node i, \({\mathbf {n}}_i\):

$$\begin{aligned} {^t{\mathbf {n}}_{i}}={^{t-\varDelta {t}}}{\mathbf {Q}} \; {^{t-\varDelta {t}}{\mathbf {n}}_{i}} \end{aligned}$$
(8)

Rotations are further handled in a similar manner as translational degrees of freedom. The updated node normal is rotated backwards to the initial element configuration by means of \({^t{\mathbf {R_e}}^T}\):

$$\begin{aligned} {^t{\mathbf {n}}_{Ri}}={^t{\mathbf {R_e}}^T}\;{^t{\mathbf {n}}_{i}} \end{aligned}$$
(9)

and further compared to the original node normal in order to determine the deformational nodal rotations, free of rigid-body rotation, and with respect to the initial configuration, Fig. 2. Now, the same approach already elaborated in Eqs. (2) and (3) is applied. The deformational translations and rotations are used with the linear stiffness matrix to obtain the internal forces and moments with respect to the initial configuration, which are finally rotated to the current element configuration.

Fig. 2
figure 2

Co-rotational concept handling of shell normals

Full size image

Obviously, extraction of the element rotation matrix from the overall motion is an important aspect in the co-rotational formulation. Generally speaking, each incremental volume of the structure may exhibit different rigid-body rotation. But in the framework of the present co-rotational FEM, a single rotation matrix is used per element which implies averaging of the rigid-body rotation over the element domain. The rotation matrix at a material point can generally be obtained by polar decomposition of the deformation gradient matrix at that point. For relatively simple elements, such as the linear tetrahedron or linear triangular element, the deformation gradient matrix is constant over the whole element domain which fits nicely into the formulation. With more complex elements (e.g. quadratic elements), the polar decomposition of the deformation gradient matrix at the element centroid is used here.

Hence, the formulation uses the element linear stiffness matrix, which is computed only once, in a pre-step. In further computation, the element rotation matrix between the initial and current configurations is determined in order to update the element stiffness matrix and compute the internal forces and moments (where applicable). The global stiffness matrix is re-assembled using the rotated element stiffness matrices and the vector of internal forces is updated, so that either static or dynamic nonlinear analysis may proceed. It should be noticed that the formulation neglects the influence of the change in the element shape and initial stress state onto the element stiffness matrix.

4 Aspect of accuracy—static shell examples

As emphasized above, the presented formulation implements certain simplifications, i.e. neglects certain geometrically nonlinear effects. An important question rises: how is the accuracy of obtained results affected by those simplifications?

The achievable accuracy in terms of numbers by means of the presented co-rotational FEM in combination with the linear tetrahedral element has been considered by Marinkovic et al. [28]. Additionally, in the same reference, a technique was proposed to improve the accuracy in cases involving moderate strains, but it implies a larger numerical effort because the co-rotational formulation is extended by a secant approach with an update of the element stiffness matrix. Another approach to improve the accuracy with some additional numerical effort is based on the so-called projector matrix [14, 34].

Thin-walled structures are known for their susceptibility to large rotations, whereby the strains remain small. This is why they represent a good candidate to consider this aspect. A couple of illustrative examples are chosen for this consideration. Those examples have also been a subject of interest of other authors (e.g. [23, 21, 19]). It is not intended here to study this aspect exhaustively but rather to get a general impression on what can be expected. In typical applications involving interactive simulations, displacements are the result of primary interest.

Two shell elements were implemented with the presented co-rotational formulation. The full biquadratic nine-node shell element, denoted here by S9 (Fig. 3, left), belongs to the family of degenerated shell elements. It was originally developed as a piezoelectric shell element by Marinković et al. [24] and tested in the commercially available FEM software package ABAQUS [33]. The linear triangular shell element, denoted by S3 (Fig. 3, right), is the mechanical part of the electro-mechanical shell element presented and tested by Marinković and Rama [25] and Rama [39]. A few remarks on the shell elements would be worthwhile at this point. Both elements implement the Mindlin–Reissner kinematics and, hence, include transverse shear. Due to the flat shape of the S3 element, a FE discretization of a curved geometry is represented as a set of facets thus demanding a finer mesh. However, the element itself is computationally very efficient and, additionally, the finer discretization also talks in favor of the applied co-rotational formulation (rigid-body rotation accounted for element-wise). The full biquadratic shape functions of the S9 element facilitate covering of a relatively large range of curvatures. Although this implies that reasonably rough meshes can be used to discretize a complex geometry with the S9 element (compared to linear elements), this advantage may easily be lost with substantial geometrically nonlinear deformations. The results obtained with the implemented shell elements are compared with those obtained using ABAQUS 3-node linear shell element (A-S3) and ABAQUS 8-node biquadratic shell element (A-S8R) and the rigorous geometrically nonlinear (updated Lagrangian) FEM formulation.

Fig. 3
figure 3

Full biquadratic quadrilateral and linear triangular shell elements

Full size image

4.1 Curled cantilever beam

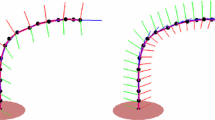
A clamped beam exposed to a bending moment at the free tip is considered in the first example. If the bending moment is slowly increased, the beam will bend until it gets curled into a complete circle. The required overall bending moment for this deformation is analytically determined as \(M = \pi Ebh^3/6l\) [3], where a denotes the length, b the width, h the thickness, and E is the Youngs modulus.

The geometry is chosen here so that \(l=10 \,\hbox {m}\) , \(b=0.5 \,\hbox {m}\) and \(h=0.01 \,\hbox {m}\), see Fig. 4. As for material properties, the Youngs modulus is taken to be \(E=2 \times 10^{11} \, \hbox {N/m}^{2}\) and in order to use the analytical solution for the beam, the Poissons coefficient is taken as equal to 0. Hence, in this specific case the edge distributed bending moment is obtained as \(M_l = (\pi /3)10^4 \,\hbox {N}\). The mesh of \(10 \times 1\) elements was used with the quadratic quadrilaterals, while the discretization with the linear triangular elements was finer in order to capture the bending adequately, so that 20 element-stripes were used along the length with each’ stripe containing 4 elements across the width, hence 80 elements altogether. These meshes give converged results with the implemented S9 and S3 element. Figure 5 shows the initial and deformed geometries computed with the S9 element and co-rotational formulation, with the intermediate configurations depicted upon each 20. The computations with the S9 and S3 elements were performed using increments of 10%. The analysis in ABAQUS was done using the same meshes (for respective elements) and it was set to use an automatic increment size with the initial increment size of 10%. With the A-S8R element ABAQUS performed 252 increments, but aborted the analysis at the load level of 87.28% due to convergence issues. The computation with A-S3 element was completed (100% of the load) and was done in 314 increments. As representative results, the displacements of the beam tip in the x- and y-directions are chosen and can be seen in Figs. 6 and 7, respectively. All the results are in very good agreement, with the given remark that A-S8R element failed to complete the analysis with the used mesh.

Fig. 4
figure 4

Geometry of the cantilever beam and loading

Full size image
Fig. 5
figure 5

Intermediate configurations at constant load increments of 20%

Full size image
Fig. 6
figure 6

Displacement of the beam tip in the x-direction

Full size image
Fig. 7
figure 7

Displacement of the beam tip in the y-direction

Full size image

It should also be emphasized that, for better accuracy of the analysis, the size of deformation in this case would also require to account for the change in the thickness (the thinning in tension and the thickening in compression) [42], which also gives rise to the neutral surface shift during the deformation. However, in this analysis the Poisson coefficient was set to zero. But even if this was not the case, this effect is neglected with all the used elements as well as in the analytical solution that yielded the bending moment required to produce the considered deformation.

4.2 Pinched hemisphere

In the second case, a structure with a doubly curved geometry is considered. It is a hemispherical shell with an 18\({^\circ }\)-hole at the top, radius \(r = 10 \,\hbox {m}\) and thickness \(h=0.04\, \hbox {m}\), Fig. 8. The Young’s modulus of the material is taken to be \(E=6.825 \times 10^{10} \,\hbox {N/m}^{2}\) and the Poisson ratio \(\nu =0.3\). The structure is exposed to two pairs of concentrated forces acting on the bottom edge of the shell. The magnitude of each of the forces is \(150 \, \hbox {kN}\). The pair of forces that is symmetric with respect to the yz-plane acts so as to stretch the hemisphere along the x-axis, while the pair symmetric with respect to the xz-plane compresses it along the y-axis.

Fig. 8
figure 8

Pinched hemisphere geometry and loads

Full size image

The double symmetry allows modeling of only a quarter of the hemisphere with the adequate kinematical boundary conditions applied (Fig. 9, left). In order to capture the local rotations appropriately, finer meshes were needed. After convergence analysis, the results obtained with the FE mesh containing 400 (\(20\times 20\)) quadrilateral elements (Fig. 10, left) and the FE mesh containing 800 triangular elements (Fig. 9, right) were taken as representative.

Fig. 9
figure 9

Pinched hemisphere—FEM mesh with quadrilateral (left) and triangular (right) elements

Full size image

For a better insight into the size of deformation the structure is exposed to, Fig. 10 depicts the original and deformed configurations at the full load from different perspectives and without scaling, i.e. the scale factor equals 1.

Fig. 10
figure 10

Initial and deformed hemisphere (scale factor equals 1)

Full size image

The diagrams in Figs. 11 and 12 show the development of the displacements of points A and B (Fig. 9) along the x- and y-axes, respectively, with the increasing load. A good agreement of the results by all four elements can be noticed. It was important in this case to use a sufficiently fine mesh so that the local rigid-body rotations are adequately captured in the co-rotational formulation. Whereas in the first considered case the element rigid-body rotation was practically around one axis, the overall displacement field in this case is more complex.

Fig. 11
figure 11

Displacement of point A in the x-direction

Full size image
Fig. 12
figure 12

Displacement of point B in the y-direction

Full size image

5 Aspect of efficiency

In various applications that involve interactive simulation, the simulation speed is the primary aspect. A distinctive example of such an application is a surgical simulator, e.g. for the laparoscopic surgery. Due to the high level of complexity of this type of surgery, surgeons frequently emphasize their wish for high-quality VR-based simulators for the purpose of training. Obviously, the real-time requirement has the highest priority in such an application, while the accuracy requirement is not defined in terms of numbers and may be violated as long as the on-screen behavior appears realistic to human perception. Though in many commercially available devices this is achieved by means of the simplest approach, namely the mass-spring systems, the presented co-rotational FEM formulation represents a more sophisticated alternative.

Beside the formalism used for the computation of deformable body behavior, there are some further computational parameters that play a very important role with respect to the defined objective. They are not in the very focus of this paper, but need to be addressed briefly for adequate comprehension of the results given below.

The FE mesh plays an important role in every FEM analysis. In typical engineering FE analyses it needs to be set with very special care. However, if the required minimum accuracy is defined as plausible behavior, then the idea of coupled meshes can be applied. Namely, a relatively fine mesh of surface vertices can be used to represent the actual object geometry in sufficient detail, while a relatively rough FE mesh can be used for the computation. The surface vertices are connected into triangles to give a triangulated surface representation, see Fig. 13, right. The two meshes are coupled to each other based on the local element coordinates of the surface vertices with respect to the finite elements. A vertex that is inside an element is assigned to that element. Upon deformation the global vertex coordinates are recovered based on its element local coordinates and global position of the element nodes. Hence, the FE mesh does not have to fit the actual geometry, but can instead only resemble the actual geometry with more (Fig. 14b) or less precision (Fig. 14c). In this manner the computational burden can be adjusted to the available hardware and other simulation parameters and requirements.

Fig. 13
figure 13

Liver model geometry: 2598 vertices and 5192 faces

Full size image
Fig. 14
figure 14

a Geometric liver model with two FE meshes: b FE mesh A (846 nodes, 2945 elements), c FE mesh B (660 nodes, 2640 elements)

Full size image

Time integration, solver type and time-step size are important aspects in dynamic FE computations. Whereas the explicit time-integration schemes are very efficient in computing a single time-step, provided a lumped mass and damping matrix is used, the time-step size is on the other hand severely limited due to the conditional stability. Therefore, the explicit integration schemes are used for highly nonlinear (no iterations) and fast dynamics problems. In an interactive simulation, the dynamics that is visible to the human eye is of interest, i.e. relatively slow dynamics. This fact permits to simply filter high frequency dynamics out, which is effectively done by using sufficiently large time-steps. This talks in favor of an implicit time integration with a time-step that is sufficiently large not only to compensate for the larger numerical effort per time-step, but also to provide better overall numerical efficiency compared to explicit time-integration. An implicit time-integration scheme keeps the system of equations coupled [17]:

$$\begin{aligned}&{\mathbf {M}}^{t+{\varDelta {}t}} \ddot{\mathbf{u}}+{^t}{{\mathbf {C}}}^{t+{\varDelta {}t}} \dot{\mathbf{u}}^{(k)}+{^t}{\mathbf {K}}^{t+{\varDelta {}t}}\mathbf {\varDelta u}^{(k)} \nonumber \\&\quad =^{t+{\varDelta {}t}}{\mathbf {F}}_{ext}-^{t+{\varDelta {}t}}{\mathbf {F}}^{(k-1)}_{int} \end{aligned}$$
(10)

where \({\mathbf {K}}\) and \({\mathbf {C}}\) are the structural stiffness and damping matrices, respectively, \({\mathbf {u}}\) are the nodal displacements, dots above \({\mathbf {u}}\) denote the time derivatives, i.e. velocities (one dot) and accelerations (two dots), \(\varDelta\) denotes the increment, while \({\mathbf {F_{ext}}}\) and \({\mathbf {F_{int}}}\) are the nodal external and internal forces, respectively. The implicit time-integration of a nonlinear problem demands iterations and (k) in the right superscript denotes the iteration number. In each iteration, the linearized system of equations can be resolved by a direct or iterative solver. An iterative solver, such as the method of preconditioned conjugate gradients (PCG), is an interesting choice due to several reasons. In dynamics, particularly relatively slow dynamics, the velocities do not change dramatically within a time-step and, hence, a good choice of the starting vector is already available, thus reducing the number of iterations notably. A further reason would be the fact that a trade-off between the numerical efficiency and accuracy can be performed easily by limiting the number of iterations, and this can even be done dynamically, during a simulation. Finally, the PCG solver has a great parallelization potential.

Interactive simulations of three solid test objects/models are considered below to provide an insight into the aspect of efficiency by means of the presented formulation in combination with the linear tetrahedral element and the PCG solver. The time step of \(0.01\, \hbox {s}\) is used. The simulation is set so that 4 configurations are computed before the current configuration is shown on the screen, which implies that 25 frames per second would correspond to the real-time computation (\(25\times 4\times 0.01=1\)). The test objects, i.e. models used in the interactive simulations are:

  • a torus-like model, FE mesh: 2487 elements, 1956 degrees of freedom (DOFs), see Fig. 15a;

  • a spleen model, FE mesh: 2226 elements, 1656 DOFs, the geometric model: 962 vertices, 1920 faces, see Fig. 15b;

  • the liver model depicted in Figs. 13 and 14, with the finer FE mesh (Fig. 14b): 2945 elements, 2538 DOFs; the geometric model: 2598 vertices, 5192 faces, see Fig. 15c.

Obviously, the latter two models are motivated by a possible application in the field of surgical simulation and they make use of the coupled mesh technique. The spleen model uses a uniform FE mesh that only roughly resembles the geometric model, while for the liver model the adaptive FE mesh A depicted in Fig. 14b is used. This analysis represents an extension of a similar analysis given in [28], in which only uniform meshes together with older hardware configurations were considered. Figure 16 gives several screen-shots from the interactive simulations with the aforementioned models demonstrating the ability of the co-rotational FEM to cover large displacements and rotations producing plausible behavior. Based on the accuracy demonstrated in the previous section, plausible behavior is expectable, but one should also have in mind that the coupled mesh technique is applied in the later two examples.

Fig. 15
figure 15

Models for interactive simulations: a torus-like structure, b spleen and c liver

Full size image
Fig. 16
figure 16

Screen-shots from an interactive simulation: a torus model, b spleen model; c liver model

Full size image

The same settings are used for an interactive simulation of two shell models, both meshed using the S3 element:

  • an annular slit plate, with one side of the slit clamped and the other one free, meshed by 234 elements, 960 DOFs, see Fig. 17a;

  • the hemisphere from Sect. 4.2 with the edge of the 18-hole clamped, meshed by 1040 elements, 3432 DOFs, see Fig. 17b.

Fig. 17
figure 17

Shell models for interactive simulations: a slit annular plate and b hemisphere with 18-hole

Full size image

Proceeding in the similar way as with the solid structures, Fig. 18 gives several screen-shots from the interactive simulations with the considered shell structures involving rather large deformations computed by the presented co-rotational formulation. The results regarding the simulation speed are summarized in Tables 1 and 2 for different hardware configurations. Three hardware configurations have been used, all of which can be described as conventional personal computers. Information on the CPU and GPU in each configuration is given as those are the components with the main impact onto the simulation efficiency. The considered hardware configurations involve multi-core CPUs, but only one core is used for the computation, i.e. parallelization is not used. The main results in the tables are ratio and the number of frames per seconds (F/s). Ratio denotes the ratio between the clock pace of the simulation and the real time needed for the simulation. If its value is greater than 1 it means the simulation time runs at a pace faster than real time, and vice versa. Obviously, with the chosen time-step and computing 4 time-steps before the screen is refreshed, the simulation with all considered models can run on each of the used hardware configurations at a pace faster than real time or quite close to real time

Fig. 18
figure 18

Screen-shots from an interactive simulation: a slit annular plate; b hemisphere with the 18-hole

Full size image
Table 1 Simulation pace of different hardware configurations with solid models
Full size table
Table 2 Simulation pace of different hardware configurations with shell models
Full size table

6 Conclusions

VR- and AR-based environments call for adequate solutions for the background physics of deformable objects in the framework of interactive simulations that are supposed to run at the same speed as a real clock or somewhat slower but without a delay that would affect the aimed functionality. The essence of the presented solution is the simplified co-rotational FEM formulation. The implemented simplifications obviously make the formulation unsuitable for certain analysis types, such as buckling analysis. It was shown that, despite the simplification implemented in the formulation, it can cover the geometric nonlinearities to a significant extent with accuracy that can be acceptable in certain fields of applications. The examples with the shell elements were focused on this aspect. But it should be emphasized that the achievable accuracy strongly depends on the character of geometrically nonlinear behavior. If it is dominated by large local rigid-body rotations whereby strains and stress stiffening effects remain small, then the presented formulation, which keeps the element elastic behavior linear with respect to the co-rotational reference frame, is expected to yield good accuracy. The prerequisite for this is adequate FE meshing as the rigid-body rotation is accounted for element-wise. This implies that the areas characterized by substantial gradients of rigid-body rotation upon deformation require finer meshing (of course, standard criteria for FE meshing apply as well).

It was shown that FE models with several thousands elements may run in real-time with conventional hardware configurations. Some of the hardware configurations used in the tests contain components that could even be described as outdated. Shell elements are obviously more demanding as they employ both nodal translations and rotations, whereby handling the latter is numerically more expensive. A suitable solution may be sought in solid-shell elements [43] that use only translations as nodal degrees of freedom. Certainly, the mentioned FE model sizes can be described as modest compared to the FE models used in typical engineering tasks, but the objectives of engineering FE models and performed simulations are also substantially different. In addition, the formulation can be enriched by the coupled mesh technique, which together with the adequate choice of the integration scheme (time-step size) and solver provides vast options for the trade-off between the numerical effort and accuracy.

As examples suggest, the approach can be applied for the purpose of surgical simulation. If the real-time requirement is not strict, i.e. if it is relaxed to, say, numerically very efficient then the approach may also find its application in MBS dynamics for flexible bodies experiencing geometrically nonlinear deformation with respect to the floating reference frame. This would eliminate the need to superpose the large rigid-body motion with the deformational motion, as the former is readily incorporated into the co-rotational FEM. Finally, considering the computational power of commercially available hardware components (personal computers meant here), the approach may represent a well-balanced alternative to the available solutions for the current needs of interactive simulations. Beside the considerations related to shells, further work should also tackle the challenges of implementing efficient solutions for material nonlinearities, contact and tear and adequate estimation of the average element rigid-body rotation.