Introduction

Despite a large amount of research in spray drying (Langrish and Fletcher 2003; Masters 1996), the activity of spray-dried materials before and after drying has not been widely studied. Thermal degradation of powders that are produced by spray dryers may be an important consideration in the production of functional food powders. The short residence time of particles inside spray dryers, of the order of minutes or less (Masters 1996), may be a significant factor affecting thermal degradation in this type of equipment, but the high temperatures, 200 °C at the inlet, also need to be considered.

On one hand, spray drying is currently used in the dairy industry to prepare stable powdered milk products that can be stored for up to 6 months. The key components of milk are lactose, casein and fat and these are known to be preserved by spray drying (Masters 1996). Indyk et al. (1996) found that the amount of thermal degradation of vitamin D3 during the spray drying (149 °C) and fluidised-bed drying (107 °C) of milk powder was negligible. High-performance liquid chromatography was used to analyse the concentrations of vitamin D3 before and after spray drying.

However, there is clearly some level of thermal degradation for some classes of chemicals. Some thermal degradation when spray drying folic acid was found by Hawkes and Villota (1989). Inlet temperatures of 200 to 300 °C and outlet temperatures of 100 to 130 °C were used, and they found that folic acid was retained best at an inlet temperature of 260 °C and an outlet temperature of 108 °C. Folate retention was increased at higher feed rates. They used multiple-regression analysis and response surfaces to fit their data, but such an approach has limited predictive power outside the immediate scope of the equipment and operating conditions of their experiments, compared with a mechanistic approach to modelling.

A Buchi-191 miniature spray dryer was used to dry tomato powders by Goula and Adamopoulos (2005) at air-inlet temperatures of 110, 120, 130 and 140 °C and main air-flow rates of 17.50, 19.25, 21.00 and 22.75 m3 h−1. The loss of lycopene in the tomato material was studied using spectrophotometric analysis, with losses ranging from 8.1 to 20.9% and being influenced by most of the operating variables, including air temperature, liquid feed rate, the solids concentration in the feed, the air-flow rate through the nozzle and the main flow rate into the dryer.

Hence, there is evidence both for spray dryers causing thermal degradation of the materials being processed in them and for an insignificant degree of degradation, depending on the type of material present. For vitamin C, Goula and Adamopoulos (2006) measured the thermal degradation of vitamin C in tomato pulp, both as tomato halves and as tomato pulp, where the pulp was sprayed in a Buchi-191 spray dryer. More degradation was seen inside the spray dryer due to the high droplet and particle surface area in contact with the gas, and liquid–liquid and liquid–gas shear. The relationship between the thermal degradation and the temperature and moisture-content profiles during spray drying is explored in this work, using the simulation of Hanus and Langrish (2007). In particular, the location of the maximum rate of thermal degradation is explored.

Simulation Approach and Method: Parallel-Flow Design Equations

Tall-form dryers, such as this Buchi-191 that have an aspect ratio significantly different to 1:1 (height/diameter) may be modelled by treating them as parallel-flow dryers to a first approximation. A clear description of equations for these situations is given in Truong et al. (2005) and given below. The approach and the equations in it actually date back at least as far as Keey and Pham (1976). In the following equations, the subscripts p, a and s represent the droplet, air and solids, respectively.

Model Assumptions

The model assumes that the air and the gas move in parallel flow from the inlet to the outlet through the spray dryer with no backmixing, and it is assumed that the air temperature, humidity and axial velocity at any cross-section of the drying chamber are uniform. One-way gas-droplet coupling is assumed, which is possible since the momentum of the water droplets contributes only a small percentage (7.3 to 20%) of the total momentum of air and water in the Buchi B-290 spray dryer (Best 2005). Following from this assumption, the droplets are therefore assumed to not significantly affect the gas-flow patterns, although the droplets are affected by the gas-flow patterns. The low particle-number concentrations and modest shear stresses mean that no agglomeration or breakup of droplets or particles is assumed to take place in the dryer. The following equations are, with these assumptions, quite general (Keey and Pham 1976; Zbicinski 1995; Truong et al. 2005; Hanus and Langrish 2007) and apply to any materials treated in this way.

Droplet Trajectory Equations

The droplet trajectory equations (Truong et al. 2005; Hanus and Langrish 2007) are droplet axial, radial and tangential momentum balances. U p and U a represent the velocity (m s−1) of the particles (or droplets) and the air, respectively. The subscripts x, r and t represent the axial, radial and tangential components, respectively. The variable h is the axial distance from the atomiser.

$$\frac{{dU_{{\text{px}}} }}{{dh}} = \left[ {\left( {1 - \frac{{\rho _{\text{a}} }}{{\rho _{\text{p}} }}} \right)g - \frac{3}{4}\frac{{\rho _{\text{a}} C_{\text{D}} U_{\text{R}} \left( {U_{{\text{px}}} - U_{{\text{ax}}} } \right)}}{{\rho _{\text{p}} d_{\text{p}} }}} \right]\frac{1}{{U_{{\text{px}}} }}$$
(1)
$$\frac{{dU_{{\text{pr}}} }}{{dh}} = \left[ { - \frac{3}{4}\frac{{\rho _{\text{a}} C_{\text{D}} U_{\text{R}} \left( {U_{{\text{pr}}} - U_{{\text{ar}}} } \right)}}{{\rho _{\text{p}} d_{\text{p}} }}} \right]\frac{1}{{U_{{\text{px}}} }}$$
(2)
$$\frac{{dU_{{\text{pt}}} }}{{dh}} = \left[ { - \frac{3}{4}\frac{{\rho _{\text{a}} C_{\text{D}} U_{\text{R}} \left( {U_{{\text{pt}}} - U_{{\text{at}}} } \right)}}{{\rho _{\text{p}} d_{\text{p}} }}} \right]\frac{1}{{U_{{\text{px}}} }}$$
(3)

Here, ρ is the density (kg m−3), d p is the particle or droplet diameter (m), U R is the relative velocity between the particle or droplet and the air (m s−1), and C D is the drag coefficient. The subscripts a and p refer to the air and the particle or droplet, respectively. U R and C D are calculated as follows (Rhodes 1998).

$$U_{\text{R}} = \sqrt {\left( {U_{{\text{px}}} - U_{{\text{ax}}} } \right)^2 + \left( {U_{{\text{pr}}} - U_{{\text{ar}}} } \right)^2 + \left( {U_{{\text{pt}}} - U_{{\text{at}}} } \right)^2 } $$
(4)
$$C_{\text{D}} = \frac{{24}}{{Re_{\text{p}} }}\left( {1 + 0.15Re_{\text{p}} ^{0.687} } \right)$$
(5)

The particle Reynolds number is defined as:

$$Re_{\text{p}} = \frac{{\rho _{\text{a}} U_{\text{R}} d_{\text{p}} }}{{\mu _{\text{a}} }}$$
(6)

Here μ is the viscosity (kg m−1 s−1).

The radial distance from the dryer axis, r, of particles or droplets as a function of axial distance from the atomiser is estimated as follows.

$$\frac{{dr}}{{dh}} = \frac{{U_{{\text{pr}}} }}{{U_{{\text{px}}} }}$$
(7)

Droplet Mass Balance Equations

Based on the concept of a characteristic drying curve, the unsteady-state mass balance for the droplet can be stated as follows (Truong et al. 2005):

$$\frac{{dm_{\text{p}} }}{{dh}} = - \xi \frac{{A_{\text{p}} K_{\text{m}} }}{{U_{{\text{px}}} }}\left( {p_{{\text{vs}}} - p_{{\text{vp}}} } \right)$$
(8)

Here m p is the mass of the particle or droplet (kg), ξ is the relative drying rate, A p is the particle or droplet surface area (m2), K p is the mass-transfer coefficient (partial-pressure based; kg m−2 s−1 Pa−1), p vs is the partial pressure of the surface of the particle or droplet (Pa), and p vb is the partial pressure of water vapour in the bulk air (Pa). A p can be calculated as follows.

$$A_{\text{p}} = \pi d_{\text{P}}^2 $$
(9)

The droplet diameter is expected to change due to shrinkage. The particle or droplet diameter, d p, is updated based on the assumption of balloon shrinkage without crust or skin formation. It has been suggested that free shrinkage of the sodium chloride droplets is a reasonable assumption (Langrish and Zbicinski 1994). Unlike milk droplets, sodium chloride droplets do not form a skin.

$$d_{\text{p}} = d_{{\text{pi}}} \left( {\frac{{\rho _{{\text{pi}}} - 1,000}}{{\rho _{\text{p}} - 1,000}}} \right)^{\frac{1}{3}} $$
(10)
$$\rho _{\text{p}} = \frac{{1 + X}}{{1 + X\frac{{\rho _{\text{s}} }}{{\rho _{\text{w}} }}}}\rho _{\text{s}} $$
(11)

Here, the variables that have not been defined previously are d pi, the initial droplet diameter (m), and ρ pi, the initial droplet density (kg m−3). The gas-phase mass-transfer coefficient is defined by the following equations:

$$K_{\text{p}} = \frac{{M_{\text{w}} K_{\text{m}} }}{{M_{\text{a}} P}}$$
(12)
$$K_{\text{m}} = \frac{{\rho _{\text{a}} D_{\text{v}} Sh}}{{d_{\text{p}} }}$$
(13)

Here, K p is the mass-transfer coefficient (partial-pressure based; kg m−2 s−1 Pa−1), M w is the molecular weight of water (g mol−1), M a is the molecular weight of air (g mol−1), K m is the mass-transfer coefficient (kg m−2 s−1), D v is the diffusivity of water in air (m2 s−1), Sh is the Sherwood number and P is the total pressure (Pa). The diffusivity can be estimated from the equation (Perry et al. 1997):

$$D_{\text{v}} = \frac{{1.17564 \times 10^{ - 9} \times T_{{\text{abs}}} ^{1.75} \times 101325}}{P}$$
(14)

The Sherwood and Schmidt numbers are calculated from the equations:

$$Sh = 2.0 + 0.6Re_{\text{p}} ^{0.5} Sc^{0.33} $$
(15)
$$Sc = \frac{{\mu _{\text{a}} }}{{\rho _{\text{a}} D_{\text{v}} }}$$
(16)

Here, T abs is the absolute temperature of the droplet or particle (K) and Sc is the Schmidt number.

Droplet Heat Balance Equations

The unsteady-state heat balance for the droplet or particle is (Truong et al. 2005):

$$\frac{{dT_{\text{p}} }}{{dh}} = \frac{{\pi d_{\text{p}} k_{\text{a}} Nu\left( {T_{\text{a}} - T_{\text{p}} } \right) + \frac{{dm_{\text{p}} }}{{dh}}U_{{\text{px}}} H_{{\text{fg}}} }}{{m_{\text{s}} \left( {C_{{\text{ps}}} + XC_{{\text{pw}}} } \right)U_{{\text{px}}} }}$$
(17)

The Nusselt (Nu) and Prandtl (Pr) numbers are calculated from the equations (Ranz and Marshall 1952):

$$Nu = 2.0 + 0.6Re_{\text{p}} ^{0.5} Pr^{0.33} $$
(18)
$$Pr = \frac{{C_{{\text{pa}}} \mu _{\text{a}} }}{{k_{\text{a}} }}$$
(19)

Other product and particle properties are calculated from the equations:

$$H_{{\text{fg}}} = 2.792 \times 10^6 - 160T_{{\text{abs}}} - 3.43T_{{\text{abs}}} ^2 $$
(20)
$$m_{\text{s}} = \frac{{Xm_{\text{p}} }}{{100}}$$
(21)

Here, T is the temperature, k a is the thermal conductivity of humid air (W m−1 K−1), Nu is the Nusselt number, H fg is the latent heat of water evaporation (J kg−1), m s is the mass of solids in the droplet (kg),and C p is the specific heat capacity (J kg−1 K−1).

Mass and Energy Balance Equations for Drying Medium

The mass-balance equation for the drying air is:

$$\frac{{dY_{\text{b}} }}{{dh}} = \frac{{\Sigma _{{\text{droplets}}} \left( { - \frac{{dm_{\text{p}} }}{{dh}}} \right)n_{{\text{droplets}}} }}{G}$$
(22)

Here, G is the mass flow rate of the dry air (kg s−1), and n droplets is the flow rate of droplets (number s−1). The corresponding heat-balance equation for the drying air is:

$$\frac{{dH_{\text{h}} }}{{dh}} = - \frac{1}{G}\left( {\Sigma _{{\text{droplets}}} \left( {m_{\text{s}} \left( {C_{{\text{ps}}} + XC_{{\text{pw}}} } \right)\frac{{dT_{\text{p}} }}{{dh}}} \right) - \frac{{UA\left( {T_{\text{a}} - T_{{\text{amb}}} } \right)}}{L}} \right)n_{{\text{droplets}}} $$
(23)

Here, H h is the enthalpy of the humid air (J kg−1), UA is the heat-transfer coefficient for heat loss from the dryer (W K−1), and L is the length of the spray-drying chamber (m).

Thermal Degradation Kinetics

Goula and Adamopoulos (2006) have measured the following degradation kinetics for vitamin C during spray drying:

$${\text{ }}\Delta \left( {\frac{C}{{C_{\text{i}} }}} \right) = - k\left( {\frac{C}{{C_{\text{i}} }}} \right)\Delta t$$
(24)

Here C is the concentration of ascorbic acid at any time t, C i is the initial concentration, k is the rate constant for the first-order degradation reaction, and Δt is the time step. In this equation, the rate constant was given by the following equations (from Goula and Adamopoulos, 2006):

$${\text{ }}k = K \bullet 278.6624 \bullet \exp \left( {0.0660w} \right) \bullet \exp \left( { - {{5348} \mathord{\left/ {\vphantom {{5348} {T_{{\text{abs}}} }}} \right. \kern-\nulldelimiterspace} {T_{{\text{abs}}} }}} \right){\text{(min}}^{{\text{ - 1}}} {\text{)}}$$
(25)

for w ≤ 65 (R 2 = 0.993)

$${\text{ }}k = K \bullet 7480.089 \bullet \exp \left( { - 0.0115w} \right) \bullet \exp \left( { - {{4718} \mathord{\left/ {\vphantom {{4718} {T_{{\text{abs}}} }}} \right. \kern-\nulldelimiterspace} {T_{{\text{abs}}} }}} \right){\text{(min}}^{{\text{ - 1}}} {\text{)}}$$
(26)

for w > 65 (R 2 = 0.993)

$${\text{ }}K = - 37613 + 178 \bullet T_{{\text{ai}}} - 0.0158\left( {{{Q_{\text{a}} } \mathord{\left/ {\vphantom {{Q_{\text{a}} } {Q_{\text{f}} }}} \right. \kern-\nulldelimiterspace} {Q_{\text{f}} }}} \right) - 1.27{\text{MSD}}^2 \left( {R^2 {\text{ = 0}}{\text{.939}}} \right)$$
(27)

Here T ai is the inlet air temperature (°C), Q a is the drying air-flow rate (m3 h−1), Q f is the feed flow rate (m3 h−1), and MSD is the Sauter mean diameter of the atomized droplets (mm). The particle temperature (T abs) has units of Kelvin, w is the wet-basis moisture content, in % [100X/(1 + X)], and K is a correction factor to account for the higher degradation rate of vitamin C when spray drying, due to the large surface area in contact with air enhancing the rate of ascorbic acid oxidation, exposure of the droplets and particles to light, and shear within the liquid and between the liquid and the gas. It is important to note that Eqs. 25 to 27 arise from the experimental data and analysis of Goula and Adamopoulos (2006) for vitamin C degradation in spray dryers, which include the combined effects of both thermal degradation and oxidation. In addition, they considered the same design of spray dryer as used here, so any wall-abrasion effects are also likely to be the same.

Drying Kinetics

Particulate drying kinetics are included, and the concept of a characteristic drying curve has been used here (Keey and Suzuki 1974; Keey and Pham 1976; Langrish and Kockel 2001), although other approaches are possible, including a shortcut solution to the diffusion equation (Liou and Bruin 1982; Kieviet 1997) and other diffusion models (Adhikari et al. 2003; Chen 2004) or receding-plane type models (Chen et al. 1999). These drying kinetics allow for hindered drying below the critical moisture content of the droplet due to the presence of the solids. The general form of the characteristic drying curve (Keey 1978) is that the relative drying rate (ξ), which is the actual drying rate of the solids relative to the unhindered drying rate, is some function of the characteristic moisture content, as follows.

$$\begin{aligned} &\begin{array}{*{20}c} {\xi = f\left( \Phi \right)}&{{\text{if}}\,X \leqslant X_{{\text{cr}}} } \\ {\xi = 1}&{{\text{if}}\,X > X_{{\text{cr}}} } \\ \end{array} \\&\Phi = \frac{{X - X_{\text{e}} }}{{X_{{\text{cr}}} - X_{\text{e}} }}\,\, \\ \end{aligned} $$
(28)

Here X is the actual average moisture content of the particle (kg kg−1), X cr is the critical moisture content (kg kg−1), X e is the equilibrium moisture content (kg kg−1), and Φ is the characteristic moisture content. The equilibrium moisture content is the moisture content of the particle in equilibrium with the gas, where no further reduction in moisture content occurs. The critical (X cr) and equilibrium (X e) moisture contents have been assumed to be the same as those given in Hanus and Langrish (2007), where the critical moisture content is assumed to be the same as the initial moisture content. The initial moisture content, for the 14% total solids solution sprayed by Goula and Adamopoulos (2006), is (1 − 0.14)/0.14 = 6.1 kg kg−1 (dry basis).

Model Solution

This model for the steady-state behaviour of the dryer is a set of ordinary differential equations (ODEs), which were implemented and solved in Mathworks’ Matlab using the inbuilt Matlab stiff ODE solver function ode23s. The air flows into the dryer with an axial component only, so the inlet boundary values of the radial and tangential inlet air velocity were both set to a value of 0 m s−1. The boundary values of other parameters, such as the inlet values of the axial velocities and gas temperatures, were based on experimental conditions described as follows. The simulations of Hanus and Langrish (2007) suggest that ten discrete-size classes are adequate to represent the continuous particle-size distribution in this type of two-fluid atomizer. Hanus and Langrish (2007) also found that an average heat loss coefficient (UA, the overall heat-transfer coefficient multiplied by the surface area of the outside of the dryer) of 2.4 W K−1 was adequate to represent the energy loss from the equipment.

The conditions used by Goula and Adamopoulos (2006) included the following ones:

  • Inlet air temperatures, 110 and 130 °C

  • Nozzle air-flow rate, 500 and 700 l h−1

  • Main air-flow rate, 17.50 and 19.25 m3 h−1

  • Total liquid flow rate, 1.75 ml min−1

  • Solids content in the feed, 14%

  • Feed liquid temperature, 32 °C

  • Dryer length, 0.48 m

  • Dryer diameter, 0.155 m

These conditions have been used in the following simulations. The particle sizes vary with the nozzle air-flow rate, and due to the assumption of balloon shrinkage, these sizes decrease through the dryer. The particle sizes for the ten size classes are shown in Table 1 (based on Hanus and Langrish 2007) as a function of nozzle air-flow rate. The simulations are based on the experimental data of Goula and Adamopoulos (2006), who have shown that both oxidation and thermal effects are significant, according to their kinetic equations (Eqs. 25 to 27). The particle sizes have been measured (Lamy et al. 2007) using a Malvern Mastersizer 2600c (Malvern Instruments, Malvern, Worchestershire, UK). The drying kinetics have also been assumed to be the same as those used in Hanus and Langrish (2007), although the sensitivity of the model predictions to different assumptions about the kinetics has also been assessed here.

Table 1 Particle sizes in microns for the size classes are shown as a function of nozzle air-flow rate (Hanus and Langrish 2007)
Full size table

Results and Discussion

The sensitivity of the model predictions for the mean ratio of final to initial vitamin C concentrations (C/C 0) has been studied with respect to the shape of the characteristic drying curve used and the presence (UA = 2.4 W K−1) or absence (UA = 0 W K−1) of heat loss from the equipment, which could be altered by insulating the equipment. A linear (ξ = Φ falling-rate curve was found by Langrish and Kockel (2001) for milk powders, while Hanus and Langrish (2007) found a quadratic (ξ = Φ2) falling-rate curve for salt solutions. The sensitivities are shown in Table 2, which shows predicted values within the range of experimental values given by Goula and Adamopoulis (2006) of 0.88 to 1, showing between 0 and 12% degradation.

Table 2 Sensitivity of the model predictions for the mean ratio of final to initial vitamin C concentrations (C/C 0) to the operating conditions, to the assumed particulate drying behaviour (quadratic or linear falling-rate kinetics) and to the presence or absence of heat loss
Full size table

While the drying kinetics have some effect, the largest effect is through removing the heat loss through insulating the equipment. A linear falling-rate curve causes faster drying than a quadratic curve, resulting in more cooling of the particles, lower particle temperatures and less thermal degradation (numbers closer to unity in Table 2). Higher inlet air temperatures result in larger amounts of thermal degradation, as shown by the lower numbers in the table, while higher nozzle air-flow rates cause finer particles, faster drying, more particle cooling, lower particle temperatures and less thermal degradation.

Higher main air-flow rates cause more thermal degradation, since the air temperatures remain higher throughout the dryer in this case, as shown in Fig. 1, which shows the results of two simulations at the normal heat loss and for an inlet air temperature of 130 °C, a nozzle air-flow rate of 500 l h−1 and main air-flow rates of 17.50 and 19.25 m3 h−1. The higher air temperatures in the dryer from higher main air-flow rates arise because more thermal energy enters the dryer. The saturation humidity does not arise at 0.06 m from the start of the dryer; this point simply shows that most of the moisture removal, overall, occurs over this section. However, such an analysis might be considered to be rather superficial because the rest of the dryer is designed to remove the moisture from the largest size class of particles. An inlet air temperature of 130 °C has been used in Figs. 1, 2, 3 and 4 for illustrative purposes. The range of inlet air temperatures from 110 to 130 °C, as per the experimental data from Goula and Adamopoulos (2006), has been used in Table 2 and Fig. 5 of this paper. It is not obvious that such temperatures cause temperature overheating because the extent of thermal degradation, in these simulations as well as in the experimental data, is small, with the ratio of final to initial concentrations being in the range of 0.88 to 1, showing between 0 and 12% degradation.

Fig. 1
figure 1

Predicted air temperatures and gas humidities as a function of distance along the dryer for an inlet air temperature of 130 °C, a nozzle air-flow rate of 500 l h−1 and main air-flow rates of 17.50 and 19.25 m3 h−1

Full size image
Fig. 2
figure 2

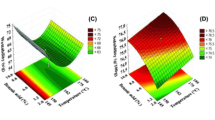
Predicted particle temperatures as a function of distance along the dryer for an inlet air temperature of 130 °C, a nozzle air-flow rate of 500 l h−1 and a main air-flow rate of 19.25 m3 h−1, normal heat loss. The size classes are given in Table 1. The smaller size classes (classes 1–8) are all shown to the left of those for size classes 9 and 10, at distances less than 0.02 m from the inlet of the dryer

Full size image
Fig. 3
figure 3

Predicted particle temperatures as a function of distance along the dryer for an inlet air temperature of 130 °C, a nozzle air-flow rate of 500 l h−1 and a main air-flow rate of 19.25 m3 h−1, no heat loss. The size classes are given in Table 1. The smaller size classes (classes 1–8) are all shown to the left of those for size classes 9 and 10, at distances less than 0.02 m from the inlet of the dryer

Full size image
Fig. 4
figure 4

Predicted degradation rates as a function of distance along the dryer for an inlet air temperature of 130 °C, a nozzle air-flow rate of 500 l h−1 and a main air-flow rate of 19.25 m3 h−1, normal heat loss. The size classes are given in Table 1. The smaller size classes (classes 1–8) are all shown to the left of those for size classes 9 and 10, at distances less than 0.02 m from the inlet of the dryer

Full size image
Fig. 5
figure 5

Predicted extents of degradation and final moisture contents as a function of inlet air temperature and nozzle air-flow rates for main air-flow rates of 17.50 and 19.25 m3 h−1, normal heat loss

Full size image

To some extent, heat loss from the dryer is partially responsible for the higher particle peak temperature inside the dryer compared with the particle temperature at the outlet, as can be seen in Fig. 2. Figure 3 is different from Fig. 2, in that Fig. 3 shows that, when this heat loss is removed in this simulation, the peak particle temperatures near the inlet of the dryer, particularly for the fine particles, are still above the particle temperatures at the outlet.

The appearance of a peak particle temperature inside the dryer that is significantly above both inlet and outlet particle temperatures is not simply a function of the linear falling-rate drying kinetics, as shown in Table 2, which shows the effect of two more very different falling-rate drying expressions, a quadratic relationship and a square-root one. The quadratic relationship gives lower drying rates than linear falling-rate behaviour and hence higher particle temperatures, while the square-root one gives the opposite type of behaviour. However, in all cases, the peak particle temperature inside the dryer is significantly above both inlet and outlet particle temperatures, independently of the assumed drying kinetics. Essentially, the continuation of particle drying after the particle and gas temperatures have approached each other in the initial stages of drying means that both gas and particle temperatures decrease after this point of initial temperature approach. The gas temperature decreases because the gas supplies energy for moisture evaporation, while the particle temperature decreases because it tracks the gas temperature.

Dryers are not heat exchangers, and the gas and temperature profiles in a cocurrent dryer do not follow the classical expectation of the gas and particle temperatures approaching each other smoothly and proportionately in a cocurrent heat exchanger. In particular, the particle temperatures typically reach a peak value in the middle of the dryer that is greater than both the inlet and outlet particle temperature, a fact that has been experimentally verified and is used in practice to sterilize meat solids that are processed inside cocurrent cascading rotary dryers (Fernando et al. 1990). In other applications, such peak particle temperatures may be undesirable or even hazardous, as in the drying of wood chips, and the drying of wood chips in cascading rotary dryers has also been reported (Kamke and Wilson 1985, 1986a, b). In particular, Fig. 4 identifies where the degradation rates are highest. Due to the higher moisture contents in the middle of the dryer and the highest particle temperatures in the middle of the dryer, these degradation rates are also predicted to be highest in the middle of the dryer. Comparing Figs. 2 and 4, it appears that the peak temperatures coincide with the peak degradation rates, so the effect of the peak temperatures is dominant compared with the effect of changing moisture content.

Given this simulation, it is also possible to answer the question of what the optimal spray drying conditions would be if the inlet conditions were varied over the following ranges for inlet air temperatures (110–130 °C) and nozzle (500–700 L h−1) and main air (17.50–19.25 m3 h−1) flow rates. For this purpose, it is necessary to specify how the objective function and the constraints might be defined. One possible objective function is to minimize the amount of thermal degradation, and a possible constraint might be the achievement of a suitably low final moisture content. For dairy powders, a final moisture content of 5% or under in the powder is often specified. Fixed variables have included the following ones:

  • Total liquid flow rate, 1.75 ml min−1

  • Solids content in the feed, 14%

  • Feed liquid temperature, 32 °C

  • Dryer length, 0.48 m

  • Dryer diameter, 0.155 m

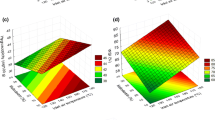
For quadratic drying kinetics, Fig. 5 shows the predicted extents of degradation and final moisture contents as a function of inlet air temperature and nozzle air-flow rates for main air-flow rates of 17.50 m3 h−1 (Fig. 5a,b) and 19.25 m3 h−1 (Fig. 5c,d). For moisture contents and other parameters, wet bases and dry bases are interconvertable, in the sense that a quantity per unit dry mass (dry basis) can be converted to a quantity per unit wet mass (wet basis) by dividing the quantity by (1 + X), where X is the dry-basis moisture content. For example, the wet-basis moisture content (w, %) can be obtained from the dry-basis moisture content (X, kg kg−1) according to the relationship w = 100X/(1 + X). The results shown in Figs. 1, 2, 3, 4 and 5 include the integrated effects of the degradation kinetics, which include the effect of moisture content, as shown in Eqs. 25 to 27. Although crust formation affects the drying kinetics, the peak particle temperature inside the dryer has been shown here (Figs. 2, 3 and 4) to be significantly above both inlet and outlet particle temperatures, independently of the assumed drying kinetics.

The lowest amount of degradation (the closest value of the degradation indicator to unity) occurs for both main air-flow rates (at the extreme ends of the range of air-flow rates) at the lowest inlet air temperature and the highest nozzle air-flow rate. The thermally labile nature of the material means that the use of the lowest inlet air temperature is understandable. As previously noted, higher nozzle air-flow rates cause finer particles, faster drying, more particle cooling, lower particle temperatures and less thermal degradation. As also previously noted, lower main air-flow rates cause less thermal degradation, since the air temperatures remain higher throughout the dryer in this case. Higher inlet air temperatures and higher nozzle air-flow rates (giving finer droplets) are predicted to result in lower final moisture contents. Higher main air-flow rates mean higher air velocities and greater relative velocities between gas and solids, giving faster drying rates, as well as meaning larger energy flow rates into the dryer (at a given inlet air temperature, the energy flow rate into the dryer is proportional to the main air-flow rate).

Conclusions

Regardless of the amount of heat loss from the dryer, the key results are that the particle temperatures in a cocurrent spray dryer are likely to reach peak values shortly after the inlet of the dryer and that the occurrence of this peak value near the inlet of the dryer does not depend, in general, on the extent of heat loss. Such maximum particle temperatures also lead to the greatest degradation rates there. Another key result is that the lowest amount of degradation (the closest value of the degradation indicator to unity) occurs, for both main air-flow rates (at the extreme ends of the range of air-flow rates), at the lowest inlet air temperature and the highest nozzle air-flow rate.