Introduction

The titanium (Ti) alloy Ti-6Al-4V is most commonly used in the aerospace industry and for medical prostheses, where weight and material strength considerations are critical.1,2 The material strength of these alloys has been shown to be heavily reliant upon elemental content as well as microstructural arrangement.3,4 Oxygen and nitrogen content, in particular, greatly influence material strength of the alloy. As their content in alloys decreases, material ductility, fracture toughness, resistance to corrosion and crack initiation all improve, however at the expense of material strength.

Conventionally produced Ti-6Al-4V alloys have yield strengths between 720 MPa and 950 MPa, a wide range which is dependent upon the complex interdependence of heat treatment, processing, and chemical composition; all of which impact microstructure and residual stresses within the material.5 The morphology of the microsctructure in the alloy, dependent on processing conditions, yields either lamellar, equiaxed, or bimodal structures, in a combination of alpha and beta phases.

The mechanical properties of \(\alpha \)/\(\beta \) alloys depend heavily on the characteristics of their microstructure. In particular, the size and volume fraction of the equiaxed alpha particles, the volume fraction of total alpha and the thickness of the Widmanstätten alpha laths have been shown to yield the greatest influence on the mechanical properties of the alloy.6 Given the complex interdependency between each of these microstructural variables, no simple predictive constitutive equation for these materials based on governing physical laws exists. Recently, however, Collins et al.6 developed a phenomenological equation predicting the mechanical strength of these multi-phase materials. Their method used Bayesian neural networks in conjunction with genetic algorithms to solve for the optimized best fit between stereological and compositional measurements on \(\alpha \)/\(\beta \) Ti-6Al-4V alloys, and empirical observations of their mechanical strength.7 These mechanism-based equations suggest ways to improve control over the material strength of these alloys by controlling the relative hexagonal close-packed (hcp) alpha and body-centered cubic (bcc) beta phases by solid solution strengthening. Phenomenological relationships provided this way, however, are deterministic, and do not account for the large variability which is known to occur naturally for each material variable.8

For this reason, an additional analysis was performed here on the model generated by Collins et al.,6 to introduce a probabilistic prediction of the titanium alloy yield strength. For this approach, the variability in the phenomenological equation was described using the following cumulative distribution functions (cdfs): Weibull, Normal, and Uniform. These cdfs statistically characterize the composition and microstructure variables. This approach yields a mean square error (MSE) confidence interval prediction on the yield stress calculation obtained from the phenomenological equation and is described in more detail below. To the best knowledge of the authors, such a confidence interval prediction on the material strength of \(\alpha \)/\(\beta \) processed Ti-6Al-4V alloys has never been reported.

Phenomenological Model for Yield Stress in Titanium Alloy

A brief overview of the phenomenological process model (Eq. 1) is described below. Equation 1 was developed from wrought structures as a prototypical tool to better understand and predict the effect of the novel 3D printing process on material performance, and ultimately to ensure the performance of the material during service.9 This is the first attempt to develop such an equation for titanium alloys with the ultimate objective of providing a process-structure-property-performance relationship. The explicit equation is given below:

$$\begin{aligned} \sigma _{\rm ys} =&\; 89 {F_{\rm V}^{\text {total}{\_}\alpha }} + 45 {F_{\rm V}^{\beta }} \\&+ \text{ SSS } \times \left[ 1 + \left(1-{F_{\rm V}^{\text {equiaxed}{\_}\alpha }}\right) \times \frac{100 - {\text{ colony }}}{100} \times 0.25 \right] \\&+ 110 \times {F_{\rm V}^{\text {equiaxed}{\_}\alpha }} \times {\text {Equiaxedsize}}^{-0.5} \\&+ \left(1-{F_{\rm V}^{\text {equiaxed}{\_}\alpha }}\right) \times \frac{{\text{ colony }}}{100} \times 126 \times (\text{ LW })^{-0.26} \left(B\right) ^{0.26}, \end{aligned}$$
(1)

where SSS is the solid-solution strengthening component, defined as the following:

$$\begin{aligned} \text{ SSS } =&\; {F_{\rm V}^{\text {total}{\_}\alpha }} (149.5 \times {C_{\rm Al}}^{0.667}+745 \times {C_{\rm O}^{0.667}}) \\ &+ {F_{\rm V}^{\beta }}\left( (34\times {C_{\rm V}}^{0.765})^{0.5} + (245\times {C_{\rm Fe}}^{0.765})^{0.5}\right) ^{2.15}, \\ \end{aligned}$$
(2)

and

$$\begin{aligned} \textit{ B } = \text{ LW } (1-({F_{\rm V}^{\text {total}{\_}\alpha }} -{F_{\rm V}^{\text {equiaxed}{\_}\alpha }}). \end{aligned}$$
(3)

It should be noted that Eq. 1 is identical to the equation for \(\sigma _{\rm ys}\) in9 except for B, which is explicitly expressed here in terms of LW, \(F_{\rm V}^{\text {total}{\_}\alpha }\) and \(F_{\rm V}^{\text {equiaxed}{\_}\alpha }\).

The volume fractions of total hcp \(\alpha \), bcc \(\beta \) and equiaxed \(\alpha \) particles found in Ti-6Al-4V are represented in Eq. 1 by \(F_{\rm V}^{\text {total}{\_}\alpha }\), \(F_{\rm V}^{\beta }\) and \(F_{\rm V}^{\text {equiaxed}{\_}\alpha }\), respectively. The weight percent elemental composition of aluminum, oxygen, vanadium and iron are represented by \(C_{\rm Al}\), \(C_{\rm O}\), \(C_{\rm V}\) and \(C_{\rm Fe}\), respectively. Equiaxedsize represents the size average of the equiaxed \(\alpha \) particles, while LW is the average \(\alpha \)-lath width. The colony variable is the percentage of parallel \(\alpha \)-lath order within the crystalline structure. Colonies are adjacent laths which are both geometrically parallel and of the same crystallographic variant. There are 12 possible alpha variants that may precipitate from the parent beta phase, each obeying the Burgers orientation relationship, but which are distinct with respect to which \(<110>\) and \(<111>\) beta are parallel to the (0001) and (11–20). A colony only contains one variant, which is necessarily geometrically parallel and immediately adjacent to laths of the same orientation.

Standardized stereological protocols were used to quantify the microstructural composition of \(\alpha \)/\(\beta \) Ti-6Al-4V alloy samples within a parametric array of variables, such as microstructural volume fractions and particle geometries.6 These variables were then used within the neural networks to train and test an equation which predicts the material properties of the material within the range of data used to generate them.

There are two shortcomings of this method: (1) models generated this way will not reflect fundamental physical laws underlying the mechanisms, and (2) the equation is valid within the range of data used to generate it, but not outside of it. A solution for the first shortcoming was to provide genetic algorithms to deconstruct the neural network functions generated and include microstructure relationships and properties based on legacy understanding (for further details on the genetic algorithms, see 9). Phenomenological equations generated this way enable the prediction of material properties when no exact solution exists, as is the case for the complex interdependency of the multi-scale microstructural features and composition of titanium alloys (Fig. 1). The validity of the predictive model remains bound within the limits of the data span used to generate it, however.

Fig. 1
figure 1

Experimental yield stress data (red circle) shown, as compared to the phenomenological model prediction (black square), which shows excellent agreement between the model and data

Full size image

Probabilistic Parameter Estimation

Having established a phenomenological relationship between material parameters such as composition, volume fraction, microstructural features and the strength of the titanium alloy, it is of value to now consider the naturally occurring variability in these material properties to obtain a realistic estimation for the yield strength and subsequent confidence intervals. This modeling process involves statistically characterizing each variable in the phenomenological equation with an appropriate cdf, in order to describe its inherent variability.

The natural variability in the volume fraction of alpha and beta particles, for example, was approximated by a Normal cdf (see Fig. 2). The variability in material composition of elemental aluminum (Al), vanadium (V), iron (Fe) and oxygen (O), on the other hand, was modeled using Uniform cdfs. A two-parameter Weibull cdf was used to characterize the Equiaxedsize. The colony variable was characterized with a two-parameter Weibull cdf for the lower tail of the data, but the majority of the data were constant. Consequently, a bimodal cdf was used. Further comments for these assumptions are given below.

Fig. 2
figure 2

Graphical estimation (line) and experimental data (red circles) for variable F \(_{\rm V}^{\text {equiaxed}{\_}\alpha }\). Plotted on normal probability paper

Full size image

Determination of the appropriate cdfs to describe these material properties initially involved graphical estimation techniques. Once an acceptable cdf was determined, parametric estimation for the cdfs was completed using the data. Table I lists the variables, the assumed form of the cdf, and the mean \(\mu \), variance \(\sigma ^2\), and the coefficient of variation cv. Notice that the variables with the largest scatter are C \(_{\rm Fe}\) and C \(_{\rm O}\), respectively. There is very little variability in \(F_{\rm V}^{\text {total}{\_}\alpha }\). Since these estimated cdfs were used in subsequent Monte Carlo simulations of the phenomenological equation (Eq. 1), the scatter in each variable is critical. The simulated results provide a predictive range on the yield strength for these alloys because the model development and analysis were based on data from the alloy. Details of this approach are provided below for each of the material variables involved.

Elemental Composition (C \(_{\rm x}\))

Data for the composition of Al, V, Fe and O (C \(_{\rm x}\)) in the titanium alloy were considered to be characterized by a Uniform cdf. The primary reason for this assumption is that all compositions within the material have an equal likelihood of appearing. The Uniform cdf has the following general form:

$$\begin{aligned} F_x(x) = {\left\{ \begin{array}{ll} 0 &{} \text{ for } \textit{ x } < \textit{ a } \\ \frac{{ {x-a}}}{{ b-a}} &{} \text{ for } \textit{ a } \le \textit{ x } < \textit{ b } \\ 1 &{} \text{ for } \textit{ x } \ge \textit{ b } \end{array}\right. }, \end{aligned}$$
(4)

where a and b represent the limits on C \(_{x}\) estimated from the data of these variables. In Eq. 4, x stands for the composition (in mass %) of either Al, V, Fe or O, and F \(_x\)(x) their associated probability. Since the compositions are assumed to be well represented by Uniform cdfs, then simulation of these variables is straightforward.

Volume Fractions (\(F_\mathrm{V}^{x}\))

Graphical estimation for both \(F_\mathrm{V}^{\text {total}{\_}\alpha }\) and \(F_{\rm V}^{\text {equiaxed}{\_}\alpha }\) indicates that a Normal cdf is acceptable for their characterization. An example of this technique for the equiaxed \(\alpha \) data is shown in Fig. 2, where the data are plotted on Normal probability paper (for further details on Normal paper, see Ref. 10). Notice that the linear fit is quite good. In fact, the correlation coefficient for the fit is 0.982. The parameters \(\mu \) and \(\sigma \) (representing the mean and standard deviation, respectively) are shown in the Normal cdf (Eq. 5):

$$\begin{aligned} F_x(x) =\int _{-\infty }^{x} \frac{1}{\sqrt{2 \pi \sigma ^2}} e^{ -\frac{1}{2} \left( \frac{x-\mu }{\sigma }\right) ^2} \mathrm{d}x \end{aligned}$$
(5)

The parameters were graphically estimated and found to be \(\hat{\mu }\) = 0.56% and \(\hat{\sigma }\) = 0.12%. Furthermore, the maximum likelihood estimates (MLE) are identical. Similarly, this was repeated for total volume fractions of alpha. The correlation coefficient for this case is 0.95, which is not quite as good, but still very acceptable. The estimated parameters for this case, using graphical and MLE estimation, are \(\hat{\mu }\) = 90.2% and \(\hat{\sigma }\) = 1.69%. In addition, these two cdfs were also checked with the Kolomogorov–Smirnov (KS) and Anderson–Darling (AD) goodness of fit tests. Both cdfs are acceptable according to the KS test for any level of significance less than 20%. The AD test, however, indicated that they are acceptable for any significance less than 10%. This is due to the fact that the data in the tails exhibit more scatter (see Fig. 2). There are several algorithms for simulating Normal variables; however, the Box–Müller method11 is quite easy to use, and was implemented for the subsequent simulation of these volume fractions.

Equiaxedsize and Colony

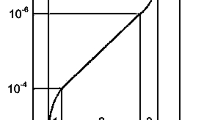
The data for equiaxed \(\alpha \) particle size (variable Equiaxedsize) were plotted on Weibull probability paper (for futher details on Weibull paper, see 12), as shown in Fig. 3. The correlation coefficient for the data is 0.969. Thus, the apparent linearity indicates that a two-parameter Weibull cdf is suitable for these data. The two-parameter Weibull cdf is shown in Eq. 6:

$$\begin{aligned} F_x(x) =1 - e^{-\left( x/{\beta }\right) ^{\alpha }}, \end{aligned}$$
(6)

where \(\alpha \) is the shape parameter and \(\beta \) is the scale parameter. The MLE values for these are \(\hat{\alpha }\) = 9.79 and \(\hat{\beta }\) = 7.27 \(\mu \)m. The KS statistic indicates that the cdf is acceptable for any significance less than 20%; however, the AD test implies that the cdf is acceptable for any significance less than 15%. Again, this is due to the deviation in the lower tail shown on Fig. 3. Simulation of Eq. 6 is straightforward.

Fig. 3
figure 3

Equiaxedsize alpha particle size data (red circles) and graphical estimation (black line). Plotted on Weibull probability paper

Full size image

The colony data are considerably different from all others in this work because they are distinctly bimodal. The first mode is the lower third of the data, which are characterized well by a two-parameter Weibull cdf. The second mode is the remaining data, which are constant at 100%. The estimated parameters for the first mode are \(\hat{\alpha }\) = 3.97 and \(\hat{\beta }\) = 66.1%. These parameters were confirmed using graphical estimation, and the goodness of fit was corroborated using the KS and AD tests, which indicate that for any significance less than 20% this cdf is acceptable. This simulation of the colony is not quite as standard as the other variables. In fact, the following describes the bimodal equation which simulates the colony variable:

$$\begin{aligned} \text {colony} = {\left\{ \begin{array}{ll} 100, &{} 66\% \text{ of } \text{ the } \text{ time } \\ \hat{\beta } (-\log (1-u_\mathrm{w}))^{\frac{1}{\hat{\alpha }}} , &{} 33\% \text{ of } \text{ the } \text{ time } \end{array}\right. } \end{aligned}$$
(7)

where \(u_\mathrm{w}\) = a uniform random number. The Weilbull portion of the simulation is truncated at 100% and represents the lower third of the distribution. Two thirds of the simulated values are identically 100%.

Analysis and Results

Figure 4 summarizes the major portion of the effort herein. The solid dots are the experimental yield stresses for which the model in Eq. 1 was developed. The open squares are the values computed using this phenomenological model. The comparison is quite good. The only significant deviation is in the lower tail where there is at most a difference of 2.5% in yield strength. The main purpose of this paper is to incorporate the inherent variablility in the underlying variables. These critical variables are listed in Table I.

Table I List of all variables found in Eq. 1 (except for \(F_\mathrm{V}^{\beta }\) = 1 − \(F_{\rm V}^{\text {total}{\_}\alpha }\)), with their respective cdfs used to model their uncertainty, including (when appropriate) the range on which these data were generated as well as the mean, variance and coefficient of variation for their distributions.
Full size table
Fig. 4
figure 4

Probability of experimental yield stress data (red circles; proprietary) shown, as compared to the phenomenological model prediction (black square) and Monte Carlo simulations (black line). A MSE confidence interval of one and two standard deviations is also shown (blue dashed lines)

Full size image

The solid line on Fig. 4 is the simulated cdf for the model, that is, the variables in Table I were simulated and inserted into Eq. 1 in order to simulate the yield stress. The experimental data correspond extremely well to the simulated values in the upper range, above approximately 780 MPa. A bifurcation in the data less than 780 MPa is the result of the wide range of elemental compositions observed in these materials, and suggests that multiple modes of material behavior exist as a function of composition variability. These data indicate that a bimodal cdf may be more appropriate. Clearly, the simulated cdf deviates from the data in this lower tail portion by as much as 6%. While that does not seem to be overly significant, the simulated estimate is greater than the actual data which means that the simulation is not a conservative estimate. Using the simulated values and the data, a mean square error (MSE) estimate can be computed. Also, a standard deviation of the MSE, \(\sigma _{\text {MSE}}\), can be used to estimate a confidence interval about the simulated cdf. The thin dashed lines correspond to the simulated cdf \(\pm \,\sigma _{\text {MSE}}\) and the bold dashed lines are the simulated cdf \(\pm \)2\(\sigma _{\text {MSE}}\). Obviously, all the data are contained within the lines using \(\pm \)2\(\sigma _{\text {MSE}}\). However, in order to capture the experimental data in the lower tail, the interval is condiserably wider. Positively, the \(\pm \)2\(\sigma _{\text {MSE}}\) interval captures the bimodal behavior even though the model did not contain that characteristic. For design allowables for structurally significant components, the lower \(\pm \)2\(\sigma _{\text {MSE}}\) line should be used because all data are bounded by it. In other words, it is the most conservative estimate for the entire collection of experimental data.

Even though the model and the simulation are reasonably representative of the data, further refinement of the probabilistic model to include the bimodal nature of the data is warranted. This will be possible given additional understanding of the material behavior and expanded data. However, this first approximation on the yield strength of Ti-6Al-4V alloys is valuable in beginning to grasp the complex relationship between probabilistically based materials modeling and experimental observations.

Conclusion

The primary purpose of this paper is to begin the development of a probabilistically based mechanistic model for the yield strength of Ti-6Al-4V wrought materials. A novel phenomenological equation has been developed, as a first attempt, using neural network analyses coupled with a genetic algorithm. The underlying variables that cause variability in experimentally determined yield strength have been statistically characterized, and their cdfs have been subsequently used in simulation to predict the yield strength, and more importantly a confidence interval based on MSE. The work shown here provides a tool which bridges the gap between material processing and performance, which will be useful in material design and optimization strategies. While significant progress has been made, further refinements on the model, characterization of the material properties, and confidence estimation are needed. As new manufacturing procedures are known to alter material microstructures and performance, the rapid development of these new technologies, such as metal 3D printing, require an equally rapid informed understanding of the resulting material properties. As such, the current model developed on wrought titanium alloys also provides the first step towards an eventual new tool in the parametric design and optimization of 3D printed titanium alloys.