Introduction

One of the main requirements for further development of present-day aircraft engine manufacture is to increase the gas turbine engine lifetime which greatly depends on the endurance of highly stressed structural components such as disks and blades. The methodology of establishing the lifetime by the concept of safe crack propagation is known [1] to be based on the knowledge of a fatigue crack growth rate (FCGR) dl dN in the above-mentioned structural components, where l is the fatigue crack length and N is the number of loading cycles. It is usually determined using the function dl/dN = f (∆K) or a kinetic diagram of FCGR (where ∆K is the stress intensity factor (SIF) range), which consists of three segments (j = 1, 2, 3) – Fig. 1.

Fig. 1
figure 1

A kinetic diagram of FCGR (segments 1, 2, and 3).

Full size image

According to the applicable standards [2, 3], the second segment of the kinetic diagram (j = 2) is used for the FCGR determination. This segment is adequately described by the Paris equation

$$ dl/dN=C{\left(\varDelta K\right)}^n, $$
(1)

where the constant C and the exponent n (hereinafter, the coefficients of the Paris equation) are found for each experimentally obtained kinetic diagram.

The reliability of the FCGR determination depends on how accurate the coefficients of Eq. (1) are found, i.e., on the correct selection of the second segment of the kinetic diagram. The standard [2] specifies that a FCGR ranging from 10−5 to 10−3 mm/cycle shall correspond to this segment. Taking into account that this range corresponds to the second segment only roughly, Potapov and Perepelitsa [4] put forward a procedure for improving the accuracy of the determination of the coefficients C and n, which permits excluding from consideration the FCGR values that do not correspond to the segment at hand.

The researchers [5–7] noted an essential relationship between the Paris equation coefficients C and n, which is represented by the regression equation

$$ \log C=a+bn, $$
(2)

where a and b are constants.

The investigations to determine the constants a and b for various grades of steels and aluminum alloys have been undertaken by many researchers. The results of testing of specimens of different widths and different extents of heat treatment, in various media, which were generalized in [8], have demonstrated stable values of the constants a and b for strongly varying C and n. Noteworthy is the assumption made in [9] that it is only the stress ratio R which may have an effect on the values of a and b.

The validity of relationship (2) is supported by the results of testing of compact specimens of nickel alloys ÉP741NP and ÉK151ID at temperatures T = 20 and 400°C [10] as well as by the generalization [11] of the test data for titanium and nickel alloys, which were reported by many researchers, including the data obtained at Pisarenko Institute of Problems of Strength of the National Academy of Sciences of Ukraine. It was inferred in [10] that relationship (2) is a universal one for the types of alloys under consideration.

The objective of this work has been to experimentally study, using a unified methodological approach, the behavior of the crack growth rate in titanium alloys taking into account the temperature effects, and to verify the validity of relationship (2) between the Paris equation coefficients.

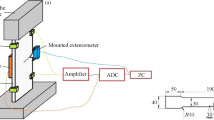
Methodological Background of Compact Specimen Testing and Determination of Fatigue Crack Growth Rate. As per requirements [2, 3] the tests for the FCGR determination were performed on compact (CT) specimens (Fig. 2).

Fig. 2
figure 2

Compact tension (CT) specimen for the FCGR investigations.

Full size image

A Mod. RUMUL TESTRONIC 50kN resonance testing machine is used for growing a precrack in a specimen. The specimen is loaded in a sinusoidal pattern with a frequency of f = 60 ± 5 Hz and stress ratio R = 0.1. During the crack growth the level of maximum cycle load decreased in steps and its value at the last step was 283.5 kgf. The fatigue precrack growth dynamics is monitored throughout the loading process by an optical method using a Mod. MBS-10 microscope. The instant the initial fatigue crack starts from a mechanical notch is detailed on both opposite sides of the specimen. The deviation of the crack front from its center line is monitored too.

For plotting the FCGR kinetic diagram the testing of compact specimens is carried out using a Mod. BiSS-100 servo-hydraulic testing machine with a high-temperature furnace SEL (Instron) mounted on the load frame of the machine.

A high-temperature strain gauge (Instron) is applied to record the crack face displacement that is used for the computational determination of the crack length. In the case of testing at room temperature (20°C), the crack length increment is also recorded by an optical method on both opposite sides of the specimen.

During the tests the specimen temperature is monitored by a Cr-Al thermocouple that is welded by a spotter to lower part of the specimen, i.e., below the expected fatigue crack front.

Upon pre-loading of the specimen, a high-temperature strain gauge is put on the side part of the specimen; the gauge rods are positioned according to the markers made on this part of the specimen, such that the strain gauge center coincides with the notch center. The installed strain gauge is pressed with its elastic elements to the specimen; the furnace is closed by latch locks and heat-insulated. Then, the thermocouple contacts welded to the specimen are connected to the temperature measuring system that provides real-time recording through the test (from the start of heating till completion of the test).

To check functionality of the whole testing system (loading circuits, strain gauge records, temperature measuring system, software), we carry out a test cycling on the specimen (four to six cycles) in a sinusoidal pattern with the maximum cycle load being 80% of that recorded on the last step of the fatigue precrack growing, with a stress ratio R = 0.1 and loading frequency f = 1 Hz. In the course of cycling, the fatigue crack length in the specimen is computed in real time by software using the elastic compliance method. The computed value is compared with the arithmetic mean value over two physical measurements of the crack length (on two sides of the specimen) by the optical method. If the computed and physical values coincide the further testing of the specimen is performed.

The specimen is loaded with a force of 30.6 kgf, the testing machine is now controlled via the load channel (in order to avoid any damage of the specimen due to a linear expansion of the power train) and a stepwise heating of the furnace is started to smoothly reach the preset temperature. Once the required temperature is attained, the specimen is held for 15 min and then tested.

The loading of the specimen is carried out in a stress-controlled mode by a sinusoidal pattern with the following parameters: frequency f = 1 Hz, stress ratio R = 0.1, and maximum cycle load P max = const, which is preset for each test temperature.

During the testing the following characteristics are recorded at 0.05-mm increments of the computed crack length or every 50 cycles of loading: actual maximum cycle force on the specimen P max, displacement of marker points on the side part of the specimen, and number of cycles. Using the data obtained and the initial geometrical dimensions of the specimen and the elastic modulus of the test material, the software calculates, in real time, the maximum and minimum values of the cycle stress intensity factor K, the fatigue crack length l, the crack growth rate dl dN, and the elastic compliance coefficient. The tests are continued until K max = 161.3 kgf/mm3/2 and terminated before the specimen failure.

The fatigue crack front is analyzed by the fracture surfaces as per the requirements [2] and we define more accurately the crack parameters, namely: the initial crack length l 0, the final crack length l f , and the crack front curvature. Thereupon, we adjust, if necessary, the values of the computed crack length using a correction factor.

The computational method of determination of the fatigue crack length is based on the elastic compliance approach. Using the test results for some standard types of specimens [12], a functional relationship between the fatigue crack length and the compliance coefficient of the specimen; it represents an inverse value of the slope ratio of the load–displacement straight line.

We introduce the following notation: W is the characteristic dimension of the specimen, in this case its width, α = l/W is the relative fatigue crack length, EvB/P is the dimensionless compliance coefficient, where E is the elastic modulus, P is the cycle load, v is the crack face displacement, and B is the specimen thickness.

Then, a relation between the relative fatigue crack length and the dimensionless compliance coefficient can

be written as

$$ \upalpha =l/W={C}_0+{C}_1{u}_X+{C}_2{u}_X^2+{C}_3{u}_X^3+{C}_4{u}_X^4+{C}_5{u}_X^5, $$
(3)

where \( {u}_X=1/\left(\sqrt{EvB/P}+1\right),\ {\mathrm{C}}_k\left(k=1,\dots, 5\right) \) are the constants that are determined in [3] for a specific type of specimens.

To solve the problem of computational determination of the fatigue crack length using relation (2) a deformation diagram in the load–displacement coordinates is recorded at each loading cycle; in the general case, this diagram is a nonlinear one. Therefore, for the determination of the specimen elastic modulus, at the ith loading cycle we considered only the diagram linear portion (which is a segment between 20 and 95% along the abscissa axis, see Fig. 3) in order to exclude any possible “rounding-off” at the limiting points of the diagram. In this case, the displacement is taken to mean the magnitude of the crack face opening. Using the slope of this straight-line portion we compute the elastic modulus E and re-calculate the compliance coefficient that corresponds to the given loading cycle. Noteworthy is the fact that the slope varies with crack length, which is clearly seen from the linear segments of the deformation diagram for three successive loading cycles (Fig. 3).

Fig. 3
figure 3

Load as a function of the crack opening displacement for three successive loading cycles.

Full size image

Based on the test results for each loading cycle, the relative crack length is calculated using relation (2). According to the standard requirements [3], at least one reading of the crack length – at the beginning or upon completion of the test – shall be taken when applying the above method.

Since the values of the elastic modulus involved in relation (2) may differ slightly, there may occur a discrepancy between the computed crack length and the optically recorded one. If such a discrepancy is insignificant, the value of the elastic modulus is adjusted using a correction coefficient, until the computed and the physical crack lengths are identical.

Where necessary, the entire computational relation between the crack length and the number of loading cycles is adjusted by changing the correction coefficient. In the case of a nonlinear fatigue crack growth, which is represented by the crack branching or deviating from the straight-line direction, or if the correct determination of the final physical crack length l is impossible, the adjustment is performed by the refined (physically measured) value l 0.

In the tests at room temperature, the crack length is determined by two methods – computational and optical. In the optical method, the crack length is recorded on two opposite side of the specimen, and an arithmetic mean of the measurements is taken to be the physical crack length. In this case, the range for measuring the crack length is 400 cycles of loading.

By way of example, Fig. 4 shows the relations between crack length and the number of cycles, which were obtained by the computational and optical methods. It is evident that the computational method gives a slightly larger (by about 0.4 mm) fatigue crack length at the final growth stage in comparison with the optical method. This is due to the fact that the computational method takes into account the crack branching and considers the entire crack front, while the optical method covers only the visible portion of the crack front on the opposite surfaces of the specimen. The initial and final crack lengths measured from the fracture surface of the specimen broken after the tests coincide with the respective values found by the computational method. The stress intensity factor K is determined by the formula for a rectangular compact specimen with an edge crack under eccentric tension,

Fig. 4
figure 4

The relations between the fatigue crack growth rate and the number of loading cycles, as obtained by the optical method (▲) and computations (●).

Full size image
$$ K=\frac{P}{B\sqrt{W}}\frac{\left(2+\upalpha \right)}{{\left(1-\upalpha \right)}^{3/2}}\left(0.866+4.64\upalpha -13.32{\upalpha}^2+14.72{\upalpha}^3-5.6{\upalpha}^4\right). $$
(4)

The fatigue crack growth rate dl dN is found by the differential method of polynomials, i.e., through approximation (2q ± 1) of successive values of the crack length l i–q , …, l, …, l i+q and the number of cycles N i–q ,…, N, …, N i+q by a polynomial of 2nd degree, where q is usually 1, 2, 3, or 4 [2].

In the ith cycle of loading, for the fatigue crack length l i obtained we determine the SIF range in the cycle by the formula

$$ \varDelta K={K}_{\max }-{K}_{\min } $$
(5)

and plot the kinetic FCGR diagram in the coordinates dl/dN – ∆K as per [2].

From the points plotted on the kinetic diagram we exclude those which correspond to its first segment. The remaining ones are used for the determination of the coefficients of Paris equation (1) which, after taking the logarithm, becomes

$$ \log \left( dl/dN\right)= \log C+n \log \left(\varDelta K\right). $$

The values of the coefficients C and n in Eq. (1) are found from the sampling {(dl/dN) i ; ∆K i } by the least-squares method. The entire mathematical treatment of the results is performed by means of applications MS Excel and OriginPro in Windows 7 environment.

Test Results. To solve the problem stated above we carried out tests to determine FCGR and then derive coefficients of the Paris equation for two titanium alloys (hereinafter, grades 1 and 2) at temperatures of 20, 200, 300, and 400°C.

Six specimens were tested at each temperature. Based on the test results we plotted FCGR kinetic diagrams; Fig. 5 provides a representative example of such diagrams.

Fig. 5
figure 5

FCGR kinetic diagram for the alloy of grade 2.

Full size image

In what follows, the test results are shown in the form of adjusted values of the characteristics to be determined. This is due to the requirement of nondisclosure of information; this, however, does not limit the possibility of solving the problem at hand.

In accordance with the methodological background outlined above, a steady-state portion of the FCGR kinetic diagram is used when deriving the Paris equation.

Arithmetic mean values of the coefficients C and n for the specimens tested are given in Table 1, and the temperature dependence of these coefficients is illustrated in Fig. 6. It follows from the test results that the influence of temperature on the coefficients C and n depends on the alloy grade. Thus, at this stage of investigations, with the set of experimental data available it seems to be impossible to interpolate, with an adequate confidence, the values of the Paris equation coefficients between limiting values of the test temperature. Incorrectness of this approach to interpolation of data is confirmed by the uniaxial tension test results, in particular, by the determination of the elastic modulus E. This is also demonstrated (Fig. 7) by the temperature dependence of mean values of the elastic modulus of titanium alloy of grade 1, where no correlation between them is revealed.

Table 1 Arithmetic Mean Adjusted Values of the Paris Equation Coefficients C and n for Titanium Alloys of Grades 1 and 2
Full size table
Fig. 6
figure 6

Adjusted values of the coefficients C (a) and n (b) vs. the test temperature for the titanium alloys of grades 1 (★) and 2 (●).

Full size image
Fig. 7
figure 7

Experimental values of log C and n for the alloys of grades 1 (solid symbols) and 2 (open symbols): (★, ✰) T = 20°C, (●, ○) T = 200°C, (▲, △) T = 300°C, (◆, ◇) T = 400°C.

Full size image
Fig. 8
figure 8

Adjusted elastic modulus vs. the test temperature for the alloy of grade 1.

Full size image

Based on the test results, we plotted relations (2) – solid lines in Fig. 8. The dashed line in Fig. 8 represents the same relation for alloys ÉP741NP and ÉK151ID, which was obtained in [10].

The values of the coefficients of Eq. (2) are summarized in Table 2.

Table 2 Adjusted Values of the Coefficients of Eq. (2) for the Materials under Study and for Alloys ÉP741NP and ÉK151ID
Full size table

The data obtained support the hypothesis of validity of correlation (2) between the Paris equation coefficients for titanium alloys [11]. However, it is seen from Fig. 8 that this relationship is not a universal one for titanium alloys of the same type, which was stated in [10] on the basis of test results for nickel alloys with different technological heredity.

Conclusions

1. We have put forward a procedure for the experimental–computational determination of fatigue crack growth rate characteristics including the influence of temperature in accordance with the standard requirements.

2. The validity of the hypothesis of a linear correlation between the Paris equation coefficients has been verified.

3. A comparison between the present findings and those reported elsewhere has demonstrated that for each material there is a set of coefficients of the above correlation.

4. It has been found out that at this stage of investigations it is impossible to apply interpolation between the Paris equation coefficients and the test temperature.