Abstract
In this paper recent developments for mesolevel modeling of failure in composite laminates are reviewed. The complexity of failure processes in composite laminates presses the need for reliable computational tools that can predict strength and damage tolerance. In mesolevel modeling, where individual layers are modeled separately but individual fibers are not, different failure processes are distinguished such as delamination, fiber failure and matrix failure. This paper deals with the question how these different processes should be treated for efficient and realistic computational modeling of failure. The development that is central in this review is the use of the extended finite element method (XFEM) for matrix cracks. Much attention is also paid to algorithmic aspects of implicit analysis of complex failure mechanisms, particularly but not exclusively in relation to XFEM. Furthermore, the remaining limitations and challenges for mesolevel analysis of composite failure are discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Composite laminates are attractive engineering materials for their high strength and stiffness with low weight. They are increasingly applied in the aircraft, automotive and wind turbine industry and they have potential for use in slender structures in civil and building engineering. Different composite designs exist such as woven, braided and non-crimp fabric, but the relatively traditional laminate made of unidirectional plies remains a dominant form. Yet, limitations in the understanding and modeling of the behavior of these composite laminates slows down their rise in engineering practice.
The advantageous properties of composite laminates stem partially from the same feature as the challenges in understanding and predicting their behavior, namely from the multiscale nature of the material (see Fig. 1). The composite is made of stiff and strong fibers (e.g. glass, carbon or aramide) and a thermoset or thermoplastic resin material, the matrix. In laminates, the fibers are straight and long and have a fixed orientation within each layer or ply. The laminate is then formed by stacking a number of plies with different fiber orientations, such that a material is obtained with directional properties that suit the application. Because it are the fibers that are stiff and strong, the design is optimal when the load is carried by the fibers. The function of the matrix material is merely to keep the fibers in place and as such to eliminate the poor resistance to bending of individual fibers and fiber bundles.
Optimal use of composites is held back because reliable prediction of their damage tolerance and strength is still challenging. As a consequence, the safety of a certain composite structure under given load conditions can only be ensured with many expensive and laborious tests or with high safety factors. For example, the number of tests on components and structural parts that is required to achieve safety certification of a typical large composite airframe is of the order 10,000 [1]. If more reliable computational analysis were possible, real-life tests could partially be replaced with simulations, or virtual tests. Moreover, efficient computational tools could aid the material researcher in improving the material and give the engineer more freedom to optimize the design. Here, reliability and efficiency are two goals for the developer of numerical methods that are typically at odds with one another. It is a huge challenge to formulate computational models with which reliable results can be obtained quickly.
The main complicating aspect for laminate failure analysis is that different processes may occur during failure (see e.g. Fig. 2). Plasticity and cracking of the matrix material may occur, as well as fracture of fibers in tension or kinking of fibers in compression, possibly accompanied by debonding in the fiber-matrix interface. Matrix failure is classified as delamination when it occurs between the plies or as matrix cracking or ply splitting when the crack is oriented through the thickness of the ply. Here, the term ‘transverse matrix cracking’ is generally used for cracks oriented perpendicular to the load direction and ‘splitting’ for cracks in load direction. Reliable failure analysis of a composite structure must include a representation of each of the possible processes as well as their interaction. For most purposes, prediction of the onset of failure processes is not sufficient, because initial local failure does not necessarily lead to loss of integrity of the structure. Especially after matrix failure, the load bearing capacity of the composite is not immediately exhausted, since stress can be redistributed over the fibers. Therefore, failure analysis has to be ‘progressive’, i.e. the progression of failure through the material should be simulated.
Laminate analysis can be performed on three different scales (see Fig. 1). On the microlevel, the composite material is considered in most detail with distinction of individual fibers and the matrix material. On the mesolevel, each ply is homogenized to an orthotropic material in which the fiber direction is implicitly present in the ply properties. On the macrolevel, a single equivalent material is used, for which the laminate properties are obtained with through-thickness homogenization, e.g. with classical lamination theory [2]. Macrolevel computational analysis of failure has been done by Williams et al. [3]. However, the idea of through-thickness homogenization only stays valid in failure analysis when cracks cut the laminate through the thickness; delamination is naturally excluded from macrolevel analysis which limits the applicability of this approach. Microlevel computational analysis of failure, on the other hand, has been done by González and LLorca for both fiber failure [4] and transverse failure [5, 6]. Microlevel simulations are important for understanding the mechanical behavior of composites during failure, but limitations with respect to computational costs are soon met. Nevertheless, the need to incorporate the microlevel failure mechanisms in a multiscale framework is often stressed [1, 7–10], where the idea is to couple models from different scales, such that detailed analysis is performed locally to provide information for a global coarse-scale analysis. To meet this need, sequential multiscale models for composite materials have been proposed in recent years by different authors [11–14], involving a priori homogenization of lower scale results to generate input for higher scale simulations. The ideal, however, would be to have fully-coupled multiscale failure analysis with concurrent simulations on different scales. For this, great care is needed to formulate the right microscale model and coupling to avoid pathological behavior that is particular for failure analysis [15]. A promising framework for multiscale failure analysis has recently been developed by Nguyen et al. [16], but this has not yet been applied to composites. Moreover, because computational costs associated with multiscale analysis remain tremendous, tools for monoscale analysis will remain useful.
In this paper, the focus is on mesolevel analysis. The benefit of the mesolevel is that the relevant failure processes can all be described, but the challenge is to represent the micromechanical behavior realistically in the mesolevel idealization. This challenge will receive attention in this paper both in the discourse on recent methods and in the discussion of their limitations. Before the paper goes into detail about the computational modeling of failure in laminates, Sect. 2 contains an overview of some of the basic concepts and notations that are used from both fields on which the discussed research builds: numerical methods on the one hand and composite materials on the other. Subsequently, in Sect. 3 computational modeling of delamination is discussed. In Sect. 4 the possibility to model ply failure with a continuum approach is explored and discarded. An alternative approach is presented in the more lengthy Sect. 5 where a discrete representation of matrix cracks is central. The formulation of a discrete model for matrix cracks is discussed, as well as the way this interacts with formulations for the other failure processes. Next to assessment of different kinematic and constitutive models for the different failure processes, this paper deals with the algorithmic treatment of those models in implicit analysis. The competition and interaction between the different failure processes and the brittleness of composite laminates endanger the stability of the iterative procedure with which the solution for each time step is found. The meticulous algorithmic treatment that is necessary for implicit analysis of cases with complex failure mechanisms is exemplified in detail in Sect. 6. Numerical results obtained with the finite element framework for failure analysis described in Sects. 5 and 6, are presented and discussed in Sect. 7.
2 Preliminaries
In this section the basic concepts and notations used in the paper are briefly introduced: the nonlinear finite element method, computational failure analysis, mechanics of composite laminates and failure theories for composites.
2.1 The Nonlinear Finite Element Method
Models for progressive failure in composites are generally embedded in the framework of the finite element method [17, 18]. The main emphasis in this paper lies on methods for implicitly solving the quasi-static equilibrium equation, which means that momentum balance is solved neglecting inertia terms. Many of the material models can also be used for explicit finite element analysis, but optimality for implicit analysis is primary here.
The fundamental unknown in the considered finite element techniques is the displacement field. In each time step the displacement field that satisfies equilibrium as well as the essential boundary conditions, is approximated by solving the discretized weak form of the momentum balance or equilibrium equation, which is written as a set of equations
where the external force vector f ext represents external loading, and the internal force vector f int is a function of the displacement field.
In Eq. (1), the order of the problem has been reduced by discretizing the displacement field with a finite set of degrees of freedom and an equally sized set of shape functions. The shape functions are defined such that the degrees of freedom can be interpreted as nodal displacements. The nodes are defined in a mesh which divides the problem domain into elements. With the shape function matrix N and nodal displacement vector a, the displacement field u T={u x ,u y ,u z } is expressed element-wise as:
with


where n is the number of nodes of the element, N 1…N n are the shape functions defined over the element domain and a ij is the displacement of node i in direction j.
The strain field is defined with the strain nodal displacement matrix B as
with B(x)=LN(x) and

Stress σ is a function of strain ε,
which can be nonlinear and history dependent. This relation, the constitutive law, describes the material behavior. The simplest constitutive law is Hooke’s law:
where D e is the (constant) elasticity matrix, related to the Young’s modulus and Poisson’s ratio.
With Eqs. (5) and (7), the stress field can be computed from the (history of) the nodal displacements. The left hand side of the equilibrium equation (1) is evaluated from the stress field in a loop over the elements:
where Ω e is the element domain and M e maps the element vector to the corresponding entries in the global vector. The fact that the B matrix from Eq. (5) reappears in Eq. (9) is related to the Galerkin approximation method [17]. To keep the notation compact, the assembly of element integrals \([\sum_{\mathrm{e}}\mathbf{M}_{\mathrm{e}}\int_{\varOmega_{\mathrm{e}}}\ldots ]\) is from here on written as an integral over the global domain [∫ Ω …].
When f int(a) is nonlinear, the set of equations in (1) cannot be solved for a directly. The solution is then found iteratively with the Newton-Raphson procedure. In this iterative procedure a linearized system is solved in each iteration to approach the solution of the true system. The solution vector is updated in iteration j by solving
where K j−1 is the global tangent matrix evaluated at a j−1:
The update is repeated until the desired level of accuracy is obtained. After that, the next time step is entered.
The global tangent matrix K is evaluated in a loop over the elements. For the relations above, it takes the form of
where D, the material tangent, is a linearization of the constitutive law:
The integrals in Eqs. (9) and (12) which are both defined over the element domain are evaluated numerically in a loop over integration points.
2.2 Computational Failure Analysis
In this section, some of the key concepts in computational modeling of failure of materials are reviewed. Different methods for the modeling of cracks can be divided into two categories: the continuum approach and the discontinuous approach. In the continuum approach, the crack is smeared over a band with finite width. This is conceptually appealing, because the intact material is already modeled as a continuum, and it is convenient if the failure of the material can be represented in the same model. However, the discontinuous approach, in which the crack is modeled as a jump in the continuum, does justice to the elementary notion that a crack is not just a weaker kind of material but rather a new interior boundary. Both will be briefly discussed here, as well as the necessary material parameters for failure analysis.
2.2.1 Continuum Approach
Continuum models fit directly into the finite element framework presented in Sect. 2.1, as they are implemented in the relation between stress and strain, Eq. (7).
Plasticity
The continuum nonlinear material law with most history in finite element modeling is based on the theory of plasticity [19]. This theory has its root in metals analysis, and is built on the idea that deformation can be decomposed in an elastic part and a permanent or plastic part. The basic form of the constitutive law with plasticity is
Typically, the plastic strain ε p is unknown and computed such that the stress satisfies a certain criterion. This makes Eq. (14) an implicit set of equations which in most cases has to be solved iteratively with the so-called return mapping algorithms [20]. For modeling of failure, the stress criterion can be formulated such that the stress must vanish upon increasing plastic strain.
Damage
A more straightforward option is offered by the continuum damage theory [21]. Here, the basic idea is that the stiffness of the material decreases as a consequence of the reduction of the effective cross section when microcracks appear. The simplest formulation, assuming isotropic stiffness degradation is written as
where ω is the damage variable, which grows from 0 to 1 during failure. Generally, the stiffness degradation is computed explicitly from the strain, which grants continuum damage the advantage over plasticity of implementational simplicity and algorithmic robustness.
Practically, the main difference between plasticity and damage is in the unloading of the material. In the case of plasticity, constant ε p gives unloading with the initial stiffness, while in the case of damage, constant ω gives secant unloading (see Fig. 3).
Regularization
Continuum models for failure suffer from severe mesh-dependency. In softening, the nonlinear behavior tends to localize in a single row of elements. The amount of energy that is dissipated in the crack that is smeared over this band depends on the size of the elements, vanishing to nonsensical zero dissipation in the limit of very fine discretization.
This can be mitigated with the crack band method, in which the local stress strain behavior depends on the element size as first proposed by Bažant and Oh [22]. However, this does not solve the mesh sensitivity problem completely; element shape and orientation still influence the solution. More advanced localization limiters such as non-local [23] and gradient models [24–26], which introduce an internal length scale are to be preferred for reliable accurate representation of softening material behavior. These methods however, require a very fine mesh in the failure zone and considerable implementation effort. Another option is to introduce a rate dependent term [27], which has physical meaning for high rate problems, but can also be used artificially with quasi-static problems to resolve the mesh dependency problem.
2.2.2 Discontinuous Approach
The alternative to smearing a crack over the continuum is to insert a discontinuity in the displacement field. Although this is a more intuitive approach to failure, since displacements really are discontinuous over a crack, it requires more fundamental changes to the finite element formulation. One way or the other, the kinematical formulation has to be adapted to accommodate the discontinuity. To control the amount of energy that is dissipated in the crack as it propagates and to remove the singularity from the stress field at the crack tip, cohesive forces are applied on the crack surface, following early work by Barenblatt [28]. This means that a second constitutive law is introduced besides the constitutive law for the continuum. This ‘cohesive law’ relates the cohesive traction t to the size of the displacement jump over the crack 〚u〛:

The cohesive law can, just like the continuum models, be based on plasticity and/or damage. However, it does not require special regularization because it is acting on a surface instead of in a volume.
Interface Elements
The most straightforward discontinuous approach is to have the discontinuity between the elements. Duplicate nodes are used along the crack path to describe a jump in the displacement field (see Fig. 4). The cohesive forces can be defined on a node to node (lumped) basis [29, 30], or in a continuous interface element [31, 32]. These two are connected through the fact that the often used nodal (Newton-Cotes) integration scheme in the continuous interface element renders it essentially similar to the lumped elements. In fact, it has been shown by Schellekens and De Borst [33] that a nodal integration scheme leads to better performance for interface elements, and the same thing has been shown for lumped versus continuous interface elements by Rots [34].
The interface element consists of two surfaces which are connected to adjacent solid elements. Initially the two surfaces coincide, but they may be driven apart mechanically. The displacement jump is defined as the difference between the displacement fields of the two surfaces, which are in turn defined with standard finite element interpolation functions from Eq. (2):

with
The contribution of the interface element to the internal force vector is then defined as an integral over the interface surface Γ i :
and the contribution to the global tangent matrix likewise as
where

Partition of Unity Finite Element Method
An increasingly popular class of methods for modeling of cracks is based on enrichment of the solution basis with discontinuous functions, referred to as the Partition-of-Unity Finite Element Method (PUFEM) [35], the eXtended Finite Element Method (XFEM) [36] or the Generalized Finite Element Method (GFEM) [37]. Melenk and Babuška [35] introduced PUFEM as an easy way to include information about the problem being solved to the finite element basis. Exploiting the partition of unity property of the finite element shape functions, any function can be added to the basis in order to improve its approximability. This includes the possibility to add a discontinuous function for the modeling of cracks, which has been done first by Belytschko and Black [38] and Moës et al. [39]. In this way, a discontinuity is running through the elements (see Fig. 5), which obviously offers more flexibility for the crack path than interface elements. In the original publications, asymptotic functions are used for enrichment around the crack tip to approximate the singular stress field. Alternatively, it is possible to add cohesive tractions on the crack surface, as proposed by Wells and Sluys [40] and Moës and Belytschko [36]. In this case the crack tip singularity is removed from the stress field.
In this method, the displacement field is defined as the sum of two independent fields, one of which is multiplied with the Heaviside step function \(\mathcal{H}\):
where \(\tilde{\mathbf{a}}\) are additional degrees of freedom defined only on the nodes of those elements that contain the crack and \(\mathcal{H}\) is equal to 1 on one side of the crack and equal to 0 on the other side. The displacement jump is defined on the cracked surface Γ c as

Hansbo’s Version of XFEM
An alternative method has been proposed by Hansbo and Hansbo [41], in which two overlapping elements are introduced with independent displacement fields which are partially active. Cohesive tractions were applied in this method by Mergheim et al. [42], after which Song et al. [43] proved it to be equivalent to PUFEM with Heaviside function and coined the term ‘phantom node method’. Because of this equivalence, the term XFEM has grown to be used for crack modeling with both PUFEM and Hansbo’s method.
An advantage of Hansbo’s method over PUFEM is that it is more simple to implement, because the method does not require any changes to be made in the elements adjacent to the cracked elements. Moreover, in dynamic methods, Hansbo’s method allows for straightforward lumping of the mass matrix in contrast with PUFEM. However, there is no similar extension to enrichment with asymptotic functions to approximate the singular stress field around the crack tip. Therefore, for modeling of cohesive cracking Hansbo’s method is to be preferred, while for modeling of crack propagation in a fracture mechanics approach, PUFEM is the better alternative.
Hansbo’s version of XFEM is illustrated in Fig. 6. An element with original nodes n 1…n 4 is crossed by a crack at Γ c , dividing the element domain into two complementary sub-domains, Ω A and Ω B . Phantom nodes (labeled \(\tilde{n}_{1}\ldots\tilde{n}_{4}\)) are added on top of the existing nodes. The existing element is replaced by two new elements, referred to as element A and element B. The connectivity of the overlapping elements in the illustration is

The elements do not share nodes, and therefore have independent displacement fields. Both elements are only partially active: the active part of element A is Ω A and the active part of element B is Ω B . This is represented numerically in the definition of the displacement field: the displacement of a point with coordinates x is computed with the standard finite element shape functions N(x) and the nodal displacement values from either of the overlapping elements, depending on the location of the point:
The displacement jump over the crack is defined as the difference between the displacement fields of the two elements.

When this definition of the displacement field is combined with constitutive laws for the bulk stress and the cohesive traction, it follows from standard variational principles that the contribution to the internal force vector on the degrees of freedom corresponding with element A and B are defined as
and
Because \(\mathbf{f}^{\mathrm{int}}_{A}\) is coupled to u B (and \(\mathbf{f}^{\mathrm{int}}_{B}\) to u A ) via t(〚u〛) and Eq. (26), the linearization also involves cross terms and the total contribution to the global tangent matrix is

with


Because the law for the normal component is typically different from that for the shear component(s), transformations from the global coordinate frame to an orthonormal frame that is aligned with the crack (see Fig. 6) and back are wrapped around the evaluation of the constitutive law. The displacement jump in local {n,s,t}-frame is related to the displacement jump in global {x,y,z}-frame with

where, with t-axis parallel to the z-axis, the transformation matrix R is given as

Similarly, it holds
and (with R −1=R T)
In the remainder of this document, cohesive laws are presented in the local frame, omitting the overbars for notational simplicity and omitting the transformations for brevity.
2.2.3 Material Parameters
Whether the description of choice is a continuum model with a stress-strain relation, or a discontinuous model with a traction-separation relation, in either case a constitutive law is needed to characterize the fracture behavior of the material. In formulating the constitutive law, a choice has to be made for the fundamental parameters. Ideally, the model contains only parameters that can be obtained from simple experiments and that are objective material constants. A common choice is to use strength and fracture energy (or ‘fracture toughness’). The strength of the material is the maximum stress the material can sustain, which is the peak level of the stress in Fig. 3, while the fracture energy is the amount of energy that is required to form a unit area of new crack surface, which is related to the area under the curves in Fig. 3. In a traction-separation law, the fracture energy is equal to the area under the curve, but in a stress-strain relation, the area under the curve is of the dimension energy per volume and has to be multiplied with the width of the failure zone in order to obtain the fracture energy.
In fracture mechanics, distinction is made between mode I (opening), mode II (sliding) and mode III (tearing), each of which is associated with a distinct value for the fracture energy [44]. In computational practice, it can be hard to distinguish between mode II and mode III and therefore often only two modes are considered for the fracture energy: opening (mode I) and shearing (mode II/III). For strength, there can also be different values related to different loading directions. When uniaxial strength and pure mode fracture energy are determined, more assumptions and/or parameters are needed to interpolate for general stress state. In general stress space, strength becomes an envelope around the admissible stress states. And for general mixed mode fracture, the fracture energy becomes a function of the mode ratio.
In an idealized homogeneous material, strength and fracture energy can be related to fundamental bond forces on the nanolevel. In a heterogeneous material, however, the strength is dominated by irregularities in the microstructure. The failure load measured in a simple experiment is governed by stress concentrations due to stiffness inhomogeneity and/or triggered by spatial variation of the strength due to the presence of weak spots. Therefore size effects may play a role [45, 46]. Similarly, the fracture energy in a heterogeneous material is supposed to lump everything that is happening in the fracture process zone. The validity of the assumption that strength and fracture energy are fundamental material parameters for composites will be discussed at several points in this paper.
2.3 Mechanics of Composite Materials
2.3.1 Elasticity
The starting point for the constitutive modeling of composite laminates is a law for the elastic behavior of the elementary ply. Considering the fact that the ply is stiff in fiber direction and compliant in other directions, the transversely isotropic version of Hooke’s law is used, which is defined as
with

where E 1 and E 2 are the Young’s moduli of the ply in fiber direction and transverse direction respectively, ν 21 and ν 23 are the longitudinal and transverse Poisson’s ratios, and G 12 is the longitudinal shear modulus. Under the assumption of transverse isotropy, the transverse shear modulus G 23 is a dependent quantity, defined as:
The overbars in Eq. (36) are used to indicate that the measures are expressed in the local material frame. In this frame, the 1-axis is aligned with the fiber direction in the ply, as illustrated in Fig. 7. In computational analysis transformations are required to relate stress and strain quantities in the global coordinate frame (e.g. σ={σ x ,σ y ,σ z ,τ yz ,τ zx ,τ xy }) to those in the local coordinate frame (e.g. \(\bar{\boldsymbol{\sigma}}= \{\sigma_{1},\sigma_{2},\sigma_{3},\tau_{23},\tau_{31},\tau_{12} \}\)) [47]. Here too, overbars and transformations are omitted in the remainder for brevity.
2.3.2 Residual Stress
An important aspect of laminate analysis is the residual stress due to fabrication. The difference in thermal properties of fiber and matrix causes the thermal expansion behavior of the ply to be orthotropic. When the laminate is cooled during fabrication, the plies tend to shrink in transverse direction, but, since the plies are connected, this contraction is constrained. The transverse tensile stress that is caused by the mismatch in thermal properties can be significant with respect to the transverse tensile strength of the ply. Therefore it is important to take these residual stresses into account. The linear elastic constitutive law after a temperature change is
where the total strain is decomposed into a mechanical part and a thermal part:
with
where ΔT is the magnitude of the change in temperature and α 1 and α 2 are the coefficients of thermal expansion in fiber direction and transverse direction, respectively.
2.4 Failure Theories for Composite Materials
The ply is the elementary building block for the mesolevel approach to laminates. Therefore, mesolevel failure analysis requires criteria for predicting failure of the ply. The concept of strength is not as clearly defined for a homogenized composite as it is for a homogeneous material. Therefore, the composite nature of the ply complicates the formulation of a stress based criterion for onset of failure. Unidirectional strength properties are measured for the characterization of the material in its principal directions, but in failure analysis, these have to be interpolated in order to get a general failure criterion (or set of criteria) to be able to evaluate any three dimensional stress state for failure. Early work in the development of an orthotropic failure envelope was done by Hill [19], Tsai [48] and Hoffman [49], who formulated criteria that consist of a single relation for the interaction of the different stress components in the material frame. For composite materials, the most popular version of these interactive criteria is the one formulated by Tsai and Wu [50]. The transversely isotropic version of the Tsai-Wu criterion can be written as:
with

where F 1t and F 1c are the tensile and compressive strength in longitudinal direction, F 2t and F 2c the tensile and compressive strength in transverse direction and F 23 and F 12 the transverse and longitudinal shear strength.
However, a single interactive criterion does not sufficiently reflect the level of complexity that is inherent to composite materials. A smooth failure envelope does not match the fact that, due to the inhomogeneity of the material, discrete switches from one type of failure to another are involved when the load direction is gradually changed. Therefore, failure-mode-based theories have been proposed, with a number of independent criteria corresponding to an equal number of failure modes. The first failure theories that distinguished between fiber failure and matrix failure were developed by Hashin [7, 51]:
-
Fiber tension:
$$ \frac{\sigma_1}{F_{1\mathrm{t}}}=1 $$(44) -
Fiber compression:
$$ -\frac{\sigma_1}{F_{1\mathrm{c}}}=1 $$(45) -
Matrix tension:
$$ \sqrt{ \frac{ (\sigma_2+\sigma_3 )^2}{F_{2\mathrm {t}}^2} + \frac{\tau_{23}^2-\sigma_2\sigma_3}{F_{23}^2} + \frac{\tau_{31}^2+\tau_{12}^2}{F_{12}^2} }=1 $$(46) -
Matrix compression:
The World Wide Failure Exercise organized by Hinton et al. (see [52, 53] and references therein) has been an attempt to decide which failure theory is most appropriate. Although clear difference in predictions of different models were reported, there was no uniform conclusion in favor of a single approach. A trade-off between accuracy of the criterion and the number of material parameters or assumptions involved will remain present, considering the fact that “a criterion is only as good as the data available” [54]. Another problem with the failure criterion approach is that it is based on homogeneous stress, while, as soon as failure has started somewhere in the specimen, stress is not homogeneous anymore. Size effects do play a role, which blurs the meaning of the concept of strength.
Furthermore, there is a statistical size effect that is of importance for the phenomenon of fiber failure. The unidirectional ply strength in fiber direction is best described with a weakest link theory and a statistical distribution of the strength [46]. Numerous models have been developed to predict the ply strength in fiber direction as a function of the specimen size (see e.g. [55–57]). However, such models are not readily available for progressive failure analysis because they tend not to predict the location of failure, which is necessary information to continue the analysis beyond the first failure event. A Weibull criterion can be used to predict brittle fiber failure (Hallett et al. [58]), but when it is applied to cases with progressive fiber failure, as has been done by Li et al. [59], it is necessary to assume that failure occurs at the location where stress is the highest, which contradicts the Weibull assumption that failure may occur anywhere.
Another complicating factor is that ply failure can be influenced by the presence of neighboring plies when the ply is embedded in a laminate. The neighboring plies have a constraining effect on the failure which makes it uncertain to what extent the failure can be characterized accurately with properties measured for the isolated ply. A well-known example of this is the increase in transverse strength upon decreasing ply thickness, a phenomenon first reported by Parvizi et al. [60] and comprehensively reviewed by Nairn [61]. Theories exist to predict the in situ strength see e.g. Camanho et al. [62]. An open issue here is that the use of in situ strength parameters is more obvious for ply discount methods [63] than for progressive failure analysis where onset of failure is followed by softening or decohesion. In the latter case, the fracture energy is already present in the post-peak response, and onset of failure is not the same as appearance of (visible) cracks. However, when crack growth is brittle, i.e. cracks grow in a snapback, the post peak response becomes more of a numerical artifact needed for well-posedness and robustness. In that case, the use of in situ strengths is also appropriate with softening or decohesion.
In reaction to the World Wide Failure Exercise, Dávila et al. [64] developed another set of failure criteria. These criteria, referred to as LaRC03, were designed for plane stress. In a later publication by Pinho et al. [65], the set of criteria were completed for full three-dimensional stress states, referred to as LaRC04. They are considerably more elaborate than the criteria by Hashin, but the LaRC criteria do not require additional material parameters. They differ from Hashin’s on the following points. Firstly, for all matrix failure mechanisms, in situ strength values are used. Secondly, for matrix compression, they are based on Mohr-Coulomb friction following Puck and Schürmann [66]. Thirdly, for fiber compression, an initial misalignment of the fibers is assumed, and three different failure scenarios related to different stress states around the misaligned fibers result in three different criteria: one for kink-band formation, one for matrix failure under biaxial compression and one for matrix tensile failure.
As an alternative to explicit failure criteria, a micromechanical approach can be adopted to obtain a failure envelope. González et al. [5, 6] performed micromechanical simulations on a representative volume element to get the ply strength for different loading conditions. The idea is that this requires less assumptions and material parameters: only the simpler constituents need to be characterized, while the behavior of the composite is virtually determined.
However, even when an accurate general failure criterion for the elementary ply can be formulated or virtually obtained, a ply failure criterion is not sufficient for the prediction of laminate failure. One could use it to assess laminate failure in a First Ply Failure approach [67], equating failure of a single ply to failure of the laminate, but in general, local failure of a ply does not necessarily lead to global laminate failure. Redistribution of stress may be possible such that the structure can be loaded beyond the load level at which first local failure occurs. In that case, in order to predict the load bearing capacity of a structure or structural part under specific load conditions, progressive failure analysis is required. That is, the failure criteria must be extended with a theory on what happens after failure. Furthermore, the failure process of delamination has to be included to do complete laminate analysis.
3 Delamination Modeling
The two most popular computational methods for the analysis of delamination are the Virtual Crack Closure Technique (VCCT) [68, 69] and interface elements with a cohesive law [32, 70]. Disadvantages of the former are that it cannot deal with initiation and that the crack front has to coincide with element boundaries in a regular mesh. For these reasons, cohesive elements are gaining popularity, particularly for progressive failure analysis with non-self-similar crack growth and interaction with other failure processes.
In mesolevel modeling of laminates, each ply is modeled independently, which means that the boundaries between the plies always coincide with an element boundary. Interface elements can therefore be inserted easily by doubling the nodes on the existing element boundary. Moreover, they offer an efficient method to get realistic values for the interfacial tractions. Alternatively, a fine discretization through the thickness would be needed to model delamination in a continuum sense [71] or with XFEM [72, 73], because the through thickness variations in the stress field must then be computed accurately for correct initiation and propagation of cracks. Therefore, interface elements are the method of choice for mesolevel delamination modeling.
3.1 Cohesive Law
Modeling of delamination with interface elements was first done by Schellekens and De Borst [32] and Allix and Ladevèze [70]. Schellekens and De Borst developed a plasticity formulation which was further pursued by Hashagen and De Borst [74]. However, robustness and ease of implementation renders damage formulations favorable.
Delamination fracture tends to be a mixed-mode phenomenon, because the direction of crack propagation is given by the topology of the interface, while the orientation of the loading is variable. A simple bilinear softening law for mixed-mode failure with constant fracture toughness was proposed by Mi et al. [75]. However, it is important to take into account that the fracture toughness, which is a key parameter in the cohesive law, is not a material constant [76–78]. Camanho et al. [79] developed a cohesive law in which the fracture toughness is a phenomenological function of mode mixity as formulated by Benzeggagh and Kenane [80]. This cohesive law was improved for thermodynamical consistency by Turon et al. [81]. Alternative formulations have been proposed among others by Allix and Corigliano [82], Yang and Cox [83], Högberg [84] and Jiang et al. [85]. Below, the cohesive law as formulated by Turon [81] is outlined.
Starting point is the phenomenological relation between fracture energy and mode ratio by Benzeggagh and Kenane [80]:
where G c is the fracture energy as a function of the mode ratio G II /G with material parameters G Ic , G IIc and η. In case of three-dimensional analysis, mode II and mode III are taken together (in fact, it is hard to distinguish between the two in interface elements, since there is no well-defined crack front and consequently no well-defined tangent vector to the crack front). Then there is a decomposition of displacement and traction vectors into a normal part (mode I) and a shear part (mode II/III). When the normal to the interface plane is aligned with the global z-axis, decomposition between normal and shear displacement jump is straightforward:


Before the evaluation of the cohesive law, the values of the displacement jump for onset and propagation of pure mode opening are calculated from the material parameters:


where K is the initial dummy stiffness, F n and F sh are the normal and shear strength of the interface and G Ic and G IIc are the mode I and mode II fracture toughness.
Then the current displacement jump is used to compute an equivalent opening displacement:

and the mode ratio B:

Normal relative displacements only contribute when positive, hence the use of the Macauley operator, which is defined as 〈x〉=max(x,0). It can be shown that B is related to the mode ratio in Eq. (48) as B=G II /G, when it is assumed that B is constant inside the cohesive zone.
Subsequently, the onset criterion and propagation criterion related to the current mode ratio (see Fig. 8) are computed with:


The damage variable ω d is defined such that the traction-separation law is bilinear for any fixed mode ratio:

Finally, the traction t is computed with isotropic damage as

where δ ij is the Kronecker delta and the part between square brackets is included to cancel the damage for the normal traction component when the normal displacement jump is negative. That way, interpenetration of opposite crack faces is prevented through a penalty approach with K as penalty parameter.
The consistent tangent is defined as [86]:

with


3.2 Open Issues
In later work, Turon et al. [87] have shown that the energy dissipation does not follow the assumed Benzeggagh-Kenane relation under all circumstances. This is due to the fact that in mixed-mode cracking the mode ratio varies over the length of the cohesive zone, see Fig. 9, which is in contrast with model assumption of a constant mode ratio as visualized in Fig. 8. Turon et al. [87] have shown that proper behavior is obtained when the strength parameters are in accordance with the following relation:
Alternatively, it is possible to adopt an orthotropic relation for the penalty stiffness, such that
The latter choice is somewhat more laborious because the orthotropic stiffness relation must be accommodated in the implementation, but theoretically more appealing because the penalty stiffness is already a numerical artifact, as opposed to the strength parameters which have physical meaning. Nevertheless, applying Eq. (62) can also be defended arguing that the shear strength is not unambiguously defined and that the exact magnitude of strength parameters has only limited influence on the results in many delamination cases (provided that the ratio is such that Eq. (62) is satisfied).
Evolution of traction and displacement jump components in a single integration point for mixed-mode bending test with G II /G=0.5 (see van der Meer and Sluys [88] for details)
Notwithstanding this improvement by Turon et al., Goutianos and Sørensen [89] have shown that a theoretical path-dependency exists for all truss-like cohesive laws that have a mode-dependent fracture toughness. With truss-like they mean that the ratio in traction components is fixed to the ratio in opening displacements, as it is in Eq. (58). Gutianos and Sørensen have shown that the dissipation for such cohesive laws depends on the complete opening history rather than on the mode ratio only. Although there might be something physical to this path-dependency, it should be regarded a flaw as long as the basic assumption that the fracture toughness only depends on mode ratios (see Eq. (48)) has not been revised explicitly. Notably, the cohesive law by Yang and Cox [83] does not suffer from this path-dependency, because it works with fixed pure mode behavior and a mixed-mode cut-off criterion rather than with isotropic damage.
Next to this issue with a discrepancy between theory and results of cohesive laws, there are some physical phenomena that are not included the theory behind the laws. Like most cohesive laws, the one outlined in Sect. 3.1 makes use of a penalty approach to prevent interpenetration and allow for compressive forces to be transmitted through the interface. What is not taken into account, however, is the possibility of a significant increase in strength and mode II fracture energy in the presence of compressive stress. This issue has been addressed by Li et al. [90] but is still ignored in most formulations.
Even in the absence of compressive stress, the fracture toughness is not always constant for a given mode ratio. Wisnom has observed a size effect in the fracture toughness [91] and several authors have reported a dependence on the relative fiber orientations of the neighboring plies [92–94]. Davidson et al. [95] have given further evidence that different cases with the same mode ratios do not necessarily display the same fracture toughness. Part of this can be attributed to the fact that delamination is not necessarily the only dissipative process in a characterization test with which the fracture toughness is measured. In reality, there may be interaction between delamination and transverse damage. A formulation in which constitutive coupling between matrix cracking and delamination exists is the mesomodel by Ladevèze et al. [96]. How much constitutive coupling is realistic has not been characterized properly and is indeed very hard to quantify. This should be distinguished from mechanical coupling, for instance when delamination is triggered by the presence of matrix cracks. Such mechanical interaction between different failure processes can be captured well and will be given attention in the Sect. 5.3.
3.3 Element Size Requirement
One drawback of cohesive methods is that the cohesive zone has a given length and that robust and accurate simulations require the elements to be several times smaller than this cohesive zone. In (quasi-)infinite continua, the length of the cohesive zone is related to the fracture energy, stiffness and strength, but for delamination cracks in thin laminates, the thickness is an additional influence [83, 97, 98]. The length of the cohesive zone may vary for different loading conditions, generally the cohesive zone is longer for mode II than for mode I, but the length of the cohesive zone in typical laminates is of the order of 1 mm. Since elements must be several times smaller than the cohesive zone length, typical element sizes of around 0.2–0.3 mm are commonly required for robustness and accuracy. This element size requirement seriously limits the specimen dimensions that can be simulated within reasonable computation time.
An engineering solution to this limitation has been proposed by Turon et al. [99], viz. to increase the length of the cohesive zone in the simulation artificially by reducing the interface strength. This method can push the limits of model dimensions that can be analyzed within acceptable computation times considerably but it should be handled with care because the solution may be influenced [97, 100]. Limited alleviation of the mesh-requirements can furthermore be achieved by adapting the integration scheme as proposed by Yang et al. [101].
Another direction to improve the performance of large interface elements is to locally enrich the displacement field. Improvement was already reported by Crisfield and Alfano [102] with a relatively simple hierarchical enrichment. Guiamatsia et al. [103] enriched the displacement field with the analytical solution of a beam on elastic foundation. This was based on the assumption that it is underrepresentation of the variation of the stress ahead of the crack tip which needs to be addressed. However, the real challenge is to enrich the kinematics such that deformation of an element containing the crack tip can be represented accurately, resulting in a smooth response for a smooth progression of the crack tip through the element. Such an enrichment scheme has been proposed by Samimi et al. [104], who added a hat-enrichment where the location of the peak of the enrichment is an additional degree of freedom. However, this strategy has only been shown to work in 2D with line interfaces; generalization to cases with plane interfaces is not obvious, although a step in that direction has been made by Samimi et al. [105].
The most significant gain in element size has been reported by van der Meer et al. [106] in an approach where the cohesive zone is eliminated altogether. The front is described mesh-independently with the level set method and crack growth is handled with fracture mechanics. However, this method has not yet reached such level of maturity that it can be combined with descriptions for other failure processes in laminates. Currently, the element size requirement related to cohesive methods with interface elements remains problematic for progressive failure analysis of laminates.
4 Continuum Methods for Ply Failure and Their Limitation
Next to a model for interply delamination, a model for intraply failure is needed to do progressive failure analysis of laminates. In Sect. 2.4, failure criteria for the ply have been introduced. A complicating aspect is that different failure processes may occur in the ply. For each of the failure processes, there must be a representation of what happens after the strength related with this particular failure mechanism has been reached at local level. The most simple approach to progressive failure analysis is the ply discount method, where the stiffness of a ply is suddenly reduced after the failure criterion is violated. This has been applied to matrix failure by Laš and Zemčik [107] and Liu et al. [108]. These models, however, give mesh-dependent results: the amount of energy that is dissipated when a crack is formed vanishes upon mesh refinement.
In order to obtain a unique response, models with a continuous constitutive relation must be used. For orthotropic materials, several examples are available for extension of a failure criterion with a plasticity law [109–112]. But in the context of composite materials, continuum damage formulations are more popular, because these are more easily coupled to the failure-mode-based criteria, with different stiffness degradation laws for the different failure processes. After pioneering work by Ladevèze and Le Dantec [113] and Matzenmiller et al. [114], several different formulations have been proposed in which distinction is made between fiber failure and matrix failure [115–122].
The basic relation for continuum damage models for the unidirectional ply is as follows:
with

where ω f and ω m2…ω m6 are the damage variables related to fiber failure and matrix failure, respectively. The evolution of the damaged variables is strain-driven and related to failure criteria, with coupling between the different matrix damage variables.
Although this works well in some cases, there is a pathology in the continuum approach to the modeling of composites, which can be understood from simple micromechanical considerations. When looking at the micromechanical failure process, the orientation of a band with matrix failure influences the softening behavior of the composite material. A band with shear failure that is oriented in fiber direction can develop into a macrocrack running between the fibers, which is a relatively brittle mechanism, while a band with matrix shear failure in any other direction is crossed by fibers, and the corresponding failure mechanism is therefore more ductile (see Fig. 10). In continuum models, however, this distinction cannot be made. In the homogenized continuum, both mechanisms are represented with a softening shear band with the same local stress-strain relation.
This pathology of continuum models with respect to matrix crack simulation is illustrated with the example of a uniaxial tensile test on a 10∘ unidirectional laminate. This is a standard test for the determination of the in-plane shear strength [123, 124]. The test is performed on a specimen with the shape of a parallelogram, where the oblique ends are used to remove stress concentrations from the boundaries. Experiments show brittle matrix failure; in a sudden event, the specimen breaks, with the crack running in fiber direction. The case has been simulated by van der Meer and Sluys [125] with a continuum damage model of the type of Eq. (65) as well as with a softening plasticity model for orthotropic materials, both regularized with a rate-dependent term. With both models, the same erroneous response was obtained.
The results obtained with the continuum damage model are shown in Fig. 11: the load-displacement diagram for two different meshes and the final deformation. The influence of the element size on the load-displacement behavior is negligible, which is related to the fact that the band with localized strain is wider than the elements, due to the viscosity term. The deformed mesh, which is taken from the coarse mesh analyses, clearly shows a failure pattern that is different from that observed in experiments; the failure band is not aligned with the fibers.
Off-axis tensile test: geometry and experimentally observed crack path (top) and load-displacement relation and final deformed mesh with regularized continuum damage model (bottom) [125]
Notably, there is a significant displacement perpendicular to the load direction. The deformation in the localization area is such that the strain in fiber direction ε 1 remains relatively small. In the damage model, this is a consequence of the distinction that is made between fiber failure and matrix failure. Because of this, the model gives locally correct behavior, where a stress state for which the transverse strength is exceeded never gives rise to large strains in fiber direction. However, although the local behavior is correct, the global behavior is not. The fact that ε 1 remains small, is not sufficient to ensure that matrix failure develops in fiber direction. The cause for this behavior lies in the fact that the direction of failure propagation in the model is governed by the stress concentration rather than by the fiber direction. This is a consequence of the homogenization which is fundamental to continuum models. In a homogenized model the smeared crack will always propagate there where the stress is highest, whereas in the real material the very fact that the material is inhomogeneous causes the crack to grow differently, as shown in Fig. 12.
With this example, the consequences of the limitation of the continuum approach are clearly visible. The micromechanical cause for cracks to grow in fiber direction, is not present in continuum models, at least not as long as the model is a local model. This can be considered a special case of violation of the principle of separation of scales. In Sect. 1, the microscale has been introduced as the level where individual fibers and the matrix material are distinctively present, while on the mesoscale, the material is homogenized. As such, an individual matrix crack is a typical microscale phenomenon. When it is brought to the mesoscale through homogenization it is no longer individually represented. In reality, however, an individual matrix crack may grow very large, and play a role on a higher scale. After homogenization in the micro-meso transition, this information is lost.
It is unlikely that failure mechanisms, in which large cracks in fiber direction play a role in different plies with different fiber orientations, can be predicted using state-of-the-art continuum models for ply failure, irrespective of the failure criteria and damage evolution laws that are applied. However, for other failure mechanisms, the continuum description serves well, e.g. when failure in all plies is localized in a single plane [121, 126, 127]. In some cases the matrix crack will emerge correctly, such as the split near a circular hole as reported by Cox and Yang [1]. In other cases, a good match in peak load values may even be found, such as reported by Abisset et al. [128] with very good predicted failure load levels in a series of complex test cases. But, as far as localized matrix failure in a single ply is concerned, the predictive quality of continuum models should be doubted. Unphysical failure mechanisms are introduced in the system and these may lead to erroneous results.
5 A Strategy Around Discrete Modeling of Matrix Cracks
On the mesolevel, where matrix and fibers are not modeled separately, it is necessary to enforce the orientation of the matrix cracks in order to describe the mechanisms realistically, as argued in the previous section. This calls for a discrete representation of individual cracks with a discontinuous approach. This can be achieved by inserting interface elements through the thickness of the ply at a priori selected locations. This strategy, first employed by Wisnom and Chang [129], gives good interaction with interface elements for delamination. Similar work has been done by De Moura and Gonçalves [130] and Yang and Cox [83]. Wisnom, Hallett and coworkers have further applied this on different notched and unnotched geometries with considerable success [58, 59, 85, 131, 132]. However, this strategy requires additional meshing effort and is less predictive because the possible crack locations have to be predefined. Therefore a mesh-independent representation of discontinuities with XFEM (see Sect. 2.2) is to be preferred for the simulation of matrix cracking. Techniques for mesh-independent representation of discontinuities have been applied in the context of matrix cracking by Iarve et al. [133–136], Yang et al. [137–139] and van der Meer et al. [86, 88, 140, 141].
Iarve et al. make use of PUFEM with smooth enrichment function instead of the standard Heaviside enrichment. The model was first applied to matrix cracking by in unidirectional composites by Iarve [133] and then to laminates by Mollenhauer et al. [134]. In these references, the matrix cracks were still inserted a-priori without progressive damage modeling, but it was already shown that this representation of matrix cracks allows for accurate stress fields in damaged composites by comparing numerical results with images obtained with moiré interferometry. Progressive cracking and the interaction with delamination was added in a later publication [135], where cohesive cracks were inserted over the width of the specimen after the strength was violated in one point. Unnotched specimens with different layups were analyzed and results were compared with experimental observations from Crossman and Wang [142] and Johson and Chang [143]. A statistical strength distribution was used to obtain a random crack pattern and the number of cracks was limited to a maximum number per ply. A continuum damage model for fiber failure has been added by Mollenhauer et al. [136], based on the formulation of Maimí et al. [117, 118]. Results are compared overheight compact tension test results from Li et al. [144].
The formulation by Yang et al. is based on Hansbo’s version of XFEM, which they refer to as A-FEM. It was first introduced by Ling et al. [137] and applied to matrix cracking in laminates by Zhou et al. [138] and Fang et al. [139]. Zhou et al. [138] used the model to investigate the interaction and competition between matrix cracking and delamination and their sensitivity to the ratios between different material parameters. Fiber failure has been added by Fang et al. [139] as a sudden stiffness reduction after violation of a maximum strain criterion. Results obtained with the model are compared with experiments on double edge notched tension specimens by Hallett et al. [145] and again a good correlation in terms of damage progression and global response has been demonstrated [139].
The formulation by van der Meer et al. is also based on Hansbo’s method and introduced in Ref. [88]. Numerical aspects of the interaction between XFEM for matrix cracks and interface elements for delamination were investigated by van der Meer and Sluys [86] and a continuum damage model was added for fiber failure in a later publication [140]. There, results were validated against experiments by Spearing and Beaumont [146]. Further validation on experiments by Green et al. [147] and Li et al. [144] was presented in Ref. [141]. In the remainder of this paper, the main choices and findings by van der Meer et al. are discussed in more detail, providing an overview of the main issues for building a model around an XFEM representation of matrix cracks (in this section), as well as a detailed look under the hood of the algorithmic framework used (in Sect. 6) and a demonstration of the possibilities of the approach (in Sect. 7).
5.1 Fundamental Choices
With XFEM, initiation and growth of cracks can be simulated at arbitrary locations in the mesh. For this, generally two criteria are needed, the first is to judge whether the crack will grow and the second to determine in which direction the crack will grow. From this point of view, application of these methods to the simulation of matrix cracking in laminates is a simplification, because the second criterion becomes trivial: the direction of crack growth is always equal to the fiber direction. A matrix crack grows by definition between the fibers, and this can be numerically enforced by fixing the direction of crack growth (ϕ in Fig. 6 is set equal to θ in Fig. 7). As long as one layer of elements is used through the thickness of the ply, it is naturally assumed that matrix cracks always extend through the ply thickness. Because of this, complications in describing three dimensional crack paths (see e.g. [148]) are avoided. It is furthermore assumed that the matrix crack orientation is always perpendicular to the plane of the laminate. Therefore the crack topology can be described completely in the 2D midplane of the ply, even when 3D solid elements are used. The downside of this assumption is that the wedge effect that may occur in compressive laminate failure due to inclined matrix cracks [66] is not included. To date, XFEM for matrix cracking has only been applied to tensile load cases, where the assumption that cracks are perpendicular to the midplane is realistic.
For the simulation of propagating matrix cracks, the cohesive approach is chosen over the brittle version with crack tip enhancement. In the first place because the cohesive tractions and hence a fine mesh are needed anyway for delamination. And secondly because it is not clear what the singular functions should look like for a crack tip in an orthotropic medium that is constrained by neighboring plies. With this choice, Hansbo’s version of XFEM is from implementational point of view the most favorable choice.
For crack initiation and the insertion of new crack segments a stress-based criterion is used. The particular choice for the criterion in the work presented here is not related to a particular failure theory, but rather to the Benzeggagh-Kenane-criterion (Eq. (48)) used in the cohesive law (see Sect. 5.2). The stress is rotated to the material frame and then evaluated with the following expression, taking into account the fact that the local 2-axis is normal to the crack plane:
with


This criterion is evaluated in all elements in which cracking is allowed, taking into account the minimum crack spacing as described in Sect. 5.4. When the criterion is violated, the element is split in two and a cohesive segment is inserted between the two (see Fig. 6).
5.2 Cohesive Law
In contrast with interface elements, XFEM requires an initially rigid cohesive law, because the cohesive segments are introduced at nonzero stress level. In most texts on propagating cohesive cracks in XFEM or related formulations, decohesion is mode I driven, either by leaving out shear tractions altogether [36, 43, 149], or by assuming constant shear stiffness [42], or by assuming decreasing shear stiffness where the decrease is driven by normal crack opening only [40, 150]. This simplification is compatible with a crack propagation procedure that is based on the direction of maximum principal stress, because then mode I is the dominant cracking mode. In the present case of matrix cracking, however, the crack propagation direction is independent of the stress field, and a complete mixed-mode formulation is needed. Such formulations have not been developed in the initial explorations of XFEM.
It is possible to define an initially-rigid mixed-mode damage law that computes the traction vector from the displacement jump (see e.g. Oliver [151] and Mergheim and Steinmann [152]). However, the traction is then not uniquely defined for zero crack opening (see Fig. 13; all iso-lines for the traction go through 〚u〛=0). In a uniaxial case it is obvious that the traction should be equal to the strength. But in a mixed mode formulation the strength is a surface in the traction space and the initial traction can be any point on that surface, each with a zero opening. The traction evaluation itself remains feasible, because the crack opening after a finite load increment will not be exactly equal to zero. However, the highly nonlinear nature of the traction-separation law around the origin endangers the stability of the analysis. Very small variations in nodal displacements give rise to large changes in nodal forces and also, more critically, to large changes in the tangent matrix, which leads to ill-convergence.
However, more knowledge on the initial traction is available. Namely, that the cohesive traction acting on the crack surface must be in equilibrium with the stress in the bulk material next to the crack:
where σ is the stress tensor and n the normal vector of the crack surface. Notably, since the crack is parallel to the fiber, the vector σ n contains the material stress components σ 2, τ 12 and τ 23. The value of σ n upon crack initiation is known and can be used for the evaluation of the initial traction with two different concepts. The first has been introduced by Moonen et al. [153] and includes the term σ n from the neighboring bulk material directly in the cohesive law. The second concept, by Hille et al. [154], is to use a law with a finite initial stiffness and then shift the origin of the law such that the traction at zero opening matches the stress at the moment the crack segment is introduced.
Van der Meer et al. have developed two cohesive formulations for composites that each make use of one of these concepts and that both start from the phenomenological mixed mode law by Benzeggagh and Kenane [80]. The version based on Moonen’s idea can be found in [88], and the version based on Hille’s idea in [141]. Both implementations have been validated in simple mixed mode cases, but the second was found to be more robust in complex cases. The formulation of this cohesive law is obtained as follows. Let Turon’s damage law from Sect. 3.1 be written as an operator \(\mathcal{T}\) which relates the evolution of the traction t to the evolution of displacement jump 〚u〛:

where t is used to indicate the history-dependence. The shifted version uses exactly the same operator, but works on a translated argument:

with

where the translation 〚u〛0 is computed from the bulk stress at the location of the cohesive integration point at the instant before the crack segment is introduced:

Here, K is the initial elastic stiffness in the cohesive law and  is the traction on the crack surface computed from the bulk stress at the moment of introduction of the crack segment. This leads to the desired initially rigid behavior, as illustrated in Fig. 14. Moreover, the traction-separation relation is not singular as long as K is finite, and, initially, for the undamaged cohesive integration point with zero crack opening, the traction is in equilibrium with the stress in the adjacent bulk material.
is the traction on the crack surface computed from the bulk stress at the moment of introduction of the crack segment. This leads to the desired initially rigid behavior, as illustrated in Fig. 14. Moreover, the traction-separation relation is not singular as long as K is finite, and, initially, for the undamaged cohesive integration point with zero crack opening, the traction is in equilibrium with the stress in the adjacent bulk material.
5.3 Interaction with Delamination
This section deals with the numerical representation of the interaction between matrix cracks and delamination when the former is modeled with the Hansbo’s method and the latter with interface elements. The investigations are performed in a two-dimensional framework where each ply is modeled with a single layer of plane stress elements, but the same holds for a three-dimensional framework with one layer of solid elements per ply.
When a discontinuity appears in the displacement field of one of the planes that are connected with interface elements, this obviously affects the relative displacement field between the planes. Using XFEM for the ply theoretically requires that the interface elements connecting the plies are adapted accordingly, as shown in Fig. 15. Each of the plane displacement fields Na bottom and Na top in the definition of the interface displacement jump in Eq. (17) may become discontinuous as in Eq. (25). This should be taken into account in the evaluation of the interface displacement jump. Practically, this would entail that upon introduction of phantom nodes, the connectivity and integration scheme of the interface elements is adapted accordingly, including transfer of history variables. Moreover, the possibility that both connected planes in a single interface element are cracked has to be accounted for.
However, with Hansbo’s method, more than with traditional PUFEM, the nodal displacements related to the original nodes of a cracked element remain meaningful, due to the fact that those are always in the active part of the overlapping elements (see Fig. 6). When the interface elements are not adapted upon cracking of the plies, the inconsistency in the displacement field is limited to the interior of the element. Since high accuracy in the displacement field at sub-element level is generally not pursued in finite element analysis, the consequences of using such a nonconforming displacement field may very well be acceptable. Moreover, the significance of an error at sub element level will vanish upon mesh refinement. At the nodes, the unadapted displacement field is equal to the discontinuous field. The relative displacement between each pair of original nodes remains the real relative displacement of the corresponding pair of material points. Therefore, if a nodal integration scheme is used for the interface element, the displacement jump of the unadapted interface element evaluated at the integration points is exact. Then, not-updating the interface element means not much more than under-integration of the displacement jump field.
A schematic representation of the mechanical process in which matrix cracking and delamination interact is given in the top row of Fig. 16. The material in two plies with in-plane dimensions corresponding with a single quadrilateral finite element is considered. First, a matrix crack appears in the transverse ply. Next, significant crack opening demands that minor delamination takes place. Finally, the delamination front propagates beyond the boundaries of the element domain. The numerical representation of the interaction with an unadapted interface element and nodal integration is shown in the bottom row of Fig. 16. Integration points in the interface element are indicated as springs. With this simplified description, limited crack opening may occur without any delamination. But major delamination will still result in interface damage.
With unadapted interface elements minor delamination is not captured. However, even if they would be adapted, the complex micromechanical stress and displacement fields that correspond with this state would not be represented accurately. Furthermore, with unadapted elements, the final amount of energy dissipated will be correct when major delamination occurs on both sides of the splitting crack, and will approach the correct value upon mesh-refinement when major delamination occurs on only one side of the crack. Therefore, van der Meer and Sluys [86] have proposed to use unadapted interface elements for delamination in combination with XFEM for matrix cracking. In the following example, this choice is validated.
Open Hole Laminate
Above, it has been argued that an error is introduced by not updating interface elements when neighboring solid elements are cracked, but that this error can be expected to vanish upon mesh refinement. Here, results are shown from an investigation into the magnitude of this error with a mesh-refinement study for a case in which interaction between matrix cracking and delamination is essential [86]. A [±45]s-laminate with a circular hole under tension is considered (see Fig. 17). The location of two cracks per ply is predefined in order to keep the response relatively simple.
Matrix cracks are growing from the hole to the long edge. But these cracks alone are not sufficient to form a mechanism, because of mutual constraint between the two plies. The load is transferred via the interface, which causes delamination to grow away from those cracks, until the area between the cracks is completely delaminated. The failure mechanism is illustrated in Fig. 18 where the deformation short before final failure is shown. It can be observed that failure is complete on one side of the hole, while delamination between the matrix cracks on the other side of the hole is still developing. The asymmetry in the response is due to the unstable nature of the delamination process and is triggered in the simulations by asymmetry in the mesh.
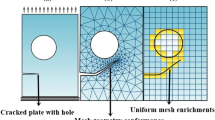
Six different meshes are used and two different integration schemes for the interface elements. All meshes are generated with the same mesh generator [155], where the typical element length is each time scaled throughout the domain with a factor \(1/\sqrt{2}\), resulting in an increase in the number of nodes with a factor of approximately two. The triangular interface elements are integrated with either a three point Gauss scheme or a three point Newton-Cotes scheme. Load-displacement diagrams for three different meshes are presented in Fig. 19. The dissipation-based arclength method (see Sect. 6.1) allows for flawless tracking of the equilibrium path with two sharp snapbacks, each corresponding with delamination on one side of the hole. It can be observed that differences between the results for the different meshes are limited. Especially with the two finer meshes, there is very good agreement between the results. Fig. 20 shows the trend in maximum load value upon mesh refinement for both integration schemes. The results are practically equal for all meshes with Newton-Cotes integration. The trend for the peak load value with Gauss integration approaches the mesh-objective value from analyses with Newton-Cotes integration.
Load-displacement relation for open hole laminate with limited number of cracks obtained with three different meshes and two different integration schemes [86]
Peak load for different meshes for open hole laminate with limited number of cracks [86]
Furthermore, in Fig. 21 the dissipation at the end of all twelve analyses is visualized. Again, the results with Newton-Cotes integration converge to a unique solution very fast. The energy dissipation due to delamination in the analyses with Gauss integration decreases upon mesh refinement. The fact that more energy is dissipated before a mechanism is formed with Gauss integration can be well understood considering that the unadapted interface elements are bridging the matrix crack. Eventually, the interface is damaged on both sides of the crack, because in the unadapted interface element relative displacements become large over the whole element domain, while in the real discontinuous displacement field significant relative displacements occur on one side of the crack only. This is illustrated in Fig. 22, showing the area with delamination damage and the location of the matrix cracks. It can be observed that with Gauss integration the final delamination front lies outside of the area bound by the splitting cracks, while with nodal integration, the delamination front lies, on average, on the cracks as it should.
Energy dissipation for different meshes for open hole laminate with limited number of cracks [86]
Final matrix cracks and delamination on one side of the hole with Gauss integration (left) and Newton-Cotes integration (right) and n n ≈2000 [86]
It is concluded from this example that unadapted interface elements can be used between elements that are cracking with the phantom node method without reservation. When unadapted interface elements are used, a nodal (Newton-Cotes) integration scheme is to be preferred because with such a scheme the displacement jump is exact in all integration points and no artificial bridging is introduced.
5.4 Crack Spacing
In a mesolevel laminate model, the strains in different plies are necessarily conforming until delamination takes place. Matrix cracks that are introduced as a discontinuity in the displacement field do not change this, except at sub-element level. In other words, introduction of transverse cracks after violation of the failure criterion does not necessarily lead to localization of deformation and hence to unloading of the surrounding material. This gives the stress-based laminate analysis with matrix cracking an ill-posed character. In absence of delamination, the stress keeps increasing in every uncracked element. Eventually, the matrix strength may be exceeded throughout the domain. With a rigid interface, the stress field may give rise to an infinite number of cohesive cracks with infinitesimal crack spacing.
Physically, the ill-posedness of the mechanical problem is reflected in the apparent randomness of the exact location of matrix cracks. The exact location of subsequently appearing matrix microcracks and the distance between those cracks depends on the microstructural fiber distribution and on the complex three dimensional displacement field in the neighborhood of existing cracks. The resolution of the mesomodel is by definition not sufficiently fine to capture this. However, this is not necessarily problematic, because in mesolevel analysis one is not really interested in finding the exact location of individual transverse cracks. It is rather the presence of matrix cracks in a certain region and the delamination that they promote that is important for mesolevel analysis. A statistical strength distribution could alleviate the ill-posedness in the analysis in the sense that a unique location can be found where cracks should initiate first. But if these first cracks do not cause significant delamination, increasing strain may still lead to a theoretically infinite number of cracks, except when the full three-dimensional problem is solved with multiple elements over the ply thickness.
In the example in Sect. 5.3, the ill-posedness was removed by predefining where matrix cracks are allowed. As a consequence, the strength criterion, Eq. (66), was not applied consistently throughout the domain. There were areas where the stress exceeded the strength but where the material was nonetheless assumed to remain intact. However, XFEM can deal with multiple parallel cracks, provided that the number of these cracks is finite. Therefore a numerical crack spacing parameter has been introduced by van der Meer and Sluys [86] to remove the ill-posedness while maintaining as much as possible the predictive quality that cracks may initiate wherever stress exceeds the strength. Because the matrix cracks are straight, the normal distance between a pair of cracks can be computed, which is used as a limiter for crack initiation.
An additional advantage of using a predefined minimum crack spacing is that this allows for the modeling of coalescing cracks. Since the cracks are straight, it can be anticipated that two cracks will meet. Practically this means that crack initiation at a location with zero normal distance to an existing crack is also allowed.
The crack propagation/initiation procedure is implemented such, that whenever the matrix strength is exceeded in an element, the projected distance from this element to existing cracks is checked. If that distance is smaller than the predefined crack spacing, it is tried to move the point of initiation of the new crack inside the failing element such that the two cracks will meet exactly. If that fails, crack initiation in this element is aborted, and the same element will not be checked for failure again. New crack segments are either an extension of an existing crack, or the initiation of a new crack with Δ≥Δmin or the initiation of a new crack that is anticipated to meet an existing crack Δ=0 (see Fig. 23).
It is not immediately clear how the value of Δmin should be chosen. A lower bound is related to the fineness of the mesh, practically because dealing with multiple cracks per element is troublesome, and philosophically because the fineness of the discretization indicates the desired resolution of the approximation.
Open Hole Laminate
The influence of the crack spacing on the results has been investigated in Ref. [86] with emphasis on the question how the spacing parameter influences the objectivity of the global response. Here, results from one of the examples are shown. The [±45]s-laminate with circular hole from the previous section (see Fig. 17) is revisited, but this time there are no predefined crack locations. Instead, the number of cracks is limited by the spacing.
Peak load values for different values of the crack spacing are displayed in Fig. 24. Two different plateaus where the maximum load is roughly constant can be observed. The cause for the drop in maximum load for (Δx<0.9 mm) is found in subcritical delamination near the hole. In all computations, the first cracks are initiated at the same location along the hole, since the crack spacing does not influence the solution before any cracks are present. The location of these first cracks is at the point where the cross section is minimal. Then, as the load continues to increase, more cracks are initiated. In case the spacing is small enough to have secondary parallel cracks that also touch the circular hole, the small triangular areas that are enclosed by these cracks delaminate before the maximum load is reached. The consequence of this subcritical delamination is that the effective cross-section is reduced and hence that the load carrying capacity drops.
Peak load value for open hole laminate for different values of the crack spacing [86]
The influence of the spacing on the final delaminated area can be observed in Fig. 25, which depicts the final crack pattern and delaminated area for four different values of the crack spacing. Load-displacement diagrams are also shown. There is no absolutely unique solution, but a strong similarity between the results with different crack spacing values can nevertheless be observed.
Load-displacement diagrams along with final delamination damage and matrix cracks for different values of the crack spacing [86]
The fact that in this case the secondary cracks eventually form the main opening macrocracks, makes predictive analysis of the failure mechanism particularly challenging. With the approach with XFEM for matrix cracking and a crack spacing parameter, this challenge can be met. The transition from the distributed phenomenon of a zone with parallel matrix cracks to the discrete phenomenon in which an individual crack from this zone becomes dominant is captured automatically as a consequence of proper ply kinematics and sound interaction between matrix cracking and delamination.
The influence of crack spacing on the final dissipation is shown in Fig. 26. Here too, the influence of the presence of subcritical damage is visible, particularly in the dissipation related to delamination. For the dissipation in the matrix cracks, a completely unique response has not been obtained. Nevertheless, the influence of crack spacing on dissipation is limited, even when only dissipation due to matrix cracking is considered. Not all cracks that are initiated are fully opening. Therefore the amount of energy that is dissipated in distributed matrix cracking is not linearly dependent on the number of cracks. That the response is not completely unique is in this case acceptable as a reflection of the fact that there is randomness in the exact location of matrix cracks. No data was obtained for crack spacing of 0.9 mm, because in that computation the secondary cracks that only just missed the hole eventually caused difficulties in the post peak analysis.
Energy dissipation for open hole laminate for different values of the crack spacing [86]
It is concluded from this example that the artificial crack spacing parameter does not have a pathological influence on the results. When the spacing is chosen sufficiently small to describe the final delamination pattern, the predicted peak load value is largely independent of the value that is used for the spacing. The total dissipation, however, a quantity strongly related to the post-peak response, remains more sensitive to this value. The optimal value for the spacing parameter remains problem and mesh-dependent, but with this approach it is possible to deal with both distributed matrix cracking and discrete splitting, and to have a transition between the two, which is governed by the mechanics in the interface as it should be.
5.5 Fiber Failure
In order to build a complete model for ply failure, the discontinuous model for matrix cracking must be combined with a model for fiber failure. Several considerations lead to the preference of a continuum model over a discontinuous approach here. Firstly, the compelling reason to use a discontinuous representation for matrix cracks, namely that the direction of crack propagation is governed by the microstructure rather than by the stress field, is not present in this case. Moreover, in the case in which a band with fiber failure grows in the direction of a matrix crack in an adjacent ply, the discontinuous approach will have more difficulty in predicting this orientation. Prior to failure there is a band of elements in which stress is high. With a continuum model this will automatically lead to failure in this band, while it is not clear how this propagation direction should be extracted from the stress field in case it is modeled as a propagating discontinuity in the displacement field. Secondly, the continuum description fits the physics well, because fiber failure is a mechanism that results in a band in which material is damaged. This is due to the fact that fibers do not fail in a smooth plane, the process generally involves pull out of fibers from a zone with extensive matrix failure.
The remaining disadvantage of the continuum approach to failure is that regularization is needed. The method for fiber failure proposed by Fang et al. [139] is not regularized, while van der Meer et al. [140] and Mollenhauer et al. [136] use the crack band method [22] for regularization of their successive fiber failure models. This simple method, in which the constitutive behavior depends on the element size, leads to mesh-size independent results, although limited dependence on the orientation of the elements may still be present. The formulation by van der Meer et al. [140] is detailed below.
Because the fiber failure mechanism does not leave the matrix intact, isotropic softening is assumed
The force that drives degradation, however, is orthotropic, motivated by the obvious fact that fiber failure only occurs due to loading in fiber direction. Puck and Schürmann [66] argued that the difference between available formulations is small as far as failure initiation is concerned. Therefore, for simplicity, maximum strain and maximum stress criteria are to be preferred. Of these, the maximum strain criterion is most appropriate to drive the degradation, because this largely rules out the influence of transverse strain on the amount of energy dissipated due to fiber failure. The variable κ f is defined as the time maximum of the normalized strain in fiber direction
where E 1 is the ply Young’s modulus in fiber direction, 〈ε 1〉 is the positive strain in fiber direction and F 1t is the ply strength in fiber direction. Damage initiates when κ f=1 and an exponential softening relation is used to compute ω f.
where β is related to the fracture energy and the element size as:
For a realistic representation of crack bridging behavior as observed by Pinho et al. [156], linear-exponential [117] or bilinear [157] softening would be more realistic than the simple exponential softening described here.
For the influence of fiber failure on the matrix cracking process the assumption of isotropic softening is maintained. That means, firstly, that the failure criterion for matrix cracking is applied on the effective stress (D e ε) instead of on the nominal stress σ and, secondly, that after crack initiation fiber damage is also applied to the cohesive traction in the matrix cracks.

where  is the traction as computed with the cohesive law in Eq. (71). In each cohesive integration point, ω
f is computed from the bulk strain at that point, which is taken as the average of the independent strains on both sides of the crack.
is the traction as computed with the cohesive law in Eq. (71). In each cohesive integration point, ω
f is computed from the bulk strain at that point, which is taken as the average of the independent strains on both sides of the crack.
5.6 Shear Nonlinearity
A final feature must be added to the constitutive model of the ply, namely a representation of the nonlinear shear deformations in the matrix. Van der Meer et al. [140] have chosen for the phenomenological model by Van Paepegem et al. [124, 158] which includes both damage and plasticity, so that it can be fitted with respect to observed loading/unloading behavior with both stiffness degradation and permanent strain, see Fig. 27(b). For failure analysis, a proper description of the unloading behavior is of importance, also under monotonic boundary conditions, because unloading of the bulk material will occur around the failure zone.
The basic relation between shear stress and shear strain with damage and plasticity is
Van Paepegem et al. [124] proposed exponential evolution relations for ω 12 and \(\gamma_{12}^{\mathrm{p}}\) in differential form. In order to obtain behavior that is independent of the time step size, the equations have been rewritten in [140] in closed form:


Apart from the elimination of the differential formulation, another change has been made in Eq. (81) with respect to the original formulation. Namely that the evolution of D depends on the total strain γ 12 rather than on the elastic strain \(\gamma_{12}^{\mathrm{e}}=\gamma_{12}-\gamma_{12}^{\mathrm{p}}\). This adaptation disentangles the influence of the four material parameters C 1…C 4 on the stress strain behavior and therefore simplifies the curve fitting exercise in which these parameters are to be obtained.
In laminate analysis, matrix cracking will not be allowed everywhere in the domain (see Sect. 5.4). As a consequence, it cannot be excluded that the stress in the bulk material between two cracks will exceed the matrix strength. For this reason, the model for shear nonlinearity, needs to remain well-posed beyond the failure strain, even though it is unclear what is the physical meaning of this part. The model by Van Paepegem et al. [124] starts to exhibit softening from a certain threshold strain. This would violate the separation between matrix nonlinearity and matrix failure and is therefore undesirable. This is solved by extending the phenomenological curve with a perfectly plastic part beyond the point where ∂τ 12/∂γ 12=0.
The interaction between shear nonlinearity and fiber damage is straightforward because the two processes are driven by independent strain components. Fiber damage is applied to the total stress after shear nonlinearity, i.e. Eq. (74) is generalized to
where \(\hat{\mathbf{D}}\) is the orthotropic material stiffness matrix with nonlinear shear component \(\hat{D}_{66}= (1-\omega_{12} )G_{12}\) and ε e is the elastic strain with \(\gamma_{12}^{\mathrm{e}}=\gamma_{12}-\gamma_{12}^{\mathrm{p}}\).
In this model, there is no coupling between hardening matrix damage ω 12 and softening matrix damage in transverse cracks (ω m) or in the interface (ω d). This can only be justified if the microcracks that are represented by ω 12 in the continuum are not aligned with the microcracks represented by ω m and ω d in the cohesive zones. For delamination this is a likely assumption, but for transverse cracking some kind of interaction would be realistic. Moreover, where parameter identification is concerned, in the measurement of G IIc,m there is definitely some energy dissipation involved that is due to the very same processes that are interpreted as shear nonlinearity in other measurements. The sharp distinction between matrix damage in transverse cracks and matrix damage due to in plane shear is debatable. This is a consequence of the mesolevel approach. Two phenomena are dealt with that are clearly distinct on the mesoscale but nevertheless connected on the microscale. To this date, this issue has been left unresolved, for reasons of simplicity, but also because energy dissipation in matrix cracks is not the most important property in the complete failure simulation.
6 Solution Algorithm for Simulations with Many Cracks
In the previous section, a numerical framework for the simulation of composites has been introduced. However, carefully constructed kinematic and constitutive models are not all that is needed for successful simulations. When the computation crashes due to non-convergence before the virtual specimen has failed, the model is of no use, and when the computation time is very high this does not encourage its use either. In order to obtain a model that is applicable to complex cases, a well-designed solution procedure is indispensable. Algorithmic details from a specific implementation are often left unpublished, because they are generally not considered pivotal, nor even always meritable. However, they are important. Robustness and efficiency are essential for numerical methods in engineering. In this section, detailed attention is therefore given to the algorithmic aspects of the computational framework developed in Refs. [86, 88, 140, 141].
The central element of the solution algorithms for implicit nonlinear finite element analysis is the Newton-Raphson method (see Sect. 2.1). Theoretically, the Newton-Raphson procedure offers quadratic convergence when linearization is exact, under the assumptions that the procedure is started within the radius of convergence and that the function for which a solution is sought is smooth [18]. On complex problems, however, such favorable convergence properties are generally not realized, either because the radius of convergence is smaller than practicable or because smoothness is absent. In these cases, there is no guarantee that the procedure converges at all. There are several possible factors that can endanger robustness of the Newton-Raphson iterative procedure. These are listed below:
-
Non-consistent linearization. Quadratic convergence requires exact linearization, but in practice, especially with complex constitutive relations, the chain rule for differentiation is not always followed to the very last terms, consciously or not. This may stay without consequences in simple verification cases but it poses a serious threat to convergence in complex cases.
-
Non-differentiability of the local response. A subtle form of non-smoothness is when there is discontinuity in the derivative of nodal forces with respect to nodal displacements. This may be caused by a kink in the constitutive law, but also by switches between loading and unloading behavior. Adaptive stepping is often a solution to solve convergence difficulties in this case, either by decreasing or by increasing the increment size.
-
Discontinuities in the local response. More severe lack of smoothness occurs when there is a discontinuity in the relation between nodal forces and nodal displacements. This is for instance the case when instant loss of stiffness is assumed in a constitutive law, but also crack growth with XFEM may lead to small sudden changes in nodal force distribution. In the latter case, the effect vanishes when elements are sufficiently small. This type of discontinuity can nevertheless be very severe, because adaptive stepping is not always effective.
-
Snapback behavior. In quasi-static analysis, snapback behavior can exist in the equilibrium solution. The cause for this can be physical (for composites: the unloading of stiff fibers after fiber breakage or after delamination) but also numerical (e.g. the use of relatively large elements with cohesive methods). When no arclength-algorithm is available, a snapback becomes a load drop, i.e. a discontinuity of the global response. The starting point of the Newton-Raphson procedure for the step in which the load drops may be outside of the radius of convergence beyond cure with adaptive stepping.
-
Bifurcations or near-bifurcations. For instance when different cracks or failure processes are competing and one has to be halted while the other continues to develop, it is possible that the iterative procedure oscillates between different solution paths. A modified Newton-Raphson strategy may be necessary: assuming secant instead of softening behavior for both competing mechanisms will help to find the one that is most critical.
Progressive failure simulations for composites have several aspects that complicate the solution procedure. In this section, the numerical algorithms used to cope with these complications for the simulation of complex failure mechanisms in Ref. [141] is outlined. Firstly sharp snapbacks are encountered. When matrix failure occurs in fibrous materials, two processes take place simultaneously: matrix material damages (by definition), and fibers unload (as a possible consequence). Because the fibers are very stiff and the matrix failure process is not very ductile, the amount of elastic energy released by the second process easily exceeds the amount of energy necessary to drive the first. Hence, damage grows in an unstable manner and snapback behavior is observed in the equilibrium path. The dissipation-based arclength method by Gutiérrez [159] has been found to be a very powerful tool for following the equilibrium path when many different failure processes are interacting and competing. The method is presented in Sect. 6.1, along with an extension of the formulation that is needed with the proposed constitutive models. Secondly, the initiation and propagation of cracks with XFEM must be given a place in the solution procedure. This is a remeshing operation that is not suitable for integration in the Newton-Raphson procedure. However, due to the possibility of distributed cracking, many cracks can be expected, which should be dealt with as efficiently as possible. The strategy for crack propagation is presented in Sect. 6.2. Thirdly, an adaptive time stepping strategy is needed. In laminate fracture, different failure processes may occur and interact. In some cases the different processes are competing, in other cases they promote one another, but in either case the system is highly nonlinear, with a varying radius of convergence. Therefore, an adaptive strategy is employed, which searches for an increment size for which the Newton-Raphson procedure does converge. The adaptive strategy is presented in Sect. 6.3. Fourthly, the fiber failure model gives particular convergence problems which cannot be solved with adaptive time stepping. Therefore, a modified Newton-Raphson scheme is used in some cases when the fully linearized iterative procedure does not converge. In Sect. 6.4 it is explained how and when this is done.
6.1 Dissipation-Based Arclength Method
Gutiérrez [159] has developed the dissipation-based arclength technique for complex failure problems. Unlike the original arclength method [160], it is also stable for highly localized behavior, and unlike the indirect displacement control method [161], which was introduced particularly for localized behavior, it is not necessary to specify in advance where failure occurs. Like with other arclength methods, a constraint equation is added to the system of equations, but in the dissipation-based arclength method, the constraint equation is based on the thermodynamical principle that energy dissipation is non-negative in each finite time increment. With this in mind, a forward marching strategy along the equilibrium path is defined by prescribing a finite amount of energy to be dissipated in each time step. In Fig. 28, it is illustrated how the equilibrium path is followed incrementally with equal energy increments. The constraint equation is defined in terms of global quantities, and therefore, there is no need to prescribe or track where the localized deformation occurs.
6.1.1 Original Formulation
In the dissipation-based arclength method, the constraint equation is formulated such that an increment in the energy dissipation is prescribed in each time step. For models with secant unloading, the constraint equation is expressed in terms of nodal quantities as:
where \(\hat{\mathbf{f}}\) is the unit load vector, λ is the load scale factor (\(\lambda\hat{\mathbf{f}}=\mathbf{f}^{\mathrm{ext}}\)), a is the nodal displacement vector, and ΔE is the prescribed amount of dissipated energy in the time step. The subscript 0 is used to refer to a quantity at the beginning of the time step, while Δ indicates an increment during the time step.
In the left diagram of Fig. 29, the quantities from Eq. (83) are illustrated for a single degree of freedom. Assuming the path between the two points on the load-displacement curve is straight, the area ΔE can be expressed as
which is strongly similar to the generalized form in Eq. (83). However, it is obvious from the figure that this expression depends on the assumption of secant unloading. In case permanent deformations are present (as in the right diagram of Fig. 29) the constraint equation has to be adapted.
6.1.2 Damage/Plasticity Formulation
In the analysis of laminate failure, the assumption of secant unloading does not hold for two reasons, firstly due to the residual stress from the curing process (see Sect. 2.3), and secondly due the permanent strain related to shear nonlinearity (see Sect. 5.6). An extension of the dissipation-based arclength method for plasticity has been derived before by Verhoosel et al. [162]. In that derivation, however, it is tacitly assumed that plasticity is the only dissipative mechanism. Another constraint equation has been derived by van der Meer et al. [140] that is generic for combined damage and plasticity, including thermal strain as a specific case of plasticity.
The presence of thermal strain and plasticity require an additional vector assembly, rendering the constraint equation as
with
where B is the strain nodal displacement matrix, D is the consistent stiffness matrix, ε th is the thermal strain from Eq. (41) which is assumed to be constant during the analysis. The derivation of Eq. (85) starts, following Gutiérrez [159] with expressing the dissipation rate \(\dot{E}\) as the difference between the exerted power P and the rate of elastic energy \(\dot{V}\):
with
where \(\hat{\mathbf{f}}\) is a unit load vector, λ is the load scale factor and \(\dot{\mathbf{a}}\) is the nodal displacement rate.
The elastic energy V is defined as

where Ω is the bulk domain and Γ is the cohesive surface, both in interface elements and in XFEM cracks. With the kinematic relations ε=Ba and 〚u〛=Za, this can be reorganized to

The two integral terms between parentheses can be eliminated, because they are equal to the internal force vector, and hence, when equilibrium is satisfied, to the external force vector. The elastic energy is therefore rewritten as
Note that the integral with the operator Z has been eliminated without specifying whether this signifies the kinematic relation in an interface element or in a pair of elements with the phantom node method. However, secant unloading in the cohesive zone has been assumed in Eq. (89).
With Eq. (91), assuming constant ε th, the rate in elastic energy is:
After substitution of \(\dot{\boldsymbol{\varepsilon}}^{\mathrm{p}}=\mathbf {F}\mathbf {B}\dot{\mathbf{a}}\) and \(\dot{\boldsymbol{\sigma}}^{\mathrm{p}} =\mathbf{D}\mathbf{B}\dot{\mathbf{a}}\) this can be reorganized to
with
where D is the consistent tangent matrix D ij =∂σ i /∂ε j and F is the gradient of plastic strain with respect to total strain \(F_{ij}={\partial\varepsilon^{\mathrm{p}}_{i}}/{\partial\varepsilon_{j}}\).
Substitution of (88) and (93) into Eq. (87) gives
With forward Euler integration, the constraint equation prescribing that a finite amount of energy, ΔE, is dissipated becomes:
The first two terms are equal to the left hand side of the original form in Eq. (83). The third therm is new and asks for the assembly of an additional vector. Due to the forward Euler integration, the vector f ∗ has to be evaluated only at the beginning of the time step. However, when the discretization changes due to crack growth with XFEM, it has to be re-evaluated.
6.2 Crack Growth
During the progressive failure process in laminates, many matrix cracks can appear. When matrix cracks are modeled with XFEM, this therefore requires a numerical framework which can handle a big number of cracks to an extent that is not known in other applications of XFEM. Therefore, an in-depth exposition of the solution procedure used in Refs. [86, 140, 141] is included here. This solution procedure has specifically been designed to efficiently accommodate a large number of propagating cracks.
6.2.1 Position in Global Algorithm
In XFEM, crack growth is dealt with outside of the Newton-Raphson loop. Doing it inside the loop would either imply that the cracks may grow based on a non-equilibrium solution, which is physically unsound, or it would require that crack growth is reversible inside the Newton-Raphson loop, which would harm the robustness of the solution procedure.
Therefore, the stress field is checked for failure after an equilibrium solution has been found. Together with the adaptive stepping, this results in a solution algorithm for the single time step with a threefold loop (see Fig. 30). The innermost loop is the Newton-Raphson loop, which is standard for nonlinear finite element computations. In step {1}, the new solution vector is initialized to be equal to that from the previous time step, and the boundary conditions are updated. In step {2}, the residual vector, is updated for the current displacement field, where the residual is the unbalance in the weak form of the equilibrium equation, cf. Eq. (1):
In step {3}, the relative magnitude of this unbalance R is computed, and it is checked whether this is small enough to consider the current displacement field an equilibrium solution. The criterion for this is:
Where ∥r∥0 is the norm of the residual vector from the first iteration. As long as the criterion (98) is not satisfied, the system is repeatedly linearized and solved with Eq. (10) in step {5}, but not before it has been checked in step {4} whether there is still hope that the Newton-Raphson procedure will converge. If the residual becomes too high (R>R max) or the number of iterations too large (n>n max), the procedure is canceled and restarted with a new increment (see Sect. 6.3).
After an equilibrium solution has been found, the corresponding stress field is checked for failure in step {6}. The solution is acceptable if the failure criterion is not violated in any of the elements where cracking is allowed. Then the solution is stored (history is updated, output is written, etc.) in step {8}. In contrast, when the failure criterion is violated, new crack segments are inserted, either as growth of existing cracks or as initiation of new cracks. After this, equilibrium is no longer satisfied. There are three options for how to continue: proceed to the next time step ({7}→{8}), restart the current time step ({7}→{1}), or continue the Newton-Raphson loop ({7}→{2}). The third option is to be preferred, which will be argued below.
As long as time steps are sufficiently small, it can still be assumed that the solution before crack growth is close to the real solution path, since with cohesive tractions the perturbation of the equilibrium is small. Therefore, one might be inclined to proceed to the next time step directly after crack growth, like Wells and Sluys [40]. This would be most efficient, and the small loss in accuracy could be acceptable. However, even the loss in accuracy is accepted regarding the gain in efficiency, robustness requires otherwise. It is possible that the Newton-Raphson scheme does not converge after crack growth. Then the algorithm will not converge in the next time step, whichever increment size is chosen. This will lead to termination of the simulation unless a more complicated adaptive scheme is implemented which can go back to the beginning of the previous time step. Therefore, the option to go from step {7} directly to step {8} is discarded. It is necessary to find equilibrium again before the solution is committed. In that case, if no convergence is found after crack growth, this crack growth can be canceled (in step {9}) to go back to the beginning of the same time step with a different increment (see Sect. 6.3). The next time step is entered if and only if a solution has been found that satisfies both equilibrium and the failure criterion.
In a given finite element implementation, it can be more straightforward to restart the time step at {1} than to continue with the converged but not-accepted solution at {2}. For efficiency, however, it is to be preferred to re-enter the Newton-Raphson loop with the latest converged solution. This displacement field, which satisfies equilibrium as well as the constraints for this time step, gives a better estimate for the final solution of the time step (see Fig. 31, \(\mathbf{a}_{i}^{0}\) is closer to a i than a i−1). Using the latest converged solution reduces the number of iterations needed to re-establish equilibrium considerably. This is especially advantageous when the crack growth loop is passed several times inside a single time step.
6.2.2 Crack Growth Procedure
It is crucial for efficiency that it is possible to introduce multiple new crack segments before the iteration loop is entered again. The computation would become unnecessarily lengthy if equilibrium would be sought for after every single insertion of a new crack segment. The procedure for crack growth in steps {6} and {7} is illustrated in more detail in Fig. 32. First, the stress is checked in all integration points in all elements where failure is allowed. The values from the failure criterion evolution are sorted in descending order and stored per ply. Then, crack segments are introduced element by element, beginning with the element with the highest violation. After each initiation of a new crack, the set of elements in which cracking is allowed is updated, considering the restrictions related to the crack spacing (see Sect. 5.3). New segments are introduced until no more elements exist in which the failure criterion is violated and in which cracking is allowed or until a maximum number of new crack segments per ply has been reached.
Algorithm for crack growth with possibly multiple new crack segments before re-entering the Newton-Raphson loop (for the location in the full procedure, see Fig. 30)
With the irreversibility of crack growth, this may in some cases cause cracks to be initiated or extended too fast. It is possible that crack growth in one place would reduce the stress elsewhere if equilibrium were re-established, and that further crack growth should therefore not take place, while it does in the proposed strategy. But generally, this is not the case because crack growth at one place rather tends to cause stress to increase elsewhere. In fact, no significant influence on the results has been found when the maximum number of simultaneously inserted new crack segments was increased from 1 to 200 per ply. At the same time, this increase did effectuate a dramatic reduction of the computation costs in cases with many cracks.
Finally, for convergence of the iterative procedure, it is important that the new degrees of freedom are initialized at values that are close to their unknown final values. With Hansbo’s version of XFEM, a very good estimate can be made by equating the displacements of a new phantom node to those of the corresponding original node. This results in a zero displacement jump in the new crack segment, and therefore to a displacement field that is optimally close to the last converged solution.
6.3 Adaptive Increment Strategy
Because laminate failure is constituted by a series of relatively brittle failure events, it is a challenge to design a loading strategy with which the capricious equilibrium path can be followed. The dissipation-based arclength method is a very powerful tool for this purpose. Nevertheless, there is no guarantee that the solution will always be found. However, a single case of non-convergence should not lead to termination of the computation, because it is very well possible that for another increment size, the analysis may be continued. Therefore, a strategy that is adaptive with respect to the increment size is necessary.
Furthermore, the dissipation-based arclength method only works when energy is actually being dissipated. When the system is completely elastic, the system of equations with the additional constraint equation becomes singular. Therefore a hybrid loading strategy is used which uses standard displacement increments in the initial stage and possibly again in later stages when no damage occurs. In short, both the size of the increment and its type (energy or displacement) are variable during the analysis (see also Verhoosel et al. [162]).
In Fig. 33, the algorithmic treatment of the possible increment changes is illustrated. The step numbers correspond with the numbering in the visualization of the global algorithm in Fig. 30, although several new steps have been inserted that were left out before, viz. steps {10} to {13}. The dotted and dashed arrows correspond with the two loops with the same line types in Fig. 30. The Newton-Raphson loop, however, is collapsed into a single box. The algorithm is presented in a different configuration with all arrows pointing downward to emphasize the implementation structure where we always go from one instance of the Newton-Raphson procedure via a possible change in the increment to the next instance of the Newton-Raphson procedure. Figure 33 is about what happens between these two instances of the iterative procedure.
Detailed algorithm for change in increment size or switch of increment type between two instances of the Newton-Raphson procedure (cf. Fig. 30)
During each instance of the Newton-Raphson procedure, the increment is fixed. But after it has been left, be it with convergence to step {6} or with non-convergence to step {9}, adaptation of the increment is possible. Especially in case of non-convergence many different actions may follow. In steps {9a} to {9f}, six different changes to the increment are possible. They are tried in the presented order until one of them succeeds. As soon as one succeeds, possible crack growth during this time step is canceled in step {9g} and the iterative procedure is restarted with the new increment. If none of the six changes can be applied, this means that there are no options left for finding a proper increment for this time step, and the computation is terminated. The order of the steps {9a} to {9f} is such that infinite loops and premature terminations are avoided.
The meaning of the steps {9a} to {9f} as well as of the newly inserted steps {10} to {13} is explained below.
6.3.1 Change in Increment Size
The size of the increment can be changed following three different rules, depending on the outcome of the Newton-Raphson procedure and on the history of tried increments in this time step.
- {11}:
-
At the end of the time step, i.e. when an equilibrium solution has been found that does not violate the failure criterion, the size of the increment is adapted according to
$$ \mathrm{increment}\leftarrow2^{-z}\cdot\mathrm{increment},\quad z= \bigl(n-n^{\mathrm{opt}}\bigr)/4 $$(99)where n opt is the optimum number of iterations. This is done irrespective of the type of increments that is used, energy or displacement. In case of crack growth, the number of iterations used in this expression, n, is the maximum number of iterations in a single cycle of the Newton-Raphson procedure; the counter is reset each time equilibrium is reached but its maximum value during the time step is used for the step size adaptation. Lower and upper bounds are given for both energy and displacement increments. If n=n opt the increment size remains unchanged.
- {9c}:
-
When convergence has not been reached, it often helps to reduce the size of the increment. In step {9c}, this is tried with a constant reduction factor c:
$$ \mathrm{increment}\leftarrow c\cdot \mathrm{increment},\quad c\in \langle0,1\rangle $$(100)The lower bounds that are enforced in step {11} are again taken into account. When the increment size is already below this lower bound, the reduction fails and we proceed to step {9d}
- {9e}:
-
In exceptional cases it happens that a very small increment does not lead to convergence, and that the difficulties can be overcome by taking a larger increment. Therefore, when small increments of both types have been tried without success, it is tried to increase the increment size. This is only done with the generally more robust energy increments. The highest value that has been tried in this time step is multiplied with 1/c.
$$ \mathrm{increment}\leftarrow\frac{1}{c} \cdot\mathrm {increment},\quad c\in\langle 0,1\rangle $$(101)The increase fails if the largest tried increment already exceeds the upper bound ΔE max.
6.3.2 Switch of Increment Type
The type of the increment (displacement or energy) can be changed on different occasions. Obviously, compatibility of the boundary conditions when switching from one type to the other is important. This is not automatically ensured, because the dissipation-based arclength method is based on a scalable external force vector rather than on scalable displacements. The additional unknown λ in the constraint equation (96) is a scale factor for the load vector. It is only compatible with displacement control when nonzero displacements are prescribed on a single degree of freedom, in which case the external force vector contains only one scalable value. But it is possible to obtain compatibility with prescribed displacements on a group of nodes, namely by adding node to node constraints for all the nodes of that group and applying an external force on one of them.
The places where a switch from one type to the other can be made are listed below:
- {10}:
-
A switch to energy increments is possible after convergence has been reached. This switch is intended to be made at least once per analysis, because the analysis always starts with displacement increments. For this purpose, the dissipated energy is computed after convergence has been obtained with a displacement increment. If this exceeds a threshold value
$$ \Delta E > \Delta E^{\mathrm{crit}} $$(102)the switch to arclength control is made. Notably, with crack growth this can happen in the middle of the time step.
- {9a}:
-
It is possible that at the low point of a snapback, the test specimen becomes completely or almost completely elastic. This state is reached with energy increments, but can be left only with displacement increments. In this case, it is a waste of resources to go through a whole series of increment reductions before the switch to displacement increments is made. Fortunately, this state can be detected very efficiently in the first iteration that is done with the arclength method. In the first iteration with an energy increment, the scaled residual is evaluated with an additional check. If there is a large increase
$$ R>R^{\mathrm{crit}} $$(103)this is taken as an indication that the system is (nearly) elastic, and the Newton-Raphson procedure is aborted straight away with a message that is caught in step {9a}. The switch to displacement increments is made and a flag is set, indicating that this type of switch has been made. This flag disallows any switching back to energy increments until step {9f} is reached.
- {12}:
-
In highly nonlinear computations, sometimes very small increments are necessary to find equilibrium. Unfortunately, the combination of the dissipation-based arclength method with very small increments on the one hand and remeshing with XFEM on the other can be problematic. The reason for this is that upon remeshing, the stiffness of the numerical model changes slightly. Typically, adding degrees of freedom makes the structure more compliant. Because the remeshing occurs at a nonzero load level, this stiffness reduction leads to spurious energy dissipation. If the mesh is sufficiently fine, this change is negligible for the global response. But for very small energy increments it is possible that the spurious dissipation is larger than the prescribed value, in which case the constraint equation can only be satisfied by global unloading. A spurious snapback is the result. This is bad for efficiency, because the model has to be reloaded carefully, and it possibly endangers robustness. Therefore, it can be useful to fix the displacement increment after crack growth for the remainder of the time step. This is especially the case when a mesh is used that is relatively coarse. This switch is made after crack propagation when the energy increment is smaller than ΔE crit.
- {13}:
-
The switch to displacement control at step {12} has to be made undone at the end of the time step. This is done in step {13}. Notably, a jump in energy increment can be made, because the final amount of dissipated energy from this time step (after crack growth with fixed displacement) is used as the next increment.
- {9b}:
-
When no convergence is reached after this temporary switch to displacement control has been made, the step is retried with the original energy increment, but with a flag that the switch at {12} is not allowed for the remainder of this time step.
- {9d}:
-
A switch from one increment type to the other is tried when reduction of the increment of the current type in step {9c} fails. After a switch to displacement control, the increment is set to the initial value Δu 0; after a switch to energy increments, it is set to the value from the last successful Newton-Raphson procedure. The switch to displacement control fails if the smallest allowed displacement increment has already been tried in this time step; the switch to energy increments fails if both the smallest and the largest allowed values have already been tried.
- {9f}:
-
Finally, in exceptional cases it is possible that the switch in step {9a} has been made for while it should not be. In case no displacement increment has been found for which convergence could be attained after this switch has been made, the search for a successful increment is continued with energy increments. Obviously, the switch in {9a} is then disallowed for the remainder of the time step. This step fails if it is passed for a second time or if it is passed when the switch in step {9a} has not been made.
If the complete series {9a}–{9f} fails, this means that all possible increment sizes of both types have been tried. It is then and only then that the computation is terminated due to non-convergence.
Several tuning parameters have been introduced in this section. Optimum values for all of these are to some extent problem dependent, particularly those that are not dimensionless. A good set of values that has been used for all open hole test simulations in Sect. 7 and [141] is presented in Table 1.
6.4 Modified Newton-Raphson Method
The continuum damage model for fiber failure introduced in Sect. 5.5 with regularization according to the crack band method gives particular convergence problems. Presumably this is due to difficulties that the Newton-Raphson procedure has in finding a single band of elements that is damaging. This particular kind of ill-convergence manifests itself in oscillatory iterations, for which it holds that
Unfortunately, when this behavior is encountered, step size reduction is often ineffective.
Therefore a modified Newton-Raphson procedure has been implemented for this case, in which a partially secant matrix is used for K instead of the fully linearized K=∂ f int/∂ a. Inside the Newton-Raphson loop a check for oscillations in the residual norm is incorporated in step {3}. When oscillations are encountered, it is tried to escape these by using a not completely consistent tangent matrix. In a select set of integration points, the secant stiffness is used. For this purpose, the loading/unloading state of all material points is compared in each iteration with that from the previous iteration. In every point where the state changes from loading to unloading or vice versa, the secant stiffness is used in the subsequent iterations. Generally, this leads to an initial increase in the residual, but after several iterations the residual starts decreasing and the procedure converges slowly to the equilibrium solution. The maximum number of iterations is increased. When the residual norm decreases in 10 subsequent iterations, this is taken as an indication that the radius of convergence of the Newton-Raphson procedure has been reached. Then, the special strategy is terminated and consistent linearization is used again, often resulting in convergence in few additional iterations.
This is a rather crude and costly technique, but it sometimes works to get beyond a critical point in the equilibrium path, which would otherwise only be passed after a long series of increment changes, if at all. This partially secant method is only performed when energy increments are applied.
7 Numerical Results on Complex Test Cases
In this section, results are shown from a validation exercise for the numerical framework that has been described in the previous two sections (see also Ref. [141]). The model with XFEM for matrix cracking, interface elements for delamination, continuum damage for fiber failure, a damage/plasticity model for shear nonlinearity and the dissipation-based arclength method for robustness has been applied to simulate several experiments that have been performed at the University of Bristol [144, 147].
7.1 Open Hole Tension
A large number of failure experiments have been performed on open hole laminates by Green et al. [147]. Size effects in laminate failure have been studied with series of quasi-isotropic specimens involving different types of scaling. In-plane scaling was analyzed as well as two types of thickness scaling: ply-level scaling [45 m /90 m /−45 m /0 m ]s with m∈[1,2,4,8], and sublaminate-level scaling [45/90/−45/0] ns with n∈[1,2,4,8]. The ply-level scaled specimens were fabricated by blocking multiple plies with the same fiber orientation together, thus increasing the effective ply thickness.
The material properties for the simulations (see Table 2) are taken from Jiang et al. [85], except for those related to shear nonlinearity, which are chosen to fit data reported by Lafarie-Frenot and Touchard [163]. Strength parameters related to matrix cracking were replaced with in situ values computed with the relations by Camanho et al. [62]. Although much effort has been paid to build a robust and efficient framework, two material parameters are adapted in order to secure robustness for feasible element sizes. For the interface elements, the strength is reduced with a factor 2 as suggested by Turon et al. [99]. Furthermore, for the matrix cracks, the fracture energy related to mode I failure is increased to the value given for mode II failure, viz. from 0.2 to 1.0 N/mm. The influence of these changes has been commented upon in the discussion of the results in [141].
The value for the ply strength in fiber direction F 1t is not uniquely defined, because the strength in unidirectional tests depends on the size of the test specimen due to the importance of the statistical strength distribution [164]. The size of the loaded volume influences the moment of onset of fiber failure. In the analyzed cases, however, with a non-uniform stress distribution and subcritical damage, the loaded volume is variable. The value of 3131 MPa is related to a loaded volume of 1 mm3. Furthermore, the spacing between the matrix cracks is set equal to 1.0 mm.
The geometry is shown in Fig. 34. The dimensions correspond with the smallest specimens as tested by Green et al. [147] which is the only in-plane size considered for the simulations. In a square region around the hole, the irregular mesh has a uniform density with typical length of the element side of 0.2 mm. In the fine mesh region, matrix cracking and delamination is allowed. Outside the region the mesh is coarser and no cracking is allowed.
7.1.1 Ply-Level Scaling
Results for the ply-level scaled specimens are presented in Fig. 35. Three different values of the maximum load level are shown for each value of m, firstly results from plane stress analysis, secondly results from three-dimensional analysis with one layer of solid elements per ply, and thirdly the averaged experimental values. For the cases in which the delamination type failure occurs (see Green et al. [147]), the plotted value corresponds with the maximum load value before the delamination in the [−45/0]-interface reaches the boundary of the fine mesh region. Notably, the delamination type failure mechanism cannot be simulated completely, because it involves delamination over the entire gauge length. But the delamination that is growing from the crack in the −45∘-ply causes a load drop and the beginning of this process can still be captured well. Therefore, limiting the zone in which delamination is allowed does not influence the peak load values.
Peak load values for ply-level scaling. Comparison between numerical and experimental results for 2D and 3D analyses [141]
The load values are divided by the unnotched cross section, to give a clear visualization of the size effect. Without any size effect, the maximum load would scale linearly with the thickness resulting in a constant maximum far field stress and hence in a horizontal line. It is concluded from Fig. 35 that the size effect in strength with respect to ply thickness scaling is captured well with the proposed framework, even in two-dimensional analysis.
Not only are the peak load values close to those measured, the failure mechanisms in the four different computations also correspond with the observed failure mechanisms. In Fig. 36 the delamination in the [−45/0]-interface and the fiber damage in the 0∘-ply are shown for a post peak time step for different values of the ply thickness. The results from the analysis with m=1 are typical for the pullout type failure as described by Green et al. [147]: fiber failure in the 0∘-ply and matrix cracking in the others, accommodated by delamination. The results obtained with other values of the ply thickness are typical for the delamination type failure: extensive delamination occurs in the [−45/0]-interface. In the case with double ply thickness, a very small amount of fiber failure is found and in the case with quadruple ply thickness, no fiber failure occurs at all. Results with m=8 are omitted here because they are very similar to those with m=4.
Typical post peak damage for pullout failure (m=1) and delamination failure (m=2,4) [141]
7.1.2 Sublaminate-Level Scaling
The thinnest laminate in the series with ply-level scaling is the same as the thinnest in the series with sublaminate-level scaling: [45/90/−45/0] ns with n=1. The analysis is repeated in 2D for n=2, and also for the limit case of [45/90/−45/0]∞. The latter is constructed with periodic boundary conditions by connecting the top ply directly to the bottom ply with interface elements (see Fig. 37). In this way the limit case of many repeated sublaminates can be approximated with limited computational costs.
The peak load values obtained with the proposed model are compared with the experimental values in Fig. 38. In this case, the size effect is not captured. The experimentally observed decrease in strength for increasing laminate thickness is not reproduced in the simulations. In all simulations the failure is of the pullout type, which does correspond with the experimental observations.
Peak load values for sublaminate-level scaling. Comparison between numerical and experimental results, for different matrix crack patterns [141]
Possibly, statistical strength distribution plays a significant role in this size effect. Fiber failure is significant in the pullout type failure and the volume of loaded fibers scales linearly with the thickness. However, in light of recent results, it is more likely that the observed size effect in the fracture toughness for fiber failure is defining for the sublaminate-level scaling size effect. Chen et al. [165] have presented much better results for the sublaminate level scaling using thickness-dependent fracture toughness values measured by Laffan et al. [166]. The double 0∘-ply in the center of the laminate is assigned a higher value for the fracture toughness (130 N/mm) than the other isolated 0∘-plies (50 N/mm). As a consequence, the averaged fracture toughness decreases for increasing number of sublaminates.
7.1.3 Fiber Strength
Considering the uncertainty of the ply strength in fiber direction, it is interesting to check the influence of varying this parameter on the results. Obviously, the fiber strength does not influence the peak load values in cases where fiber failure is not part of the global failure mechanism. For the cases with pullout failure, however, the parameter is significant, although the failure mechanism also involves delamination. In Fig. 39 the peak load value is shown for the case of n=m=1 with different values of F 1t. A clear trend is found with increasing global strength for increasing ply strength. The mean experimental value and covariance are shown with dashed lines. The influence of F 1t on the effective laminate strength indicates a drawback of the proposed framework, because, in fact, this is not a material constant but rather depends on the size of the loaded volume [164].
7.1.4 Concluding Remarks
With the simulation of open hole experiments, it has been shown that the proposed framework can be used for accurate simulation of different failure mechanisms in laminates. With the straight matrix cracks and interface elements, the failure mechanisms involving matrix cracking and delamination can be described well and as such modeled accurately.
In all cases, the failure mechanisms in the computation matched that in the experiment (pullout or delamination). Good quantitative agreement was furthermore obtained for ply-thickness scaling. The correct representation of the failure mechanism allows for the prediction of size effects in failure. However, the size effect with respect to sublaminate-level failure has not been reproduced. This is probably due to the size effect that exists in the fracture energy for fiber failure which has not been taken into account in the simulations.
7.2 Overheight Compact Tension
The overheight compact tension test has been developed to allow the growth of damage in laminates in a stable manner [167]. A series of overheight compact tension experiments on samples with different laminate designs has been performed by Li et al. [144]. Again, different failure mechanisms were obtained with ply-level scaling and sublaminate-level scaling. In this case, the failure mechanisms that involve extensive delamination are computationally very demanding. The in-plane dimensions are larger than for the open hole tests and the element size has to be equally small throughout the delaminated area. The laminates with sublaminate-level scaling however, failed without significant delamination. Fiber breakage was observed along the center line, not only in the 0∘-ply but also in the ±45∘-plies. This failure mechanism is similar to the brittle failure mechanism in the open hole test series [147]. In the compact tension test, however, failure was progressive instead of catastrophic. The failure progressed in small sudden jumps, which were reflected in a series of load drops [144]. Because the same carbon-epoxy material was used as for the open hole experiments, while the failure mechanism was different, it is a valuable validation step to simulate these with the same set of parameters. However, the mechanism without delamination is not found when the same reduced interface strength parameters are used in the simulation. In the case of the compact tension test, reducing the strength leads to a switch from the fiber failure dominated mechanism to a failure mechanism with significant delamination. This is an example of the risk of the engineering solution to alleviate mesh requirements by reducing the interface strength. The results presented in this section are obtained with the original values for the interface strength. In the absence of large scale delamination this does not endanger numerical stability.
The geometry of the test setup is shown in Fig. 40. In a band of 8 mm wide reaching to 12 mm beyond the crack tip the mesh is fine with typical element length of 0.14 mm, and only there delamination and matrix cracking is allowed. Outside this region, the plies are completely attached. The sublaminate-level scaling is simplified with periodic boundary conditions as illustrated in Fig. 37.
Overheight compact tension test (all dimensions in mm) [141]
7.2.1 Failure Mechanism
The failure mechanism in the simulation is driven by fiber failure in the ±45∘ and 0∘-plies and matrix cracking in the 90∘-ply, as illustrated in Fig. 41. Minor delamination only occurs in the narrow band with fiber failure ahead of the notch. This is the same failure mechanism as was observed experimentally. Matrix cracks are crucial to form the sawtooth-shaped cracks in the ±45∘-plies, but the energy required to form the matrix cracks is very small in comparison to the fracture energy of fiber failure. Therefore, the influence of the exact amount and location of the matrix cracks on the global response can be expected to be negligible. From the crack patterns in Fig. 41, it is concluded that limiting the size of the region with delamination and matrix cracking does not influence the results significantly in this case. Only in the 90∘-ply, the zone with distributed cracking extends up to the boundary of the fine mesh region. The distributed cracking in that ply which is apparently truncated does not interact with the main failure mechanism.
Fiber damage and matrix cracking in the four different plies in overheight compact tension analysis with crack spacing 0.5 mm [141]
7.2.2 Load-Displacement Relation
Simulations have been performed for different values of the crack spacing parameter. In Fig. 42, the obtained load-displacement curves are shown. It can be observed that the softening branch is in all cases not smooth, which is due to unsteady propagation of the fiber failure through the irregular mesh. All results fall within a band with limited width. There is a trend that the load level of the softening branch increases when spacing Δ is increased, but this trend is not monotonous. Considering the fact that fiber failure is the main dissipative process and that the level of the softening branch in compact tension tests is typically related to the fracture energy, the variation is likely to be connected to the changes in the effective fracture energy of the fiber failure mechanism. Although the fracture energy is input as a material constant, the actual dissipation in the numerical model only matches this value if the assumption of failure in a single band of elements perpendicular to the fiber direction is valid. The input value gives a lower bound, and the accuracy with which this value is approached is determined by the extent to which the mechanism is formed efficiently. This offers an explanation for the observed trend, because with larger spacing, the chance that an optimal mechanism can be formed is reduced. In Fig. 43, where the fiber failure in the 0∘-ply is visualized for Δ=0.9 mm, this can be observed in several locations where fiber failure does not form a mechanism in a single band of elements.
Load displacement relations for overheight compact tension test: [45/90/−45/0]∞ simulations with different values for crack spacing and [45/90/−45/0]2s experiments [141]
Fiber damage and matrix cracking in 0∘-ply in analysis with crack spacing 0.9 mm [141]
Load-displacement curves from the experiments are also shown in Fig. 42. The maximum load in the simulations corresponds well with the load level at which the first significant load drop occurred in the tests. However, in the experimental curves, recovery of the load after load drops is visible to an extent that does not occur in the simulations. In two of the five tests, this eventually led to a maximum load that is considerably higher than the values in the simulations.
7.2.3 Fiber Strength
Interestingly, the same influence of F 1t is not present in the compact tension test. Reducing the strength from 3131 MPa to 2800 MPa does not give any clear influence on the results, as can be observed in Fig. 44. The gray patch indicates the results obtained with F 1t =3131 MPa, the colored lines are obtained with F 1t =2800 MPa. The results fall within the same band. Although fiber failure is the dominant process in this failure mechanism, the ply strength in fiber direction is not the most important parameter. It is worth noting that even when fiber failure is dominating the response, the size effect related to statistical fiber strength distribution is not necessarily important.
7.2.4 Concluding Remarks
The simulations of the overheight compact tension test has demonstrated that the numerical model can capture yet another failure mechanism including fiber failure in off-axis plies. The complex interaction between matrix cracks and fiber failure in these plies is represented well, while the exact choice for the numerical crack spacing parameter has little effect on the global response. However, severe convergence problems with the fiber failure model in the irregular mesh have necessitated much use of the costly modified Newton-Raphson scheme proposed in Sect. 6.4.
More results from simulations of the overheight compact tension tests with a discrete representation of matrix cracks have recently been reported been reported by Mollenhauer et al. [136], providing excellent correlation in terms of damage profiles and global load-displacement response for the cases with more extensive delamination.
8 Conclusions and Discussion
In this paper, recent progress in mesolevel modeling of composite laminates has been reviewed. The use of XFEM for discrete modeling of arbitrarily located matrix cracks is a large innovation toward realistic simulations of failure mechanisms in composite laminates. This model for matrix cracking can be combined with more conventional cohesive models for delamination and continuum damage models for fiber failure to capture complete progressive failure mechanisms. With the developments described in this paper, predictive simulation of strength and damage tolerance of composite structures has come within reach, at least for tension-dominated load cases. It is emphasized that numerical algorithms have to be designed with great care to allow for robust analysis through the highly nonlinear and sometimes very brittle failure process. Consistent linearization, arclength techniques and adaptive stepping are crucial.
In spite of substantial progress, several issues remain open for further investigation.
-
There is no good model for progressive fiber failure that takes the statistical size effect into account. Fiber failure is a complicated process, which may involve individual fiber breakages at random locations which eventually join up through extensive debonding or matrix cracking. This cannot be simulated in a mesolevel framework where the fiber microstructure is not explicitly present, but complete microstructural analysis of this process is also out of reach. Need for improvement at this point is acknowledged by both Mollenhauer et al. [136] and van der Meer et al. [141].
-
Under compression matrix cracks are inclined which leads to a particular catastrophic failure mechanism [66]. It is possible to use XFEM for inclined matrix cracks, but significant additional implementation effort is required, which has to date not been attempted.
-
A number of questions surround the current practice of delamination models. There is a proven path-dependence of popular cohesive laws, pressure dependence and friction are often neglected, and there are further observations that the assumed characterization of the fracture toughness is not always realistic.
-
Element size requirements limit the applicability of the developed models. Computational costs get quickly out of hand when moving beyond the size of small coupons (∼10−1 m). Further simplifications or new algorithms will be needed to perform large scale computations.
-
An artificial crack spacing parameter is necessary for well-defined analysis with discrete matrix cracks. Use of statistical strength distribution in combination with mesh-refinement through the thickness of the ply may work to get a realistic representation of the stress relaxation behind matrix cracks, but this would excessively increase computation costs.
-
There is lack of understanding as to how in situ effects are realistically represented in a numerical that includes softening or decohesion for matrix cracks. Theoretical models that predict the in situ strength are based on fracture mechanics and therefore not consistent with the damage mechanics framework for numerical models that involve a gradual loss of integrity.
-
Not much is known about what kind of coupling between the different constitutive models is realistic. Particularly for the matrix, different models for delamination, matrix cracking and shear nonlinearity have been developed over the years and material parameters for all of them are obtained with different tests, while it is not known how much of the energy dissipation related to shear nonlinearity is related to the same microcracking that contributes to the fracture energy for transverse matrix cracking.
On another level, a challenge that arises when higher fidelity methods for mesolevel failure simulations of composites become available is to reduce the expert-level required to use these models in order to embed them in multiscale programs for virtual testing of composites. For better characterization, a link with lower scale models is desirable, and at the same time, much interest exists to be able to predict failure at a larger scale. Such multiscale programs require, however, that the models at each individual scale are robust and reliable for a wide spectrum of problems without required intervention of an expert user or developer.
References
Cox BN, Yang QD (2006) In quest of virtual tests for structural composites. Science 314(5802):1102–1107
Reddy JN (2004) Mechanics of laminated composite plates and shells: theory and analysis, 2nd edn. CRC, Boca Raton
Williams KV, Vaziri R, Poursartip A (2003) A physically based continuum damage mechanics model for thin laminated composite structures. Int J Solids Struct 40(9):2267–2300
González C, LLorca J (2006) Multiscale modeling of fracture in fiber-reinforced composites. Acta Mater 54(16):4171–4181
González C, LLorca J (2007) Mechanical behavior of unidirectional fiber-reinforced polymers under transverse compression: microscopic mechanisms and modelling. Compos Sci Technol 67(13):2795–2806
Totry E, González C, LLorca J (2008) Failure locus of fiber-reinforced composites under shear transverse compression and out-of-plane shear. Compos Sci Technol 68(3–4):829–839
Hashin Z (1980) Failure criteria for unidirectional fiber composites. J Appl Mech 47(2):329–334
Mayes JS, Hansen AC (2004) Composite laminate failure analysis using multicontinuum theory. Compos Sci Technol 64(3):379–394
Renard J, Thionnet A (2006) Damage in composites: from physical mechanisms to modelling. Compos Sci Technol 66:642–646
Kanouté P, Boso DP, Chaboche JL, Schrefler BA (2009) Multiscale methods for composites: a review. Arch Comput Methods Eng 16(1):31–75
Trias D, Costa J, Fiedler B, Hobbiebrunken T, Hurtado JE (2006) A two-scale method for matrix cracking probability in fibre-reinforced composites based on a statistical representative volume element. Compos Sci Technol 66:1766–1777
Drago A, Pindera M-J (2007) Micro-macromechanical analysis of heterogeneous materials: macroscopically homogeneous vs periodic microstructures. Compos Sci Technol 67(6):1243–1263
Ernst G, Vogler M, Hühne C, Rolfes R (2010) Multiscale progressive failure analysis of textile composites. Compos Sci Technol 70(1):61–72
LLorca J, González C, Molina-Aldareguía JM, Segurado J, Seltzer R, Sket F, Rodríguez R, Sádaba S, Muñoz R, Canal LP (2011) Multiscale modeling of composite materials: a roadmap towards virtual testing. Adv Mater 23(44):5130–5147
Gitman IM, Askes H, Sluys LJ (2007) Representative volume: Existence and size determination. Eng Fract Mech 74(16):2518–2534
Nguyen VP, Stroeven M, Sluys LJ (2012) Multiscale failure modeling of concrete: micromechanical modeling, discontinuous homogenization and parallel computations. Comput Methods Appl Mech Eng 201–204(1):139–156
Hughes TJR (1987) The finite element method: linear static and dynamic finite element analysis. Prentice-Hall, Englewood Cliffs
Belytschko T, Liu WK, Moran B (2000) Nonlinear finite elements for continua and structures. Wiley, Chichester
Hill R (1950) The mathematical theory of plasticity. Oxford University Press, London
Simo JC, Hughes TJR (1998) Computational inelasticity. Springer, New York
Lemaitre J, Chaboche JL (1990) Mechanics of solid materials. Cambridge University Press, Cambridge
Bažant ZP, Oh B (1983) Crack band theory for fracture of concrete. Mater Struct 16(3):155–177
Bažant ZP, Pijaudier-Cabot G (1989) Measurement of characteristic length of non-local continuum. J Eng Mech 115(4):755–767
de Borst R, Mühlhaus H-B (1992) Gradient-dependent plasticity: formulation and algorithmic aspects. Int J Numer Methods Eng 35(3):521–539
Peerlings RHJ, de Borst R, Brekelmans WAM, Geers MGD (1998) Gradient-enhanced damage modelling of concrete fracture. Mech Cohes-Frict Mater 3(4):323–342
Peerlings RHJ, Geers MGD, de Borst R, Brekelmans WAM (2001) A critical comparison of nonlocal and gradient-enhanced softening continua. Int J Solids Struct 38(44):7723–7746
Wang WM, Sluys LJ, de Borst R (1997) Viscoplasticity for instabilities due to strain softening and strain-rate softening. Int J Numer Methods Eng 40(20):3839–3864
Barenblatt IG (1962) The mathematical theory of equilibrium cracks in brittle fracture. Adv Appl Mech 7:55–129
Ngo D, Scordelis AC (1967) Finite element analysis of reinforced concrete beams. ACI J Proc 64(3):152–163
Xie D, Waas AM (2006) Discrete cohesive zone model for mixed-mode fracture using finite element analysis. Eng Fract Mech 73(13):1783–1796
Goodman RE, Taylor RL, Brekke TL (1968) A model for the mechanics of jointed rock. J Soil Mech Found Div 94:637–659
Schellekens JCJ, de Borst R (1994) Free edge delamination in carbon-epoxy laminates: a novel numerical/experimental approach. Compos Struct 28(4):357–373
Schellekens JCJ, de Borst R (1993) On the numerical integration of interface elements. Int J Numer Methods Eng 36(1):43–66
Rots JG (1988) Computational modeling of concrete fracture. PhD thesis, Delft University of Technology
Melenk JM, Babuška I (1996) The partition of unity finite element method: basic theory and applications. Comput Methods Appl Mech Eng 139(1–4):289–314
Moës N, Belytschko T (2002) Extended finite element method for cohesive crack growth. Eng Fract Mech 69(7):813–833
Strouboulis T, Babuška I, Copps K (2000) The design and analysis of the generalized finite element method. Comput Methods Appl Mech Eng 181(1):43–69
Belytschko T, Black T (1999) Elastic crack growth in finite elements with minimal remeshing. Int J Numer Methods Eng 45(5):601–620
Moës N, Dolbow J, Belytschko T (1999) A finite element method for crack growth without remeshing. Int J Numer Methods Eng 46(1):131–150
Wells GN, Sluys LJ (2001) A new method for modelling cohesive cracks using finite elements. Int J Numer Methods Eng 50(12):2667–2682
Hansbo A, Hansbo P (2004) A finite element method for the simulation of strong and weak discontinuities in solid mechanics. Comput Methods Appl Mech Eng 193(33–35):3523–3540
Mergheim J, Kuhl E, Steinmann P (2005) A finite element method for the computational modelling of cohesive cracks. Int J Numer Methods Eng 63(2):276–289
Song J-H, Areias PMA, Belytschko T (2006) A method for dynamic crack and shear band propagation with phantom nodes. Int J Numer Methods Eng 67(6):868–893
Broberg KB (1999) Cracks and fracture. Academic Press, San Diego
Bažant ZP, Planas J (1998) Fracture and size effect in concrete and other quasibrittle materials. CRC Press, Boca Raton
Wisnom MR (1999) Size effects in the testing of fibre-composite materials. Compos Sci Technol 58(13):1937–1957
Hyer MW (1998) Stress analysis of fiber-reinforced composite materials. McGraw-Hill, Boston
Tsai SW (1965) Strength characteristics of composite materials. NASA Contractor Report 224
Hoffman O (1967) The brittle strength of orthotropic materials. J Compos Mater 1:200–206
Tsai SW, Wu EM (1971) A general theory of strength for anisotropic materials. J Compos Mater 5(1):58–80
Hashin Z, Rotem A (1973) A fatigue failure criterion for fiber reinforced materials. J Compos Mater 7:448–464
Hinton MJ, Soden PD (1998) Predicting failure in composite laminates: the background to the exercise. Compos Sci Technol 58(7):1001–1010
Soden PD, Kaddour AS, Hinton MJ (2004) Recommendations for designers and researchers resulting from the world-wide failure exercise. Compos Sci Technol 64(3–4):589–604
Liu KS, Tsai SW (1998) A progressive quadratic failure criterion for a laminate. Compos Sci Technol 58(7):1023–1032
Harlow DG, Phoenix SL (1978) The chain-of-bundles probability model for the strength of fibrous materials I: analysis and conjectures. J Compos Mater 12(2):195–214
Okabe T, Takeda N (2002) Size effect on tensile strength of unidirectional CFRP composites—experiments and simulation. Compos Sci Technol 62(15):2053–2064
Koyanagi J, Hatta H, Kotani M, Kawada H (2009) A comprehensive model for determining tensile strength of various unidirectional composites. J Compos Mater 43(18):1901–1914
Hallett SR, Green BG, Jiang W-G, Wisnom MR (2009) An experimental and numerical investigation into the damage mechanisms in notched composites. Composites, Part A, Appl Sci Manuf 40(5):613–624
Li X, Hallett SR, Wisnom MR (2009) Numerical simulation of damage propagation in overheight compact tension tests. In: Proceedings of international conference on composite materials (ICCM-17), Edinburgh
Parvizi A, Garrett KW, Bailey JE (1978) Constrained cracking in glass fibre-reinforced epoxy cross-ply laminates. J Mater Sci 13(1):195–201
Nairn JA (2000) Matrix microcracking in composites. In: Talreja R, Månson J-AE (eds) Polymer matrix composites. Comprehensive composite materials, vol 2. Elsevier, Amsterdam, pp 403–432. Chap 13
Camanho PP, Dávila CG, Pinho ST, Iannucci L, Robinson P (2006) Prediction of in situ strengths and matrix cracking in composites under transverse tension and in-plane shear. Composites, Part A, Appl Sci Manuf 37(2):165–176
Talreja R (1985) Transverse cracking and stiffness reduction in composite laminates. J Compos Mater 19(4):355–375
Dávila CG, Camanho PP, Rose CA (2005) Failure criteria for FRP laminates. J Compos Mater 39(4):323–345
Pinho ST, Dávila CG, Camanho PP, Iannucci L, Robinson P (2005) Failure models and criteria for FRP under in-plane or three-dimensional stress states including shear non-linearity. NASA Technical Memorandum 213530
Puck A, Schürmann H (1998) Failure analysis of FRP laminates by means of physically based phenomenological models. Compos Sci Technol 58(7):1045–1067
Reddy JN, Pandey AK (1987) A first-ply failure analysis of composite laminates. Comput Struct 25(3):371–393
Rybicki EF, Kanninen MF (1977) A finite element calculation of stress intensity factors by a modified crack closure integral. Eng Fract Mech 9(4):931–938
Krueger R (2004) Virtual crack closure technique: history, approach, and applications. Appl Mech Rev 57(2):109–143
Allix O, Ladevèze P (1992) Interlaminar interface modelling for the prediction of delamination. Compos Struct 22(4):235–242
Maimí P, Mayugo JA, Camanho PP (2008) A three-dimensional damage model for transversely isotropic composite laminates. J Compos Mater 42(25):2717–2745
Wells GN, de Borst R, Sluys LJ (2002) A consistent geometrically non-linear approach for delamination. Int J Numer Methods Eng 54(9):1333–1355
Remmers JJC, Wells GN, de Borst R (2003) A solid-like shell element allowing for arbitrary delaminations. Int J Numer Methods Eng 58(13):2013–2040
Hashagen F, de Borst R (2000) Numerical assessment of delamination in fibre metal laminates. Comput Methods Appl Mech Eng 185(2):141–159
Mi Y, Crisfield A, Hellweg H-B, Davies GAO (1998) Progressive delamination using interface elements. J Compos Mater 32(14):1246–1272
Hibbs MF, Bradley WL (1987) Correlations between micromechanical failure processes and the delamination toughness of graphite/epoxy systems. In: Fractography of modern engineering materials: composites and metals (A88-16961 05-23). ASTM, Philadelphia, pp 68–97
Evans AG, Rühle M, Dalgleish BJ, Charalambides PG (1990) The fracture energy of bimaterial interfaces. Mater Sci Eng A 126(1–2):53–64
Tay TE (2003) Characterization and analysis of delamination fracture in composites: an overview of developments from 1990 to 2001. Appl Mech Rev 56(1):1–32
Camanho PP, Dávila CG, de Moura MF (2003) Numerical simulation of mixed-mode progressive delamination in composite materials. J Compos Mater 37(16):1415–1438
Benzeggagh ML, Kenane M (1996) Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed mode bending apparatus. Compos Sci Technol 56(4):439–449
Turon A, Camanho PP, Costa J, Dávila CG (2006) A damage model for the simulation of delamination in advanced composites under variable-mode loading. Mech Mater 38(11):1072–1089
Allix O, Corigliano A (1996) Modeling and simulation of crack propagation in mixed-modes interlaminar fracture specimens. Int J Fract 77(2)
Yang QD, Cox BN (2005) Cohesive models for damage evolution in laminated composites. Int J Fract 133(2):107–137
Högberg JL (2006) Mixed mode cohesive law. Int J Fract 141(3–4):549–559
Jiang W-G, Hallett SR, Green BG, Wisnom MR (2007) A concise interface constitutive law for analysis of delamination and splitting in composite materials and its application to scaled notched tensile specimens. Int J Numer Methods Eng 69(9):1982–1995
van der Meer FP, Sluys LJ (2010) Mesh-independent modeling of both distributed and discrete matrix cracking in interaction with delamination. Eng Fract Mech 77(4):719–735
Turon A, Camanho PP, Costa J, Renart J (2010) Accurate simulation of delamination growth under mixed-mode loading using cohesive elements: definition of interlaminar strengths and elastic stiffness. Compos Struct 92(8):1857–1864
van der Meer FP, Sluys LJ (2009) A phantom node formulation with mixed mode cohesive law for splitting in laminates. Int J Fract 158(2):107–124
Goutianos S, Sørensen BF (2011) Work or separation of truss-like mixed mode cohesive laws. In: Lee W-I, et al. (eds) Proceedings of 18th international conference on composite materials, Jeju, Korea, Aug 2011
Li X, Hallett SR, Wisnom MR (2008) Predicting the effect of through-thickness compressive stress on delamination using interface elements. Composites, Part A, Appl Sci Manuf 39(2):218–230
Wisnom MR (1992) On the increase in fracture energy with thickness in delamination of unidirectional glass fibre-epoxy with cut central plies. J Reinf Plast Compos 11(8):897–909
Allix O, Lévêque D, Perret L (1998) Identification and forecast of delamination in composite laminates by an interlaminar interface model. Compos Sci Technol 58(5):671–678
Andersons J, König M (2004) Dependence of fracture toughness of composite laminates on interface ply orientations and delamination growth direction. Compos Sci Technol 64(13–14):2139–2152
Greenhalgh ES, Rogers C, Robinson P (2009) Fractographic observations on delamination growth and the subsequent migration through the laminate. Compos Sci Technol 69(14):2345–2351
Davidson BD, Gharibian SJ, Yu L (2000) Evaluation of energy release rate-based approaches for predicting delamination growth in laminated composites. Int J Fract 105(4):343–365
Ladevèze P, Lubineau G (2002) An enhanced mesomodel for laminates based on micromechanics. Compos Sci Technol 62:533–541
Harper PW, Hallett SR (2008) Cohesive zone length in numerical simulations of composite delamination. Eng Fract Mech 75(16):4774–4792
Turon A, Costa J, Camanho PP, Maimí P (2008) Analytical and numerical investigation of the length of the cohesive zone in delaminated composite materials. In: Camanho PP, Pinho ST, Dávila CG, Remmers JJC (eds) Mechanical response of composites, computational methods in applied sciences. Springer, Berlin, pp 77–97. Chap 4
Turon A, Dávila CG, Camanho PP, Costa J (2007) An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Eng Fract Mech 74(10):1665–1682
Harper PW, Sun L, Hallett SR (2012) A study on the influence of cohesive zone interface element strength parameters on mixed mode behavior. Composites, Part A, Appl Sci Manuf 43(4):722–734
Yang QD, Fang XJ, Shi JX, Lua J (2010) An improved cohesive element for shell delamination analyses. Int J Numer Methods Eng 83(5):611–641
Crisfield MA, Alfano G (2002) Adaptive hierarchical enrichment for delamination fracture using a decohesive zone model. Int J Numer Methods Eng 54(9):1369–1390
Guiamatsia I, Ankersen JK, Davies GAO, Iannucci L (2009) Decohesion finite element with enriched basis functions for delamination. Compos Sci Technol 69(15–16):2616–2624
Samimi M, Van Dommelen JAW, Geers MGD (2009) An enriched cohesive zone model for delamination in brittle interfaces. Int J Numer Methods Eng 80(5):609–630
Samimi M, Van Dommelen JAW, Geers MGD (2011) A three-dimensional self-adaptive cohesive zone model for interfacial delamination. Comput Methods Appl Mech Eng 200(49–52):3540–3553
van der Meer FP, Moës N, Sluys LJ (2012) A level set model for delamination—modeling crack growth without cohesive zone or stress singularity. Eng Fract Mech 79:191–212
Laš V, Zemčik R (2008) Progressive damage of unidirectional composite panels. J Compos Mater 42(1):25–44
Liu CJ, Nijhof AHJ, Ernst LJ, Marissen R (2008) Modeling failure interaction in notched cross-ply laminates. J Compos Mater 42(20):2175–2193
Vaziri R, Olson MD, Anderson DL (1992) Finite element analysis of fibrous composite structures: a plasticity approach. Comput Struct 44(1):103–116
Li X, Duxbury PG, Lyons P (1994) Considerations for the application and numerical implementation of strain hardening with the Hoffman yield criterion. Comput Struct 52(4):633–644
Lourenço PB, de Borst R, Rots JG (1997) A plane stress softening plasticity model for orthotropic materials. Int J Numer Methods Eng 40(21):4033–4057
Hashagen F, de Borst R (2001) Enhancement of the Hoffman yield criterion with an anisotropic hardening model. Comput Struct 79(6):637–651
Ladevèze P, Le Dantec E (1992) Damage modelling of the elementary ply for laminated composites. Compos Sci Technol 43(3):257–267
Matzenmiller A, Lubliner J, Taylor RL (1995) A constitutive model for anisotropic damage in fiber-composites. Mech Mater 20(2):125–152
Pinho ST, Robinson P, Iannucci L (2006) Physically based failure models and criteria for laminated fibre-reinforced composites with emphasis on fibre kinking. Part I: Development. Composites, Part A, Appl Sci Manuf 37(1):63–73
Pinho ST, Robinson P, Iannucci L (2006) Physically based failure models and criteria for laminated fibre-reinforced composites with emphasis on fibre kinking. Part II: FE implementation. Composites, Part A, Appl Sci Manuf 37(5):766–777
Maimí P, Camanho PP, Mayugo JA, Dávila CG (2007) A continuum damage model for composite laminates: Part I—constitutive model. Mech Mater 39(10):897–908
Maimí P, Camanho PP, Mayugo JA, Dávila CG (2007) A continuum damage model for composite laminates: Part II—computational implementation and validation. Mech Mater 39(10):909–919
Laurin F, Carrère N, Maire J-F (2007) A multiscale progressive failure approach for composite laminates based on thermodynamical viscoelastic and damage models. Composites, Part A, Appl Sci Manuf 38(1):198–209
Lapczyk I, Hurtado JA (2007) Progressive damage modeling in fiber-reinforced materials. Composites, Part A, Appl Sci Manuf 38(11):2333–2341
Camanho PP, Maimí P, Dávila CG (2007) Prediction of size effects in notched laminates using continuum damage mechanics. Compos Sci Technol 67(13):2715–2727
Germain N, Besson J, Feyel F (2007) Composite layered materials: anisotropic nonlocal damage models. Comput Methods Appl Mech Eng 196(41–44):4272–4282
Chamis CC, Sinclair JH (1977) Ten-deg off-axis test for shear properties in fiber composites. Exp Mech 17(9):339–346
Van Paepegem W, De Baere I, Degrieck J (2006) Modelling the nonlinear shear stress–strain response of glass fibre-reinforced composites. Part I: experimental results. Compos Sci Technol 66(10):1455–1464
van der Meer FP, Sluys LJ (2009) Continuum models for the analysis of progressive failure in composite laminates. J Compos Mater 43(20):2131–2156
Camanho PP, Fink A, Obst A, Pimenta S (2009) Hybrid titanium-CFRP laminates for high-performance bolted joints. Composites, Part A, Appl Sci Manuf 40(12):1826–1837
Blom AW, Lopes CS, Kromwijk PJ, Gürdal Z, Camanho PP (2009) A theoretical model to study the influence of tow-drop areas on the stiffness and strength of variable-stiffness laminates. J Compos Mater 43(5):403–425
Abisset E, Daghia F, Ladevèze P (2011) On the validation of a damage mesomodel for laminated composites by means of open-hole tensile tests on quasi-isotropic laminates. Composites, Part A, Appl Sci Manuf 42(10):1515–1524
Wisnom MR, Chang F-K (2000) Modelling of splitting and delamination in notched cross-ply laminates. Compos Sci Technol 60(15):2849–2856
de Moura MFSF, Gonçalves JPM (2004) Modelling the interaction between matrix cracking and delamination in carbon-epoxy laminates under low velocity impact. Compos Sci Technol 64(7):1021–1027
Hallett SR, Wisnom MR (2006) Numerical investigation of progressive damage and the effect of layup in notched tensile tests. J Compos Mater 40(14):1229–1245
Hallett SR, Jiang W-G, Khan B, Wisnom MR (2008) Modelling the interaction between matrix cracks and delamination damage in scaled quasi-isotropic specimens. Compos Sci Technol 68(1):80–89
Iarve EV (2003) Mesh independent modelling of cracks by using higher order shape functions. Int J Numer Methods Eng 56(6):869–882
Mollenhauer D, Iarve EV, Kim R, Langley B (2006) Examination of ply cracking in composite laminates with open holes: a moiré interferometric and numerical study. Composites, Part A, Appl Sci Manuf 37(2):282–294
Iarve EV, Gurvich MR, Mollenhauer DH, Rose CA, Dávila CG (2011) Mesh-indepedent matrix cracking and delamination modeling in laminated composites. Int J Numer Methods Eng 88(8):749–773
Mollenhauer D, Ward L, Iarve E, Putthanarat S, Hoos K, Hallett S, Li X (2012) Simulation of discrete damage in composite overheight compact tension specimens. Compos part A
Ling D, Yang QD, Cox BN (2009) An augmented finite element method for modeling arbitrary discontinuities in composite materials. Int J Fract 156(1):53–73
Zhou ZQ, Fang XJ, Cox BN, Yang QD (2010) The evolution of a transverse intra-ply crack coupled to delamination cracks. Int J Fract 165(1):77–92
Fang XJ, Zhou ZQ, Cox BN, Yang QD (2011) High-fidelity simulations of multiple fracture processes in a laminated composite in tension. J Mech Phys Solids 59(7):1355–1373
van der Meer FP, Oliver C, Sluys LJ (2010) Computational analysis of progressive failure in a notched laminate including shear nonlinearity and fiber failure. Compos Sci Technol 70(4):692–700
van der Meer FP, Sluys LJ, Hallett SR, Wisnom MR (2012) Computational modeling of complex failure mechanisms in laminates. J Compos Mater (in press)
Crossman FW, Wang ASD (1982) The dependence of transverse cracking and delamination on ply thickness in graphite/epoxy laminates. In: Reifsnider KL (ed) Damage in composite materials. ASTM International, West Conshohocken, pp 118–139
Johnson P, Chang F-K (2001) Characterization of matrix crack-induced laminate failure—Part I: experiments. J Compos Mater 35(22):2009–2035
Li X, Hallett SR, Wisnom MR, Zobeiry N, Vaziri R, Poursartip A (2009) Experimental study of damage propagation in over-height compact tension tests. Composites, Part A, Appl Sci Manuf 40(12):1891–1899
Hallett SR, Wisnom MR (2006) Experimental investigation of progressive damage and the effect of layup in notched tensile tests. J Compos Mater 40(2):119–141
Spearing SM, Beaumont PWR (1992) Fatigue damage mechanics of composite materials. I: experimental measurement of damage and post-fatigue properties. Compos Sci Technol 44(2):159–168
Green BG, Wisnom MR, Hallett SR (2007) An experimental investigation into the tensile strength scaling of notched composites. Composites, Part A, Appl Sci Manuf 38(3):867–878
Jäger P, Steinmann P, Kuhl E (2008) Modeling three-dimensional crack propagation—a comparison of crack path tracking strategies. Int J Numer Methods Eng 76(9):1328–1352
Rabczuk T, Zi G, Gerstenberger A, Wall WA (2008) A new crack tip element for the phantom node method with arbitrary cohesive cracks. Int J Numer Methods Eng 75(5):577–599
Cox JV (2009) An extended finite element method with analytical enrichment for cohesive crack modeling. Int J Numer Methods Eng 78(1):48–83
Oliver J (2000) On the discrete constitutive models induced by strong discontinuity kinematics and continuum constitutive equations. Int J Solids Struct 37(48–50):7207–7229
Mergheim J, Steinmann P (2006) A geometrically nonlinear FE approach for the simulation of strong and weak discontinuities. Comput Methods Appl Mech Eng 195(37–40):5037–5052
Moonen P, Sluys LJ, Carmeliet J (2008) A continuous-discontinuous approach to simulate fracture processes in quasi-brittle materials. Philos Mag 88(28):3281–3298
Hille TS, Suiker ASJ, Turteltaub S (2009) Microcrack nucleation in thermal barrier coating systems. Eng Fract Mech 76(6):813–825
Geuzaine C, Remacle J-F (2009) Gmsh: a three-dimensional finite element mesh generator with built-in pre- and post-processing facilities. Int J Numer Methods Eng 79(11):1309–1331
Pinho ST, Robinson P, Iannucci L (2006) Fracture toughness of the tensile and compressive fibre failure modes in laminated composites. Compos Sci Technol 66(13):2069–2079
Dávila CG, Rose CA, Camanho PP (2009) A procedure for superposing linear cohesive laws to represent multiple damage mechanisms in the fracture of composites. Int J Fract 158(2):211–223
Van Paepegem W, Baere ID, Degrieck J (2006) Modelling the nonlinear shear stress–strain response of glass fibre-reinforced composites. Part II: model development and finite element simulations. Compos Sci Technol 66(10):1465–1478
Gutiérrez MA (2004) Energy release control for numerical simulations of failure in quasi-brittle solids. Commun Numer Methods Eng 20(1):19–29
Riks E (1979) An incremental approach to the solution of snapping and buckling problems. Int J Solids Struct 15(7):529–551
de Borst R (1987) Computation of post-bifurcation and post-failure behavior of strain-softening solids. Comput Struct 25(2):211–224
Verhoosel CV, Remmers JJC, Gutiérrez MA (2009) A dissipation-based arc-length method for robust simulation of brittle and ductile failure. Int J Numer Methods Eng 77(9):1290–1321
Lafarie-Frenot MC, Touchard F (1994) Comparative in-plane shear behaviour of long-carbon-fibre composites with thermoset or thermoplastic matrix. Compos Sci Technol 52(3):417–425
Wisnom MR, Khan B, Hallett SR (2008) Size effects in unnotched tensile strength of unidirectional and quasi-isotropic carbon/epoxy composites. Compos Struct 84(1):21–28
Chen B, Tay TE, Baiz PM, Pinho ST (2011) Size effects in progressive damage of notched and holed composites. In: Lee W-I, et al. (eds) Proceedings of 18th international conference on composite materials, Jeju, Korea Aug 2011
Laffan MJ, Pinho ST, Robinson P, Iannucci L (2010) Measurement of the in situ ply fracture toughness associated with mode I fibre tensile failure in FRP. Part II: size and lay-up effects. Compos Sci Technol 70(4):614–621
Kongshavn I, Poursartip A (1999) Experimental investigation of a strain-softening approach to predicting failure in notched fibre-reinforced composite laminates. Compos Sci Technol 59(1):29–40
Acknowledgements
Financial support from the Technology Foundation STW (under grant 06623) and the Ministry of Public Works and Water Management, The Netherlands, is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
van der Meer, F.P. Mesolevel Modeling of Failure in Composite Laminates: Constitutive, Kinematic and Algorithmic Aspects. Arch Computat Methods Eng 19, 381–425 (2012). https://doi.org/10.1007/s11831-012-9076-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-012-9076-y