1 Introduction

A system is called sparse if the ratio of the zero, or near-to-zero, coefficients to non-zero coefficients is relatively small. Sparse systems are usually classified into two categories: (i) exact sparse systems; in which the response of the system is zero, and (ii) near sparse systems; in which most of the response taps are close (not equal) to zero [1]. If a system did not have any of these properties, then it can be classified as a non-sparse system [2].

The knowledge of sparse approximation is very important as it spans to both fields of theoretical and practical applications such as image processing, audio analysis, system identification, wireless communication, and biology. The least mean square (LMS) adaptive algorithm, introduced by Hopf and Widrow [3], is widely used in many applications such as echo cancelation, channel estimation, and system identification, due to its simplicity and low computational complexity. Unfortunately, the conventional LMS does not exploit the sparsity of the system. It neglects the inherent sparse structural information carried by the system, and this leads to degradation in the actual performance of the system [4]. Many algorithms have been proposed to exploit this sparsity nature of a signal, and most of these algorithms apply a subset selection scheme during the filtering process [5–8]. This process of a subset selection is implemented through statistical detection of active taps or sequential tap updating [9–11]. Other variants of the LMS algorithm assign proportionate step sizes of different magnitude to each tap such as the proportionate normalized LMS (PNLMS) and improved proportionate normalized LMS (IPNLMS) [12, 13].

Recently, many norm constraint LMS-type algorithms are proposed to improve the performance of the LMS algorithm by incorporating the \(l_0\)-norm [14, 15] or \(l_1\)-norm penalty into the cost function of the conventional LMS algorithm; thereby, increasing the convergence rate and/or decreasing the mean square error (MSE). Unfortunately, most of these algorithms suffer from the adaptation of the norm constraint for identifying systems with different sparsity due to the lack of adjusting factor [4]. The variable step-size LMS (VSSLMS) was proposed by Harris et al. [16] to improve the performance of the conventional LMS, but still lacks the capability of exploiting sparsity of the system [16, 17].

In this paper, the \(p\)-norm penalty is used along with the VSSLMS algorithm to try to overcome the above mentioned limitations. This is achieved by incorporating the \(p\)-norm-like constraint into the cost function of the VSSLMS algorithm. This concept of the \(p\)-norm-like was fragmented to form a new constraint definition called the non-uniform norm which can be made more flexible for adjustment when the need arise to counter for the swap over between the point of anti-sparse and sparsity of the systems. Thus, with this knowledge of the \(p\)-norm optimization exploration, the proposed algorithm is called the \(p\)-norm constraint variable step size LMS (\(p\)-NCVSSLMS).

This paper is organized as follows. In Sect. 2, the VSSLMS algorithm is reviewed and the proposed algorithm is derived. In Sect. 3 convergence analysis of the proposed algorithm is presented and its stability criterion is derived. In Sect. 4, experimental results are presented and discussed. Finally, conclusions are drawn.

2 Proposed algorithm

2.1 Review of the variable step-size LMS algorithm

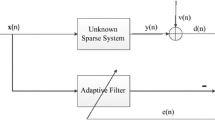
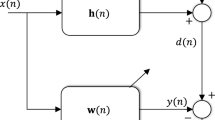
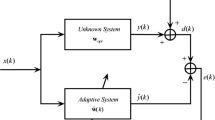
The VSSLMS algorithm is deduced from the conventional LMS algorithm with a variable step size. Let \(y(n)\) be a sample output of an observed signal

$$\begin{aligned} y(n)=\mathbf{w}^T\mathbf{x}(n)+ v(n), \end{aligned}$$
(1)

where \(\mathbf{w}=\left[ w_0w_1\ldots w_{N-1}\right] ^T\)and \(\mathbf{x}(n)=[x(n)x(n-1)\ldots x(n-N+1)]^T\) denote the filter coefficient and the input tap vector, respectively. \(v(n)\) is the observed noise which is assumed to be independent from \(x(n)\).

The main aim of the LMS algorithm is to sequentially estimate the coefficients of the filter using the input–output relationship of the signal [18]. Let \(\mathbf{w}(n)\) be the estimated coefficient vector of the adaptive filter at the \(n\)th iteration. In the conventional LMS, the cost function \(J(n)\) is defined as:

$$\begin{aligned} J(n)=\frac{1}{2}e^2(n), \end{aligned}$$
(2)

where \(e(n)\) is the instantaneous error:

$$\begin{aligned} e(n)=y(n)-\mathbf{w}^T(n)\mathbf{x}(n). \end{aligned}$$
(3)

The filter coefficients vector is then updated by

$$\begin{aligned} \mathbf{w}(n+1)&= \mathbf{w}(n)-\mu \frac{\partial J(n)}{\partial \mathbf{w}(n)}\nonumber \\&= \mathbf{w}(n)+\mu e(n)\mathbf{x}(n), \end{aligned}$$
(4)

where \(\mu \) is the step size which serves as the condition of the LMS algorithm given by,

$$\begin{aligned} 0<\mu <\frac{1}{\lambda _\mathrm{max}(\mathbf{R})}, \end{aligned}$$
(5)

where \(\lambda _\mathrm{max}\) is the maximum eigenvalue of \(\mathbf{R}\), and \(\mathbf{R}\) is the autocorrelation matrix of the input tap vector. Usually, there is a trade off between the convergence rate and MSE value in LMS algorithm. The VSSLMS algorithm uses a variable step size, as proposed in [16], in order to avoid such a trade off, and is given by,

$$\begin{aligned} \mu ^{\prime }(n+1)=\alpha \mu ^{\prime }(n)+\gamma e^2(n), \end{aligned}$$
(6)

with \(0<\alpha <1\) and \(\gamma >0\) then

$$\begin{aligned} \mu (n)=\left\{ \begin{array}{l@{\quad }l} \mu _\mathrm{max} &{} \text{ if } \mu ^{\prime }(n+1)> \mu _\mathrm{max} \\ \mu _\mathrm{min} &{} \text{ if } \mu ^{\prime }(n+1)< \mu _\mathrm{min} \\ \mu ^{\prime }(n+1) &{} \text{ otherwise }, \end{array} \right. \end{aligned}$$
(7)

where \(0<\mu _\mathrm{min}<\mu _\mathrm{max}\). Therefore, the step size is a positive value whose strength can be controlled by \(\alpha \), \(\gamma \) and the instantaneous error \(e(n)\) as in (6). In other words, if the instantaneous error is large, the step size will increase to provide faster tracking. If the prediction error decreases, the step size will be decreased to reduce the misadjustment and hence provides a small steady-state error. The perfection of the algorithm could be attained at \(\mu _\mathrm{max}\), [17]. \(\mu _\mathrm{max}\) is chosen in such a way to assure constrained MSE [19]. A sufficient condition to achieve this is

$$\begin{aligned} \mu _\mathrm{max} \le \frac{2}{\mathrm{tr }(\mathbf{R})}. \end{aligned}$$
(8)

2.2 The \(p\)-norm variable step-size LMS algorithm

Even though, the VSSLMS algorithm provides a good performance, still, its performance can be improved further by imposing the sparsity condition of the system. The proposed algorithm is derived by solving the optimization problem:

$$\begin{aligned} \mathbf{w}(n)=\mathop {\hbox {arg min}}\limits _\mathbf{w} J_{1,n}(\mathbf{w}), \end{aligned}$$
(9)

where \(J_{1,n}(\mathbf{w})\) is the modified cost function in (2) which is achieved by incorporating a \(p\)-norm penalty function as:

$$\begin{aligned} J_{1,n}(\mathbf{w})=\frac{1}{2}|e(n)|^2 +\lambda \Vert \mathbf{w}(n)\Vert _p^p. \end{aligned}$$
(10)

The last term in (10) is a \(p\)-norm-like constraint penalty, where \(\lambda \) is a positive constant whose value is used to adjust the penalty function. This function has a definition which is different from the classic Euclidean norm [4], defined as:

$$\begin{aligned} \Vert \mathbf{w}(n)\Vert _p^p=\sum _{i=1}^{n}|w_i|^p, \end{aligned}$$
(11)

where \(0\le p\le 1\) and we can deduce that:

$$\begin{aligned} \lim _{p\rightarrow 0}\Vert \mathbf{w}(n)\Vert _p^p=\Vert \mathbf{w}(n)\Vert _{0}, \end{aligned}$$
(12)

which counts the number of non-zero coefficients, and

$$\begin{aligned} \lim _{p\rightarrow 1}\Vert \mathbf{w}(n)\Vert _p^p=\Vert \mathbf{w}(n)\Vert _{1}=\sum _{i=1}^{n}|w_i|. \end{aligned}$$
(13)

Both (12) and (13) are utilized for proper solution and analysis of sparse system derived by the \(l_0\) and \(l_1\)-norm algorithms as stated in [5]. Since the \(p\)-norm has been analyzed, next is to find a solution for the optimization problem in (9) by using a gradient minimization techniques, the gradient of the cost function with respect to the filter coefficient vector \(\mathbf{w}(n)\) is

$$\begin{aligned} \widehat{\varvec{\nabla }}J_{1,n}(\mathbf{w})=\frac{\partial |e(n)|^2}{\partial \mathbf{w}}+\lambda \frac{\partial \Vert \mathbf{w}(n)\Vert _p^p}{\partial \mathbf{w}}, \end{aligned}$$
(14)

whose solution was found to be

$$\begin{aligned} \widehat{\varvec{\nabla }}J_{1,n}(\mathbf{w})=\mathbf{w}(n) + \lambda p\frac{ \mathrm {sgn}[\mathbf{w}(n)]}{\Vert \mathbf{w}(n)\Vert ^{1-p}}. \end{aligned}$$
(15)

Thus, from the gradient descent recursion,

$$\begin{aligned} w_{i}(n+1)&= w_{i}(n)-\mu (n)\widehat{\varvec{\nabla }}J_{1,n}(\mathbf{w})\nonumber \\&= w_{i}(n)+\mu (n)e(n)x(n-i)\nonumber \\&-\kappa (n) p \frac{\mathrm {sgn}[w_{i}(n)]}{\sigma +|w_{i}(n)|^{1-p}},\quad \forall 0\le i<N, \nonumber \\ \end{aligned}$$
(16)

where \(\forall 0\le i<N\), \(\mu (n)\) is the variable step size of the algorithm given by (1), \(\kappa (n)=\lambda \mu (n)>0\) is an adjustable parameter controlling the stability of the system, \(\sigma \) is a very small positive constant to avoid dividing by zero and \(\mathrm {sgn}[w_{i}(n)]\) is a component-wise sign function.

The introduction of the \(p\)-norm facilitates the optimization of the norm constraint, this can be achieved by adjusting the parameter \(p\) as in (11). This parameter has effect on both the estimation bias and the intensity of the sparsity measure, hence the trade off makes it difficult to achieve the best solution for the optimization problem.

To address these problems, the classic \(p\)-norm as in (9) is riven into a non-uniform \(p\)-norm-like [4]. In this method, a different value of \(p\) is assigned for each entry of \(\mathbf{w}(n)\) as:

$$\begin{aligned} \Vert \mathbf{w}(n)\Vert _{p,N}^p=\sum _{i=1}^{N}|w_i|^{p_i}, \end{aligned}$$
(17)

where \(0\le p_i\le 1\) and the new cost function, which is subjected to (16), can be deduced from the gradient descent recursion equation as,

$$\begin{aligned} w_{i}(n+1)&= w_{i}(n)+\mu (n) e(n)x(n-i)\nonumber \\&-\kappa (n) p_{i}\frac{\mathrm {sgn}[w_{i}(n)]}{\sigma +|w_{i}(n)|^{1-p_{i}}}, \end{aligned}$$
(18)

where \(\forall 0\le i<N\), and the introduction of \(\mathbf{p}=[p_0,p_1, \ldots ,p_{N-1}]^T\) vector makes it feasible to control the effect of estimation bias and sparsity correction measure by assigning a different value of \(p\) for every tap weight vector. The last part of (18) suggests that a metric of the absolute value of \(w_i(n)\) can be introduced to quantitatively classify the filter coefficients into small and large categories.

By considering the range of the expected value of the tap weight vector, the absolute value expectation can be defined as:

$$\begin{aligned} h_i(n)=\mathrm {E}\left[ |w_{i}(n)|\right] , \quad \forall 0\le i<N, \end{aligned}$$
(19)

since we are interested in the minimum possible value of \(\mathbf{p}\) rather than its index, and minimizing the term \(\frac{p_{i}}{|w_{i}(n)|^{1-p_{i}}}\) in (18) is equivalent to minimizing \(p_{i}|w_{i}(n)|^{p_{i}-1}\), then the optimization of the large category for each entry of \(\mathbf{p}\) can be expressed as:

$$\begin{aligned} \min _{p_i}[p_{i}|w_{i}(n)|^{p_{i}-1}]=0,\quad \mathrm {sub. to:} \quad w_{i}(n)>h_i(n), \end{aligned}$$
(20)

and for the small category, \(p_i\) is set to be unity to avoid the imbalance between the extremely great or slight intensity caused by various values of small \(w_i(n)\). Therefore, the comprehensive optimization of the non-uniform norm constraint will cause \(p_i\) to take a value of either a \(0\) or \(1\) when \(w_i(n)>h_i(n)\) or \(w_i(n)<h_i(n)\), respectively. With these, the update equation in (18) becomes

$$\begin{aligned} w_{i}(n+1)&= w_{i}(n)+\mu (n)e(n)x(n-i)\nonumber \\&- \kappa (n) f_i \mathrm {sgn}[w_{i}(n)], \quad \forall 0\le i<N, \end{aligned}$$
(21)

where \(f_{i}\) can be obtained by:

$$\begin{aligned} f_{i}=\frac{\mathrm {sgn}[\mathrm {E}\left[ |w_{i}(n)|\right] -|w_{i}(n)|] + 1}{2},\quad \forall 0\le i<N. \end{aligned}$$
(22)

The second term in (21) provides a variable step size update while the last term imposes a non-uniform norm constraint whose function is to attract small filter coefficients to zero. Unlike other norm constraint algorithms, the norm exertion here depends on the value of individual coefficient with respect to the expectation of the tap weight. Also the zero attractor of the non-uniform norm increases the convergence rate of small coefficients and eliminates the estimation bias caused by large coefficients, hence improves the performance of the algorithm.

Table 1 A summary of the proposed algorithm
Full size table

Moreover, the performance of the proposed algorithm can be improved further by reweighting the term introduced in (22) which makes it completely behaves as a reweighted zero attractor [5]. By this, the update equation of the proposed algorithm can be expressed as:

$$\begin{aligned} w_{i}(n+1)&= w_{i}(n)+\mu (n)e(n)x(n-i)\nonumber \\&-\kappa (n) f_{i}\frac{\mathrm {sgn}[w_{i}(n)]}{1+\varepsilon |w_{i}(n)|}, \quad \forall 0\le i<N, \end{aligned}$$
(23)

where \(\varepsilon >0\) is an adjustable parameter whose value controls the reweighing factor. Table 1 provides a summary of the proposed algorithm.

3 Convergence analysis of the proposed algorithm

In this section, the convergence analysis of the proposed algorithm is presented and a stability condition is derived. The essence of the convergence analysis is to ensure that the algorithm fulfills the criteria needed for the application requirements. Now, starting by substituting (22) in (23),

$$\begin{aligned} w_{i}(n+1)&= w_{i}(n)+\mu (n)e(n)x(n-i)\nonumber \\&- \kappa (n) \left( \frac{\mathrm {sgn}(\mathrm {E}\left[ |w_{i}(n)|\right] -|w_{i}(n)|) + 1}{2(1+\varepsilon |w_{i}(n)|)}\right) \nonumber \\&\times \mathrm {sgn}\left[ w_{i}(n)\right] . \end{aligned}$$
(24)

Assuming that an i.i.d zero-mean Gaussian input signal \(x(n)\) corrupted by a zero-mean white noise \(v(n)\), the filter misalignment vector can be defined as:

$$\begin{aligned} \delta \mathbf{w}(n)= \mathbf{w}(n)-\mathbf{w}_{0} \end{aligned}$$
(25)

where \(\mathbf{w}_{0}\) represents the unknown system coefficients vector.

The mean and the auto-covariance matrix of \(\delta \mathbf{w}(n)\) can be written as,

$$\begin{aligned} \varvec{\epsilon }(n)&= \mathrm {E}[\delta \mathbf{w}(n)], \end{aligned}$$
(26)
$$\begin{aligned} \mathbf{S}(n)&= \mathrm {E}\left[ \mathbf{q}(n)\mathbf{q}^{T}(n)\right] , \end{aligned}$$
(27)

where \(\mathbf{q}(n)\) is the zero-mean misalignment vector defined as:

$$\begin{aligned} \mathbf{q}(n)=\delta \mathbf{w}(n)-\mathrm {E}[\delta \mathbf{w}(n)], \end{aligned}$$
(28)

The instantaneous mean square deviation (MSD) can be defined as:

$$\begin{aligned} J(n)&= \mathrm {E}[\Vert \delta \mathbf{w}(n)\Vert _p^p]\nonumber \\&= \sum _{i=0}^{N-1}\varLambda _{i}(n), \end{aligned}$$
(29)

where \(\varLambda _{i}(n)\) denotes the \(i\)th-tap MSD and is defined with respect to the \(i\)th element of \(\delta \mathbf{w}(n)\)

$$\begin{aligned} \varLambda _{i}(n)&= \mathrm {E}[\delta _{i}^{2}(n)] \nonumber \\&= S_{ii}(n) + \epsilon _{i}^{2}(n); \quad i=0,\ldots , N-1 \end{aligned}$$
(30)

where \(S_{ii}(n)\) and \(\epsilon _{i}(n)\) are the \(i\)th diagonal element and the \(i\)th of the \(S(n)\) and \(\epsilon (n)\), respectively.

Substituting \(d(n)=\mathbf{w}_0^{T}\mathbf{x}(n) + v(n)\) and (3) in (24) gives

$$\begin{aligned} w_{i}(n+1)&= w_{i}(n)\nonumber \\&+\mu (n)[\mathbf{x}^{T}(n)\mathbf{w}_0 \!+\! v(n)\!-\!\mathbf{x}^{T}(n)\mathbf{w}(n)]x(n\!-\!i)\nonumber \\&- \kappa (n) \left( \frac{\mathrm {sgn}(\mathrm {E}\left[ |w_{i}(n)|\right] -|w_{i}(n)|) + 1}{2(1+\varepsilon |w_{i}(n)|)}\right) \nonumber \\&\times \mathrm {sgn}\left[ w_{i}(n)\right] , \end{aligned}$$
(31)

Equation (31) can be rewritten in vector form as,

$$\begin{aligned} \mathbf{w}(n+1)&= \mathbf{w}(n)\!+\!\mu (n)\mathbf{x}(n)\left[ \!\mathbf{x}^{T}\!(n)\mathbf{w}_0 \!+\! v(n)\!-\!\mathbf{x}^{T}\!(n)\mathbf{w}(n)\!\right] \nonumber \\&-\frac{\kappa (n)}{2} (\left\{ \mathrm {sgn}(\mathrm {E}\left[ |\mathbf{w}(n)|\right] -|\mathbf{w}(n)|) +\mathbf{1}\right\} \nonumber \\&\times \odot \,\mathrm {sgn}\left[ \mathbf{w}(n)\right] )\oslash \left( \mathbf{1}+\varepsilon |\mathbf{w}(n)|\right) , \end{aligned}$$
(32)

where \(|\mathbf{w}|\) is the element wise absolute of \(\mathbf{w}\), \(\mathbf{1}\) denotes a vector of ones of the same size of \(\mathbf{w}\), and \(\odot \) and \(\oslash \) denote element-by-element vector multiplication and division, respectively. Subtracting \(\mathbf{w}_0\) form both sides of (32) and substituting (25) gives

$$\begin{aligned} \varvec{\delta }(n+1)&= \mathbf{A}(n)\varvec{\delta }(n) + \mu (n)\mathbf{x}(n)v(n)\nonumber \\&-\frac{\kappa (n)}{2} (\left\{ \mathrm {sgn}(\mathrm {E}\left[ |\mathbf{w}(n)|\right] -|\mathbf{w}(n)|) +\mathbf{1}\right\} \nonumber \\&\odot \,\mathrm {sgn}\left[ \mathbf{w}(n)\right] )\oslash \left( \mathbf{1}+\varepsilon |\mathbf{w}(n)|\right) , \end{aligned}$$
(33)

where \(\mathbf{I}_{N}\) denotes the \(N\times N\) identity matrix and

$$\begin{aligned} \mathbf{A}(n)=\mathbf{I}_{N}-\mu (n)\mathbf{x}(n)\mathbf{x}^{T}(n), \end{aligned}$$
(34)

Taking the expectation of (33) and using the independence assumption [21] provide

$$\begin{aligned} \varvec{\epsilon }(n+1)&= [1-\mu (n)\sigma _{x}^{2}]\varvec{\epsilon }(n)\nonumber \\&\quad -\frac{\kappa (n)}{2}\mathrm {E}[ \left( \left\{ \mathrm {sgn}(\mathrm {E}\left[ |\mathbf{w}(n)|\right] -|\mathbf{w}(n)|) +\mathbf{1}\right\} \right) \nonumber \\&\quad \odot \,\mathrm {sgn}\left[ \mathbf{w}(n)\right] )]\oslash \left( \mathbf{1}+\varepsilon |\mathbf{w}(n)|\right) , \end{aligned}$$
(35)

where \(\sigma _{x}^{2}\) is the variance of \(x(n)\). Now, subtracting (35) from (33) and substituting (26) and (28) gives

$$\begin{aligned} \mathbf{q}(n+1)=\mathbf{A}(n)\mathbf{q}(n)+\mu (n)\mathbf{x}(n)v(n)+\frac{\kappa (n)}{2} \mathbf{Z}(n) \end{aligned}$$
(36)

where

$$\begin{aligned} \mathbf{z}(n)&= \mathrm {E}\left[ \left( \mathrm {sgn}(\mathrm {E}\left[ |\mathbf{w}(n)|\right] -|\mathbf{w}(n)|) +\mathbf{1}\right) \right. \nonumber \\&\left. \oslash \left( [\mathbf{1}+\varepsilon |\mathbf{w}(n)|]\right) \right] \odot \mathrm {sgn}\left[ \mathbf{w}(n)\right] \nonumber \\&-\left( \mathrm {sgn}(\mathrm {E}\left[ |\mathbf{w}(n)|\right] -|\mathbf{w}(n)|) +\mathbf{1}\right) \nonumber \\&\oslash \left( [\mathbf{1}+\varepsilon |\mathbf{w}(n)|]\right) \odot \mathrm {sgn}\left[ \mathbf{w}(n)\right] . \end{aligned}$$
(37)

By (27),

$$\begin{aligned} \mathbf{S}(n+1)&= \mathrm {E}\left\{ \mathbf{q}(n+1)\mathbf{q}^{T}(n+1)\right\} \nonumber \\&= \mathrm {E}\bigg \{\left[ \mathbf{A}(n)\mathbf{q}(n)+\mu (n)\mathbf{x}(n)v(n)+\frac{\kappa (n)}{2} \mathbf{z}(n)\right] \nonumber \\&\times \!\left[ \mathbf{A}(n)\mathbf{q}(n)\!+\!\mu (n)\mathbf{x}(n)v(n)\!+\!\frac{\kappa (n)}{2} \mathbf{z}(n))\right] ^{T}\bigg \}\nonumber \\&= \mathrm {E}\left\{ \mathbf{A}(n)\mathbf{q}(n)\mathbf{q}^{T}(n)\mathbf{A}^{T}(n)\right\} \nonumber \\&+\mathrm {E}\left\{ \mathbf{A}(n)\mathbf{q}(n)\mu (n)v(n)\mathbf{x}^{T}(n)\right\} \nonumber \\&+\frac{\kappa (n)}{2}\mathrm {E}\left\{ \mathbf{A}(n)\mathbf{q}(n)\mathbf{z}^{T}(n)\right\} \nonumber \\&+\mathrm {E}\left\{ \mu (n)v(n)\mathbf{x}(n)\mathbf{q}^{T}(n)\mathbf{A}^{T}(n)\right\} \nonumber \\&+ \mathrm {E}\left\{ \mu ^{2}(n)v^{2}(n)\mathbf{x}(n)\mathbf{x}^{T}(n)\right\} \nonumber \\&+\frac{\kappa (n)}{2}\mathrm {E}\left\{ \mu (n)v(n)\mathbf{x}(n)\mathbf{z}^{T}(n)\right\} \nonumber \\&+\frac{\kappa (n)}{2}\mathrm {E}\left\{ \mathbf{z}(n)\mathbf{q}^{T}(n)\mathbf{A}^{T}(n)\right\} \nonumber \\&+\frac{\kappa (n)}{2}\mathrm {E}\left\{ \mu (n)v(n)\mathbf{z}(n) \mathbf{x}^{T}(n)\right\} \nonumber \\&\quad +\left( \frac{\kappa (n)}{2}\right) ^{2}\mathrm {E}\left\{ \mathbf{z}(n)\mathbf{z}^{T}(n)\right\} . \end{aligned}$$
(38)

To evaluate (38), we use the fact that the fourth-order moment of a Gaussian variable is three times its variance squared [20], and by the independence assumption [21] and symmetric behavior of the covariance matrix \(\mathbf{S}(n)\),

$$\begin{aligned}&\mathrm {E}\left\{ \mathbf{A}(n)\mathbf{q}(n)\mathbf{q}^{T}(n)\mathbf{A}^{T}(n)\right\} \nonumber \\&\quad =\left( 1-2\mu (n)\sigma _{x}^{2} +2\mu ^{2}(n)\sigma _{x}^{4}\right) \mathbf{S}(n)\nonumber \\&\qquad +\,\mu ^{2}(n)\sigma _{x}^{4}\mathrm {tr}[\mathbf{S}(n)]I_{N}, \end{aligned}$$
(39)

and

$$\begin{aligned} \mathrm {E}\left\{ \mathbf{A}(n)\mathbf{q}(n)\mathbf{z}^{T}(n)\right\}&= \mathrm {E}^{T}\left\{ \mathbf{z}(n)\mathbf{q}^{T}(n)\mathbf{A}^{T}(n)\right\} \nonumber \\&= (1\!-\!\mu (n)\sigma _{x}^{2})\mathrm {E}\left\{ \mathbf{w}^{T}(n)\mathbf{z}(n)\right\} , \end{aligned}$$
(40)

where \(\mathrm {tr}(.)\) denotes the trace of a matrix. Now, finding the trace of (38) and by using the results of (39) and (40), we obtain

$$\begin{aligned} \mathrm {tr}[\mathbf{S}(n+1)]&= \left( 1-2\mathrm {E}\left\{ \mu (n)\right\} \sigma _{x}^{2}+2\mathrm {E}\left\{ \mu ^{2}(n)\right\} \sigma _{x}^{4}\right) \nonumber \\&\times \,\mathrm {tr}[\mathbf{S}(n)]+N\mathrm {E}\left\{ \mu ^{2}(n)\right\} \sigma _{x}^{4}\nonumber \\&\times \,\mathrm {tr}[\mathbf{S}(n)]+N\mathrm {E}\left\{ \mu ^{2}(n)\right\} \sigma _{v}^{2}\sigma _{x}^{2}\nonumber \\&+\,\kappa (n)(1-\mathrm {E}\left\{ \mu (n)\right\} \sigma _{x}^{2})\mathrm {E}\left\{ \mathbf{w}^T(n) \mathbf{z}(n)\right\} .\nonumber \\ \end{aligned}$$
(41)

From (37), it is obvious that \(\mathbf{z}(n)\) is bounded, and hence, the term in (41) \(\mathrm {E}\left\{ \mathbf{w}^T(n)\mathbf{z}(n)\right\} \) converges. Thus, the adaptive filter is stable if the following holds:

$$\begin{aligned} |1-2E\{\mu (n)\}\sigma ^2_x+(N+2)E\{\mu ^2(n)\}\sigma ^4_x|<1. \end{aligned}$$
(42)

As the algorithm converges (\(n\) is sufficiently large), the error \(e(n)\rightarrow 0\), and hence, by (6), \(\mu (n)\) becomes constant. In this case, \(E\{\mu ^2(n)\}=E\{\mu (n)\}^2=\mu ^2(n)\). Hence the above equation simplifies to

$$\begin{aligned} 0<\mu (\infty )<\frac{2}{(N+2)\sigma ^2_x}. \end{aligned}$$
(43)

This result shows that if \(\mu \) satisfies (43), the convergence of the proposed algorithm is guaranteed.

4 Experimental results

In this section, numerical simulations to investigate the performance of the proposed algorithm in terms of the steady-state MSD (\(MSD=E\Vert \mathbf{h}-\mathbf{w}(n)\Vert ^2\)) and convergence rate are carried out. The performance of the proposed algorithm is compared to those of the non-uniform norm constrained LMS (NNCLMS) [4] and ZA-LMS [5] algorithms. Two-system identification experiments have been designated to demonstrate the performance analysis. All simulations are obtained by \(100\) times independent runs.

In the first experiment, the sparse system, to be identified, is assumed to be of \(64\) taps with \(5\) random taps are assumed to be 1. The driven input and observed noise are both assumed to be white Gaussian processes with zero mean and variances \(1\) and \(0.01\), respectively. The algorithms are simulated with the following parameters: For the ZA-LMS, \(\mu =0.015\) and \(\kappa =0.0015\). For NNCLMS, \(\mu =0.015\), \(\kappa =0.0015\), and \(\epsilon =2\). For the proposed algorithm, \(\gamma =0.0005\), \(\alpha =0.97\), \(\mu _\mathrm{min}=0.011\), \(\mu _\mathrm{max}=0.017\), \(\kappa =0.0015\), and \(\epsilon =2\). As shown in Fig. 1, it can be noticed that the proposed algorithm converges at the same rate of the other algorithms with 4 and 10 dB lower MSD’s than those of the NNCLMS and ZA-LMS algorithms, respectively. Figure 2 shows the evolution curve of \(\mu (n)\) of the proposed algorithm in white Gaussian noise. From the figure, we note that \(\mu (n)\) initially is large to provide fast convergence, and as the algorithm starts converging, \(\mu (n)\) starts decreasing to provide low MSD value.

Fig. 1
figure 1

Ensemble MSD curves of the proposed, NNCLMS and ZA-LMS algorithms in white Gaussian noise

Full size image
Fig. 2
figure 2

Evolution curve of \(\mu (n)\) of the proposed algorithm in white Gaussian noise

Full size image

In order to test the performances of all algorithms due to the change of the sparsity of the unknown system, experiment one is repeated by only changing the unknown system. The unknown system is assumed to be 50 taps. As shown in Fig. 3, at the beginning, one random coefficient of the system is assumed to be 1 and the others are set to zeros. Between iterations 1,500 and 3,000, four random coefficients are set to 1 and the rest are zeros. After iteration 3,000, 14 random coefficients are set to 1 and the rest are zeros. From Fig. 3, we note that even though all the algorithms converge at the same rate, but the proposed algorithm converges to a lower MSD than the others. Also, the ZA-LMS is highly affected by the sparsity of the system. Figure 4 shows the evolution curve of \(\mu (n)\) of the proposed algorithm for the experiment in Fig. 3. Figure 5 shows the effect of sparsity on the performance of the algorithms (1 denotes \(\%100\) sparse system).

Fig. 3
figure 3

Ensemble MSD curves of the proposed, NNCLMS and ZA-LMS algorithms in white Gaussian noise (different sparsity ratios)

Full size image
Fig. 4
figure 4

Evolution curve of \(\mu (n)\) of the proposed algorithm in white Gaussian noise (different sparsity ratios)

Full size image
Fig. 5
figure 5

MSD curves versus sparsity ratio

Full size image

5 Conclusions

In this paper, a new \(p\)-norm-based VSSLMS algorithm for sparse system identification is proposed. The proposed algorithm exploits sparsity by attracting relatively small coefficients of the sparse system to zero. Convergence analysis of the proposed algorithm is presented. The performance of the proposed algorithm has been compared to those of the ZA-LMS and NNCLMS algorithms in a sparse system identification setting. Simulations results show that the proposed algorithm is superior to the other algorithms.