1 Introduction

Owing to its simplicity and robustness to signal statistics, the least mean square algorithm (LMS) is extensively applied for system identification, channel equalization, echo cancellation, interference cancellation, etc. [8]. In some scenarios, the unknown systems are sparse in nature, i.e., a small portion of the impulse response components have a significant magnitude while the rest are zero or close to zero. Representative sparse systems include echo paths, digital TV transmission channels, broadband systems, and sparse wireless multi-path channels [13, 17]. The filtering performance can be improved if sparse prior information is used in the sparse system. However, the standard LMS algorithm does not utilize such information [4]. Algorithms utilizing the sparsity, such as the proportionate normalized least mean square algorithm (PNLMS) [5] and its variations, i.e., the improved PNLMS (IPNLMS) [2], PNLMS\(++\)[9], and the mu-law PNLMS (MPNLMS) [6, 7] were previously proposed. Recently, a new frame based on the \(L_1\) norm penalty constraint was proposed. Its primary algorithms include the zero-attracting least mean square algorithm (ZA-LMS) and the reweighted zero-attracting least mean square algorithm (RZA-LMS) [4]. The zero-attracting-type algorithms outperform the standard LMS when the channel is sparse. Further, the RZA-LMS algorithm performs adequately when the number of nonzero taps increases and has just little loss in performance compared to the conventional LMS algorithm in the non-sparse channels.

The step size is a crucial parameter in determining the performance of an algorithm. A small step-size algorithm can achieve a low steady-state mean square error, whereas, the convergence speed is considerably slow. On the contrary, a large step size can provide fast convergence at the cost of a large steady-state mean square error. A fixed step-size algorithm cannot achieve a low steady-state mean square error and a fast convergence speed simultaneously. Several variable step-size algorithms have been previously proposed [1, 10, 14]. In this paper, we propose a variable step-size method based on an error function. Using the novel variable step-size method, a variable step-size RZA-LMS (VSS-RZA-LMS) algorithm and a related VSS-LMS algorithm are proposed. The performance of the LMS, RZA-LMS, and the proposed VSS-LMS and VSS-RZA-LMS, are compared and tested in a sparse system identification model that contains abrupt changes. The simulation results show that the proposed VSS-RZA-LMS algorithm has a reduced steady-state misalignment compared to the conventional RZA-LMS algorithm.

The rest of this paper is organized as follows: the review of the conventional LMS and RZA-LMS algorithms, and the introduction of the proposed algorithms are presented in Sect. 2. The simulation results are depicted in Sect. 3. In Sect. 4, the conclusion is provided.

2 Algorithms

2.1 Review

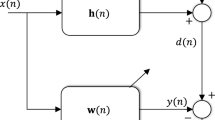
The block diagram of the sparse system identification model is depicted in Fig. 1. Define \(d\left( n \right) \) as the desired output signal of the unknown system:

$$\begin{aligned} d\left( n \right) =\mathbf{w}_o^\mathrm{T} \mathbf{x}\left( n \right) +v\left( n \right) \end{aligned}$$
(1)

where \(\mathbf{w}_o \) is the impulse response of the unknown system. \(\mathbf{x}\left( n \right) \) is the input signal and \(\mathbf{x}\left( n \right) =\left[ {x\left( n \right) ,x\left( {n-1} \right) ,\ldots ,x\left( {n-N+1} \right) } \right] ^\mathrm{T}\). Define \(\mathbf{w}\left( n \right) \) as the estimation of \(\mathbf{w}_o \) at the nth iteration. \(v\left( n \right) \) denotes the measurement noise. Although non-Gaussian noise is common in practical applications and there are several solutions to deal with it [15, 16], the performance of the RZA-LMS deteriorates sharply when non-Gaussian noise is present. Thus, in this paper, we use the Gaussian noise as the measurement noise. \(e\left( n \right) \) is the prior error and can be defined as:

$$\begin{aligned} e\left( n \right) =d\left( n \right) -y\left( n \right) =d\left( n \right) -\mathbf{w}^\mathrm{T}\left( n \right) \mathbf{x}\left( n \right) \end{aligned}$$
(2)

where T indicates the transposition.

Fig. 1
figure 1

Block diagram of the sparse system identification model

Full size image

LMS algorithm: The cost function of the LMS can be expressed as:

$$\begin{aligned} J_1 \left( n \right) =E\left( {e^{2}\left( n \right) } \right) \end{aligned}$$
(3)

Using the gradient descent method, the iteration equation can be represented as:

$$\begin{aligned} \mathbf{w}\left( {n+1} \right) =\mathbf{w}\left( n \right) +\mu e\left( n \right) \mathbf{x}\left( n \right) \end{aligned}$$
(4)

where \(\mu \) is the step size.

RZA-LMS: The RZA-LMS algorithm introduces a log-sum penalty in its cost function. It has been proved in compressed sensing that the \(L_0\) norm performs better than the \(L_1\) and \(L_2\) norms in a sparse channel. The log-sum penalty is the approximation of the \(L_0\) norm. The cost function of the RZA-LMS can be expressed as:

$$\begin{aligned} J_2 \left( n \right) =\frac{1}{2}e^{2}\left( n \right) +\gamma \sum _{i=1}^N {\log } \left( {1+\frac{\left| {w_i } \right| }{\varepsilon ^{{\prime }}}} \right) \end{aligned}$$
(5)

\(\varepsilon ^{{\prime }}\) is the threshold value that the RZA-LMS algorithm utilizes to selectively shrink taps with small magnitudes and \(\gamma \) is a controllable parameter that determines the degree of the reweighted zero attraction of the filter tap coefficients. Utilizing the gradient descent method, the iteration formula can be written as:

$$\begin{aligned} w_i \left( {n+1} \right) =w_i \left( n \right) -\rho \frac{\hbox {sgn}\left( {w_i \left( n \right) } \right) }{1+\varepsilon \left| {w_i \left( n \right) } \right| }+\mu e\left( n \right) x_i \left( n \right) \end{aligned}$$
(6)

It can also be expressed equivalently in the vector form:

$$\begin{aligned} \mathbf{w}\left( {n+1} \right) =\mathbf{w}\left( n \right) -\rho \frac{\hbox {sgn}\left( {\mathbf{w}\left( n \right) } \right) }{1+\varepsilon \left| {\mathbf{w}\left( n \right) } \right| }+\mu e\left( n \right) \mathbf{x}\left( n \right) \end{aligned}$$
(7)

where \(\rho ={\mu \gamma }/{\varepsilon ^{{\prime }}}\), \(\varepsilon =1/{\varepsilon ^{{\prime }}}\).

Compared with the LMS, it can be seen that the iteration equation of the RZA-LMS has an extra term, \(-\rho \frac{\hbox {sgn}\left( {\mathbf{w}\left( n \right) } \right) }{1+\varepsilon \left| {\mathbf{w}\left( n \right) } \right| }\), called the reweighted zero attractor that always tends to shrink the tap coefficients to zero. The reweighted zero attractor reacts only on those taps whose magnitudes are comparable to \(\varepsilon ^{{\prime }}\) and there is a negligible shrinkage for taps with \(\left| {w_i } \right| \gg \varepsilon ^{{\prime }}\).

2.2 The Proposed Algorithms

The fixed step-size (FSS) algorithms cannot usually obtain a suitable balance between a fast convergence speed and a low steady-state mean square error. In [10, 14], several variable step-size algorithms based on the nonlinear relationship between the step size and \(\left| {e\left( n \right) } \right| \) or \(\left| {e\left( n \right) } \right| ^{2}\) are proposed. However, the noise, \(v\left( n \right) \), existing in \(e\left( n \right) \) may influence the performance of the algorithm. In this paper, we propose a variable step-size method based on a modified error function. It is expressed as follows:

$$\begin{aligned} \mu \left( n \right) =\beta \,\hbox {erf}\,\left[ {\sigma _{e_{f}}^2 \left( n \right) } \right] \end{aligned}$$
(8)

where the standard error function can be defined as:

$$\begin{aligned} \hbox {erf}\,\left( x \right) =\frac{2}{\sqrt{\pi }}\int _0^x {\exp } \left( {-\eta ^{2}} \right) \mathrm{d}\eta \end{aligned}$$
(9)

The figure of the modified error function, \(f\left( x \right) =\hbox {erf}\,\left( {x^{2}} \right) \), is shown in Fig. 2. In (8), \(\beta \) is the positive scale factor and \(e_f \left( n \right) \) is the noise-free prior error that can be expressed as [3]:

$$\begin{aligned} e_f \left( n \right) =e\left( n \right) -v\left( n \right) =\left( {\mathbf{w}_o -\mathbf{w}\left( n \right) } \right) ^\mathrm{T}{} \mathbf{x}\left( n \right) \end{aligned}$$
(10)

In (8),

$$\begin{aligned} \sigma _{e_{f}}^2 \left( n \right) =E\left( {e_f^2 \left( n \right) } \right) \end{aligned}$$
(11)

\(\sigma _{e_{f}}^2 \left( n \right) \) is the power of \(e_f \left( n \right) \). It can be obtained recursively as [11, 12]:

$$\begin{aligned} \sigma _{e_{f}}^2 \left( n \right) =\sigma _e^2 \left( n \right) -\sigma _v^2 \left( n \right) =\frac{1}{\delta +\sigma _x^2 \left( n \right) }R_{e\mathbf{x}} \left( n \right) ^\mathrm{T}R_{e\mathbf{x}} \left( n \right) \end{aligned}$$
(12)

where \(\delta \) is a small regularization factor for avoiding the stalling of the estimation equation (12) when \(\sigma _x^2 \left( n \right) =0\). \(\sigma _e^2 \left( n \right) \) and \(\sigma _v^2 \left( n \right) \) are the power of the prior error and the system noise power, respectively. \(R_{e\mathbf{x}} \left( n \right) \) denotes the cross-correlation matrix between \(e\left( n \right) \) and \(\mathbf{x}\left( n \right) \). \(\sigma _x^2 \left( n \right) \) is the

Fig. 2
figure 2

Curve of the error function with a variable, x

Full size image

input signal power. \(R_{e\mathbf{x}} \left( n \right) \) and \(\sigma _x^2 \left( n \right) \) can be estimated by [11, 12]:

$$\begin{aligned} R_{e\mathbf{x}} \left( n \right)= & {} \lambda R_{e\mathbf{x}} \left( {n-1} \right) +(1-\lambda )e\left( n \right) \mathbf{x}\left( n \right) \end{aligned}$$
(13)
$$\begin{aligned} \sigma _x^2 \left( n \right)= & {} \lambda \sigma _x^2 \left( {n-1} \right) +\left( {1-\lambda } \right) x^{2}\left( n \right) \end{aligned}$$
(14)

where \(\lambda \) is the positive smoothing factor.

Using the variable step-size strategy mentioned above, two novel algorithms are proposed in this paper. The first algorithm is a variable step-size LMS algorithm (VSS-LMS) based on an error function. Its step size is controlled by (8) and the iteration formula can be expressed as:

$$\begin{aligned} \mathbf{w}\left( {n+1} \right) =\mathbf{w}\left( n \right) +\mu \left( n \right) e\left( n \right) \mathbf{x}\left( n \right) \end{aligned}$$
(15)

The second algorithm is the variable step-size RZA-LMS (VSS- RZA-LMS) and it can be expressed as:

$$\begin{aligned} w_i \left( {n+1} \right) =w_i \left( n \right) +\mu \left( n \right) e\left( n \right) x_i \left( n \right) -\rho \frac{\hbox {sgn}\left( {w_i \left( n \right) } \right) }{1+\varepsilon \left| {w_i \left( n \right) } \right| } \end{aligned}$$
(16)

The step size is controlled by (8).

Fig. 3
figure 3

Performance curves with a 1/16 sparsity for a 16-tap sparse system

Full size image

3 Simulation Results

The performance of the proposed algorithms are tested in a sparse system identification model that contains abrupt changes, wherein, the \(\mathbf{w}_o \) abruptly changes to \(-\mathbf{w}_o \). The input signals are zero-mean, white, Gaussian random signals. The convergence performance is assessed by the normalized mean square deviation (NMSD) calculated by \(\hbox {NMSD}=10\log \left( {{\left\| {\tilde{\mathbf{w}}} (n) \right\| }_2^2 /{\left\| {\mathbf{w}_o } \right\| }_2^2 } \right) \), where, \({\tilde{\mathbf{w}}} (n)=\mathbf{w}_o -\mathbf{w}(n)\). Three experiments are performed to evaluate the performance of the proposed algorithms. The output signal-to-noise ratios (SNR) of the first two experiments are set to 30 dB for the additive white Gaussian noise; the performance of the proposed algorithms with different SNR levels will be discussed in the last experiment.

Fig. 4
figure 4

Performance curves with a 8/16 sparsity for a 16-tap half-sparse system

Full size image
Fig. 5
figure 5

Performance curves with a 16/16 sparsity for a 16-tap non-sparse system

Full size image
Fig. 6
figure 6

Performance curves with a 16/128 sparsity for a 128-tap sparse system

Full size image

In the first experiment, the sparse system to be identified is randomly generated with 16 taps. In order to compare the performance of several algorithms with different sparsities, we formulate three cases for the sparse channel with 16 taps. In case 1, we set the coefficient of the \(5^\mathrm{th}\) tap to unity and the other 15 taps are set to zero, setting the system sparsity to 1/16. In case 2, the even terms among the 16 taps are set to zero, while the odd taps all are changed to one. Thus, the system sparsity is 8/16. In the last case, we change all the even taps to −1 and the odd terms remain as one. In this situation, the system becomes non-sparse. The simulation results of cases 1, 2, and 3 are depicted in Figs. 3, 4 and 5, respectively. The step size, \(\mu =0.05\), for both the LMS and the RZA-LMS. We set \(\rho =7\times 10^{-4}\) and \(\varepsilon =20\) for both the VSS-RZA-LMS and the RZA-LMS. In the proposed VSS-RZA-LMS and VSS-LMS, we set \(\beta =0.05\), \(\lambda =0.995\), and \(\delta =0.0001\). The initial values of \(\sigma _x^2 \) and \(\sigma _{e_{f}}^2 \) are equal to zero. The simulation results are obtained from the ensemble averages of over 300 independent runs.

In the second experiment with 128 taps, 16 taps are set to one and the others are zero. The values of \(\varepsilon \), \(\lambda \), and \(\delta \) are the same as in the first experiment. The step size, \(\mu \), for both the LMS and the RZA-LMS are changed to 0.01. The values of \(\rho \) are set to \(2\times 10^{-4}\) for both the VSS-RZA-LMS and the RZA-LMS. We set \(\beta =0.006\) for the VSS-RZA-LMS and the VSS-LMS. The initial values of \(\sigma _x^2 \) and \(\sigma _{e_{f}}^2 \) are equal to zero. The simulation results are obtained from the ensemble averages of over 100 independent runs. The simulation results of the second experiment are shown as Fig. 6.

Fig. 7
figure 7

Effects of the different SNR levels

Full size image

The system model and parameters of the third experiment are the same as those of the second. In this experiment, we test the proposed algorithms with different SNR levels. The SNRs are set to be 15, 25 and 35 dB, separately. The simulation results are obtained from the ensemble averages of over 30 independent runs. The simulation results of the third experiment are illustrated in Fig. 7.

Comparing Figs. 3, 4 and 5, we can see that the proposed algorithms have a lesser steady-state mean square error than the conventional LMS and RZA-LMS algorithms. The proposed VSS-RZA-LMS algorithm shows robustness when the number of nonzero taps increases, with little loss in performance compared to the VSS-LMS in non-sparse situations. In Fig. 6, the flexibility and robustness of the proposed algorithms are presented, when the number of taps increases. The simulation results in Fig. 7 clearly depict the effect with different SNR levels.

Although the proposed VSS method can achieve a better performance than the original fixed step-size algorithms, certain objective limitations for its practical application continue to exist. The step size of the RZA-LMS becomes considerably small when the number of taps is significant; in this situation, the VSS method will be unsuitable. Thus, the improvement of the performance of a large sparse system is a valuable topic for future research.

4 Conclusion

In this paper, a novel variable step-size method based on an error function for sparse system model is proposed. Using the nonlinear relationship between the step size and the power of the noise-free prior error, the proposed variable step-size algorithm balances the steady-state mean square error and the convergence speed satisfactorily. The simulation results show that the proposed variable step-size RZA-LMS can obtain a better performance than the fixed step-size algorithm.