A smooth simultaneous confidence band for conditional variance function

Abstract

A smooth simultaneous confidence band (SCB) is obtained for heteroscedastic variance function in nonparametric regression by applying spline regression to the conditional mean function followed by Nadaraya–Waston estimation using the squared residuals. The variance estimator is uniformly oracally efficient, that is, it is as efficient as, up to order less than $n^{-1/2}$, the infeasible kernel estimator when the conditional mean function is known, uniformly over the data range. Simulation experiments provide strong evidence that confirms the asymptotic theory while the computing is extremely fast. The proposed SCB has been applied to test for heteroscedasticity in the well-known motorcycle data and Old Faithful geyser data with different conclusions.

1 Introduction

Conditional variance function is an important ingredient in regression analysis, as many statistical applications require knowledge of the variance function, such as weighted least squares estimation of the mean function and construction of confidence intervals/bands for the mean function. Compared to mean function estimation, the literature on the estimation of variance function is rather sparse. Fan and Yao (1998) proved efficiency of the residual-based kernel variance estimator, Müller and Stadtmüller (1987) and more recently, Levine (2006) and Brown and Levine (2007) proposed difference-based kernel estimator and obtained its asymptotic normality, while Wang et al. (2008) derived the minimax rate of convergence for variance function estimation and constructed minimax rate optimal kernel estimators. For applications of variance estimation in the analysis of assay and microarray data, see Davidian et al. (1988) and Cai and Wang (2008).

Existing literature had mostly overlooked one crucial aspect of the problem, that is, simultaneous confidence band (SCB) for the variance function, which is an extremely powerful tool for inference on the global shape of curves, see for instance, Bickel and Rosenblatt (1973), Hall and Titterington (1988), Härdle (1989), Xia (1998), Claeskens and Van Keilegom (2003), Ma et al. (2012), Wang et al. (2014), Zheng et al. (2014) for theoretical works on SCB. This paper provides a spline–kernel two-step estimator of the variance function that is oracally efficient and comes equipped with a smooth SCB that substantially improves over the spline SCB of Song and Yang (2009), both theoretically and computationally.

To describe the problem, let observations $\left\{ \left( X_{i},Y_{i}\right) \right\} _{i=1}^{n}$ and unobserved errors $\left\{ \varepsilon _{i}\right\} _{i=1}^{n}$ be i.i.d copies of $\left( X,Y,\varepsilon \right)$ satisfying the regression model

$$\begin{aligned} Y=m\left( X\right) +\varepsilon , \end{aligned}$$

(1)

where $\mathsf {E}\left( \varepsilon \mid X\right) =0,\mathsf {E}\left( \varepsilon ^{2}\mid X\right) =\sigma ^{2}\left( X\right)$, and the conditional mean function $m\left( x\right)$ and variance function $\sigma ^{2}\left( x\right)$, defined on a compact interval $\left[ a,b\right] ,$ are unknown. Note that with squared errors $Z_{i}=\varepsilon _{i}^{2},1\le i\le n,\mathsf {E}\left( Z_{i}\mid X_{i}\right) =\sigma ^{2}\left( X_{i}\right)$, hence the variance function $\sigma ^{2}(x)$ is in fact the conditional mean function of $Z_{i}$ on $X_{i}$. If $\sigma ^{2}(\cdot )$ is constant, the model is homoscedastic, otherwise heteroscedastic, see Dette and Munk (1998) for testing of heteroscedasticity, Carroll and Ruppert (1988), Akritas and Van Keilegom (2001), Cai and Wang (2008) for regression methods in the presence of heteroscedastic errors, and Hall and Marron (1990) for rate-optimal estimator of homoscedastic variance.

Suppose for the sake of discussion that the mean function $m\left( x\right)$ were known by “oracle”, one could obtain a new data set $\left\{ \left( X_{i},Z_{i}\right) \right\} _{i=1}^{n}$, in which $Z_{i}=\left\{ Y_{i}-m\left( X_{i}\right) \right\} ^{2},1\le i\le n$ , and estimate the function $\sigma ^{2}(x)$ by a regressor $\tilde{\sigma } ^{2}(x)$ of the $Z_{i}$’s on the $X_{i}$’s, a would-be estimator called “infeasible estimator” as it is based on unavailable knowledge, serves as a useful benchmark against which feasible ones can be compared to. Fan and Yao (1998) had obtained two-step estimator $\hat{\sigma }^{2}\left( x\right)$ of $\sigma ^{2}\left( x\right)$ by local linear regression of $\hat{Z} _{i}=\{ Y_{i}-\hat{m}\left( X_{i}\right) \} ^{2}$ on $X_{i}$, in which $\hat{m}\left( x\right)$ is a first-step local linear estimator of $m\left( x\right)$, and shown that for any fixed $x\in \left( a,b\right)$, $\hat{\sigma }^{2}\left( x\right)$ was asymptotically as efficient as the “infeasible local linear estimator” $\tilde{\sigma }^{2}(x)$. Since this efficiency was merely pointwise, it allowed only the construction of confidence interval for $\sigma ^{2}\left( x\right)$ at a single point $x$, not at every point $x\in \left[ a,b\right]$ with simultaneous coverage, see also Hall and Carroll (1989) for the negligible effect of mean on the estimation of variance function.

Song and Yang (2009) had formulated a two-step estimator $\hat{\sigma } ^{2}\left( x\right)$ of $\sigma ^{2}\left( x\right)$ by spline regression of $\hat{Z}_{i}=\{ Y_{i}-\hat{m}\left( X_{i}\right) \} ^{2}$ on $X_{i}$, in which $\hat{m}\left( x\right)$ is a first step spline estimator of $m\left( x\right)$, and established asymptotic efficiency of $\hat{\sigma }^{2}\left( x\right)$ relative to an “infeasible spline estimator” $\tilde{\sigma }^{2}(x)$ over the data range $[a,b]$, and as a result an SCB was obtained for the whole variance curve as formulated in Wang and Yang (2009). There are some serious theoretical shortcomings, however with the shortcomings, however, with the spline SCB of Wang and Yang (2009) and hence also of Song and Yang (2009): the constant spline SCB is too wide and inaccurate; the linear spline SCB is narrow but its coverage probability is higher than the nominal level.

We propose a two-step estimator of $\sigma ^{2}(x)$ by spline estimator $\hat{m}\left( x\right)$ of $m\left( x\right)$ in step one and kernel estimator $\hat{\sigma }^{2}\left( x\right)$ of $\sigma ^{2}\left( x\right)$ in step two, which is uniformly as efficient as the infeasible kernel estimator, and hence oracally efficient. It is smooth as it comes from kernel smoothing, and enjoys excellent convergence rate of kernel smoother as well as coverage probability quickly approaching the nominal value. As an illustration, consider the motorcycle data, with Fig. 4 depicting the spline–kernel SCB of its variance function, at confidence levels 99.991 and 98.698 %, overlaid with a constant variance estimate which is either a consistent estimate $n^{-1}\sum \nolimits _{i=1}^{n}\hat{ \varepsilon }_{i,p}^{2}$ or the maximum of lower confidence line, the constant variance hypothesis is rejected in both scenarios, with $p$ value $=0.00009$ or $0.01302$. While the proposed SCB is superior to the SCB of Song and Yang (2009), the spline–kernel estimator is computationally much faster than the kernel–kernel estimator of Fan and Yao (1998), due to using spline instead of kernel in step one, which cuts computing burden substantially, see Xue and Yang (2006) and Wang and Yang (2007) for speed comparison of spline and kernel smoothing. The new spline–kernel estimator is shown in Theorem to be globally as efficient as the “infeasible kernel estimator” while the kernel–kernel estimator of Fan and Yao (1998) is as efficient as the “infeasible kernel estimator” only at a fixed point, see also Equation (3.2) of Hall and Carroll (1989) for pointwise oracle efficiency. Furthermore, oracle efficiency in Theorem 1 is of order smaller than $n^{-1/2}$, which had not existed in previous works.

The paper is organized as follows. Section 2 presents main theoretical results and Sect. 3 provides insights of proofs, Sect. 4 gives concrete steps to implement the SCB, while Sects. 5 and 6 report simulation results and analysis of the motorcycle data and Old Faithful geyser data. Section 7 concludes, and technical proofs are in the “Appendix”.

2 Main result

Without loss of generality, we take $\left[ a,b\right] =\left[ 0,1\right]$. An asymptotic $100\left( 1-\alpha \right) \%$ simultaneous confidence band (SCB) for the unknown variance function $\sigma ^{2}\left( x\right)$ over a sequence of subintervals $\left[ a_{n},b_{n}\right] \subseteq \left[ 0,1\right]$ where $a_{n}\rightarrow 0,b_{n}\rightarrow 1$ as $n\rightarrow \infty$, consists of an estimator $\hat{\sigma }^{2}\left( x\right)$ of $\sigma ^{2}\left( x\right)$, lower and upper confidence limit $\hat{\sigma }^{2}\left( x\right) -l_{n,L}\left( x\right) ,$ $\hat{ \sigma }^{2}\left( x\right) +l_{n,U}\left( x\right)$ at every $x\in \left[ a_{n},b_{n}\right]$ such that

$\underset{n\rightarrow \infty }{\lim }P\left\{ \sigma ^{2}\left( x\right) \in \left[ \hat{\sigma }^{2}\left( x\right) -l_{n,L}\left( x\right) ,\hat{ \sigma }^{2}\left( x\right) +l_{n,U}\left( x\right) \right] ,\quad \forall x\in \left[ a_{n},b_{n}\right] \right\} =1-\alpha .$

Our goal is to construct error bound function $l_{n,L}(x)$, $l_{n,U}(x)$ based on data $\left\{ \left( X_{i},Y_{i}\right) \right\} _{i=1}^{n}$ drawn from model (1). We describe briefly below the ideas of oracally efficient estimation, which will be shown later to yield the SCB.

If the mean function $m\left( x\right)$ were known by “oracle ”, one could compute the errors $\varepsilon _{i}=Y_{i}-m\left( X_{i}\right)$ and the squared errors $Z_{i}=\varepsilon _{i}^{2},1\le i\le n$, and then smooth the data $\left\{ \left( X_{i},Z_{i}\right) \right\} _{i=1}^{n}$, taking advantage of the fact that $\mathsf {E}\left( Z_{i}\mid X_{i}\right) \equiv \sigma ^{2}\left( X_{i}\right)$. Specifically, denote by $K$ a kernel function, $h=h_{n}$ a sequence of smoothing parameters called bandwidth, and $K_{h}\left( u\right) =K\left( u/h\right) /h$, an “infeasible kernel estimator” of the variance function is

$$\begin{aligned} \tilde{\sigma }_{\text {K}}^{2}\left( x\right) =\frac{\sum _{i=1}^{n}K_{h} \left( X_{i}-x\right) Z_{i}}{\sum _{i=1}^{n}K_{h}\left( X_{i}-x\right) }. \end{aligned}$$

(2)

To mimic this would-be kernel estimator $\tilde{\sigma }_{\text {K}}^{2}\left( x\right)$ of $\sigma ^{2}\left( x\right)$, a spline–kernel oracally efficient estimator $\hat{\sigma }_{\text {SK}}^{2}\left( x\right)$ of $\sigma ^{2}\left( x\right)$ is

$$\begin{aligned} \hat{\sigma }_{\text {SK}}^{2}\left( x\right) =\frac{\sum _{i=1}^{n}K_{h}\left( X_{i}-x\right) \hat{Z}_{i}}{\sum _{i=1}^{n}K_{h}\left( X_{i}-x\right) }, \end{aligned}$$

(3)

where $\hat{Z}_{i}=\hat{\varepsilon }_{i,p}^{2}$ are the square of residuals $\hat{\varepsilon }_{i,p}$ obtained from spline regression,

$$\begin{aligned} \hat{\varepsilon }_{i,p}=Y_{i}-\hat{m}_{p}\left( X_{i}\right) ,\quad 1\le i\le n, \end{aligned}$$

(4)

the spline estimator $\hat{m}_{p}\left( x\right)$ is defined as follows, for some positive integer $p$,

$$\begin{aligned} \hat{m}_{p}\left( x\right) =\underset{g\in G_{N}^{\left( p-2\right) }\left[ 0,1\right] }{\arg \min }\sum \nolimits _{i=1}^{n}\left\{ Y_{i}-g\left( X_{i}\right) \right\} ^{2}, \end{aligned}$$

(5)

in which $G_{N}^{\left( p-2\right) }$ is the space of functions that are piecewise polynomials of degree $\left( p-1\right)$ on interval $\left[ 0,1 \right]$, defined below.

The interval $\left[ 0,1\right]$ is divided into $\left( N+1\right)$ subintervals $J_{j}=[ t_{j},t_{j+1}) ,j=0,\ldots ,N-1,J_{N}=[ t_{N},1]$ by a sequence of equally spaced points $\{ t_{j}\} _{j=1}^{N}$, called interior knots, given as

$$\begin{aligned} t_{0}=0<t_{1}<\cdots <1=t_{N+1},\quad t_{j}=jH,\quad j=0,1,\ldots ,N+1, \end{aligned}$$

in which $H=1/\left( N+1\right)$ is the distance between neighboring knots. We denote by $G_{N}^{\left( p-2\right) }=G_{N}^{\left( p-2\right) }\left[ 0,1\right]$ the space of functions that are polynomials of degree $\left( p-1\right)$ on each $J_{j}$ and have continuous $\left( p-2\right)$th derivative. In particular, $G_{N}^{\left( 0\right) }$ denotes the space of functions that are linear on each $J_{j}$ and continuous on $\left[ 0,1\right]$, with linear B-spline basis $\{ b_{j,2}( x) \} _{j=-1}^{N}$ being

$$\begin{aligned} b_{j,2}\left( x\right) =K_{0}\left( \frac{x-t_{j+1}}{H}\right) ,\quad j=-1,0,\ldots ,N,\quad \text {for}\quad K_{0}\left( u\right) =\left( 1-\left| u\right| \right) _{+}. \end{aligned}$$

Alternatively, one can estimate $\sigma ^{2}\left( x\right)$ by spline local linear estimator $\hat{\sigma }_{\text {SLL}}^{2}\left( x\right)$ based on $\{ X_{i},\hat{Z}_{i}\} _{i=1}^{n}$, which mimics the would-be local linear estimator $\tilde{\sigma }_{\text {LL}}^{2}\left( x\right)$ based on $\left\{ X_{i},Z_{i}\right\} _{i=1}^{n}$,

$$\begin{aligned} \left\{ \hat{\sigma }_{\text {SLL}}^{2}\left( x\right) ,\tilde{\sigma }_{\text { LL}}^{2}\left( x\right) \right\} =\left( 1,0\right) \left( \mathbf {X}^{ \scriptstyle {T}}\mathbf {WX}\right) ^{-1}\mathbf {X}^{\scriptstyle {T}}\mathbf {W }\left( {\hat{\mathbf {Z}}},\mathbf {Z}\right) , \end{aligned}$$

in which the oracle and pseudo-response vectors are

$$\begin{aligned} \mathbf {Z}=\left( Z_{1},\ldots ,Z_{n}\right) , \quad {\hat{\mathbf {Z}}}=\left( \hat{Z }_{1},\ldots ,\hat{Z}_{n}\right) \end{aligned}$$

with the same weight and design matrices

$$\begin{aligned} \mathbf {W}=\text {diag}\left\{ K_{h}\left( X_{i}-x\right) \right\} _{i=1}^{n}\!, \quad \mathbf {X}^{\scriptstyle {T}}=\left( \begin{array}{ccc} 1 &{} \quad ,\ldots , &{}\quad 1 \\ X_{1}-x &{}\quad ,\ldots , &{}\quad X_{n}-x \end{array} \right) . \end{aligned}$$

The idea of synthesizing spline and kernel smoothing in one estimator appeared first in Wang and Yang (2007), Wang and Yang (2009) for additive model and later extended to generalized additive model in Liu et al. (2013).

To formulate the necessary technical assumptions, for sequences of real numbers $c_{n}$ and $d_{n}$, one writes $c_{n}\ll d_{n}$ to mean $c_{n}/d_{n}\rightarrow 0$, as $n\rightarrow \infty$.

• (A1) The function $m\left( \cdot \right) \in C^{p}\left[ 0,1 \right]$, $p>1$.

• (A2) The joint distribution of $(X,\varepsilon )$ is bivariate continuous with $\mathsf {E}(\varepsilon \mid X) =0$, $\mathsf {E}(\varepsilon ^{2}\mid X) =\sigma ^{2}(X)$, and for some $\eta >1/2$,$\sup _{x\in [ 0,1] }\mathsf {E}(\vert \varepsilon \vert ^{4+2\eta }\mid X=x) =M_{\eta }<+\infty$.

• (A3) The density function $f( x) \in C[ 0,1 ]$, the variance function $\sigma ^{2}( x) \in C^{2}[ 0,1]$, and $0<c_{f}\le f( x) \le C_{f}<+\infty ,0<c_{\sigma }\le \sigma ( x) \le C_{\sigma }<+\infty$ for $x\in [ 0,1]$.

• (A4) The kernel function $K\in C^{( 1) }( \mathbb {R})$ is a symmetric probability density function supported on $[ -1,1]$.

• (A5) The bandwidth $h$ satisfies $n^{2\alpha -1}(\log n) ^{4}\ll h\ll n^{-1/5}(\log n) ^{-1/5}$, for some $\alpha$ such that $\alpha <2/5$, $\alpha (2+\eta ) >1$, $\alpha (1+\eta ) >2/5$.

• (A6) The number of interior knots $N=N_{n}$ satisfies

  $$\begin{aligned} \max \left\{ \! \left( \frac{n}{h^{2}}\right) ^{1/4p}\!,\left( \frac{\log n}{h} \right) ^{1/2\left( p-1\right) }\!\right\} \!\ll \! N\!\ll \! \min \left\{ n^{1/2}h,\left( \frac{nh}{\log n}\!\right) ^{\!1/3}\!,\left( \frac{n}{h}\right) ^{1/5}\!\right\} . \end{aligned}$$

Assumptions (A1)–(A3) are adapted from Song and Yang (2009), Assumption (A4) is standard for kernel regression, and Assumptions (A5) and (A6) are general conditions on the choice of number of knots $N$ and bandwidth $h$ to ensure oracle efficient and the extreme distribution result in (6) below. In particular, one may take the mean squared error optimal order $N$ $\sim n^{1/\left( 2p+1\right) }$ and an undersmoothing $h=n^{-1/5}\left( \log n\right) ^{-1/5-\delta }$ for any $\delta >0$, which satisfy all the requirements in Assumptions (A5) and (A6). As an example, data-driven implementation of $N$ and $h$ is given in Sect. 4, aided by explicit formulae (13) for BIC and (15) for rule-of-thumb bandwidth.

It follows from Assumption (A2) that the conditional variance of $Z=\varepsilon ^{2}$ is $v_{Z}^{2}\left( x\right) \equiv \text {var}\left( Z\mid X=x\right) \equiv \mu _{4}\left( x\right) -\sigma ^{4}\left( x\right)$ in which $\mu _{4}\left( x\right) \equiv \mathsf {E}(\varepsilon ^{4}\mid X=x)$. In addition

$$\begin{aligned} \sup _{x\in \left[ 0,1\right] }\mathsf {E}\left( \left| Z-\sigma ^{2}\left( X\right) \right| ^{2+\eta }\mid X=x\right)&\le \sup _{x\in \left[ 0,1\right] }\mathsf {E}\left( Z^{2+\eta }+\sigma \left( X\right) ^{4+2\eta }\mid X=x\right) \\&< M_{\eta }+C_{\sigma }^{4+2\eta }<+\infty . \end{aligned}$$

Consequently, under Assumptions (A2)–(A5), by applying classic SCB theory to the unobservable sample $\left\{ \left( X_{i},Z_{i}\right) \right\} _{i=1}^{n}$, one has

$$\begin{aligned} P\left[ a_{h}\left\{ \underset{x\in \left[ h,1-h\right] }{\sup }\left| \tilde{\sigma }_{\text {K}}^{2}\left( x\right) -\sigma ^{2}\left( x\right) \right| /V_{n}-b_{h}\right\} \le t\right] \rightarrow e^{-2e^{-t}},\quad t\in \mathbb {R} \end{aligned}$$

(6)

where

(7)

From (6) one obtains an asymptotic $100\left( 1-\alpha \right) \%$ oracle SCB for $\sigma ^{2}\left( x\right)$ over $\left[ h,1-h\right]$ ,

$$\begin{aligned} \tilde{\sigma }_{\text {K}}^{2}\left( x\right) \pm V_{n}\left( 2\log h^{-1}\right) ^{1/2}Q_{n}\left( \alpha \right) , \end{aligned}$$

(8)

where

$$\begin{aligned} Q_{n}\left( \alpha \right) =1+\frac{\log \left\{ C\left( K\right) /2\pi \right\} -\log \left\{ -\frac{1}{2}\log \left( 1-\alpha \right) \right\} }{ 2\log h^{-1}}. \end{aligned}$$

(9)

In stating our main theoretical results in the next two Theorems, and throughout this paper, we denote by $\left\| \cdot \right\| _{\infty }$, the supremum norm of a function $r$ on $\left[ 0,1\right]$, i.e., $\left\| r\right\| _{\infty }=\sup _{_{x\in \left[ 0,1\right] }}\left| r\left( x\right) \right|$.

Theorem 1

Under Assumptions (A1)–(A6), as $n\rightarrow \infty$ , the estimator $\hat{\sigma }_{\text {SK}}^{2}\left( x\right)$ is asymptotically as efficient as the “infeasible estimator”, $\tilde{\sigma }_{ \text {K}}^{2}\left( x\right)$ i.e.,

$$\begin{aligned} \left\| \hat{\sigma }_{\text {SK}}^{2}-\tilde{\sigma }_{\text {K} }^{2}\right\| _{\infty }=o_{p}\left( n^{-1/2}\right) . \end{aligned}$$

As commented in the introduction, the oracle efficiency stated in Theorem 1 is of the unprecedented small order $o_{p}\left( n^{-1/2}\right)$, and the next result follows immediately.

Theorem 2

Under Assumptions (A1)–(A6), an asymptotic $100\left( 1-\alpha \right) \%$ oracally efficient SCB for $\sigma ^{2}\left( x\right)$ over $\left[ h,1-h\right]$ is

$$\begin{aligned} \hat{\sigma }_{\text {SK}}^{2}\left( x\right) \pm V_{n}\left( 2\log h^{-1}\right) ^{1/2}Q_{n}\left( \alpha \right) \end{aligned}$$

(10)

with $V_{n}$ and $Q_{n}\left( \alpha \right)$ given in (7) and (9) respectively. In other words,

$$\begin{aligned} \underset{n\rightarrow \infty }{\lim }P\left\{ \sigma ^{2}\left( x\right) \in \hat{\sigma }_{\text {SK}}^{2}\left( x\right) \pm V_{n}\left( 2\log h^{-1}\right) ^{1/2}Q_{n}\left( \alpha \right) ,\forall x\in \left[ h,1-h \right] \right\} =1-\alpha . \end{aligned}$$

The proofs of Theorems 1 and 2 depend on Propositions 1, 2 and 3 given in Sect. 3. The proofs of these Propositions are based on Lemmas 1, 4 and 2. All of them are provided in the “Appendix”. Both Theorems 1 and 2 remain true with spline–kernel estimator $\hat{\sigma }_{\text {SK} }^{2}\left( x\right)$ replaced by spline-local linear estimator $\hat{\sigma }_{\text {SLL}}^{2}\left( x\right)$, but detailed proofs for local linear estimator are omitted as in Wang and Yang (2007, 2009).

3 Error decomposition

To break the estimation error $\hat{\sigma }_{\text {SK}}^{2}\left( x\right) - \tilde{\sigma }_{\text {K}}^{2}\left( x\right)$ into simpler parts, we begin by discussing the spline space $G^{(p-2)}_{N}$ and the representation of the spline estimator of $\hat{m}_{p}(x)$ in Eq. (5).

Denote by $\left\| \phi \right\| _{2}$ the theoretical $L^{2}$ norm of a function $\phi$ on $\left[ 0,1\right]$ , i.e., $\left\| \phi \right\| _{2}^{2}=\mathsf {E}\{ \phi ^{2}( X) \} =\int _{0}^{1}\phi ^{2}\left( x\right) f\left( x\right) dx$, the empirical $L^{2}$ norm as $\left\| \phi \right\| _{2,n}^{2}=n^{-1}\small {\sum _{i=1}^{n}}\phi ^{2}\left( X_{i}\right)$, and then define the rescaled B-spline basis $\{ B_{j,p}( x) \} _{j=1-p}^{N}$ for $G_{N}^{\left( p-2\right) }$, each with theoretical norm equal to $1$

$$\begin{aligned} B_{j,p}\left( x\right) \equiv b_{j,p}\left( x\right) \left\| b_{j,p}\left( x\right) \right\| _{2}^{-1},\quad 1-p\le j\le N. \end{aligned}$$

The estimator $\hat{m}_{p}\left( x\right)$ in Eq. (5) can then be expressed as

$$\begin{aligned} \hat{m}_{p}\left( x\right) =\underset{G_{N}^{\left( p-2\right) }}{\text {Proj} }\mathbf {Y}=\sum \limits _{j=1-p}^{N}\hat{\lambda }_{j,p}B_{j,p}\left( x\right) , \end{aligned}$$

where the vector $\{ \hat{\lambda }_{1-p,p},\ldots ,\hat{\lambda } _{N,p}\} ^{\scriptstyle {T}}$ solves the following least-squares problem

$$\begin{aligned} \left\{ \hat{\lambda }_{1-p,p},\ldots ,\hat{\lambda }_{N,p}\right\} ^{ \scriptstyle {T}}=\underset{R^{N+p}}{\arg \min }\sum \limits _{i=1}^{n}\left\{ Y_{i}-\sum \limits _{j=1-p}^{N}\hat{\lambda }_{j,p}B_{j,p}\left( X_{i}\right) \right\} ^{2}. \qquad \quad \end{aligned}$$

(11)

We write $\mathbf {Y}$ as the sum of a signal vector $\mathbf {m}$ and a noise vector $\mathbf {E}$,

$$\begin{aligned} \mathbf {Y}=\mathbf {m}+\mathbf {E},\quad \mathbf {m}=\left\{ m\left( X_{1}\right) ,\ldots ,m\left( X_{n}\right) \right\} ^{\scriptstyle {T}},\quad \mathbf {E}=\left\{ \varepsilon _{1},\ldots ,\varepsilon _{n}\right\} ^{\scriptstyle {T}}. \end{aligned}$$

Projecting this relationship into the space $G_{n}^{\left( p-2\right) }$, one obtains

$$\begin{aligned} \hat{\mathbf {m}}_{p}=\left\{ \hat{m}_{p}\left( X_{1}\right) ,\ldots ,\hat{m} _{p}\left( X_{n}\right) \right\} ^{\scriptstyle {T}}=\underset{G_{n}^{\left( p-2\right) }}{\text {Proj}}\mathbf {Y}=\underset{G_{n}^{\left( p-2\right) }}{ \text {Proj}}\mathbf {m}+\underset{G_{n}^{\left( p-2\right) }}{\text {Proj}} \mathbf {E}. \end{aligned}$$

Correspondingly, in the space $G_{N}^{\left( p-2\right) }$, one has $\hat{m} _{p}\left( x\right) =\tilde{m}_{p}\left( x\right) +\tilde{\varepsilon } _{p}\left( x\right) ,$ where

$$\begin{aligned} \tilde{m}_{p}\left( x\right) =\sum _{J=1-p}^{N}\tilde{\lambda } _{J,p}B_{J,p}\left( x\right) ,\quad \tilde{\varepsilon }_{p}\left( x\right) =\sum _{J=1-p}^{N}\tilde{a}_{J,p}B_{J,p}\left( x\right) , \end{aligned}$$

(12)

with the vectors $\left\{ \tilde{\lambda }_{1-p,p},\ldots ,\tilde{ \lambda }_{N,p}\right\} ^{\scriptstyle {T}}$ and $\left\{ \tilde{a} _{1-p,p},\ldots ,\tilde{a}_{N,p}\right\} ^{\scriptstyle {T}}$ being solutions to (11) with $Y_{i}$ replaced by $m(X_{i})$ and $\varepsilon _{i}$ respectively.

Regarding variance estimator in (2) and (3)

$$\begin{aligned} \hat{\sigma }_{\text {SK}}^{2}\left( x\right) -\tilde{\sigma }_{\text {K} }^{2}\left( x\right)&= \frac{\sum _{i=1}^{n}K_{h}\left( X_{i}-x\right) \left( \mathrm{I}_{i,p}+\mathrm{II}_{i,p}+\mathrm{III}_{i,p}\right) }{\sum _{i=1}^{n}K_{h}\left( X_{i}-x\right) } \\&= \hat{f}^{-1}\left( x\right) \left\{ \mathrm{I}+\mathrm{II}+\mathrm{III}\right\} , \end{aligned}$$

in which $\hat{f}\left( x\right) =n^{-1}\sum _{i=1}^{n}K_{h}\left( X_{i}-x\right)$,

$$\begin{aligned} \mathrm{I}&= \mathrm{I}\left( x\right) =n^{-1}\sum \limits _{i=1}^{n}K_{h}\left( X_{i}-x\right) \mathrm{I}_{i,p},\\ \mathrm{II}&= \mathrm{II}\left( x\right) =n^{-1}\sum \limits _{i=1}^{n}K_{h}\left( X_{i}-x\right) \mathrm{II}_{i,p},\\ \mathrm{III}&= \mathrm{III}\left( x\right) =n^{-1}\sum \limits _{i=1}^{n}K_{h}\left( X_{i}-x\right) \mathrm{III}_{i,p},\\ \mathrm{I}_{i,p}&= \left\{ m\left( X_{i}\right) -\tilde{m}_{p}\left( X_{i}\right) \right\} ^{2}+\tilde{\varepsilon }_{p}^{2}\left( X_{i}\right) +2\left\{ \tilde{m}_{p}\left( X_{i}\right) -m\left( X_{i}\right) \right\} \tilde{ \varepsilon }_{p}\left( X_{i}\right) ,\\ \mathrm{II}_{i,p}&= -2\varepsilon _{i}\tilde{\varepsilon }_{p}\left( X_{i}\right) ,\mathrm{III}_{i,p}=\left\{ m\left( X_{i}\right) -\tilde{m}_{p}\left( X_{i}\right) \right\} \varepsilon _{i}. \end{aligned}$$

By Assumption (A3), $\hat{f}\left( x\right) =f\left( x\right) +u_{p}\left( 1\right) \ge c_{f}+u_{p}\left( 1\right)$, hence Theorem 1 follows from the next three Propositions on I, II, III.

Proposition 1

Under Assumptions (A1)–(A6), as $n\rightarrow \infty ,$

$$\begin{aligned} \left\| \mathrm{I}\right\| _{\infty }=\mathcal {O}_{p}\left\{ h^{-1}\left( H^{2p}+{(nH)}^{-1}\right) \right\} =o_{p}\left( n^{-1/2}\right) . \end{aligned}$$

Proposition 2

Under Assumptions (A1)–(A6), as $n\rightarrow \infty$,

$$\begin{aligned} \left\| \mathrm{II}\right\| _{\infty }=\mathcal {O}_{p}\left( n^{-1}h^{-1/2}H^{-3/2}\log ^{1/2}n+n^{-1}h^{1/2}H^{-5/2}\right) =o_{p}\left( n^{-1/2}\right) . \end{aligned}$$

Proposition 3

Under Assumptions (A1)–(A6), as $n\rightarrow \infty$,

$$\begin{aligned} \left\| \mathrm{III}\right\| _{\infty }=\mathcal {O}_{p}\left\{ n^{-1/2}h^{-1/2}H^{p-1}\log ^{1/2}n+n^{-1/2}h^{1/2}H^{p-2}\right\} =o_{p}\left( n^{-1/2}\right) . \end{aligned}$$

4 Implementation

We describe in this section one concrete procedure that implements the oracally efficient SCB in Theorem 2, and is used throughout Sects. 5 and 6 for both simulated and real data examples. Given any sample $\left\{ \left( X_{i},Y_{i}\right) \right\} _{i=1}^{n}$ from model (1), let $a=\min \left( X_{1},\ldots ,X_{n}\right) ,b =\max \left( X_{1},\ldots ,X_{n}\right)$ and transform the data range from $\left[ a,b\right]$ into $\left[ 0,1\right]$ by the linear transformation $x\rightarrow$ $(x-a)/(b-a)$. If this linear operation fails to make design variable $X$ conform to Assumption (A3), one applies the quantile transformation $x\rightarrow$ $F_{n}=n^{-1}\sum \nolimits _{i=1}^{n}\mathrm{I}\left( X_{i}\le x\right)$.

To select the number of interior knots $N$, let $\hat{N}^{\text {opt}}$ be the minimizer of BIC defined below, over integers from $\left[ 0.5N_{r},\min \left( 5N_{r},Tb\right) \right]$, with $N_{r}=n^{-1/\left( 2p+1\right) }$ and $Tb=n/4-1$, which ensures that $\hat{N}^{\text {opt} }$ is order of $n^{-1/\left( 2p+1\right) }$ and the number of parameters in the least-squares estimation is less than $n/4$. The chosen $\hat{N}^{\text {opt}}$ obviously satisfies Assumption (A6), but other choices of $N$ remain open possibility. For any candidate integer $N\in \left[ 0.5N_{r},\min \left( 5N_{r},Tb\right) \right]$, denote the predictor for the $i$-th response $Y_{i}$ by $\hat{Y} _{i}=\hat{m}_{p}(X_{i})$, and let $q_{n}=\left( 1+N_{n}\right)$ be the number of parameters in (11), the BIC value corresponding to $N$ is,

$$\begin{aligned} \text {BIC}=\log \left( \text {MSE}\right) +q_{n}\log \left( n\right) /n,\text { MSE}=n^{-1}\sum \limits _{i=1}^{n}\left\{ Y_{i}-\hat{Y}_{i}\right\} ^{2}. \end{aligned}$$

(13)

Algebra shows that the least-squares problem in Eq. (11) can be also solved via the truncated power basis $\left\{ 1,x,\ldots ,x^{p-1}\!,\left( x-t_{j}\right) _{+}^{p-1}\!,j=1,2,\ldots N\right\}$, see de Boor (2001), which is regularly used in implementation. In other words,

$$\begin{aligned} \hat{m}_{p}\left( x\right) =\overset{p-1}{\underset{k=0}{\sum }}\hat{r} _{k}x^{k}+\overset{N}{\underset{j=1}{\sum }}\hat{r}_{j,p}\left( x-t_{j}\right) _{+}^{k}, \end{aligned}$$

(14)

where the coefficients $\left( \hat{r}_{0},\ldots ,\hat{r}_{p-1},\hat{r} _{1,p},\ldots ,\hat{r}_{N,p}\right) ^{\scriptstyle {T}}$ are solutions to the least squares problem

$\left( \hat{r}_{0},\dots ,\hat{r}_{N,p}\right) ^{\scriptstyle {T}}\!=\!\mathop {\text {argmin}}\limits _{\left( r_{0},\dots ,r_{N,p}\right) \in \mathbb {R}^{N+P}}\sum \limits _{ i=1}^{n}\left\{ \! Y_{i}\!-\!\sum \limits _{k=0}^{p-1} r_{k}X_{i}^{k}\!-\!\sum \limits _{j=1}^{N}r_{j,p}\left( X_{i}-t_{j}\right) _{+}^{k}\right\} ^{2}\!.$

To choose an appropriate bandwidth $h=h_{n}$ for computing $\hat{\sigma }_{ \text {SK}}^{2}\left( x\right)$, one adopts the following rule-of-thumb (ROT) bandwidth of Fan and Gijbels (1996), Equation (4.3):

$$\begin{aligned} h_{\text {rot}}=\left\{ \frac{35\sum \nolimits _{i=1}^{n}\left( \hat{Z} _{i}-\sum \nolimits _{k=0}^{4}\widehat{a}_{k}X_{i}^{k}\right) ^{2}}{ n\sum \nolimits _{i=1}^{n}\left( 2\widehat{a}_{2}+6\widehat{a}_{3}X_{i}+12 \widehat{a}_{4}X_{i}^{2}\right) ^{2}}\right\} ^{1/5} \end{aligned}$$

(15)

in which $\left( \widehat{a}_{k}\right) _{k=0}^{4}=\text {argmin}_{\left( a_{k}\right) _{k=0}^{4}\in \mathbb {R}^{5}}\sum \nolimits _{i=1}^{n}\left( \hat{ Z}_{i}-\sum \nolimits _{k=0}^{4}a_{k}X_{i}^{k}\right) ^{2}$. One then sets $h=h_{n}=h_{\text {rot}}(\log n)^{-1/2} \sim n^{-1/5}\left( \log n\right) ^{-1/2}$, which clearly satisfies Assumption (A5), especially the undersmoothing condition $h\ll n^{-1/5}\left( \log n\right) ^{-1/5}$.

For constructing the SCB, the unknown functions $v_{Z}^{2}\left( x\right)$ and $f\left( x\right)$ are evaluated and then plugged in, the same approach taken in Hall and Titterington (1988), Härdle (1989), Xia (1998), Wang and Yang (2009), Song and Yang (2009). Let $\tilde{K}\left( u\right)$ $=15\left( 1-u^{2}\right) ^{2}\mathrm{I}\left\{ \left| u\right| \le 1\right\} /16$ be the quadratic kernel and $s_{n}$ be the sample standard deviation of $\left\{ X_{i}\right\} _{i=1}^{n}$ and

$$\begin{aligned} \hat{f}\left( x\right) =n^{-1}\overset{n}{\underset{i=1}{\sum }}h_{\text {rot} ,f}^{-1}\tilde{K}\left( \frac{X_{i}-x}{h_{\text {rot},f}}\right) ,\quad h_{\text {rot },f}=\left( 4\pi \right) ^{1/10}\left( \frac{140}{3}\right) n^{-1/5}s_{n}, \end{aligned}$$

(16)

where $h_{\text {rot},f}$ is the rule-of-thumb bandwidth in Silverman (1986). Define $\mathbf {\nabla }^{\scriptstyle {T}}=\{ \nabla _{i},1\le i\le n\}$, $\nabla _{i}=\{ \hat{Z}_{i}-\hat{\sigma }_{\text {SK} }^{2}\left( X_{i}) \right\} ^{2}$, and

$$\begin{aligned} \mathbf {X}=\mathbf {X}\left( x\right) =\left( \begin{array}{ccc} 1 &{} ,\ldots , &{} 1 \\ X_{1}-x &{} ,\ldots , &{} X_{n}-x \end{array} \right) ^{\scriptstyle {T}},\quad \mathbf {W}=\mathbf {W}\left( x\right) =\text {diag} \left\{ \tilde{K}\left( \frac{X_{i}-x}{h_{\text {rot},\sigma }}\right) \right\} _{i=1}^{n} \end{aligned}$$

where $h_{\text {rot},\sigma }$ is the ROT bandwidth of Fan and Gijbels (1996) Equation (4.3), as $h_{\text {rot}}$ in (15), but with the $\hat{Z}_{i}$’s replaced by $\nabla _{i}$’s, and define the following estimator of $v_{Z}^{2}\left( x\right)$

$$\begin{aligned} \hat{v}_{Z}^{2}\left( x\right) =\left( 1,0\right) \left( \mathbf {X}^{ \scriptstyle {T}}\mathbf {WX}\right) ^{-1}\mathbf {X}^{\scriptstyle {T}}\mathbf {W }\mathbf {\nabla }. \end{aligned}$$

(17)

The following results follow from Bickel and Rosenblatt (1973) and Fan and Gijbels (1996)

$$\begin{aligned} \underset{x\in \left[ 0,1\right] }{\sup }\left| \hat{v}_{Z}^{2}\left( x\right) -v_{Z}^{2}\left( x\right) \right| +\underset{x\in \left[ 0,1 \right] }{\sup }\left| \hat{f}\left( x\right) -f\left( x\right) \right| =o_{p}\left( 1\right) . \end{aligned}$$

(18)

The function $V_{n}$ is approximated by the following, with $\hat{f}\left( x\right)$ and $\hat{v}_{Z}^{2}\left( x\right)$ defined in Eqs. (16) and (17)

$$\begin{aligned} \hat{V}_{n}=\hat{v}_{Z}\left( x\right) {\left\{ \hat{f}\left( x\right) nh\right\} }^{-1/2}C_{K}^{1/2}. \end{aligned}$$

Then Eq. (18) and Theorem 2 imply that as $n\rightarrow \infty$, the SCB below is asymptotically $100\left( 1-\alpha \right) \%$

$$\begin{aligned} \hat{\sigma }_{\text {SK}}^{2}\left( x\right) \pm \hat{V}_{n}\left( 2\log h^{-1}\right) ^{1/2}Q_{n}\left( \alpha \right) . \end{aligned}$$

(19)

The construction described above of SCB according to Theorem 2, is over an interior portion of the data range $\left[ 0,1\right]$, namely $\left[ a_{n},b_{n}\right] =\left[ h_{n},1-h_{n}\right] \subseteq \left( 0,1\right)$, as seen in the SCB plots of Figs. 3, 2, 4 and 5. It should be emphasized, however, that the interval sequence $\left[ h_{n},1-h_{n}\right]$ covers the entire interior $\left( 0,1\right)$ as sample size $n\rightarrow \infty$ and $h_{n}\rightarrow 0$, which reflects, for instance, the widening range in Fig. 3 of SCB in (c) and (d) over (a) and (b).

Although any spline order $p>1$ can be employed, we have used only linear splines $\left( \text {with }p=2\right)$ for simplicity. It is well-known that the choice of kernel function is of less importance, according to Assumptions (A4) and (A5), the kernel function $K$ is chosen to be the quadratic kernel. Simulation comparison will be made in Sect. 5 of the above oracally efficient SCB with the infeasible SCB, which is computed from (8) with $v_{Z}^{2}(x)$ and $f(x)$ replaced by $\tilde{v} _{Z}^{2}(x)$ and $\hat{f}(x)$ in (16), respectively, where $\tilde{v}_{Z}^{2}(x)$ is the right side of (17) with $\mathbf {\nabla }$ substituted by $\tilde{\mathbf {\nabla }}$, where $\tilde{\mathbf {\nabla }}^{\scriptstyle {T}}=\{ \tilde{\nabla }_{i},1\le i\le n\}$, $\tilde{\nabla }_{i}=\{ {Z}_{i}-\tilde{\sigma }_{\text { K}}^{2}\left( X_{i}\right) \} ^{2}$.

5 Simulation

In this section, simulation results are presented to illustrate the finite-sample behavior of the oracally efficient SCB, on data sets generated from model (1), with $X\sim U[-1/2,1/2]$, and

$$\begin{aligned} m\left( x\right) =\sin \left( 2\pi x\right) ,\quad \sigma \left( x\right) =1/2-cx^{2},\quad \varepsilon \mid x\sim N\left\{ 0,\sigma ^{2}\left( x\right) \right\} . \end{aligned}$$

(20)

We choose $c=1,c=0.5$, which have included variance functions $\sigma ^{2}\left( x\right)$ that are strongly heteroscedastic $\left( c=1\right)$ and nearly homoscedastic $\left( c=0.5\right)$, while sample sizes are taken to be $n=100,200,500$ and the confidence levels are $1-\alpha =0.99,0.95$. Table 1 contains the coverage frequency of the true curve $\sigma ^{2}\left( x\right)$ at all data points $\left\{ X_{i}\right\} _{i=1}^{n}$ by the oracally efficient SCB whose construction details are in Sect. 4 over $500$ replications of sample size $n$. Coverage frequency over the same data sets of the infeasible SCB in (8) is also listed in the table. In all cases, the coverage improves with increasing sample size, which confirms to Theorem 2, and the two SCBs are quite close to each other in terms of coverage frequency, showing positive confirmation of Theorem 1. For both cases $c=1$ and $c=0.5$, the oracally efficient SCB has coverage frequency approaching the nominal level for sample size as low as $n=200$.

Table 1 Coverage frequency of the oracally efficient SCB in Theorem (2) and the infeasible SCB in (8) from $500$ replications

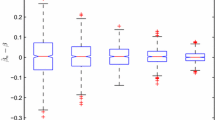
Figure 1 depicts the boxplots over $500$ replications of $\Delta _{n}=\sqrt{n}\max$ $\big \vert \tilde{\sigma }_{\text {K}}^{2}\left( x_{j}\right) -\hat{\sigma }_{ \text {SK}}^{2}\left( x_{j}\right) \big \vert$, where {$x_{j},j=1,2,\ldots n_{\text {grid}}$} points on $\left[ -0.5+h,0.5-h\right]$ with $n_{\text { grid}}=401$, $h$ being the chosen bandwidth of estimator (3 ). it can be seen that the boxplot of $\Delta _{n}$ becomes narrower as $n$ increases, implying that difference between the spline–kernel variance estimator and the infeasible estimator with known mean function is asymptotically of smaller order than $n^{-1/2}$, which confirms Theorem 1. For visual impression of the SCB, Figs. 3 and 2 are created based on sample sizes $n=100,500$, and $c=1,0.5$, respectively, each with symbols: center thick line (true curve), center solid line (the estimated curve), upper- and lower-dashed line (SCB). In all figures, the SCB becomes narrower and fit better for $n=500$ than for $n=100$.

Fig. 1

Boxplots of $\Delta _{n}$ with a $c=1$; b $c=0.5$

Fig. 2

Plots of SCB for variance function (dashed) which is computed according to (19), the estimator $\hat{\sigma }_{\text {SK}}^{2}\left( x\right)$ (solid), the true function $\sigma ^{2}\left( x\right)$ with $c=0.5$ (thick). a $n=100$, 95 % SCB; b $n=100$, 99 % SCB; c $n=500$, 95 % SCB; d $n=500$, 99 % SCB

Fig. 3

Plots of SCB for variance function (dashed) which is computed according to (19), the estimator $\hat{\sigma }_{\text {SK}}^{2}\left( x\right)$ (solid), the true function $\sigma ^{2}\left( x\right)$ with $c=1$ (thick). a $n=100, 95\%$ SCB; b $n=100, 99\%$ SCB; c $n=500$, 95 % SCB; d $n=500$, 99 % SCB

6 Empirical examples

In this section, we test the null hypothesis of homoscedasticity $H_{0}:\sigma ^{2}(x)=\sigma _{0}^{2}>0$ for two well-known data sets. The first is the motorcycle data with $n=133$ observations, with $X=$ time (in milliseconds) after a simulated impact on motorcycles, $Y=$ the head acceleration of a PTMO (post mortem human test object). The data can be called in R by the command “data(motorcycledata)”, see http://www.inside-r.org/node/52453. In Fig. 4, the center thick lines are the spline–kernel estimator $\hat{\sigma }_{\text {SK}}^{2}(x)$ for $\sigma ^{2}(x)$, the upper/lower solid lines represent the SCB for the variance function. Since the $100(1-0.00009)\%$ SCB in (a) does not contain the consistent estimate of $\sigma _{0}^{2}$ under the null hypothesis, which equals $n^{-1}\sum \nolimits _{i=1}^{n}\hat{\varepsilon } _{i,p}^{2}$, one rejects the null hypothesis of homoscedasticity with $p$ value $<0.00009$.

Fig. 4

For the motorcycle data, plots of SCB (solid) computed according to the (19), the spline–kernel estimator $\hat{\sigma }_{\text {SK}}^{2}(x)$ (thick), the scatterplot of $\hat{Z}_{i}=\hat{ \varepsilon }_{i,p}^{2}$ a $99.991\%$ SCB, a constant variance fit which equals $n^{-1}\sum \nolimits _{i=1}^{n}\hat{\varepsilon } _{i,p}^{2}$, $\alpha =0.00009$; b 98.698 % SCB, a constant variance fit which equals the maximum of upper SCB, $\alpha =0.01302$

Song and Yang (2009) had obtained a $p$ value of $0.008$ with spline SCB, as minimum of the upper confidence line equals the maximum of the lower confidence line for the spline SCB of confidence level $99.2~\%=1-0.008$. The $99.2~\%$ spline SCB therefore contains completely a horizontal line, even though its height is not equal to $n^{-1}\sum \nolimits _{i=1}^{n}\hat{\varepsilon }_{i,p}^{2}$. For comparison, we have computed the confidence level at which the upper and lower lines of the spline–kernel SCB coincide, which turns out to be $98.698~\%$, thus one rejects the null hypothesis of homoscedasticity with $p$ value $\le 0.01302$. Figure 4b depicts the $98.698~\%$ spline–kernel SCB and the horizontal line that completely fits inside the SCB. We have also constructed ad hoc local linear SCBs by substituting $\hat{ \sigma }_{\text {SK}}^{2}\left( x\right)$ in (19) with the two-step local linear estimator of $\sigma ^{2}\left( x\right)$ in Fan and Yao (1998), and with minimum of upper line and maximum of lower line equal, the confidence level is $99.999865~\%$, thus the $p$ value is $0.00000135$ for rejecting the null hypothesis of homoscedasticity. To sum up, for the motorcycle data, homoscedasticity is rejected by all four approaches, with $p$ values ranging from $0.00000135$ to $0.01302$.

The second data set is the Old Faithful geyser data, which can be downloaded from http://www.stat.cmu.edu/~larry/all-of-statistics/=data/faithful.dat. Geysers are a special kind of hot springs that erupt a mixture of hot water, steam and other gases, and by studying geysers scientists obtain useful information about the structure and the dynamics of earth’s crust. The data consists of $n=272$ observations for the Old Faithful geyser in Yellowstone National Park, Wyoming, USA: $X=$ eruption time in mins, $Y=$ the waiting time to next eruption. Figure 5 shows that for the geyser data one can not reject the null hypothesis of homoscedasticity with a $p$ value $0.12$.

Fig. 5

For the Old Faithful geyser data, plots of SCB (solid) computed according to the (19), the spline–kernel estimator $\hat{\sigma }_{\text {SK}}^{2}(x)$ (thick), a constant variance fit which equals $n^{-1} \sum \nolimits _{i=1}^{n}\hat{\varepsilon } _{i,p}^{2}$, the scatterplot of $\hat{Z}_{i}=\hat{\varepsilon } _{i,p}^{2}$ a 95 % SCB, $\alpha =0.05$, b 88 % SCB, $\alpha =0.12$

7 Conclusions

A spline–kernel estimator is proposed for the conditional variance function in nonparametric regression model, which is shown to be oracally efficient, that is, it uniformly approximates an infeasible kernel variance estimator at the rate of $o_{p}\left( n^{-1/2}\right)$. A powerful technical Lemma 4 is used in the proofs of Propositions 2 and 3, both indispensable in establishing oracle efficiency. A data-driven procedure implements the kernel SCB centered around the oracally efficient two-step estimator, with limiting coverage probability equal to that of the infeasible kernel SCB. As illustrated by both the motorcycle and the Old Faithful geyser data, the theoretically justified kernel SCB is also a useful tool for testing hypotheses on the conditional variance function, and is expected to find wide applications in many scientific disciplines.

Appendix A

Throughout this Appendix, we denote by $\left\| \xi \right\|$ the Euclidean norm and $\left| \xi \right|$ means the largest absolute value of the elements of any vector $\xi$. We use $c$, $C$ to denote any positive constants in the generic sense. We denote for any given constant $C>0$, a class of Lipschitz continuous functions by $\text {Lip}\left( \left[ 0,1\right] ,C\right) =\left\{ \varphi \left| \left| \varphi \left( x\right) -\varphi \left( x^{\prime }\right) \right| \le C\left| x-x^{\prime }\right| \text {, }\forall x,x^{\prime }\in \left[ 0,1\right] \right. \right\}$.

1.1 A.1 Preliminaries

The Lemmas of this Subsection are needed for the proof of Propositions 1, 2 and 3. These Propositions clearly establish Theorems 1 and 2.

Lemma 1

Under Assumptions (A1)–(A5), there exists a constant $C_{p}>0$, $p>1$, such that for any $m\in C^{p}\left[ 0,1\right]$ there is a spline function $g_{p}\in G_{N}^{\left( p-2\right) }$ satisfying $\left\| m-g_{p}\right\| _{\infty }$ $\le CH^{p}$ and $m-g_{p}\in \text {Lip}\left( \left[ 0,1\right] ,CH^{p-1}\right)$. The function $\tilde{m}_{p}\left( x\right)$ given in Equation (12)

$$\begin{aligned} \left\| \tilde{m}_{p}\left( x\right) -m\left( x\right) \right\| _{\infty }\le C_{p}\underset{g\in G_{N}^{\left( p-2\right) }}{\inf }\ \left\| g-m\right\| _{\infty }=\mathcal {O}_{p}\left( H^{p}\right) . \end{aligned}$$

Moreover, for the function $\tilde{\varepsilon }_{p}\left( x\right)$ given in Equation (12)

$$\begin{aligned} \left\| \tilde{\varepsilon }_{p}\left( x\right) \right\| _{2,n}= \mathcal {O}_{p}\left( n^{-1/2}N^{1/2}\right) ,\left\| \tilde{ \varepsilon }_{p}\left( x\right) \right\| _{\infty }=\mathcal {O}_{p}\left( n^{-1/2}N^{1/2}{(\log n)}^{1/2}\right) . \end{aligned}$$

See Lemma A.1 of Song and Yang (2009), and also Wang and Yang (2009) for detailed proof.

Lemma 2

Under Assumption (A6), as $n\rightarrow \infty$,

$$\begin{aligned} \underset{x\in \left[ 0,1\right] }{\sup }\left\{ \left| \left\{ B_{j,p}\left( x\right) \right\} _{j=1-p}^{N}\right| +\left\| \left\{ B_{j,p}\left( x\right) \right\} _{j=1-p}^{N}\right\| \right\} =\mathcal {O} \left( H^{-1/2}\right) \end{aligned}$$

(21)

See Lemma A.4 of Song and Yang (2009) for detailed proof.

The strong approximation result of Tusnády (1977) is also needed.

Lemma 3

Let $U_{1},\ldots ,U_{n}$ be i.i.d. r.v.’s on the $2$ -dimensional unit square with $P\left( U_{i}<\mathbf {t}\right) =\lambda \left( \mathbf {t}\right) ,\mathbf {0\le t\le 1,}$ where $\mathbf {t=(} t_{1,}t_{2}\mathbf {)}$ and $\mathbf {1=(}1,1\mathbf {)}$ are $2$-dimensional vectors, $\lambda \left( \mathbf {t}\right) =t_{1}t_{2}.$ The empirical distribution function $F_{n}^{u}\left( \mathbf {t}\right)$ based on sample $\left( U_{1},\ldots ,U_{n}\right)$ is defined as $F_{n}^{u}\left( \mathbf {t} \right) =n^{-1}\sum _{i=1}^{n}\mathrm{I}_{\left\{ U_{i}<\mathbf {t}\right\} }$ for $\mathbf {0}\le \mathbf {t\le 1.}$ The $2$-dimensional Brownian bridge $B\left( \mathbf {t}\right)$ is defined by $B\left( \mathbf {t}\right) =W\left( \mathbf {t}\right) -\lambda \left( \mathbf {t}\right) W\left( \mathbf { 1}\right)$ for $\mathbf {0}\le \mathbf {t\le 1}$, where $W\left( \mathbf {t} \right)$ is a $2$-dimensional Wiener process. Then there is a version $B_{n}\left( \mathbf {t}\right)$ of $B\left( \mathbf {t}\right)$ such that

$$\begin{aligned} P\left[ \sup _{\mathbf {0\le t\le 1}}\left| n^{1/2}\left\{ F_{n}^{u}\left( \mathbf {t}\right) -\lambda \left( \mathbf {t}\right) \right\} -B_{n}\left( \mathbf {t}\right) \right| >\left( C\log n+x\right) \frac{ \log n}{n^{1/2}}\right] <Ke^{-\lambda x} \end{aligned}$$

holds for all $x$, where $C,K,$ $\lambda$ are positive constants.

Denote the well-known Rosenblatt transformation for bivariate continuous $\left( X,\varepsilon \right)$ as

$$\begin{aligned} \left( X^{\prime },\varepsilon ^{\prime }\right) =M\left( X,\varepsilon \right) =\left\{ F_{X}\left( x\right) ,F_{\varepsilon |X}\left( \varepsilon |x\right) \right\} , \end{aligned}$$

(22)

so that $\left( X^{\prime },\varepsilon ^{\prime }\right)$ has uniform distribution on $\left[ 0,1\right] ^{2}$, therefore

$$\begin{aligned} Z_{n}\left\{ M^{-1}\left( x^{\prime },\varepsilon ^{\prime }\right) \right\} =Z_{n}\left( x,\varepsilon \right) =\sqrt{n}\left\{ F_{n}\left( x,\varepsilon \right) -F\left( x,\varepsilon \right) \right\} , \end{aligned}$$

(23)

with $F_{n}\left( x,\varepsilon \right)$ denoting the empirical distribution of $\left( X,\varepsilon \right)$. Lemma 3 implies that there exists a version $B_{n}$ of $2$-dimensional Brownian bridge such that

$$\begin{aligned} \sup _{x,\varepsilon }\left| Z_{n}\left( x,\varepsilon \right) -B_{n}\left\{ M\left( x,\varepsilon \right) \right\} \right| =\mathcal {O} _{a.s.}\left( n^{-1/2}\log ^{2}n\right) . \end{aligned}$$

(24)

Lemma 4

Under Assumptions (A2)-(A5), as $n\rightarrow \infty$, for any sequence of functions $r_{n}$ $\in \text {Lip}\left( \left[ 0,1\right] ,l_{n}\right) ,l_{n}>0$ with ${\left\| r_{n}\right\| _{\infty }=\rho }_{n}\ge 0$

$$\begin{aligned} {n}^{-1}\sum _{i=1}^{n}K_{h}\left( X_{i}-x\right) r_{n}\left( X_{i}\right) \varepsilon _{i}=\mathcal {\ U}_{p}\left( n^{-1/2}h^{-1/2}{\rho }_{n}\log ^{1/2}n+n^{-1/2}h^{1/2}l_{n}\right) \nonumber \\ \end{aligned}$$

(25)

Proof

Step 1. We first discretize the problem by letting $0=x_{0}<x_{1}\,<\cdots <x_{M_{n}}=1,M_{n}=n^{4}$ by equally spaced points, the smoothness of kernel $K$ in Assumption (A4) imples that

$$\begin{aligned}&\!\!\!\underset{x\in \left[ 0,1\right] }{\sup }\left| n^{-1}\sum _{i=1}^{n}K_{h}\left( X_{i}-x\right) r_{n}\left( X_{i}\right) \varepsilon _{i}\right| \le \underset{0\le j\le M_{n}}{\max } \left| n^{-1}\sum _{i=1}^{n}K_{h}\left( X_{i}-x_{j}\right) r_{n}\left( X_{i}\right) \varepsilon _{i}\right| \\&\!\!\!\qquad +\underset{0\le j<M_{n}}{\max }\sup _{x\in \left[ x_{j},x_{j+1}\right] }\left| n^{-1}\sum _{i=1}^{n}K_{h}\left( X_{i}-x_{j}\right) r_{n}\left( X_{i}\right) \varepsilon _{i}-n^{-1}\sum _{i=1}^{n}K_{h}\left( X_{i}-x\right) r_{n}\left( X_{i}\right) \varepsilon _{i}\right| \\&\!\!\!\quad \le \underset{0\le j<M_{n}}{\max }\left| n^{-1}\sum _{i=1}^{n}K_{h}\left( X_{i}-x_{j}\right) r_{n}\left( X_{i}\right) \varepsilon _{i}\right| +CM_{n}^{-1}h^{-2}n^{-1}\sum _{i=1}^{n}\left| r_{n}\left( X_{i}\right) \varepsilon _{i}\right| \end{aligned}$$

and the moment conditions on error $\varepsilon$ in Assumption (A2), the rate of $h$ in Assumption (A5) imply next that

$$\begin{aligned}&\underset{x\in \left[ 0,1\right] }{\sup }\left| n^{-1}\sum _{i=1}^{n}K_{h}\left( X_{i}-x\right) r_{n}\left( X_{i}\right) \varepsilon _{i}\right| \nonumber \\&\quad \le \underset{0\le j<M_{n}}{\max }\left| n^{-1}\sum _{i=1}^{n}K_{h}\left( X_{i}-x_{j}\right) r_{n}\left( X_{i}\right) \varepsilon _{i}\right| +\mathcal {O}_{p}\left\{ {\rho } _{n}n^{-2}\right\} . \end{aligned}$$

(26)

Step 2. To truncate the error, we denote $D_{n}=n^{\alpha }$ with $\alpha$ as in Assumption (A5). Assumption (A5) implies that $D_{n}n^{-1/2}h^{-1/2} \log ^{2}n\rightarrow 0,$ $n^{1/2}h^{1/2}D_{n}^{-\left( 1+\eta \right) }\rightarrow 0$, $\sum _{n=1}^{\infty }D_{n}^{-\left( 2+\eta \right) }<\infty$. Write $\varepsilon _{i}=\varepsilon _{i,1}^{D_{n}}+\varepsilon _{i,2}^{D_{n}}$, where $\varepsilon _{i,1}^{D_{n}}=\varepsilon _{i}\mathrm{I}\left\{ \left| \varepsilon _{i}\right| >D_{n}\right\} ,\varepsilon _{i,2}^{D_{n}}=\varepsilon _{i}\mathrm{I}\left\{ \left| \varepsilon _{i}\right| \le D_{n}\right\}$, and denote $\mu ^{D_{n}}\left( x\right) =\mathsf {E}\left\{ \varepsilon _{i}\mathrm{I}\left\{ \left| \varepsilon _{i}\right| \le D_{n}\right\} \mid X_{i}=x\right\}$. One immediately obtains that

$$\begin{aligned} \underset{x\in \left[ 0,1\right] }{\sup }\left| \mu ^{D_{n}}\left( x\right) \right| \le \mathsf {E}\left\{ \left| \varepsilon \right| ^{2+\eta }\mid X=x\right\} D_{n}^{-\left( 1+\eta \right) }=o\left( n^{-1/2}h^{-1/2}\right) , \nonumber \\ \underset{x\in \left[ 0,1\right] }{\sup }\left| \mathsf {E} n^{-1}\sum _{i=1}^{n}K_{h}\left( X_{i}-x\right) r_{n}\left( X_{i}\right) \mu ^{D_{n}}\left( X_{i}\right) \right| =o\left( n^{-1/2}h^{-1/2}{\rho } _{n}\right) . \end{aligned}$$

(27)

Next, since $P\left( \left| \varepsilon _{i}\right| >D_{n}\right) \le \mathsf {E}\left| \varepsilon \right| ^{2+\eta }D_{n}^{-(2+\eta )}$, $\sum \nolimits _{n=1}^{\infty }P\left( \left| \varepsilon _{n}\right| >D_{n}\right) \le$ $\mathsf {E}\left| \varepsilon \right| ^{2+\eta }\sum \nolimits _{n=1}^{\infty }D_{n}^{-\left( 2+\eta \right) }<+\infty$, Borel–Cantelli Lemma then implies that

$$\begin{aligned} P\left\{ \omega \mid \exists N\left( \omega \right) ,\varepsilon _{i,1}^{D_{n}}\left( \omega \right) =0,i=1,2,\ldots n,\text {for }n>N\left( \omega \right) \right\} =1. \end{aligned}$$

So one has for any $k>0$

$$\begin{aligned} \underset{x\in \left[ 0,1\right] }{\sup }{n}^{-1}\left| \sum \nolimits _{i=1}^{n}K_{h}\left( X_{i}-x\right) r_{n}\left( X_{i}\right) \varepsilon _{i,1}^{D_{n}}\right| =\mathcal {O}_{a.s.}\left( n^{-k}{\rho } _{n}\right) . \end{aligned}$$

(28)

Step 3. The truncated sum $n^{-1}\sum _{i=1}^{n}K_{h}\left( X_{i}\!-\!x\right) r_{n}\left( X_{i}\right) \varepsilon _{i,2}^{D_{n}}$ equals $\int _{\left| \varepsilon \right| \le D_{n}}K_{h}\left( u\!-\!x\right) r_{n}\left( u\right) \varepsilon dF_{n}\left( u,\varepsilon \right)$, while

$$\begin{aligned}&\int _{\left| \varepsilon \right| \le D_{n}}K_{h}\left( u-x\right) r_{n}\left( u\right) \varepsilon dF\left( u,\varepsilon \right) =\mathsf {E} n^{-1}\sum _{i=1}^{n}K_{h}\left( X_{i}-x\right) r_{n}\left( X_{i}\right) \varepsilon _{i,2}^{D_{n}} \\&\quad =\mathsf {E}n^{-1}\sum _{i=1}^{n}K_{h}\left( X_{i}-x\right) r_{n}\left( X_{i}\right) \mu ^{D_{n}}\left( X_{i}\right) =u\left( n^{-1/2}h^{-1/2}{\rho } _{n}\right) , \end{aligned}$$

according to (27). The above two Equations imply that

$$\begin{aligned} n^{-1}\sum _{i=1}^{n}K_{h}\left( X_{i}-x\right) r_{n}\left( X_{i}\right) \varepsilon _{i,2}^{D_{n}}&= n^{-1/2}\int _{\left| \varepsilon \right| \le D_{n}}K_{h}\left( u-x\right) r_{n}\left( u\right) \varepsilon dZ_{n}\left( u,\varepsilon \right) \nonumber \\&+u\left( n^{-1/2}h^{-1/2}{\rho }_{n}\right) . \end{aligned}$$

(29)

Step 4. The term $n^{-1/2}\int _{\left| \varepsilon \right| \le D_{n}}K_{h}\left( u-x\right) r_{n}\left( u\right) \varepsilon dZ_{n}\left( u,\varepsilon \right)$ equals

$$\begin{aligned}&-n^{-1/2}\int _{\left| \varepsilon \right| \le D_{n}}d\left\{ K_{h}\left( u-x\right) r_{n}\left( u\right) \varepsilon \right\} Z_{n}\left( u,\varepsilon \right) \\&\quad =n^{-1/2}\int _{\left| \varepsilon \right| \le D_{n}}d\left\{ K_{h}\left( u-x\right) r_{n}\left( u\right) \varepsilon \right\} \left[ B_{n}\left\{ M\left( u,\varepsilon \right) \right\} -Z_{n}\left( u,\varepsilon \right) \right] \\&\qquad -n^{-1/2}\int _{\left| \varepsilon \right| \le D_{n}}d\left\{ K_{h}\left( u-x\right) r_{n}\left( u\right) \varepsilon \right\} B_{n}\left\{ M\left( u,\varepsilon \right) \right\} . \end{aligned}$$

Note that

$$\begin{aligned}&n^{-1/2}\int _{\left| \varepsilon \right| \le D_{n}}d\left\{ K_{h}\left( u-x\right) r_{n}\left( u\right) \varepsilon \right\} \left[ B_{n}\left\{ M\left( u,\varepsilon \right) \right\} -Z_{n}\left( u,\varepsilon \right) \right] \nonumber \\&\quad =n^{-1/2}\!\int _{\left| \varepsilon \right| \le D_{n}}\!\left\{ dK_{h}\left( u\!-\!x\right) \!r_{n}\left( u\right) \!+\!K_{h}\left( u\!-\!x\right) dr_{n}\!\left( u\right) \right\} d\varepsilon \left[ B_{n}\!\left\{ M\left( u,\varepsilon \right) \right\} \!-\!Z_{n}\left( u,\varepsilon \right) \right] \nonumber \\&\quad =U_{a.s.}\left\{ n^{-1/2}\log ^{2}n\times D_{n}\left( h^{-1}{\rho } _{n}+l_{n}\right) n^{-1/2}\right\} \nonumber \\&\quad =U_{a.s.}\left\{ D_{n}n^{-1}h^{-1}\log ^{2}n\left( {\rho } _{n}+hl_{n}\right) \right\} \nonumber \\&\quad =u_{a.s.}\left\{ n^{-1/2}h^{-1/2}\left( {\rho }_{n}+hl_{n}\right) \right\} \end{aligned}$$

(30)

by the growth constraint on $D_{n}=n^{\alpha }$. Note also that

$$\begin{aligned}&-n^{-1/2}\int _{\left| \varepsilon \right| \le D_{n}}d\left\{ K_{h}\left( u-x\right) r_{n}\left( u\right) \varepsilon \right\} B_{n}\left\{ M\left( u,\varepsilon \right) \right\} \\&\quad =n^{-1/2}\int _{\left| \varepsilon \right| \le D_{n}}K_{h}\left( u-x\right) r_{n}\left( u\right) \varepsilon dB_{n}\left\{ M\left( u,\varepsilon \right) \right\} \\&\quad =n^{-1/2}\int _{\left| \varepsilon \right| \le D_{n}}K_{h}\left( u-x\right) r_{n}\left( u\right) \varepsilon dW_{n}\left\{ M\left( u,\varepsilon \right) \right\} \\&\qquad -n^{-1/2}\int _{\left| \varepsilon \right| \le D_{n}}K_{h}\left( u-x\right) r_{n}\left( u\right) \varepsilon dF\left( \varepsilon \left| u\right. \right) f\left( u\right) duW_{n}\left( 1,1\right) \end{aligned}$$

in which

$$\begin{aligned}&\left| n^{-1/2}\int _{\left| \varepsilon \right| \le D_{n}}K_{h}\left( u-x\right) r_{n}\left( u\right) \varepsilon dF\left( \varepsilon \left| u\right. \right) f\left( u\right) duW_{n}\left( 1,1\right) \right| \nonumber \\&\quad \le n^{-1/2}\int _{\left| \varepsilon \right| \le D_{n}}\left| \varepsilon \right| dF\left( \varepsilon \left| u\right. \right) \int K_{h}\left( u-x\right) \left| r_{n}\left( u\right) \right| f\left( u\right) du\left| W_{n}\left( 1,1\right) \right| \nonumber \\&\quad \le n^{-1/2}\mathsf {E}\left| \varepsilon \right| ^{2+\eta }D_{n}^{-\left( 1+\eta \right) }{\rho }_{n}C_{f}\left| W_{n}\left( 1,1\right) \right| =U_{p}\left( n^{-1/2}D_{n}^{-\left( 1+\eta \right) }{ \rho }_{n}\right) . \qquad \end{aligned}$$

(31)

Meanwhile

$$\begin{aligned}&\mathsf {E}\left[ n^{-1/2}\int _{\left| \varepsilon \right| \le D_{n}}K_{h}\left( u-x\right) r_{n}\left( u\right) \varepsilon dW_{n}\left\{ M\left( u,\varepsilon \right) \right\} \right] ^{2} \\&\quad =n^{-1}\int _{\left| \varepsilon \right| \le D_{n}}K_{h}\left( u-x\right) ^{2}r_{n}^{2}\left( u\right) \varepsilon ^{2}dF\left( \varepsilon \left| u\right. \right) f\left( u\right) du \\&\quad =n^{-1}\int \left\{ \int _{\left| \varepsilon \right| \le D_{n}}\varepsilon ^{2}dF\left( \varepsilon \left| u\right. \right) \right\} K_{h}\left( u-x\right) ^{2}r_{n}^{2}\left( u\right) f\left( u\right) du \\&\quad \le n^{-1}\int K_{h}\left( u-x\right) ^{2}r_{n}^{2}\left( u\right) \sigma ^{2}\left( u\right) f\left( u\right) du\le n^{-1}h^{-1}{\rho } _{n}^{2}C_{\sigma }^{2}C_{f}, \end{aligned}$$

so the $M_{n}$ Gaussian variables $n^{-1/2}\int _{\left| \varepsilon \right| \le D_{n}}K_{h}\left( u-x_{j}\right) r_{n}\left( u\right) \varepsilon dW_{n}\left\{ M\left( u,\varepsilon \right) \right\} ,0\le j<M_{n}$ each has variance less than $n^{-1}h^{-1}{\rho }_{n}^{2}C_{\sigma }^{2}C_{f}$, hence

$$\begin{aligned}&\underset{0\le j<M_{n}}{\max }\left| n^{-1/2}\int _{\left| \varepsilon \right| \le D_{n}}K_{h}\left( u-x_{j}\right) r_{n}\left( u\right) \varepsilon dW_{n}\left\{ M\left( u,\varepsilon \right) \right\} \right| \nonumber \\&\quad =\mathcal {O}_{p}\left( n^{-1/2}h^{-1/2}{\rho }_{n}\log ^{1/2}n\right) . \end{aligned}$$

(32)

Finally, putting together Eqs. (26), (28 ), (29), (30), (31 ) and (32) proves the Lemma.

1.2 A.2 Proof of Propositions

Proof of Proposition

1 It is obvious that $\left| \mathrm{I}_{i,p}\right| \le 2\left\{ \tilde{m}_{p}\left( X_{i}\right) -m\left( X_{i}\right) \right\} ^{2}+2\tilde{\varepsilon }_{p}^{2}\left( X_{i}\right) .$ Meanwhile applied Lemma 1, $\left\| m-\tilde{m}_{p}\right\| _{2,n}^{2}\le \left\| m-\tilde{m} _{p}\right\| _{\infty }^{2}=\mathcal {O}_{p}\left( H^{2p}\right)$, $\left| \mathrm{I}\right|$ is bounded by

$$\begin{aligned}&2{n}^{-1}{h}^{-1}c^{-1}\sum \nolimits _{i=1}^{n}\left| K\left\{ (X_{i}-x)/h\right\} \right| \left\{ \left( m\left( X_{i}\right) -\tilde{m }_{p}\left( X_{i}\right) \right) ^{2}+\tilde{\varepsilon }_{p}^{2}\left( X_{i}\right) \right\} \\&\quad \le 2{h}^{-1}c^{-1}\left\| K\right\| _{\infty }\left\{ \left\| m- \tilde{m}_{p}\right\| _{2,n}^{2}+\left\| \tilde{\varepsilon } _{p}^{2}\right\| _{2,n}^{2}\right\} \\&\quad \le 2c^{-1}\left\| K\right\| _{\infty }\left\{ h^{-1}\left( H^{2p}+n^{-1}H^{-1}\right) \right\} . \end{aligned}$$

Proof of Proposition

2 By (12), $\tilde{\varepsilon }_{p}( X_{i}) =\sum _{J=1-p}^{N}\tilde{a}_{J,p}B_{J,p}( X_{i})$, Lemma 1 and Wang and Yang (2009) entail that $(\sum _{J=1-p}^{N}\tilde{a}_{J,p}^{2}) ^{1/2}=\mathcal {O}_{p}(\Vert \tilde{\varepsilon }_{p}(x) \Vert _{2,n}) =\mathcal {O}_{p}(n^{-1/2}N^{1/2})$. Set $r_{n}\left( x\right) =B_{J,p}\left( x\right)$, then Lemma 2 entails that $\rho _{n}=\mathcal {O}\left( H^{-1/2}\right)$ and it is easy to verify that $l_{n}=\mathcal {O}\left( H^{-3/2}\right)$. Applying Lemma 4, one obtains that

$$\begin{aligned}&{n}^{-1}\sum \limits _{i=1}^{n}K_{h}\left( X_{i}-x\right) \varepsilon _{i}B_{J,p}\left( X_{i}\right) \nonumber \\&\quad =\mathcal {U}_{p}\left( n^{-1/2}h^{-1/2}H^{-1/2}\log ^{1/2}n+n^{-1/2}h^{1/2}H^{-3/2}\right) \end{aligned}$$

(33)

and hence

$$\begin{aligned} \left| \mathrm{II}\left( x\right) \right|&= \left| {n} ^{-1}\sum \limits _{i=1}^{n}K_{h}\left( X_{i}-x\right) 2\varepsilon _{i} \tilde{\varepsilon }_{p}\left( X_{i}\right) \right| \\&= \left| 2{n}^{-1}\sum \limits _{i=1}^{n}K_{h}\left( X_{i}-x\right) \varepsilon _{i}\sum \limits _{J=1-p}^{N}\tilde{a}_{J,p}B_{J,p}\left( X_{i}\right) \right| \\&\le c^{-1}\left\{ \sum \limits _{J=1-p}^{N}\tilde{a}_{J,p}^{2}\sum \limits _{J=1-p}^{N}\left\{ 2{n}^{-1}\sum \limits _{i=1}^{n}K_{h}\left( X_{i}-x\right) \varepsilon _{i}B_{J,p}\left( X_{i}\right) \right\} ^{2}\right\} ^{1/2} \\&= \mathcal {O}_{p}\left( n^{-1/2}N^{1/2}\right) \times \left( N+p\right) ^{1/2}\\&\,\times \mathcal {U}_{p}\left( n^{-1/2}h^{-1/2}H^{-1/2}\log ^{1/2}n+n^{-1/2}h^{1/2}H^{-3/2}\right) \\&= \mathcal {U}_{p}\left( n^{-1}h^{-1/2}H^{-3/2}\log ^{1/2}n+n^{-1}h^{1/2}H^{-5/2}\right) , \end{aligned}$$

the lemma is proved.

Proof of Proposition

3

$$\begin{aligned} \mathrm{III}\left( x\right)&= 2{n}^{-1}\sum \limits _{i=1}^{n}K_{h}\left( X_{i}-x\right) \left\{ \left( m\left( X_{i}\right) -g_{p}\left( X_{i}\right) \right) \varepsilon _{i}\right\} \\&+2{n}^{-1}\sum \limits _{i=1}^{n}K_{h}\left( X_{i}-x\right) \left\{ \left( g_{p}\left( X_{i}\right) -\tilde{m}_{p}\left( X_{i}\right) \right) \varepsilon _{i}\right\} \end{aligned}$$

in which the spline function $g_{p}\in G_{N}^{\left( p-2\right) }$ satisfies $\left\| m-g_{p}\right\| _{\infty }$ $\le CH^{p},m-g_{p}\in \text {Lip }\left( \left[ 0,1\right] ,CH^{p-1}\right)$ as in Lemma 1. Set $r_{n}\left( x\right) =m\left( x\right) -g_{p}\left( x\right)$, then $\rho _{n}=\mathcal {O}\left( H^{p}\right) ,l_{n}=\mathcal {O} \left( H^{p-1}\right)$, so applying Lemma 4 yields

$$\begin{aligned}&{n}^{-1}\sum _{i=1}^{n}K_{h}\left( X_{i}-x\right) \left\{ \left( m\left( X_{i}\right) -g_{p}\left( X_{i}\right) \right) \varepsilon _{i}\right\} \nonumber \\&\quad = \mathcal {U}_{p}\left\{ {(nh/\log n)}^{-1/2}H^{p}+n^{-1/2}h^{1/2}H^{p-1} \right\} . \end{aligned}$$

(34)

Denoting $g_{p}\left( x\right) -\tilde{m}_{p}\left( x\right) =\sum _{J=1-p}^{N}\gamma _{J,p}B_{J,p}\left( x\right)$ and applying Lemma 1, one has

$$\begin{aligned} \left( \sum \nolimits _{J=1-p}^{N}\gamma _{J,p}^{2}\right) ^{1/2}\le C\left\| g_{p}\left( x\right) -\tilde{m}_{p}\left( x\right) \right\| _{2}=\mathcal {O}\left( H^{p}\right) , \end{aligned}$$

which, together with (33) imply that

$$\begin{aligned}&\left| 2{n}^{-1}\sum \limits _{i=1}^{n}K_{h}\left( X_{i}-x\right) \left\{ g_{p}\left( X_{i}\right) -\tilde{m}_{p}\left( X_{i}\right) \right\} \varepsilon _{i}\right| \\&\quad =\left| 2{n}^{-1}\sum \limits _{J=1-p}^{N}\gamma _{J,p}\sum \nolimits _{i=1}^{n}K_{h}\left( X_{i}-x\right) B_{J,p}\left( X_{i}\right) \varepsilon _{i}\right| \\&\quad \le \left( \sum \limits _{J=1-p}^{N}\gamma _{J,p}^{2}\right) ^{1/2}\left[ \sum \limits _{J=1-p}^{N}\left\{ 2{n}^{-1}\sum \nolimits _{i=1}^{n}K_{h}\left( X_{i}-x\right) B_{J,p}\left( X_{i}\right) \varepsilon _{i}\right\} ^{2} \right] ^{1/2} \\&\quad =\mathcal {O}\left( H^{p}\right) \times \mathcal {O}\left( N^{1/2}\right) \times \mathcal {U}_{p}\left( n^{-1/2}h^{-1/2}H^{-1/2}\log ^{1/2}n+n^{-1/2}h^{1/2}H^{-3/2}\right) \\&\quad =\mathcal {U}_{p}\left( n^{-1/2}h^{-1/2}H^{p-1}\log ^{1/2}n+n^{-1/2}h^{1/2}H^{p-2}\right) , \end{aligned}$$

which, together with (34), prove the lemma.