Introduction

Cracks initiated by fatigue are a major problem in the dynamic structure of industrial machinery where they can cause accidents and failures [1]. The vibration behavior of beams changes when cracks occur, so action can be taken to prevent more damage [2]. Natural frequencies and mode shapes can be used to distinguish between healthy and unhealthy structures [3]. Cantilever beams are used in many mechanical structures, and researchers have studied cracked cantilever beams [4,5,6]. Choudhury et al. [3] carried out a theoretical analysis of a cracked cantilever beam and observed that frequency values change along with crack depth and crack location. They observed changes in frequency behavior in the first three modes of vibrations. Their results indicated that the range of natural frequency increased for different crack locations and depths at higher modes of vibration. They outlined a new optimization method for estimation of results based on location and depth of crack. The maximum error in this proposed method is 0.3 and 0.05% based on crack depth and crack location, respectively. Liu et al. [7] investigated the vibration of a cantilever beam with a closed, fully embedded horizontal crack and developed a new three-segment beam model with local flexibilities at the crack tips. They obtained the natural frequencies and mode shapes of the cracked cantilever beam using the transfer matrix method and compatibility conditions at the crack tips. They determined compliance at the crack tips using a J-integral approach. They validated the J-integral approach by comparing their results with those calculated using finite element analysis and found only small differences between the two methods. Zeng et al. [8] established the finite element model of cracked cantilever beams and introduced the use of the area damage factor when evaluating crack levels. They discussed vibration response and crack level identification in three cases of crack severity. They inferred that a combination of the acceleration–velocity phase portraits in the excitation direction and lateral velocity–displacement phase portraits perpendicular to the excitation direction can be used to identify the crack severity. Mia et al. [9] have extracted modal analysis, natural frequencies and mode shapes of transverse vibrations for the first three modes of both intact and cracked cantilever beams. They used commercial finite element analysis software ABAQUS to analyze various crack depths and locations and concluded that natural frequency is reduced when a crack is present. The amount of the reduction depends on the crack location, depth and opening size. Nandwana and Maiti [10] used a rotational spring for modeling transverse vibrations of a slender beam in the presence of an inclined edge or internal normal crack to detect crack location based on measurement of natural frequencies. They plotted spring stiffness versus crack locations for the three lowest transverse modes. Their prediction of crack location was less than 4.5% when an inclined edge crack was present. Khalkar and Ramachandran [11] investigated the effects of transverse cracks and oblique cracks at different locations and depths on the dynamic responses of the cantilever beam. They observed that when crack depth increases to 80% of the depth of the beam, a significant reduction in the natural frequency of the beam occurs. They also observed that when crack depth is 20% or less of the depth of the beam, the reduction in the natural frequency of the beam is least affected. Batabyal et al. [12] carried out parametric studies using ANSYS software to evaluate natural frequencies and mode shapes for different crack parameters. They plotted the contour lines of the cracked beam frequencies so that any point represents the frequency at a specific crack location and depth. They inferred that both crack location and crack depth have noticeable effects on the modal parameters of the cracked cantilever beam. Djidrov et al. [13] introduced a single transversal crack at the surface of a cantilever beam and presented changes in natural frequency and FRF amplitude attributable to the effect of different crack depths at different crack positions. Their results indicated that when a crack is located near the middle of the beam, there are noticeable shifts in both FRF amplitude and frequency where the severity of the crack depth is perceptible. In this study, rotational stiffness and flexibility in a crack are analytically calculated and plotted for various crack depth ratios, using a described model on a cracked isotropic aluminum cantilever beam. ANSYS v16 was used to perform finite element analysis (FEA), including calculations of the modal, harmonic and structural frequencies for both the intact and cracked cantilever beams. The natural frequencies for the first three bending vibration modes for the intact cantilever beam obtained using FEA were validated with the results obtained through analytical calculations. Modal analysis was used to derive the first sixth mode shapes and its natural frequencies, including the modes of bending vibration, torsional vibration and deformation in Z. The relationship between the frequency ratios and the crack depth ratios was plotted and studied for various crack locations on the cracked beam. Structural analysis was used to calculate zero frequency deflection for the intact and cracked beams. The stiffness of the intact and cracked beams was analytically calculated using zero frequency deflection and the natural frequency of the first mode of bending vibration to determine the percent of error. Deformation response in the Y-direction was plotted and studied for both the intact and cracked beams. Structural analysis was also used to determine longitudinal stress at the crack tips in the cracked cantilever beam. The stress intensity factor for mode I of the crack (opening edge crack) was analytically estimated for the cracked cantilever beam. The schematic for the present work is shown in Fig. 1.

Fig. 1
figure 1

Schematic of present work

Full size image

Description of Model

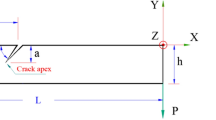
For this study, the selected isotropic material for the intact and cracked cantilever beams is aluminum. The properties [14] for this material are Young’s modulus of elasticity (E) = 70 GPa, Poisson’s ratio (ν) = 0.346 and density (ρ) = 2710 kg/m3. The model used for the cracked cantilever beam is shown in Fig. 2. The dimensions and parameters of the intact and cracked cantilever beam are length (L) = 600 mm, width (W) = 45 mm, thickness (t) = 30 mm and load (F) = 150 N. In the analytical calculations and finite element analysis, the crack is single transversal, assumed to be open edge, and listed based on crack depth ratio (d/t) and crack location ratio (e/L) where d is the depth of the crack and e is the distance from the crack to the fixed end of the cantilever beam. For this analysis, the crack is present at crack location ratios of 0.1, 0.5 and 0.9. For every crack location, the crack depth ratio was varied as 0.25, 0.4, 0.55 and 0.7.

Fig. 2
figure 2

Model of cracked cantilever beam

Full size image

Rotational Stiffness and Flexibility

Beam cracks can be modeled as equivalent internal springs, and the linear-moment law can be applied when a crack opens [15]. To simulate a uniform depth one-dimensional beam crack, the torsional spring separates an intact beam into two segments [16]. The approach that replaces the crack with a rotational spring has been used to analyze a cracked beam with a rectangular cross section [17, 18]. In the massless rotational spring model, the stiffness is inversely proportional to the crack size [10]. The presence of the crack in the component is informed by local flexibility [19]. The presence of the crack influences the dynamic response of the system under an external force with constant amplitude and frequency, and local flexibility can then be determined based on crack depth [20]. Flexibility was treated as a dimensionless parameter related to the severity of damage [15]. In this study, rotational stiffness and flexibility in crack were calculated using multiple methods: rotational stiffness using Eq 1 [21] and Eq 2 [15], and flexibility using Eq 3 [21] and Eq 4 [15]. The calculated values of rotational stiffness and flexibility are plotted versus the crack depth ratios in Figs. 3 and 4, respectively, showing that as crack depth increases, rotational stiffness decreases and flexibility increases.

$$Kz = Wt^{2} E/72\pi \left( {\frac{d}{t}} \right)^{2} f_{z} \left( {\frac{d}{t}} \right)$$
(1)
$$\begin{aligned} f_{Z} \left( {\frac{d}{t}} \right) &= 0.6384 - 1.035\left( {\frac{d}{t}} \right) + 3.7201\left( {\frac{d}{t}} \right)^{2} - 5.1773\left( {\frac{d}{t}} \right)^{3} \\ & \quad + {\kern 1pt} 7.553\left( {\frac{d}{t}} \right)^{4} - 7.332\left( {\frac{d}{t}} \right)^{5} + 2.4909\left( {\frac{d}{t}} \right)^{6} \\ \end{aligned}$$

where Kz is rotational stiffness in crack

$$Kj = \frac{EI}{t}\frac{{0.9\left[ {\left( {{d \mathord{\left/ {\vphantom {d t}} \right. \kern-0pt} t}} \right) - 1} \right]^{2} }}{{\left( {{d \mathord{\left/ {\vphantom {d t}} \right. \kern-0pt} t}} \right)\left[ {2 - \left( {{d \mathord{\left/ {\vphantom {d t}} \right. \kern-0pt} t}} \right)} \right]}}$$
(2)
Fig. 3
figure 3

Relation between rotational stiffness in crack and crack depth ratio

Full size image
Fig. 4
figure 4

Relation between flexibility in crack and crack depth ratio

Full size image

\(I = \frac{1}{12}Wt^{3}\), where Kj is rotational stiffness in crack

$$\theta = 6\pi \left( {\frac{d}{t}} \right)^{2} f_{z} \left( {\frac{d}{t}} \right)\left( {{\raise0.7ex\hbox{$t$} \!\mathord{\left/ {\vphantom {t L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}} \right)$$
(3)

where θ is flexibility at crack location

$$\alpha = \frac{EI}{{\left( {Kj} \right)L}}$$
(4)

where α is a dimensionless parameter related to the severity of the damage, E is the modulus of elasticity, I is the moment of inertia, W is beam width, t is beam thickness, d is crack depth, and L is beam length.

Finite Element Analysis (FEA)

ANSYS v16 [22] is used to perform finite element analysis (structural, modal and harmonic) of a 3D model of the intact and cracked cantilever beams. The finite element analysis of the cracked cantilever beam is performed at different crack locations and depths. The solid 185 element used in the analysis is suitable for modeling the 3D solid structure and has special features such as large deflection, large strain, plasticity, hyper-elasticity, stress stiffening and fracture parameter calculations. The solid 185 element is defined along eight nodes with three degrees of freedom at each node: translations in the nodal x, y and z directions. The region around the crack tip is crucially important in the finite element modeling where it has high gradients of stress and deformation fields. A refined mesh in the region around the crack tip should be used to pick up the rapidly varying stress and deformation fields. In linear elastic problems, the displacements near the crack tip (or crack front) vary as a function of √r, where r is the distance from the crack tip. The stresses and strains are singular at the crack tip, varying as a function of 1/√r. The crack faces should be coincident, and the elements around the crack tip (or crack front) called singular elements should be quadratic, with the mid-side nodes placed at the quarter points to capture the singularity in stresses and strains. In the finite element analysis, the singular elements are used for meshing the region around the crack tip, as shown in Fig. 5. For meshing 2D cracked beam model, plane 183 element type is used and then the 2D model is extruded in Z-direction to obtain 3D cracked beam model. The plane 183 element is changed to solid 185 element type for meshing 3D cracked model. The applied load (F) = 150 N is applied at the free end of the 3D model of the intact and cracked cantilever beams during structural and harmonic analysis. The cracked beam and its crack tip are meshed in ANSYS v16, as shown in Fig. 5.

Fig. 5
figure 5

FEM model of the cracked beam: (d/t) = 0.7, (e/L) = 0.5

Full size image

Validation of FEA Results

A comparison between the ANSYS FEA natural frequencies of the first three modes of bending vibration and those obtained by Mia et al. [9] for cracked cantilever beam model is carried out. The material properties and geometry for the cracked cantilever beam model are given in Table 1 [9]. In the finite element analysis, the crack is a V-shaped notched of opening 2 mm as described in [9]. The solid 185 element is applied for meshing the 3D cracked beam in the ANSYS analysis. Figure 6 shows FEA results for the cracked cantilever beam mode shapes of bending vibration. Table 2 presents the results at different crack locations for crack depth 0.1 m obtained by 3D ANSYS analysis and those obtained by Mia et al. [9] using 3D ABAQUS analysis. Plot of comparison results of frequency versus crack location from fixed end at the first three modes of bending vibration is presented in Fig. 7. The results in Table 2 and Fig. 7 showed that the variations can give validation for ANSYS FEA results, where the maximum variation is 1.86%.

Table 1 Material properties and geometry for cracked cantilever beam model [9]
Full size table
Fig. 6
figure 6

FEA results for the cracked beam model modes of bending vibration

Full size image
Table 2 Frequency at different crack locations for crack depth 0.1 m
Full size table
Fig. 7
figure 7

Frequency vs. crack location for crack depth 0.1 m at the first three modes

Full size image

Modal Analysis

The block Lanczos method was used to extract mode shapes and natural frequencies [23,24,25,26]. The natural frequencies of the first three modes of bending vibration for the intact cantilever beam model were validated by comparing the ANSYS FEA results to the values obtained using the analytical equation in Eq 5 [27]. The results of the two methods are listed in Table 3. The differences do not exceed − 2.4%.

$$\omega_{n} = \left( {\beta_{n} l} \right)^{2} \sqrt {\frac{EI}{{\rho Al^{4} }}}$$
(5)

where ωn is the natural frequency describing the n-th mode of bending vibrations, E is Young’s modulus, I is the moment of inertia, ρ is the material density, A is the area of cross section, and l is the length of cantilever beam.

$$\beta_{1} l = 1.875,\;\beta_{2} l = 4.694,\;{\text{and}}\;{\text{for}}\;n \ge 3\;\beta_{n} l = \left( {2n - 1} \right)\pi /2$$
Table 3 Comparison between the FEA and analytically natural frequencies of the intact cantilever beam
Full size table

The first sixth natural frequencies of the intact and cracked cantilever beams are listed in Table 4. Figures 8, 9, 10, 11, 12, 13, 14 and 15 show mode shapes for the cracked cantilever beam with a specified crack depth and crack location ratio. For the first three bending vibration mode shapes, the frequency ratio for the cracked beam was determined by calculating the ratio of the frequency of the cracked beam to that of the intact beam. The first three bending frequency ratios were plotted as a function of the crack depth ratio (d/t) for varying crack location ratios (e/L) in Figs. 16, 17 and 18. For the first mode of bending vibration, the frequency ratio decreased when the crack depth ratio increased and the crack location ratio decreased. For the second mode of bending vibration, the frequency ratio versus crack depth ratio at (e/L) = 0.5 was less than that at (e/L) = 0.1, as shown in Fig. 17. This result was inconsistent because as the crack neared the fixed end of the beam, the frequency ratio should decrease. Further analysis showed that the Y-deformation that occurred at (e/L) = 0.5 in the pattern of the second mode shape of bending vibration was greater than that at (e/L) = 0.1, as shown in Figs. 9 and 10. Also, the pattern of the third mode shape of bending vibration obtained using Fig. 18 where Y-deformation of this mode shape occurred at (e/L) = 0.5 is slightly similar to that of the intact beam, as shown in Fig. 12. As a result, the frequency ratio versus crack depth ratio at (e/L) = 0.5 is nearly equal to one. Y-deformation in the third mode of bending vibration occurred at (e/L) = 0.9, which is greater than that at (e/L) = 0.1, as shown in Figs. 11 and 13; this explains why the reason the frequency ratio for (e/L) = 0.9 is less than that at (e/L) = 0.1 in Fig. 18.

Table 4 The first sixth natural frequencies for intact and cracked cantilever beam
Full size table
Fig. 8
figure 8

Third mode shape (second mode of bending vibration): cracked beam; (d/t) = 0.7, (e/L) = 0.9

Full size image
Fig. 9
figure 9

Third mode shape (second mode of bending vibration): cracked beam; (d/t) = 0.7, (e/L) = 0.5

Full size image
Fig. 10
figure 10

Third mode shape (second mode of bending vibration): cracked beam; (d/t) = 0.7, (e/L) = 0.1

Full size image
Fig. 11
figure 11

Sixth mode shape (third mode of bending vibration): cracked beam; (d/t) = 0.55, (e/L) = 0.9

Full size image
Fig. 12
figure 12

Sixth mode shape (third mode of bending vibration): cracked beam; (d/t) = 0.55, (e/L) = 0.5

Full size image
Fig. 13
figure 13

Sixth mode shape (third mode of bending vibration): cracked beam; (d/t) = 0.55, (e/L) = 0.1

Full size image
Fig. 14
figure 14

Sixth mode shape (first mode of torsional vibration): cracked beam; (d/t) = 0.7, (e/L) = 0.9

Full size image
Fig. 15
figure 15

Fifth mode shape (first mode of torsional vibration): cracked beam; (d/t) = 0.55, (e/L) = 0.1

Full size image
Fig. 16
figure 16

Frequency ratio vs. crack depth ratio at first mode of bending vibration

Full size image
Fig. 17
figure 17

Frequency ratio vs. crack depth ratio at second mode of bending vibration

Full size image
Fig. 18
figure 18

Frequency ratio vs. crack depth ratio at third mode of bending vibration

Full size image

Stiffness of Intact and Cracked Cantilever Beam

Khalkar and Ramachandran [28] obtained the stiffness of the cracked beam by dividing the applied load at the free end of the cracked beam by the zero frequency deflection. The zero frequency deflection is obtained through a structural analysis of the deflection at the free end of the cantilever beam. The stiffness was validated using modal analysis to obtain the natural frequency of the first mode of bending vibration for the cracked beam and substituting it in Eq 6 [28]. There was agreement in the computed stiffness calculated under the two methods. In this analysis, the stiffness of the intact and cracked beam was calculated using the same two methods indicated in [28]. The mass of the cracked cantilever beam was treated as identical to the mass of the intact cantilever beam, as the computed difference between these two masses was very small to negligible.

$$f_{n} = \frac{1}{2\pi }\sqrt {\frac{k}{0.2357m}}$$
(6)

where k is the stiffness of an intact cantilever beam and 0.2357 m is the effective mass of an intact cantilever beam. Plots of the natural frequencies of the first mode of bending vibration and zero frequency deflection are shown in Figs. 19, 20, 21 and 22. The computed stiffness values for the intact and cracked cantilever beam are listed in Table 5.

Fig. 19
figure 19

Zero frequency deflection: cracked beam; (d/t) = 0.7, (e/L) = 0.1

Full size image
Fig. 20
figure 20

Zero frequency deflection: cracked beam; (d/t) = 0.25, (e/L) = 0.5

Full size image
Fig. 21
figure 21

Natural frequency of the first mode of bending vibration: cracked beam; (d/t) = 0.7, (e/L) = 0.1

Full size image
Fig. 22
figure 22

Natural frequency of the first mode of bending vibration: cracked beam; (d/t) = 0.25, (e/L) = 0.5

Full size image
Table 5 Stiffness of the intact and cracked cantilever beam
Full size table

Harmonic Analysis

Harmonic analysis involves plotting the calculated response of a structure to cyclic loads over a frequency range on an amplitude versus frequency graph [23, 25]. Harmonic analysis is used to determine shifts in the natural frequencies and study the frequency response functions for the cracked beam [13]. The frequency response diagram is an important tool which can be used to detect a crack in the beam [2]. Ma et al. [29] analyzed the effects of excitation load and crack parameters on slant-cracked cantilever beam vibration responses. They used the amplitude frequency responses in three frequency regions to describe the super-harmonic resonance, resonance and sub-harmonic resonance. In this study, harmonic analysis was used to examine the difference in the deformation responses in the Y-direction for the intact and cracked cantilever beams at different crack depth ratios in specified crack locations. The deformation responses in the Y-direction in the range of 0–40 Hz are shown in Figs. 23, 24 and 25 for both the intact and cracked cantilever beams. The natural frequencies of the cracked beam differ from those of the intact beam in the following ways:

Fig. 23
figure 23

Deformation response in Y-direction for the cracked cantilever beam; (e/L) = 0.1

Full size image
Fig. 24
figure 24

Deformation response in Y-direction for the cracked cantilever beam; (e/L) = 0.5

Full size image
Fig. 25
figure 25

Deformation response in Y-direction for the cracked cantilever beam; (e/L) = 0.9

Full size image
  1. 1.

    For the first mode of bending vibration, (a) at (e/L) = 0.9, it is very small (at its lowest), (b) at (e/L) = 0.5, it increases, and (c) at (e/L) = 0.1, it increases more.

  2. 2.

    For the second mode of bending vibration, (a) at (e/L) = 0.9, it is very small (at its lowest), (b) at (e/L) = 0.1, it increases, and (c) at (e/L) = 0.5, it increases more (to its highest).

  3. 3.

    For the third mode of bending vibration, (a) at (e/L) = 0.5, it is very small (at its lowest), (b) at (e/L) = 0.1, it increases, and (c) at (e/L) = 0.9, it increases more (to its highest).

The observations in Figs. 23, 24 and 25 are used to establish the information in Figs. 16, 17 and 18 of the modal analysis and the pattern of mode shapes.

Stress Intensity Factor

Stress intensity factor is defined as the crack driving force; its critical value is fracture toughness, a material property which reflects resistance to extension of the crack [30]. Stress intensity factor can be evaluated for three crack modes: mode I the crack is opening under tensile stress, mode II the crack is sliding under applied shear stress, and mode III the crack is tearing under applied shear stress [31]. The stress intensity factor denotes the severity of the crack. Many authors have presented studies on estimating the stress intensity factor for cracks [32,33,34,35,36,37].

The stress intensity factor for mode I (opening edge crack) was determined using Eq 7 [21]. ANSYS was used for a structural analysis of the stresses inside the crack. The contour of the longitudinal stress distribution around the crack tip for cracked cantilever beam (d/t) = 0.7, (e/L) = 0.1 is shown in Fig. 26. The SIF versus crack depth ratio was plotted for various crack locations in Fig. 27, showing that as crack depth ratio increased and crack location ratio decreased, the SIF values increased.

$${\text{SIF}} = \sigma \sqrt {\pi d} f\left( {{d \mathord{\left/ {\vphantom {d t}} \right. \kern-0pt} t}} \right)$$
(7)
$$f\left( {{d \mathord{\left/ {\vphantom {d t}} \right. \kern-0pt} t}} \right) = 1.13 - 1.374\left( {{d \mathord{\left/ {\vphantom {d t}} \right. \kern-0pt} t}} \right) + 5.749\left( {{d \mathord{\left/ {\vphantom {d t}} \right. \kern-0pt} t}} \right)^{2} - 4.464\left( {{d \mathord{\left/ {\vphantom {d t}} \right. \kern-0pt} t}} \right)^{3}$$

where SIF is the first stress intensity factor,\(\sigma\) is stress in the crack, d is crack depth, and t is the thickness of the cantilever beam.

Fig. 26
figure 26

Enlarged view of the longitudinal stress distribution around the crack tip; (d/t) = 0.7, (e/L) = 0.1

Full size image
Fig. 27
figure 27

Plot of SIF vs. crack depth ratio

Full size image

Conclusions

Based on the results obtained in this study, the following conclusions were drawn:

  1. 1.

    An increase in crack depth led to decreased rotational stiffness and increased flexibility in the crack.

  2. 2.

    At specific crack locations, the reduction in the natural frequencies of the cracked cantilever beam was proportional to the depth of crack.

  3. 3.

    For the first bending vibration mode, the natural frequency of the cracked cantilever beam was proportional to the distance of the crack from the fixed end of the cantilever beam.

  4. 4.

    For the second and third bending vibration modes, the pattern of mode shapes was vital to understanding the variation in the natural frequency of the cracked cantilever beam.

  5. 5.

    In the modal analysis, plotting the deformation responses in the Y-direction for the intact and cracked cantilever beams revealed a noticeable shift in the natural frequencies.

  6. 6.

    Where the depth of the crack was constant, the stiffness of the cracked beam increased as the distance of the crack from the fixed end of the cantilever beam increased.

  7. 7.

    Where the location of the crack was constant, the stiffness of the cracked beam decreased as the crack depth increased.

  8. 8.

    Stress intensity factor values in mode I increased as crack depth increased and the distance of the crack from the fixed end of the cantilever beam decreased.