Determination of the Effect of a Mode I Surface Crack Cross-Sectional Shape on the Characteristics of the Forced Bending Vibrations of a Cantilever Beam

The results of computational experiments for determining the effect of a mode I surface fatigue crack cross-sectional shape in a rectangular cantilever beam on the characteristics of its free and forced bending vibrations with varying cross-sectional dimensions of the crack and its longitudinal position are presented. Finite-element models of beams with 8-node 3D finite elements were developed for carrying out investigations. Three types of a breathing crack cross-section were considered: rectangular, triangular, and trapezoidal one, with the solution of a contact problem to ensure the non-penetration of crack edges. Plots of relative change in the natural frequency of vibration, the amplitudes of the first and second harmonics and their ratios at the main, super- and subharmonic resonances versus the shape, relative area and location of the crack were obtained. It is shown that when bending vibrations of the beam with a rectangular crack, are excited along the axis Oy, there arise displacements only in the direction of driving force, while in the case of triangular and trapezoidal cracks, there arise additional displacements along the axis of minimum stiffness, Oz. It was found that the change in the natural frequency of the beam, as well as the ratio of the amplitudes of dominant harmonics during the recording of vibrations along the excitation axis at the main, super- and subharmonic resonances increase with increasing relative area of the crack cross-section. Under this condition, their largest value was characteristic of a rectangular crack, and the smallest of a triangular one. It was noted that a characteristic indicator of the asymmetric shape of the crack was the appearance of vibrations in the plane perpendicular to the excitation plane.

Problem Statement. The nucleation and development of surface fatigue cracks in structural elements is a complex process, which depends on many factors, such as the presence of stress concentrators, load type, operating conditions and time, etc. But, regardless of the conditions of the occurrence and growth rate of such damages, their timely detection will allow to avoid further negative consequences associated with the failure of machine parts. In order to solve this urgent scientific and technical problem, intensive research is carried out, as evidenced by the large volume of publications. However, the results of their analysis show that today there is no universal way to diagnose the presence of such fatigue cracks.

The most effective methods include vibrodiagnostic methods, which are based on the inter relationship between the characteristics of the crack (depth or sectional area, location) and change in the stiffness of structural elements and, as a consequence, change in the natural frequency and mode of vibrations [1,2,3], dissipative properties [4], as well as the appearance of nonlinear effects upon the excitation of forced vibrations [5,6,7].

The Pisarenko Institute of Problems of Strength of the National Academy of Sciences of Ukraine proposed approximate analytical and numerical methods for determining the vibration diagnostic parameters indicating the presence of a mode I breathing crack in beams of rectangular cross-section and showed their significant dependence on the crack size and location, and the features of bending vibration excitation [8,9,10]. However, the methods have been developed under the condition that the front of the fatigue crack is a straight line parallel to the neutral line of the beam cross-section, that is, its shape is rectangular. In the general case, the crack front can represent a straight line at an angle to the neutral line or a curve, such as a parabola [11, 12].

Papers [13,14,15,16] present the results of computational and experimental studies to determine the influence of the rectangular and trapezoidal shapes of cracks on the natural frequencies of the vibrations of a cantilever beam of rectangular cross-section in a wide range of varying their dimensions and location along the beam length. Note that in these works, when modeling the crack, only its influence on the change in the elastic properties of the beam was taken into account. However, taking into account the change in the inertial characteristics of the beam due to the presence of a crack makes it possible to establish more generalized laws of formation of its natural frequencies of vibrations [17]. In addition, note that in [17], as well as in [13,14,15,16], the nonlinearity of the beam vibrations caused by the presence of a breathing fatigue crack was not studied.

The possibility of nonlinear effects under forced vibration of a beam with fatigue crack and their influence on its natural frequencies and the vibration amplitude spectrum were considered in [1,2,3,4,5,6,7,8,9,10,11, 18, 19].

Analysis of the known results of studies of forced vibrations of beams with fatigue cracks shows that the influence of the geometry of the front on the formation of their characteristics has not been studied enough.

The aim of this study is to computationally investigate the influence of the position of the mode I fatigue crack front as a straight line relative to the neutral line of a solid beam on its characteristics of free and forced vibrations when varying the cross-sectional dimensions of the crack and its longitudinal position.

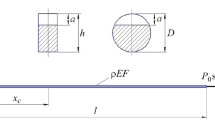
The Object of the Study and Its Finite-Element Modeling. We consider a cantilever beam of rectangular cross-section with appropriate geometric parameters: l = 0.23 m, h = 0.02 m, and b = 0.004 m (Fig. 1). The material properties are as follows: elastic modulus E = 2 ·10¹¹ Pa, density ρ = 7800 kg/m³, Poisson’s ratio μ = 0.3, logarithmic decrement of vibration δ = 0.01, and friction coefficient f = 0.2.

Fig. 1

FE model of a cantilever beam of rectangular cross-section with a breathing fatigue crack: x₀ and x_c are the site of recording vibration characteristics and the crack position, respectively.

To solve the problem, modern software packages based on the finite element method allow one to consider different types of modeling the research object (linear, two-dimensional or three-dimensional ones) and to take into account its loading conditions, close to operational ones, as well as the full interaction of the crack edges in the vibration process according to the results of solving the contact problem.

When creating a finite-element (FE) calculation model of the beam, we used eight-node elements. Each node of had three degrees of freedom, which made it possible to determine the displacements in any node of the beam along each of its axes.

The breathing crack was constructed in the form of a mathematical cross-section, i.e., two surfaces (crack edges) with zero distance between them, which had a common section line – the front as a straight line at an arbitrary angle to the median plane of the beam. It was assumed that during its vibrations, the cross-sectional dimensions of the crack remained unchanged. The mechanism of alternating crack opening and super closure was taken into account by solving a contact problem. Considering this, contact elements are imposed on the crack edges. To ensure FE contact, the mesh on both surfaces must be identical. The crack edges were considered as a contact pair, which consisted of a target surface and a contact surface with a given coefficient of friction, which ensured their mutual non-penetration. So, in the process of vibrations, the stiffness of the beam changed depending on the contact of the crack edges. If the surfaces were not in contact, the crack was completely open, when they were in direct contact, the crack was closed, and the beam behaved as a solid body. If the surfaces were partially in contact, there was a transient crack opening and closure process.

Since we considered a cantilever beam, any displacement of its end elements at the position x = 0 were zero.

The forced vibrations of the beam were excited by a harmonic force P sin(ωt ), where P is the driving force amplitude, and ω is the excitation frequency applied to the free end.

The Main Principles of Numerical Calculation of the Forced Vibrations of a Beam. To carry out the research on determining the characteristics of the forced vibrations of a beam with a breathing fatigue crack, we used a numerical method of calculation using the created FE model of the beam. The forced bending vibrations of the FE model of the beam are described by the differential equation

$$ \left[M\right]\left\{\ddot{u}\right\}+\left[D\right]\left\{\dot{u}\right\}+\left[K\right]\left\{u\right\}=\left\{P(t)\right\}, $$

(1)

where [M] and [D] are the inertial and dissipative matrices of the system, [K] is the stiffness matrix, {u}, $\left\{\dot{u}\right\}$, and $\left\{\ddot{u}\right\}$ are the column vectors of displacement, velocity, and acceleration, respectively, and {P(t )} is the column vector of the external harmonic load. The stiffness matrix [K] depends on the mutual position of contacting crack surfaces and is determined using the Newton–Raphson method. The dissipative matrix [D] is represented in the form of the Rayleigh model, which in the case of internal energy dissipation, has the form

$$ \left[D\right]=\upbeta \left[K\right], $$

(2)

where $\upbeta =\frac{\delta }{2{\uppi}^2{\upomega}_0}$ for the decrement of vibration δ, which is independent of the amplitude of deformation, ω₀ is the natural frequency of beam vibrations.

The solution of Eq. (1) was carried out by time integration using Newmark’s method [20] with the following initial conditions: ${\left\{u\right\}}_0=0,{\left\{\dot{u}\right\}}_0=0,$ and ${\left\{\ddot{u}\right\}}_0=0.$ The vibrations of the beam were studied in the 1s time interval, which was approximately 300 periods of vibrations. This number of periods at the decrement of vibration δ = 0.01 was sufficient to fix steady-state vibrations (Fig. 2).

Fig. 2

Time dependence of the displacement of the free end of a cracked rod.

The fast Fourier transform (FFT) procedure was used to determine such characteristics as the resonant frequency and amplitude spectrum of beam vibrations.

Results of Numerical Studies. According to the problem statement, three types of the cross-section of a breathing fatigue crack were considered (Fig. 3).

Fig. 3

Cross-sectional shapes of a breathing crack: (a) rectangular; (b) triangular; (c) trapezoidal.

The geometric dimensions of the crack cross section for the three values of its relative area γ =F_c/bh , are given in Table 1, where F_c is the area of the crack.

Table 1 Geometric Dimensions of the Cross Section of Cracks under Investigation (m)

Numerical studies of forced vibrations of the beam were carried out at a disturbing force P amplitude of 1 N for the main resonance and 100 N for the super- and subharmonic resonances.

Let us analyze the influence of the crack model on the resonant frequency of the beam at the main resonance. The amplitude-frequency characteristics (AFC) of an intact beam and a beam with an open and a breathing triangular crack with a relative cross-sectional area γ = 0.125 and the location x_c= 0.1l were determined (Fig. 4). For the beam with a breathing crack, the conditions of contact of its edges were set after the calculation of the natural frequencies of vibrations of the intact beam and the beam with an open crack, after which the problem of its forced vibrations was solved. The vibration excitation frequency of such a beam was chosen between the natural frequencies of the first two beams.

Fig. 4

AFC of an intact beam(solid line), with an open (dashed line) and a breathing (dash-dotted line) triangular crack with the relative cross-sectional area γ = 0.125 and position x_cl = 0.1.

Analysis of the obtained AFCs shows that the maximum value of the amplitude of the main resonance at the assumed constant decrement of vibrations practically does not depend either on the presence of the crack or on its model. This means that, in this case, this characteristic of forced vibrations cannot be used as a vibrodiagnostic indicator of the presence of a crack.

Under real conditions, some change in the damping properties of the beamin the presence of a crack and, accordingly, a change in the value of the maximum amplitude are possible. However, it is practically impossible to estimate the presence and size of the crack from the value of this amplitude, since a number of operational factors, such as amplitude level, frequency value, cyclic loading time and temperature conditions before performing vibrodiagnostics, can influence the value of the damping property of the beam before the appearance of a crack of any size.

In [17, 21], it was shown that the following characteristics of forced vibrations can be used as vibrodiagnostic parameters indicating the presence of cracks: the change in the natural vibration frequency of the damaged beam $\varDelta \overline{\upomega}=1-{\upomega}_c/{\upomega}_0,$ where ω_c is the natural vibration frequency of the beam with a breathing crack, and the ratio of the amplitudes of dominant harmonics the main resonance A_2/1 = A₂/A₁. Noteworthy is that under monoharmonic vibration excitation for the beam in the absence of or with an open crack, we have A_2/1 = 0.

Further numerical studies of the forced vibrations of the beam were carried out in the presence of breathing cracks (Fig. 3). Considering this, a study was performed for three variants of their dimensions, which were chosen so that for each of them, the relative cross-sectional area of the cracks remained constant.

Figure 5 shows plots of first and second harmonic vibration amplitudes under excitation at the main resonance of the beamversus the vibration recording site at the relative parameters of the crack γ = 0.25 and x_c/l = 0.1.

Fig. 5

Plots of the first (■) and second (□) harmonics vibration amplitudes versus the site of vibration recording along the axes Oy (solid lines) and Oz (dashed lines) for rectangular (a), triangular (b) and trapezoidal (c) cracks with the relative parameters γ = 0.25 and x_cl = 0.1.

As can be seen from the obtained data, the displacements of the beamwith a rectangular crack occur only along the Oy-axis, that is, in the direction of driving force. In the case of triangular and trapezoidal cracks, there arise additional displacements along the minimum stiffness axis Oz, which also decompose into two dominant harmonics (Fig. 5b and c).

Plots of the change in the natural frequency of the rod, $\varDelta \overline{\upomega}$, and the ratio of the amplitudes of the dominant harmonics along each of the axes [A_2/1(y) = A₂(y)/A₁(y), A_2/1(z) = A₂(z)/A₁(z)] under main resonance excitation for selected shapes of a transverse crack versus its relative area γ and location x_c/l were also obtained (Fig. 6).

Fig. 6

Plots of the relative change in the natural frequency of vibration ( dashdot lines) and the ratio of the amplitudes of the dominant harmonics along the axes Oy (solid lines) and Oz (dashed lines) of a beam with rectangular (■), triangular (▲), and trapezoidal (●) cracks versus the relative area γ at x_cl = 0.1 (a) and the location x_cl at γ = 0.25 (b).

As can be seen from the above data, the change grows with increasing relative cross-sectional area of the crack regardless of its shape. In this case, the largest value of $\varDelta \overline{\upomega}$ is characteristic of a rectangular crack and the smallest of a triangular one. As the crack moves to the free end of the rod, this value decreases.

The analysis of the obtained plots for the amplitude ratio A_2/1 shows: along the axis Oy, the value of the parameter A_2/1(y) for the triangular crack practically does not change with increase in γ, while for the other two shapes it slightly increases, but does not exceed 0.012; along the Oz axis, the values of A_2/1 (z) significantly increase and change from 0.06 to 0.2 with increasing γ. For the trapezoidal crack, they are somewhat larger. When the crack position along the beam length changes, the largest value of the vibration parameter A_2/1(z) is achieved at x_c = 0.4l. So, the mode of beam vibrations along the Oz-axis changes significantly.

The presence of multiple harmonics in the forced vibration spectrum at the frequency which is equal to the resonance vibration frequency of the beam with a breathing crack makes possible the excitation of resonant modes at multiple frequencies. Therefore, similarly to the main resonance, a study was conducted to determine the effect of selected shapes of transverse crack on the excitation of vibrations at the frequencies of the superharmonic resonance of order 1/2 and subharmonic resonance of order 2. Figure 7 shows plots of dominant harmonics versus the vibration recording site at γ = 0.25 and x_c = 0.1l, and Fig. 8 shows the corresponding values of the ratio of the amplitudes of dominant harmonics: second-to-first one $\left({\overline{A}}_{2/1}={A}_2/{A}_1\right)$ at the superharmonic resonance and first-to-second one $\left({\overline{A}}_{2/1}={A}_1/{A}_2\right)$ at the subharmonic resonance.

Fig. 7

Plots of first (■) and second (□) harmonic vibration amplitudes versus the site of vibration recording along the axes Oy (solid lines) and Oz (dashed lines) for rectangular (a, b), triangular (c, d), and trapezoidal (e, f) cracks during the excitation of super- (a, c, e) and subharmonic (e, d, f) resonances.

Fig. 8

Plots of the ratio of the amplitudes of the dominant harmonics at the super- (a) and subharmonic (b) resonances along the axes Oy (solid lines) and Oz (dashed lines) of a beam with rectangular (■), triangular (▲), and trapezoidal (●) cracks versus the relative cross-sectional area γ at x_cl = 0.1.

As with the main resonance, the beam with a rectangular crack vibrates only along the axis of vibration excitation and has the greatest value of the amplitude ratio in both nonlinear resonant modes compared with the other two crack shapes. The trend of the plots of ${\overline{A}}_{2/1}=\left(\upgamma \right)$ for triangular and trapezoidal cracks is almost identical and differs only quantitatively.

As can be seen from Fig. 8, the ratio of the amplitudes of the dominant harmonics when recording vibrations along the excitation axis at both super- and subharmonic resonances increases with cross-sectional area of cracks. However, along the Oz-axis, first an increase in the ratio of the amplitudes of the dominant harmonics, followed by a decrease for both types of nonlinear resonance are noted.

Let us consider the influence of the crack shape on the percentage change in natural frequency and the value of the ratio of the amplitudes of the dominant harmonics at the main, super- and subharmonic resonances in the Oy plane. Thus, at the relative crack area γ = 0.125, 0.1875, and 0.25, the $\varDelta \overline{\upomega}$ value for the trapezoidal crack reaches 80, 77, and 75%, respectively; for the triangular crack, it is 40, 45, and 50% of the value for the rectangular crack.

For A_2/1, in the case of trapezoidal crack we get 95, 83, and 70% for triangular crack, 85, 81, and 40%, respectively.

For ${\overline{A}}_{2/1},$ in the case of trapezoidal crack we get 90, 81, and 83%, for triangular crack 40, 60, and 66%. For ${\overline{A}}_{1/2},$ in the case of trapezoidal crack we get 80, 65, and 70%, for triangular crack 20, 11, and 45%. That is, these values are lower and, in some cases, significantly lower than those for the rectangular crack.

A characteristic indicator of the asymmetric shape of the crack, as was shown above, is the appearance of vibrations in the plane perpendicular to the excitation plane. Taking this into account, at relatively smaller γ values, the indicators ${\overline{A}}_{2/1}$ and ${\overline{A}}_{1/2}$ in the plane Oz are even higher than those in the plane of excitation for a rectangular crack. But the ignorance of the crack shape creates a problem in estimating its possible area.

Figure 9 shows plots of the amplitude ratio of the dominant harmonics versus the location of a triangular crack at γ = 0.25. It can be seen that as the crack approaches the free end of the beam, both at the super- and subharmonic resonances, the value of the amplitude ratio decreases. Only for the crack x_cl = 0.4, the value of this ratio along the Oz axis is higher than along the Oy axis, which can be explained by a significant change in the mode of vibrations in the presence of a crack in this position. Even in the case of quite a large crack of the size γ = 0.25 in the position near the free end of the rod, this value is very small at both super- and subharmonic resonances. So, in this case, it is practically impossible to detect a crack using the ratio of the amplitudes of dominant harmonics.

Fig. 9

Plot of the ratio of the amplitudes of the dominant harmonics at the super- (▲) and subharmonic (∆) resonances along the axes Oy (solid lines) and Oz (dashed lines) versus the location x_c/ l of a triangular crack at γ = 0.25.

Conclusions. Based on the results of numerical studies of the forced vibrations of a cantilever beam of rectangular cross-section with cracks of different configurations, it was established that when a non-uniform triangular or trapezoidal crack appeared, there arised additional displacements in the plane of minimum stiffness upon the excitation of bending vibrations. The ratio of the amplitudes of the dominant harmonics of displacements both at the main resonance and at the nonlinear super- and subharmonic resonances depended largely on the crack configuration. These ratios reached their maximum in rectangular cracks and minimum in triangular cracks. So, if these ratios are observed, a problem arises not only in determining the size or location of the crack, but also in establishing the geometric shape of the damage, since the same values of the vibration characteristics correspond to different damage values of structural elements.