Numerical Simulation to Predict the Effect of Process Parameters on Hardness during Martempering of AISI4140 Steel

Abstract

Martempering is a widely practiced industrial heat treatment process to harden steel parts with minimum distortion. A numerical experiment to predict hardness distribution in AISI 4140 steel cylinders of various diameters during martempering is presented in this work. Apart from the diameter (D), the effect of other process variables such as heat transfer coefficient (h), bath temperature (T_b), and residence time (t_r) was also studied. The relationship between hardness distribution and the aforementioned process variables was highly nonlinear. An artificial neural network (ANN) model with a single hidden layer and 30 hidden layer neurons was thus developed to predict the hardness distribution in martempered AISI 4140 steel cylinders. The increase in bath temperature, diameter, and residence time decreased the average hardness, and an increase in the heat transfer coefficient increased the average hardness of martempered AISI 4140 cylinders. The weights of the ANN model were used to calculate the relative importance of all input variables and they followed a decreasing order of T_b>D>t_r>h.

Introduction

The time quenching technique involves the use of two or more quenching media on a timed basis. Partial quenching in water, followed by quenching in oil or molten salt, followed by air cooling are some examples of the time quenching process. Interrupted quenching, martempering, and rinse quenching are commercial examples of this type of quenching practice. The quenched part is cooled in the medium at a high cooling rate until martensitic start temperature and then cooled in another medium at a moderate cooling rate to room temperature. The practice is to avoid quench defects in the heat-treated part (Ref 1).

Figure 1 shows clearly the difference between conventional quench hardening, martempering, and modified martempering. In conventional quench hardening, a large temperature gradient exists between the surface and core of the part through the cooling. During martempering (Fig. 1b), the austenitized steel part is quenched in a quenchant maintained just above M_s, the part is held in the quenchant until the temperature is equalized throughout its cross section. The part is then removed from a high-temperature quench bath and cooled in the air to room temperature allowing austenite to transform to martensite. The temperature gradient between the surface and the core, observed in the parts quenched in high-temperature quenchant is much less than in conventional quenchants (water, mineral oil, aqueous polymer, etc.). This reduces both thermal and transformational stresses, which aids to minimize the distortion and susceptibility to cracking in the quenched part.

The marquenched parts are subsequently subjected to tempering. Carbon steels, low alloy steels, and gray cast iron parts can be subjected to martempering. There are many variants of martempering. Figure 1(c) shows one of the variations of the martempering process. Low hardenability steel parts are subjected to this process. In this process, the part is quenched in quenchant maintained at a temperature just below M_s. The low temperature of the quenchant (150-175 °C) increases the severity of the quenchant. Higher cooling rates thus offered by the quenchants help in evading high-temperature pearlitic transformation in the quenched part. Another variant of the martempering process is used to heat treat steel parts with a large cross-sectional area. In this process, the part is first quenched in water or brine for a very short time and subsequently transferred to a martempering bath. This process increases the depth of hardening as compared to the conventional martempering process.

Mathematical Modelling of Hardness Evolution

Quench hardening is a complex multi-physics process that involves heat transfer, phase transformation, and mechanical stress fields acting in the quenched body. Generally, TTT and CCT diagrams have been used to predict the microstructure of the hardened steel part (Ref 2). Dean et al. (Ref 3) and Rao B. Smoljan et al. (Ref 4) and Prabhu (Ref 5) used a cooling curve parameter t₈₅ defined as the time needed to cool from 800 to 500 °C to predict the hardness of hardened steel parts. This method cannot be used for predicting hardness during martempering because of the interrupted nature of cooling and high bath temperature involved in the martempering process.

Tensi (Ref 6) suggested rewetting time, i.e., the time corresponding to the collapse of vapor blanket stage as a parameter to predict hardness. Martempering is generally carried out in molten salt mixture. Rao and Prabhu (Ref 7) showed that there is no vapor blanket stage during quenching in molten salt media. Hence, rewetting time cannot be used to predict hardness during martempering in salt media. Zehtab et al. (Ref 8) suggested the use of quench factor analysis to predict the hardness of Jominy end quench steel specimens.

The most widely used method to predict phase distribution in the quenched steel part was described by Simsir and Gur (Ref 9, 10). This FEM-based method is based on modified JMAK (Johnson–Mehl–Avrami–Kolmogorov) and KM equations (Koistinen–Marburger). Babu and Kumar (Ref 11) modified this method by incorporating temperature equilibrium phase limitation for ferrite and bainite to successfully predict interfacial heat flux at the metal quenchant and phase distribution during quenching of the AISI 4140 steel probe in water and air.

It is evident that most of the models available in the literature are focused on predicting hardness during the conventional quench hardening process. The increasing emphasis on distortion control heat treatment processes provides us a scope for developing similar models to predict hardness during distortion control heat treatment process. The purpose of the present work is to modify the phase transformation models described in the above-mentioned works to model phase transformations and hardness distributions during the martempering process.

Details of the Numerical Model

FEM-Based Phase Transformation Model

The phase transformation during quench hardening of steel is a complex process that involves the thermal, metallurgical effect, and mechanical stress effects interacting with each other. In the present model, the effect of mechanical stress was neglected. The thermal field/ heat transfer in the steel is the driving force for metallurgical transformations. The heat transfer during quench cooling of a 1-d cylinder is governed by Eq 1. The heat transfer equation coupled with the phase transformation field was solved using the FEM method.

$${\rho C}_{{\text{p}}} \frac{{\partial {\text{T}}}}{{\partial {\text{t}}}} = \frac{1}{r}\frac{\partial }{{\partial {\text{r}}}}\left( {{\text{kr}}\frac{{\partial {\text{T}}}}{{\partial {\text{r}}}}} \right) + {\text{Q}}$$

(1)

Here, ${\uprho }$ is density, C_p is the specific heat at constant pressure, k is thermal conductivity, T is temperature, r represents radial coordinate and Q is latent heat. The two physical phenomena that result in the interaction of the phase transformation field with the thermal field are

• (i) Variation of thermophysical properties (${\uprho },{\text{Cp}},{\text{k}}$) of the steel with temperature and the phase composition of the steel.

• (ii) Latent heat evolution is associated with the transformation of austenite to product phases.

Equation 2 shows the linear mixture rule used to determine the thermophysical property of a mixture consisting of ‘N’ phases.

$${\text{P}}\left( {{\text{T}},\xi_{k} } \right) = \mathop \sum \limits_{k = 1}^{N} P_{k} \xi_{k}$$

(2)

where, $P_{k}$ and $\xi_{k}$ are the thermophysical property and volume fraction of the phase ‘k,’ respectively. Phase variable ’k’ in Eq 2 refers to austenite, ferrite, pearlite, bainite, and martensite.

$${\text{Q}} = \mathop \sum \limits_{k = 1}^{N} \left( {\rho_{k} \Delta {\text{H}}_{k} \dot{\xi }_{k} } \right)$$

(3)

In Eq 3, Q is the latent heat that is generated when austenite transforms to any phase ‘k’ (ferrite, pearlite, bainitic, or martensite) and $\Delta {\text{H}}_{k}$ and $\dot{\xi }_{k}$ are the latent heat per unit volume and the rate of evolution of phase k from austenite, respectively. Figure 2 shows the temperature-dependent thermophysical properties of AISI 4140 steel. These properties were obtained from JMatPro software (Ref 12). The ASTM grain size of 9 and the composition of the AISI 4140 steel probe presented in Fig. 2 were provided as input to JMatPro software to calculate thermophysical properties and TTT diagram. Figure 3 shows the TTT diagram and the critical temperature obtained for 4140 steel.

Fig. 1

Cooling curve superimposed on TTT diagram for (a) conventional quench hardening (b) Martempering (c) Modified martempering [2]

Fig. 2

Temperature-dependent variation of (a) Density, (b)Thermal conductivity, (c) Specific heat (d) enthalpy of transformations for different phases

The transformations of austenite to ferrite, pearlite, and bainite are diffusional transformations. The transformation of austenite to martensite is diffusionless transformation. The isothermal diffusional transformations can be modelled using the JMAK equation shown in Eq 4.

$$\xi_{k} = \left( {1 - \exp \left( { - b_{k} \left( T \right)t^{{n_{k} \left( T \right)}} } \right)} \right)$$

(4)

In Eq 4, b_k and n_k are material parameters that were obtained from the TTT diagram. In the TTT diagram, transformation start phase fraction ($\xi_{ki}$) and transformation finish phase fraction ($\xi_{kf}$) were 0.1% and 99.9%, respectively.

$$n_{k} = \frac{{ln\left( {\frac{{\ln \left( {\xi_{ki} - 1} \right)}}{{\ln \left( {\xi_{kf} - 1} \right)}}} \right)}}{{\ln \left( {\frac{{t_{i} }}{{t_{f} }}} \right)}}$$

(5)

$$b_{k} = - \frac{{\ln \left( {\xi_{ki} - 1} \right)}}{{t_{i}^{{n_{k} }} }}$$

(6)

Equations 5 and 6 show the formulae used to calculate n_k and b_k, respectively. Where t_i and t_f are the transformation times corresponding to $\xi_{ki}$ and $\xi_{kf}$, respectively, at a given temperature (T).

Diffusion-based transformations occur in two stages, nucleation and growth. Schiel’s additive rule was adopted to describe the non-isothermal nucleation process that occurs during quenching. The cooling was divided into small intervals of $\Delta t_{i}$. The time for the start of transformation ($\tau \left( {\xi_{{k_{i} }} ,T_{i} } \right)$) was extracted from TTT. Schiel’s sum was then calculated at each time step as shown in Eq 7.

$$S_{k = f,p,b} = \mathop \sum \limits_{i = 1}^{n} \frac{{\Delta t_{i} }}{{\tau_{i} \left( {\xi_{k} ,T} \right)}}$$

(7)

When Schiel’s sum exceeded the value of 1, the nucleation stage was presumed to be complete. After completion of the nucleation stage, the growth of phases was modelled using the JMAK (Johnson–Mehl–Avrami–Kolmogorov) equation as described in Eq 8 and 9.

$$\xi_{k}^{^{\prime}} \left( {\text{t}} \right) = \frac{{\xi_{k}^{t} }}{{\xi_{k}^{max} \left( {\xi_{\gamma }^{t} + \xi_{k}^{t} } \right)}}{ }$$

(8)

$$\tau_{f} = \left( { - \frac{{\ln \left( {1 - \xi^{\prime}_{k} \left( t \right)} \right)}}{{b_{k} \left( T \right)}}} \right)^{{\frac{1}{{n_{k} \left( T \right)}}}}$$

(9)

$$\xi_{k}^{t + \Delta t} = \xi_{k}^{max} \left( {\xi_{\gamma }^{t} + \xi_{k}^{t} } \right)\left( {1 - \exp \left( {b_{k} \left( {\tau_{f} + \Delta t} \right)^{{n_{k} }} } \right)} \right)$$

(10)

where fictitious time ($\tau_{f}$) is defined as the time required for the formation of phase fraction $\xi^{\prime}_{k} \left( t \right)$ at constant temperature T. Later this fictitious time was used to calculate the phase fraction at the next time step $(\xi_{k}^{t + \Delta t}$) as described in Eq 10.

With known values of Ae₃ and composition, the eutectoid composition, and carbon equivalent of the AISI 4140 steel was calculated using Eq 11 (Ref 13). The maximum ferrite composition ($\xi_{Fe}^{max}$) was calculated using the lever rule. Maximum fraction transformed for pearlite and bainite was 1.

$$\begin{aligned} \% {\text{C}} = & \left( {\left( {{912} {-+}{15}.{2}\% {\text{Ni}} + {44}.{7}\% {\text{Si}} - {1}0{4}\% {\text{V}} + {31}.{5}\% {\text{Mo}} + {13}.{1}\% {\text{W}}{-} {3}0\% {\text{Mn}} - {11}*{\text{Cr}}{-}{2}0\% {\text{Cu }}} \right.} \right. \\ & \left. {\left. {\; + {7}00\% {\text{P}} + {4}00\% {\text{Al}} + {12}0\% {\text{As}} + {4}00\% {\text{Ti}} - {\text{Ae}}_{{3}} } \right)/{2}0{3}} \right)^{2} \\ \end{aligned}$$

(11)

The diffusionless martensitic transformation was modelled using the Koistinen-Marburger model shown in Eq 12. ${\Omega }$ in the equation was assumed to be 0.011 (Ref 14).

$$\xi_{M}^{t + \Delta t} = \left( {\xi_{\gamma }^{t} + \xi_{M}^{t} } \right)\left( {1 - \exp \left( { - {\Omega }\left( {M_{s} - T^{t + \Delta t} } \right)} \right)} \right)$$

(12)

Simulation of the Effect of Heat Transfer Coefficient, Bath Temperature, Section Thickness, and Residence Time on Hardness

As shown in Fig. 4, a simulation study on the effect of four important process variables during martempering of AISI 4140 steel cylinders was performed. Heat transfer coefficient (h), quench bath temperature (T_b), diameter (D), and residence time (t_R) were considered as the four process variables

Fig. 3

TTT diagram of AISI 4140 steel probe obtained from JMatPro

The maximum residence time (t_Rmax) was defined as the time required to cool the quenched part surface from austenitizing temperature (850 °C) to the quench bath temperature and also fulfil following two conditions

• (1) The temperature difference between the surface and center of the steel cylinder below 1 °C

• (2) The surface temperature is less than 5 °C.

The component was subjected to air cooling at a time greater than residence time. To ensure residence time is less than the maximum residence time, the residence time fraction (f) was defined as the ratio of residence time to maximum residence time (f=t_R/t_RMax). The ambient air temperature was assumed to be 30 ± C. The air heat transfer coefficient was obtained from the work of Kothandaraman et al. (Ref 15). The equation used to determine the surface temperature-dependent air heat transfer coefficient is given in Fig. 4.

Daniel H Herring (Ref 16) discussed the average heat transfer coefficients for various quench media like air, salt, gas, oil, polymer, water, and brine. In the simulations, the quench heat transfer coefficient was varied from 500 to 3500W/m² °C in steps of 500 W/m² °C. Bath temperature was varied in steps of 50 °C from M_s − 100 to M_s+100 in intervals of 50 °C. The diameter of the steel bar was varied in steps of 2, 5, 7.5, 10, 20, 30, 40, 60, 80, and 100 mm. A detailed description of the time step size and mesh size used in the FEM model is given in Fig. 4. At each node, the kinetics of diffusion-based and diffusionless transformations and phase-dependent thermophysical properties were modelled as discussed in section 1.1. The FEM-based code to solve phase transformation coupled heat transfer equation (Eq 1-12) was coded in MATLAB compiler (Ref 17). The calculation was stopped when the temperature at the center of the probe decreased below M_S of the steel grade. As shown in Eq 13 , 14, the volume fraction of austenite and martensite at room temperature was assumed to be 5% and 95% of total austenite available for martensitic transformation at each node at M_s.

$$\xi_{A}^{T = 25^\circ C} = 0.05\left( {\xi_{A}^{{T = M_{s} }} } \right)$$

(13)

$$\xi_{M}^{T = 25^\circ C} = 0.95\left( {\xi_{A}^{{T = M_{s} }} } \right)$$

(14)

Yield strength was calculated using the linear mixture rule shown in Eq 15. The hardness (H) was modelled as a function of yield strength (σ_y). The hardness-yield strength relationship was obtained from JMatPro software and is shown in Fig. 5. Table 1 shows yield strength at room temperature for different phases obtained from JMatPro.

$$H = \mathop \sum \limits_{k = A,F,P,B,M} \sigma_{k} \xi_{k}$$

(15)

Fig. 4

Flowchart of the numerical experiment

Table 1 Yield strength of different phases

The phase transformation coupled heat transfer equation was solved for all combinations of varying input variables shown in Fig. 4. The total number of simulations performed was 10×7×5×6=2100, where 10, 7, 5 and 6 were the number of levels of input variables D, h, T_b, and f, respectively

Results and Discussion

The results of the simulations for an AISI 4140 steel cylinder of 60mm diameter quenched in a medium that offers a heat transfer coefficient of 1000W/m² K maintained at a bath temperature of 323.6 °C and held for a residence time of t_Rmax is shown in Fig. 6. A sharp change in the thermal profile after residence time (t_r) was due to a change of boundary conditions to air cooling boundary conditions. The volume % of austenite (1.14%), ferrite (0.73%%), pearlite (0%), bainite (73.39%), and martensite (21.69%) phases at room temperature was calculated at the geometric center.

Fig. 5

Hardness as a function of yield strength

Similarly, phase fractions were obtained at all the nodes of the axisymmetric model of the cylinder and these phase fractions were further used to predict hardness distribution in the cylinder. Figure 7(a) and (b) shows the distribution of phase fractions and predicted hardness from surface to center of the steel. A detailed description of the procedure adopted for the calculation of these phase fractions and predicting hardness was provided in Section 2.2. The higher hardness near the surface of the cylinder was due to a higher volume fraction of martensite near the surface.

Fig. 6

(a) Transient variation of temperature at geometric center and the surface of the cylinder and (b) Volume fraction of various phases at the geometric center of the cylinder obtained for numerical experiment with D = 60mm, h = 1000W/m2K, Tb=Ms (323.6 °C) and f=1

As shown in Fig. 7, the average hardness, H_Avg, was calculated based on the hardness distribution (H(r)) in the steel cylinder. The average hardness was calculated using the fundamental theorem of calculus, i.e., $H_{Avg} = \frac{1}{{r_{max} }}\mathop \smallint \limits_{0}^{{r_{max} }} H\left( r \right){\text{d}}r$.Similar procedure was followed and the value of H_Avg was calculated for all 2100 simulations. Appendix A shows the variation of average hardness in 4140 steel cylinders of different diameters with heat transfer coefficient, bath temperature, and residence time fraction during martempering.

Effect of Section Thickness, Heat Transfer Coefficient, Bath Temperature, and Residence Time on the Hardness of AISI 4140 Steel Cylinders during Martempering

Appendix A shows the variation of mean hardness in AISI 4140 steel probes of different diameters (D) with bath temperature (T_b), heat transfer coefficient (h), and residence time fractions (f).

For cylinders of diameters lesser than 5mm, variation in the h, Tb, and f did not have a significant effect on hardness evolution. The mean hardness calculated in this case was very high.

For cylinders of diameter greater than 10mm, there was a significant drop in the hardness for low values of h and high values T_b. This effect of lower hardness at higher h and T_b increased with increasing diameter. This was evident from the increase in the lower mean hardness area in the h v/s T_b contour plots with increasing diameters.

There was no significant effect of residence time fraction (f) on the hardness for cylinders with diameters less than 10mm. The decrease in the residence time fraction resulted in decreased mean hardness values in cylinders with diameters greater than 15mm as observed in Fig. 16, 17, 18, 19, 21, 22. This decrease in mean hardness was initially observed to concentrate in high heat transfer coefficient and high bath temperature region. However, with an increase in the diameter of the cylinder, the effect of ‘f’ on mean hardness was observed in the low heat transfer coefficient and low bath temperature region. From the contour plots, it is very clear that the mean hardness is significantly affected by all the four process parameters and the variation was observed to be nonlinear. Modelling such a complex process is thus not possible using conventional regression models.

Variation of Maximum Residence Time

Residence time is one of the important process variables during martempering of steel parts. Figure 8 shows the variation of maximum and minimum values of t_Rmax with diameter, heat transfer coefficient, and bath temperature. The maximum and minimum values of t_Rmax were significantly dependent on the diameter of the cylinder. The minimum values of t_Rmax decreased with increasing heat transfer coefficient and bath temperatures. The maximum value of t_Rmax was independent of heat transfer coefficient and bath temperature.

Fig. 7

(a) Phase fractions and (b) Predicted hardness as a function of radial distance obtained for numerical experiment with D = 60mm, h = 1000 W/m²K, T_b = M_s (323.6 °C) and f = 1

An Artificial Neural Network Model for Predicting Hardness Distribution in AISI 4140 Steel Cylinder

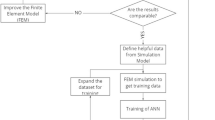
Artificial neural network (ANN) is a powerful machine learning algorithm that is inspired by biological neuronal networks in animal brains. The neural network toolbox in MATLAB was used to model the hardness in the AISI 4140 steel cylinder during martempering. Figure 9 shows the architecture of the artificial neural network model used to predict hardness distribution in martempered AISI 4140 steel cylinders

Fig. 8

Variation of maximum residence time with (a) diameter of steel cylinder

As described in section 2.2, 2100 simulation experiments were performed for AISI 4140 steel cylinders by varying diameter, heat transfer coefficient, bath temperature, and residence time fractions. The hardness values were extracted at various radial locations in the cylinder of radius r_o. These locations were defined by the dimensionless radial location (r/r_o). The hardness values were extracted at 11 equally spaced radial locations between the center (r/r_o=0) and surface (r/r_o=1) for each simulation experiment with incremental steps of 0.1. The total number of input/output data set available for training neural network model was thus 23,400 (2100 simulations × 11 radial locations).

A single hidden layer neural network architecture shown in Fig. 9 was used to model the hardness distribution in martempered AISI 4140 steel cylinders. The neural network consists of 3 layers input, hidden, and output layers. Equation 16 shows the scheme adapted to calculate the weighted summation of normalized input (x_i) for each neuron (N_j) in the hidden layer. Where W_i,j, and b_j correspond to weight and bias for ith input variable and jth hidden layer neuron, respectively. z_j is the input to the hidden layer.

$$z_{j} = b_{j} + \sum\limits_{{i = 1}}^{5} {(W_{{i,j}} x_{i} )}$$

(16)

The output from the hidden layer X_o,j was calculated by applying tan sigmoidal activation function on z_j in MATLAB algorithm as shown in Eq 17.

$${\text{x}}_{{{\text{O}},{\text{j}}}} = \frac{{{\text{e}}^{{{\text{z}}_{{\text{j}}} }} - {\text{e}}^{{ - {\text{z}}_{{\text{j}}} }} }}{{{\text{e}}^{{{\text{z}}_{{\text{j}}} }} + {\text{e}}^{{ - {\text{z}}_{{\text{j}}} }} }}$$

(17)

A linear activation function was applied on the weighted sum of x_o,j in the output layer to calculate the output Y_o as shown in Eq 18. The output of the ANN model is the normalized hardness value (Y_O).

$$Y_{O} = b_{o} + \mathop \sum \limits_{j = 1}^{{N_{HL} }} (W_{{\text{O,j}}} x_{{\text{o,i}}} )$$

(18)

Data Pre-Processing

There is a large difference between the magnitude of different input/output variables used in the ANN model. For instance, h varies between 3500 and 500 whereas D varies between 2 and 100. To avoid the adverse effects of magnitude on the convergence of network parameters, the input and output variables were normalized and scaled between 0 and 1. The maximum and minimum values of input and output variables used for normalization are shown in Table 2. Equation 19 shows the formula used to normalize the values of D, h, T_b, t_r (f×t_Rmax) r/r_o, and H.

$$X_{{{\text{Norm}}}} = \frac{{\left( {X - X_{{{\text{Min}}}} } \right)}}{{(X_{{{\text{Max}}}} - X_{{{\text{Min}}}} )}}$$

(19)

Table 2 Parameters used to normalize inputs and outputs of the ANN model

Normalization of input and output data is a very important step in training the neural network. However, for the prediction of hardness, normalized output data, Y_o, needs to be denormalized. Equation 20 shows the formula used to calculate the hardness from the normalized output from the ANN model.

$$X = X_{Norm} (X_{Max} - X_{Min} ) + X_{Min}$$

(20)

Training and Validation of the ANN Model

Training a neural network involves the calculation of weights (W_i,j and W_O,j) and biases (b_j and b_O) by minimizing the error in the output variables. MATLAB uses the Levenberg–Marquardt algorithm to minimize the error of the output variable and calculate weights and biases.

To avoid overfitting, 70% of the total data set was randomly selected to train the neural network. The balance of 30% of the total data was equally divided and used to validate and test the neural network model.

The number of neurons in the hidden layer (N_HL) is an important parameter that defines the architecture of an ANN model. Equation 21 shows the procedure adapted to calculate the mean square error (MSE). The mean square error was calculated using the whole data set consisting of 23400 input/output data set.

$$MSE = \frac{1}{n}{ }\mathop \sum \limits_{i = 1}^{n} \left( {H_{Sim} - H_{ANN} } \right)^{2} n = 23400$$

(21)

As shown in Fig. 10(a), the mean square error decreased with the number of neurons in the hidden layer. Beyond 30 neurons in hidden layers, there is no significant reduction in the mean square error with further increases in the number of neurons in the hidden layer.

Fig. 9

Architecture of artificial neural network model used to predict hardness distribution in martempered AISI 4140 steel cylinders

A single hidden layer neural network with 30 neurons was thus used to model the hardness distribution in AISI 4140 cylinders during martempering. Figure 10(b) shows the error between hardness values over the entire range. The hardness values predicted by the ANN model were in fair agreement with hardness values from the simulations.

Figure 11 shows the hardness distribution in AISI 4140 steel cylinders as predicted using the simulations and ANN model. The process variables causing the hardness distribution in Figure 11were chosen to demonstrate the accuracy of hardness prediction in low and high average hardness regimes, respectively.

Fig. 10

(a) Variation of standard error with the number of neurons in the hidden layer (b) Error plot for N_HL=30

The Relative Importance of Input Variables

Table 3 presents values of all weights and biases of the suggested neural network model. Equation 22 shows the procedure suggested by Ibrahim (Ref 18) to calculate the relative importance (RI) of input variables based on the connection weights in the neural network. Table 3 shows the relative importance of parameters calculated for all input variables neural network model.

$$RI_{i} = \frac{{\mathop \sum \nolimits_{j = 1}^{{N_{HL} }} |W_{i,j } W_{O,j} |}}{{\mathop \sum \nolimits_{i = 1}^{5} \left( {\mathop \sum \nolimits_{j = 1}^{{N_{HL} }} |W_{i,j } W_{O,j} |} \right)}}$$

(22)

Table 3 Weights (W_i,j) and bias (b_j) of artificial neural network model

From Fig. 12 which shows the proportions from Table 4, it is clear that both temperature and diameter are the most important input variables, followed by the residence time and heat transfer coefficient. The dimensionless radial position was the least important input variable in the neural network model. The relative importance of input variables should be analyzed in conjunction with the trends in Fig. 13, 14, 15, 16, 17, 18, 19, 20, 21, 22. Analysis of larger trends in the simulation results reveals that increased bath temperature, diameter, and residence time results in decreased hardness whereas, an increased heat transfer coefficient increased average hardness in martempered AISI 4140 cylinders. Also from Fig. 11, hardness increased with an increase in r/r_o.

Fig. 11

Distribution of hardness predicted by simulation experiment and ANN model in AISI 4140 cylinder of a) 80mm diameter and h=1000W/m²K T_b=373.6 °C and f=0.99 b) 100mm diameter and h=3000W/m²K T_b=273.6 °C and f=0.5

Table 4 Relative importance parameter calculated for input variables of neural network model

Fig. 12

Pie chart showing the percentage of relative importance input variables

Conclusions

In martempering, for a given section thickness of the part, the heat transfer coefficient, quench bath temperature and residence time are the process variables that need to be controlled by the heat treaters. The present work proposes a FEM model to simulate martempering process and further uses the simulation results to formulate an artificial neural network model to predict hardness in the steel cylinder. These models are beneficial for the heat-treating community for designing martempering process. The following are the important conclusions from the work.

• 1. An increase in bath temperature, diameter, and residence time results in a decrease in hardness whereas, an increase in heat transfer coefficient results in an increase of average hardness in martempered AISI 4140 cylinders.

• 2. The artificial neural network model was trained to predict hardness distribution in martempered AISI 4140 steel cylinders.

• 3. The weights of the neural network were used to calculate the relative importance parameter for each input variable. The ability of input variables to influence the hardness is arranged in the following increasing order: T_b > D > t_r > h > r/r_o.

• 4. The proposed model for the prediction of hardness considers the effects of bath temperature, part diameter, residence time, and the heat transfer coefficient as well.

Appendix A

See Figures 13, 14, 15, 16, 17, 18, 19, 20, 21, 22.

Fig. 13

Effect of heat transfer coefficient and bath temperature on the average hardness in AISI 4140 cylinder of 2mm diameter for residence time fraction of (a) 1, (b) 0.99, (c) 0.95, (d) 0.9, (e) 0.75, (f) 0.5

Fig. 14

Effect of heat transfer coefficient and bath temperature on the average hardness in AISI 4140 cylinder of 5 mm diameter for residence time fraction of (a) 1, (b) 0.99, (c) 0.95, (d) 0.9, (e) 0.75, (f) 0.5

Fig. 15

Effect of heat transfer coefficient and bath temperature on the average hardness in AISI 4140 cylinder of 10 mm diameter for residence time fraction of (a) 1, (b) 0.99, (c) 0.95, (d)0.9, (e) 0.75, (f) 0.5

Fig. 16

Effect of heat transfer coefficient and bath temperature on the average hardness in AISI 4140 cylinder of 15 mm diameter for residence time fraction of (a) 1, (b) 0.99, (c) 0.95, (d) 0.9, (e) 0.75, (f) 0.5

Fig. 17

Effect of heat transfer coefficient and bath temperature on the average hardness in AISI 4140 cylinder of 20 mm diameter for residence time fraction of (a) 1 (b) 0.99, (c) 0.95, (d) 0.9, (e) 0.75, (f) 0.5

Fig. 18

Effect of heat transfer coefficient and bath temperature on the average hardness in AISI 4140 cylinder of 30 mm diameter for residence time fraction of (a) 1, (b) 0.99, (c) 0.95 (d) 0.9, (e) 0.75, (f) 0.5

Fig. 19

Effect of heat transfer coefficient and bath temperature on the average hardness in AISI 4140 cylinder of 40 mm diameter for residence time fraction of (a) 1, (b) 0.99, (c) 0.95, (d) 0.9, (e) 0.75, (f) 0.5

Fig. 20

Effect of heat transfer coefficient and bath temperature on the average hardness in AISI 4140 cylinder of 60 mm diameter for residence time fraction of (a) 1 (b) 0.99, (c) 0.95, (d) 0.9 (e) 0.75, (f) 0.5

Fig. 21

Effect of heat transfer coefficient and bath temperature on the average hardness in AISI 4140 cylinder of 80 mm diameter for residence time fraction of (a) 1, (b) 0.99, (c) 0.95, (d) 0.9, (e) 0.75, (f) 0.5

Fig. 22

Effect of heat transfer coefficient and bath temperature on the average hardness in AISI 4140 cylinder of 100 mm diameter for residence time fraction of (a) 1, (b) 0.99, (c) 0.95, (d) 0.9, (e) 0.75, (f) 0.5