1 Introduction

Martensite, being one of the quench-hardening constituent in steels, is a microstructure with great practical importance.[1] The transformation from austenite to martensite can also increase the strain-hardening and the ductility through a transformation-induced plasticity (TRIP) effect. Many steels are partially martensitic, e.g., dual phase steels, quenching and partitioning steels, TRIP steels. In order to optimize the performance of these steels, the fraction of each constituent must be carefully considered.

In low alloy steels, austenite transforms into martensite at a very high rate when the temperature is lower than the martensite start temperature, M s, and no more martensite forms by prolonging the isothermal holding time but by decreasing the temperature. This type of martensite is denoted as athermal martensite, and the fraction of athermal martensite is thus a function of temperature but independent of time.[1–6]

With the demand of improved high-performance steels, much attention is currently paid toward the design of new steels and the optimization of their production with the aid of computational tools. These tools are preferentially based on physical models and should have predictive capability and satisfactory accuracy. During the past several decades, many models, both theoretical and empirical have been developed to describe the fraction of martensite as a function of undercooling.[3–9] However, most theoretical models lack parameter determination and are not predictive, while the empirical models are only useful in a limited alloying range and under certain conditions since they cannot account for the underlying physics. Hence, it seems that a semi-empirical phenomenological model is preferred at the present stage. All the previous models apply the temperature as the variable while using the chemical driving force, i.e., the difference of Gibbs energy between austenite and martensite, would link directly to thermodynamics. Furthermore, a model based on thermodynamics could be further developed and would be compatible with other physical models, as the semi-empirical model by Stormvinter et al.[10] (SBÅ model), which predicts M s based on the thermodynamic driving force for steels. Following the same path, a model is established based on the relationship between the driving force from thermodynamic calculations and the fraction of martensite from experimental results. Part of the model was presented in a short paper in a conference proceeding,[11] and this paper describes the details of the model and the predictions are validated vs experimental data from the literature.

2 Previous Models

Early works on modeling of the fraction of athermal martensite dates back to the 1940s when Harris and Cohen[3] proposed the following formula (HC model)

$$ f = 1 - 6.95 \times 10^{ - 15} \left[ {455 - \left( {M_{\text{s}} - T} \right)} \right]^{5.32} $$
(1)

in which and in the rest of this paper, f is the volume fraction of martensite, M s is the martensite start temperature, and T is the temperature the alloy is quenched to. The equation was derived from experimental data for four 1.1 wt pct carbon steels with various contents of chromium and nickel. In the original equation, the temperature was given in the Fahrenheit scale. The fraction of martensite was measured by a metallography method proposed by Greninger and Troiano[12] where a sample is quenched to the target temperature, held at that temperature or at a higher temperature for a certain time, and finally quenched to room temperature. The martensite formed during the first quench is tempered and appears dark in the light optical microscope (LOM) after etching, and thus it can be distinguished from the martensite formed during the second quench to room temperature, which appears bright in the LOM. This technique has, since then, been applied extensively for the measurement of the M s temperature and the fraction of martensite.[3,13–15]

At the same time, Fisher et al.[4] developed a model (FHT model) based on nucleation theory

$$ f = 1 - \left( {qn + 1} \right)^{ - m} $$
(2)

in which q is related to the grain size, n is the number of martensite plates, and m is related to the shape of the martensite units. The authors applied Eq. [2] to fit the experimental data of two steels from the work by Harris and Cohen.[3]

The model that has been applied most frequently was proposed by Koistinen and Marburger (KM) in 1959[5]

$$ f = 1 - \exp \left[ {\alpha \left( {M_{\text{s}} - T} \right)} \right] $$
(3)

in which α is a constant depending on the material. In their study, four Fe-C alloys with 0.37 to 1.10 wt pct carbon were quenched to room or sub-room temperatures, and the volume fraction of retained austenite was measured using X-ray diffraction. By plotting logarithmically the fraction of retained austenite vs the difference of M s and T, a linear relationship was found and α was determined to be −0.011. Due to the shape of the function, the M s used in Eq. [3] should be the extrapolated temperature from experimental data and differs slightly from the true measured M s.

In a work by Mendiratta and Krauss,[15] the parameter α was reported to be −0.008 for a Fe-C binary alloy with 1.86 wt pct carbon. The alloy was quenched to room and sub-room temperatures, and the fraction of retained austenite was measured using the metallography method.

Van Boheman and Sietsma[16] used experimental data from 19 plain carbon and low alloy steels to determine the parameter α in Eq. [3]. The composition ranges of these steels were 0.26 to 1.86 wt pct C, 0.1 to 14.9 wt pct Ni, 0.2 to 8.7 wt pct Cr, with small amount of Mn and Si. The fraction of martensite was determined using metallography or dilatometry data. They presented the following expression (BS model)

$$ \alpha_{\text{BS}} = - 0.0224 + 0.0107{\text{C}} + 0.0007{\text{Mn}} + 0.00005{\text{Ni}} + 0.00012{\text{Cr}} + 0.0001{\text{Mo}} $$
(4)

with each alloying element content given in mass percent.

The KM equation was later derived theoretically for plate martensite by Magee in 1970, giving it a physical background.[17] It was assumed that the number of newly formed martensite plates dN is proportional to the chemical driving force ΔG as

$$ {\text{d}}N = \varphi {\text{d}}\Delta G^{{\gamma - \alpha^{\prime } }} $$
(5)

where φ is a constant, and γ and α′ represent austenite and martensite, respectively. By assuming that the average volume of each plate is V, then the newly formed volume fraction of martensite is

$$ df = V\left( {1 - f} \right){\text{d}N} $$
(6)

where (1 − f) is the retained austenite from which martensite forms. Combining Eqs. [5] and [6] gives

$$ df = V\left( {1 - f} \right)\varphi \frac{{{\text{d}}\Delta G^{{\gamma - \alpha^{\prime } }} }}{{{\text{d}}T}}{\text{d}}T $$
(7)

By assuming that V and \( \frac{{{\text{d}}\Delta G^{{\gamma - \alpha^{\prime } }} }}{{{\text{d}}T}} \) are constants, the integration yields

$$ f = 1 - \exp \left[ {V\varphi \frac{{{\text{d}}\Delta G^{{\gamma - \alpha^{\prime } }} }}{{{\text{d}}T}}\left( {M_{\text{s}} - T} \right)} \right] $$
(8)

in which \( V\varphi \frac{{{\text{d}}\Delta G^{{\gamma - \alpha^{\prime } }} }}{{{\text{d}}T}} \) is constant.

One drawback with the KM equation is that the function has a C-shape instead of an S-shape which is observed experimentally, and it is necessary to apply an extrapolated M s value instead of the measured or calculated M s. The equation describes the experimental data quite well above about 20 pct of martensite, but deviates significantly from the experiments below 10 pct, the reason being the shape of the curve which is not in accordance with the true transformation curve. To solve this problem, Lee and van Tyne[18] added an extra parameter, n, to the KM equation

$$ f = 1 - \exp \left[ {\alpha_{\text{LT}} \left( {M_{\text{s}} - T} \right)^{n} } \right] $$
(9)

M s in Eq. [9] is the actual M s temperature of the steel and they determined the two parameters from experimental data (LT model)

$$ \alpha_{\text{LT}} = - 0.0231 + 0.0105{\text{C}} + 0.0017{\text{Ni}} - 0.0074{\text{Cr}} + 0.0193{\text{Mo}} $$
(10)
$$ n = 1.4304 - 1.1836{\text{C}} + 0.7527{\text{C}}^{2} - 0.0258{\text{Ni}} - 0.0739{\text{Cr}} + 0.3108{\text{Mo}} $$
(11)

with alloying content given in mass percent. The chemical composition ranges used were 0.2 to 1.2 wt pct C, 0 to 2.1 wt pct Ni, 0 to 1.2 wt pct Cr, with small amount of Mn and Si.

Skrotzki[6] used the following formula

$$ f = 1 - \exp \left[ {\frac{{T - M_{\text{f}} }}{{M_{\text{s}} - M_{\text{f}} }}} \right]^{n} $$
(12)

in which M f is the martensite finish temperature, representing 99 pct of martensite formation, and n is a material dependent constant. Equation [12] was fitted to experimental data from several different materials with good fitting results, including carbon steels, high Ni ferrous alloy, high Mn ferrous alloy, and Cu-based and NiTi shape memory alloys.

Yu[7] also included both M s and M f, and derived

$$ f = \frac{{M_{\text{s}} - T}}{{M_{\text{s}} - \beta M_{\text{f}} - \left( {1 - \beta } \right)T}} $$
(13)

in which β is the quotient of the entropy of martensite and austenite. Equation [13] was fitted to data from Harris and Cohen,[3] arbitrarily choosing β = 0.4 for all four alloys examined. Equations containing both M s and M f are applied more frequently in shape memory alloys where M f has been determined more often than in steels.

Based on nucleation theory, Guimaraes and Rios[8] derived an equation

$$ f = 1 - \exp \left( { - \Gamma \frac{T^{*} - T}{T}} \right) $$
(14)

where Γ can be theoretically expressed as a function of mean volume of each martensite plate, the change of entropy in the transformation and the grain size, and T* is defined as the highest temperature where martensite embryos can propagate.

Lee and Lee[9] applied a differential equation based on the converted fraction from dilatometry results for an AISI 5120 steel

$$ \frac{df}{{{\text{d}}T}} = Kf^{\alpha } \left( {1 - f} \right)^{\beta } $$
(15)

where K is a function of temperature and composition, and the parameters α and β are functions of the carbon content.

Comparing with other models, KM type of models are convenient to use, and the parameters have been determined in several works for some plain carbon and low alloy steels. However, since KM type of models are purely empirical, the determined parameters could only be applied to a limited range of compositions. Other models, which are mostly derived theoretically, are more often applied as a fitting function but the parameters have been determined only for a few steels and thus they cannot be applied for predictions in most cases.

3 Present Approach

3.1 Model Derivation

The martensitic transformation starts at a temperature lower than where austenite and martensite have the same Gibbs energy, i.e., at T 0, due to dissipation of energy related to elastic and plastic deformation, called the barrier of the transformation. In other words, the transformation starts at the temperature where the chemical driving force equals the barrier of the transformation. Based on experimental values of M s for several binary and ternary systems, Stormvinter et al.[10] established a relationship between the barrier of transformation and the alloying content that could be used to predict the M s temperature. The same idea is used in the present work to model the fraction of martensite formed below the M s temperature, where the extra chemical driving force triggers more martensite to form.

It is assumed that the fraction of newly formed lath or plate martensite, df, is proportional to the change of the molar driving force,\( {\text{d}}(\Delta G_{m}^{{\gamma - \alpha^{\prime}}} ) \), similar to Magee’s derivation in Eq. [7], and the following equation is proposed

$$ df = Bf\left( {1 - f} \right)\frac{1}{{\Delta G_{\text{m}}^{{\gamma - \alpha^{\prime } }} }}{\text{d}}\left( {\Delta G_{\text{m}}^{{\gamma - \alpha^{\prime } }} } \right) $$
(16)

where B is a material constant, f is added in the consideration of a self-catalyzed effect from the previously formed martensite, and \( \frac{1}{{\Delta G_{\text{m}}^{{\gamma - \alpha^{\prime } }} }} \) is related to deformation energy in the untransformed austenite, (1 − f). The untransformed austenite is stabilized by the deformation and if it is assumed that the stored deformation energy is proportional to the driving force, the increase of the martensite fraction, df, is inversely proportional to the driving force \( \Delta G_{\text{m}}^{{\gamma - \alpha^{\prime}}} \).

By integrating from M s to a certain temperature T below M s, one obtains

$$ f = \frac{1}{{1 + A^{ - 1} \left( {\Delta G} \right)^{ - B} }} $$
(17)

in which A is a constant and ΔG is denoted as the excess driving force which is the difference of driving force at T and at M s as

$$ \Delta G = \Delta G_{\text{m}}^{{\gamma - \alpha^{\prime } \left( T \right)}} - \Delta G_{\text{m}}^{{\gamma - \alpha^{\prime } \left( {M_{\text{s}} } \right)}} $$
(18)

3.2 Parameter Determination

The chemical driving force is calculated as

$$ \Delta G_{\text{m}}^{{\gamma - \alpha^{\prime } }} = G_{\text{m}}^{\gamma } - G_{\text{m}}^{{\alpha^{\prime } }} - \Delta G_{\text{Z}} $$
(19)

in which \( G_{\text{m}}^{\gamma } \) and \( G_{\text{m}}^{{\alpha^{\prime } }} \) are the molar Gibbs energies of austenite and martensite, respectively, calculated from the Thermo-Calc software package and the TCFE6 database,[19] and ΔG Z is the Zener ordering energy, related to the carbon redistribution after martensite formation. After the martensitic transformation, carbon atoms still reside in the interstitial sites inherited from austenite, but have a tendency to move to one of the three families of interstitial sites preferred.

ΔG Z is modeled using an expression proposed by Fisher,[20] and adopted in the same way as in the SBÅ model,[10] assuming complete ordering during the whole transformation.

Since the calculated value of the excess driving force is most often in the order of a few thousand J/mol, and to avoid a very small value of the parameter A, Eq. [17] is modified for the fit of experimental data as

$$ f\left( \text{Pct} \right) = \frac{100}{{1 + A^{\prime - 1} \left( {\frac{\Delta G}{100}} \right)^{{ - B^{\prime } }} }} $$
(20)

in which f has the unit of percent.

Equation [20] is first applied to several groups of experimental data[3,12,13,15,21] with least square fitting. The fitted values of parameters A′ and B′ are plotted vs M s in Figure 1.

Fig. 1
figure 1

Fitted values of (a) parameters A′ and (b) parameters B′ in Eq. [20] vs the experimental M s temperatures

Full size image

From Figure 1, parameter A′ was approximately 0.05 and therefore it was fixed to 0.05 in the further fitting. Parameter B′ seems to increase with increasing M s.

To take into account the influence from different types of measurement on the shape of the transformation curves, another parameter C was introduced in the equation

$$ f\left( \text{Pct} \right) = \frac{100}{{1 + A^{\prime \prime - 1} \left( {\frac{\Delta G - C}{100}} \right)^{{ - B^{\prime \prime } }} }} $$
(21)

Parameter C has the same unit as the Gibbs energy and could be converted to a temperature difference, which could be viewed as a shift of M s.

One example of the difference in shape is shown in Figure 2. In Figure 2(a), the transformation curve of an SAE-52100 steel[13] measured using metallography is compared with a fitted curve using Eqs. [20] or [21]. Parameter C, indicated in the diagram, corresponds to 21 K (21 °C). In Figure 2(b), the transformation curve of a Fe-0.80 wt pct C steel[16] measured with dilatometry is compared with the fitted results using Eqs. [20] or [21]. The correlation is very good, giving a small value of parameter C, corresponding to 0.1 K (0.1 °C). The difference between M s measured using the two different methods is noticeable. The reason is that using dilatometry most often one sample is tested during relatively fast continuous cooling, and the macroscopic dilatation is evaluated to find the starting temperature. Clearly, a certain volume fraction of martensite must form before any macroscopic dilatation can be observed. On the contrary, using the metallography method several samples from the same alloy are tested, each data point being one test sample. The metallography method is more sensitive than the dilatometry method. When the temperature is close to M s, the formation of the first several plates of martensite could be influenced dramatically by defects, such as e.g., inclusions, and thus a very small amount of martensite could be observed in a wide range of temperature. This would result in a transformation curve similar to the diagram shown in Figure 2(a). Moreover, in several cases where experimental results were tested using metallography, the M s was reported as the temperature where a few percent of martensite formed. Since Eq. [20] always begins where ΔG = 0 and f = 0, the parameter C is necessary in the fitting for these cases where f ≠ 0. Generally, parameter C is added in the present model only as a fitting means due to the uncertainty in the M s measurements.

Fig. 2
figure 2

Transformation curves fitted to experimental data using Eqs. [20] or [21] for (a) a SAE-52100 steel determined by metallography and (b) an Fe-0.80C steel determined by dilatometry

Full size image

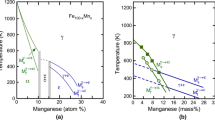
Equation [21] is applied in the second round of fitting with parameter A′ fixed to 0.05, and the fitted values of parameter B″ as a function of M s are shown in Figure 3, categorized by authors or testing methods.[3,6,13–16,21–25] It is found that parameter B″ fitted to metallography results, shown in black points, has a rather linear relationship with M s. Hence, linear fitting was applied for B″, giving

$$ B^{\prime \prime } = 0.006 * M_{\text{s}} - 0.1369 $$
(22)

with M s in Kelvin.

Fig. 3
figure 3

Fitted values of parameter B″ in Eq. [21] vs the experimental M s temperatures, black solid points determined by metallography with a linear fitting, red open points determined by dilatometry, and blue crosses determined by magnetization

Full size image

When parameter A″ is fixed, parameter B″ represents the steepness of the function, and a smaller parameter B″ means a less steep curve, or lower overall transformation rate. Here the transformation rate is the percentage of transformation with respect to temperature. It thus means that a lower M s gives a smaller B″ value, and this indicates that the interval of M s and M f increases with decreasing of M s.

Figure 3 also shows that, the results of parameter B″ fitted to dilatometry data, shown in red open points, fall lower than the results fitted to metallography data, shown in black solid points. It thus seems like the transformation rate measured using dilatometry is lower than that measured using metallography, even though the data are evaluated for different steels and not directly comparable.

The conversion of parameter C into temperature shows that, among the total of 46 steels applied in the fitting, 25 steels drop in the range of ±5 K (±5 °C), 14 steels in the range of ±10 K (±10 °C), and 7 in the range of ±22 K (±22 °C). Comparing with the uncertainties of M s determined by experiments or M s predicted by various models, parameter C is smaller or in the similar range. Thus parameter C is only used in the fitting of the experimental data, aiming to obtain a more predictable B′ (B″) value (comparing Figures 1(b) and 3), and hence C is eliminated in the predictive model.

To verify the choice of parameter A″ equal to 0.05, it has also been fixed to 0.03 or 0.07, and the fitted results are quite similar as the results show in Figure 3, with a slightly different linear function for parameter B″ than Eq. [22]. Thus in the present model, parameter A″ is chosen as 0.05.

In summary, the present model is expressed in Eq. [20] with parameter A′ set to 0.05 and parameter B′ is equal to B″ in Eq. [22]. The model should be applied in the case when the steel is quenched directly to a certain temperature using water, brine, or oil. Continuous fast cooling seems to show less fraction of martensite compared with direct quenching to the same temperature. At the present stage, no quantitative conclusion can be made for the results tested by dilatometry due to lack of sufficient experimental results.

Figure 4 shows some transformation curves predicted by the present model using the measured M s and comparing to experimental data evaluated using metallography. Most of the predicted curves show very good agreement with the experimental data.

Fig. 4
figure 4

Experimental data determined by metallography from (a) Harris and Cohen,[3] (b) Grange and Stewart,[13] and (c) Morgan and Ko,[14] compared with predicted transformation curves as the dashed lines by the present model

Full size image

3.3 Validation

The present model and models by HC,[3] FHT,[4] BS,[16] and LT[18] are applied to calculate M 50 and M 90 temperatures, representing 50 and 90 pct of martensite formation, respectively, for 25 different steels, see Figure 5. The detailed experimental data, including steel grade, chemical compositions, and temperatures, are listed in the paper by Lee[26] in which the rest of the models except the present model were compared. The original data are taken from an atlas of isothermal transformation diagrams.[27] In Figure 5, the M s temperature used in the present model is taken either from experimental data or calculated using the SBÅ model, while the M s temperature used in other models is only using the experimental data. The comparison in Figure 5 shows that, all models predict M 50 rather satisfactorily, while the present model and the LT model[18] predict M 90 more satisfactorily. The predictions from the present model using experimental M s and calculated M s give quite similar result, since SBÅ model could give quite accurate predictions for the examined alloys. The results show that, combined with the SBÅ model, the present model can predict the full transformation curve satisfactorily.

Fig. 5
figure 5

Comparisons of (a) experimental M 50 temperatures and (b) experimental M 90 temperatures with predictions by present model and other models, and M s temperatures used in the present model are from either experimental data or from calculations using SBÅ model, while M s temperatures used in the other models are from experimental data

Full size image

4 Discussion

A distinguishing feature of the present model is that the cooling method is considered, although a quantitative model considering cooling rate is not obtained yet. The effect of cooling methods on the transformation curve has been reported since early works. In the work from Steven and Haynes,[28] the transformation in a low alloy steel was measured using metallography and dilatometry. Their results show that both methods give similar values when the transformation is below about 60 pct, however, when it is higher than 60 pct, the fraction measured using dilatometry is lower than if it is evaluated using the metallography method. This observation was attributed by the authors to the stabilization of austenite. In the work from Morgan and Ko,[14] mercury, saturated brine, and oil were applied as quenchants. The oil quench resulted in less martensite at a specific temperature compared to the mercury quench for several Fe-C-Ni alloys with about 1 wt pct C and up to about 10 wt pct Ni. The authors attributed this phenomenon to the stabilization of austenite above M s during quenching. These experimental observations illustrate that, for a specific steel, the transformation rate increases with increasing cooling rate.

The middle part of the transformation curve could be treated approximately linear, and the slope of this linear part has been studied in several previous works. Brook and coworkers[29] examined the slopes of two groups of Fe-C-Ni and Fe-C-Cr alloys with the metallography method. They calculated the slopes between about 5 and 50 pct of transformation, and found that in both groups of alloys, the slope is approximately linearly increasing with increasing M s. Another study[30] also shows that, with increasing the carbon content in steels, M s decreases, and the interval of M s and M f increases. These two results are consistent with the present work. In another work, Pradhan and Ansell[21] applied a magnetization method and examined the slopes of several Fe-C-Ni-Cr alloys. They found that the slope is decreasing with increasing M s, which is in contrast with the work by Brook et al. and the present work. Their data are shown in blue crosses in Figure 3, in which a decreasing parameter B″ with increasing M s is observed. However, their data drop in the vicinity of the data from which the present model is derived. In the present model, parameter B′ (B″) is linearly increasing with M s, and it is suspected by the present authors that this is due to the increasing mechanical energy accompanied by the transformation with decreasing temperature, i.e., a steel with lower M s needs more driving force to further deform the retained austenite. The present model predicts that, for different steels, the transformation rate increases with increasing M s.

At present, parameter B′ (B″) is expressed only with M s, thus those factors which influence M s also influence the subsequent transformation, e.g., grain size. It has been shown that a smaller grain size of prior austenite decreases the M s and accelerates transformation rate.[24] These factors were not considered in the present model but should be included in future work.

5 Summary

In this work, a thermodynamically based model is proposed to predict the fraction of martensite with undercooling. The present model is based on the chemical driving force, instead of temperature. In the parameter determination, the effect of the cooling method on the transformation was considered. The model can be applied to predict the fraction of athermal martensite with quenching for plain carbon and low alloy steels. The only model parameter is a linear function of M s, and the present model predicts that the transformation rate increases with increasing M s. Comparing with experimental data of M 50 and M 90 temperatures from literature, the present model gives satisfactory predictions.