Physical Properties, Complex Impedance, and Electrical Conductivity of Double Perovskite LaBa_0.5Ag_0.5FeMnO₆

Abstract

Double perovskite oxide with general formula LaBa_0.5Ag_0.5FeMnO₆ (LBAFMO) has been prepared by the sol–gel-based Pechini method. To study and compare its electrical properties, impedance spectroscopy was carried out in the temperature ranging from 200 K to 340 K and frequency range from 100 Hz to 1 MHz. At room temperature, x-ray diffraction analysis revealed the compound to be single phase and to crystallize in the cubic system in space group Pm-3m. The imaginary part of the impedance (Z″) as a function of frequency indicated non-Debye model relaxation. Impedance data in a Nyquist plot (Z″ versus Z′) was used to determine an equivalent circuit. The complex impedance of LBAFMO revealed the presence of grain and grain-boundary contributions. The alternating-current (AC) conductivity as a function of frequency was interpreted by applying Jonscher’s law to determine the activation energy. Modulus analysis revealed the occurrence of a relaxation process supplemented by a conduction phenomenon.

Introduction

Double perovskite compounds have general formula A₂B′B″O₆ or A′A″B′B″O₆, where the cations occupying the A site are essentially ions of alkaline-earth metals or rare earths, while the B′ and B″ sites are occupied by two transition metals that are likely to be ordered at octahedral sites, thus forming B′O₆ and B″O₆ octahedra. In recent years, these materials have attracted interest from many researchers because of their various physical properties. The variation of the choice of the cations B′ and B″ in such compounds can result in a wide range of electrical and magnetic properties, including metallicity, half-metallicity, insulation, as well as ferromagnetism (FM), ferrimagnetism (FIM), and antiferromagnetism (AFM).^1,2 Multiferroic materials exhibit more than one ferroic order.

Such coexistence of ferromagnetic and ferroelectric materials has attracted great attention in fundamental physics and chemistry.^3,4,5 In the case of ferroelectrics, “ferro” indicates that a material exhibits a permanent electrical polarization even in the absence of an electric field, while in the case of ferromagnetic, the residual magnetization intensity can be reversed by applying a magnetic field.

In addition, early studies were devoted to oxides of the type Ln_1−xA_xMnO₃, x $\in$ [0, 1] (Ln = rare earth, A = Ca, Ba, Sr, etc.).^6,7 Manganese exhibits very important magnetic properties (ferromagnetic and antiferromagnetic). Indeed, with the development of new concepts in solid-state physics, these oxides have been the subject of active studies, which formed the basis for the development of the theory of double exchange (DE)⁸ and superexchange (SE).⁹

Over recent decades, numerous doped perovskites have drawn broad attention from researchers thanks to their substantial electrical properties,^10,11,12,13 such as the compound LaMnO₃. Nonetheless, the observation of uncommon electrical features in perovskite oxide LaAMnO₃ with rare-earth element A (Ba, Ca, Sr, etc.) has revived interest in this type of materials. Doping LaMnO₃ material with aliovalent ions leads to the conversion of a fraction of Mn³⁺ to Mn⁴⁺. This results in an interaction between the Mn³⁺ and Mn⁴⁺ ions, which is responsible for the properties of these manganese oxides.¹⁴ Moreover, other studies have been carried out on the electrical properties of LaBaFe_0.5Zn_0.5Mn${\text{O}}_{{6 - {\updelta }}}$ compound.¹⁵ Indeed, the latter has been explored using x-ray diffraction and electrical impedance spectroscopy and found to crystallize at room temperature in cubic systems.¹⁵

Impedance spectroscopy (IS) is a further technique that can be used to investigate the electrical characteristics of samples. It allows the determination of the relaxation frequency as well as grain, grain-boundary, and grain-electrode effects. The IS technique enables the measurement of the real and imaginary parts of the impedance over a wide range of frequency.

In the work presented herein, LaBa_0.5Ag_0.5FeMnO₆ compound was prepared by the sol–gel-based Pechini method. The aim of this work is to synthesize the proposed compound (LBAFMO) ceramic and study its physical properties to understand the characteristics of the crystal structure and its dielectric properties at different frequencies and temperatures.

Experimental Procedures

LaBa_0.5Ag_0.5FeMnO₆ compound was synthesized by means of the sol–gel-based Pechini method. Stoichiometric amounts of analytical-grade La₂O₃, BaCO₃, Ag, Fe₂O₃, and MnO₂ were solvated in citric acid solution to which ethylene glycol and diluted nitric acid were added.

After calculating the proportions of the precursors, they were weighed using a balance then placed in an Erlenmeyer flask fit with a magnetic bar; 40 ml nitric acid and 20 ml distilled water were added. This mixture was dissolved using a hot plate equipped with a magnetic stirrer at 80°C for 4 h. Citric acid and ethylene glycol were then added to homogenize the reaction medium. The obtained mixture was brought to a temperature of 170°C. Afterwards, heat treatment at 500°C for 6 h was carried out, and the obtained powder was crushed then pressed in a mold with the application of 4 tons/cm² to form circular pellets with thickness of 1.68 mm and diameter of 11 mm. The thus-obtained pellets were subject to annealing cycles from 600°C to 900°C to obtain dense material, each lasting 12 h.

Several samples were prepared using the same method and steps but different chemical precursors. Then, several techniques, such as electron diffraction and scanning transmission electron microscopy, were applied to confirm the purity of the samples and their oxygen stoichiometry. The results of these different techniques showed that this preparation method can achieve pure compounds with low oxygen deficiency.¹⁶ The structure, phase purity, and homogeneity of the prepared sample were determined by x-ray powder diffraction (XRD) analysis (PHILIPS diffractometer, X'PertPRO MPD) at room temperature in the Bragg angle range from 2$\theta$ = 20° to 80° using anticathode copper radiation (λ_CuKα = 1.54060 Å) with step size of $\Delta \theta$ = 0.02°. The analysis of the x-ray pattern was carried out using the FullProf program.¹⁷ Dielectric measurements were conducted using a precision impedance analyzer (Agilent 4294A) in C_p–R_p configuration in the frequency range from 100 Hz to 1 MHz and temperature range from 200 K to 340 K using a bath cryostat. The sample was placed under helium atmosphere to improve the heat transfer and avoid moisture. Besides, the compounds were used in disk form (diameter 11 mm, thickness 1.68 mm), with opposite surfaces painted with conductive silver paste for connection to the electrodes.

Results and Discussion

Structural Analysis

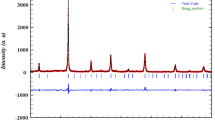
Figure 1 shows the x-ray diffraction pattern of LBAFMO at room temperature. The intensities of the measured diffraction lines are in good accordance with the calculated ones, indicating good crystallization of the material. Furthermore, all peaks could be indexed to the cubic system in space group Pm-3m.

Fig. 1

X-ray powder diffraction of LaBa_0.5Ag_0.5FeMnO₆ recorded with Cu K_α radiation.

LaBa_0.5Ag _0.5FeMnO₆ compound is monophasic according to Rietveld refinement. To achieve charge balance, the material contains Mn⁴⁺, Fe³⁺, and some Fe⁴⁺ to compensate the incorporation of Ag⁺. No structural transition is seen in Fig. 1, indicating not only that these peaks are very low but also that the sample is monophasic and pure. Therefore, the x-ray powder diffraction pattern of BaLaFe₂ ${\text{O}}_{{6 - {\updelta }}}$ compound corresponds to the simple cubic structure in space group Pm-3m.¹⁶ Rietveld refinement was performed on the XRD diffractograms to estimate the lattice parameters, yielding results of a = b = c = 3.8955 Å with volume V of 59.1139 ų. The reliability factors were found, giving goodness factors of $\chi^{2}$ = 1.56, R_F = 1.76, and Bragg factor R_B = 1.89. The exact processing temperature used for the sample for structural study was 900°C. To confirm the perovskite-like structure and the degree of distortion in the compound, the Goldschmidt tolerance factor t was calculated¹⁸ as

$$ t = \frac{{r_{\rm A} + r_{\rm O} }}{{\sqrt 2 (r_{\rm B} + r_{\rm O } )}}, $$

(1)

where r_A = r (La, Ba, Ag), r_B = r (Fe, Mn), and r_O are the ionic radii for the A and B site cations, and oxygen, respectively. The evolution of the crystal structure as a function of the value of the parameter is explained below: 0.75 < t  < 0.96: Orthorhombic distortion, 0.96 < t < 0.99: rhombohedral distortion, and 0.99 < t < 1.06: cubic.

According to Shannon, the ionic radii are r(Ba²⁺) = 1.61 Å, r(Ag⁺) = 1.28 Å, r(La³⁺) = 1.36 Å, r(Mn⁴⁺) = 0.53 Å, r(Fe³⁺) = 0.49 Å, r(Fe⁴⁺) = 0.585 Å, and r(O²⁻) =1.4 Å.^19,20 For this material, the t value larger than 1 confirms the cubic structure of the material. Figure 1 also shows the (111) and (200) reflection peaks, confirming the accuracy of the Rietveld refinement and the formation of cubic phase. For morphological study of grains, the Debye–Scherrer method²¹ can be applied to determine the crystallite size based on the x-ray diffractogram as

$$ D = \frac{K \cdot \lambda }{{\beta \cdot {\text{cos}} \,\theta }}, $$

(2)

where D is the average crystallite size, K = 0.89, λ is the wavelength (1.54060 Å), β is the width at mid-height of the peak, and θ is the diffraction angle of the peak considered. A grain size of 36 nm was obtained, and scanning electron microscopy (SEM) was performed to study the sample morphology, observe the crystallinity of the sintered powder, and detect the growth of grains (Fig. 2a). This figure also shows FESEM images of the sample obtained using ImageJ software to calculate the average size of the nanoparticles. The method consists in measuring the sizes of the maximum possible clear particles from the SEM image, which are of different sizes. A frequency plot for the particle size is then presented. The average size of the nanoparticles can then be estimated by applying a Lorentzian fit to this diagram (Fig. 2b). The morphology was found to be dense and uniform, with grains of 467 nm, each consisting of 13 crystallites.

Fig. 2

FESEM images of LaBa_0.5Ag_0.5FeMnO₆ nanoparticles.

Impedance Analysis

Complex impedance spectroscopy is an efficient, simple, and adaptable method for analysis of the frequency-dependent response of various electrical parameters and effects (grain, grain boundary, electrode effect, etc.) of samples through a simple impedance formulation. In literature, the electrical conduction of oxide materials results essentially from hopping between ions such as Mn³⁺, Mn⁴⁺, and Fe³⁺, or overlapping of d orbital of cations.²² Under the application of an electric field, electrons will migrate from one site to another, giving an electrical response.

The dependence of the complex impedance of the LaBa_0.5Ag_0.5FeMnO₆ sample on temperatures is shown in Fig. 3. The obtained spectra are made up of a single semicircular arc. It can be concluded that the compound exhibits not only grain but also grain-boundary effects in its electrical properties. In addition, the radius of the semicircles corresponding to the resistance decreases with increase in the temperature. Besides, the Nyquist diagram (Fig. 3) shows a non-Debye model²³ of relaxation behavior. A distribution of relaxation times (instead of a single relaxation time) in the sample is suggested by the depressed semicircular arc (with the plot center line lie below the real axis), resulting from flaws in the majority of solids.^24,25

Fig. 3

Complex impedance spectrum at different temperatures with equivalent electrical circuit.

To study the properties of LBAFMO, the complex impedance spectra were measured using ZView software. The fit was obtained using an equivalent circuit that can be described as a parallel (R₁.C₁) circuit in series with an (R₂–CPE₁) circuit, where R₁ is the grain resistance, C₁ is the grain capacitance, R₂ is the grain-boundary resistance, and CPE₁ is the constant-phase element (Fig. 3). The parameters of the equivalent circuit are obtained from the fitting at selected temperatures and are summarized in Table I. Indeed, transport in grains, which are purely resistive, occurs mainly at high frequencies, while conduction at grain boundaries generally takes place at low frequencies. The constant-phase element (Z_CPE) is determined by the equation²⁶

$$ Z_{{{\text{CPE}}}} = \frac{1}{{Q\left( {{\rm j}w} \right)^{\alpha } }}. $$

(3)

Table I The parameters for the equivalent circuit of LaBa_0.5Ag_0.5FeMnO₆.

The resistance values R, Q and $\alpha$ are determined by minimizing the difference between the calculated and experimental data. While Q denotes the value of the pseudocapacity of the CPE element, α represents the material’s capacitive nature. If α = 0, it behaves as an Ohmic resistance, whereas if α = 1, it becomes an ideal capacitor.

The real (Z′) and imaginary (−Z″) parts of the complex impedance were calculated according to the following formulas:

$$ Z^{\prime } = \frac{{R^{ - 1 } + Q\omega^{\alpha } {\text{Cos}} \left( {\frac{\alpha \pi }{2} } \right) }}{{\left( {R^{ - 1 } + Q\omega^{\alpha } {\text{cos}} \left( {\frac{\alpha \pi }{2}} \right)^{2} } \right) + \left( {C\omega + Q\omega^{\alpha } \sin \left( {\frac{\alpha \pi }{2})^{2} } \right)} \right) }}, $$

(4)

$$ - Z^{\prime \prime } \, = \frac{{R^{ - 1 } + Q\omega^{\alpha } \sin \left( {\frac{\alpha \pi }{2} } \right) }}{{\left( {R^{ - 1 } + Q\omega^{\alpha } {\text{cos}} \left( {\frac{\alpha \pi }{2}} \right)^{2} } \right) + \left( {C\omega + Q\omega^{\alpha } \sin \left( {\frac{\alpha \pi }{2}} \right)^{2} } \right) }}, $$

(5)

respectively. Figure 4 presents the difference of the real part of the impedance Z′ as a function of frequency at different temperatures. In the region of low frequencies and temperatures, the impedance value is higher but then it gradually decreases with increase in frequency. For certain frequencies (> 10⁵ Hz), Z′ is almost constant, but then decreases. Moreover, the values of Z′ converge at high frequencies towards a minimal value. This result can be attributed to the release of space-charge polarization, decreasing the potential barrier in the material.²⁷ Figure 5 plots the imaginary part of the complex impedance Z″ as a function of frequency at different temperatures. From Fig. 5, we can clearly see peaks where the corresponding frequency of the Z″ maximum is shifted to higher frequencies with increase in temperature. The displacement of this maximum confirms the occurrence of a dielectric process that is characteristic of the material. This relaxation can be explained by the accumulation of charges at grain boundaries, which polarize under the effect of an electric field.²⁸ This relaxation can be interpreted based on charge accumulation at grain boundaries that are polarized under the action of an electric field.²⁸

Fig. 4

Evolution of real part of impedance as function of frequency at various temperatures.

Fig. 5

Variation of imaginary part of impedance as function of frequency at various temperatures.

Dielectric Studies

The complex permittivity of a dielectric material following a non-Debye model can be obtained from the relationship²⁹

$$ \varepsilon^{*} \left( w \right) = \varepsilon_{\infty } + \frac{{\left( {\varepsilon_{{\text{S}}} - \varepsilon_{\infty } } \right)}}{{(1 + {\rm j}\omega \tau )^{1 - \alpha } }} + \frac{{\sigma_{{{\text{DC}}}} }}{{{\rm j}\omega \varepsilon_{0} }}, $$

(6)

where $\varepsilon_{\infty }$ is the high-frequency permittivity, $\varepsilon_{{\text{S}}}$ is the static permittivity, $\varepsilon_{0}$ is the permittivity of free space, τ is the relaxation time, ω is the angular frequency, α is a parameter between 0 and 1, with the former value giving the characteristic result of Debye relaxation, and $\sigma_{{{\text{DC}}}}$ represents the Ohmic conductivity.^30,31,32 As clearly seen from Fig. 6a, the discrepancy of the real part ε′ of the complex permittivity versus frequency increases with temperature, but it decreases with an increase in frequency. This is likely explained by the material’s dielectric polarization mechanism. Actually, the values of ε′ are very high at low frequencies, which can be attributed to the accumulation of charge carriers between the sample and electrodes, e.g., interfacial polarization.^33,34 Figure 6b shows the variation of the imaginary part ε″ of the complex permittivity as a function of frequency at different temperatures. Indeed, a decrease of ε″ with increase in frequency is visible, which can be ascribed not only to the presence of a relaxation time distribution but also to the contribution of charge carrier density.^35,36

Fig. 6

Variation of (a) real and (b) imaginary part of the permittivity as functions of frequency at different temperatures.

Electrical Modulus Studies

The electrical modulus can be used to explore the conduction mechanism and relaxation behavior of a compound.³⁷ It can be determined from the following mathematical formalism:³⁸

$$ M^* = M^{{\prime }} + {\rm j}M^{{\prime \prime }} = {\rm j}\omega C_{0} \quad Z^* = \frac{1}{{\varepsilon^{*} }}. $$

(7)

The real (M′) and imaginary (M″) parts of the complex modulus can be obtained from the complex impedance data Z^*($\omega$) = Z′ − jZ″) using the expressions

$$ M^{\prime } = \omega C_{0} Z^{\prime } $$

(8)

$$ M^{\prime \prime } = \omega C_{0} Z, $$

(9)

where C₀ is the vacuum capacitance of the cell.

Figure 7a shows the difference of the real part of the electrical modulus at different temperatures as a function of frequency. Although the values of M′ are very low at low frequency, they attain a maximum at elevated frequency for all temperatures. In addition, if ε′ decreases, M′ increases, while it was noted above that the permittivity values are large. This can be explained by charge accumulation between the electrode and material. This result confirms the dielectric characterization. The dependence of the imaginary part of the modulus M″ on frequency (Fig. 7b) reveals a relaxation process. M″ is initially low but increases with frequency at some temperature until reaching a maximum that represents a peak of relaxation. If the temperature increases, the modulus values shift to the maximum at higher frequency. The relaxation peaks show that the sample is an ionic conductor. The imaginary part of the modulus is maximal at $\omega \tau$ = 1.

Fig. 7

Variation of (a) the real part (M′) and (b) the imaginary part (M″) of the modulus as functions of frequency at various temperatures.

The activation energy of the relaxation processes can be determined through the expression³⁹

$$ F_{{\text{P}}} = f_{0} \exp \left( { - E_{{\text{a}}} /K_{{\text{B}}} T} \right), $$

(10)

where $f_{0}$ is the frequency at high temperature, $K_{{\text{B}}}$ is the Boltzmann constant, $E_{{\text{a}}}$ is the activation energy, and T is temperature. By plotting the relaxation frequency $F_{{\text{p}}}$ as a function of inverse temperature (1000/T) (Fig. 8), a linear dependence is obtained, obeying Arrhenius behavior.⁴⁰ The resulting activation energy value is 0.386 eV.

Fig. 8

Variation of F_p frequency relaxation with temperature.

Electrical Conductivity Studies

Conductivity measurements are significant for all dielectric materials as they can provide a great deal of information about the conduction mechanism. Besides, the electrical conduction mechanism relies on the movement of electrically charged particles through a transmission medium. Such movement, whose basic mechanism depends on the material, can result in the flow of an electric current in response to an electric field. Two kinds of conduction mechanism exist in a dielectric, namely the electrode-limited conduction mechanism and the bulk-limited conduction mechanism.

The electrode-limited conduction mechanism depends on the electrical characteristics at the electrode–dielectric interface. Considering this type, one can extract the physical features of the barrier height at the electrode–dielectric interface and the effective mass of the conduction carriers in the dielectric material. Meanwhile, the bulk-limited conduction mechanism depends on the electrical properties of the dielectric itself. Through its analysis, one can obtain several important physical parameters of the dielectric, including the trap level, trap spacing, trap density, carrier drift mobility, dielectric relaxation time, and density of states in the conduction band. Figure 9 shows the frequency dependence of the AC conductivity at different temperatures. In addition, the variation of the conductivity reveals two zones, at low and elevated frequency. While the conductivity shows a large plateau corresponding to the direct current (Dc) conductivity at low frequencies, it gradually increases with increase in the frequency at elevated frequency.

Fig. 9

Frequency dependence of AC conductivity at various temperatures.

Moreover, the conductivity curves can be expressed using the Jonscher relation,⁴¹

$$ \sigma \left( \omega \right) = \sigma_{{{\text{DC}}}} + A\omega^{s}, $$

(11)

where $\sigma_{{{\text{DC}}}}$ is the DC conductivity, ω is the frequency, A is a constant that depends on temperature, and s (0 ≤ s ≤ 1) is a dimension lessparameter that characterizes the dispersion in the material.20 As illustrated in Fig. 10, the dependence of the conductivity on inverse temperature follows the Arrhenius law:⁴²

$$ \sigma_{{{\text{DC}}}} = \sigma_{0} \exp \left( {\frac{{ - E_{{\text{a}}} }}{{K_{{\text{B }}} T }}} \right), $$

(12)

where $E_{{\text{a}}}$ is the activation energy, $\sigma_{0}$ is the preexponential term, and $K_{{\text{B}}}$ is Boltzmann’s constant. The activation energy value obtained for LaBa_0.5Ag_0.5FeMnO₆ is 0.392 eV, which may differ from that obtained from the modulus analysis, indicating that the charge transport properties result from the AC conduction mechanism. The temperature dependence of the exponent s was explored to identify the conduction model in the material. The obtained values of s vary from 0.993 to 0.664, depending on temperature. Numerous models can be applied to illustrate the conduction mechanism in samples. Examples including quantum-mechanical tunneling (QMT), correlated barrier hopping (CBH), nonoverlapping small-polaron tunneling (NSPT), and overlapping large-polaron tunneling (OLPT) can be cited. In the case of CBH, s decreases linearly with increase in temperature.⁴³ In overlapping large-polaron tunneling (OLPT), s decreases monotonically with increase in temperature until reaching a minimum. For high temperatures, beyond this minimum, s increases again.⁴⁴ Figure 11 shows the variation of the parameter s as a function of temperature for LBAFMO. The variation of the parameter s thus follows the OLPT conduction mechanism.⁴⁴

Fig. 10

Variation of ln($\sigma_{{{\text{DC}}}} \times T$) with 1000/T.

Fig. 11

Variation of universal exponent s with temperature.

Conclusions

LaBa_0.5Ag_0.5FeMnO₆ compound was synthesized by the sol–gel-based Pechini technique. x-Ray diffraction analysis indicated the cubic structure of the material, while complex impedance spectroscopy confirmed the occurrence of both grain and grain-boundary contributions to the relaxation process of LBAFMO. The electrical properties of LBAFMO can be described by an RC equivalent circuit. Furthermore, the Z′ and Z″ curves merging above 10⁵ Hz for different temperatures demonstrate the occurrence of a relaxation phenomenon. The variation of the AC conductivity is shown to obey Jonscher's law. Moreover, the activation energies resulting from the conductivity and modulus analyses are very similar, confirming that the charge transport between ions occurs via a jump mechanism correspond to the OLPT conduction model.