Structural, AC conductivity, conduction mechanism and dielectric properties of La_0.62Eu_0.05Ba_0.33Mn_0.85Fe_0.15O₃ ceramic compound

Abstract

The new perovskite compound La_0.62Eu_0.05Ba_0.33Mn_0.85Fe_0.15O₃ was successfully synthesized via the sol–gel process. X-ray diffraction revealed that our sample is pure and crystallizes in the orthorhombic structure with Pbnm space group. Electrical properties were performed using the complex impedance spectroscopy technique in the range of frequency (40–10 MHz) and at various temperatures (80–400 K). AC-conductivity results are well described by the universal Jonsher’s power law at low temperatures and the DC-conductivity data are well fitted by the small polaron hopping model at high temperatures. Impedance results show a negative temperature coefficient of resistance (NTCR) which discloses the semiconductor behaviour of the studied sample. Nyquist plots were well fitted by an equivalent circuit involving the contribution of grain and grain boundaries in the conduction process. Giant dielectric values, useful in electronic devices, were obtained. Moreover, a relaxation diffuse phase transition is attributed to a strong heterogeneity in A and B sites of the studied perovskite.

1 Introduction

The manganese family with the general formula ${\text{M}}_{{ 1- {\text{x}}}} {\text{M}}_{\text{x}}^{{\prime }} {\text{MnO}}_{ 3}$ (M = La, Pr, Nd, … and M′ = Ba, Sr, Ca …) has been intensively studied in the last decennies [1,2,3]. Research based on these compounds was motivated by the diversity of behaviours they exhibited such as paramagnetic-ferromagnetic (PM-FM) phase transition [4], magnetoelectric properties [5], charge ordering [6], colossal magnetoresistance (CMR) [7] and large magnetocaloric effect (MCE) [8,9,10]. As a consequence, many technological applications may be developed on the basis of manganite compounds in the field of information storage (computer memory systems, sensors and magnetic devices, infrared detectors, etc.…). From a fundamental point of view, the ferromagnetic character of these materials is due essentially to the double exchange (DE) interaction between Mn³⁺ and Mn⁴⁺ ions via oxygen [11]. Doping the Mn site by non-magnetic transition elements such as titanium [12] and chromium [13] affects the Mn⁴⁺/Mn³⁺ ratio leading to the destruction of the Mn–O–Mn networks. Consequently, the DE interaction is reduced and the MCE and magneto-transport properties of related materials are strongly affected.

In our laboratory, Boujelben et al. [14] and Ammar et al. [15] studied the effect of substitution of manganese with iron in Pr_0.67Sr_0.33Mn_1−xFe_xO₃ and Pr_0.5Sr_0.5Mn_1−xFe_xO₃ respectively. They have demonstrated that this substitution weakens the ferromagnetism and causes a decrease in the Curie temperature in the substituted compounds. Electrical characterizations showed that the substitution of manganese by iron in the Pr_0.67Sr_0.33Mn_1−xFe_xO₃ [14] compounds preserves the semiconductor–metal transition, but with a significant decrease in the electrical transition temperature. In the Pr_0.5Sr_0.5Mn_1−xFe_xO₃ [15] samples, the semiconductor behaviour was confirmed throughout the temperature range 50–325 K. Snini et al. [16] have shown that doping with iron in Pr_0.67Ba_0.22Sr_0.11Mn_1−xFe_xO₃ (0 ≤ x ≤ 0.15) compounds causes a decrease in MCE.

Other works were interested in the study of europium substitution in A-site on electrical and dielectric properties of manganites [17, 18]. They have demonstrated a reduction in the conductance of these materials with the increase of Eu content.

This article is one of several studies carried out in our laboratory to try to obtain materials with remarkable electrical, dielectric and magnetic characteristics. These materials, with relatively low cost, can be used in order to miniaturize the size of electronic components with the increase of their performances.

In a previous work [19], we have studied the electrical and dielectric properties of La_0.67−xEu_xBa_0.33Mn_0.85Fe_0.15O₃ (x = 0.0, 0.1) manganites prepared via sol–gel route. These compounds possess a semiconductor character in the whole temperature range of study and dielectric results show high values of the permittivity required to miniaturize the size of capacitors. In order to confirm these results, we have elaborated, using the same method, a sample with an europium content equal to 0.05.

In the present paper, we report a detailed investigation on the electrical and dielectric features of the La_0.62Eu_0.05Ba_0.33Mn_0.85Fe_0.15O₃ compound synthesized by sol–gel method as a function of frequency and temperature using the impedance spectroscopy technique.

2 Experimental details

In order to prepare the La_0.62Eu_0.05Ba_0.33Mn_0.85Fe_0.15O₃ (noted E05) ceramic compound, we have used as starting materials, high purity La₂O₃, MnO₂, BaCO₃, Eu₂O₃ and Fe₂O₃ oxides. The precursors were at first dried, then mixed according to the following chemical reaction:

(1)

Details of the preparation method were described in our previous work [19]. The structural properties were investigated using a Panatycal type RX (θ–2θ) powder diffractometer at room temperature with Cu-K_α radiation (λ_Kα = 1.5406 Å). The diffraction (XRD) pattern was scanned between 15 and 100°. The structural parameters of the synthesized sample were determined from powder X-ray diffractogram using the Rietveld method and the FULLPROF program [20]. Besides, the homogeneity of the sample and its elemental composition were examined using a semi-quantitative analysis by energy dispersion spectroscopy (EDX). In order to perform electrical measurements, the sample was sandwiched between two thin silver layers representing the ohmic contacts. Conductance measurements were conducted with an Agilent 4294 analyzer using an AC signal amplitude of 50 mV where the frequency varies from 40 Hz to 10 MHz. The evolution of temperature (from 80 to 400 K) was insured by a liquid nitrogen cooled VPF-400 cryostat from Janis Corporation (Table 1).

Table 1 The principle results of Rietveld refinements for the La_0.62Eu_0.05Ba_0.33Mn_0.85Fe_0.15O₃ compound

3 Results and discussion

3.1 Structural characterization

The EDX spectrum of the studied compound, shown in Fig. 1, reveals the presence of all chemical elements used during the preparation step and confirms the absence of any other impurities. Additionally, the chemical composition of the studied compound is given in the inset of Fig. 1. We can verify, from these results, that there is no loss of any integrated chemical element during the sintering process.

Fig. 1

Energy dispersive X-ray spectra (EDX) of La_0.62Eu_0.05Ba_0.33Mn_0.85Fe_0.15O₃ compound. The inset shows the chemical composition of the same sample

We must notice that this method is not accurate for quantitative elemental analysis, especially with low-substitution concentrations [21, 22].

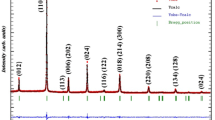
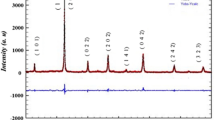
Figure 2a shows the X-ray powder pattern of the E05 sample determined at room temperature. The crystal structure, refined using the Rietveld’s profile-fitting method, shows that our sample crystallizes in the orthorhombic system with Pbnm space group. This result is confirmed by the determination of the tolerance factor given by Goldschmidt [23]:

Fig. 2

a Rietveld-refined XRD profile of La_0.62Eu_0.05Ba_0.33Mn_0.85Fe_0.15O₃ compound at room temperature, b evolution of β cos θ versus 4sin θ and c the SEM micrograph of the studied sample

$$t = \frac{{r_{A} + r_{O} }}{{\sqrt 2 \left( {r_{B} + r_{O} } \right)}}$$

(2)

In this expression, r_A, r_B and r_O represent the average ionic radii of the A-site, the B-site and oxygen respectively. The obtained value (t = 0.9416) confirms that the studied compound crystallizes in the orthorhombic structure. The results of the refinement which contains the cell parameters, the Mn–O bond length distances and the Mn–O–Mn bond angles are gathered in Table 1. As seen, the determined lattice parameters a, b and c verified the relation $a \approx b \approx c/\sqrt 2$ which indicates the presence of a cooperative Jahn–Teller distortion characterizing an orthorhombic distortion in perovskites [24]. These results are in good agreement with those obtained in our previous work for La_0.67−xEu_xBa_0.33Mn_0.85Fe_0.15O₃ (x = 0.0, 0.1) compounds [19]. The Mn³⁺ and Fe³⁺ have almost the same ionic radii, then the lattice distortion effect due to the presence of iron can be neglected. Thus, the orthorhombic distortion can be attributed to the difference in the ionic radii between Eu³⁺ and La³⁺ [25].

The X-ray volumetric mass density ρ_th of the studied compound is calculated according to the relation [26]:

$$\rho_{th} = \frac{{Z{\text{x}}M}}{{N_{A} {\text{x}}V}}$$

(3)

In this expression, Z stands for the number of atoms (Z = 1), M is the molecular weight, N_A = 6.023 × 10²³ denotes the Avogadro’s number and V (= axbxc) represents the volume of the unit cell determined from the X-ray measurements. The value of ρ_th is compared to the experimental one ρ_exp given by:

$$\rho_{exp} = \frac{{4{\text{xm}}_{\text{p}} }}{{\pi {\text{x}}D^{2} {\text{x}}e}},$$

(4)

where m_p, e, and D are respectively the mass, the thickness and the diameter of the ceramic pellet under investigation. The values of ρ_th and ρ_exp are used to calculate the compactness defined by C = ρ_exp/ρ_th. The obtained value of C is 94.55% (then the porosity is evaluated at 5.45%) which confirms the good quality of our compound. The sintered density was measured also by the well-known Archemedian method in water. The obtained value was d ≈ 91% dense.

The average crystallite size of the studied sample can be evaluated by two methods: The Scherrer’s model and the Williamson–Hall method. In the first one, the crystallite size D_S can be calculated using the relation given by [27]:

$$D_{S} = \frac{{0.9\, {\uplambda}_{{{\text{K}}\upalpha}} }}{{\beta \,cos\, \theta_{Max} }}$$

(5)

where β denotes the full width at half maximum of the most intense peak and θ_Max its position. D_S is found to be 47 nm.

The crystallite size is also determined by means of the Williamson–Hall method. The main advantage of this method is that it can separate both effects: the distortion and the size ones [28]. In this evaluation, we have considered only the prominent peaks, located at θ, in the X-ray diffraction pattern. Mathematically, ε which is a coefficient related to strain effect and the crystallite size D_W can be determined by the following expression [28]:

$$\beta cos\theta = \frac{0.9 \lambda }{{D_{W} }} + 4\varepsilon sin\theta$$

(6)

In this expression, the instrumental corrected broadening β which corresponds to each diffraction peak can be determined using the relation:

$$\beta = \left[ {\beta_{measured}^{2} - \beta_{instrumental}^{2} } \right]^{1/2}$$

(7)

In the Bragg peaks, the silicon is used as standard material in order to determine the instrumental broadening. In Fig. 2b, we have plotted the evolution of βcosθ versus 4sinθ. Accordingly, using the obtained linear fit, we have calculated the microstrain ε from the slope of this curve and the crystallite size from its intercept with vertical axis. The calculated values are, respectively, 1.1 × 10⁻³ and 68 nm. As can be seen, D_W is larger than D_S. This result can be explained by the fact that the broadening effect originating from the presence of the strain, is completely excluded in Scherrer’s model [29].

Figure 2c indicates the scanning electron microscope (SEM) micrograph of our sample. The average grain size is estimated at about 111 nm. It is worth noticing that the value calculated from XRD data is significantly lower than that estimated from SEM micrograph. This difference is generally due to the fact that each grain observed by SEM is formed by several crystal domains.

Furthermore, it is clear from XRD pattern that no secondary phase exists in the compound. The white dots seen in the SEM image are purely superficial (they do not appear in the pores). They come from the BaSO₄ powder used when the pellet was tested in optical measurements.

3.2 DC conductivity analysis

Figure 3a shows the temperature evolution of the DC electrical conductivity σ_DC relative to the E05 compound. The experimental σ_DC values were obtained from AC measurements at the lowest frequency used (40 Hz). As clearly seen, σ_DC increases with the increase of temperature indicating that the studied sample exhibits a semiconducting character in the whole temperature range explored. This behaviour is usually encountered in perovskite materials such as BaTi_0.5Mn_0.5O₃ [30], Pr_0.5−xGd_xSr_0.5MnO₃ (0  ≤  x  ≤  0.3) [31] and La_0.8Ba_0.1Ca_0.1Mn_1−xRu_xO₃ (x = 0 and 0.075) [32]. Contrariwise, a metallic to semiconductor behaviour or a semiconductor to metallic one may be obtained in other compounds such as La_0.7−xEu_xBa_0.3MnO₃ and Pr_0.75Bi_0.05Sr_0.1Ba_0.1Mn_1−xTi_xO₃ [21, 33]. In a previous work [34], we have obtained a metallic behaviour followed by a semiconductor one in Pr_0.8Sr_0.2MnO₃ prepared by sol–gel method. By doping the latter compound by bismuth in the praseyodyme site, the metallic behaviour is suppressed completely.

Fig. 3

a Temperature dependence of σ_DC for the La_0.62Eu_0.05Ba_0.33Mn_0.85Fe_0.15O₃ compound at different temperatures. The inset shows σ_DC for La_0.67−xEu_xBa_0.33Mn_0.85Fe_0.15O₃ (0 ≤ x ≤ 0.1) as comparaison and b evolution of Ln (σ_DCT) versus 1000/T. The inset illustrates the variation of Ln(σ_DC) with T^−0.25 for the E05 compound

It is well known that the electrical properties of the doped manganite systems are governed by the double exchange mechanism. This phenomenon governs the overlap between the 2p orbital of the oxygen and 3d orbital of the manganese ions. A reduction in this overlap, described usually by the bandwidth W [35] causes a decrease in conductivity and may induce either a metal to semiconductor transition or an enhancement of the semiconductor behaviour.

We can notice that, by comparing the conductivities obtained with this compound and those obtained with the La_0.67−xEu_xBa_0.33Mn_0.85Fe_0.15O₃ (x = 0.0, 0.1) samples in the inset of Fig. 3a, we can confirm that the conductivity in these compounds decrease with the Eu content as proposed in our previous work [19].

We report in Fig. 3b, the variation of Ln (σ_DC · T) against the inverse of the temperature for our studied compound. At high temperatures, σ_DC is described by the following expression [36]:

$$\sigma_{DC} T = \sigma_{0} \cdot e^{{ - \frac{{E_{a} }}{{{\text{k}}T}}}}$$

(8)

In this relation, E_a is the activation energy, k is the Boltzmann constant and σ₀ is a constant.

The obtained linear evolution suggests that the hopping mechanism in this compound is thermally activated. The calculated activation energy is 126 meV, which is in the same order of magnitude of that obtained with the La_0.57Eu_0.1Ba_0.33Mn_0.85Fe_0.15O₃ compound [19].

At low temperatures, the experimental values of conductivity can be analyzed with the variable range hopping model (VRH). This model can be described by the following equation [37]:

$$\sigma_{DC} \left( T \right) = \sigma_{0} exp\left( { - \frac{{T_{0} }}{T}} \right)^{0.25}$$

(9)

The curve of Ln(σ_DC) as a function of T^−0.25, illustrated in the inset of Fig. 3b, is linear which confirms the validity of this model. The change of conduction mechanism obtained in our compound is generally observed at low temperatures in semiconductor oxides and manganites of the perovskite type [21]. The linear curve extends to high temperature. We can conclude that both mechanisms described by Eqs. (8) and (9) are implied at high temperature.

3.3 AC-conductivity analysis

Figure 4a shows the frequency evolution of AC conductivity σ_AC at various temperatures for the E05 ceramic compound. As we can see, below 10⁴ Hz, the σ_AC curves are characterized by the appearance of a plateau, for each temperature, showing the frequency-independent nature of σ_AC. In this region, the σ_AC measurements can be confused by σ_DC values.

Fig. 4

a Frequency evolution of the conductivity σ_AC(ω) at various temperatures and b temperature evolution of σ_AC(ω) at two selected frequencies for the E05 compound

But in the high frequency region, two behaviours can be selected: Towards low temperatures, σ_AC increases with frequency which represents the typical behaviour of a semiconductor compound and at high temperatures, σ_AC decreases with frequency as observed in metallic materials. We can conclude from this result that the studied material evolves from semiconductor to metallic when the temperature increases. At two selected frequencies: 10⁵ Hz (in the plateau region) and 2 × 10⁶ Hz (in the dispersion region), we have plotted the evolution of σ_AC against temperature. The determined transition temperature T_SC-M is estimated at 180 K (see Fig. 4b).

For 80 ≤ T ≤ 175 K, the E05 compound shows a semiconductor behaviour which is usually described by the Jonscher power law given by [38]:

$$\sigma_{AC} \left( \omega \right) = \sigma_{DC} + A_{1} \omega^{s}$$

(10)

where ω represents the angular frequency, s is a parameter describing the degree of interaction between charge carriers and their environment and A₁ denotes a parameter that depends only on temperature. The s values can be determined by fitting the σ_AC(ω) experimental data with relation (10). Results of this refinement at different temperatures are gathered in Table 2. We can notice, particularly, that s exceeds 1 which corresponds to a hopping of charge carriers between neighbouring sites [39].

Table 2 Refinement parameters using Jonsher model for the E05 compound

As shown in Fig. 5a, all experimental curves are well refined by Jonscher’s power law. The inset of this figure shows a linearity between (− ln A₁) and the s parameter as confirmed by Papathanassiou [40]. The frequency exponent s obtained from this fitting is then plotted as a function of temperature in Fig. 5b. It is well known that, in disordered perovskite compounds, the s parameter plays a key role in the determination of the conduction mechanism.

Fig. 5

a Fitting of the conductivity σ_AC by the Jonscher power law. The inset shows the variation of Ln(A) according to the exponent s and (b) temperature dependence of the exponent s and (1 − s) for the La_0.62Eu_0.05Ba_0.33Mn_0.85Fe_0.15O₃ compound

Indeed, in Fig. 5b, s shows two behaviours:

• From 80 to 100 K, s decreases with increasing temperature, which indicates that the correlated barrier hopping (CBH) is the most appropriate model for describing conductivity in this region. s is given by [41]:

  $$s\left( {T,} \right) = 1 - \frac{6kT}{{W_{M} + kTln\left( {\omega \tau_{0} } \right)}}$$

  (11)

  In this expression, τ₀ is the characteristic relaxation time and W_m denotes the binding energy required to move a charge carrier from one site to another. If $W_{M} \gg kTln(\omega \tau_{0} ),$, relation (11) can be simplified as:

  $$s\left( T \right) = 1 - \frac{6kT}{{W_{M} }}$$

  (12)

  In the studied region of temperature, the plot of (1–s) versus temperature shown in Fig. 5b, gives us the average binding energy W_M of the studied compound which is evaluated at 115 meV.

• For 110 K ≤ T ≤ 175 K, s increases with increasing temperature. So this evolution can be described by the non-overlapping small polaron tunnelling (NSPT) model where the s parameter is given by [30]:

  $$s\left( {T,} \right) = 1 + \frac{4}{{\frac{{W_{H} }}{kT} - Ln\left( {\omega \tau_{0} } \right) }}$$

  (13)

  In this relation, W_H is the polaron hopping energy. For larger values of W_H/k_BT, s can be written as:

  $$s\left( T \right) = 1 + \frac{{4 k_{B} T}}{{W_{H} }}$$

  (14)

  The temperature evolution of (1 − s) gives W_H = 34 meV (see also Fig. 5b). The same evolution of the s parameter (from CBH model to NSPT one) was observed in the La_0.57Eu_0.1Ba_0.33Mn_0.85Fe_0.15O₃ ceramic compound [19].

  As seen, an increase in temperature induces a decrease in the binding energy of the charge carriers, which can jump easily from one site to another with low energy required.

  In order to confirm this result, we have compared the hopping distance R_ω in the two models. Indeed, according to the CBH model, R_ω is given by:

  $$R_{{\omega_{1} }} = \frac{{e^{2} }}{{\pi \varepsilon \varepsilon_{0} \left[ {W_{M} - kTln\left( {\frac{1}{{\omega \tau_{0} }}} \right)} \right]}}$$

  (15)

For the NSPT model, R_ω can be written as:

$$R_{{\omega_{2} }} = \frac{1}{2\alpha }\left[ {ln\left( {\frac{1}{{\omega \tau_{0} }}} \right) - \frac{{W_{H} }}{kT}} \right]$$

(16)

In these expressions, α⁻¹ is the spatial extension of the polaron and τ₀ is the relaxation time given by τ₀ = 1/(2πf₀) where f₀ = 10¹³ Hz [42, 43].

The temperature evolution of the hopping distance R_ω (R_ω1 and R_ω2) at different frequencies is plotted in Fig. 6. These values, which increase with increasing temperature at fixed frequency, are in the same order of magnitude as the interatomic spacing. Thus, the increase in temperature gives charge carriers additional thermal energy, allowing them to easily jump from one site to another. At a given temperature, the hopping distances decrease with frequency which induce an increase of the AC conductivity. The decrease of hopping distances (as illustrated in Fig. 6) induces an increase in the density of charge carriers and consequently the AC conductivity increases.

Fig. 6

Temperature evolution of R_ω and N_EF) at various frequencies for the La_0.62Eu_0.05Ba_0.33Mn_0.85Fe_0.15O₃ studied compound

In the range of temperatures (180 ≤ T ≤ 400 K) and at high frequencies, the conductivity decreases with the increase of temperature and frequency, a typical behaviour of a metallic compound [22].

In this region, σ_AC can be described by the simplified Drude’s model. According to this theory, the conductivity is determined by the following expression [44]:

$$\sigma_{AC} = \sigma_{DC} /\left( {1 + \omega^{2} \tau_{e}^{2} } \right)$$

(17)

τ_e represents the relaxation time, which describes the electron–phonon scattering.

These conductivity results are well fitted by relation (17) as shown in Fig. 7. The temperature evolution of τ_e plotted in the inset of the same figure confirms the metallic behaviour of our sample in this range of temperature [45].

Fig. 7

Adjustment of the conductivity σ_AC(ω) in the metallic region by Drude’s model. The inset shows the temperature dependence of the relaxation time

3.4 Complex impedance analysis

The complex impedance spectroscopy is a powerful method which provides the separation of the bulk (grain), grain boundary and electrode contributions [46].

The evolution of the real part of impedance (Z′) versus frequency at temperatures varying from 80 to 160 K is shown in Fig. 8a. As observed, at low frequencies, the magnitude of Z′ is frequency independent and decreases with increasing temperature. By further increasing frequencies, the experimental values of Z′ are found to decrease gradually with the rise of temperature. This phenomenon can be attributed to the increase of mobility of charge carriers through the structure indicating an increase in σ_AC values. One can see also a shift in Z′ plateau indicating the existence of a frequency relaxation phenomenon in the E05 compound. In addition, in this range of frequency, the decrease of the Z′ magnitude with the increase in temperature indicates a negative temperature coefficient of resistance (NTCR) which is typical behaviour of semiconductor materials [47].

Fig. 8

Frequency evolution of a the real part of the complex impedance Z′(ω) and (b) the imaginary part Z″ at various temperatures. The inset shows the evolution of Ln (τ) versus 1000/T

At higher frequencies, the Z′ values merge irrespective to the temperature which may be related to the release of space charge polarization which induce a reduction of the barrier properties in the studied compound [48, 49].

Figure 8b shows the frequency evolution of the imaginary impedance (− Z″) at different temperatures for our compound. As illustrated, these curves show peaks at (${\text{f}}_{ \hbox{max} } , - Z_{max}^{{\prime \prime }}$) where f_max is the relaxation frequency which shifts to higher frequencies when the temperature increases indicating a thermally activated relaxation phenomenon. The merger of the studied plots at high frequencies indicates a possible accumulation of space charge in the studied compound [50].

The relaxation time calculated from the relation τ = 1/(2πf_max) and plotted against 1000/T, shows an activation energy equal to 81 meV (see the inset of Fig. 8b). The origin of this relaxation process may be defects at higher temperatures and the presence of electrons and/or immobile species at low temperatures [34].

In order to further illustrate this relaxation phenomenon and calculate the activation energy with precision, we have reported in Fig. 9a the normalization curves of ${\text{Z}}^{{\prime \prime }} /{\text{Z}}_{\hbox{max} }^{{\prime \prime }}$ at different temperatures for this compound. These spectra shift towards high frequencies with the increase of temperature. The asymmetry of these peaks confirms that the relaxation in our material is non-Debye. The calculated activation energy shown in the inset of Fig. 9a is equal to 83 meV, which is similar to that determined previously.

Fig. 9

a Variation of ${\text{Z}}^{{\prime \prime }} /{\text{Z}}_{\hbox{max} }^{{\prime \prime }}$ with frequency at different temperatures. The inset represents the variation of f_max as a function of 1000/T and (b) frequency dependence of ${\text{d(Z}}^{{\prime }} / {\text{Z}}_{\hbox{max} } )/{\text{df}}$ and ${\text{Z}}^{{\prime \prime }} /{\text{Z}}_{\hbox{max} }^{{\prime \prime }}$ with frequency at 80 K

At a fixed temperature (T = 80 K as an example), we have plotted in Fig. 9b the frequency evolution of ${\text{d(Z}}^{{\prime }} / {\text{Z}}_{\hbox{max} }^{{\prime }} )/{\text{df}}$ and ${\text{Z}}^{{\prime \prime }} /{\text{Z}}_{\hbox{max} }^{{\prime \prime }}$ for the E05 sample. As seen, the minimum of the first curve and the maximum of the second one do not coincide confirming the deviation from the Debey’s model [51].

Figure 10a illustrates the Nyquist plots (− Z″(ω) vs. Z′(ω)) associated with our studied compound at various temperatures. All these curves are characterized by the presence of two semicircles indicating the existence of two contributions: the first one, detected at low frequencies describes the grain boundary contribution which is due mainly to space charge polarization and the second one, which appears at high frequencies, shows the effect of grains and can be attributed to the orientational polarization [52]. It is worth noticing that the centre of these plots is localized below the real axis confirming the Cole–Cole formalism [53].

Fig. 10

a Nyquist plots (− Z″ vs. Z′) with the corresponding electrical equivalent circuit and b temperature dependence of Ln(Rgb/T) for the studied compound. The inset shows the temperature evolution of the blocking factor

The obtained Nyquist plots were modelled by an equivalent circuit shown in the inset of Fig. 10a where R_g and R_gb are respectively the grain and grain boundary resistances. CPE_gb is a constant phase element given by the relationship [54]:

$$Z_{{CPE_{gb} }} = \frac{1}{{Q_{gb} \left( {j\omega } \right)^{\alpha } }}\qquad{\text{where }} - 1 \le {\upalpha} \le 1$$

(18)

where α describes the degree of deviation from the Debey model and Q_gb the capacitance value of the CPE_gb impedance. Consequently, the real and the imaginary parts of the impedance will be given by the following relations:

$${\text{Z}}^{{\prime }} ({{\upomega }}) = {\text{R}}_{\text{g}} + \frac{{{\text{R}}_{\text{gb}} \left[ {1 + {\text{R}}_{\text{gb }} {\text{Q}}_{\text{gb}} {\upomega}^{{{\upalpha}_{\text{gb}} }} { \cos }\left( {\frac{{{\upalpha}_{\text{gb}} {{\uppi }}}}{2}} \right)} \right]}}{{\left( {1 + {\text{R}}_{\text{gb }} {\text{Q}}_{\text{gb}} {\upomega}^{{{\upalpha}_{\text{gb}} }} { \cos }\left( {\frac{{{\upalpha}_{\text{gb}} {{\uppi }}}}{2}} \right)} \right)^{2} + \left( {{\text{R}}_{\text{gb }} {\text{Q}}_{\text{gb}} {\upomega}^{{{\upalpha}_{\text{gb}} }} { \sin }\left( {\frac{{{\upalpha}_{\text{gb}} {{\uppi }}}}{2}} \right)} \right)^{2} }}$$

(19)

and

$$Z = \frac{{R_{gb}^{2} Q_{gb} \omega^{\alpha } sin\left( {\frac{\alpha \pi }{2}} \right)}}{{\left( {1 + R_{gb} Q_{gb} \omega^{\alpha } cos\left( {\frac{\alpha \pi }{2}} \right)} \right)^{2} + \left( {R_{gb} Q_{gb} \omega^{\alpha } sin\left( {\frac{\alpha \pi }{2}} \right)} \right)^{2} }}$$

(20)

Results of the refinement are presented in Table 3. The choice of this equivalent circuit is confirmed. Indeed, we have shown in Figs. 8a, b and 10a the fit of all experimental curves by the simulated ones (solid lines) using relations (19) and (20). The superposition of these plots reveals the good quality of the fit. Table 3 demonstrates that R_gb shows higher values due to the accumulation of defects at grain boundaries [31].

Table 3 Extracted parameters of the equivalent circuit for the La_0.62Eu_0.05Ba_0.33Mn_0.85Fe_0.15O₃ compound

The evolution of R_gb according to 1000/T can be analysed using the Arrhenius law described by:

$$R_{gb} = R_{0} T exp\left( { - \frac{{E_{a} }}{kT}} \right)$$

(21)

We report in Fig. 10b the evolution of Ln(R_gb/T) versus 1000/T. The obtained activation energy is 102 meV which is of the same order of magnitude as those obtained in our previous study for La_0.67−xEu_xBa_0.33Mn_0.85Fe_0.15O₃ (x = 0 and x = 0.1) compounds [19] and not far from that obtained by DC conductivity analysis. On the other hand, the decrease in R_g values with the rise in temperature confirms the NTCR behaviour of the sample.

The inset of Fig. 10b illustrates the temperature evolution of the blocking factor $\gamma_{f}$ given by [55]:

$$\gamma_{f} \left( \% \right) = \frac{{R_{gb} }}{{\left( {R_{g} + R_{gb} } \right)}} \times 100$$

(22)

This factor describes the percentage of the charge carriers blocked at the grain boundaries compared to the total number of charge carriers responsible for the conduction phenomenon.

At low temperatures, almost all carriers are blocked by grain boundary effects. By increasing temperature, the thermal energy of the charge carriers becomes larger which allows them to jump easily over the barriers created by defects accumulated at grain boundaries. Accordingly, the grain boundary effect decreases progressively and the total conductivity tends to that of grains.

3.5 Dielectric results

As a matter of fact, the dielectric permittivity reflects the polarization state of a dielectric. The dielectric measurements for the E05 compound carried out in the frequency range of 40–10 MHz at different temperatures can be computed from the relation [56]:

$$\sigma_{AC} (\omega ) = \varepsilon_{0 } \omega \varepsilon^{{\prime \prime }} = \omega \varepsilon_{0 } \varepsilon^{{\prime }} tan \delta$$

(23)

where ε′ is the real part of the complex dielectric permittivity which presents the storage of energy, ε″ the imaginary part of the dielectric permittivity describing the loss of energy and tan δ is the dielectric loss factor. As known, the complex permittivity can be written as:

$$\varepsilon^{\ast} \left( \omega \right) = \varepsilon^{{\prime }} \left( \omega \right) - j\varepsilon^{{\prime \prime }} \left( \omega \right)$$

(24)

The frequency dependence of ε′ at different temperatures is presented in Fig. 11a. At low frequencies, ε′ which tends to be frequency independent shows colossal values that can be attributed to the coexistence of electronic, dipolar, ionic and mainly interfacial polarization [34]. Similar behavior has been obtained in compounds and in other amorphous semiconductors [29,30,31]. At high frequencies, ε′ shows a dispersion with frequency due to the Maxwell–Wagner interfacial polarization originating from the accumulation of inhomogeneities at grain boundaries. At fixed frequency, the disorder induced by the increase of temperature can explain the decrease of the dielectric permittivity in our compound.

Fig. 11

a Frequency evolution of ε′ at various temperatures. The inset shows the fit of ɛ′(ω) by the Cole–Cole model and b evolution of the imaginary part of permittivity ε″(ω) at different temperatures. The inset indicates the adjustment of Ln (ε″) by Giuntini theory

The inset of Fig. 11a shows that the ε′(ω) experimental results are well described by the Cole–Cole model. According to this model, the complex dielectric permittivity is described by the following equation:

$$\varepsilon^{\ast} \left( \omega \right) = \varepsilon_{\infty } + \frac{{\varepsilon_{s} - \varepsilon_{\infty } }}{{1 + (j\omega \tau )^{\alpha } }}$$

(25)

From relations (24) and (25), ε′(ω) can be written as:

$$\varepsilon^{{\prime }} (\omega ) = \varepsilon_{\infty } + \frac{{(\varepsilon_{\text{s}} - \varepsilon_{\infty } )\left[ {1 + ({{\upomega \uptau }})^{{\upalpha}} { \cos }\frac{{{{\upalpha \uppi }}}}{2}} \right]}}{{1 + ({{\upomega \uptau }})^{{2{\upalpha}}} + 2({{\upomega \uptau }})^{{\upalpha}} {\text{cos}}\frac{{{{\upalpha \uppi }}}}{2}}}$$

(26)

ε₀ and $\varepsilon_{\infty }$ are respectively the values of the constant static dielectric at low and at high frequencies, τ is the relaxation time and α describes the distribution of the relaxation times. The fit parameters are gathered in Table 4.

Table 4 The adjustment parameters of ɛ’(ω) by the Cole–Cole model

In the metallic regime (at high temperatures), the real part of the permittivity in La_0.67−xEu_xBa_0.33Mn_0.85Fe_0.15O₃ (x = 0.0, 0.1) manganites show negative values which may characterize metamaterials [19]. This behavior wasn’t confirmed in this compound.

Figure 11b shows the frequency evolution of the imaginary part ε″(ω) of the complex permittivity at various temperatures. As can be seen, the presented curves shows a linear evolution with frequency. At low frequencies, the obtained high values of ε″ prove the existence of all polarization effects in our structure. But with increasing frequency, the dielectric loss decreases since the electric dipoles present in the E05 compound cannot follow the AC applied electric field [57]. It worth be noticing that the absence of peaks in ε″(ω) plots confirms that the polarization phenomenon in this compound is governed by a hopping process as demonstrated previously [21].

Mathematically, ε″(ω) can be described by the simplified Giuntini law given by [58]:

$$\varepsilon^{{\prime \prime }} (\omega ) = D(T) \omega^{m}$$

(27)

where

$$m = - 4kT/W_{C}$$

(28)

In these expressions, D is a constant depending only on temperature, W_C is the maximum potential barrier height and m is an exponent describing the interaction between electric dipoles. In the inset of Fig. 11b we have plotted the variation of the Ln (ε″) against Ln (ω) at various temperatures. These obtained linear curves whose slopes are of the order of − 1 indicate the dielectric losses are governed by the DC conduction mechanism [59]. The same behavior was obtained in LiNa₃P₂O₇ [57] and in La_0.67−xEu_xBa_0.33Mn_0.85Fe_0.15O₃ (x = 0.0, 0.1) compounds [19].

Figure 12a displays the temperature evolution of the real part of the permittivity of the studied compound at some selected frequencies. Two behaviours were reported in the literature depending on the degree of substitution of ions in A or B site of the ABO₃ perovskite: a classic or a relaxor ferroelectric. In our case, the intensity of ε′(ω) decreases with increasing frequency. Interestingly, ε′(ω) shows a broad peak which shifts to high temperatures with the increase of frequency. In addition, the maximum of ε′(ω) decreases with the increase in frequency. This dispersion proves the appearance of a dielectric relaxation behavior which can be correlated with the thermally activated process attributed to the grain boundary contribution. The obtained maximum of ε′(ω), located at T_m, corresponds to the Curie temperature of the ferroelectric-paraelectric phase transition can be ascribed to the strong heterogeneity introduced in both the A-site and the B-site of the Pr_0.67Sr_0.33MnO₃ perovskite. Indeed, the radii difference between La and Eu ions in A-site [r(La³⁺) = 1.216 Å and r(Eu³⁺) = 1.12 Å] and between Mn and Fe ions in B-site(r(Mn³⁺) = 0.645 Å and r(Fe³⁺)=0.78 Å [25]) increases the driving force leading to a tilting of the substituted MnO₆ octahedra. As a consequence, local fluctuations in A-site and B-site appear and disturb the Coulomb interactions at a long distance [45]. As a result, the order becomes a short distance.

Fig. 12

Temperature evolution of ε′ (a) and 1/ε′ (b) at different frequencies for the studied compound. The inset shows the variation of Ln $\left( {\frac{1}{{\varepsilon^{{\prime }} }} - \frac{1}{{\varepsilon_{m}^{{\prime }} }}} \right)$ versus Ln (T − T_m)

Figure 12b shows the temperature evolution of 1/ε’ at various frequencies. Above T_m, the real part of the permittivity can be described by the Curie–Weiss law given by:

$$\varepsilon^{{\prime }} = \frac{C}{{T - T_{0} }}$$

(29)

In this relation, C is a constant and T₀ represents the Curie–Weiss temperature. In fact, this parameter describes the degree of deviation from the Curie–Weiss law. By analysing this figure, we can notice that T₀ > T_m, which confirms the diffuse phase transition and the relaxor character of the studied compound.

The real part of dielectric permittivity follows the Curie–Weiss law at T larger than deviation temperature T_dev (at which the curve devuiates from the linear fit) estimated at 150 K for f = 10⁶Hz and deviates from it in the region T_m ≤ T≤T_dev.

The diffuseness of the obtained relaxor can be determined using the empirical modified Curie–Weiss formula proposed by Uchino and Nomura [60]:

$$\frac{1}{{\varepsilon^{{\prime }} }} - \frac{1}{{\varepsilon_{\hbox{max} }^{{\prime }} }} = \frac{{\left( {T - T_{m} } \right)^{\gamma } }}{{C_{m} }}$$

(30)

where $\varepsilon_{max}^{{\prime }}$ represents the maximum of ε′ and C_m is a constant. The critical factor γ characterises the disordered perovskite structures and reflects the nature of the diffusion. Indeed, if γ = 1, the material is considered as a classical ferroelectric and the relation (29) is obtained. But, if γ = 2, the compound is called a relaxor ferroelectric and expression (30) describes a complete diffuse phase transition.

In the inset of Fig. 12b, we have shown the evolution of Ln ($1/\varepsilon^{{\prime }} - 1/\varepsilon_{max}^{{\prime }}$) as a function of ln (T − T_m). The calculated values of γ, gathered in the same figure, confirms the strong diffuse nature for the relaxation behaviour in our studied compound. Similar behavior was obtained in the Pr_0.8Sr_0.2MnO₃ compound prepared by the solid-state process.

4 Conclusion

We have reported in this research work the structure, electrical and dielectric properties of La_0.62Eu_0.05Ba_0.33Mn_0.85Fe_0.15O₃ ceramic material prepared by sol–gel route. X-ray diffraction revealed that our compound posses nanometric crystallite size and crystallizes in the orthorhombic structure with Pbnm space group. Moreover, the study of DC electrical properties proves the presence of a semiconductor character. From the AC study, we have demonstrated that the AC conductivity σ_AC(ω) follows the Jonscher power law and the conduction mechanism is governed by the correlated barrier hopping (CBH) from 80 to 100 K and the NSPT model for 100 ≤ T ≤ 1750 K. The complex impedance study shows the presence of an electrical relaxation phenomenon in the our sample. The real part of the dielectric permittivity, which follows the Cole–Cole model, shows that our compound shows a ferroelectric relaxor character confirmed by the Curie–Weiss law. The diffuseness of this relaxor, calculated at several frequencies, shows an important disordered material. This disorder can be attributed to a strong heterogeneity in A and B sites of the studied perovskite.