Thermodynamic-Based Model Coupled with Phase Transformation Simulation to Predict the Ms Temperature in the Case of Two-Phase Steel

Abstract

A thermodynamic prediction model of the austenite-to-martensite phase transformation kinetics and of the martensitic transformation start temperature ($M_{{\text{s}}}$) has been developed. A strong drop in $M_{{\text{s}}}$ temperature was experimentally observed on a state containing 60 pct martensite. The classical hypothesis of austenite carbon enrichment and grain size refinement on the $M_{{\text{s}}}$ temperature is not sufficient to explain this drop. The partitioning of substitutional elements at the interface is responsible for the phase transformation delay. Two heat treatments have been proposed to obtain a different partitioning at the interface for an identical phase fraction. A coupling of the $M_{{\text{s}}}$ temperature prediction model with a phase transformation prediction model allowed reproducing the experimental results. Finally, the prediction of the martensitic transformation kinetics was validated compared to the experimental kinetics.

1 Introduction

The development of new steels such as dual-phase (DP), transformation-induced plasticity (TRIP)^[1] or more recently quench and partitioning (Q&P)^[2] steels with new thermal routes generates a higher interest in the understanding of the austenite-to-martensite phase transformation in the case of multiphase steels. Tools for predicting the martensite start ($M_{{\text{s}}}$) temperature as a function of the chemical composition and the microstructure parameters (grain size and austenite fraction) are thus required to design thermal treatments and to guarantee mechanical properties.

In the literature, many models^{[3,4,5,6,7,8,9,10,11,12,13,14,15]} were developed to predict the $M_{{\text{s}}}$ temperature of steels quenched from the fully austenitic domain. These models are based on an empirical approach and generally account for the effect of alloying elements on $M_{{\text{s}}}$ temperature value. Among all these elements, carbon plays a major role, as it is known to impact the austenite-to-martensite transformation driving force strongly, leading thus to a large decrease in the $M_{{\text{s}}}$ temperature. However, it has to be noted that the above-mentioned models often neglect the effect of the prior austenite grain size on the transformation, although it has been widely reported^{[16,17,18,19]} that the $M_{{\text{s}}}$ temperature is shifted toward lower temperatures with a decrease in the austenite grain size. This is often explained by a Hall-Petch mechanism: fine austenite grains could increase the resistance of austenite to plastic deformation and thus retard martensite transformation.

To improve preceding models, two recent approaches have been developed: (1) neural networks using artificial intelligence and numerous input variables to refine the result^[20,21,22] and (2) predictive models based on thermodynamics. The main drawback of the first type of approach is its lack of physical basis and the delicate calibration of the models, which limits their versatility. By contrast, for the predictive models based on thermodynamics,^[23,24] new contributions can be added. This is the case of the model developed by Bohemen et al.^[24] who improved the basic model of Gosh and Olson^[23] by integrating the grain size effect on the $M_{{\text{s}}}$ prediction. They added two contributions enabling to take into account the $M_{{\text{s}}}$ temperature decrease resulting from a grain size refinement and the change in the martensite lath aspect ratio. However, this model can only be applied to steels quenched from a fully austenitic state and cannot be generalized to two-phase states such as DP steels, which are mainly heated at an intercritical annealing temperature. In this case, the martensitic transformation occurs at much lower temperature than for the fully austenitic steels. This can be attributed to several reasons: (1) the austenite grain size of two-phase states is globally smaller, (2) the austenite carbon content is higher because of ferrite rejection, (3) austenite/ferrite interfaces are present in the microstructure and (4) substitutional elements (such as manganese) may enrich austenite at the ferrite-austenite interfaces at a level depending on the austenitization conditions.

In this context, the aim of the present paper is to propose a new approach to predict the $M_{{\text{s}}}$ temperature in the case of two-phase steels (such as dual-phase steels). The approach's originality consists of coupling the thermodynamic model developed by Bohemen et al.^[24] for the $M_{{\text{s}}}$ prediction with a phase transformation model^[25] likely to determine the composition in alloying elements at the ferrite-austenite interfaces before quenching. In the present study, to highlight the manganese enrichment influence at the ferrite-austenite interface on the $M_{{\text{s}}}$ temperature, two thermal cycles were carried out with the aim of obtaining the same austenite fraction before cooling but with two different manganese enrichments. In the model, several hypotheses were applied to take into account the observed experimental fall, namely: (1) a grain size decrease and (2) the chemical composition of the elements at the interface.

2 Materials and Procedure

This study was carried out on an industrial DP1000 steel. Its chemical composition is $\text {Fe}{-}0.17\text {C}{-}1.7\text {Mn}{-}0.5\text {Cr}{-}0.3\text {Si}$ with a 5 μm mean grain size. The DP1000 steel has been hot-rolled in the austenitic domain, coiled around 873 K ($600\ ^{\circ }\hbox {C}$) and then slowly cooled to obtain a ferrite-pearlite microstructure. The sheets were then finally cold rolled with a 55  reduction ratio to obtain sheets 1.5 mm thick.

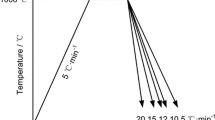
To investigate the influence of the microstructural state before cooling on the $M_{{\text{s}}}$ temperature, three different states (fully or partially austenitic) were produced in a Gleeble thermo-mechanical simulator using heating by Joule effect and cooling through direct air projection on the specimens. For this purpose, samples (10 mm wide by 100 mm long) were heated to the chosen temperature with a heating rate of 5 K/s and then isothermally treated with a precise temperature control (± 3 K) thanks to the use of type-K thermocouples welded on the surface of the specimens. A fully austenitic state (denoted $100\, \text{}\gamma$ state herafter) was obtained after 120 seconds of holding at 1123 K ($850\ ^{\circ }\hbox {C}$) (Figure 1(a)). In addition, two partially austenitic states, for which the target austenite fraction was 60 pct, were produced thanks to (1) an annealing treatment at 1033 K (760$^{\circ }\hbox {C}$) for 300 seconds, thus allowing a manganese peak at the interface to be created ($60\, \text{} \gamma _{-1}$ state) (Figure 1(b)), and (2) a continuous heating up to 1078 K (805$^{\circ }\hbox {C}$) followed by a subsequent rapid cooling ($60\, \text{} \gamma _{-2}$ state).

Fig. 1

Optical microscopy micrographs of (a) the $100\, \text{}\gamma$ state cooled at $R_{\text{C}}=30\,\hbox {K}/\hbox {s}$ and (b) the $60\, \text{}\gamma _{-_1}$ state cooled at $R_{\text{C}}=40\,\hbox {K}/\hbox {s}$. Quantified phase fractions evaluated by dilatometry analysis are reported in the caption of each micrograph after nital etching

An optical LED dilatometer was used to monitor the sample length changes during martensite transformation and to determine the $M_{{\text{s}}}$ temperature from the three initial states. The tangent method was applied to determine the kinetics of transformation.

Led dilatometry was also employed during the continuous cooling of the steel starting from the $100\, \text{} \gamma$ state and from the $60\, \text{} \gamma _{-1}$ state to build the continuous cooling transformation (CCT) diagrams obtained from these two states when the cooling rate was varied between 1 and 40 K/s.

3 Theory

3.1 General Equation for $M_{{\text{s}}}$ Prediction

The massive transformation of austenite into martensite is assumed to occur when the change in free energy ($\Delta G_{\text{c}}$) accompanying the transformation is greater than the energy required to achieve it. This energy is generally related to the energy required to overcome expansion resistance, deformation energy and the creation of new interfaces.

As already mentioned, the model used in the present study was developed by Bohemen et al.^[24] It enables to consider the effect of the chemical composition and that of the austenitic grain size on the $M_{{\text{s}}}$ temperature using the following formula:

$$\begin{aligned} M_{\text{s}}=T_1- \left( \dfrac{\Delta G_{\text{c}} }{S}\right) \end{aligned}$$

(1)

where (1) $T_1$ is the temperature where $\alpha$ and $\gamma$ have the same Gibbs energy, (2) $\Delta G_c$ is the driving force necessary to achieve austenite $\rightarrow$ martensite transformation at $T= M_{\text{s}}$, and (3) S is the assumed constant entropy of the steel.

3.2 Thermodynamic Model for the Prediction of $T_1$

To determine the chemical energy gain when transforming austenite into martensite, it is possible to use a thermodynamic simulation software (such as Thermocalc or FactStage) or to assume a linear variation of the free energy as a function of temperature for different compositions over a certain range of values. This simplification makes it possible to determine the value of $T_1$ as a function of the alloy composition using the following formula:

$$\begin{aligned} T_1=T_0+\sum _i K_0^ix_i \end{aligned}$$

(2)

for steels with $x_{\text{C}}<1\,\hbox {wt}\, \text{},~x_{\text{Mn}}<5\,\hbox {wt}\, \text{}, x_{Si}<3\,\hbox {wt}\, \text{}$, $x_{\text{Cr}}<3\,\hbox {wt}\, \text{}, x_{\text{Ni}}<6\,\hbox {wt}\, \text{}, x_{\text{Mo}}<4 \,\hbox {wt}\, \text{}$. The values of $T_0$ and the various $K_0^i$ coefficients were determined using a linear extrapolation of FactStage thermodynamic data^[24] (see Table I).

Table I Summary of the Constants Used in Eq. [2]

3.3 Grain Size Effect

The novelty of Bohemen’s model compared to that of Ghosh and Olson^[23] is based on the addition of two terms ($\Delta G_{\text{HP}}$ and $\Delta G_{\text{SH}}$) in the expression of the critical driving force $\Delta G_{\text{c}}$ to consider the grain size effect. This leads to the following equation for $\Delta G_{\text{c}}$ :

$$\begin{aligned} \Delta G_{\text{c}}&=\Delta G_0+\Delta G_{\text{HP}} ( K_{\text{HP}}, D^\gamma )\nonumber \\&\quad +\Delta G_{\text{SH}} ( K_{\text{SH}}, D_c^\gamma , D^\gamma ) +\Delta G_\mu (K_\mu ^i,x_i) \end{aligned}$$

(3)

with $\Delta G_0$ a constant, $\Delta G_{\text{HP}}$ the free energy due to grain refinement (Hall and Petch mechanism), $\Delta G_{\text{SH}}$ the free energy due to the martensite unit shape factor and $\Delta G_{\mu }$ the additionnal free chemical energy due to the friction forces coming from the alloying elements.

The term $\Delta G_\mu$ is given by the following equation:

$$\begin{aligned} \Delta G_{\mu }=K_{\mu }^C\sqrt{x_C} +\sqrt{\sum _i \left( K_{\mu }^i \sqrt{x_i}\right) ^2} \end{aligned}$$

(4)

The different values of the $K_{\mu }^i$ coefficients have been from a database of 120 steels and are reported in Table II.^[24]

Table II Summary of the Constants Used in Eq. [4]

In Eq. [3], two mechanisms are supposed to contribute to the $M_{{\text{s}}}$ temperature variation when the grain size varies.

The first mechanism corresponds to a hardening of Hall and Petch type as proposed by Ansell et al.^[26,27,28] It results from the fact that the increase in the autenite grain size leads to a local reduction of plastic deformations in austenite. Brofman and Ansell^[26] have shown that the $M_{{\text{s}}}$ reduction is proportional to the square root of the austenitic grain size. This dependence leads to the following expression of $\Delta G_{\text{HP}}$:

$$\begin{aligned} \Delta G_{\text{HP}}=\dfrac{K_{\text{HP}}}{\sqrt{D^\gamma }} \end{aligned}$$

(5)

The second mechanism is due to an increase in the martensite unit aspect ratio (c/a)^[28] with a grain size decrease. This shape change can only occur with a higher driving force and therefore with a lower $M_{{\text{s}}}$ temperature. The free chemical energy associated with this shape change is described by the following formula:

$$\begin{aligned} \Delta G_{\text{SH}}=K_{\text{SH}} \exp {\left( -\dfrac{6D^{\gamma }}{D_{\text{C}}^{\gamma }}\right) } \end{aligned}$$

(6)

where $D_C^{\gamma }$ is the austenitic critical grain diameter before the formation of a martensitic sub-unit single package.

The coefficients present in the various contributions defined above are summarized in Table III.

Table III Summary of the Constants Used in the Model

3.4 Austenite to Martensite Transformation Kinetics

Classically several equations are used to model the austenite to martensite transformation kinetics such as the well-known Koistinen–Marburger law (KM) or the Strotsky equation.^{[14,29,30,31,32]} The KM law is defined by the following equation:

$$\begin{aligned} f_{\alpha '}=1 - \exp \left( -\alpha _m \left( M_s - T \right) \right) \end{aligned}$$

(7)

with $M_{{\text{s}}}$ the martensitic start temperature and $\alpha _m$ the parameter governing the slope of the curve. $\alpha _m$ is expressed as a function of the steel chemistry according to Eq. [8] and Table IV.^[14]

$$\begin{aligned} \alpha _m=(\alpha _0-\alpha _1(1 - \exp (-K_{\alpha }^Cx_C)) -\sum _i K_{\alpha }^ix_i \end{aligned}$$

(8)

Table IV Summary of the Constants Used in Eq. [8] (All Values are Dimensionless)

4 Results and Discussion

4.1 Preliminary Work-CCT Diagrams from a Fully or Partially Austenitic State

First, the continuous cooling transformation (CCT) diagrams of the insvestigated steel were built, using LED dilatometry, starting from the $100\, \text{} \gamma$ and $60\, \text{} \gamma _{-1}$ states for cooling rates between 1 and 40 K/s (Figure 2(b)). Dilatation curves were analyzed using the tangent method to obtain the austenite decomposition kinetics (Figure 2(a)) and to determine the start and finish temperatures for ferrite and pearlite ($\left( F+P \right) _{\text{S}}, \left( F+P \right) _{\text{F}}$), bainite $\left( B_{\text{S}}, B_{\text{F}} \right)$, and martensite $\left( M_{\text{s}},M_{\text{F}} \right)$.

The main conclusions which can be drawn from Figure 2(b) are the following:

• (1) The domain associated with ferrite and pearlite remains globally unchanged regardless of the initial austenite fraction but it is slightly shifted toward lower temperatures with decreasing the austenite fraction (i.e., with increasing the austenite carbon content).

• (2) The bainitic domain is extended for the $60\, \text{}\gamma _{-1}$ state. Bainite is obtained for a larger range of cooling rate (10 to 30 K/s) compared to only 20 K/s for the $100\, \text{} \gamma$ state.

• (3) The martensitic domain is shifted toward lower temperatures when the austenite proportion decreases.This is in agreement with the austenite carbon enrichment in the partially austenitic steel. Table V summarizes the $M_{{\text{s}}}$ temperatures obtained for the different initial states, and Figure 3 shows the dilatometry curves associated with the three initial states of the steel.

Fig. 2

(a) Austenite decomposition fractions of the 100 $\gamma$ state during continuous cooling from 1123 K (850 $^{\circ }\hbox {C}$) to room temperature at 1, 5, 10, 20, 30 and 40 K/s and (b) comparison of the CCT diagrams obtained during continuous cooling of the $100\, \text{}\gamma$ state (dashed lines) and of the $60\, \text{}\gamma _{-1}$ state (full lines)

Fig. 3

Dilatometry curves associated with the three initial states of the steel reflecting the austenite-to-martensite transformation starting at different temperatures

Table V Summary of the Experimental Values for the $M_{{\text{s}}}$ Temperature and for the Prior Austenite Grain Size Obtained for all Initial States

4.2 Prediction of the $M_{{\text{s}}}$ Temperature in Two-Phase Steels

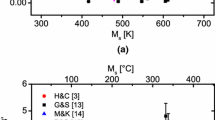
Figure 4 presents the results of the different prediction models for the $M_{{\text{s}}}$ temperature found in the literature. These models can be divided in two categories: (1) the empirical models based only on the steel chemistry and (2) the thermodynamic model of Bohemen et al. presented in this paper, which also enables considering the grain size.

For the application of the models to the case of the $100\, \text{}\gamma$ state, its $M_{{\text{s}}}$ temperature was calculated using the DP1000 steel bulk composition and a mean austenitic grain size of 3.8 μm in the direction perpendicular to the cold-rolling direction. As Figure 4 shows, most models are able to reproduce the $100\, \text{}\gamma$ experimental data. This is consistent with the fact that the models were developed for fully austenitic steels. In the following, the objective is to discuss the application of these models to the case of the $60\, \text{}\gamma$ states by considering, in a first approach, that the only change to consider is due to the austenite carbon enrichment. Then, due to the inability of this assumption to account for the experimental results, the effect of other factors (grain size, substitutional enrichment of austenite) will be discussed in the case of the thermodynamic model of Bohemen.

Fig. 4

Comparison of the different $M_{{\text{s}}}$ prediction models in the literature on the $100\, \text{}\gamma$ and $60\, \text{}\gamma _{-1}$ states. The colored horizontal domains give an estimation of the error on the measured Ms values

4.3 Austenite Carbon Enrichment

To apply the preceding models to the case of the $60\, \text{}\gamma _{-1}$ state, it was first considered that the only change to bring is a modification of the austenite carbon content in the chemical composition of the steel. The carbon enrichment of austenite can be calculated from the mass balance of carbon in the steel expressed by the following formula:

$$\begin{aligned} \left( x_C^{\gamma }=\frac{x_C^0-\left( 1-f_{\gamma }\right) x_C^{\alpha }}{f_{\gamma }} \right) \end{aligned}$$

(9)

where $x_C^{\gamma }$, $x_C^{\alpha }$ and $x_C^{0}$ are respectively the austenite, ferrite $(0.015 wt\, \text{})$ and bulk carbon composition. Including the hypothesis of austenite carbon enrichment for the two-phase $60\, \text{}\gamma _{-1}$ state, no model presented in Figure 4 faithfully reproduces the observed experimental drop of about 100 K since the predicted $M_{{\text{s}}}$ values are overestimated of approximatively 50 to 100 K.

The present results thus disagree with the works of Bohemen and Sietsma^[32] who showed that the carbon content is the only parameter to modify in the chemical composition to predict the $M_{{\text{s}}}$ temperature of partially austenitized steels. These discrepancies could be because their expriments were performed on steels with a much higher carbon content (0.46 to 0.8 wt pct) and with a much lower content of alloying elements (Mn 0.7 wt pct).

Considering the results obtained in this work on the two-phase states, it seems necessary to consider that other factors are likely to play a role in the $M_{{\text{s}}}$ temperature value in the case of flat multiphase steels (low carbon concentration and presence of alloying elements such as Mn, Cr, Si, etc.). Only the thermodynamic model developed by Bohemen et al.^[24] allows including all these potential contributions. This is why this model was retained in the following study.

4.4 Austenite Grain Size Refinement

To consider the grain refinement in the thermodynamical model,^[24] it is necessary to evaluate the average distance between grain boundaries perpendicular to the direction of cold rolling, which may be different from the average grain size depending on the cold-rolling reduction ratio. Using microscopic observations and Fiji software, a local thickness algorithm^[33,34] was applied to each investigated state of this study leading to the grain size values given in Table V. In this study only the values measured by microscopic observation were used in the simulations. Nevertheless, for the sake of simplicity, to estimate the $\gamma$ grain size in two-phase steel, we propose the following formula:

$$\begin{aligned} D_{60\, \text{}\gamma }=f_{\gamma }D_{100\, \text{}\gamma } \end{aligned}$$

(10)

where $D_{60\, \text{}\gamma }$ and $D_{100\, \text{}\gamma }$ are respectively the austenitic grain size of two- and single-phase steel. This relationship assumes a constant grain number between $f_{\gamma }=60\, \text{}\gamma$ and $f_{\gamma }=100\, \text{}\gamma$. It slightly overestimates the observed experimental value but allows an efficient estimation.

Although the addition of the grain size refinement hypothesis reduces the $M_{{\text{s}}}$ temperature in the case of $60\, \text{}\gamma _{-1}$ steel, Figure 5(a) shows that it is not yet sufficient to fully explain the drop observed experimentally. However, in the case of the $60\, \text{}\gamma _{-2}$ steel, the addition of the grain size refinement hypothesis is sufficient to explain the observed experimental drop, leading to a correct prediction of the $M_{{\text{S}}}$ temperature (see Figure 5(b)).

Fig. 5

Comparison of the model predictions for $M_{{\text{S}}}$ with the experimental data for: (a) the $60\, \text{}\gamma _{-1}$ state and (b) the $60\, \text{}\gamma _{-2}$ state

4.5 Alloying Element Enrichment at the Interface

The heat treatment necessary for austenite formation in the case of two-phase steels can, depending on the annealing conditions, lead to a partitioning of the substitutional elements at the interface, which can delay the austenite-martensite transition. To predict and model the substitutional element enrichment at the interface, the Gibbs energy minimization (GEM) model^[25] was used considering a 5 μm 1-D simulation cell (10,000 nodes and interface width of 2.5 nm) with closed boundary conditions for each element, corresponding to half-spacing between the pearlitic zones. Diffusion coefficients and chemical potential have been extracted from the MOBFE3 mobility and TCFE8 database. The simulation starts with an austenitic region of 2.4 volume fraction (containing 6.67 wt pct C and 10 wt pct Mn), resulting from the fast transformation of cementite into austenite. A mass balance is performed to determine the flat profile concentrations within the ferrite (containing 0.0066 wt pct C and 1.55 wt pct Mn).

The model used in this work allows predicting the austenite fraction formed during heating from the initial state at room temperature as well as the different diffusion profiles. According to this model, the phase transformation occurring in the DP1000 steel to reach the $60\, \text{}\gamma _{-2}$ state is not characterized by a manganese enrichment in austenite at the interface as can be seen in Figure 6(d). In this case, the $M_{{\text{s}}}$ modeling, shown in Figure 6(b), can be performed by considering only the carbon enrichment in austenite and the grain refinement compared to that of the $100\, \text{pct}\gamma$ state. By contrast, for the $60\, \text{}\gamma _{-1}$ state, a manganese enrichment at the interface of 2.4 (wt pct) is clearly shown in Figure 6(c). In this case, the $M_{{\text{s}}}$ prediction requires considering this enrichment (see Figure 6(a)). By combining all factors involved in the model (C and Mn enrichment in austenite and grain refinement), it is possible to obtain a $M_{{\text{s}}}$ drop of about 85 K, which is consistent with experimental observation and measurements. Therefore, both two-phase steel states highlight the effect of the interface enrichment in manganese which may occur during a conventional industrial thermal cycle and lead to a drop of the $M_{{\text{s}}}$ temperature of the order of 30 K. In conclusion, the $M_{{\text{s}}}$ prediction models can be extended under the condition of knowing precisely the microstructural changes occurring during the thermal cycle. A coupling with a phase transformation model seems an essential point to efficiently predict the $M_{{\text{s}}}$ temperature in the case of two-phase steels containing alloying elements.

Lastly, it has to be pointed out here that the situation investigated in the present paper is very different from that described by Tsuchiyama et al.^[35] who observed a nucleation of martensite at the center of austenite islands and not at the phase boundary during cooling. This can be attributed to the fact that these authors worked on a medium manganese steel with a manganese content of 5 wt pct leading to a much more marked manganese partitioning at the interface (9 vs 2.4 wt pct). With such high chemical composition in manganese, it seems realistic that the energy necessary for the martensite nucleation in an austenite region with a low Mn content is negligible compared to the austenite stabilization by a high manganese composition. In addition, it should be noted that the martensite formation at the center of austenite islands as described in the paper of Tsuchiyama et al.^[35] was obtained from a microstructure combining the presence of residual austenite with a high Mn enrichment and tempered martensite. This situation is thus very different from that studied in our paper where the phase in contact with austenite is ferrite and not martensite. This could significantly modify the nucleation of “fresh martensite” during cooling as the mechanical stresses at the interface can be quite different in the presence of martensite instead of ferrite.

Fig. 6

Comparison of the model predictions for Ms with the experimental data for: (a) the $60\, \text{}\gamma _{-1}$ state and (b) the $60\, \text{}\gamma _{-2}$ state. Concentration profiles within the sample for: (c) the $60\, \text{}\gamma _{-1}$ state and (d) the $60\, \text{}\gamma _{-}2$ state

4.6 Prediction of the Austenite-to-Martensite Transformation Kinetics

Once the $M_{{\text{s}}}$ temperature has been modeled, the martensitic transformation kinetics can be calculated using different formulas. Using the Koistinen-Marburger law (Eq. [7]) with the parameter $\alpha _{\text{m}}$ calculated with the data of Table IV and the predicted $M_{{\text{s}}}$ values of this study, the austenite-to-martensite kinetics were modeled starting from the $100\, \text{}\gamma$ and $60\, \text{}\gamma _{-1}$ states. Figure 7(b) shows that the experimental kinetics prediction gives good results in the case of the $100\, \text{}\gamma$ state. On the other hand, for the $60\, \text{}\gamma _{-1}$ state, the only carbon mass balance assumption is not sufficient to reproduce the experimental kinetics because of an $M_{{\text{s}}}$ overestimation. The additional assumptions (grain size refinement and substitutional element segregation at the interface) provided in this paper allow approaching the experimental kinetics as presented in Figure 7(a). In view of the results, it seems that the key parameter needed to model the martensitic transformation kinetics is based on a accurate description of the $M_{{\text{s}}}$ temperature. The consideration of all the elements that can delay the phase transformation, such as grain size refinement and the addition of alloying elements that can be partitioned at interfaces, is thus required for an accurate prediction of martensitic transformation kinetics in high-strength steels. These modifications make it possible to consider an extension of the martensitic transformation kinetics prediction in the case of two-phase steels.

Fig. 7

Comparison of the martensitic transformation kinetics for: (a) the $60\, \text{}\gamma _{-1}$ state and (b) the $100\, \text{}\gamma$ state

5 Conclusion

Following the development of predictive models for $M_{{\text{s}}}$ in recent years based on thermodynamic models and considering the grain size effect, it is now possible to predict the $M_{{\text{s}}}$ temperature and the austenite-to-ferrite kinetics with accuracy for fully austenitic steels. However, very few studies have examined the case of the two-phase steels on the martensitic transformation, even though most new-generation high-strength steels include several phases and high content of alloying elements. The purpose of this study was to model the considerable drop in experimental $M_{{\text{s}}}$ temperatures observed in the two-phase states that no model in the literature was able to capture. As this drop cannot be totally explained in some cases by the carbon austenite enrichment and by the grain austenite refinement, it was assumed that the substitutional enrichment at the austenite/ferrite interface level can be partly responsible for the $M_{{\text{s}}}$ fall. A phase transformation model was thus used to predict this enrichment and then to predict successfully the $M_{{\text{s}}}$ temperature of dual-phase steels. These hypotheses make it possible to support the model thermodynamic foundations applied to the $100\, \text{}\gamma$ states when the exact chemical element profile is known within the material, allowing thus its extension for two-phase states and other applications than dual phases.