1 Introduction

Bulk metallic glasses (BMGs) exhibit many desirable properties, e.g., high strengths and hardness, large elastic limits, and excellent corrosion and oxidization resistance,[1–7] which make them potential candidates as new structural materials. However, BMGs are notorious for their brittle nature upon loading due to the formation of the highly localized shear bands. In a monolithic BMG, a major shear band will run through the entire sample once it initiates from some weak locations. To circumvent this disadvantage, a class of metallic-glass-matrix composites (MGMCs), with ductile dendritic crystalline phases dispersed in the metallic-glass (MG) matrix, has emerged with improved toughness, due to the stabilization against shear localization and propagation of critical shear bands upon loading.[8–13] The primary objective will be clearly directed to how to design such a microstructure and control the internal strain fields so that the ductility enhancement can be manipulated.

A number of studies have been conducted to investigate the deformation mechanisms in the dendrite-dispersed MGMCs. For example, Hofmann et al.[10] and Qiao et al.[8,9,14–16] found that the MGMCs had substantially improved malleability and tensile ductility compared with monolithic BMGs, presumably by blocking the propagation of shear bands by soft crystalline phases in MGMCs under loading.[10,17,18] This mechanism can be revealed by post-mortem observations, while only limited in situ studies have been performed by synchrotron X-ray and neutron diffraction measurements on the microstructural origin of these deformation mechanisms.[19–23] We note that the synchrotron X-ray diffraction measurement has unique advantages, compared with the neutron diffraction in respect of resolution, which tends to be more sensitive to structural disorder and fluctuations, and allows the background intensities between peaks to be estimated more reliably.[24]

In the X-ray diffraction, lattice strain can be calculated from the shift of diffraction peaks, which corresponds to the elastic lattice distortion of grains in different crystallographic directions. From the micromechanics standpoint, the lattice strain relies on the intergranular interactions of inhomogeneous deformation fields in neighboring grains, which is also called Type-II strains.[25] In diffraction analysis, the lattice strain in the 〈hkl〉 direction, ɛ hkl , is calculated from the interplanar spacing (d hkl ), based on the change of values d hkl before and after deformation, which can be measured from the {hkl} peak shift in the diffraction pattern. In elastic deformation, the evolution and anisotropy of ɛ hkl are determined by the elastic anisotropy and texture of materials, while in plastic deformation, they are mainly contributed by plastic slips and intergranular interactions among neighboring grains. The deviation of the measured ɛ hkl from the extrapolated curve of the measured elastic–elastic portion is denoted as intergranular strains.[25,26]

In the reported diffraction works, Ott et al.[23] studied the elastic strain evolution of particle-reinforced MGMCs in single crystal direction using the synchrotron X-ray diffraction and finite element modeling (FEM) during compressive loading. Their simulations are based on continuum Mises plasticity without any reference to the plastic anisotropy in the inclusions, and also there is no reference to the strain localization in the matrix. Clausen et al.[21,22] investigated the lattice-strain evolution of dendrite-crystal-strengthened MGMCs by neutron diffraction and self-consistent models. Their self-consistent model is based on the Eshelby inclusion model and gives a neat treatment of how a crystalline grain deforms within other grains, which clearly has difficulties in describing dendritic crystals. Deformation in the matrix involves strain localization, which again cannot be addressed by the self-consistent model. Limitations in these literature works have prevented a full understanding of deformation mechanisms in these composites.

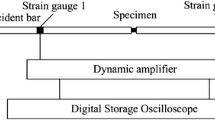
In the current work, a synergistic experimental/modeling study is reported to investigate the lattice-strain evolution of crystalline phases in the dendritic-inclusion-dispersed MGMCs under in situ uniaxial compressive deformation in both elastic and plastic stages. The composition of the selected MGMC system is Zr58.5Ti14.3Nb5.2Cu6.1Ni4.9Be11.0 in atomic percent (at. pct). The final microstructure of the MGMC, as shown in the scanning-electron-microscopy (SEM) image of Figure 1(a), consists of metallic-glass matrix and crystalline phase. During the transition from elastic-to-plastic deformation in the crystalline phase (~450 MPa under uniaxial compression), we are interested in the sequence of yielding in different grain families. In other words, which grains are “hard” or “soft” when the crystalline microstructure is dendritic and the surrounding matrix is elastic? During the transition from elastic-to-plastic deformation in the matrix phase (~1450 MPa under uniaxial compression), the emphasis is placed on the load partitioning between the MG matrix and crystalline dendrites. For example, how would the shear bands affect the lattice-strain evolution in the second phase? Deformation behavior was identified using high-energy synchrotron X-ray diffraction, with the schematic in Figure 1(b) illustrating the experimental set-up. Procedures to obtain representative diffraction results in Figures 1(c) and (d) are explained in Section II.

Fig. 1
figure 1

(a) Scanning electron microscope image of the dendritic crystalline phase (β) in the metallic-glass matrix with the composite composition of Zr58.5Ti14.3Nb5.2Cu6.1Ni4.9Be11.0 (at. pct) and the crystalline phase volume percentage of ~55 pct. (b) Schematic illustration of the in situ synchrotron X-ray diffraction experiment on the compression sample. (c) X-ray diffraction pattern of the as-cast specimen before deformation. (d) Line profiles for the specimens before deformation and at an applied stress of ~1500 MPa

Full size image

Deformation mechanisms can be studied from a microstructure-based finite element method in which the crystalline phase and matrix are explicitly modeled in Figure 2. Appropriate geometric information (such as crystallographic orientation and shape) and constitutive models (including crystal plasticity for the inclusion and free-volume model for the matrix) can be assigned to the finite elements. The connection between the synchrotron X-ray diffraction measurements and the finite element simulation lies on the lattice strain, which can be extracted by finding the grains that satisfy the diffraction condition, as schematically shown in Figure 2(c). Details of modeling and simulation, as well as lattice-strain extraction procedure, are given in Section III. Lattice strains will provide the unprecedented information on the underlying deformation mechanism at microstructural scales, and our explicit microstructure-based simulations differ from many previous studies in this class of materials. Consequently, effects of dendrite shape, crystalline orientations, and strain localization in the matrix on lattice-strain evolution can be investigated and be used to understand the deformation mechanisms.

Fig. 2
figure 2

(a) The finite element simulation is conducted on a compression specimen with cubic elements in ABAQUS model. (b) and (c) display all the crystalline grains and the {310} grains, respectively

Full size image

2 Experimental Methods

2.1 Sample Preparation

The MGMCs were prepared by arc-melting a mixture of Zr, Ti, Ni, Cu, Nb, and Be with purities greater than 99.9 pct in weight percent (wt pct) under a Ti-gettered argon atmosphere. The liquid alloys were sucked into a cylindrical copper mold with a diameter of 3 mm and a length of around 70 mm. Upon cooling from a high-temperature melt, the alloy undergoes partial crystallization by nucleation and subsequent growth of the β phase in the remaining liquid, producing a two-phase microstructure containing β-phase dendrites in the MG matrix. The energy-dispersive spectrometry (EDS) analysis revealed the compositions of the dendrites and the glass matrix to be Zr66Ti15Nb8Cu10Ni1 and Zr50Ti13Nb3Cu20Ni14, respectively. It should be note that the element Be cannot be detected by EDS, and it is almost wholly enriched in the MG matrix.[15] The volume fraction of the dendrites was found to be approximately 55 pct by analyzing the contrast on the SEM images. For mechanical experiments, the samples were still in a cylindrical geometry, and machined to 6 mm in length with an aspect ratio of 2:1. The ends of samples for mechanical tests were polished to a 1200 grit SiC surface to ensure alignment.

2.2 Synchrotron X-ray Measurements

The high-energy synchrotron X-ray diffraction was carried out at the beamline, 11ID-C, of the Advanced Photon Source (APS), Argonne National Laboratory, USA. As schematically shown in Figure 1(b), a digital image plate (MAR 345, with a 200 × 200 μm2 pixel size) was positioned 1,800 mm downstream from the sample to record the scattered intensity in transmission through the specimens, with a beam size of 0.2 × 0.2 mm2. A two-dimensional (2D) ring pattern was recorded on the image plate, as shown in Figure 1(c). Scattering patterns were extracted by azimuthally averaging the ring pattern over an arc of approximately 5º centered on the vertical (loading) direction using the FIT2D software.[27] The specimens were loaded incrementally in uniaxial compression using a motorized screw-driven load cell, and the data were collected automatically every 20 seconds, without stopping the load. All the samples were tested under compression at a strain rate of 2 × 10−4 s−1.

The interplanar spacing of the {hkl} planes, d hkl , was determined in terms of the Bragg’s law, d hkl  = λ/2sin θ hkl , where 2θ hkl is the diffraction angle of different {hkl} planes and determined by fitting the position of an individual Debye cone on the diffraction spectra. Due to the high angular resolution of the synchrotron-based X-ray diffraction technique, the slight shift of diffraction patterns could be tracked during the course of loading. The lattice strain, ɛ hkl , can thus be obtained by

$$ \varepsilon_{hkl} = \frac{{d_{hkl} - d_{hkl}^{0} }}{{d_{hkl}^{0} }}, $$
(1)

where d 0 hkl is the interplanar spacing in the undeformed state. The diffraction peaks of {110}, {200}, {211}, {220}, and {310} planes of the β phase in the MGMCs with a BCC structure before and after deformation are exhibited in Figure 1(d) under compressive deformation.

3 Modeling

3.1 Microstructure-Based Finite Element Simulations

In contrast to the self-consistent model in which a grain of interest is embedded in an effective homogeneous medium,[21,22] the microstructure will be explicitly simulated with appropriate constitutive models assigned to each phase as shown in Figure 2. The crystalline phase can be assigned with a slip-based crystal plasticity model,[25,26] which describes the Schmid law, slip anisotropy, and hardening behavior. The constitutive parameters include elastic constants C11, C12, and C44; the critical resolved shear stress τ 0; and those describing strain-rate dependence and hardening behavior. Details are given in Section III–B. This model has been implemented in ABAQUS, a commercial finite element software, through the user-defined material (UMAT) subroutine,[28] which has been modified further for the lattice-strain analysis. The MG matrix can be assumed to be elastic-perfect plastic solids in some cases for the sake of simplicity with the constitutive parameters of Young’s modulus E, Poisson’s ratio ν, and yield stress σ YBMG . However, at the late stage of deformation, the localized deformation in the narrow shear bands will give a stress field that cannot be faithfully described by the elastic–plastic model. To this end, we adopt the free-volume-based constitutive model for more elaborate studies since it is capable of capturing the shear-banding events,[29,30] with details being given in Section III–C. This constitutive model has been implemented into ABAQUS using the UMAT subroutine in Reference 29 which allows us to study the interaction between individual shear bands and the background stress fields.[31,32]

Compared with the traditional MGMCs with particle-like crystalline inclusions in the MG matrix,[23,33–36] the typical characteristic of this kind of composite is that a large amount of dendritic single crystals with random crystallographic orientations precipitate in the MG matrix. However, a full 3D mesh of the dendritic microstructure in Figure 1(a) is not feasible because of the fine geometric details. Here, we adopt a uniaxial specimen in Figure 2(a) with 7,986 cubes.[25] Half of these cubes belong to the MG matrix, while the other half are of the crystalline phase, as shown in Figure 2(b). This configuration is close to the experimental condition, where the crystalline phases have a volume percentage of ~50 pct in the MGMC specimens. Each grain in Figure 2(b) has eight C3D8R elements with the same crystal orientation, in which the C3D8R element is a 3D-reduced-integration hexahedral element. Note in Figure 1(a), each crystalline inclusion is dendritic and actually consists of multiple grains. All the crystalline grains are assigned with the same crystal plasticity constitutive parameters but with different crystallographic orientations. The boundary conditions in the current models are with an applied load at one end and pinned boundary at the other end.

The extraction and calculation of lattice strains, ɛ hkl , are specified as follows. A subset of grains is selected, 〈hkl〉 directions of which are parallel (or within a small tolerance angle) to the diffraction vector, q. The tolerance, which is the maximum deviation between the 〈hkl〉 direction and q, is chosen in the simulations to ensure that a large amount of {hkl} grains could be selected to improve the statistical quality (e.g., ±4 deg in our simulation). Figure 2(c) exhibits the selected grains with the 〈310〉 crystallographic orientation in the model. The lattice strain, ɛ hkl , is a volume average of the projected elastic strain, given by[25]

$$ \varepsilon_{hkl} = \frac{{\sum\limits_{N = 1}^{{N_{\text{grain}} }} {\int {\varepsilon_{ij}^{\text{elastic}} q_{i} q_{j} {\text{d}}\varOmega_{N} } } }}{{\sum\limits_{N = 1}^{{N_{\text{grain}} }} {\int {{\text{d}}\varOmega_{N} } } }}, $$
(2)

where dΩ N is the differential volume of the Nth grain, and N GRAIN is the total number of grains in 〈hkl〉 directions.

3.2 Crystal Plasticity for Crystal Inclusions

In the slip-based crystal plasticity theory,[37,38] the crystal will yield when the revolved shear stress reaches a critical strength on a given slip system (i.e., the Schmid law), and the constitutive model also needs to specify the flow behavior and hardening law. From the kinematics point of view, the deformation behavior of the material elements is characterized by the deformation gradient:

$$ F_{ij} = \frac{{\partial x_{i} }}{{\partial X_{j} }}, $$
(3)

where x i and X i are the current (deformed) and initial coordinates, respectively. The total deformation gradient can be decomposed into elastic and plastic parts, F ij  = F e ik F p kj , where F e ik and F p kj denote elastic and plastic deformation components, respectively. The plastic rate of deformation is

$$ \dot{F}_{ik}^{\text{p}} F_{kj}^{{{\text{p}} - 1}} = \sum\limits_{\alpha = 1}^{{n_{\text{s}} }} {\dot{\gamma }\left[ {\tau^{(\alpha )} ,\tau_{\text{flow}}^{(\alpha )} } \right]} s_{i}^{(\alpha )} m_{j}^{(\alpha )} , $$
(4)

where n s is the total number of slip systems, \( \dot{\gamma } \), s (α) i , and m (α) j are the shear rate, slip direction, and slip plane normal of the αth slip system, respectively. The shear rate is a function of the resolved shear stress, τ (α), acting on the slip plane and the flow strength of the slip system, τ (α)flow . The resolved shear stress is computed as

$$ \tau^{(\alpha )} = m_{i}^{(\alpha )} F_{ij}^{{{\text{e}} - 1}} J\sigma_{jk} F_{kl}^{\text{e}} s_{l}^{(\alpha )} $$
(5)

where J = det(F e). The elastic part of the deformation gradient is related to stress through

$$ T_{ij} = C_{ijkl} E_{kl}^{\text{e}} , $$
(6)

where \( E_{ij}^{\text{e}} = \frac{1}{2}(F_{ki}^{\text{e}} F_{kj}^{\text{e}} - \delta_{ij} ) \) is the elastic Lagrange-Green strain, and T ij is the material stress tensor, which is related to the Cauchy stress by

$$ J\sigma_{ij} = F_{ik}^{\text{e}} T_{kl} F_{jl}^{\text{e}} $$
(7)

The Pierce–Asaro–Needleman’s constitutive law is used to characterize the plastic flow and strain hardening, given by

$$ \dot{\gamma }^{(\alpha )} = \dot{\gamma }_{0} |\frac{{\tau^{(\alpha )} }}{{\tau_{\text{flow}}^{(\alpha )} }}|^{n} {\text{sgn}}[\tau^{(\alpha )} ], $$
(8)
$$ \dot{\tau }_{\text{flow}}^{(\alpha )} = \sum\limits_{\beta } {h_{\alpha \beta } } |\dot{\gamma }^{(\beta )} |, $$
(9)

where the self-hardening modulus is given by

$$ h_{\alpha \alpha } = h(\gamma ) = h_{0} \sec h^{2} |\frac{{h_{0} \gamma }}{{\tau_{\text{s}} - \tau_{0} }}|({\text{no}}\;{\text{sum}}\;{\text{on}}\;\alpha ) $$
(10)

Here h 0 is the initial hardening modulus, τ 0 is the initial yield stress, τ s is the saturation slip strength (the stress at which the large plastic flow initiates), and \( \gamma = \int\limits_{0}^{t} {\sum\limits_{\alpha } {|\dot{\gamma }^{(\alpha )} |} } {\text{d}}t \) is the total accumulated shear strain on all slip systems. The latent hardening moduli, h αβ , are given by

$$ h_{\alpha \beta } = h(\gamma )[q + (1 - q)\delta_{\alpha \beta } ](\alpha \ne \beta ), $$
(11)

where q is the ratios of latent to self-hardening.

To summarize, the constitutive behavior of crystals is characterized by a set of parameters, including the elastic constants in principal directions (C11, C12, and C44), characteristic strain rate (\( \dot{\gamma }_{0} \)), stress exponent (n), initial yield stress (τ 0), saturated yield stress (τ s), and initial hardening rate (h 0).

3.3 Free-Volume Model for the Metallic-Glass Matrix

Following the Spaepen’s free-volume model,[30] the stress-driven increase in the free volume reduces the viscosity, thus leading to strain-softening behavior of MGs. In the pure shear case, the plastic-strain rate (\( \dot{\gamma }^{\text{p}} \)) is represented by

$$ \frac{{\partial \gamma^{\text{p}} }}{\partial t} = 2f\exp \left( { - \frac{{\alpha v^{*} }}{{v_{\text{f}} }}} \right)\exp \left( - \frac{{\Delta G^{\text{m}} }}{{k_{\text{B}} T}}\right)\sinh \left( {\frac{\tau \varOmega }{{2k_{\text{B}} T}}} \right), $$
(12)

where f is the frequency of atomic vibration, α is a geometric factor of order 1, v* is the hard-sphere volume of an atom, v f is the average free volume per atom, ΔG m is the activation energy, Ω is the atomic volume, τ is the shear stress, k B is the Boltzmann constant, and T is the absolute temperature.

The evolution of free volumes is determined by two competing processes during deformation: the stress-driven creation and diffusion-dominated annihilation. Thus, the net change rate of the free volume is given by

$$ \frac{{\partial v_{\text{f}} }}{\partial t} = v^{*} f\exp \left( { - \frac{{\alpha v^{*} }}{{v_{\text{f}} }}} \right)\exp \left( { - \frac{{\Delta G^{\text{m}} }}{{k_{\text{B}} T}}} \right)\left\{ {\frac{{2\alpha k_{\text{B}} T}}{{v_{\text{f}} C_{\text{eff}} }}\left[ {\cosh \left( {\frac{\tau \varOmega }{{2k_{\text{B}} T}}} \right) - 1} \right] - \frac{1}{{n_{\text{D}} }}} \right\}, $$
(13)

where n D is the number of atomic jumps needed to annihilate a free volume equal to v*, and n D = 3 in the current calculation, and the effective elastic modulus is C eff = E/3(1 − υ). Using the small-strain and rate-dependent plasticity framework, the plastic strain is assumed to be proportional to the deviatoric stress, as generalized from Eq. [12], while the temporal change in the free volume is also coupled with the Mises stress, as generalized in Eq. [13]. This constitutive model allows us to study the interaction between individual shear bands and between the shear bands and the background stress fields.[31,32]

4 Results

4.1 Lattice-Strain Evolution in MGMCs

The compressive engineering stress–strain curve of a cylindrical MGMC specimen is shown Figure 3(a). Note that the compressive stress/strain is denoted as positive throughout this paper. Under quasi-static compressive loading, the composite exhibits a yield stress of σ y  = ~1.5 GPa, with a corresponding elastic strain limit, ε y  = 1.2 pct. After further deformation, linear work hardening prevails until the failure occurs for the MGMC specimen, with the fracture strength of σ f = ~1800 MPa and plastic strain of ɛ p y  = ~5.6 pct. It could be noted that the yielding strength of the MGMCs is much higher than that of single β-phase specimens, which is ~450 MPa in the current case.[15,22] But there is no indication of yield and subsequent plastic deformation of the second phase (β) from the macroscopic stress–strain curve in Figure 3(a).

Fig. 3
figure 3

(a) The macroscopic compressive engineering stress–strain curve shows considerable plastic deformation. (b) A representative stress–lattice-strain curve can be divided into 3 stages. This example is particularly for grains with their 〈310〉 directions parallel to the loading direction

Full size image

Figure 3(b) displays the applied stress vs the longitudinal lattice-plane-specific elastic strain (i.e., lattice strain) curves of the β-Zr crystalline phase in the MGMCs for {310} grains. Three stages of deformation can be identified. In Stage I (0 to 450 MPa, an elastic–elastic stage), the lattice strain of the β-phase crystals increases linearly with the applied stress, since both the dendritic crystalline phases and MG matrix are under elastic deformation. In Stage II (450 to 1480 MPa, an elastic–plastic stage), the β phase yields at around 450 MPa, and plastic deformation starts thereafter, which can be concluded from the deviation of lattice strains in this stage from the extrapolated straight line from Stage I. In Stage III (1480 to 1550 MPa, a plastic–plastic stage), both the crystals and MG matrix deform plastically after 1480 MPa, and the lattice strain decreases with increasing the applied stress thereafter, until the ultimate failure of MGMC specimens. We denote this lattice strain decrease in Stage III as a “turnover” phenomenon, which results from an elastic relaxation near the second phase. The microscopic mechanisms responsible for these three stages and their transitions will be investigated in detail as described in next section.

4.2 Elastic–Elastic Deformation of the β-Zr Crystalline Phase and MG Matrix (Stage I)

Figure 4 gives the measured stress–lattice-strain curves of the β phase for several grain families. In Stage I, when the applied stress is below 450 MPa, these curves are straight lines with different slopes, which are governed by the elastic constants of both the crystal and MG phases, the geometric shape of crystalline phases, and crystallographic orientations of these dendrites. In this study, the elastic constants (C11, C12, and C44) can be fitted from the comparison between the predicted and the measured slopes of stress–lattice-strain curves in Stage I. These slopes are denoted as k hklExp and k hklFEM , respectively. The elastic constants are optimized to minimize the following objective function:

$$ \varphi = \left( {k_{\text{Exp}}^{200} - k_{\text{FEM}}^{200} } \right)^{2} + \left( {k_{\text{Exp}}^{211} - k_{\text{FEM}}^{211} } \right)^{2} + \left( {k_{\text{Exp}}^{220} - k_{\text{FEM}}^{220} } \right)^{2} + \left( {k_{\text{Exp}}^{310} - k_{\text{FEM}}^{310} } \right)^{2} $$
(14)

The resulting elastic constants are C11 = 91.0, C12 = 69.5, and C44 = 31.0 GPa, while the reported elastic constants by the self-consistent model are C11 = 90.0, C12 = 68.0, and C44 = 33.0 GPa.[21,22]

Fig. 4
figure 4

Stress vs lattice-strain curves from the X-ray diffraction with the extrapolated lines from the elastic stage of each curve. Four grain families, {200}, {211}, {220}, and {310}, have been measured

Full size image

4.3 Elastic–Plastic Transition of the β-Zr Crystalline Phase (Stage II)

When the second phase deforms plastically and the MG matrix deforms elastically, the lattice strains deviate from the straight lines extrapolated from Stage I, which can be characterized by the intergranular strains (Δɛ hkl ):[25,26]

$$ \Delta \varepsilon_{hkl} = \varepsilon_{hkl}^{\text{Experiment}} - \varepsilon_{hkl}^{\text{Extrapolation}} $$
(15)

as plotted against the applied stress in Figure 5. The deviation is a result of load partitioning between “hard” and “soft” phases or grains.[26,39] When two solids are under an isostrain condition (which corresponds to the Taylor model of a polycrystal in which all grains have the same strain field as the macroscopic one), the one with a high ratio of yield stress to modulus, σ Y/E, will yield later and is the “hard” solid. Once the “soft” solid (with a low σ Y/E) yields, the load will be supported by the “hard” solid so that the corresponding elastic strain in the “hard” solid significantly increases. In other words, the “hard” solid will experience positive intergranular strains, and the “soft” one with negative intergranular strains.

Fig. 5
figure 5

Stress vs intergranular strain curves for {200}, {211}, {220}, and {310} grains in the transition from Stages I to II

Full size image

The load partitioning occurs not only between the two phases but also among the grains. As presented in Figure 5, at the transition from Stage I to Stage II, Δɛ 200 is the most positive, and Δɛ 220 is about zero, indicating that {200} grains are the “hardest,” followed by {310} and {211} grains, while {220} grains are the “softest.” The ‘‘hardest’’ {200} grains will carry more applied loads, and their further deformation will decrease the slope of the σ − ε 200 curve in Stage II, as shown in Figure 4. In order to testify these experimental results, the “hard” and “soft” crystal directions could be further demonstrated by calculations from the strength-to-stiffness ratio, r hklcry , as given by[39]

$$ r_{\text{cry}}^{hkl} = \frac{{\sigma_{Y}^{hkl} }}{{E^{hkl} }} = \frac{{\tau_{0} }}{{m^{hkl} E^{hkl} }} $$
(16)

where r hklcry and m hkl are the strength-to-stiffness ratio and Schmid factor in the 〈hkl〉 direction, respectively; and τ 0 is the critical resolved shear stress. The first grain family to yield will be the one with the lowest strength-to-stiffness ratio, which is the “softest” grain family. Three sets of slip systems for BCC materials, {110}〈111〉, {112}〈111〉, and {123}〈111〉, are considered in the current calculation. In Table I, for the {110}〈111〉 slip system, the “hardest” grain family is {200} with a r hklcry value of 2.85 × 10−3, followed by {310} grains with a r hklcry value of 1.67 × 10−3, and the {220} and {211} grain families are the “softest” with a r hklcry value of 1.17 × 10−3. For the {112}〈111〉 and {123}〈111〉 slip systems, the “hardest”-to-“softest” grain sequence is in the order: {200}, followed by {310} grains, then {220}, and finally, {211} grain families, and the r hklcry values are all listed in Table I. Therefore, {200} and {310} grain families are much “harder” than the {211} and {220} grain families for all these three slip systems. However, all the intergranular strains of {hkl} grains will become positive, when the applied stress increases to high enough (e.g., 1000 MPa), since the MG matrix has a much higher r MG value of 20.22 × 10−3 than the crystalline phases, indicating that the matrix is much “harder” than all the crystal grain families.

Table I Strength-Stiffness Ratios of a Number of {hkl} Grains in the Crystalline Phase and the Metallic-Glass (MG) Matrix, with an Initial Yield Stress of 150 MPa for the Crystalline Phase
Full size table

4.4 Elastic–Plastic Transition of the MG Matrix (Stage III)

In uniaxial compression, when the applied stress reaches ~1480 MPa, the deformation behavior of crystals enters the Stage III in Figure 3(b), in which both the MG matrix and crystal inclusions deform plastically. Then, the lattice strain in each crystalline orientation decreases with the increasing applied stress until the ultimate failure of the MGMCs specimens occurs.

Our initial ABAQUS simulations employ cubic grains of random crystal orientations and the elastic–plastic matrix to simulate the lattice-strain evolution of crystals in MGMCs. The overall trends of the lattice-strain evolution of the crystalline phase in MGMCs can be obtained in Figure 6 with both experimental and simulated results, after carefully choosing the constitutive parameters for the three families of slip systems, {110}〈111〉, {112}〈111〉, and {123}〈111〉, in the crystal-plasticity theory and for the Mises plasticity in MG matrix, which are all listed in Table II. In Figure 6, it can be observed that the simulation results have a good agreement with the experimental results in Stage I, while some discrepancy appears in Stages II and III. Although the simulation results exhibit some deviation from the experimental results in the end Stage II and Stage III, we obtain the same sequence of different grain families at various stress levels, such as 800, 1400, and 1500 MPa, i.e., red–blue–green–black ({220}–{211}–{310}–{200}) from left to right in Figure 6. The discrepancy near the end of Stage II may result from the highly idealized microstructure in simulations, as opposed to the actual dendritic structure, as well as from the hardening law that may not faithfully represent the deformation behavior in the crystalline phase.

Fig. 6
figure 6

Experimental and finite element simulation results of the lattice-strain evolution curves for {200}, {211}, {220}, and {310} grains

Full size image
Table II Parameters Used in the Finite Element Simulations with Results Matching the Lattice-Strain Evolution in the Composites, as Shown in Fig. 6
Full size table

It should also be noted that thermal residual stress might exist in the MGMCs, which is developed during rapid cooling due to the difference in thermal expansion coefficients between the MG matrix and dendrite crystals. The magnitude of thermal residual stress can be calculated using the Eshelby equivalent inclusion method.[40] The residual stress in MGMCs has been extensively reported to be in the range of 100 to 300 MPa for crystalline inclusions and less than 100 MPa in the matrix.[20,41–44] For the MGMCs in the current study, there is an initial tensile longitudinal residual stress in the β phase and a compressive stress in the MG matrix, which will slightly affect the initial yield of inclusions in MGMCs, as pointed out in Clausen et al.[22] Similar to Clausen et al.[22] who used a self-consistent model but not considered residual stress, thermal residual stress is not introduced in our FEMs, but it will be clearly an important future research line.

5 Discussion

5.1 Effects of Inclusion Shape and Dendrite Orientation on Lattice-Strain Relaxation in Stage III

The crystalline phases in the FEM capture some but not all the features of the dendritic microstructure. Therefore, it is necessary to examine the effect of geometric parameters on the predictability of the FEM results. Using a single-inclusion model, three kinds of geometric shapes (cubic, spherical, and dendritic morphologies) are employed in the inset of Figure 7. Stress–elastic strain curves of these different models under uniaxial compression are presented. The yield stresses for the inclusion and matrix are 450 and 1400 MPa, respectively. It could be observed that the slopes of stress–elastic strain curves increase at ~450 MPa, and the turnover behavior occurs at ~1400 MPa with an enlarged view in the inset of Figure 7. It should be noted that the change in slopes in Stage II are almost the same for the inner cubic and spherical models, while the elastic-strain evolution is very different for the dendritic model. This is due to the introduction of high aspect-ratio features in the dendrite, and, thus, the severe stress concentration. However, the trend of lattice-strain evolution is similar for these three different shapes. Near the end of these curves, the plastic zone in the matrix will expand as the applied stress increases, and the load partitioning by the matrix will relax the elastic strain in the inclusion that is responsible for the turnover behavior in the stress vs lattice-strain curves for the crystalline inclusions. However, we note that this analysis is based on a continuum plastic model for the matrix, while the actual deformation is by the shear bands. This issue will be further illustrated later by the free-volume model.

Fig. 7
figure 7

Stress vs ɛ elastic33 curves of the single inclusion model with cubic-, spherical-, and dendritic-inclusion shapes (inset)

Full size image

Another variable is the orientation of the dendritic inclusions with respect to the loading direction, since this trend will directly affect the resulting plastic-zone development. To reduce the simulation effort, 2D uniaxial compression simulations on the MGMCs with 45- and 90-deg-oriented dendrite inclusions were performed to investigate the influence of orientations of the dendrite inclusions on the lattice-strain evolution, respectively. It is found that in the MGMCs with a 45-deg-oriented dendrite inclusion, no relaxation occurs, as indicated by (iii) and (iv) in Figure 8(a). In contrast, slight relaxation can be observed in the model with a 90-deg-oriented dendritic inclusion, as shown in Figure 8(c). As discussed in References 45 through 47, complex stress states under loading can be beneficial in improving the plasticity of MGMCs. In the 45-deg dendritic model, the stress concentration initiates from four corners of the dendrite inclusion and propagates throughout the entire sample, as shown in the Mises stress contour in Figure 8(b). In contrast, stress concentration only starts from two horizontal dendrite vertexes, and the other two perpendicular dendrite vertexes have low stresses, as shown in Figure 8(d). Therefore, this inclusion-geometry study can provide some guidance on the design and preparation of MGMCs.

Fig. 8
figure 8

(a) Stress vs ɛ elastic22 curves for both the inclusion and matrix in the composite with the dendrite inclusion shown in (b), which shows the Mises stress contours at stress level (iv). Both the matrix and inclusion are simulated as elastic-perfectly plastic solids, with Young’s modulus, Poisson’s ratio, and yield stress being 89 GPa, 0.37, and 1.4 GPa for the matrix, and 60 GPa, 0.37, and 0.45 GPa for the inclusion. (c) Everything else being the same as (a), the rotation of the dendritic crystalline phase by 45 deg leads to a dramatic change of the lattice-strain evolution when the matrix yields (i.e., at the very end of the stress–ɛ elastic22 curves). (d) The Mises stress contours of model in (c) at stress level (iv)

Full size image

5.2 Effects of Localized Deformation in Metallic Glass on Lattice-Strain Evolution

The studies above successfully predict the lattice-strain evolution of crystalline phases in MGMCs. However, the role played by the localized deformation in shear bands in the MG matrix remains unclear. Thus, the free-volume-based constitutive model for the MG matrix is employed to investigate the shear-band initiation and propagation in the MGMC upon uniaxial compression. The material parameters for the MG matrix are v f/αv* = 0.05, EΩ/2k B T = 200, v = 0.37, n D = 3, α = 0.15, and v*/Ω = 1, and the normalized applied strain rate is 10−3 s−1. In simulations shown in Figure 9, the inclusions are assumed to be an elastic-perfectly plastic body, with the Young’s modulus, Poisson’s ratio, and yield stress being 60 GPa, 0.37 and 0.45 GPa, respectively. For comparison, two types of MGMCs with different inclusion shapes—dendritic and circular morphologies—are employed for calculations.

Fig. 9
figure 9

Stress vs ɛ elastic22 curves for both the inclusion and matrix in the composite with multiple circular (a) and dendritic (c) inclusions, respectively. The Mises stress contours are shown at stress level (iv) for circular (b) and dendritic (d) model, respectively. The matrix is described by the free-volume constitutive model, with the Young’s modulus and Poisson’s ratio being 200 GPa and 0.37, respectively. Other parameters can be found in the text. The inclusion phase is an elastic-perfectly plastic solid with the Young’s modulus, Poisson’s ratio, and yield stress being 60 GPa, 0.37, and 0.45 GPa, respectively. All figures are given in a deformed mesh with a displacement magnification ratio of 1, and the state-dependent variable 1 (SDV1) specifies the free volume

Full size image

Figure 9(a) describes the lattice-strain evolution for both the MG matrix and crystalline inclusion in the circular-inclusion model under compressive loading. Here, the lattice strain is in fact the elastic strain in the loading direction, and the applied stress is the one on the entire specimen. The ultimate lattice strain in the crystalline inclusion is obtained by averaging the values of all inclusion grains. As observed in Figure 9(a), with increasing the applied stress, the lattice strain in both the matrix and inclusion rises linearly at the beginning till a deviation occurs at a stress of ~0.8 GPa. Afterward, the lattice strain of the MG matrix still increases linearly, while that of inclusions increases at a much lower rate. This trend is due to the load partitioning following the yielding of the crystalline inclusion. When the applied stress reaches ~ 1.7 GPa, the difference of stress/lattice-strain slopes between the MG matrix and inclusion becomes more significant. With the further increase in the applied stress, the lattice strain of the matrix increases significantly, while that of the inclusions begins to decrease, i.e., turnover phenomenon happens. To obtain insights into the mechanism responsible for the stress/lattice-strain slope change in the matrix and inclusion, particularly on the turnover behavior, the free-volume contours at stress level (iv) are plotted in Figure 9(b). Note that SDV1 in Figure 9(b) denotes the first solution-dependent state variable (SDV), which is employed to represent the free volume in the UMAT code.[29] At the stress level (i), although inclusions have already yielded at a nominal yield stress of 0.45 GPa, and the free volume in the matrix starts to localize around the matrix/second phase interface, no stress/lattice-strain slope change occurs. This trend indicates that the load partitioning in the MGMCs does not happen immediately following the yielding of inclusions. When the load is increased to 1.2 or 1.7 GPa, localized deformation begins to form in shear bands, typically as demonstrated in stress levels, (ii) and (iii). At these two stages, more loads will be transferred to the matrix, resulting in much increased lattice strains, while the lattice strain in the crystalline inclusion tends to evolve slowly. In Figure 9(b), the shear bands can be observed to initiate at an angle of ~45 deg from the matrix/inclusion interface and propagate outward. Ultimately, when the localized shear bands propagate and link with each other, the lattice-strain relaxation in the inclusions become more significant, and the turnover behavior will emerge at the stress level (iv).

The study on the dendritic-inclusion-embedded MGMCs with the free-volume model is presented in Figures 9(c) and (d), which exhibit similar trends with the circular-inclusion model. The only difference is that the shear bands preferentially initiate from vertexes of the dendritic inclusions in Figure 9(d). This trend demonstrates that the geometry of the inclusions does not exert significant influence on the lattice-strain evolution. Note that in these simulations, MGMCs contain roughly 20 pct (volume percent) of crystalline inclusions. However, in the real specimens, the volume percentage of crystals is ~50 pct. The only difference between the high-volume and low-volume percentage cases is that the chance of forming a dominant shear band by connecting many minor ones is much lower for the high-volume percentage case, due to the enhanced blocking effect of second phases. Clearly, the success of the MGMCs in the ductility enhancement needs to reach the percolation limit, below which the plasticity of MGMC specimens cannot be enhanced significantly.

6 Conclusions

In summary, microscopic deformation mechanisms in the in situ MGMCs have been examined using synchrotron X-ray scattering and FEM under compressive loading in the current study. In a uniaxial compression, the σ − ε hkl curves of the crystalline inclusions could be divided into three stages. In Stage I, both the inclusion and matrix are elastic, before the crystalline inclusions yield at an applied stress of ~450 MPa. In Stage II, crystals undergo plastic deformation, while the amorphous matrix remains elastic until ~1480 MPa. In Stage III, beyond 1480 MPa, both the crystal and matrix yield and are subjected to the plastic deformation until the ultimate failure of specimens occurs. After the β phase yields, the stress concentrations appear in the MG matrix, resulting in the yielding behavior of the matrix at an applied stress slightly lower than its macroscopic yield stress. Different crystal geometries, including cubes/spheres/dendrites, are used to examine the inclusion-shape effects on the elastic strain evolution of the inclusions. Both the elastic-perfectly plastic model and the free-volume-based model are used for the MG matrix, which successfully explain the relaxation of elastic strains in the second phase and also the effects of geometric shape and dendrite orientations. Moreover, the current study can provide some guidelines in the design and preparation of MGMCs. For example, the 45-deg dendritic inclusions should work better in improving the ductility of MGMCs, compared with the 90-deg case, because more stress concentration is introduced into the MGMC specimens upon loading for the 45-deg case. The percentage of crystalline inclusions should be above the percolation limit so as to block and deflect the shear-band propagation to form a major shear band, which can lead to the catastrophic failure of MGMC specimens.