1 Introduction

The inhomogeneous deformation behavior of bulk metallic glasses (BMGs) corresponds to strain localization into narrow shear bands, and these shear bands, if unconstrained, may catastrophically propagate throughout the specimen.[1–4] It has been widely demonstrated that if the shear bands can be blocked by external or internal constraints, the plastic strain on each shear band is minimized and therefore additional shear bands have to be initiated to accommodate the applied strain fields, thus delaying the catastrophic failure and leading to enhanced ductility.[5–9] Consequently, the understanding of shear band patterns will help design these constraints to confine shear bands and to prevent brittle failure of BMGs.

It has been found that shear bands in BMGs deviate, although slightly, from the principal shear stress directions. In uniaxial tension and compression tests of BMGs, the angle between shear band plane and loading direction falls in the range of 50 to 60 deg for tension tests and 40 to 45 deg for compression test.[10–16] Such deviation was explained using the Mohr–Coulomb yield criterion.[10–15] As pointed out by Zhao and Li,[17,18] the Mohr–Coulomb model, however, gives the same amount of deviation in both tension and compression conditions, and therefore is unable to predict the observed asymmetric deviation of shear band angles from 45 deg in tension and compression tests. In our recent work,[19] shear bands in metallic glasses are modeled as a result of material instability (which can be predicted from constitutive parameters and loading conditions), which does not corresponds to material yield condition. Using the classic Rudnicki–Rice model,[20] we found that the shear band directions depend on Poisson’s ratio ν, the ratios of three deviatoric principal stresses to Mises stress, the coefficient of internal friction μ, and the dilatancy factor β. As shown in Figure 1, the shear band makes an angle θ 0 to the largest principal stress σ I with

Fig. 1
figure 1

Schematic illustration of the shear band direction in the principal stress space with principal stresses \( \sigma_{\text{I}} \ge \sigma_{\text{II}} \ge \sigma_{\text{III}} \)

Full size image
$$ \theta_{0} = \pm \tan^{ - 1} \sqrt {\frac{{\xi - N_{\min } }}{{N_{\max } - \xi }}} $$
(1)

where \( \xi = \frac{1}{3}\left( {1 + \nu } \right)\left( {\beta + \mu } \right) - N\left( {1 - \nu } \right), \, N_{\max } = {{\sigma_{I}^{\prime } } \mathord{\left/ {\vphantom {{\sigma_{I}^{\prime } } {\bar{\tau }}}} \right. \kern-\nulldelimiterspace} {\bar{\tau }}}, \, N = {{\sigma_{\text{II}}^{\prime } } \mathord{\left/ {\vphantom {{\sigma_{\text{II}}^{\prime } } {\bar{\tau }}}} \right. \kern-\nulldelimiterspace} {\bar{\tau }}}, \, N_{\min } = {{\sigma_{\text{III}}^{\prime } } \mathord{\left/ {\vphantom {{\sigma_{\text{III}}^{\prime } } {\bar{\tau }}}} \right. \kern-\nulldelimiterspace} {\bar{\tau }}}, \, \bar{\tau } = {{\sigma_{mises} } \mathord{\left/ {\vphantom {{\sigma_{mises} } {\sqrt 3 }}} \right. \kern-\nulldelimiterspace} {\sqrt 3 }}, \) and \( \sigma_{I}^{\prime } \), \( \sigma_{\text{II}}^{\prime } \), and \( \sigma_{\text{III}}^{\prime } \) are the principal deviatoric stresses. On \( \left( {\sigma_{\text{I}} ,\sigma_{\text{II}} } \right) \) and \( \left( {\sigma_{\text{II}} ,\sigma_{\text{III}} } \right) \) planes, there will be only one kind of shear band, which is parallel to the \( \sigma_{II} \) direction. Throughout this article, we denote the shear band pattern in the \( \left( {\sigma_{I} ,\sigma_{\text{III}} } \right) \) plane as case I and that in plane \( \left( {\sigma_{I} ,\sigma_{II} } \right) \) and plane \( \left( {\sigma_{\text{II}} ,\sigma_{\text{III}} } \right) \) as case II. It is clear from Eq. [1] that the shear band does not follow the principal shear stress direction, which is 45 deg to the maximum principal stress.

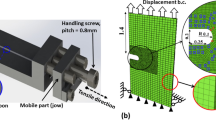
Indentation tests have been widely used to investigate the elastic/plastic behavior of metallic glasses, due to the highly localized plastic deformation near indenter tips. In order to visualize shear band patterns, various kinds of indentation tests were performed by using the “bonded interface” technique in Vickers indentation[21–25] and spherical indentation.[19,26–31] In this technique, two samples are bonded and the subsequent indentation is made into the center of and parallel to the bonded interface. Since the stress fields will be significantly affected by this interface, we need to understand whether the observed shear bands using the bonded-interface technique represent the actual ones when the interface constraint is absent. Consequently, this article is concerned with the shear band patterns under indentation with the presence of two types of internal constraints: (1) the bonded cross-sectional interface and (2) the film/substrate interface, as shown in Figure 2. Our previous work is limited to analytical solutions of Hertzian spherical and cylindrical contacts.[19] In this article, we extend the Rudnicki–Rice instability analysis by performing detailed finite element models (FEMs), so that the calculated stress fields in bonded plates under indentation tests can be used to predict the shear band directions, since no analytical stress solutions are available under these conditions.

Fig. 2
figure 2

Finite element simulations for (a) Vickers indentation and (b) spherical indentation. A half substrate is adopted because of symmetry. (c) Schematic illustration of microindentation test on the bonded-interface (shaded area) metallic glass films on a steel substrate

Full size image

It should be noted that the model in Eq. [1] does not predict when and where the strain localization occurs; it only gives the direction of the shear band if it is initiated. Therefore, with the elastic stress fields calculated from the FEM, the principal stresses are determined and Eq. [1] and Figure 1 are used to determine the orientation of the possible shear band. The plotted shear bands in this article are contours generated from predefined seeding points. In our modeling work, we simulate Vickers indentation on BMGs with and without the bonded interface in Section II, and spherical indentation on metallic glass plates with and without the bonded interface, or with and without the film/substrate interface in Section III. Experimentally, we performed spherical indentation on Zr-based metallic glass plates on stainless steel substrate in order to study the effect of the film/substrate interface on shear band directions.

Another concern is that the actual stress field differs from the elastic or continuum plasticity simulations because of the strain localization associated with shear bands. To be exact, the elastic stress field can be used to predict the directions of first shear bands, while the elastic-plastic stress fields can only be trusted outside the plastic zone when a large number of shear bands are contained in the plastic zone. An explicit history of shear band nucleation and propagation is required to validate the preceding predictions. An implicit finite element method was previously developed for the free-volume-based constitutive model.[32,33] Simulations performed using this methodology will be presented and compared to the continuum plasticity predictions in Section IV.

2 Vickers Indentation

The finite element setup is schematically shown in Figure 2(a) using the commercial software package, ABAQUS. The geometric symmetry associated with the rigid Vickers indenter allows us to use half of the deformable substrate with 37,887 C3D4 elements. The bottom and side surfaces of the substrate are clamped. In the case of a full substrate, the boundary condition for the cross-sectional surface is the displacement symmetric condition about the z-axis. If the substrate is made by bonding two specimens (as in Figure 2(c)), the boundary condition for the cross-sectional surface is traction free. Two frictionless contact pairs are defined between the indenter and the specimen and between the film and substrate in Figure 2(c). As discussed in Section I, the BMG specimen is modeled as an elastic or elastic-perfectly plastic solid with the Young’s modulus, Poisson’s ratio, and yield strength being 80 GPa, 0.36 GPa, and 1.8 GPa, respectively. In the case of a BMG film on the steel platen, these parameters for steel are 210, 0.33, and 0.46 GPa, respectively. The choice of β and μ will be discussed later. The stress fields are analyzed on deformed mesh at the maximum indentation load.

2.1 Vickers Indentation on a BMG Substrate Without Any Internal Constraints

Because of the traction-free condition, the top surface in the substrate outside the contact area is in a plane stress condition, and the stress normal to the top surface, which vanishes (being zero), is one of the three principal stresses. For elastic contact, the two in-plane principal stresses, σ max,i , σ min,i , are found to be σ max,i  > σ min,i  > 0 in the plotted region in Figure 3(a). According to Figure 1, the shear band direction should follow the second largest principal stress (case II), being σ min,i in the elastic contact simulations. For elastic-plastic contact, the plastic deformation of the sample underneath the contact leads to the development of compressive stresses on the top surface. We found that 0 > σ max,i  > σ min,i on the plotted region in Figure 3(b) and shear bands should follow the direction of σ max,i (case II). In both elastic and elastic-plastic contacts, the shear bands on the top surface and outside the contact area exhibit circular shape, as shown in Figure 3. These curves are actually trajectories predicted from Eq. [1], which start from the seeding points (small dots in Figure 3). As explained in Section I, our model does not predict where the shear band is initiated and how far a shear band extends.

Fig. 3
figure 3

Shear band patterns on the top surface of the metallic glass substrate (without interface constraints) under Vickers indentation: (a) elastic contact and (b) elastic-plastic contact

Full size image

Because of symmetry, the shear stress components, σ xz and σ yz , on the cross-sectional plane (z = 0) vanish, and thus, σ zz on this plane is a principal stress. For both elastic and elastic-plastic contacts, the finite element simulations show that the two in-plane principal stresses, σ max,i and σ min,i , underneath the contact center obey the following relationship: 0 > σ max,i  > σ zz > σ min,i . According to Figure 1, the shear band directions should be at θ 0 off the maximum in-plane principal stress and form the radial shear bands, as shown in Figures 4(a) and (b) for elastic and elastic-plastic contacts, respectively. The red solid curves show the direction of the principal shear stress that is 45 deg to the in-plane principal stresses. The black dashed curves and blue dashed curves show the predictions using β + μ = 0.1 and β + μ = 0.5, respectively. The sum of the internal friction coefficient, μ, and dilatancy factor, β, has strong effects on the radial shear band directions, especially for large β + μ. The black dashed curves almost collapse onto the red ones, showing that the principal shear stress direction seemingly works for BMG material with β + μ = 0.1 and ν = 0.36. This is, however, merely a coincidence. Other combinations of β + μ and ν lead to deviation from the principal shear stress.

Fig. 4
figure 4

Shear band patterns on the cross-sectional interface of the metallic glass substrate (without interface constraints) under Vickers indentation: (a) elastic contact and (b) elastic-plastic contact

Full size image

Following our previous work,[19] we choose the value of β + μ in the range from 0 to 0.5, as justified in the following. First, the measurement of the pressure sensitivity coefficient μ in the literature is mostly based on the shear band angle analysis in the Mohr–Coulomb framework (which, however, is unable to predict the observed asymmetric deviation of shear band angles from 45 deg in tension and compression) or on the indentation hardness response[14,30,31] (which again assumes the Mohr–Coulomb model with associative flow). Nevertheless, the measured values of μ from these methods are typically around 0.05 to 0.25. Second, these methods are unable to give any information on the dilatancy factor β; instead, associative flow (so that β = μ) is often assumed. Third, the Rudnicki–Rice model in Eq. [1] predicts the dependence of the shear band angle on β + μ, and experimental comparisons suggest a range of 0 to 0.5.[19] Consequently, two representative values of β + μ, i.e., 0.1 and 0.5, are used in this work.

2.2 Vickers Indentation on the Bonded-Interface BMG Substrate

As shown in Figure 5, the bonded interface (z = 0) is represented by a slit, and the resulting stress relaxation will change the stress fields in the BMG specimen. For elastic contact, immediately outside the contact area, the minimum in-plane principal stress is very close to zero. We note that σ yy  = 0 outside the contact on the surface. Following case I in Figure 1, we will obtain radial-like shear bands, as shown in Figure 5, for β + μ = 0.1. Moving away from the contact area, the minimum in-plane principal stress is noticeably larger than zero, i.e., σ max,i  > σ min,i  > 0, so that circular shear bands will be initiated (case II in Figure 1). Experimental observations[21–25] found the co-existence of both circular and radial shear bands, as well as sometimes only one family of radial shear bands. The latter may be caused by the fact that the indentation is not perfectly symmetric, or the material is not uniformly fabricated, so pre-existing casting defects might prefer a certain orientation.

Fig. 5
figure 5

Shear band patterns on the top surface of the bonded-interface metallic glass substrate under elastic Vickers indentation

Full size image

The bonded interface at z = 0 is also in a plane stress condition, since the normal stress component is released. Semicircular shear bands are plotted, as in Figures 6(b) and (d), for both elastic contact and elastic-plastic contact because 0 > σ max,i  > σ min,i . The semi-sphere shear bands were plotted only on the right half of the bonded surface. Due to geometric symmetry, the left half should be a mirror reflection of the right half. In reality, the coexistence of radial and semicircular shear bands was demonstrated. Our simulations in this subsection assume that no tensile stress can be developed in the bonded interface, while in the experiments, the interface gradually delaminates with the increase of the indentation load (which is similar to a wedging-crack test). Consequently, radial shear bands can form in the early stage (when the interface is still bonded), as discussed in Section II–A, and may still remain when the semicircular shear bands are initiated in a later stage for the debonded interface. For comparison purposes, using the two in-plane principal stresses in the (x,y) plane at z = 0, the radial shear bands are plotted on the bonded interface for both elastic contact and elastic-plastic contact in Figures 6(a) and (c), respectively. The intersection angle in the family of red curves is 90 deg, and the angle for β + μ = 0.5 is about 72 deg. Thus, the radial shear bands that are formed in the early stage may remain and propagate in directions that are very similar to the predictions in Figure 4, indicating that the stress relaxation has little effect in the orientations of these radial shear bands.

Fig. 6
figure 6

Shear band patterns on the cross-sectional interface of the bonded-interface metallic glass substrate under Vickers indentation: (a) elastic contact and radial shear bands, (b) elastic contact and semicircular shear bands, (c) elastic-plastic contact and radial shear bands, and (d) elastic-plastic contact and semicircular shear bands

Full size image

2.3 Vickers Indentation on Bonded-Interface BMG Films on a Steel Substrate

With the presence of two types of internal constraints, i.e., bonded interface at z = 0 and film/substrate interface at y = −d, with d being the film thickness, the radial and semicircular shear bands in Figure 6 will be modified. As shown in Figure 7, the film/substrate interface does not noticeably change the interaction angle between radial shear bands (72 to 90 deg), but blocks the radial shear bands from extending through the entire BMG specimen. As discussed previously, the radial shear bands can propagate in either positive θ 0 or negative θ 0 directions. When a radial shear band propagates along one θ 0 direction and is blocked by the interface, the only way for it to continue propagation is to reflect back into the film but in the other θ 0 direction. The semicircular shear bands under the contacted center region are similar to Figure 6, but those away from the center are no more continuous when they reach the film/substrate interface.

Fig. 7
figure 7

Shear band patterns on the cross-sectional interface of the bonded-interface metallic-glass film on a steel substrate under Vickers indentation: (a) elastic contact and radial shear bands, (b) elastic contact and semicircular shear bands, (c) elastic-plastic contact and radial shear bands, and (d) elastic-plastic contact and semicircular shear bands

Full size image

3 Spherical Indentation

3.1 Spherical on a BMG Substrate Without Any Internal Constraints

For spherical indentation on a BMG specimen without any internal constraints, the top surface outside the contact area is in a plane stress condition. Both radial shear band and semicircular shear band directions were plotted on the top surface, as in Figure 8(a) for elastic contact and Figure 8(b) for elastic-plastic contact. The red solid curves representing semicircular shear bands are plotted for σ max,i  > σ min,i  > 0 in the elastic contact and for 0 > σ max,i  > σ min,i in the plastic case, respectively. Under spherical indentation, the stress state is spherical symmetric, leading to near perfect circular shape shear bands on the top surface in both cases, in contrast to the Vickers indentation case. Experimental results of semicircular shear bands under Vickers indentation[25] and spherical indentation[29–31] show the same trend. The blue dashed curves, which represent the radial shear bands, are plotted for σ max,i > 0 > σ min,i and β + μ = 0.1. Such a stress state exists right outside the contact area in the elastic case and far from the contact area in the elastic-plastic case. Unlike Vickers indentation with bonded interface constraints, the radial shear bands intersect with different angles on the top surface under spherical indentation. The calculated intersection angle ranges from 70 to 82 deg in the case of elastic contact and 80 to 90 deg for elastic-plastic contact. Therefore, these ranges recover the experimental results in Reference 27 (77.7 to 81.3 deg) and Reference 28 (78 to 88 deg).

Fig. 8
figure 8

Shear band patterns on the top surface of the metallic glass substrate (without interface constraints) under spherical indentation: (a) elastic contact and (b) elastic-plastic contact. Refer to the text for the discussion on the boundaries between the radial and circular shear bands

Full size image

As shown in Figure 9, the shear band patterns on the cross-sectional interface in spherical indentation are similar to the results in Vickers indentation. For the deviation of radial shear bands from the principal in-plane shear stress, we find that the black dashed curves (β + μ = 0.1) almost overlap with the red ones.

Fig. 9
figure 9

Shear band patterns on the cross-sectional interface of the metallic glass substrate (without interface constraints) under spherical indentation: (a) elastic contact with contact radius to indenter radius ratio of \( {a \mathord{\left/ {\vphantom {a R}} \right. \kern-\nulldelimiterspace} R} \) = 0.26 and (b) elastic-plastic contact with \( {a \mathord{\left/ {\vphantom {a R}} \right. \kern-\nulldelimiterspace} R} \) = 0.28

Full size image

3.2 Spherical Indentation on the Bonded-Interface BMG Substrate

The findings in this subsection are similar to those in Section II–B with some noticeable differences. On the top surface outside the contact area, both radial and semicircular shear bands are plotted in Figure 10(a) for elastic contact and Figure 10(b) for elastic-plastic contact. The bonded interface reduces the axisymmetry of the stress field to a twofold symmetry. In addition, the stress relaxation at the bonded interface changes the degrees of sink-in or pileup near the contact edge, and the stress state is also affected as indicated by the highly curved radial shear bands in Figure 10(a) and the semicircular shear bands near z = 0 that become nearly parallel to the z-axis in Figure 10(b). The difference between Figures 8(b) and 10(b) is due to the presence of the stress relaxation at the bonded interface. Shear band patterns on the bonded interface are given in Figure 11, which are almost identical to those in Figure 6 for Vickers indentation. This can be explained by the St. Venant principle, which states that the stress fields at a distance of about the contact size away from the contact center are insensitive to the indenter shape or to the exact pressure distribution in the contact area.

Fig. 10
figure 10

Shear band patterns on the top surface of the bonded-interface metallic glass substrate under spherical indentation: (a) elastic contact with \( {a \mathord{\left/ {\vphantom {a R}} \right. \kern-\nulldelimiterspace} R} \) = 0.26 and (b) elastic-plastic contact with \( {a \mathord{\left/ {\vphantom {a R}} \right. \kern-\nulldelimiterspace} R} \) = 0.28. Refer to the text for the discussion on the boundaries between the radial and circular shear bands

Full size image
Fig. 11
figure 11

Shear band patterns on the cross-sectional interface of the bonded-interface metallic glass substrate under spherical indentation: (a) and (b) elastic contact with \( {a \mathord{\left/ {\vphantom {a R}} \right. \kern-\nulldelimiterspace} R} \) = 0.26 and (c) and (d) elastic-plastic contact with \( {a \mathord{\left/ {\vphantom {a R}} \right. \kern-\nulldelimiterspace} R} \) = 0.28

Full size image

3.3 Spherical Indentation on Bonded-Interface BMG Films on a Steel Substrate

Similar to the Vickers indentation results in Figure 7, shear band patterns in bonded-interface BMG films on a steel substrate under spherical indentation will be affected by the film/substrate interface. Next, we first illustrate our experimental observations. A (Zr55Cu30Al10Ni5)Y1 metallic glass was prepared by arc melting the constituent elements in a purified argon atmosphere. To obtain homogeneity, the alloy ingots were melted for several times before casting into a water-cooled copper mold using a suction casting facility. The resulting cylindrical BMG rods have a dimension of 6 mm in diameter and 60 mm in length. The amorphous structure of metallic glass was examined by X-ray diffraction using a Philips X’pert X-ray diffractometer (Amsterdam, The Netherlands). Rectangular plates with the thickness of around 0.5 mm were cut from the ingot. Two specimens were ground with 1200 grit sand papers, followed by mechanical polishing with a 1-μm diamond paste. Then, the two surfaces were bonded together with super glue under a tight clamping force. The bonded metallic glass plates were mounted on a steel substrate and were polished to a mirror finish with the thickness of around 0.34 mm, as shown in Figure 2(c). The United Tru-BlueTM Rockwell Hardness Testing System (United Calibration Corporation, Huntington Beach, CA) with a 1/16-in. steel ball indenter was used for the indentation study with a 100-kg load. After the indentation test, the bonded plates were separated by dissolving the super glue in the acetone. The scanning electron microscope images in Figure 12 reveal the shear band arrangements on the boned interface.

Fig. 12
figure 12

Scanning electron microscope images of shear band patterns on the bonded interface with \( {a \mathord{\left/ {\vphantom {a R}} \right. \kern-\nulldelimiterspace} R} \) = 0.27. In (a) and (b), the interface is largely debonded except for the regime near the steel platen. Radial shear bands “reflect” from the film/substrate interface. In another test shown in (c) and (d), the interface is completely debonded during the test. The observed semicircular shear bands change directions near the film/substrate interface

Full size image

When the two BMG plates are still partially bonded, as shown in Figures 12(a) and (b), radial shear bands can be observed and they are reflected at the film/substrate interface. Predictions in Figures 13(a) and (c) indicate that the reflected angle is θ 0 to the second largest principal stress, yet with an opposite sign of the incident angle. The red solid curves indicate the radial shear band directions with no deviation from the principal shear stress. The black and blue dash curves indicate the radial shear band directions with β + μ = 0.1 and β + μ = 0.5, respectively. For the completely debonded case in Figures 12(c) and (d) (which is a different test from Figures 12(a) and (b)), the semicircular shear bands are observed and they change directions near the film/substrate interface. Predictions in Figures 13(b) and (d) agree qualitatively with these observations.

Fig. 13
figure 13

Shear band patterns on the cross-sectional interface of the bonded-interface metallic glass film on a steel substrate under spherical indentation: (a) elastic contact and radial shear bands, (b) elastic contact and semicircular shear bands, (c) elastic-plastic contact and radial shear bands, and (d) elastic-plastic contact and semicircular shear bands

Full size image

4 Shear Band Patterns from the Free Volume Model

As discussed in Section I, the stress fields calculated by using the continuum plasticity model do not consider the strain localization. To validate the predictions in Sections II and III, here, we present our finite element simulations based on the free volume model and the explicit history of shear band nucleation and propagation under indentation. Following the classic Spaepen model,[32] the stress-driven increase in the free volume reduces the viscosity and thus leads to strain softening behavior. In the pure shear case, the plastic strain rate is represented by the flow equation.:

$$ \frac{{\partial \gamma^{p} }}{\partial t} = 2f\exp \left( { - \frac{{\alpha v^{ * } }}{{v_{f} }}} \right)\exp \left( { - \frac{{\Updelta G^{m} }}{{k_{B} T}}} \right)\sinh \left( {\frac{\tau \Upomega }{{2k_{B} T}}} \right) $$
(2)

where f is the frequency of atomic vibration, α is a geometric factor of order 1, v* is the hard-sphere volume of an atom, v f is the average free volume per atom, ΔG m is the activation energy, Ω is the atomic volume, τ is the applied shear stress, kB is the Boltzmann constant, and T is the absolute temperature. The evolution of the free volume is determined by two competing processes: stress-driven creation process and diffusion-dominated annihilation process. The net rate of the free volume change is

$$ \frac{{\partial v_{f} }}{\partial t} = v^{*} f\exp \left( { - \frac{{\alpha v^{*} }}{{v_{f} }}} \right)\exp \left( { - \frac{{\Updelta G^{m} }}{{{\text{k}}_{\text{B}} T}}} \right)\left\{ {\frac{{2\alpha {\text{k}}_{\text{B}} T}}{{v_{f} C_{\text{eff}} }}\left( {\cosh \left( {\frac{\tau \Upomega }{{2{\text{k}}_{\text{B}} T}}} \right) - 1} \right) - \frac{1}{{n_{D} }}} \right\} $$
(3)

where n D is the number of atomic jumps needed to annihilate a free volume equal to v* and is usually taken to be 3 to 10, and the effective elastic modulus is \( C_{\text{eff}} = {E \mathord{\left/ {\vphantom {E {3\left( {1 - \nu } \right)}}} \right. \kern-\nulldelimiterspace} {3\left( {1 - \nu } \right)}} \). Using the small-strain and rate-dependent plasticity framework, the plastic strain is assumed to be proportional to the deviatoric stress, as generalized from Eq. [2], while the temporal change in the free volume is also coupled with the Mises stress, as in Eq. [3]. Nonlinear equations from the incremental finite element formulation are solved by the Newton–Raphson method, in which the corresponding material tangent is obtained by simultaneously and implicitly integrating the plastic flow equation and the evolution equation of the free-volume field. This model was implemented into ABAQUS using the user define material subroutine.[33] This micromechanical model allows us to study the interaction between individual shear bands and between the shear bands and the background stress fields.

Because of symmetry, a quarter of the substrate was constructed for 3D indentation simulation using 37,490 C3D8 elements in ABAQUS, and the region underneath the indenter was finely meshed for accurate calculation consideration. The spherical indenter was modeled as a rigid body with a radius of R, and the contact between the indenter and the substrate was frictionless. Symmetric boundary conditions were assigned to two lateral faces (normal to positive X and positive Z), and the bottom was completely pinned. Specifically, the initial free volume is given by \( {{v_{f} } \mathord{\left/ {\vphantom {{v_{f} } {\alpha v^{*} }}} \right. \kern-\nulldelimiterspace} {\alpha v^{*} }} = 0.05 \), and other constitutive parameters are \( {{E\Upomega } \mathord{\left/ {\vphantom {{E\Upomega } {2{\text{k}}_{\text{B}} T}}} \right. \kern-\nulldelimiterspace} {2{\text{k}}_{\text{B}} T}} = 240 \), ν = 0.333, n D  = 3, α = 0.15, and \( {{v^{*} } \mathord{\left/ {\vphantom {{v^{*} } \Upomega }} \right. \kern-\nulldelimiterspace} \Upomega } \) = 1. The normalized loading rate is \( \frac{{\dot{h}}}{Rf}\exp ( {\frac{{\Updelta G^{m} }}{{{\text{k}}_{\text{B}} T}}} ) = 3.0 \times 10^{ - 7} \). When \( {a \mathord{\left/ {\vphantom {a R}} \right. \kern-\nulldelimiterspace} R} \approx 0.14 \), the first shear band has initiated and extended to a distance of about 0.5a. Two interesting observations can be obtained from the cut-and-view plots in Figure 14. First, the first shear band is actually a conical shear surface, which resembles a radial shear band from the side view. This is essentially consistent with the predicted shear band directions in Figure 9. The minor difference is that the former looks like an inverse conical shear surface, while the latter is more like hour-glass shapes since predictions in the latter are based on predefined seed points. We also note that such a perfect axisymmetry as a cone may not be attained in reality because of sample defects or loading misalignment. Second, how far a shear band extends depends on the material constitutive parameters and, most importantly, the strain and strain rate fields. Indentation-induced stress fields decay rapidly, so the observed shear bands rarely extend far beyond about twice the contact size.

Fig. 14
figure 14

To clearly visualize the three-dimensional conical shear band, free volume contours (SDV1 = \( {{v_{f} } \mathord{\left/ {\vphantom {{v_{f} } {\alpha v^{*} }}} \right. \kern-\nulldelimiterspace} {\alpha v^{*} }} \)) were plotted (a) on a vertical plane that makes an angle of 60 deg from the backside surface and (b) on a horizontal plane at a distance of 0.07R below the top surface. Finite element simulations were performed in a quarter of the substrate under spherical indentation with symmetry boundary conditions prescribed on the two side surfaces. These plots are given in deformed mesh with displacement magnification ratios being 10, 2, and 10 in X, Y, and Z directions, respectively. Refer to Fig. 2 for the coordinate system

Full size image

The bonded-interface case can be simulated by prescribing traction-free boundary conditions on one side surface, as shown in Figure 15. Different from the conical shear surface, a spadelike shear band is initiated inside the specimen but away from the contact axis and then extends to the center of the contact area. As stated in Section III–B, this is the result of stress relaxation at the bonded surface. In other words, stress relaxation leads to shear band deviating from a regular conical configuration. Subsequent loading leads to the second shear band initiated on the traction-free surface, as shown in Figure 15(c), which corresponds to a shear band on the bonded surface but deeper underneath the indenter in Figure 11. Note the change of view direction in Figure 15(c). Further simulations were not performed since the shear band simulation suffers mesh sensitivity problems; i.e., shear band width is set by the mesh resolution, and a fine mesh calculation is not readily feasible. The mesh sensitivity problem can be resolved by introducing a length scale in the constitutive law.[34,35] Nevertheless, these simulations clearly demonstrate that the interface relaxation has a critical effect on the shear band formation, and after the first shear band (which is hidden in the sample), semicircular shear bands are initiated on the bonded interface. These results confirm the validity of predictions in Sections II–B and III–B.

Fig. 15
figure 15

(a) When the traction free boundary condition is prescribed on one side surface, the first shear band becomes spadelike with the initiation site marked by “X.” (b) A horizontal cut at a distance of 0.03R below the top surface. These two plots are given in deformed mesh with displacement magnification ratios being 10, 2, and 2 in the X, Y, and Z directions, respectively. (c) A slight increase of the indentation load leads to the second shear band, which is initiated on the free surface, as shown by the free volume contours in undeformed mesh

Full size image

5 Conclusions

The initiation of shear bands in metallic glasses corresponds to the loss of stability in the constitutive model, and the classic Rudnicki–Rice theory gives the shear band direction as a function of the constitutive parameters and the applied stress state. It is incorrect to relate the shear band direction to the principal shear stress. We apply these results to the indentation tests on BMG materials without or with the presence of two types of internal constraints: (1) bonded interface and (2) film/substrate interface, as schematically shown in Figure 2. In the early stage of the indentation, before the bonded interface delaminates, two families of radial shear bands will form, as predicted by Eq. [1] and Figure 1. The indentation force will eventually wedge the bonded interface apart, so that semicircular shear bands will form, and they follow one of the in-plane principal stresses. The radial shear bands that were initiated in the early stage will remain, and their extension directions will be close to the two in-plane principal shear stresses. On the top surface, a mixture of radial and semicircular shear bands may be observed, because the stress state varies when moving away from the contact edge (i.e., Figures 5, 8, and 10). The film/substrate interface will block shear bands. Radial shear bands will get reflected, while semicircular shear bands will change their directions and end at the interface. These predictions agree well with our experimental observations on Zr-based metallic glass films on a steel platen under spherical microindentation.

We note that the stress field obtained from continuum plasticity simulation may differ from the actual one because of the strain localizations associated with shear bands. A finite element simulation based on the free volume model is conducted, and the resulting shear band nucleation and propagation confirm the validity of our predicted shear band patterns. Although not investigated here, one can tune the elastic and plastic mismatch between the BMG phase and the other phase (e.g., a weak glue layer in the bonded interface technique, or a substrate, or an alloy phase in composite), as well as the geometric and topological features of these phases, so that the stress fields near the internal interfaces and, thus, the shear bands can be manipulated.