Numerical Simulation of Pressure Infiltration Process for Making Metal Matrix Composites Using Dual-Scale Fabrics

Abstract

Correct modeling of flow and solidification of metal melt in the pressure infiltration process (PIP) is important for accurate simulation and process optimization of the mold-filling process during the making of metal matrix composites. The fiber reinforcements used in this process often consist of fiber tows or bundles that are woven, stitched, or braided to create a dual-scale preform. The physics of melt flow in the dual-scale preform is very different from that in a single-scale preform created from a random distribution of fibers. As a result, the previous PIP simulations, which treat the preform as being single scale, are inaccurate. A pseudo dual-scale approach is presented where the melt flow through such dual-scale porous media is modeled using the conventional single-scale approach using two distinctly different permeabilities in tows and gaps. A three-dimensional finite difference model is developed to model the flow of molten metal in the dual- and single-scale preforms. To track the fluid front during the mold filling and infiltration, the volume of fluid method is used. A source-based method is used to deal with transient heat transfer and phase changes. The computational code is validated against an analytical solution and a published result. Subsequent study reveals that infiltration of an idealized dual-scale preform is marked by irregular flow fronts and an unsaturated region behind the front due to the formation of gas pockets inside fiber tows. Unlike the single-scale preform characterized by sharp temperature gradients near mold walls, the dual-scale preforms are marked by surging of high-temperature melts between tows and by the presence of sharp gradients on the gap-tow interfaces. The parameters such as the (gap-tow) permeability ratio, the (gap-tow) pore volume ratio, and the inlet pressure have a strong influence on the formation of the saturated region in the dual-scale preform.

1 Introduction

The metal matrix composites (MMCs) have been shown to significantly improve the mechanical properties of metals, such as specific stiffness, wear resistance, and high-temperature performance, while lowering their densities by reinforcing metals through the use of silicon carbide or carbon fibers. In the past few decades, these advantages promoted the MMCs to be used widely in the automobile and aerospace industries as high-performance engineering materials.[1] But, the higher costs of manufacturing near-net-shape MMCs and the associated fabrication difficulties, such as requirement of great care in the higher-pressure apparatus design and operation, have been major reasons for limiting their further commercial applications.

The fabrication techniques for MMCs can be broadly divided into two categories: solid- and liquid-state techniques. Compared to the solid-state fabrication methods, the liquid-state processing route works out to be simpler, economical, and versatile, especially for pure metals or alloys with low melting points and low viscosity.[2] Among the liquid-state fabrication methods, the pressure infiltration process (PIP) is one of the most important techniques used for making MMCs where a liquid metal or an alloy under an applied pressure is injected and solidified in a mold packed with a woven or stitched fiber mat. Using this method, MMCs with higher melting-temperature matrices, and with more complex and precise geometries, can be produced. In addition, a wider variety of molds and infiltration temperatures can be used with the gas pressure infiltration process. Since the preform¹ and mold can both be heated to temperatures above the matrix solidification range, this lowers the pressure required; hence, the preform deformation during PIP is more easily avoided.[3,4]

The PIP process for making MMCs is quite similar to the resin transfer molding (RTM) process for making polymer composites. In RTM, a dry preform made from reinforcing fibers is placed in a closed mold under compression and a thermosetting resin (Newtonian liquid) is injected into the preform through inlet ports.[5] The filling resin displaces air from pores of the reinforcement and leads to complete saturation of the preform. Once the mold is thus filled, the resin is allowed to cure (i.e., allowed to undergo an exothermic reaction that transforms it into a hard solid) in order to make the final composite part.

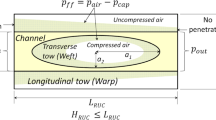
The fabrication techniques for MMCs also depend very much upon the choice of the reinforcing fiber and the matrix. As in RTM, depending upon the porous media created inside a PIP mold, the fiber reinforcement used in PIP can be classified into two categories: single-scale and dual-scale fiber reinforcements.[6] The simplest reinforcement (especially in RTM) is a random mat, which is composed of continuous strands of fibers loosely organized in no particular order. These fibrous preforms are viewed as porous media with uniform pore size distributions and, hence, they are also treated as single-scale porous media that are characterized with a single permeability value. When thousands of individual fiber filaments are bundled into tows and are either woven or stitched to form the fiber preforms, such preforms contain two distinctly different sized pores. The inter-fiber distance within the tows is in the order of micrometers, whereas the distance between the fiber bundles, also called gaps and constituting the inter-tow region, is in the order of millimeters. This kind of porous medium with two different length scales in pore size is called a dual-scale porous medium. Because of this dual-scale nature of fiber preforms, the invading liquid fills the pore spaces between the tows at a much faster rate than the filling of empty pore spaces within the tows, as can be seen in Figure 1. The delayed impregnation of tows leads to the presence of a partially saturated region behind the macroscopic flow front during mold filling and thus profoundly affects the mold-filling dynamics in RTM.[7] Such macro- and micro-flows due to the dual-scale nature of the fiber preforms will have an obvious influence on the infiltration and solidification during the mold filling in PIP as well. For the dual-scale flow behavior observed in an RTM mold, extensive studies[8–19] have been conducted to describe the unsaturated flow in RTM. However, no researcher has investigated the effect of dual-scale preforms in PIP processing.

Fig. 1

A schematic of the typical unsaturated flow pattern observed in dual-scale fiber mats[8,9]

In PIP, the phenomena governing infiltration are very complex. A number of physical, mechanical, and chemical phenomena play their roles, including the flow of liquid metal in a porous medium, the heat and mass transfer associated with matrix solidification, the chemical interfacial reactions, and even the preform deformation. For these complex phenomena, many mathematical models and associated numerical simulations have been developed to predict and understand the many features of the infiltrated metal composites over the past few decades. The first attempt to model the PIP can be attributed to Mortensen et al.,[20] where the traditional equations for flow in single-scale porous medium were employed to develop an analytical model to describe fluid flow and heat transfer during the infiltration of fibrous preforms by a pure metal. Thereafter, Mortensen et al. did numerous studies on the PIP for making MMCs by means of simulation and experimental methods.

In PIP, the rate of infiltration and the position of infiltration front are very important in controlling the infiltration process and improving the composites’ quality. Some RTM models[21–27] were based on the finite element method used in conjunction with a control volume-based approach (called FE/CV or finite element/control volume method) for tracking the resin front displacement in single-scale preforms. In each time step, the FE/CV method calculates the fraction of control volumes (defined around the FE nodes) filled with the invading resin and thus defines the position of the front. In these flow-front tracking methods, the assumption of quasi-steady flow is employed. Another technique[27–31] applied to porous media is based on the volume of fluid (VOF) method developed originally to study the displacement of metal–air interface in a fluid environment. Kuan and El-Gizawy,[28] Voller and Peng,[29] Shojaei et al.,[27] Lin et al.,[30] and Xie et al.[31] have successfully used this method to track front movement in RTM and PIP.

When the MMC processing is not assumed isothermal, the heat transfer must be taken into account, in particular when the fibrous preform and the mold are initially preheated to a temperature lower than the metal solidification temperature. Mortensen and Michaud[32–37] developed a mathematical model to study PIP under such circumstances and explain their experimental observations and results. Meanwhile, Andrews and Mortensen[38] studied the infiltration process driven by Lorentz force with the help of the Forchheimer’s equation. Lacoste et al.[39–43] presented a control volume formulation based on the enthalpy method to simulate infiltration of aluminum into a preform while accounting for the phase change phenomena and metal-front geometry during infiltration in some simple cases. Tong and Khan[44,45] modeled the infiltration and solidification/remelting of a pure metal and alloy in a single-scale porous preform using the finite difference method. The slug flow approximate was employed with Darcy’s law; mold walls were assumed to be insulated, while heat transfer between fibers and metal was taken into account. Lee et al.[46] developed a two-dimensional model to investigate solidification process in MMCs where ends of the fibers are extending out of the mold and are cooled by a heat sink. This simulation was based on the source-based enthalpy method with finite volume discretization and the simulation showed a reasonable agreement with the experimental data. Recently, Jung et al.[47] developed a finite element model to simulate the squeeze casting process for making MMCs; during the movement of liquid metal through packed fibers, the slug flow model with single-phase Darcy flow behind a clear front was used to track the preform wetting, while the enthalpy model was adopted to deal with the phase change.

Although the above-given models, by using the Darcy’s law for single-scale porous-medium flows, have been applied to model the isothermal/non-isothermal mold filling in RTM and PIP over the past two decades, research in RTM has indicated that there are some obvious discrepancies between the numerical predictions and experiments for the dual-scale fiber mats.[12–14] Because of this dual-scale nature of woven or stitched fabrics, the delayed impregnation of tows leads to the presence of a partially saturated region behind the macroscopic flow front during RTM mold filling (Figure 1). The delayed impregnation of tows, causing removal of liquid from the main flow, can be viewed as having “sinks” of liquid in the macroscopic flow field.[7] Parnas and Phelan[15] assumed the impregnation of liquid into the tows to be transversely radial and derived a mathematical expression for the sink term in terms of the penetration of micro-fronts into cylindrical tows; using this model, they succeeded in predicting the experimentally observed phenomenon of variation in liquid pressure with time after the mold has been filled. Pillai and co-workers[9,10] provided a theoretical framework for the governing equations for the dual-scale porous media encountered in dual-scale porous media using the volume-averaging method. And, Pillai and Advani[16] also developed sink functions for a variety of simplified gap-tow geometries as well as fabric unit cells,[8] and successfully replicated the drooping inlet pressure profile typically witnessed in 1-D flow experiments with dual-scale fabrics. Wang and Grove[19] determined the function of tow saturation rate by conducting the transient tow impregnation simulation in a local 2-D unit cell that represented the architecture of a plain-woven fabric; using such a determination of the sink function, they replicated the droop seen in the experimental pressure histories of the 1-D experiments. Recently, in order to capture the effects of sink phenomenon during nonisothermal reactive flows, Hua et al.[9–11] numerically simulated the RTM flows in dual-scale porous media after coupling the inter-tow (macroscopic) flow with the intra-tow (microscopic) flow through a true multi-scale approach. A coarse global mesh was used to solve the global flow equations over the entire domain, while fine local meshes are employed to solve the local tow impregnation process. The good comparison between predictions by the multi-scale model and experiments indicated that the approach could be used to simulate the unsaturated flow through dual-scale fabric mats in RTM.

Although significant work has been done to model the dual-scale flows in RTM, no equivalent research on the effect of impregnating a dual-scale fiber mat with liquid metal in PIP is investigated. In this article, we present the development of a three-dimensional numerical simulation tool for the pressure infiltration processing of a dual-scale fiber preform under a constant applied pressure. A finite difference code has been developed to study the metal flow, the infiltration-front movement, and the accompanying solidification process from a macroscopic point of view. A clear understanding of these transport phenomena is necessary in order to control and optimize PIP for manufacturing MMCs; hence, the code is used to predict the PIP phenomena under various conditions. In this simulation, the PIP flows are predicted for the single-scale fiber mats and dual-scale fabrics. Using a pseudo dual-scale approach,² the dual-scale infiltration is creating by assigning different permeabilities and porosities to the inside (intra-tow) and outside (inter-tow) regions of tows while using the same set of governing equations.

2 Description of PIP

As described in the last section, the pressure infiltration process or PIP is a widely used method to produce the MMCs. PIP is characterized by an application of pressure to the molten metal to overcome the adverse capillary forces that oppose the flow of liquid metal (matrix) into and subsequent wetting of the preform.³ The two principal methods used for pressure infiltration in non-wetting systems are (1) mechanical force applied via a piston and (2) injection pressure applied through a pressurized gas. This process (Figure 2) comprises four main steps: (1) preparation of the preform, typically a net-shape porous structure made from fabrics or fiber mats, (2) melting of the metal, (3) infiltration of the preform with molten metal, and (4) solidification of the metallic matrix.[3,37,48]

Fig. 2

Schematic representation of the PIP. (1) Preparation, (2) Melting of metal, (3) Pressure infiltration, and (4) Solidification

The present simulation of PIP is based on a process used with the pressure infiltration setup available at the Composite Materials Center, University of Wisconsin-Milwaukee (Figure 3); this setup can apply infiltration pressures up to 250 psi into the fibers packed in a small quartz tube. In this setup, a tube filled up to half of its height with the reinforcement is held by a container. Finally, an aluminum block, which is to be melted to provide the liquid aluminum for infiltration, is placed on the top of the preform inside the tube. Thus, the prepared container is put into the pressure infiltration chamber. Then, the chamber is closed and the air is evacuated to a certain vacuum pressure. Then, the chamber is heated while the vacuum is maintained. When the metal has melted, the gas is let into the chamber and the gas pressure is increased to a threshold value required for initiating infiltration. After completion of the infiltration process, either the whole system is allowed to cool down or the container is removed and cooled by air or water. The MMC sample can then be extracted from the mold.

Fig. 3

A picture (left) and a schematic (right) of the pressure infiltration setup used at the University of Wisconsin-Milwaukee

3 Numerical Model

3.1 Flow and Solidification Physics

3.1.1 Basic assumptions

The PIP for making MMCs of molten metal flowing through a porous preform can be regarded as a series of quasi-steady steps where the steady mass-flow equation in conjunction with the momentum and energy balance equations is solved in a domain changing with time. During PIP, the preform has two distinct regions: the infiltrated region and the uninfiltrated region; these are separated by the infiltration front. The heat transfer and solidification occur during infiltration. For simplifying our simulations, several assumptions are made as follows:

• (1) The metal flow is modeled as a fully saturated, single-phase flow of Newtonian Fluid in the wetted regions of the preform. Darcy’s law is valid with pore-based Re ≪ 1 everywhere inside the preform, which means that the inertial effects are neglected.

• (2) To simulate the dual-scale effect in PIP, the porous preform is divided into two regions: the gap and tow regions. The preform is assumed to be isotropic in the gap region with K _gap as the permeability scalar, and is assumed to be anisotropic in the tow region with K _tow as the permeability tensor.⁴

• (3) The tow shapes are simplified and are chosen such that the principal components of K _tow are along the x, y, and z directions.

• (4) Since pressure gradient is the dominant motive force that drives the infiltration process, gravitational effects on infiltration and solidification are neglected, as they are small compared to the imposed pressure gradient. Similarly, effects of the capillary pressure induced at the front due to surface tension and contact angle are ignored as they too are small.

• (5) The injection pressure is held constant during infiltration.

• (6) The porosity in both the gap and tow regions reduces due to deposition of solid metal on pore walls due to solidification. Hence, changes in permeability within the solidification region due to changes in the local porosity (or solid volume fraction) have been considered. (However, if the initial preform temperature is sufficiently high, the permeability will remain unchanged, except by solidification due to cooling at the mold walls.)

• (7) The physical properties of the pure metal are assumed constant. The metal density remains constant during the solid/liquid phase change as well.

• (8) Natural convection during the phase change process is negligible.

3.1.2 The governing equations

Under the above assumptions, the momentum balance equation for the porous-media flows observed in a PIP mold is equivalent to the Darcy’s law in a three-dimensional form:

$$ u = - \frac{{K_{x} }}{\mu }\frac{\partial P}{\partial x},\quad v = - \frac{{K_{y} }}{\mu }\frac{\partial P}{\partial y},\quad w = - \frac{{K_{z} }}{\mu }\frac{\partial P}{\partial z} $$

(1)

Here, μ is viscosity of liquid metal; K _x , K _y , and K _z are the principal permeability components of the fibrous preform along the three coordinate directions⁵; P is the pore-average or intrinsic phase-average pressure; u, v, and w are the x, y, and z components of the phase-average⁶ or Darcy velocity, respectively.

The volume-averaged continuity equation for the flow of incompressible metal in a non-deforming preform is given as

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0 $$

(2)

The governing equation for pressure⁷ can then be deduced by combining Eqs. [1] and [2]:

$$ K_{x} \frac{{\partial^{2} P}}{{\partial x^{2} }} + K_{y} \frac{{\partial^{2} P}}{{\partial y^{2} }} + K_{z} \frac{{\partial^{2} P}}{{\partial z^{2} }} = 0 $$

(3)

Note that this equation can be used to find the liquid (metal) pressure only in the wetted region of the preform behind a moving front. For solving the flow-front progression during the filling process, the VOF method is used:

$$ \frac{\partial F}{\partial t} + \frac{u}{\varepsilon }\frac{\partial F}{\partial x} + \frac{v}{\varepsilon }\frac{\partial F}{\partial y} + \frac{w}{\varepsilon }\frac{\partial F}{\partial z} = 0 $$

(4)

Here, F represents the fraction of a control volume filled with the liquid metal and ε is the porosity of the fibrous preform.

The averaged energy equation is given by

$$ \left[ {\varepsilon (\rho c_{\text{p}} )_{\text{m}} + (1 - \varepsilon )(\rho c_{\text{p}} )_{\text{p}} } \right]\frac{\partial T}{\partial t} + \left( {\rho c_{\text{p}} } \right)_{\text{m}} \left( {u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} + w\frac{\partial T}{\partial z}} \right) = k_{cx} \frac{{\partial^{2} T}}{{\partial x^{2} }} + k_{cy} \frac{{\partial^{2} T}}{{\partial y^{2} }} + k_{cz} \frac{{\partial^{2} T}}{{\partial z^{2} }} + \varepsilon \rho_{\text{m}} \Updelta h_{\text{m}} \frac{{\partial f_{\text{s}} }}{\partial t}, $$

(5)

where ρ is the density; c _p is the specific heat; T is the volume-averaged temperature; k _cx , k _cy , and k _cz are the x, y, and z components of thermal conductivity tensor of the metal-fiber composite, respectively; ∆h _m is the latent heat associated with the solid/liquid phase change in the metal matrix; and f _s is defined as the ratio of volume of solidified metal to the total volume of metal in the solidification region. The subscripts, m, p, and c refer to the properties of the metal matrix, the preform, and the metal-fiber composite, respectively.

3.2 Physical Domain and Problem Description

The physical domain consisting of the preform packed within a PIP mold cavity is shown schematically in Figure 4. A cubic mold is used for making composites, and the size of the mold cavity is 0.01 m × 0.01 m × 0.01 m. Tows under compression are not circular, but highly elliptical with a large aspect ratio. Illustrated in Figure 4(b) is the cross section and geometry dimension of a fiber tow used in our model.

Fig. 4

A schematic describing the structure and geometry of gap and tows in an idealized dual-scale porous medium created by packing a fiber preform within a PIP mold. Note that Section A in the central X to Z plane is perpendicular to fiber tows direction. (a) 3-D schematic of PIP in the mold, (b) Geometry of an idealized fabric

The mold wall may be assumed to be adiabatic or at a given constant temperature. The molten metal is driven to infiltrate the porous preform placed in the mold by an externally applied pressure from the top of the mold. The inlet pressure and temperature, P _in and T _in, respectively, are constant. The Preform initial temperature is T _pre.

The porous preform is assumed to be homogeneous in terms of global distribution of gap and tow properties, but not necessarily isotropic. If the preform is made from single-scale fiber mats (typically made of randomly laid fibers), the preform is assumed to be isotropic, i.e., K _x  = K _y  = K _z . On the other hand, preforms made from dual-scale fabrics contain two distinctly different gap and tow regions interspersed with each other (Figure 4). The gap region is assumed to be isotropic, while the tows regions are transversely isotropic with their X and Z principal permeability components, K _x and K _z , equal, i.e., K _x  = K _z . (Note that K _y  ≠ K _x , K _z since permeability along the fiber axes (Y direction) is different from the permeability transverse to the fiber direction.) Hence, the two porous-medium properties needed to characterize the flow in a dual-scale preform are the gap permeability (K _gap), a scalar quantity, and the tow permeability (K_tow), a second-order tensor. If the flow rate is rapid enough between the tows, a gas pocket surrounded by the fluid metal, regarded as the closed microscopic flow front, will be formed inside tows, as shown in Figure 1. The gas inside the pocket, undergoing progressive compression due to the rising gap pressure behind the moving macroscopic front, will obey the ideal gas law.

3.3 Boundary and Initial Conditions

In order to compute the mathematical model, the governing equations must be solved in conjunction with an appropriate set of boundary and initial conditions. The initial temperature of the fiber preform and the aluminum melt is set as T _pre = 900 K (627 °C) and T _in = 1000 K (727 °C), respectively. The initial value of volume fraction of fluid is set to zero, i.e., F = 0, in the dry preform.

The boundaries of the wetted preform are divided into three types: the mold walls, the inlet gate, and the flow front. The corresponding boundary conditions are as follows. At the mold walls, there is no flow in the normal direction and the corresponding boundary condition (from Darcy’s law) is expressed as $\frac{\partial P}{\partial n} = 0$. For heat transfer at the mold walls, we can set two types of boundary conditions: (1) a given temperature of the mold wall, i.e., T _w = 900 K (627 °C), or (2) the adiabatic boundary condition at the mold wall, i.e., $\frac{\partial T}{\partial n} = 0$. At the inlet gate, an applied constant pressure (P = P _in) is set at the inlet nodes; the inlet temperature, equal to the melt temperature, is set to T = T _in. At the flow front, the pressure may be set to zero gage pressure or a specified vacuum pressure for the single-scale fiber mats: P = P _gage = 0.

Our dual-scale flow model will produce two distinct types of flow fronts that must be tracked; hence, two distinct boundary conditions will be set for the two flow fronts. The first will correspond essentially to the gap (inter-tow) flow and is to be called the open flow front (Figure 5). At the open flow front(s), the pressure will be set to zero gage pressure, i.e., P = P _gage = 0. Due to different infiltration velocities in the gap and tow regions, the second flow fronts, which form gas pockets inside the tows and which are to be called the closed flow fronts, will appear. As seen in Figure 5, the closed flow fronts will be formed behind the open flow fronts and will be surrounded by the melt. (Note that the open flow front will also be called the macroscopic flow front, while the closed flow fronts inside the tows will also be described as the microscopic flow fronts.) The effect of capillary pressure and entrapped air bubbles must be considered in this model in order to obtain appropriate pressure boundary conditions for the closed flow fronts. As the outside melt pressure increases with the progress of the infiltration front, these air pockets will gradually shrink and become small,⁸ while the pressure inside air pockets will increase. The pressure boundary condition imposed at the closed flow front is

$$ P = P_{\text{gas}} - P_{\text{s}} . $$

(6)

Fig. 5

A schematic describing the formation of two types of flow fronts during the pressure infiltration of a dual-scale porous preform

Note that P _gas is the pressure inside the air pocket and is obtained using the ideal gas law as

$$ \frac{{P_{0} V_{0} }}{{T_{0} }} = \frac{{P_{\text{gas}} V_{\text{gas}} }}{{T_{\text{gas}} }}, $$

(7)

where P, V, and T are the pressure inside the air pocket, volume of the air pocket, and temperature inside the air pocket, respectively. The subscript 0 corresponds to the last time step, while the subscript gas represents the current time step. Now P _s is the suction pressure created at the liquid front due to the capillary action. Since the porous medium inside the tows consists of bundles of aligned fibers, the suction pressure through the use of the Laplace equation[50–52] is given by

$$ P_{\text{s}} = P_{\text{c}} = \frac{{2\gamma_{\text{l}} \cos (\alpha )}}{{r_{\text{e}} }} $$

(8)

where P _c is the capillary pressure, γ _l is the surface tension of the liquid, α is the contact angle of liquid at the solid–liquid interface, and r _e is the equivalent capillary radius given through the expression [ε/(1 − ε)] * r _f.[52] Use of Eqs. [7] and [8] with the closed flow-front boundary condition of Eq. [6] results in the following expression for the pressure boundary condition at the closed front:

$$ P = P_{0} \cdot \frac{{V_{0} }}{{V_{\text{gas}} }} \cdot \frac{{T_{\text{gas}} }}{{T_{0} }} - \frac{{2\gamma_{\text{l}} \cos (\alpha )}}{{r_{\text{e}} }}, $$

(9)

Note that for a non-wetting situation typical during using of PIP, α is likely to be greater than 90 deg for the typical (liquid–metal + silica fiber) systems used in MMCs and hence the second term on the right-hand side of Eq. [9] will be positive. As a result, a pressure greater than the thermodynamic gas pressure will be required to impregnate the fiber tows. Note that in the single-scale preforms, only open flow fronts will be created as there is no trapping of gas pockets inside tows.

Another important parameter is the fraction solid metal f _s, which appears in Eq. [5]. According to references,[44,53] if the initial fiber temperature is far below the melting point of the metal (T _m), some solid metal will form at the infiltration front so that the fibers are heated up to the metal melting point through the release of latent heat. When the heat transfer ahead of the infiltration front is negligible, the fraction solid metal f _s is simply given by this thermal equilibration at the infiltration front:

$$ f_{\text{s}} = \frac{{(1 - \varepsilon )(\rho c_{\text{p}} )_{\text{p}} (T_{\text{m}} - T_{\text{pre}} )}}{{\varepsilon \rho_{\text{m}} \Updelta h_{\text{m}} }} $$

(10)

3.4 Material Properties

The preform permeability and the composite thermal conductivity are very important parameters for the simulation of flow and solidification in PIP. Here, we describe the estimation of these parameters.

The existing experimental and theoretical work indicates that the solidification of metal on fiber surfaces would decrease the permeability of the preform significantly. Of the various models proposed,[20,47] we chose to use the following expressions. For the flow perpendicular to fiber axes, the equation of permeability is

$$ K = \frac{{2\sqrt 2 r^{2}_{\text{sf}} }}{{9V_{\text{sf}} }}\left[ {1 - \sqrt {\frac{{4V_{\text{sf}} }}{\pi }} } \right]^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} $$

(11)

which is valid for solid volume fractions ranging from ~0.2 to π/4. In addition, the gap permeability was estimated according to Gebart’s formula[54] as $K_{ \bot } = C_{1} \left( {\sqrt {\frac{{V_{\text{fmax}} }}{{V_{\text{f}} }}} - 1} \right)^{5/2} r_{\text{f}}^{2}$ and was assumed fixed after ignoring the effects of solidification in the gap region. The parameters C ₁ and V _fmax depend on the fiber arrangement.

During solidification, it is assumed that the metal near the reinforced fiber solidifies first and the fiber radius grows as the solidification progresses, while the porosity of the preform decreases. The new fiber radius, r _sf, and the volume fraction of the net solid material, V _sf, can be calculated from the solid fraction, f _s, as

$$ V_{\text{sf}} = V_{\text{f}} + (1 - V_{\text{f}} )f_{\text{s}} $$

(12)

$$ r_{\text{sf}} = r_{\text{f}} \sqrt {\frac{{V_{\text{sf}} }}{{V_{\text{f}} }}} , $$

(13)

where r _f is the fiber radius and V _f is the fiber volume fraction in the dry, unprocessed preform.

According to Reference 20, the thermal conductivity of a single-scale composite medium is equated to the thermal conductivity for heat flow in the direction perpendicular to parallel, continuous fibers arranged in a square array. Such conductivity for the single-scale preform is given as

$$ k_{\text{c}} = k_{\text{m}} \frac{{(k_{\text{f}} + k_{\text{m}} ) + (k_{\text{f}} - k_{\text{m}} )(1 - \varepsilon )}}{{(k_{\text{f}} + k_{\text{m}} ) - (k_{\text{f}} - k_{\text{m}} )(1 - \varepsilon )}}, $$

(14)

where k _c, k _m, and k _f are the thermal conductivities of the composite, metal, and fiber, respectively.

The effective thermal conductivity of a dual-scale composite medium needs to be estimated in different heat flow directions due to the anisotropic nature of the medium created from fiber tows consisting of aligned fibers. Several authors have proposed formulae for the thermal conductivity of fiber composites.[20,55] For the present model, the thermal conductivity of the composite for different heat-flow directions inside and outside tows is as follows.

In the wetted infiltrated regions of the tows, the thermal conductivity in the direction along the fiber axes is given by the rule of mixtures:

$$ k_{\text{c}} = \varepsilon k_{\text{m}} + (1 - \varepsilon )k_{\text{f}} $$

(15)

In the wetted infiltrated regions of the tows, the thermal conductivity in the direction perpendicular to the fiber axes is

$$ k_{\text{c}} = \frac{{k_{\text{f}} }}{{\varepsilon \frac{{k_{\text{f}} }}{{k_{\text{m}} }} + 1 - \varepsilon }} $$

(16)

In the dry, uninfiltrated regions of the tows, the thermal conductivity along the fibers axes can be given by

$$ k_{\text{c}} = \varepsilon k_{\text{air}} + (1 - \varepsilon )k_{\text{f}} \simeq (1 - \varepsilon )k_{\text{f}} $$

(17)

In the dry, uninfiltrated regions of the tows, the thermal conductivity perpendicular to fibers axes can be expressed as

$$ k_{\text{c}} = \frac{{k_{\text{f}} }}{{\varepsilon \frac{{k_{\text{f}} }}{{k_{\text{air}} }} + 1 - \varepsilon }} \simeq \frac{{k_{\text{air}} }}{\varepsilon }\quad {\text{for}}\quad k_{\text{f}} \gg k_{\text{air}} $$

(18)

Outside the tows in the inter-tow gaps, only the metal will be involved in heat conduction. So, the thermal conductivity in the gap region is the isotropic conductivity of the infiltrated metal: $k_{\text{c}} \simeq k_{\text{m}}$.

We note that Peclet number, Pe = (ρC _p)_f ur _f /k _f, is an important dimensionless parameter signifying the relative strengths of the convective and diffusive transports. For the typical (carbon fiber + aluminum melt) system, when u is on the order of 10⁻¹ m/s and the average radius of fibers r _f ≈ 10 μm, the Peclet number is estimated to be 10⁻². Since Pe < 0.1, the effect of hydrodynamic dispersion on the thermal conductivity is neglected.

3.5 Numerical Solution

The pressure governing equation, Eq. [3], the flow-front (VOF) governing equation, Eq. [4], and the energy equation, Eq. [5], were discretized by using a control volume-based finite difference method. The hybrid discretization scheme[56] was employed to evaluate the fluxes. The movement of the infiltration front was predicted by applying the “quasi-stationary” approximation, under which the pressure field was solved at each time step in the wetted region of the preform with the pressure being zero at the macroscopic front, and by solving the VOF equation, the resultant F values (with F = 0.5 set as the front) describe the infiltration process. Note that in order to apply the closed-front boundary condition on gas pockets inside the tows, we developed an algorithm for finding the location of closed flow fronts inside tows and calculating the volume enclosed by individual closed flow fronts. An iterative algorithm based on using the tri-diagonal matrix algorithm (TDMA) along the three directions was developed to solve the pressure in the wetted region. In this way, the pressure field was calculated at the each time step. The iterative procedure was continued until the point pressure values converged. Once the pressures were determined, the velocity field, as calculated by using the Darcy’s law, Eq. [1], was then used to solve the energy equation, Eq. [5]. The method described in Reference 29 was employed to solve the VOF and energy equation at the same time step. The calculating procedure stopped when the mold was completely filled. (The flow charts of the numerical solution procedure developed for this code are illustrated in Figure 6.) The conservation equations were solved using our in-house code Metal IMpregnation Process Simulation (MIMPS).

Fig. 6

Flow chart of the numerical solution procedure adapted to model mold filling in PIP

For the present problem, a 22 × 22 × 22 (X × Y × Z) grid was selected to describe the whole computational domain (Figure 4(a)) in a Cartesian system. As a part of the grid-refinement study, the computational grid was refined from 22 × 22 × 22 to 62 × 62 × 62 in order to study numerical convergence. Good convergence was achieved for the single-scale porous medium results where little difference could be observed for temperature, flow-front progress, and pressure distribution. However, the situation was a bit more complex for the dual-scale porous medium considered. The refinement test showed that certain numerical results, including global tow saturation and temperature at selected points, produced using a 22 × 22 × 22 grid are more or less in agreement with the results obtained from other more refined grids. However, some variations in the flow-front location at a given time were observed for the different grids. We could not refine the mesh indefinitely, since beyond the 62 × 62 × 62 grid, the memory requirement became very large and the time required to complete the filling simulation became very big (few days in an ordinary non-parallel workstation). As a result, the final grid was selected as a compromise between perfect numerical convergence and computational cost for the three-dimensional problem considered here—we decided to stick to a 22 × 22 × 22 grid for simulating this complex metal infiltration process in single- and dual-scale porous media.

During the presentation of the results, all the variables involved in the governing equations are rendered dimensionless as

$$ x^{*} = \frac{x}{L},\quad y^{*} = \frac{y}{W},\quad z^{*} = \frac{z}{H},\quad t^{*} = \frac{t}{{t_{\text{fill}} }},\quad P^{*} = \frac{P}{{P_{\text{int}} }},\quad \theta = \frac{{T - T_{\text{w}} }}{{T_{\text{in}} - T_{\text{w}} }} $$

(19)

These non-dimensional variables are used in the following sections.

4 Validation of Numerical Simulation

The predictions of the developed computer code are validated by comparing them with two analytical solutions of the flow-front locations predicted as a function of time for some simple mold geometries and simplified injection conditions.

The analytical expressions for the flow-front locations of one-dimensional isothermal flows in single-scale preforms packed in flat rectangular molds (with injection from one side) are given for both the cases of the constant flow rate and the constant-pressure injections as[27]

$$ x(t)_{\text{front}} = \frac{{q_{\text{in}} t}}{\varepsilon HW}\quad {\text{for}}\;{\text{the}}\;{\text{constant}}\;{\text{flow-rate}}\;{\text{case}} $$

(20a)

$$ x(t)_{\text{front}} = \sqrt {\frac{{2Kp_{\text{in}} t}}{\varepsilon \mu }} \quad {\text{for}}\;{\text{the}}\;{\text{constant}}\;{\text{pressure}}\;{\text{case,}} $$

(20b)

where $x(t)_{\text{front}}$ is the location of the flow front, t is the infiltration time, K is the preform permeability, ε is the preform porosity, μ is the viscosity of the liquid metal, H and W are the thickness and width of the mold cavity, respectively, q _in is the constant incoming flow rate, and p _in is the constant pressure at the inlet gate. Figure 7 shows a good agreement between simulation results and the analytical solution for the flow-front location varying with time for both the cases.⁹ In this isothermal study, only the infiltration process was validated, while the effect of solidification on flow-front progress was ignored.

Fig. 7

Comparison of the simulation results for flow-front progress with the analytical results for both the cases of (a) constant flow rate and (b) constant pressure, at the inlet gate

The present code was also verified with the results reported by Tong and Khan[44] for numerical modeling of a two-dimensional infiltration accompanied by solidification and remelting. Figure 8 compares the remelting-front evolution for the same process conditions: The results from the present numerical code show a reasonably good qualitative agreement with the results obtained by Tong and Khan. Generally, the infiltrated region has two subregions: the melting region and the solidification region, separated by the melting front. In here, the isothermal lines of the melting point of the infiltrated metal at the different times are estimated by the extent of the remelting region.

Fig. 8

A comparison of predictions for the evolution of the remelting front: (a) present numerical simulation using a 42 × 42 × 7 grid and (b) Tong and Khan[44] numerical results

5 Results and Discussion

In the present study, the aluminum melt is pressurized by the applied pressure and infiltrated into the mold packed with the fiber preform. The physical properties of the pure melt and the reinforcement fiber used in the numerical simulation are presented in Table I. Table II lists the process parameters used in this simulation. And, Table III shows the dimension and properties of the dual-scale porous mediums created in Figures 4 and 5 for our simulation.

Table I Material Properties of the Chosen Metal and Fibers

Table II Process Parameters Used in the Present Simulation

Table III The Dimension and Properties of the Dual-Scale Porous Medium Created in Figs. 4 and 5 for our Simulation

5.1 Infiltration of Single-Scale Preforms

First, we will study the metal infiltration pattern in the single-scale preform during PIP. Figure 9 shows the progress of the molten metal flow front in Section A of Figure 4 of the considered mold. Since the fiber preform is isotropic and the gate width is equal to the width of the mold, the flow front at each time is planar. Figure 10 presents the distribution of the pressure and velocities in the central x to z section of the mold at various times. From these figures, it can be seen that the pressure distribution is uniform perpendicular to the infiltration direction and the infiltration velocities change rapidly with time. For a preform cross section of 1 cm × 1 cm, the total infiltration time is very short and is about 0.032 second. Note that in the present study, we did include the effect of solidification on preform permeability through the use of Eq. [11].

Fig. 9

Location of the flow front of molten metal inside the fibrous preform corresponding to Section A of Fig. 4 at the different infiltration (dimensionless) times: (a) 0.154, (b) 0.332, (c) 0.695, and (d) 1.0 (t _fill = 0.032 second and flow front is given by the F = 0.5 curve)

Fig. 10

The pressure distribution and velocity field corresponding to Section A of Fig. 4 at different infiltration (dimensionless) times: (a) 0.154, (b) 0.332, (c) 0.695, and (d) 1.0. (t _fill = 0.032 second and P _in = 3 atm)

Figure 11 shows the temperature distribution at different infiltration times. It is clear that with increasing time, a sharp temperature gradient develops near the mold walls. The temperature distributions inside the PIP mold are dependent on the thermal properties of the materials, and the boundary and initial conditions. Since the temperature history is important for predicting nucleation and grain growth during solidification in PIP, such sharp gradients are likely to have important impact on the microstructural indicators in the final part such as the grain size and inter-dendritic spacings.

Fig. 11

The dimensionless temperature $\left( {\theta = \frac{{T - T_{\text{w}} }}{{T_{\text{in}} - T_{\text{w}} }}} \right)$ distribution corresponding to section A of Fig. 4 at the different infiltration (dimensionless) times: (a) 0.332 and (b) 1.0

5.2 Infiltration of a Dual-Scale Preform

We will now study the infiltration and solidification of liquid metal in the dual-scale preforms of PIP which are made from woven or stitched fabrics. Figure 12 shows the movement of flow front with time. Note that the front moves down and reaches the bottom surface of the mold in ~0.067 second, which signifies the end of the infiltration process. Comparing Figure 12 with Figure 9, we also note that the flow-front shape in the dual-scale preforms is distinctly different from those found in the single-scale preforms. The molten metal aluminum infiltrates the empty spaces between the tows at a much faster rate than the empty spaces within the tows. The delay in the infiltration velocity leads to the presence of a partially saturated region behind the flow front in the dual-scale porous media. We will do well to recall that the partially saturated tows behind the macroscopic infiltration front constitute the unsaturated region (Figure 5). From this figure showing the evolution of the infiltration front, it can be seen that there are some gas pockets and a partially saturated region behind the front due to the dual-scale nature of the preform. With the progress in infiltration, the macroscopic flow front moves down along the infiltration direction and reaches the various locations at the different times. Due to the delayed impregnation of tows, the shape of the macroscopic flow front is wavy, unlike the plain front seen in the single-scale preform. Apart from this open macroscopic flow front, there also exist a few closed flow fronts inside the unsaturated tows. We can also regard the closed flow fronts or gas pockets as the tow saturation distribution that changes with the infiltration time. It is clear that the length of the unsaturated region increases during the mold-filling process (Figure 12); it can be seen that a growing, partially saturated region with gas pockets is always present behind the macroscopic flow front. If we stop the injection when the macroscopic flow front reaches the mold end, the partially saturated region with gas pockets representing the non-wetted tows will be retained inside the produced composite. These non-wetted tows may then lead to the formation of “porosity” in the final MMC part and will seriously compromise the quality of the part. Hence, we conclude that the injection can be stopped only after the melt metal has fully saturated the tows. Our numerical simulation indicates that the mold-filling time based on the macroscopic flow-front traversing the whole mold is 0.067 second. After the mold filling, either the flow should be continued for some time to flush out the gas pockets or extra inlet pressure is applied to shrink (and eventually collapse) the pockets. The size and location of the gas pockets, which also depend on the size and location of the closed flow fronts, are dependent on the permeabilities of the tows and gaps. As depicted in Figure 12, gas pockets are formed inside tows, where the permeability inside the tows is around three times smaller than the permeability between the tows. As we shall see later, the ratio of the two permeabilities of a dual-scale porous medium has important effect on the pressure distribution and velocity field during the infiltration process. A smaller tow permeability compared to the gap permeability leads to the formation of gas pockets in PIP.

Fig. 12

The flow-front evolution with time in the dual-scale preform corresponding to Section A of Fig. 4 at the different infiltration (dimensionless) times: (a) 0.08, (b) 0.21, (c) 0.67, and (d) 1.0 (t _fill = 0.067 second and P _in = 3 atm and flow front is given by F = 0.5 curve)

Figure 13 shows the pressure and velocity-vector distributions at various infiltration times at the center section of the mold. Because of the pressure boundary conditions at the closed flow front (Eq. [6]: the gas pressure within the gas pockets added to the capillary pressure) as well as the permeability change within the tows, the flow inside the mold becomes quite complex. As seen in Figure 13, the flow velocity based on Darcy’s law changes greatly both in direction and magnitude with the spatial coordinates and is no longer parallel as seen for the single-scale preform in Figure 10.

Fig. 13

The pressure and velocity distributions in Section A of Fig. 4 at the different infiltration (dimensionless) times: (a) 0.08, (b) 0.21, (c) 0.67, and (d) 1.0 (t _fill = 0.067 second and P _in = 3 atm)

The formation and compression (and even possible dissolution and flushing down¹⁰) of the gas pockets are dependent on the local pressure around the gas pocket, which in turn is a function of the applied inlet pressure. Figure 14 presents changes in the formation and compression of the gas pockets with an increase in the inlet pressure: It is clear that the pockets are becoming smaller with an increase in the pressure.

Fig. 14

The effect of inlet pressure on the formation of gas pockets during the PIP infiltration process at the dimensionless infiltration time of unity: (a) P _in = 1 atm, (b) P _in = 10 atm

Compared to Figure 12(d), it is apparent that the gas pockets shown in Figure 14(a) will have larger volumes and will stay trapped for the too small outside pressure, whereas, for a higher pressure, the gas pockets formed will be smaller (and may partially be dissolved or flushed away). Hence, in PIP, we recommend applying a higher pressure at the inlet to reduce the volume of trapped gas pockets, which in turn would lead to a reduction of porosity in the final MMC parts.

Figure 15 shows the changes in the temperature distribution with time during the infiltration process at the central section of the mold. The main feature of the temperature profile is that it does not exactly follow the filling pattern seen in Figure 12, i.e., it is not marked by “gas pocket” zones inside the tows. But, the presence of tows does affect the temperature distribution—the temperature has a tendency to “race” along the inter-tow gap region as the higher temperatures are carried by the faster-moving gap flows. Note also that the high-temperature region in single-scale preform (Figure 11) appears as a single, thick “peak” and the sharp temperature gradients mainly appear at the mold boundaries, whereas the high-temperature region in dual-scale preform (Figure 15) appears as multiple, sharp “peaks” and the sharp temperature gradients are concentrated near gap-tow interfaces. These results may be very helpful in understanding the solidification process, in refining the grains, and in improving the quality of MMCs made using PIP. (Sharp temperature gradients may have an important effect on the development of microstructure¹¹ in the final MMCs.)

Fig. 15

Evolution of the dimensionless temperature $\left( {\theta = \frac{{T - T_{\text{w}} }}{{T_{\text{in}} - T_{\text{w}} }}} \right)$ distribution with time during PIP injection in the dual-scale preform shown in section A of Fig. 4 The four plots correspond to four different (dimensionless) times: (a) 0.08, (b) 0.21, (c) 0.67, and (d) 1.0

Let us now study the temperature histories at other points inside the mold of Figure 4(a). Three points in the central section A of the mold shown in Figure 4(b) will be considered: point P1 at the center of the mold; point P2 at the center of the mold bottom; point P3 on the inner surface of the mold sidewall, at the same height as that of point P1. Figure 16 shows the temperature-rise curves for the three points. We see that temperatures at points P1 and P3 rise almost simultaneously as the infiltration front reaches these two points at around the same time (since they are at the same elevation). We also note that although the temperatures at these two points show similar trends, i.e., both drop a little before steadily rising later on, the P1 temperature is much higher as compared to the P2 temperature. This is because the former is at the mold center, while the latter is near the mold side-wall that is maintained at a lower temperature. As expected, the temperature at point P2 rises much later, after the infiltration front has traversed almost the entire mold length.

Fig. 16

The temperature plots predicted for the points P1, P2, and P3 of Fig. 4(b)

5.3 Effect of Various Parameters on Saturation of Dual-Scale Preforms

During the pressure infiltration of our dual-scale preform when the macroscopic flow front has reached the end of the mold (Figure 12(d)), there still exists a partially saturated region behind the front due to the creation of gas pockets. A variable called tow saturation has been introduced to indicate the status of local tow impregnation in RTM processes.[8,9] In this paper, a new parameter called global tow saturation is defined to represent the fraction of saturated region in all the tows at the end of infiltration. For this parameter, a value of 0 means that all tows are empty or dry, while a value of 1 means that all tows are completely filled or saturated with the liquid metal; a value between 0 and 1 implies that the tows are partially filled with the metal. The global tow saturation, S _tow, is obtained from the formula S _tow = volume of tows occupied by metal/total tow volume in the preform, i.e.,

$$ S_{\text{tow}} = \sum\limits_{i = 1}^{{N_{\text{tows}} }} {\frac{{V_{{{\text{saturated}}\,{\text{by}}\,{\text{metal}},{\text{i}}}} }}{{V_{{{\text{tow}},{\text{i}}}} }}} , $$

(21)

In the study of resin flow through the dual-scale preforms in the RTM process for making polymer composites, the parameters such as the permeability ratio and the pore volume ratio have often been found to be important in governing the unsaturated flow.[7–10,18] Hence, we will study the effect of the pore volume ratio, the permeability ratio, and the inlet pressure on global tow saturation during pressure infiltration of the considered dual-scale preform.

The permeability ratio is defined as the ratio of the permeability in gaps, K _gap, to the permeability inside tows, K _tow. Figure 17 illustrates the effect of permeability ratio on the global tow saturation. The permeability ratio ranges from 10¹ to 10⁶ in this parametric study and was achieved by varying K _tow, while keeping K _gap fixed. The plot shows that the value of global tow saturation decreases as the permeability ratio increases. Implications are that as the tows become less permeable with an increase in the permeability ratio, more air pockets are likely to appear inside tows.¹² Note that the tow permeability, which is a function of both the fiber diameter and the tow porosity, will decrease as finer fibers are used in densely packed tows to weave or stitch the PIP preforms.

Fig. 17

Effect of permeability ration, K _gap/K _tow, on global tow saturation, S _tow

Let us now consider the pore volume ratio, which is defined as the ratio of pore volume available inside the tows to the pore volume available in the gaps of the dual-scale preform. As described in Reference 16, a higher pore volume ratio means that tows are close to each other with very little gap between them. In this study, the pore volume ratio was changed by changing the distance between tows, while keeping the tow size as well as the porosity inside tows constant. The effect of increase in the pore volume ratio on the global tow unsaturation is illustrated in Figure 18: It is clear that the global tow saturation decreases as the pore volume ration increases. This seems plausible because an increasing pore volume ratio is accompanied by smaller gap volumes, which means that smaller volumes of liquid metal in the gaps are available for wetting the fiber tows and hence they are likely to remain dry.

Fig. 18

Effect of pore volume ratio on global tow saturation, S _tow

The pressure at the inlet, which decides how fast the liquid metal travels through the gaps as well as how much the gas pockets shrink at the end of filling, is an important parameter for PIP. Figure 19 shows the effect of inlet pressure on global tow unsaturation: It is clear that the globe tow saturation increases with an increase in the inlet pressure. It can be noted that at lower pressures, i.e., when the inlet pressures are 1, 2, and 3 atm, changes in the values of global tow saturation are very small. But, when the inlet pressure is larger than 3 atm, the global tow saturation rises very rapidly with the inlet pressure. However, after this sudden rise, the global tow saturation again increases very slowly with the inlet pressure. Hence, this observation implies the existence of a critical pressure of around 3 atm when S _tow rises very rapidly. From a practical point of view, a lower inlet pressure with the smaller tow saturation is acceptable for the manufacture of MMCs using PIP, since a higher injection pressure will necessitate the use of more expensive equipment.

Fig. 19

Effect of inlet pressure on global tow saturation, S _tow

6 Summary and Conclusions

The present study investigated the infiltration and solidification process of a pure metal in a three-dimensional PIP mold used for making MMCs where both the single- and dual-scale preforms made from reinforcing fibers were considered. A pseudo dual-scale approach is adapted to model the process in the dual-scale preform where the simulation for the single-scale preform (after including Darcy’s law, the continuity equation, the energy equation after accounting for solidification, the VOF method for front tracking) is adapted for the former by assigning different permeabilities in the gap and tow regions. The entrapment of gas pockets inside fiber tows is modeled after imposing the pressure boundary condition on the closed fronts inside tows using the Ideal Gas law and the capillary pressure. A 3-D flow, perpendicular to the tows as well as fibers inside tows, is modeled in PIP molds where regularly spaced elliptical tows are used to make idealized dual-scale porous media. The numerical study is validated by achieving a good agreement with an analytical solution for front progress in a 1-D flow with no solidification as well as by achieving reasonable replication of a previous published result on front progress in a 2-D mold with solidification. Later, the study investigated the differences in flow and temperature distributions in the single- and dual-scale PIP preforms.

The following important conclusions are drawn from this study:

• 1. The infiltration and solidification processes are predicted in the single-scale and dual-scale preforms; these simulation results will be helpful in understanding the flow and solidification phenomena in the real-life PIP and in explaining the experimental results.

• 2. During the constant-pressure injection, a flat flow front develops in the single-scale preforms, whereas a highly irregular flow-front profile, marked by gas pockets entrapped inside fiber tows, develops in the dual-scale preforms. Such a flow front in the latter case leads to the creation of an unsaturated zone behind the flow front. The degree of tow saturation in such a zone is shown to be a function of not only the structural parameters, such as the ratio of permeabilities in the tow and gap regions and the ratio of pore volumes in the tow and gap regions, but also of the pressure imposed at the mold inlet.

• 3. The temperature distributions in the mold for dual-scale preform are characterized by racing of high-temperature liquids through the inter-tow gaps and sharp temperature gradients at gap-tow interfaces, unlike the distribution in single-scale preform marked by sharp gradients near the mold boundaries.