Boundary element techniques for multiscale filling simulations in dual-scale fibrous reinforcements using two lumped approaches

Abstract

Non-uniform filling of dual-scale fibrous reinforcements is crucial in modelling and simulation of liquid composites molding processes since this poses several challenges at mesoscopic (void formation) and macroscopic scale (irregular global saturation). This problem is tackled here using two lumped approaches: sink-term and effective-unsaturated permeability lumped functions are obtained from mesoscopic filling simulations, and introduced into Richards and equivalent Darcy equations to conduct macroscopic simulations. Boundary Element Techniques to solve governing equations, a fluid-front-tracking method, a Stokes-Darcy-based methodology to simulate intra-tow liquid absorption considering air compressibility and dissolution, flow-direction dependent capillary pressure, vacuum pressure and dynamic void evolution, are representative contributions of this work. Macroscopic results show that both sink-term and Richards approach are in acceptable agreement with experiments, with former approach providing more accurate results. BEM-based codes are used to study the influence of inlet pressure and flow rate, vacuum pressure, air compressibility and dissolution on the saturation behaviour.

1 Introduction

The processing of composites materials is an engineering area that has aroused a lot of interest in the scientific community. The development of new processing techniques and the improvement of the existing ones are tightly linked to the advancement of the simulation methods. In that area, one of the principal concerns is the dual-scale nature of some fibrous reinforcements that are used in the manufacturing of parts by Liquid Composite Molding (LCM), because such a nature supposes flow imbalances inside the Representative Unitary Cell (RUC), which in turn, cause uncontrolled defects (voids) and could considerably affect the global flow behavior during the filling of cavities, leading to non-uniform saturation fields.

In dual-scale fibrous reinforcements used in liquid composites molding, there exist three well-differentiated sub-domains at mesoscopic scale: channels, longitudinal tows and transverse tows, as can be observed in Fig. 1, where the yellow colour represents the fluid in the channels, whereas the green-grey colour, the fluid present inside the tows at certain time instant. The channels are considerably more permeable than the tows, leading to a non-uniform saturation of the preform as the filling takes place. At the mesoscopic level, differences between the fluid flows in these sub-domains depend on the relationship between the viscous and capillary forces. These differences significantly affect the pressure and velocity fields at the macroscopic level. For instance, in unidirectional injections, pressure reduction is linear along the mold length in single-scale fibrous reinforcements. In contrast, this reduction is almost parabolic for the unsaturated zone in dual-scale fibrous reinforcements [1]. On the other hand, in unidirectional constant flow rate injections, the inlet pressure increment with time is linear for single-scale fibrous reinforcements. Conversely, a pressure drooping occurs for dual-scale fibrous reinforcements [1, 2].

Fig. 1

Scheme of the mesoscopic problem assuming full-filled channels

The simulations of filling of dual-scale fibrous reinforcements can be classified into two main categories: mesoscopic and macroscopic simulations. Mesoscopic simulations consist of the filling of the Representative Unitary Cell (RUC). They can be carried out to: (1) determine the effective properties of the porous medium, such as the effective unsaturated and saturated permeabilities, and the constitutive relationships of these properties [3,4,5, 13]–[12], (2) compute the coupling terms between the mesoscopic and macroscopic governing equations to deduce lumped functions in terms of volume-averaged quantities [2, 14]–[18].

On the other hand, macroscopic simulations refer to those carried out in cavities, where the porous medium is initially dry. Then a liquid pass throughout it, driven by positive pressure, gravity and/or capillary pressure. During the filling, dual-scale reinforcement is not uniformly impregnated because of the differences between the channel and tow permeabilities, which originates partial saturation effects. Two strategies can be considered to determine the influence of such effects on the macroscopic variables (pressure, velocity, saturation, etc.). In the first one, simultaneous and iterative-corrected simulations are conducted at both scales (macroscopic and mesoscopic) [19]–[22], whereas in the second one, which is less rigorous but computationally cheaper, lumped functions for the effective properties or the coupling terms are obtained by running several mesoscopic simulations of the RUC filling, and those functions can be used afterwards in the macroscopic equations [2, 3, 23]–[4, 25]–[6, 12, 14]–[17]. This second strategy, in turn, can be divided into two main approaches. In the first approach, some constitutive relationships for permeability vs. saturation are obtained at the mesoscopic scale, and then, Richards equation is solved using these constitutive equations [3]–[5]. In the second approach, sink functions, $S_{g}$, are obtained by running several mesoscopic simulations and these functions are used afterwards in the solution of a Poisson type equation, which is obtained from the mass conservation equation and the Darcy law with an equivalent channel permeability, $K_{g}$ [2, 6, 14]–[17, 23]–[25].

In the present work, the Boundary Element Method (BEM) is applied for the filling simulation of dual-scale fibrous reinforcements used in the manufacturing of composite materials. A Stokes-Darcy formulation is used for the mesoscopic simulations, whereas the abovementioned lumped approaches (Richards and equivalent Darcy) are deemed for the macroscopic simulations. Some previous representative researches and the principal contributions of the present work can be summarized as follows:

• The problem of multiscale filling of dual-scale fibrous reinforcements has been tackled mostly using domain mesh techniques. For instance, the Finite Element/Control Volume (FEM/CV) conforming method was used in [24] by introducing ‘slave’ elements into the original nodes of the FEM mesh, with the purpose to simulate the delayed saturation of the tows as the macroscopic fluid front progresses. On the other hand, Park et al. [26] used a modified FEM-CV method to predict void content and saturation changes along the mold length; such work introduced an improvement of the original void formation model proposed by Kang and Lee [27], namely, a more accurate consideration of the micro-architecture of the fabric. It is important to highlight that for the macroscopic unidirectional simulations carried out in Park et al. [26], the fluid front refinement technique proposed by Kang and Lee [28] was used. In such a technique, the mesh in the neighbourhood of the fluid front is adaptively refined by using floating imaginary nodes that are placed in the contour of the FEM elements taking into account the fill factor; a smoother fluid front is achieved regarding the traditional FEM/CV methods but at the expense of the increase of computational cost. The change of the saturation at both mesoscopic (tows) and macroscopic (cavity) levels and the drooping of pressure in constant flow rate injections were studied in [2] using FEM to solve the governing equations and the nodal saturation method to track the fluid front [29]. The FEM/CV conforming method was also used in coupled multiscale simulations of unsaturated flow for isothermal [19], non-isothermal [20], and reactive [30] conditions, where two FEM meshes and the corresponding CV meshes were required since the mesoscopic (filling of tows) and macroscopic (filling of the cavity) simulations were run simultaneously, which entails a high computational cost. The FEM/CV method was employed in [18] to conduct filling simulations of tows, including the effects of capillary pressure, void pressure and non-uniform fiber volume fraction distribution. This method was used in [17] to study the influence of intra-tow resin release in reactive injection conditions of high-speed reactive RTM processes. On the other hand, an Algebraic Sub-Grid Scale (ASGS) FEM approach was used in [10] to study the effective permeability of 2D and 3D fibrous media based on the Stokes-Darcy formulation. In the present work, the use of BEM techniques implies reducing the mesh requirements in one dimension, which is convenient when dealing with moving boundary problems where the domain changes with the time as the process evolves. In our numerical scheme, direct integration of the kinematic condition interface is used to advance the fluid front (Euler method). Smoothing and re-meshing algorithms are implemented, assuring a higher-order accuracy of the fluid front shape regarding FEM/CV techniques. In this sense, the fluid front position is directly obtained from the moving interface velocity field without using interface capturing schemes for its reconstruction. Some works that use BEM techniques have also dealt with simulations of unsaturated flow in porous media [31]–[34], but the partial saturation effects were taken into account by using experimental constitutive laws for the permeability. In the present work, as demanded by Richards approach, constitutive relationships for the permeability in terms of the saturation are obtained from the results of mesoscopic simulations.

• Another contribution of the present work is referred to as the problem of considering the partial saturation of the RUC’s in the behaviour of some macroscopic variables during the filling of the cavity. As it was mentioned before, there are two main numerical strategies to tackle this problem: (1) to carry out simultaneous and iterative-corrected simulations at both scales or (2) to conduct several simulations at the mesoscopic scale for obtaining lumped functions to be used at the macroscopic scale. The second strategy is employed in the present work because it implies a lower computational cost. Still, it is introduced an important modification in the methodology to simulate the liquid absorption into the tows. This modification is motivated by some physical incongruences between numerical [2, 15, 24, 35] and experimental results [36]–[43]. When it is assumed that the channels are filled with liquid before any infiltration of the tows can take place, it is usually supposed that the tows saturation rate inside the RUC, $\dot{S}_{t}$, is function of the uniform pressure of the liquid contained in the channels, $\left\langle {P_{g} } \right\rangle^{g}$ [2, 15, 24, 35]. This methodology has some drawbacks due to its simplifications: (1) the impregnation of tows takes place towards the center of them, no matter the magnitude or direction of the channel fluid velocity, which is not in accordance with other researches [27, 36]–[38, 44, 45]; (2) the air compressibility and partial air dissolution are not taken into account, thereby leading to a constant air pressure in the fluid front during the whole filling of the tows, which does not necessarily reproduce the real situation of liquid composites molding (LCM) processes [39, 46]; (3) the capillary pressure is assumed constant during the whole RUC filling and the model to compute this pressure is employed indistinctively for the warps and the wefts; (4) vacuum pressure is not considered as an initial condition for the air pressure, which is not coherent with some applications of composites manufacturing where the vacuum pressure plays a major role [40, 41, 47, 48]; (5) the prescription of a constant pressure in the channels of the RUC is not physically consistent with the fact that the fluid is actually moving; (6) the processes of void displacement, migration and subsequent splitting, which have been reported in previous experimental researches [36]–[38, 42, 43], are not captured using this simplified methodology. Consequently, this methodology to account for the tows saturation is modified here by prescribing a pressure gradient along the RUC, $\Delta P/\Delta x,$ and imposing matching conditions between the tows and the channel sub-domains to determine the filling of the former ones; applying mass conservation, the saturation rate of the tows, $\dot{S}_{t}$, is established in terms of the difference between the inlet and outlet flow rates of the RUC, which in turns can be directly accomplished from the BEM simulations. The present methodology tackles the aforementioned drawbacks as follows: (1) decentered voids are obtained in the tows due to the prescription of a pressure gradient, which is more coherent with previous works; (2) air compressibility and partial air dissolution are considered by means of an air entrapment parameter, $\lambda$, proposed in [39]; (3) a flow-direction dependent model for the capillary pressure not involving experimental shape factors is considered [49]; (4) vacuum pressure, $P_{vac}$, is taken into account as an independent variable of the lumped functions; (5) there exists a velocity field in the channel consistent with the fluid flow direction; (6) displacement, migration and splitting of voids can be present. Using the proposed methodology, lumped functions are obtained for the sink term, $S_{g}$, and the effective unsaturated permeability, $K_{eff}$, after running a considerable amount of mesosocopic simulations (RUC fillings), and then, the macroscopic unidirectional filling is considered using the Dual Reciprocity Boundary Element Method (DR-BEM) in order to assess the reliability of the present methodology regarding previous works [1] and experimental results, and to analyse the time and space behaviour of the global saturation under both constant pressure and constant flow rate regimes.

Summarizing, given the importance of the filling simulations of dual-scale fibrous reinforcements in the composites processing, the present work is focused on the development and implementation of a BEM-based numerical methodology to tackle this problem using two lumped approaches: Richards and equivalent Darcy. The present development is boosted by the necessity to deem the influence of several aspects at mesoscopic scale (absorption into the tows considering the fluid motion at channels, air compressibility, air dissolution, flow-direction dependent capillary pressure, vacuum pressure and dynamic evolution of voids) in the behaviour of the field variables at the macroscopic scale (pressure, velocity, saturation, etc.) in a lumped fashion. It is worth noting that the present work is supported by previous developments [49]–[51], where the benefits of the reduction of meshing requirements associated to BEM techniques and the use of Euler Method, smoothing and remeshing algorithms to track the fluid front, were discussed.

2 Governing equations, boundary conditions and matching conditions

2.1 Volume-averaged variables

In the volume averaging method [52], a phase volume-averaged variable, $\left\langle {B_{\beta } } \right\rangle$, refers to the average of the variable in the phase “β” with respect to the total RUC volume, $V_{RUC}$, while an intrinsic-phase volume-averaged variable, $\left\langle {B_{\beta } } \right\rangle^{\beta }$, is the average with respect to the volume of the phase “β”, $V_{\beta }$, as shown in the following equations:

$$ \left\langle {B_{\beta } } \right\rangle = \left( {1/V_{RUC} } \right)\int\limits_{{V_{\beta } }} {B_{\beta } dV_{\beta } } $$

(1)

$$ \left\langle {B_{\beta } } \right\rangle^{\beta } = \left( {1/V_{\beta } } \right)\int\limits_{{V_{\beta } }} {B_{\beta } dV_{\beta } ,} $$

(2)

where $B_{\beta }$ is the pointwise variable in the phase “$\beta$”. The relationship between $\left\langle {B_{\beta } } \right\rangle$ and $\left\langle {B_{\beta } } \right\rangle^{\beta }$ is as follows:

$$ \left\langle {B_{\beta } } \right\rangle = \varepsilon_{\beta } \left\langle {B_{\beta } } \right\rangle^{\beta } , $$

(3)

being $\varepsilon_{\beta } = V_{\beta } /V_{RUC}$ the porosity of the phase “$\beta$”.

2.2 Modelling at the mesoscopic scale

As the channel Reynolds number and the tows permeability are supposed small, the coupling problem between the fluid in the channel and the fluid in the porous media (tows in this case) can be defined by a Stokes-Darcy formulation as follows:

For the channel (Stokes flow)

$$ \mu \left( {\partial^{2} u_{i} /\partial x_{j} x_{j} } \right) - \partial p/\partial x_{i} = 0 $$

(4)

$$ \partial u_{i} /\partial x_{i} = 0 $$

(5)

For the porous media (Darcy flow in the principal directions of permeability)

$$ \left\langle {u_{f} } \right\rangle_{i} = - \left( {K_{i} /\mu } \right) \cdot \left( {\partial \left\langle {{\text{p}}_{{\text{f}}} } \right\rangle^{{\text{f}}} /\partial x_{i} } \right) $$

(6)

$$ \partial \left\langle {u_{f} } \right\rangle_{i} /\partial x_{i} = 0, $$

(7)

where $u_{i}$, $p$, $\mu$, $K_{i}$, $\left\langle {{\text{p}}_{{\text{f}}} } \right\rangle^{{\text{f}}}$ and $\left\langle {u_{f} } \right\rangle_{i}$ represent the channel velocity, pressure in the channel, liquid viscosity, main permeabilities, pressure in the porous medium, and velocity in the porous medium, respectively.

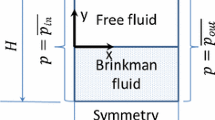
For the Stokes-Darcy problem, the matching conditions used here for the channel-tows coupling were discussed in previous works [49, 50]. On the other hand, the boundary conditions can be classified into three types (see Fig. 1):

• Inlet and outlet conditions at the Stokes domain (channel or gap):

  $$ t_{1}^{inl} = - \overline{{p_{inl} }} \cdot \widehat{{n_{1} }},\;\;u_{2}^{inl} = 0 $$

  (8)
  $$ t_{1}^{out} = - \overline{{p_{out} }} \cdot \widehat{{n_{1} }},\;\;u_{2}^{out} = 0 $$

  (9)

  where $t_{1}^{inl}$ and $t_{1}^{out}$ are the inlet and outlet surface tractions in the horizontal direction, while $\overline{{p_{inl} }}$ and $\overline{{p_{out} }}$ stand for the prescribed inlet and outlet pressures of the RUC. In a similar fashion, $u_{2}^{inl}$ and $u_{2}^{out}$ are the inlet and outlet vertical velocities, which are set to zero.

• No penetration conditions at the Darcy domains (tows):

  $$ \partial p/\partial \hat{n} = 0 $$

  (10)

• Free-surface conditions are applied at the moving boundaries between the liquid and air phases, which correspond to the fluid fronts inside the tows and the bubble front in the channels when void migration is present. Free-surface conditions are given by:

Kinematic condition:

$$ dx_{i} /dt = u_{n} \widehat{{n_{i} }} = \left( {u_{j} \cdot \widehat{{n_{j} }}} \right)\widehat{{n_{i} }} $$

(11)

Dynamic condition:

$$ p - P_{air} = - P_{cap} , $$

(12)

where $P_{air}$ is the air pressure, $P_{cap}$ is the capillary pressure and $u_{n}$ is the normal velocity of the moving boundary, which is equivalent to the normal pore velocity, $u_{n} = - \left[ {K_{i} /\left( {\varepsilon_{t} \mu } \right)} \right] \cdot \left( {\partial p/\partial x_{i} } \right)\widehat{{n_{i} }}$, in the porous medium. In this expression, $K_{i}$, $\varepsilon_{t}$, $\mu$, $p$ and $\widehat{{n_{i} }}$ stand for tow permeability in “i” direction, tow porosity, liquid viscosity, pressure, and outward normal vector. At the liquid–air interface corresponding to the bubble front when void migration occurs, the capillary pressure is computed as $P_{cap} = - \sigma \kappa = - \sigma \left( {\nabla \cdot \hat{n}} \right)$, where $\sigma$ and $\kappa$ are the surface tension and curvature of the liquid–air interface, respectively, with the last one computed as previously shown in [49, 51]. On the other hand, the models used for the calculation of the flow direction- dependent capillary pressure, $P_{cap}$, in both the longitudinal tows (warps) and the transverse tow (weft) are detailed in [49].

It is worth noting that the air sub-domain is not directly modelled in the present work. The time evolution of this sub-domain is determined by the velocity field calculated along the liquid–air interphase at each time step, which in turns depends on the dynamic condition, Eq. (12). Therefore, the Stokes-Darcy formulation used in the mesoscopic simulations is always applied for fully saturated zones in both the channel and the tows, and compressibility is not directly included on the corresponding governing equations, but instead on the dynamic condition, Eq. (12).

In this work, the architecture of the porous media is considered as a bank of aligned micro-cylinders, and the main permeabilities can be computed using the model proposed by Gebart [53]:

$$ K_{1} = 8R_{f}^{2} \cdot \left( {1 - V_{f} } \right)^{3} /\left( {c \cdot \left( {V_{f} } \right)^{2} } \right) $$

(13)

$$ K_{2} = c_{1} \left( {\sqrt {V_{f,\max } /V_{f} } - 1} \right)^{5/2} R_{f}^{2} , $$

(14)

where $R_{f}$ and $V_{f} = 1 - \varepsilon_{t}$ are the fiber radius and the fiber volume fraction of tow, respectively. In this case, a hexagonal array of fibers is considered for the tows.

In Fig. 2, it is shown the Representative Unitary Cell (RUC) of a hexagonal array of fibers, where the fiber radius, $R_{f}$, and half distance between fibers, $d$, are identified. The tow porosity, maximum fiber volume fraction and Gerbart parameters for such particular RUC are given by: $\varepsilon_{t} = 1 - \pi R_{f}^{2} /\left( {2\sqrt 3 \left( {R_{f} + d} \right)^{2} } \right)$, $V_{f,\max } = \pi /\left( {2\sqrt 3 } \right)$, $c_{1} = 16/\left( {9\pi \sqrt 6 } \right)$ and $c = 53$.

Fig. 2

Hexagonal array of fibers

2.3 Modelling at the macroscopic scale

At the macroscopic scale, two approaches to model the unsaturated filling are deemed here: Richards and equivalent Darcy. In the first one, two sub-domains are considered, namely, saturated and non-saturated, with the former one including both the channel and the filled zones of the tows. In this approach, an effective permeability function in terms of the RUC saturation is required. On the other hand, the equivalent Darcy approach is obtained from the application of the method of volume averaging to two sub-domains that are conceived as different phases, namely, the channel and the tows. In this approach, a non-linear sink function in terms of the tows saturation and other volume-averaged variables, which accounts for the mass absorption into the tows, is necessary.

In the Richards approach, a fluid phase $\left( f \right)$, including both liquid $\left( l \right)$ and gas $\left( g \right)$, is considered, and the gas density and velocity are neglected, obtaining the following mass conservation equation:

$$ \frac{{\partial \varepsilon_{l} }}{\partial t} + \frac{{\partial \left\langle {u_{i} } \right\rangle_{l} }}{{\partial x_{i} }} = - \frac{1}{{V_{RUC} }}\int\limits_{{A_{f} }} {u_{{i_{f} }} \widehat{{n_{{i_{f} }} }}dA_{f} } $$

(15)

where $\varepsilon_{l}$, $\left\langle {u_{i_{l}} } \right\rangle$, $V_{RUC}$, $A_{f}$, $u_{{i_{f} }}$ and $\widehat{{n_{{i_{f} }} }}$ are the liquid phase porosity, phase volume-average liquid velocity, the RUC volume, fiber-fluid interphase area, pointwise fluid velocity, and the normal unit vector of fiber-fluid interphase, respectively. By defining saturation as the ratio between the volume of the liquid and fluid phase, $s = V_{l} /V_{f}$, considering that $\varepsilon_{l} = V_{l} /V_{RUC}$ and assuming the impermeability and non-deformability of the fibers, i.e., $u_{{i_{f} }} = 0$ in $A_{f}$, Eq. (15) can be written as:

$$ \varepsilon_{f} \frac{\partial s}{{\partial t}} + \frac{{\partial \left\langle {u_{{i_{l} }} } \right\rangle }}{{\partial x_{i} }} = 0 $$

(16)

where $\varepsilon_{f}$ is the porosity of the fluid phase, which remains constant.

On the other hand, considering the assumptions mentioned above for the fluid and fibers, neglecting gravitational effects, and deeming scale constraints of Darcian fluids, the following momentum equation is obtained:

$$ \left\langle {u_{{i_{f} }} } \right\rangle = - \frac{{K_{{ij_{f} }} }}{{\mu_{f} }}\frac{{\partial \left\langle {p_{f} } \right\rangle^{f} }}{{\partial x_{j} }} $$

(17)

As $\left\langle {u_{{i_{f} }} } \right\rangle \approx \left\langle {u_{{i_{l} }} } \right\rangle$ and considering that both the permeability and the pressure shall be regarded as a function of the saturation, $s$, Eq. (17) can be substituted into Eq. (16) to obtain the Richards equation:

$$ \varepsilon_{f} \frac{\partial s}{{\partial t}} - \frac{\partial }{{\partial x_{i} }}\left( {\frac{{K_{{ij_{f} }} \left( s \right)}}{{\mu_{f} }}\frac{{\partial \left\langle {p_{f} } \right\rangle^{f} \left( s \right)}}{{\partial x_{j} }}} \right) = 0 $$

(18)

where $K_{{ij_{f} }} \left( s \right)$ is known as the effective unsaturated permeability.

On the other hand, the equivalent Darcy approach employed in the present work for the macroscopic modelling of dual-scale porous media was proposed by [54]. Two phases are considered (Fig. 1): channels or gaps (g), which are assumed to be initially filled with liquid, and bundles or tows (t), which are considered initially empty. The mass conservation equation is given by:

$$ \frac{{\partial \left\langle {u_{{i_{g} }} } \right\rangle }}{{\partial x_{i} }} = - S_{g} $$

(19)

where $\left\langle {u_{{i_{g} }} } \right\rangle$ is the phase volume-average channel or gap velocity and $S_{g}$ is the sink term accounting for the flow absorption through the tows as given by:

$$ S_{g} = - 1/V_{RUC} \int_{{A_{gt} }} {u_{{i_{gt} }} \widehat{{n_{{i_{gt} }} }}dA_{gt} } $$

(20)

where $A_{gt} ,\;u_{{i_{gt} }}$ and $\hat{n}_{{i_{gt} }}$ stand for the area, liquid velocity, and unit normal vector in the gap-tow interface, represented by subscript “gt”. On the other hand, the momentum equation in this approach is given by:

$$ \left\langle {u_{ig} } \right\rangle = - \frac{{K_{ig} }}{\mu } \cdot \frac{\partial }{{\partial x_{i} }}\left\langle {P_{g} } \right\rangle^{g} , $$

(21)

where $\left\langle {u_{{i_{g} }} } \right\rangle$ and $\left\langle {P_{g} } \right\rangle^{g}$ stand for the phase volume-averaged velocity and intrinsic phase volume-averaged pressure in the channels, respectively, whereas $K_{{i_{g} }}$ represents the equivalent channel or gap permeabilities in the principal directions “i" assuming impermeable tows.

For the particular case of unidirectional filling at the macroscopic scale, the non-dimensionalization of the variables depends on the injection regime, as follows (volume-averaged symbols are omitted for sake of simplicity):

• For both constant pressure and constant flow rate regimes:

  $$ \hat{x} = x/L $$

  (22)
  $$ \hat{L}_{ff} = L_{ff} /L $$

  (23)

• For a constant pressure regime only:

  $$ \hat{t} = t/\left( {L^{2} \mu /\left( {\left| {P_{inj} - P_{vac} } \right|K_{g} } \right)} \right) $$

  (24)
  $$ \hat{p} = p/\left| {P_{inj} - P_{vac} } \right| $$

  (25)
  $$ \widehat{{u_{1} }} = u_{1} /\left( {\left( {\left| {P_{inj} - P_{vac} } \right|K_{g} } \right)/\left( {L\mu } \right)} \right) $$

  (26)

• For a constant flow rate regime only:

  $$ \hat{t} = t/\left( {LA/Q_{inj} } \right) $$

  (27)
  $$ \hat{p} = p/\left( {Q_{inj} L\mu /\left( {A \cdot K_{g} } \right)} \right) $$

  (28)
  $$ \widehat{{u_{1} }} = u_{1} /\left( {Q_{inj} /A} \right), $$

  (29)

  where $x$, $L_{ff}$, $t$, $p$ and $u_{1}$ are the horizontal coordinate, fluid front position, time, pressure, and horizontal velocity, respectively; whereas, $\hat{x}$, $\hat{L}_{ff}$, $\hat{t}$, $\hat{p}$ and $\widehat{{u_{1} }}$ are the corresponding non-dimensionalized variables. On the other hand, $L$, $\mu$, $P_{inj}$, $P_{vac}$, $K_{g}$, $A$ and $Q_{inj}$ stand for the domain length, liquid viscosity, injection pressure, vacuum pressure, gap permeability, cross-section area of cavity, and injection flow rate, respectively.

3 Integral equation formulations and numerical techniques

3.1 Integral equations at the mesoscopic scale

At the mesoscopic scale (RUC filling), the boundary integral formulations for Stokes [55] and Darcy [56, 57] equations are given in terms of the corresponding Green’s integral formulae:

$$ c_{ij} \left( \xi \right)u_{j} \left( \xi \right) = \int\limits_{S} {K_{ij} \left( {\xi ,y} \right)u_{j} \left( y \right)dS_{y} - \int\limits_{S} {U_{i}^{j} \left( {\xi ,y} \right)t_{j} \left( y \right)dS_{y} } } $$

(30)

$$ c\left( \xi \right)p\left( \xi \right) = \int\limits_{S} {p^{*} \left( {\xi ,y} \right)q\left( y \right)dS_{y} - \int\limits_{S} {q^{*} \left( {\xi ,y} \right)p\left( y \right)dS_{y} ,} } $$

(31)

where $c_{ij} \left( \xi \right) = \left( {\alpha /2\pi } \right)\delta_{ij}$, with $\alpha$ as the solid angle at the source point, $\xi$, whose value is $\alpha = \pi$ for points located over a smooth contour. For points located inside the domain, $c_{ij} = \delta_{ij}$. In a similar fashion, $c\left( \xi \right)$ is equal to $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$ for points over a smooth surface and 1 for points inside the domain. The integral kernels in Eqs. (30) and (31) are given in terms of the corresponding fundamental solutions, which are the following:

$$ U_{i}^{j} \left( {\xi ,y} \right) = - \frac{1}{4\pi }\left[ {\ln \left( \frac{1}{r} \right)\delta_{ij} + \frac{{\left( {\xi_{i} - y_{i} } \right)\left( {\xi_{j} - y_{j} } \right)}}{{r^{2} }}} \right] $$

(32)

$$ K_{ij} \left( {\xi ,y} \right) = - \frac{1}{\pi }\frac{{\left( {\xi_{i} - y_{i} } \right)\left( {\xi_{j} - y_{j} } \right)\left( {\xi_{k} - y_{k} } \right)n_{k} \left( y \right)}}{{r^{4} }} $$

(33)

$$ p^{*} \left( {\xi ,y} \right) = - \frac{1}{2\pi }\ln \left( {r_{e} } \right) $$

(34)

$$ \begin{aligned} q^{*} \left( {\xi ,y} \right) = & \frac{{K_{i} }}{{K_{e} }}\frac{{\partial p^{*} }}{{\partial y_{i} }}\left( {\xi ,y} \right)\widehat{{n_{i} }}\left( y \right) \\ = & - \frac{{\left[ {\left( {y_{1} - \xi_{1} } \right)\widehat{{n_{1} }}\left( y \right) + \left( {y_{2} - \xi_{2} } \right)\widehat{{n_{2} }}\left( y \right)} \right]}}{{2\pi \left( {r_{e} } \right)^{2} }}, \\ \end{aligned} $$

(35)

where $r = \left| {\xi - y} \right|$, $r_{e} = \left[ {\left( {K_{2} /K_{1} } \right)^{\frac{1}{2}} \left( {y_{1} - \xi_{1} } \right)^{2} + \left( {K_{1} /K_{2} } \right)^{\frac{1}{2}} \left( {y_{2} - \xi_{2} } \right)^{2} } \right]^{1/2}$ and $K_{e} = \left( {K_{1} K_{2} } \right)^{1/2}$, with $\xi$ and $y$ as the source and field points, respectively. The integrals present in the fundamental solutions, $U_{i}^{j} \left( {\xi ,y} \right)$ (Stokes) and $p^{*} \left( {\xi ,y} \right)$ (Darcy), correspond to the single-layer potentials (SLP), and those present in $K_{ij} \left( {\xi ,y} \right)$ (Stokes) and $q^{*} \left( {\xi ,y} \right)$ (Darcy), to the double layer potentials (DLP).

3.2 Integral equations at the macroscopic scale

As abovementioned, two approaches are considered for the macroscopic modelling in the present work: Richards and Equivalent Darcy. In the first one, considering the principal directions of permeability in Eq. (18) and applying the property of the derivative of a product, the next equation is obtained:

$$ \frac{{K_{{i_{f} }} \left( s \right)}}{{\mu_{f} }}\frac{{\partial^{2} \left\langle {p_{f} } \right\rangle^{f} \left( s \right)}}{{\partial x_{i}^{2} }} = - \frac{\partial }{{\partial x_{i} }}\left( {\frac{{K_{{i_{f} }} \left( S \right)}}{{\mu_{f} }}} \right)\frac{{\partial \left\langle {p_{f} } \right\rangle^{f} \left( s \right)}}{{\partial x_{i} }} + \varepsilon_{f} \frac{\partial s}{{\partial t}} $$

(36)

In the second approach, the combination of the mass conservation, Eq. (19), and momentum conservation, Eq. (21), leads to the following equation:

$$ \frac{{K_{{i_{g} }} }}{\mu } \cdot \frac{{\partial^{2} \left\langle {P_{g} } \right\rangle^{g} }}{{\partial x_{i}^{2} }} = S_{g} $$

(37)

The integral formulation for Eqs. (36) and (37) is given by:

$$ c\left( \xi \right)p\left( \xi \right) = \int\limits_{S} {p^{*} \left( {\xi ,y} \right)q\left( y \right)dS_{y} - \int\limits_{S} {q^{*} \left( {\xi ,y} \right)p\left( y \right)dS_{y} + \int\limits_{\Omega } {b\left( y \right)p^{*} \left( {\xi ,y} \right)d\Omega_{y} } } } , $$

(38)

where the fundamental solutions, $p^{*}$ and $q^{*}$, considering a uniform anisotropic ratio (K₁/K₂) at macroscopic scale, have the same form as the ones presented in Eqs. (34) and (35), whereas the non-homogeneous terms for Eqs. (36) and (37) are given by:

$$ b = - \frac{{\mu_{f} }}{{K_{{e_{f} }} \left( s \right)}} \cdot \left[ {\frac{\partial }{{\partial x_{i} }}\left( {\frac{{K_{{i_{f} }} \left( S \right)}}{{\mu_{f} }}} \right)\frac{{\partial \left\langle {p_{f} } \right\rangle^{f} \left( s \right)}}{{\partial x_{i} }}} \right] + \varepsilon_{f} \frac{\partial s}{{\partial t}} $$

(39)

$$ b = \frac{\mu }{{K_{{e_{g} }} }}S_{g} = - \frac{\mu }{{K_{{e_{g} }} }}\left( {\frac{1}{{V_{RUC} }}\int\limits_{{A_{gt} }} {u_{{i_{gt} }} \widehat{{n_{{i_{gt} }} }}dA_{gt} } } \right), $$

(40)

where $K_{{e_{f} }} \left( s \right) = \left( {K_{1f} \left( s \right) \cdot K_{2f} \left( s \right)} \right)^{1/2}$ and $K_{{e_{g} }} = \left( {K_{1g} \cdot K_{2g} } \right)^{1/2}$ are the equivalent quasi-isotropic unsaturated and gap permeabilities, respectively. The domain integral of Eq. (38) can be transformed into boundary integrals using the Dual Reciprocity Boundary Element Method (DR-BEM) [58]. Firstly, the non-homogenous term, $b$, is approximated using Radial Basis Function (RBF) interpolation with Augmented Thin Plate Splines (ATPS) of order $n = 2$, which are given by the next formulae:

$$ f^{m} \left( y \right) = \left\{ {\begin{array}{*{20}l} {r^{2} \ln \left( r \right)} \hfill & {{\text{for}}\;m \in \left[ {1,N_{B} + N_{I} } \right]} \hfill \\ 1 \hfill & {{\text{for}}\;m = N_{B} + N_{I} + 1} \hfill \\ {y_{1} } \hfill & {{\text{for}}\;m = N_{B} + N_{I} + 2} \hfill \\ {y_{2} } \hfill & {{\text{for}}\;m = N_{B} + N_{I} + 3} \hfill \\ \end{array} } \right\}, $$

(41)

where $N_{B}$ is the number of boundary points, $N_{I}$ is the number of interior points and $r\left( {y,z^{m} } \right) = \left| {y - z^{m} } \right|$ is the distance between the field points, $y$, and the trial points, $z^{m}$. The non-homogeneous term can be expanded as follows:

$$ b\left( y \right) = \mathop \sum \limits_{m = 1}^{{N_{B} + N_{I} + 3}} \alpha^{m} f^{m} \left( y \right), $$

(42)

where $\alpha^{m}$ represent the approximation coefficients. The ATPS defined in Eq. (41) requires the addition of orthogonality conditions, as shown in the following equation:

$$ \mathop \sum \limits_{m = 1}^{{N_{B} + N_{I} }} \alpha^{m} = \mathop \sum \limits_{m = 1}^{{N_{B} + N_{I} }} \alpha^{m} x_{1}^{m} = \mathop \sum \limits_{m = 1}^{{N_{B} + N_{I} }} \alpha^{m} x_{2}^{m} = 0 $$

(43)

After substituting Eq. (42) into Eq. (38), the integral representation takes the following form:

$$ c\left( \xi \right)p\left( \xi \right) = \int\limits_{S} {p^{*} \left( {\xi ,y} \right)q\left( y \right)dS_{y} - \int\limits_{S} {q^{*} \left( {\xi ,y} \right)p\left( y \right)dS_{y} + \sum\limits_{m = 1}^{{N_{B} + N_{I} + 3}} {\alpha^{m} \int\limits_{\Omega } {p^{*} \left( {\xi ,y} \right)f^{m} \left( y \right)d\Omega_{y} } } } } $$

(44)

The transformation of the domain integral into a boundary integral is accomplished by defining the following auxiliary pressure field:

$$ \frac{{\partial^{2} \hat{p}^{m} }}{{\partial y_{k} \partial y_{k} }} = f^{m} \left( x \right), $$

(45)

with the particular solutions for the ATPS (Eq. (41)), $\hat{p}^{m}$ and $\hat{q}^{m}$, given in [59].The substitution of Eq. (45) into Eq. (44) and the application of Green’s identities in the domain integral lead to the following boundary-only integral representation:

$$ c\left( \xi \right)p\left( \xi \right) = \int\limits_{S} {p^{*} \left( {\xi ,y} \right)q\left( y \right)dS_{y} - \int\limits_{S} {q^{*} \left( {\xi ,y} \right)p\left( y \right)dS_{y} + \sum\limits_{m = 1}^{{N_{B} + N_{I} + 3}} {\alpha^{m} \left( {c\left( \xi \right)\hat{p}^{m} \left( \xi \right) - \mathop \smallint \limits_{S}^{{}} p^{*} \left( {\xi ,y} \right)\hat{q}^{m} \left( y \right)dS_{y} + \mathop \smallint \limits_{S}^{{}} q^{*} \left( {\xi ,y} \right)\hat{p}^{m} \left( y \right)dS_{y} } \right)} } } $$

(46)

where the coefficients $\alpha^{m}$ are obtained from the inverse of the matrix $\left[ F \right]$, which, in turns, is obtained by collocation of $N_{B}$ boundary nodes and $N_{I}$ internal nodes.

3.3 Numerical solution

The boundary and the physical variables are discretized using quadratic isoparametric interpolation in both problems, i.e., the mesoscopic and macroscopic problems. In the corners, discontinuous shape functions with a collocation factor of $\alpha_{dis} = 2/3$ are used [60]. Standard Gaussian interpolation is implemented to compute the regular integrals. The singularities of DLP integrals are treated using the rigid body motion principle [56] and the singular integrals of the SLP, using the Telles transformation [61].

At the mesoscopic scale, i.e., the coupled problem Stokes-Darcy, after the discretization of the contour and physical variables of the problem and applying the boundary and matching conditions, a system of equations is obtained. That system is solved using a singular value decomposition (SVD) algorithm due to the ill-conditioning of the system. More details about the numerical treatment of the Stokes-Darcy formulation considered here can be found in previous works [49, 50]. On the other hand, at the macroscopic scale, the final system can be written as:

$$ \left[ H \right]_{{\left( {N_{B} + N_{I} } \right) \times \left( {N_{B} + N_{I} } \right)}}^{\left( d \right)} \vec{p} - \left[ G \right]_{{\left( {N_{B} + N_{I} } \right) \times N_{B} }}^{\left( d \right)} \vec{q} = \left[ M \right]_{{\left( {N_{B} + N_{I} } \right) \times \left( {N_{B} + N_{I} + 3} \right)}} \cdot \vec{b}, $$

(47)

where the matrix $\left[ M \right]$ is as follows:

$$ \left[ M \right]_{{\left( {N_{B} + N_{I} } \right) \times \left( {N_{B} + N_{I} + 3} \right)}} = \left( {\left[ H \right]_{{\left( {N_{B} + N_{I} } \right) \times \left( {N_{B} + N_{I} } \right)}}^{\left( d \right)} \widehat{\left[ p \right]}_{{\left( {N_{B} + N_{I} } \right) \times \left( {N_{B} + N_{I} + 3} \right)}} - \left[ G \right]_{{\left( {N_{B} + N_{I} } \right) \times N_{B} }}^{\left( d \right)} \widehat{\left[ q \right]}_{{N_{B} \times \left( {N_{B} + N_{I} + 3} \right)}} } \right) + \left[ {F^{ - 1} } \right]_{{\left( {N_{B} + N_{I} + 3} \right) \times \left( {N_{B} + N_{I} + 3} \right)}} $$

(48)

with $\widehat{\left[ p \right]}$ and $\widehat{\left[ q \right]}$ as the matrices corresponding to the evaluation of the particular solutions, $\hat{p}^{m}$ and $\hat{q}^{m}$, in all field points, whereas $\left[ {F^{ - 1} } \right]$ is the inverse of the matrix $\left[ F \right]$. In Eq. (47), the term $\vec{b}$ is highly non-linear and the system is solved using Picard iteration.

3.4 Tracking of the fluid front

The numerical technique used to track the moving boundaries is based on a first-order Euler integration of the kinematic condition, Eq. (11). A detailed description of the numerical implementation of this technique for these particular problems can be found in the Appendix of [50]. Once the meshes of the moving boundaries have been reconstructed at the current time step, and the normal vector and curvatures have been computed, the BEM and DR-BEM algorithms are used to calculate the velocity at the moving boundaries. The cycle is repeated in a quasi-static approach, given the low Reynolds approximation of the problem.

3.5 Post-processing calculations

At the mesoscopic scale, i.e., coupled problem Stokes-Darcy, the fluid velocity inside the channel is computed using Eq. (30) with $c_{ij} = \delta_{ij}$ and the integral representation for the pressure is used to compute the pressure field [56]:

$$ p\left( \xi \right) = 2\mu \int\limits_{S} {\prod\nolimits_{ik} {\left( {\xi ,y} \right)\widehat{{n_{k} }}\left( y \right)u_{i} \left( y \right)dS_{y} - \int\limits_{S} {p_{i} \left( {\xi ,y} \right)t_{i} \left( y \right)dS_{y} ,} } } $$

(49)

where $p_{i} \left( {\xi ,y} \right) = - \frac{1}{{2\pi r^{2} }}\left( {\xi_{i} - y_{i} } \right)$ is the fundamental solution for the pressure and $\prod\nolimits_{ik} {\left( {\xi ,y} \right)} = \frac{1}{2\pi }\left[ {\frac{{\delta_{ik} }}{{r^{2} }} - \frac{2}{{r^{4} }}\left( {\xi_{i} - y_{i} } \right)\left( {\xi_{k} - y_{k} } \right)} \right]$ corresponds to the fundamental solution for the pressure gradient.

In the porous media, the pressure in the interior points is estimated from Eq. (31) doing $c\left( \xi \right) = 1$, while the velocities are given by the Darcy’s law, approximating the pressure gradient in the source point as follows:

$$ \frac{\partial p\left( \xi \right)}{{\partial \xi_{i} }} = \int\limits_{S} {\frac{{\partial p^{*} \left( {\xi ,y} \right)}}{{\partial \xi_{i} }}q\left( y \right)dS_{y} - \int\limits_{S} {\frac{{\partial q^{*} \left( {\xi ,y} \right)}}{{\partial \xi_{i} }}p\left( y \right)dS_{y} } } $$

(50)

At the macroscopic scale, the calculation of the pressure in the interior collocation points is straightforward by solving the system defined in Eq. (47).

4 Methodology for calculation of lumped functions of unsaturated permeability and sink term

4.1 Main assumptions and simplifications

In the present work, the methodology to compute the lumped functions considers both the air compressibility and air dissolution. When air dissolution is present, it is possible to reach the total tow saturation $\left( {S_{t} = 1} \right)$; otherwise, an equilibrium saturation, $S_{t}^{eq}$, is reached. An essential difference between the present methodology and the one employed in [2, 14, 15, 23]–[25] is the prescription of a pressure gradient in the channel rather than a constant pressure; hence, flow in the channel is modelled using Stokes equation and the tows filling is determined by the Darcy law and the matching conditions Stokes-Darcy. The RUC geometry and boundary conditions are sketched in Fig. 1, where three sub-domains can be differentiated: longitudinal tows (warps), transverse tow (weft) and channel.

The RUC geometry chosen here is a very simple idealization of cross-ply or low-crimp degree woven fabrics; this allows reducing the dimensionality of the problem from 3D to 2.5D or 2D, with the consequent reduction in the computational cost. Similar simplifications has been reported before in [2, 9, 13, 18, 26, 27, 45, 62, 65]–[64]. In other works, fully 3D simulations have been performed, leading to more realistic results, but at the expense of an increase of the computational cost [6, 10, 11, 16, 20]. In general, the shape of a fiber fabric is not entirely constant in the transverse direction, but this change is less influential as the yarns spacing and transverse crimp-degree is small; in such a case, 2D simplifications can be suitable. On the other hand, when positioned in the mold, four principal deformation mechanisms arises in bi-directional fabrics [66]: inter-fiber shear, inter-fiber slip, fiber buckling and fiber extension; additionally, nesting occurs during the ply stacking due to the relative layer shift. This causes a more intricated RUC geometry regarding the simple idealization deemed in Fig. 1. However, it is worth mentioning that, in a real application, these deformation phenomena are not uniform along the injection domain, and therefore, a RUC representation accounting for them, is not necessarily replicable to all points of the domain. The consideration of a particular 3D, more complex RUC geometry considering these deformation phenomena, is out of the scope of the present work, but this can be tackled in future researches using the present methodology.

As observed in Fig. 1, the air compressibility is considered for the weft, and total tow saturation is thus not possible when the air dissolution is neglected. For the warps, on the contrary, uncompressed air is deemed because it is considered that air can displace towards the adjacent RUC in the flow direction, considering that, when the problem is conceived at the macroscopic frame (filling of cavities), this adjacent RUC is less saturated than the analysed RUC.

4.2 Definition of scale constraints

As aforementioned, the tows are considered as a bank of aligned fibers, and two phases can be identified: fibers (fb) and fluid (fl). For the modeling of the tows, a Darcy approximation is considered in the present work, which is valid provided that the following conditions are fulfilled [52]:

• The characteristic length of the fluid phase, $L_{fl}$, is significantly smaller than characteristic length of the RUC of the tow, $L_{RUC,tow}$, namely $L_{fl} \ll L_{RUC,tow}$.

• The following length scale constraints are fulfilled: $L_{RUC,tow}^{2} \ll L_{\varepsilon } L_{p1}$ and $L_{RUC,tow}^{2} \ll L_{\varepsilon } L_{v2}$, where $L_{\varepsilon }$, $L_{p1}$ and $L_{v2}$ are the characteristic lengths associated with the change of porosity of fluid phase $\left( {\varepsilon_{fl} } \right)$, the change of first derivate of the intrinsic-phase fluid average pressure $\left( {\nabla \left\langle {P_{fl} } \right\rangle^{fl} } \right)$ and the change of second derivative of the intrinsic-phase fluid average velocity $\left( {\nabla \nabla \left\langle {v_{fl} } \right\rangle^{fl} } \right)$, respectively. If the porous medium is homogeneous and the porosity can be considered uniform, these scale restrictions are fulfilled since $L_{\varepsilon } \to \infty$.

• The following length scale constraint is satisfied: $\left| {\left\langle {y_{fl} } \right\rangle^{fl} } \right| \ll L_{v}$ and $\left| {\left\langle {y_{fl} } \right\rangle^{fl} } \right| \ll L_{fl}$, where $\left\langle {y_{fl} } \right\rangle^{fl}$ is the intrinsic phase position vector of the fluid phase regarding the RUC centroid and $L_{v}$ is the characteristic length associated with the change of the intrinsic-phase fluid average velocity $\left( {\left\langle {v_{fl} } \right\rangle^{fl} } \right)$. These restrictions are satisfied for well-arranged porous media where local porosity changes are negligible.

• The next length scale restriction is fulfilled: $L_{RUC,tow}^{2} \ll L_{v} L_{v1}$, where $L_{v1}$ is the characteristic length associated to the change of first derivative of the intrinsic-phase fluid average velocity $\left( {\nabla \left\langle {v_{fl} } \right\rangle^{fl} } \right)$. This is valid when large gradients of $\left\langle {v_{fl} } \right\rangle^{fl}$ are not present in the porous medium, where the Brinkman correction term can be ignored.

In the particular case of the tows considered in the present work, the first and second condition are fulfilled since the tow porosity is very low and uniform. The third condition is valid because the Representative Unit Cell of the tow is assumed well-ordered and local porosity changes are not relevant. Finally, the fourth condition is satisfied considering the small velocity gradients in the tows, which allows neglecting the Brinkman correction term.

Several simulation cases of the RUC filling are carried out to obtain lumped functions for the unsaturated permeability, $K_{{i_{f} }} \left( s \right)$, and the sink term, $S_{g}$. The RUC geometry and prescribed inlet and outlet pressures of these cases shall comply with several scale constraints that lead to Darcian fluid flow according to [52]. Additionally, the LCM processes entail another scale restrictions. First of all, applying the constraints given in [52] on the gap phase, Darcy’s simplification is possible provided that the following equation is valid for the phase volume-averaged pressure gradient, $\left\langle {\partial P_{g} /\partial x_{i} } \right\rangle$:

$$ \left\langle {\partial P_{g} /\partial x_{i} } \right\rangle = \varepsilon_{g} \left( {\partial \left\langle {P_{g} } \right\rangle^{g} /\partial x_{i} } \right) + \left( {1/V_{RUC} } \right)\int\limits_{{A_{gt} }} {\widetilde{{P_{g} }} \cdot \hat{n}_{gt} dA} , $$

(51)

where $P_{g}$ stands for the pointwise pressure in the channel sub-domain, whereas $\widetilde{{P_{g} }} = P_{g} - \left\langle {P_{g} } \right\rangle^{g}$ is defined as the local variation of the pressure and $\varepsilon_{g} = V_{g} /V_{RUC}$ is the gap volume fraction, with $V_{g}$ as the channel volume. Equation (51), in turns, is valid under the next scale restrictions:

$$ L_{g} \ll L_{RUC} $$

(52)

$$ \left( {L_{RUC} } \right)^{2} \ll L_{\varepsilon g} L_{p1g} , $$

(53)

where $L_{RUC}$ and $L_{g}$ are the characteristic length-scales of the RUC and the channel or gap phase, respectively. On the other hand, $L_{\varepsilon g}$ and $L_{p1g}$ are the characteristic length-scales defined by the estimates $\nabla \varepsilon_{g} = {\mathcal{O}}\left( {{\Delta }\varepsilon_{g} /L_{\varepsilon g} } \right)$ and $\nabla \nabla P_{g}^{g} = {\mathcal{O}}\left( {\nabla P_{g}^{g} /L_{p1g} } \right)$, respectively. In the latter, ${\Delta }$ stands for the absolute change of the variable, while $\nabla$ and $\nabla \nabla$ represent the first and second derivative, respectively. On the other hand, the symbol ${\mathcal{O}}$ is used to denote the order of magnitude. The constraint of Eq. (52) is satisfied in the present work because the average inter-tow distance, which is an acceptable approximation for $L_{g}$, is smaller than the RUC length, $L_{RUC}$ (See Fig. 1). Similarly, the constraint of Eq. (53) is also satisfied here because the porous medium is homogeneous at the macroscopic scale, leading to $L_{\varepsilon g} \to \infty$ [52].

Moreover, in LCM processes, the assumption of full-filled channels is more realistic as the viscous forces exceed the capillary ones. This can be valid when: (1) tows permeabilities, $K_{1}$ and $K_{2}$, are very small regarding the gap permeability, $K_{g}$, and (2) inlet injection pressure, $P_{inj}$, is at least one order of magnitude larger than capillary pressure, which has an order of magnitude of ${\mathcal{O}}\left( 3 \right)$ for LCM processes [5, 67]–[69]. The first condition is fulfilled since $K_{1}$ and $K_{2}$ have an order of ${\mathcal{O}}\left( { - 13} \right)$ and ${\mathcal{O}}\left( { - 14} \right)$, respectively, while the gap permeability has an order of ${\mathcal{O}}\left( { - 9} \right)$, as shown later. To satisfy the second condition, a minimum injection pressure of order ${\mathcal{O}}\left( 4 \right)$ is considered in the macroscopic simulations. On the other hand, according to Park et. al [1], pressure profiles for unidirectional injections in dual-scale fibrous reinforcements can be divided into three categories, as shown in Fig. 3a–c. For the fully saturated zone $\left( {S_{t} = 1} \right)$, pressure profile is linear, while in the partially saturated zone $\left( {S_{t} < 1} \right)$, pressure profile is non-linear and can be approximated by parabolic curves, being concave (Fig. 3a), convex (Fig. 3b) or both ones (Fig. 3c) depending on the magnitude of the mass absorption into the tows; in general, the larger this absorption, the more concave the profile is [70, 71], while a convex shape is liable to be obtained as the mass absorption decreases [72]. Taking into account the possible forms of the pressure profile and considering a minimum order for the injection pressure, $P_{inj}$, of ${\mathcal{O}}\left( 4 \right)$, and a maximum order for the length scale of macroscopic problem, $L$, of ${\mathcal{O}}\left( 0 \right)$, it is expected a minimum order for the pressure gradient of around ${\mathcal{O}}\left( 3 \right)$. As the order of $L_{RUC}$ is ${\mathcal{O}}\left( { - 3} \right)$ in the present work, as shown later, the minimum order for the change of pressure along the RUC, $\Delta p$, could be taken as ${\mathcal{O}}\left( 0 \right)$.

Fig. 3

Common pressure profiles in unidirectional injections for dual-scale fibrous reinforcements. a Linear-Concave, b Linear-Convex, c Linear-Convex-Concave [1]

On the other hand, the maximum order for the pressure gradient is determined by considering a mesoscopic scale restriction for the local velocity variation in the channel phase, $\widetilde{{u_{g} }}$, which establishes that [52]:

$$ \left\langle {\left| {\widetilde{{u_{g} }}} \right|} \right\rangle^{g} \ll \left\langle {u_{g} } \right\rangle^{g} , $$

(54)

where $\widetilde{{u_{g} }} = u_{g} - \left\langle {u_{g} } \right\rangle^{g}$, with $u_{g}$ and $\left\langle {u_{g} } \right\rangle^{g}$ as the pointwise and volume-average gap velocity, respectively.

In some researches about LCM processes, the maximum order for the volume-averaged velocity in the channel, $\left\langle {u_{g} } \right\rangle^{g}$, has been taken as ${\mathcal{O}}\left( { - 1} \right)$ [62, 73, 74] and the maximum order for the fluid viscosity is ${\mathcal{O}}\left( { - 1} \right)$. Consequently, taking into account this, together with the fact that the order of magnitude of gap volume fraction is ${\mathcal{O}}\left( { - 1} \right)$ and the order of magnitude of gap permeability is ${\mathcal{O}}\left( { - 9} \right)$, the maximum order for the pressure gradient, according to Darcy’s law, is ${\mathcal{O}}\left( 6 \right)$, which corresponds to a pressure change along the RUC, $\Delta p$, of order ${\mathcal{O}}\left( 3 \right)$. Additionally, to be consistent with the Stokes approximation for the channels, it is necessary to check that the gap Reynolds number, $R_{eg}$, as defined by Eq. (55), remains small.

$$ R_{eg} = \rho \left\langle {u_{g} } \right\rangle^{g} L_{g} /\mu , $$

(55)

where $\rho$, $\mu$ and $L_{g}$ stand for the liquid density, liquid viscosity and characteristic length of the channel or gap sub-domain, respectively.

4.3 Calculation of effective unsaturated permeability and sink functions

Studies about the effect of saturation on the effective permeability, $K_{eff}$, of fibrous reinforcements, have been conducted before. For instance, Landeryou et al. [4] carried out some experiments in nonwoven samples at different flow rates. They found that the relationship between unsaturated permeability and saturation does not depend on the flow rate. Afterwards, Ashari [3, 5] run some FEM simulations to study the influence of the saturation, fibre diameter and fibre content on the unsaturated permeability of nonwoven reinforcements. Recently, He et al. [6] presented a method to obtain the random permeability field of single-layer woven fabrics using fluid dynamics simulations in ANSYS/CFX, the Karhuven-Loéve expansion method and dimension reducing techniques. On the other hand, the influence of intra-yarn flows on 3D woven fabrics permeability was tackled using Stokes-Darcy simulations by Julien et al. [10]. In the present work, curves of $K_{eff}\,vs\,S_{t}$ are obtained by computing the value of $K_{eff}$ in several time instants as follows:

$$ K_{eff} = - \left\langle {u_{l} } \right\rangle \mu /\left( {{\Delta }P/{\Delta }x} \right), $$

(56)

where ${\Delta }P/{\Delta }x$ is the pressure gradient along the RUC and $\left\langle {u_{l} } \right\rangle$ is the phase volume-averaged velocity of the liquid obtained from the BEM simulations, which includes the channel and the saturated volume of the tows.

On the other hand, the sink term, $S_{g}$, defined in Eq. (20), can be characterized in terms of some volume-averaged variables of the RUC. According to Simacek and Advani [24], $S_{g}$ can be taken as a function of the volume-averaged pressure, $\left\langle {P_{g} } \right\rangle^{g}$, and the tows saturation, $S_{t}$. A sink function, $S_{g}$, of this kind was implemented in macroscopic filling simulations in [16, 17, 23, 25, 35]. A lumped function for $S_{g}$ was deduced in [14, 15] as follows:

$$ S_{g} = \left( {f_{1} \left( {\left\langle {P_{g} } \right\rangle^{g} } \right)/\mu } \right)\left\{ {e^{{A_{2} \left( {1 - S_{t} } \right)^{{A_{3} }} }} - 1} \right\}, $$

(57)

being $f_{1} \left( {\left\langle {P_{g} } \right\rangle^{g} } \right) = \varepsilon_{t} \left( {1 - \varepsilon_{g} } \right)A_{1} \left( {\left\langle {P_{g} } \right\rangle^{g} } \right)$ and $A_{1} \left( {\left\langle {P_{g} } \right\rangle^{g} } \right) = \left( {A_{1}^{*} /\beta^{*} } \right)\left\langle {P_{g} } \right\rangle^{g}$, while the fitting coefficients $A_{1}^{*}$, $A_{2}$, $A_{3}$ and $\beta^{*}$ are determined after running several simulations of the tows filling assuming a constant liquid pressure in the channels.

In the present work, the sink term, $S_{g}$, shall fulfil the principle of mass conservation in the gap or channel sub-domain. Accordingly, for a unitary width RUC, the following is valid:

$$ S_{g} = \frac{{\left( {\overline{u}_{in} - \overline{u}_{out} } \right)H_{g} }}{{H_{RUC} \cdot L_{RUC} }}, $$

(58)

where the mean inlet and outlet velocities of the RUC, $\overline{u}_{in}$ and $\overline{u}_{out}$, are defined by:

$$ \overline{u}_{in} = \left( {\mathop \smallint \limits_{{ - H_{g} /2}}^{{H_{g} /2}} u_{in}\,dy} \right)/H_{g} $$

(59)

$$ \overline{u}_{out} = \left( {\mathop \smallint \limits_{{ - H_{g} /2}}^{{H_{g} /2}} u_{out}\,dy} \right)/H_{g} , $$

(60)

where $u_{in}$ and $u_{out}$ are the pointwise inlet and outlet velocities obtained from the BEM simulations, whereas $H_{g}$ is the gap or channel height.

The sink term, $S_{g}$, and tows saturation rate, $\dot{S}_{t}$, are directly related by the following expression:

$$ S_{g} = \varepsilon_{t} \dot{S}_{t} \left( {1 - \varepsilon_{g} } \right) $$

(61)

where $\varepsilon_{t}$ and $\varepsilon_{g}$ are the tow porosity and gap volume fraction, respectively.

4.4 Characterization of the RUC and tows

Geometrical data used for BEM simulations were obtained from the characterization of a bidirectional fabric. The in-plane dimensions of the RUC were found by visual characterization using stereomicroscopy. In Fig. 4, it is shown how the idealized 2D RUC considered here (Fig. 1) fits to the real fabric architecture. According to such figure, tow width is 2800 µm and distance between bundles is 700 µm, leading to a 2D RUC length of 3500 µm. On the other hand, the natural thickness of the textile preform was measured following the ASTM D-1777 standard, obtaining a value of 0.847 mm. However, it is well known that the real preform thickness depends on the cavity where it is positioned and a larger compaction implies a greater RUC deformation, moving away from the idealized 2D RUC represented in Fig. 1. Therefore, mould thickness and number of plies for experimental tests were selected in order to obtain a similar thickness to the natural one and perverse the original RUC configuration. Accordingly, cavity thickness is 3.2 mm and number of stacked fabrics are 4, reaching an RUC thickness of 0.8 mm, which is very close to the natural one (0.847 mm).

Fig. 4

In-plane characterization of RUC using a stereomicroscope

For the sake of the RUC idealization, to be consistent with the inter-tow free-liquid passage in some parts of the fibrous reinforcement generated by the injection pressure and with the assumption of full filled channels, it is included a small gap between warps and weft (see Fig. 1). The presence of small inter-tow liquid passages has been considered in other works as well [13, 26, 27, 62]–[65].

For the tow characterization, Scanning Electron Microscopy (SEM) was used, as can be observed in Fig. 5. Several zones of the tow were zoomed in and the average fiber radius was found to be $R_{f} = 9.96\;\upmu {\text{m}}$. The tow porosity for each zone was estimated by thresholding binarization image analysis using free software ImageJ, obtaining an average value of $\varepsilon_{t} = 0.19$. Using the Gebart model [53], this leads to main permeabilities of $K_{1} = 1.53 \times 10^{ - 13} \;{\text{m}}^{2}$ and $K_{2} = 1.80 \times 10^{ - 14} \;{\text{m}}^{2}$. Similar values of tow porosity and permeabilities have been considered in previous works [2, 7, 10, 69, 75].

Fig. 5

Tow characterization using Scanning Electron Microscopy and free image analysis software ImageJ. a Front view of one bundle, b Front view of zoomed-in zone of the bundle and corresponding thresholding binarization, c Top view of several bundles and diameter measurements

5 Simulation planning, results and discussion

5.1 Analysis of saturation at the mesoscopic scale

5.1.1 Saturation curves assuming a uniform channel pressure

Firstly, some filling simulations of the RUC represented in Fig. 1 are run using BEM and assuming a uniform channel pressure, as done in [2, 14, 15, 23]–[25]. Additionally, air compressibility, partial air dissolution and vacuum pressure are not considered, and it is assumed full air dissolution. Data to run these simulations are shown in Table 1, where the channel pressures, $\left\langle {P_{g} } \right\rangle^{g}$, coincide with the ones used in [2, 14]. Dimensions of the RUC geometry considered here (Fig. 1) are reported in Table 1, namely, L_RUC, H_RUC, H_g, a₁ and a₂.

Table 1 Data of simulations with the uniform-pressure methodology

It is defined a normalized time to construct the saturation curves, as follows:

$$ \tau = t/t_{fill}, $$

(62)

where $t_{fill}$ is the total filling time, which is obtained from the BEM simulations and is reported in Table 2. The RUC geometries considered in Wang and Grove [2] and Tan [14] are represented in Fig. 6a, b, respectively, while the RUC geometry of the present work is displayed again in Fig. 6c. Using BEM results, the curves of $S_{t} vs. \, \tau$ for all values of $\left\langle {P_{g} } \right\rangle^{g}$ of Table 1 were obtained as shown in the Fig. 6f. When these curves are compared to the curves of the Fig. 6d, e, which correspond to the saturation curves obtained in [2] and [14] using FEM, respectively, some similarities can be identified. As can be observed, results converge into a single master curve; besides, despite curves are not the same since RUC geometries are different, a similar general behaviour of the saturation rate is observed: it is significant at the beginning of the injection and decreases as the filling occurs.

Table 2 Filling times obtained from BEM simulations with the uniform-pressure methodology

Fig. 6

Comparison of saturation curves. a RUC geometry of Wang and Grove [2], b RUC geometry of Tan [14], c RUC geometry of present work, d Saturation curve of Wang and Grove [2], e Saturation curve of Tan [14], f Curve $S_{t}\,vs.\,\tau$ of present work

5.1.2 RUC filling using the present methodology

Two BEM simulations of the RUC filling are compared to each other (Figs. 7a–c and 8a–k) to illustrate the principal differences between the constant-pressure methodology and the present one. In both simulations, for each filling instant, they are shown: the ratio of the current time to the total simulation time $\left( {t/t_{sim} } \right)$, warps saturation ($S_{warps} )$, weft saturation ($S_{weft} )$ and total tow saturation ($S_{t} )$. In those figures, $x$ and $y$ coordinates are reported in normalized form as $x^{*} = x/L_{RUC}$ and $y^{*} = y/L_{RUC}$. The geometric and material inputs of both simulations are shown in Table 1. On the other hand, the processing inputs for the simulation of Fig. 7a–c are a uniform channel pressure of $\left\langle {P_{g} } \right\rangle^{g} = 122\;{\text{kPa}}$ and a fluid front pressure equal to the atmospheric one, i.e., $P_{vac} = 0\;{\text{kPa}}$, whereas, for simulation of Fig. 8a–k, inlet and outlet pressures of $p_{in} = 125.5\;{\text{kPa}}$ and $p_{out} = 118.5\;{\text{kPa}}$ are considered, which originates a pressure gradient along the RUC of $\Delta P/\Delta x = 2.00 \times 10^{3} \;{\text{kPa/m}}$, with a corresponding average pressure of $\left\langle {P_{g} } \right\rangle^{g} = 122\;{\text{kPa}}$, coinciding with the average pressure of the other simulation (Fig. 7a–c). For the simulations with the present methodology (Fig. 8a–k), a vacuum pressure of $P_{vac} = - 75\;{\text{kPa}}$ is taken into account, remaining constant in the warps and changing in the weft in virtue of the air compression. The case analysed in Fig. 8a–k corresponds to full air compressibility, but the present methodology also allows considering the partial air dissolution, as shown later.

Fig. 7

Instants of filling with the constant-pressure methodology. a Warps and weft unsaturated, b Total saturation of warps, c Total saturation of the RUC

Fig. 8

Instants of filling with the proposed Stokes-Darcy methodology assuming full air compressibility. a Warps and weft unsaturated, b Total saturation of warps, c Instant of end of void compression and the onset of void mobilization, d Motion towards the right extreme of the weft, e Detail of Fig. 6d, f Arrival of a bubble to right extreme of the weft and onset of void migration, g Detail of Fig. 6f, h Stage 1 of void migration, i Stage 2 of void migration, j Stage 3 of void migration (until the bubble is in the neighborhood of the RUC’s edge), k Detail of void migration

Several filling instants for the simulation with the constant-pressure methodology are shown in Fig. 7a–c. As can be observed in all sub-plots and confirmed with the data tips of Fig. 7a, the fluid front moves uniformly, namely, parallel to the superior and inferior edges for the warps, and towards the center of the RUC for the weft, which is reasonable since the pressure is uniform along the channel-tows interface. According to this approach, the air in the weft escapes at the same tow saturation rate (full air dissolution), leading to the total RUC saturation.

For the present methodology, several filling instants are represented in Fig. 8a–k. Contrarily to the previous case, as the filling occurs, the fluid fronts in the warps and weft are not uniform (see data tips of Fig. 8a) since the pressure in the channel-tows interface is variable. From Fig. 8a–c, the bubble in the weft compresses; but, when air pressure has reached the value of the maximum pressure of liquid surrounding the weft plus the capillary pressure, the bubble compression stops, and the onset of void mobilization takes place (green line in Fig. 8c). From this time instant onwards, the change of the weft saturation, $S_{weft}$, is negligible and an equilibrium saturation, $S_{t}^{eq}$, is achieved because the bubble moves towards the right extreme of the weft, changing its shape without changing its volume (Fig. 8d–g). The details of Fig. 8d, f are shown in Fig. 8e, g, respectively, where green lines represent the void displacement. The process of void migration can be seen in Fig. 8h–k, where the ratios $t/t_{sim}$ are very close to the unity because this process is much faster than the other two processes undergone by the bubble (compression and displacement at constant volume). Although the analysis of compression, displacement and migration of intra-tow voids is not the focus of the present work, it is essential to highlight that the current methodology allows simulating these processes, as previously detailed in [50].

To conclude the present section, the fulfilment of the constraint of Eq. (54) is verified considering the horizontal velocities in the channel sub-domain obtained by BEM at the filling instants represented in Fig. 8a–j. The ratio $\left\langle {\left| {\widetilde{{u_{g} }}} \right|} \right\rangle^{g} /\left\langle {u_{g} } \right\rangle^{g}$ for each of these instants is computed, obtaining the results shown in Table 3, where it is appreciated that this restriction is satisfied in all moments.

Table 3 Ratio $\left\langle { \left| {\widetilde{{u_{g} }}} \right|} \right\rangle^{g} /\left\langle {u_{g} } \right\rangle^{g}$ for filling instants of Fig. 6a-j

5.2 Calculation of the lumped functions

5.2.1 Statement of the problem and simulation data

The air dissolution dynamics is a complex phenomenon that mainly depends on the partial air pressure (which is function on the air composition), temperature and liquid composition. The Henry´s law approach has been frequently used to estimate the solubility of gases into liquids [76], but the determination of the Henry´s laws constants is not a simple task. Experimental, semi-analytical and numerical methods have been employed before, but they could have some drawbacks. For instance, experimental methods usually demand a considerable amount of tests to obtain statistically confident values, whereas computational methods, like Monte Carlo [77, 78] and Molecular dynamics simulations [79, 80], do not provide a satisfactory trade-off between time–cost and accuracy in complex molecules. On the other hand, the application of semi-analytical models is limited and implies the availability of other experimental constants, like the solubility, which in turns depends on another parameters like volatilization, entropy, enthalpy of solvation, intrinsic hydrophobicity, among others. Many semi-analytical, molecular models are based on the supposition that the free energy change on dissolution is a linear function of the molecular properties; these are known as LSER models and have shown an acceptable accuracy for the dissolution of some organic compounds into water [81]–[84]. In the particular case of air dissolution in polymeric resins, some phenomena entail additional complexity [85]–[87]: the continuous change of composition of the entrapped air due to the styrene vapour formation, the change of the resin temperature, viscosity and species concentration during the curing process, the possible change of the resin composition near the void due to the fiber sizing wash-out, among others.

Bearing in mind the complexity of the air dissolution mechanism, this has been considered at the macroscopic equations in a lumped fashion [39, 86] by introducing a weighting factor, λ, in the pressure boundary condition of the fluid front, in such a way that for λ = 0, the rate of air dissolution is so fast that air entrapment is neglected and initial air pressure remains constant (full air dissolution), whereas for λ = 1, no air dissolution is present and the air pressure increases obeying the ideal gas law (full air compressibility). Both extreme situations were compared in the previous section, Figs. 7a–c and 8a–k. According to [39, 69, 86, 88], these extreme conditions are not feasible to occur in a real situation and the behaviour of the air entrapped inside the tow can be considered as a weighted average between both limits, with the following equation describing the fluid front pressure at the liquid–air interphase:

$$ P_{ff} = \left( {1 - \lambda } \right)P_{ff}^{lower} + \lambda P_{ff}^{upper} , $$

(63)

where $P_{ff}$, $P_{ff}^{lower}$ and $P_{ff}^{upper}$ stand for the fluid front pressure, and lower and upper bounds of the fluid front pressure, respectively, whereas $\lambda$ is the air entrapment parameter or dissolution factor, ranging between 0 and 1. The values of $P_{ff}^{lower}$ and $P_{ff}^{upper}$ are given by the following equations assuming an ideal gas [88]:

$$ P_{ff}^{lower} = P_{vac} - P_{cap} $$

(64)

$$ P_{ff}^{upper} = \min \left( {P_{vac} /\left( {1 - S_{weft} } \right),P_{liquid} } \right) - P_{cap} , $$

(65)

with $P_{vac}$, $P_{cap}$ and $P_{liquid}$ as the vacuum pressure, capillary pressure, and maximum pressure of the liquid surrounding the tow. When $\lambda = 0$, the case of full air dissolution is obtained (Fig. 7a–c), while for $\lambda = 1$, the case of full air compressibility is reached (Fig. 8a–k).

In the present section, the deduction of the lumped functions is carried out by running several simulations at the mesoscopic scale. As shown in Table 4, 56 sets of simulations are considered and, for each set, five air entrapment parameters are taken into account; namely, $\lambda = 1$ (full air compressibility), $\lambda = 0.75$, $\lambda = 0.50$, $\lambda = 0.25$ and $\lambda = 0$ (full air dissolution), obtaining a total of 280 simulations for the parametric study. Geometric and material data that are kept constants in the simulations are presented in Table 1, except for the viscosity, which is changed in the last four sets of simulations (53 to 56 in Table 4). The flow orientation-dependent capillary pressure, $P_{cap}$, is computed according to the models presented in [49].

Table 4 Sets of simulations for the determination of the lumped functions

5.2.2 Influence of average pressure and pressure gradient on the saturation curves

Firstly, to study how the average pressure and pressure gradient affect the behaviour of the total saturation, $S_{t}$, several curves of $S_{t}\,vs.\,\tau$ are shown in Fig. 9 for the case of full air compression, taking $P_{vac} = - 75\;{\text{kPa}}$. In this case, time is non-dimensionalized with the equilibrium time, which is the time to reach the equilibrium saturation, $S_{t}^{eq}$. Curves of Fig. 9 correspond to some simulations from sets 1 to 31 of Table 4 considering $\lambda = 1$. In all curves, time instant from which the total tow saturation, $S_{t}$, remains nearly constant, and void mobilisation occurs (see Fig. 8c) corresponds to $\tau= 1$. As can be observed, all simulations having the same average pressure, $\left\langle {P_{g} } \right\rangle^{g}$, tend to converge into a single curve for the present small-Reynolds-number simulations, no matter the value of the pressure gradient, $\Delta P/\Delta x$; however, the prescription of a pressure gradient, $\Delta P/\Delta x$, different to zero, induces several physically consistent phenomena at the mesoscopic scale that cannot be captured when uniform pressure is deemed for the channels, as aforementioned (Fig. 8a–k). The same conclusion can be addressed for the other values of the air entrapment parameter, $\lambda$, where the total tow saturation is possible.

Fig. 9

Influence of $\left\langle {P_{g} } \right\rangle^{g}$ and $\Delta P/\Delta x$ on the saturation curve $S_{t}\,vs.\,\tau$ considering full air compression $\left( {\lambda = 1} \right)$

5.2.3 Equilibrium saturation

For $\lambda < 1$, the equilibrium saturation is $S_{t}^{eq} = 1$ since full filling is possible, whereas for $\lambda = 1$, the value of $S_{t}^{eq}$ is not known a priori and shall be determined using the results of BEM simulations. According to the curves presented in Fig. 9, the equilibrium saturation,$S_{t}^{eq}$, depends on the average pressure, $\left\langle {P_{g} } \right\rangle^{g}$, in such a way that the larger $\left\langle {P_{g} } \right\rangle^{g}$, the higher $S_{t}^{eq}$. This poses the necessity to obtain a function for $S_{t}^{eq}$ when $\lambda = 1$. Accordingly, several curves of $S_{t}^{eq}$ vs. $\left\langle {P_{g} } \right\rangle^{g}$ for different values of vacuum pressure, $P_{vac}$, are presented in Fig. 10, where it can be observed that a bi-exponential fitting is suitable in this case for all values of $P_{vac}$, obtaining the following regression equation:

$$ S_{t}^{eq} = a_{eq} \left( {\left| {P_{vac} } \right|} \right) \cdot e^{{b_{eq} \left( {\left| {P_{vac} } \right|} \right) \cdot \left\langle {P_{g} } \right\rangle^{g} }} + c_{eq} \left( {\left| {P_{vac} } \right|} \right) \cdot e^{{d_{eq} \left( {\left| {P_{vac} } \right|} \right) \cdot \left\langle {P_{g} } \right\rangle^{g} }} $$

(66)

Fig. 10

Influence of $\left\langle {P_{g} } \right\rangle^{g}$ and $P_{vac}$ on the equilibrium saturation, $S_{t}^{eq}$, for $\lambda = 1$

The change of the fitting coefficients $a_{eq}$, $b_{eq}$, $c_{eq}$ and $d_{eq}$ with the magnitude of the vacuum pressure, $\left| {P_{vac} } \right|$, is shown in Figs. 11a, b, where some tendencies can be noticed. For the fitting coefficients $a_{eq}$ and $c_{eq}$ (Fig. 11a), a linear regression is adequate, whereas for $b_{eq}$ and $d_{eq}$ (Fig. 11b), an exact bi-exponential interpolation can be deemed. Regression equations, fitting coefficients and determination coefficients are shown in such figures.

Fig. 11

Change of fitting coefficients of the function $S_{t}^{eq}$ with the vacuum pressure. a $a_{eq}$, $c_{eq}$ vs. $\left| {P_{vac} } \right|$, b $b_{eq}$, $d_{eq}$ vs. $\left| {P_{vac} } \right|$

5.2.4 Determination of the sink function, ${\text{S}}_{{\text{g}}}$

Two procedures can be implemented for the determination of the sink term, $S_{g}$. In the first one, the saturation rate, $\dot{S}_{t}$, is computed from the plot of $S_{t}\,vs\,t$ taking the numerical derivatives and then, Eq. (61) is used to calculate $S_{g}$; the gap volume fraction, $\varepsilon_{g}$, can be computed as follows (see Fig. 1 for identification of geometrical variables):

$$ \varepsilon_{g} = 1 - \frac{{\left( {H_{RUC} - H_{g} } \right)L_{RUC} + \pi a_{1} a_{2} }}{{H_{RUC} \cdot L_{RUC} }}, $$

(67)

corresponding to a value of $\varepsilon_{g} = 0.202$ in the present work. This indirect procedure for the calculation of $S_{g}$ has been previously used in [2, 14, 15]. On the other hand, in the second procedure, $S_{g}$ is directly acquired from the mass transfer from the channels towards the tows, which can be estimated once the velocity field along the channel-tows interface is known from the BEM solution. The comparison among both procedures is shown in Fig. 12a, b considering $\lambda = 1$, where the plots of $S_{g} vs. S_{t}$ for several combinations of $\left\langle {P_{g} } \right\rangle^{g}$ and $P_{vac}$ are presented. Considering all points of these figures, the average relative difference between both procedures, defined here as $L_{1} = \left( {1/N_{point} } \right)\mathop \sum \nolimits_{i = 1}^{{N_{point} }} \left| {S_{g}^{ind} - S_{g}^{dir} } \right|/S_{g}^{dir}$, where $N_{point}$, $S_{g}^{ind}$ and $S_{g}^{dir}$ are the number of points, sink term computed by the indirect procedure and sink term computed by the direct procedure, respectively, is $L_{1} = 0.0554$, obtaining a good coincidence.

Fig. 12

Comparison between direct and indirect procedures for the calculation of $S_{g}$. a Complete range of $S_{g}$, b Reduced range of $S_{g}$. In the indirect procedure, the saturation rate is obtained from numerical derivatives of $S_{t}\,vs\,t$ curves and $S_{g}$ is computed using Eq. (61). In the direct procedure, $S_{g}$ is obtained from the mass transfer from channels towards tows computed in the BEM solution

Using results of FEM simulations, a three-parameter regression function for the sink term, $S_{g}$, has been adopted in previous works [2, 14, 15]. The form of this function was presented in Eq. (57) and is the starting point to propose another lumped function here. Initially, it is essential to highlight that in the case of full air compressibility, $\lambda = 1$, the total tow saturation is not possible, and Eq. (57) is thereby modified with the purpose to set $S_{g}$ to zero when the equilibrium saturation, $S_{t}^{eq}$, is reached. Accordingly, Eq. (57) is rewritten as Eq. (68), which can be used for any value of $\lambda$, considering that $S_{t}^{eq} = 1$ when $\lambda < 1$:

$$ S_{g} = \left( {f_{1} \left( {\left\langle {P_{g} } \right\rangle^{g} } \right)/\mu } \right)\left\{ {e^{{A_{2} \left( {S_{t}^{eq} - S_{t} } \right)^{{A_{3} }} }} - 1} \right\} $$

(68)

Additionally, to evaluate the convenience of the model of Eq. (68), some regression curves of this model for the BEM results, computing $S_{g}$ by the direct method, are considered. The case of full air compressibility, $\lambda = 1,$ considering $\left\langle {P_{g} } \right\rangle^{g} = 202\;{\text{kPa}}$ and $P_{vac} = - 75\;{\text{kPa}}$, is represented in Fig. 13a, whereas a second case corresponding to partial air dissolution with $\lambda = 0.5$, $\left\langle {P_{g} } \right\rangle^{g} = 62\;{\text{kPa}}$ and $P_{vac} = - 25\;{\text{kPa}}$, is represented in Fig. 13b. In both cases, some significant differences between the fitting model and BEM results can be noticed. Similar differences were found in the work of Wang and Grove [2], as shown in Fig. 13c. A potential type function is added here to improve this fitting model with an extra free parameter, $A_{4}$, as shown in Eq. (69). It is worth-mentioning that this equation also fulfils the physical condition of zero net infiltration into the tows, $S_{g} = 0$, when the equilibrium saturation is reached, $S_{t} = S_{t}^{eq}$.

$$ S_{g} = \left( {f_{1} \left( {\left\langle {P_{g} } \right\rangle^{g} } \right)/\mu } \right)\left\{ {e^{{A_{2} \left( {S_{t}^{eq} - S_{t} } \right)^{{A_{3} }} }} - 1 + \left( {S_{t}^{eq} - S_{t} } \right)^{{A_{4} }} } \right\} $$

(69)

Fig. 13

Comparison between fitting models. a Original fit model for $\lambda = 1,$ $\left\langle {P_{g} } \right\rangle^{g} = 202\;{\text{kPa}}$ and $P_{vac} = - 75\;{\text{kPa}}$, b Original fit model for $\lambda = 0.5,$ $\left\langle {P_{g} } \right\rangle^{g} = 62\;{\text{kPa}}$ and $P_{vac} = - 25\;{\text{kPa}}$, c Original fit model in the work of Wang and Grove [2], d Improved fit model for $\lambda = 1,$ $\left\langle {P_{g} } \right\rangle^{g} = 202\;{\text{kPa}}$ and $P_{vac} = - 75\;{\text{kPa}}$, e Improved fit model for $\lambda = 0.5,$ $\left\langle {P_{g} } \right\rangle^{g} = 62\;{\text{kPa}}$ and $P_{vac} = - 25\;{\text{kPa}}$

The fitting curves of the modified model for the two cases referred to before are presented in Fig. 13d, e, respectively, where it can be observed a better correlation with BEM results. The value of the determination coefficient of the modified model is $R^{2} = 0.995$ for the first case (Fig. 13d) and $R^{2} = 0.996$ for the second one (Fig. 13e), whereas, for the original model, these values are $R^{2} = 0.941$ (Fig. 13a) and $R^{2} = 0.949$ (Fig. 13b), respectively.

Considering the dependency of fitting coefficients of Eq. (69) on $\left\langle {P_{g} } \right\rangle^{g}$, $P_{vac}$ and $\lambda$, a more general form of this equation can be written as:

$$ S_{g} = \left( {f_{1} \left( {\left\langle {P_{g} } \right\rangle^{g} ,P_{vac} ,\lambda } \right)/\mu } \right). $$

$$ \left\{ {\begin{array}{*{20}c} {e^{{A_{2} \left( {\left\langle {P_{g} } \right\rangle^{g} ,P_{vac} ,\lambda } \right) \cdot \left( {S_{t}^{eq} - S_{t} } \right)^{{A_{3} \left( {\left\langle {P_{g} } \right\rangle^{g} ,P_{vac} ,\lambda } \right)}} }} } \\ { - 1 + \left( {S_{t}^{eq} - S_{t} } \right)^{{A_{4} \left( {\left\langle {P_{g} } \right\rangle^{g} ,P_{vac} ,\lambda } \right)}} } \\ \end{array} } \right\} $$

(70)

Using a similar approximation to previous works [2, 14, 15], the function $f_{1}$ of Eq. (70) can be written as: $f_{1} \left( {\left\langle {P_{g} } \right\rangle^{g} ,P_{vac} ,\lambda } \right) = \varepsilon_{t} \left( {1 - \varepsilon_{g} } \right) \cdot A_{1} \left( {\left\langle {P_{g} } \right\rangle^{g} ,P_{vac} ,\lambda } \right)$. The fitting parameters $A_{1} , A_{2} , A_{3}$ and $A_{4}$ for each combination of $\left\langle {P_{g} } \right\rangle^{g}$ and $P_{vac}$ are obtained using the curve fitting toolbox of Matlab with a non-linear least square, bi-square weighted method employing the truss-region algorithm; this tool is integrated with an in-house algorithm to estimate the upper and lower bounds of the fitting parameters to reach monotonic relationships between these parameters and $\left\langle {P_{g} } \right\rangle^{g}$, $P_{vac}$ and $\lambda$ based on prescribed trend equations.

To illustrate how parameters $A_{1} , A_{2} , A_{3}$ and $A_{4}$ are achieved, the case of full air dissolution, $\lambda = 0$, is considered. Initially, fitting parameters are not bounded, and their behaviour with $\left\langle {P_{g} } \right\rangle^{g}$ and $P_{vac}$ is observed to establish possible monotonic trends. Then, the upper and lower bounds of the fitting parameters are recursively modified to improve the observed correlations, aiming to maintain the precision of the fitting model, Eq. (70). This process is done with the help of the Matlab curve fitting toolbox and the in-house algorithm developed here; this is not carried out simultaneously in all parameters, but consecutively, since the modification of the bounds of one parameter can lead to the change of the remaining parameters as well, with the possible modification of their behaviour with $\left\langle {P_{g} } \right\rangle^{g}$ and $P_{vac}$. Using this procedure, a linear relationship between $A_{1}$ and $\left\langle {P_{g} } \right\rangle^{g}$ can be achieved when vacuum pressure,$P_{vac}$, is constant, as shown in Fig. 14a. Additionally, the fit curves are nearly parallel each other, as it can be confirmed by comparing the slopes of the regression equations; the average slope of these curves is $m_{1}^{av} = 9.88 \times 10^{ - 7}$. On the other hand, according to Fig. 14b, the intercepts of the fitting curves of Fig. 14a change almost linearly with $\left| {P_{vac} } \right|$, and the slope of the linear fitting curve for the plot of Intercept vs $\left| {P_{vac} } \right|$ shown in Fig. 14b is $m_{1}^{*} = 1.051 \times 10^{ - 6}$. As $m_{1}^{av}$ and $m_{1}^{*}$ are similar, it is reasonable to suppose that $A_{1}$ is approximately a linear function of $\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|$, which can be confirmed in Fig. 14c. A similar analysis can be done for the parameter $A_{2}$, which can also be conceived as a linear function of $\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|$, see Fig. 14d. Considering the linear variation of parameters $A_{1}$ and $A_{2}$ with $\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|$, parameters $A_{3}$ and $A_{4}$ are found to fit well to a power-type function in terms of $\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|$, as shown in Fig. 14e, f. Accordingly, Eq. (70) can be expressed as a function of $\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|$ as follows:

$$ S_{g} = \left( {f_{1} \left( {\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|} \right)/\mu } \right) \cdot \left\{ {e^{{A_{2} \left( {\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|} \right) \cdot \left( {S_{t}^{eq} - S_{t} } \right)^{{A_{3} \left( {\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|} \right)}} }} - 1 + \left( {S_{t}^{eq} - S_{t} } \right)^{{A_{4} \left( {\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|} \right)}} } \right\} $$

(71)

where:

$$ f_{1} \left( {\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|} \right) = \varepsilon_{t} \left( {1 - \varepsilon_{g} } \right)A_{1} \left( {\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|} \right) $$

(72)

$$ A_{1} \left( {\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|} \right) = \alpha_{1} \left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right| + \beta_{1} $$

(73)

$$ A_{2} \left( {\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|} \right) = \alpha_{2} \left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right| + \beta_{2} $$

(74)

$$ A_{3} \left( {\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|} \right) = \alpha_{3} \left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|^{{\beta_{3} }} $$

(75)

$$ A_{4} \left( {\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|} \right) = \alpha_{4} \left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|^{{\beta_{4} }} $$

(76)

and the fitting coefficients obtained are given in Table 5. The abovementioned procedure is repeated for the other values of $\lambda$ considered in this work $\left( {\lambda = \left[ {0.25, 0.5,0.75,1} \right]} \right)$. According to the BEM results, the functions for $A_{1} , A_{2} , A_{3}$ and $A_{4}$ have the same form as for the last case of $\lambda = 0$ (Eq. (73) to Eq. (76)), with fitting coefficients also given in Table 5.

Fig. 14

Plots to find the fitting coefficients of the sink function, $S_{g}$, for $\lambda = 0$. a $A_{1} \;vs\;\left\langle {P_{g} } \right\rangle^{g}$ for several values of $P_{vac}$, b Intercept vs $\left| {P_{vac} } \right|$, c $A_{1} \;vs\;\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|$, d $A_{2} \;vs\;\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|$, e $A_{3} \;vs\;\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|$, f $A_{4} \;vs\;\left| {P_{vac} - \left\langle {P_{g} } \right\rangle^{g} } \right|$

Table 5 Fitting coefficients of the regression model for $S_{g}$

5.2.5 Determination of the effective unsaturated permeability function, $K_{eff}$

Equation (56) is used to compute the effective unsaturated permeability, $K_{eff}$, of the fibrous reinforcement. In that equation, $\left\langle {u_{l} } \right\rangle$ is the phase volume-averaged horizontal velocity in the liquid phase, which can be obtained from the BEM simulations as follows:

$$ \left\langle {u_{l} } \right\rangle = \frac{{\left( {\int\limits_{{A_{g} }} {u_{g} \cdot dA_{g} + \int\limits_{{A_{tows}^{sat} }} {\left\langle {u_{l}^{tows} } \right\rangle^{l} \cdot dA_{tows}^{sat} } } } \right)}}{{A_{RUC} }}, $$

(77)

where $u_{g}$ is the pointwise horizontal velocity of liquid in the channel or gap sub-domain, $A_{g}$ is the area of the channel sub-domain, $\left\langle {u_{l}^{tows} } \right\rangle^{l}$ is the intrinsic-phase volume-averaged horizontal velocity of liquid in the tows, $A_{tows}^{sat}$ is the saturated area of the tows and $A_{RUC}$ is the total area of the RUC. It is important to remark that the numerical calculation of the velocity fields of channel and tows by BEM techniques was presented in Sect. 3. Equation (77) can also be written in terms of the phase volume-averaged velocity of the channel sub-domain, $\left\langle {u_{g} } \right\rangle$, as follows:

$$ \left\langle {u_{l} } \right\rangle = \left\langle {u_{g} } \right\rangle + \left( {\int\limits_{{A_{tows}^{sat} }} {\left\langle {u_{l}^{tows} } \right\rangle^{l} \cdot dA_{tows}^{sat} } } \right)/A_{RUC} $$

(78)

Simulations considered for calculation of $S_{g}$ (see Table 4) were considered as well for calculation of $K_{eff}$. Curves of $K_{eff}\,vs.\,S_{t}$ for different values of $\left\langle {P_{g} } \right\rangle^{g}$, $P_{vac}$ and $\lambda$ are presented in Fig. 15a–c, where it is observed that these curves are not significantly dependent on the vacuum pressure, $P_{vac}$; they are functions of the average pressure, $\left\langle {P_{g} } \right\rangle^{g}$, and the dissolution factor, $\lambda$. The behavior of the $K_{eff}$ vs $S_{t}$ curve depends on the micro-structure of the porous medium. In the present case, an increase in the curve slope can be noticed as S_t tends to 1. This behavior has been previously reported for the in-plane effective permeability in non-woven fabrics [4, 89, 90] and wicks [91] in a more noticeable way, but, to the best of our knowledge, no additional works have been conducted in cross-ply or low-crimped woven fabrics to validate this behavior. For the through-plane permeability of non-woven fabrics, an opposite behavior has been reported, namely, curve slope decreases with saturation [5].

Fig. 15

a Curves of $K_{eff}\,vs.\,S_{t}$ for different values of $\left\langle {P_{g} } \right\rangle^{g}$ and $P_{vac}$, with $\lambda = 0$, b Curves of $K_{eff}\,vs.\,S_{t}$ for different values of $\left\langle {P_{g} } \right\rangle^{g}$ and $P_{vac}$, with $\lambda = 0.5$, c Curves of $K_{eff}\,vs.\,S_{t}$ for different values of $\left\langle {P_{g} } \right\rangle^{g}$ and $\lambda$, with $P_{vac} = 0 kPa$

On the other hand, the ratios between the saturated and unsaturated permeabilities reached from Fig. 15a–c are greater than one, with a maximum ratio of 1.47. According to Park and Lee [1], this ratio can be larger or lower than the unity, but in an experimental benchmark exercise conducted by recognized universities [92], it was found that this ratio is larger than one for bidirectional fabrics, agreeing with the present numerical results. It is important to mention that the maximum ratio found here (1.47) could be in the range of experimental uncertainty of the tests used for the permeability characterization. For instance, in the benchmark exercise previously mentioned [92], the uncertainty of some saturated and unsaturated permeability tests, as quantified by the ratio between the maximum and minimum measurement, exceed this value; however, the average values reported for the saturated and unsaturated permeabilities in such a work are consistent with the results of saturated/unsaturated permeability ratios greater than one obtained here.

In Fig. 16, they are considered several plots of $K_{eff} vs S_{t}$ for the full air dissolution case, $\lambda = 0$, with their respective third-order polynomial fitting curves, regression equations and determination coefficients (R²), obtained with the Matlab's curve fitting toolbox. As can be observed, a third-order polynomial fitting is suitable to represent $K_{eff}$ in terms of $S_{t}$, in such a way that the following regression equation can be considered:

$$ K_{eff} \left( {S_{t} } \right) = P_{1} \left( {\left\langle {P_{g} } \right\rangle^{g} ,\lambda } \right) \cdot S_{t}^{3} + P_{2} \left( {\left\langle {P_{g} } \right\rangle^{g} ,\lambda } \right) \cdot S_{t}^{2} + P_{3} \left( {\left\langle {P_{g} } \right\rangle^{g} ,\lambda } \right) \cdot S_{t} + P_{4} \left( {\left\langle {P_{g} } \right\rangle^{g} ,\lambda } \right) $$

(79)

with $P_{1}$, $P_{2}$, $P_{3}$ and $P_{4}$ as fitting coefficients linearly dependent on $\left\langle {P_{g} } \right\rangle^{g}$, as shown in Fig. 17; this way, any fitting parameter of Eq. (79), $P_{i}$, with i = 1,2,3,4, can be written as:

$$ P_{i} = m_{pi} \cdot \left\langle {P_{g} } \right\rangle^{g} + b_{pi} $$

(80)

where $m_{pi}$ and $b_{pi}$ stand for the slope and intercept of the fitting curve for $P_{i}$ in terms of the average pressure, $\left\langle {P_{g} } \right\rangle^{g}$. For the other values of the dissolution factor, $\lambda$, the fit model given by Eq. (79) and Eq. (80) is applicable as well. Fitting coefficients $m_{pi}$ and $b_{pi}$ of the regression model for the effective unsaturated permeability, $K_{eff}$, are shown in Table 6. In this point, it is essential to remark that $S_{t}$ refers to the total tows saturation and is related to the total RUC saturation, s, as follows: $s = S_{ch} \varepsilon_{g} + S_{t} \left( {1 - \varepsilon_{g} } \right)$, where $S_{ch}$ is the saturation of the channel or gap sub-domain; since it is supposed that the time scale of the gap filling is several orders of magnitude lower than such of the tows filling, $S_{ch}$ can be set to one in the last expression.

Fig. 16

Fitting curves of K_eff vs S_t for several values of $\left\langle {P_{g} } \right\rangle^{g}$, with $\lambda = 0.$

Fig. 17

Fitting parameters, $P_{i}$, in terms of the average pressure, $\left\langle {P_{g} } \right\rangle^{g}$, with the corresponding linear regression equations, for $\lambda = 0$

Table 6 Fitting coefficients of the regression model for $K_{eff}$

5.2.6 Determination of the gap permeability, ${\text{K}}_{{\text{g}}}$

Gap permeability, $K_{g}$, accounts for the easiness of impregnation of the channels considering that the tows are impermeable. Accordingly, this property is only dependent on the channels architecture in the RUC. This is estimated in the present work by setting the normal permeability of tows to zero and using the following equation:

$$ K_{g} = \left\langle {u_{g} } \right\rangle \mu /\left( {{\Delta }P/{\Delta }x} \right) $$

(81)

where $\left\langle u_{g}\right\rangle$ is the phase volume-averaged horizontal velocity in the channel or gap sub-domain obtained by BEM.

In Fig. 18, $K_{g}$ is reported for several values of ${\Delta }P/{\Delta }x$ and $\left\langle {P_{g} } \right\rangle^{g}$, finding a negligible standard deviation for the results, ${\text{SD}} = 6.56 \times 10^{ - 14}$, which corroborates that $K_{g}$ should remain constant, independent of the processing parameters, as long as the RUC geometry is not altered. Therefore, the gap permeability can be reported here as the average value shown in Fig. 18, i.e., $K_{g} = 1.98 \times 10^{ - 9} m^{2}$. It is imperative to notice that this value of $K_{g}$ confirms the principal assumption of the present work: gap permeability is several orders of magnitude larger than tows permeabilities.

Fig. 18

Non-dependency of $K_{g}$ on the processing parameters

It is important to emphasize that the gap permeability, $K_{g}$, accounts for the easiness of impregnation of the channels network of the fabric, assuming that tows are impermeable. Therefore, in the numerical computations, the main difference between $K_{g}$ and $K_{eff}$ when $S_{t} = 0$ is that the last one considers the mass absorption rate from the channels towards the tows (warps and weft), which is usually very small regarding the fluid flow rate in the channels domain (even for $S_{t} = 0$ when this mass absorption is the maximum). This is the reason why the gap or channel permeability, $K_{g}$, approximates to $K_{eff}$ when $S_{t} = 0$. Since the gap permeability, $K_{g}$, does not consider the tows saturation, it does not tend to $K_{eff}$ when $S_{t} = 1$.

5.3 Macroscopic unidirectional simulations

5.3.1 Assessment of the accuracy of the DR-BEM scheme

In this section, the DR-BEM scheme presented in Sect. 3 is used to simulate the macroscopic unidirectional filling of dual-scale fibrous reinforcements using the sink term approach. This numerical scheme is validated with the analytical solution proposed in [25] for unidirectional fillings, in which the non-dimensional position of the macroscopic fluid front in the time, $\hat{L}_{ff}$, and the non-dimensional length of the unsaturated region, $\hat{L}_{us}$, at a constant injection pressure regime, are predicted as follows:

Non-dimensional position of the macroscopic fluid front, $\hat{L}_{ff}$ :

$$ \hat{L}_{ff} = \frac{1}{{k_{1} }}\cosh^{ - 1} \left( {\frac{{\psi_{1}^{2} \hat{t}}}{{\varepsilon_{g} }} + 1} \right),\;\;\;0 \le \hat{t} \le \widehat{{t_{s} }} $$

(82)

$$ \hat{L}_{ff} = \frac{{ - \sqrt {\left( {\varepsilon_{RUC} } \right)^{2} - \left( {\varepsilon_{g} } \right)^{2} } + \sqrt {\left( {\varepsilon_{RUC} } \right)^{2} - \left( {\varepsilon_{g} } \right)^{2} + 2\varepsilon_{RUC} \psi_{1}^{2} \left( {\hat{t} - \widehat{{t_{s} }}} \right)} }}{{k_{1} \varepsilon_{RUC} }} + \frac{1}{{k_{1} }}\cosh^{ - 1} \left( {\frac{{\varepsilon_{RUC} }}{{\varepsilon_{g} }}} \right), \;\;\;\widehat{{t_{s} }} \le \hat{t} \le \widehat{{t_{fill} }} $$

(83)

$$ \widehat{{t_{s} }} = 1/\psi_{2} $$

(84)

Non-dimensional length of the unsaturated region, $\hat{L}_{us}$:

$$ \hat{L}_{us} = \frac{1}{{k_{1} }}\cosh^{ - 1} \left( {\frac{{\varepsilon_{RUC} }}{{\varepsilon_{g} }}} \right), $$

(85)

where $\widehat{{t_{s} }}$ and $\widehat{{t_{fill} }}$ are the dimensionless times (see Eq. (24)) when total saturation is reached at the inlet and when the fluid front arrives at the end of the domain, respectively, while $\varepsilon_{RUC}$, $\psi_{1}$ and $\psi_{2}$ are the bulk porosity of the RUC and two model parameters, respectively, defined by:

$$ \varepsilon_{RUC} = \frac{{\sum V_{pt}^{\left( i \right)} + V_{g} }}{{V_{RUC} }} = \frac{{\varepsilon_{t} \sum V_{t}^{\left( i \right)} + V_{g} }}{{V_{RUC} }} = \varepsilon_{t} \left( {1 - \varepsilon_{g} } \right) + \varepsilon_{g} $$

(86)

$$ \psi_{1} = \sqrt {\frac{{a\left( {1 - \varepsilon_{g} } \right)L^{2} K_{t} }}{{h_{t}^{2} K_{g} }}} $$

(87)

$$ \psi_{2} = \frac{{k_{1}^{2} }}{{\left( {1 - \varepsilon_{g} } \right)\varepsilon_{t} }}, $$

(88)

where $V_{g}$, $V_{t}^{\left( i \right)}$, $V_{pt}^{\left( i \right)}$ and $V_{RUC}$ represent the channel or gap volume, the volume of tow “i”, the porous volume of tow “i” and RUC volume, respectively. On the other hand, in the calculation of $\psi_{1}$ and $\psi_{2}$(Eqs. (87) and (88)) three parameters of the tows are considered, namely, minor permeability $\left( {K_{2} } \right)$, tow height $\left( {h_{t} } \right)$ and tow porosity $\left( {\varepsilon_{t} } \right)$. The details of the calculation of the fitting parameter “a” appearing in Eq. (87) can be found in [25]. A pressure-dependent linear function for the sink term, $S_{g}$, is considered, as required in [25]:

$$ S_{g} = c\left\langle {P_{g} } \right\rangle^{g} $$

(89)

$$ c = \frac{{aK_{t} }}{{h_{t}^{2} \varepsilon_{t} \mu }} $$

(90)

The fixed and computed parameters used in the present validation are summarized in Table 7. The comparison between the analytical and numerical results is carried out based on the $L^{2}$ relative error norm and the relative error,$E$, which are defined as follows:

$$ L^{2} = \sqrt {\mathop \sum \limits_{i} \left( {\hat{L}_{ff,anal}^{\left( i \right)} - \hat{L}_{ff,drbem}^{\left( i \right)} } \right)^{2} /\mathop \sum \limits_{i} \left( {\hat{L}_{ff,anal}^{\left( i \right)} } \right)^{2} } $$

(91)

$$ E = \sqrt {\left| {\hat{L}_{us,anal} - \hat{L}_{us,drbem} } \right|/\hat{L}_{us,anal} } , $$

(92)

where $\hat{L}_{ff,anal}^{\left( i \right)}$ and $\hat{L}_{ff,drbem}^{\left( i \right)}$ are the analytical and DR-BEM solutions of the non-dimensional fluid front position in the time instant “i”, whereas $\hat{L}_{us,anal}$ and $\hat{L}_{us,drbem}$ represent the analytical and DR-BEM solutions of the non-dimensional length of the unsaturated region, $\hat{L}_{us}$.

Table 7 Data for comparison between the analytical and DR-BEM results of macroscopic unidirectional simulations

The plots of $L^{2}$ relative error norm vs. Mesh size for several values of the constant of Courant-Friedrich-Levy, ${\text{CFL}}$, which is used in the advancement of the moving interface, are presented in Fig. 19a, where the mesh size is reported as $h = e/L$, with $e$ as the size of one quadratic element and $L$ as the domain length. The results allow concluding that the DR-BEM scheme is accurate enough to conduct macroscopic filling simulations of dual-scale fibrous reinforcements for a pressure-dependent linear sink function. Additionally, the relative errors, $E$, between the analytical and the numerical solutions of the non-dimensional length of the unsaturated region, $\hat{L}_{us}$, which are shown in Fig. 19b, confirms the accuracy of the present DR-BEM scheme. The graphical comparison between the analytical and numerical non-dimensional fluid front positions is shown in Fig. 20 for $h = 1.11 \times 10^{ - 2}$ and ${\text{CFL}} = 1$, which are the parameters employed in the forthcoming simulations.

Fig. 19

Plots of convergence for the solution of macroscopic unidirectional filling using the present DR-BEM scheme. a L² relative error norm vs Mesh-size for the fluid front positions,$\hat{L}_{ff}$ b Relative error, $E$, vs. Mesh-size for the length of the unsaturated region, $\hat{L}_{us}$

Fig. 20

Comparison between analytical and DR-BEM fluid front positions for macroscopic unidirectional injections

5.3.2 Sets of simulations

After having validated the DR-BEM scheme presented here, this is employed for unidirectional macroscopic simulations using the lumped functions obtained for the sink term, $S_{g}$, and the effective unsaturated permeability, $K_{eff}$. The material parameters and RUC geometry data of the following simulations are the same as in Table 1. On the other hand, the characteristics of the macroscopic domain and the processing data are presented in Table 8. In Set 1, it is considered a constant pressure regime with two inlet pressures, i.e., $P_{inj} = \left[ {10,100} \right]\;{\text{kPa}}$, a single vacuum pressure of $P_{vac} = 0\;{\text{kPa}}$ and five cases of air dissolution, namely, full air dissolution $\left( {\lambda = 0} \right)$, partial air dissolution $\left( {\lambda = 0.25, \lambda = 0.50, \lambda = 0.75} \right)$ and full air compressibility $\left( {\lambda = 1} \right)$. On the other hand, Set 2 corresponds to constant pressure injections where two vacuum pressures are considered, i.e., $P_{vac} = \left[ {0, - 75} \right]\;{\text{kPa}}$, while the inlet pressure is kept constant in $P_{inj} = 50\;{\text{kPa}}$ and the air entrapment parameters are the same as in Set 1, namely, $\lambda = \left[ {0,0.25,0.50, 0.75, 1} \right]$. In Set 3, a constant flow rate regime is considered with inlet flow rates of $Q_{inj} = \left[ {7 \times 10^{ - 7} ,2 \times 10^{ - 6} } \right] {\text{m}}^{3} /{\text{s}}$, a single vacuum pressure of $P_{vac} = 0\;{\text{kPa}}$ and $\lambda = \left[ {0, 0.75, 1} \right]$. In Set 4, both constant pressure $\left( {P_{inj} = 100\;{\text{kPa}}} \right)$ and constant flow rate ($Q_{inj} = 1 \times 10^{ - 6} {\text{m}}^{3} /{\text{s}}$) regimes are taken into account, for the case of full air compressibility $\left( {\lambda = 1} \right)$, with vacuum pressures of $P_{vac} = \left[ {0, - 50, - 75} \right]\;{\text{kPa}}$.

Table 8 Data of macroscopic unidirectional simulations

5.3.3 Comparison between sink term and Richards approach

Experimental injections at constant pressure regime were carried out in the unidirectional permeability mold shown in Fig. 21. The arrival time of the fluid front at predetermined positions equally spaced by 20 mm can be captured using a manual push button. Geometrical dimensions of the mold are given in Table 8, namely, length of 400 mm, width of 100 mm and thickness of 3.2 mm; four preforms were positioned on the cavity to obtain similar RUC dimensions to the ones reported in Table 1. Three cases were considered with constant injection pressures of $P_{inj} = \left[ {10,50,100} \right]\;{\text{kPa}}$ and vacuum pressure of $P_{vac} = 0\;{\text{kPa}}$ (no vacuum), taking five replications for each case. These experiments are numerically reproduced using the two lumped approaches considered in the present work, with the lumped functions for the sink term, $S_{g}$, and the effective unsaturated permeability, $K_{eff}$, previously deduced in Sects. 5.2.4 and 5.2.5, respectively.

Fig. 21

Unidirectional permeability mold

Firstly, the curves of saturation $\left( {S_{t} } \right)$ vs normalized longitudinal position $\left( {\hat{x}} \right)$ obtained by both approaches (Richards and sink term) are shown in Fig. 22a–f for several fluid front positions and $\lambda = \left[ {0,0.5,1} \right]$. As can be observed, both approaches describe a similar general behaviour of the saturation, $S_{t}$, along the longitudinal direction, although Richards approach predicts larger values of $S_{t}$ as points are farther from the fluid front. Thereby, for all injection pressures and $\lambda = \left[ {0,0.5} \right]$ (Fig. 22a,b,d,e,g,h), the inlet becomes totally saturated for a lower fluid front position in the Richards approach and the fully saturated length for a determined fluid front position is greater for this approach as well. For the full compressibility case, $\lambda = 1$ (Fig. 22c,f,i), which is an extreme scenario where total saturation is not possible, the equilibrium saturation at the inlet is reached for a lower fluid front position in the Richards approach. Both approaches predict a similar influence of the injection pressure, $P_{inj}$, on the saturation, $S_{t}$, namely, for a determined fluid front position, the higher $P_{inj}$, the larger the fully saturated length for $\lambda = \left[ {0,0.5} \right]$; for the full compressibility case, $\lambda = 1$, the equilibrium saturation at the inlet is more significant as $P_{inj}$ increases, as it is reasonable.

Fig. 22

Curves of saturation $\left( {S_{t} } \right)$ vs. Normalized longitudinal position $\left( {\hat{x}} \right)$. a $P_{inj} = 10\;{\text{kPa}}$ and $\lambda = 0$, b $P_{inj} = 10\;{\text{kPa}}$ and $\lambda = 0.5$, c $P_{inj} = 10\;{\text{kPa}}$ and $\lambda = 1$, d $P_{inj} = 50\;{\text{kPa}}$ and $\lambda = 0$, e $P_{inj} = 50\;{\text{kPa}}$ and $\lambda = 0.5$, f $P_{inj} = 50\;{\text{kPa}}$ and $\lambda = 1$, g $P_{inj} = 100\;{\text{kPa}}$ and $\lambda = 0$, h $P_{inj} = 100\;{\text{kPa}}$ and $\lambda = 0.5$, i $P_{inj} = 100\;{\text{kPa}}$ and $\lambda = 1$

In the experimental tests carried out in the present work, it is not possible to directly obtain the air dissolution factor, $\lambda$, that better describes the evolution of the air pressure inside the tows. In order to estimate this value, the arrival times of the fluid front to the 20 fixed positions along the mold (20 mm, 40 mm, 60 mm, until 400 mm) are retrieved from the DR-BEM simulations for $\lambda = [0,0.25,0.50,0.75,1]$, and then, these numerical results are compared with the experimental ones taking the L² relative error norm, in such a way that the value of $\lambda$ leading to the minimum error is selected to evaluate the accuracy of the sink term and Richards approaches. For instance, in Fig. 23a–e, they are shown the dimensionless times at several fluid front positions and considering $P_{inj} = 50\;{\text{kPa}}$, obtained from experiments $\left( {\hat{t}_{exp} } \right)$ and DR-BEM simulations by the sink term approach at different dissolution factors $\left( {\hat{t}_{\lambda = 0} ,\hat{t}_{\lambda = 0.25} ,\hat{t}_{\lambda = 0.5} ,\hat{t}_{\lambda = 0.75} ,\hat{t}_{\lambda = 1} } \right)$; in Fig. 24a–e, an analogous comparison is carried for the Richards approach. According to the L² relative error norm, $\lambda = 0.75$ is the more suitable approximation for both approaches, with corresponding errors of L² = 5.20% and L² = 7.35% for the sink term and Richards approach, respectively. For the other values of injection pressure, $P_{inj} = 10\;{\text{kPa}}$ and $P_{inj} = 100\;{\text{kPa}}$, $\lambda = 0.75$ is the more appropriate dissolution factor as well. In Fig. 25, the L² relative error norms for the three injection pressures (10 kPa, 50 kPa and 100 kPa) and five dissolution factors (0,0.25,0.50,0.75,1) are shown, confirming that $\lambda = 0.75$ leads to the lower error regarding experimental results.

Fig. 23

Dimensionless times obtained from experiments and DR-BEM simulations for several fluid front positions considering the sink term approach. a $\hat{L}_{ff} = 0.2$, b $\hat{L}_{ff} = 0.4$, c $\hat{L}_{ff} = 0.6$, d $\hat{L}_{ff} = 0.8$, e $\hat{L}_{ff} = 1$

Fig. 24

Dimensionless times obtained from experiments and DR-BEM simulations for several fluid front positions considering the Richards approach. a $\hat{L}_{ff} = 0.2$, b $\hat{L}_{ff} = 0.4$, c $\hat{L}_{ff} = 0.6$, d $\hat{L}_{ff} = 0.8$, e $\hat{L}_{ff} = 1$

Fig. 25

L² relative error norm vs. Air dissolution factor for Richards and sink term approaches at several injection pressures

The experimental and numerical curves of the normalized fluid front position $\left( {\hat{L}_{ff} } \right)$ vs. dimensionless time $\left( {\hat{t}} \right)$ for the three injection cases, $P_{inj} = \left[ {10,50,100} \right]\;{\text{kPa}}$, considering $\lambda = 0.75$, are compared to each other in Fig. 26a–c. In each figure, it is also represented the curve corresponding to a single-scale porous medium (sink term, $S_{g}$, is neglected in the mass conservation equation), taking the fully saturated effective permeability, $K_{eff}^{sat}$, as computed by doing $S_{t} = 1$ in Eq. (79); in that case, the closed analytical expression for the normalized fluid front position, $\hat{L}_{ff}$, is given by:

$$ \hat{L}_{ff} = \sqrt {\frac{{2.K_{eff}^{sat} }}{{\varepsilon_{RUC} .K_{g} }}.\hat{t}} $$

(93)

where $\varepsilon_{RUC}$ is the bulk porosity of the RUC as computed by Eq. (86). Firstly, it is worth-noting that the curves obtained by the sink term and the Richards approach have a similar behaviour to the experimental curve for all values of $P_{inj}$ considered, whereas the curve for the single scale porous medium noticeably differs from these three curves, denoting the importance of considering the sink effect during the preform filling. In general, results obtained by the sink term approach are in better agreement with experimental results than those obtained by the Richards approach, which can be confirmed with the L² relative error norms (see Fig. 25 for $\lambda = 0.75$); for the sink term approach, this error norm is 4.84%, 5.20% and 3.81% for $P_{inj} = 10\;{\text{kPa}}$, $P_{inj} = 50\;{\text{kPa}}$ and $P_{inj} = 100\;{\text{kPa}}$, respectively, whereas the corresponding values for the Richards approach are 6.41%, 7.35% and 5.67%.

Fig. 26

Experimental and numerical curves of Normalized fluid front position $\left( {\hat{L}_{ff} } \right)$ vs. Dimensionless time $\left( {\hat{t}} \right)$. a $P_{inj} = 10\;{\text{kPa}}$, b $P_{inj} = 50\;{\text{kPa}}$, c $P_{inj} = 100\;{\text{kPa}}$

The differences obtained between the experimental and numerical results can be attributable to different types of errors: idealization, modelling, discretization, solution and experimental errors. The geometrical simplifications of the RUC, as dimensionality reduction, not consideration of deformation mechanisms, generation of pressure-independent liquid passages, assumption of hexagonal arrays of fibers, among others, are sources of idealization errors. On the other hand, the consideration of the air dissolution phenomenon in a lumped fashion by means of the parameter $\lambda$, which is assumed constant during the whole injection, can represent a source of modelling errors. The selection of the slip coefficient of the Stokes-Darcy matching condition is another source of modelling errors; details about this selection are given in [49, 50]. Additionally, the mesh density in both the mesoscopic and macroscopic simulations is tightly associated to spatial discretization errors since this have an influence on the solution of field variables and tracking of the fluid front; it is important to remark that mesh-dependency analyses for the mesoscopic BEM simulations were previously carried out in [50], whereas these analyses for the macroscopic DR-BEM simulations were performed here in Sect. 5.3.1. The choice of the time step based on the CFL condition and other constraints described in [50], is the principal source of the time discretization error. On the other hand, solution errors of BEM-based techniques are present as well, with the singularity errors when computed the layers potentials and the ill-conditioning errors as ones of the most important in the present case. Errors associated to the interpolation order, choice of the collocation factor for corner treatments, numerical integration and post-processing operations can be influential as well.

On the other hand, experimental errors can be classified into image analysis errors and injection test errors. Despite not quantified in this study, image analysis carried on several kinds of errors: preparation (saturation, shadowing, etc.), integration (number, density and location of discrete pixels) and analysis errors (segmentation and measurement calibration). On the other hand, unidirectional injection tests could entail several errors as well: uncontrolled capillary effects, racetracking, variations of inlet pressure during injection, measurement errors associated to inadequate parallax, erroneous time response, non-uniform fluid fronts, incorrect contrast perception; fabric shearing by careless manipulation, which in turns can lead to significant through-plane flow even for in-plane injections. To minimize these error sources, recommendations of two benchmark exercises about permeability measurement were followed here in the experimental tests [92, 93].

5.3.4 Parametric study on the influence of the inlet pressure, vacuum pressure, inlet flow rate and air dissolution factor on the saturation behaviour

In the present section, the sink term approach is used to study the influence of several variables on the behaviour of the saturation along the longitudinal direction. Curves of tows saturation $\left( {S_{t} } \right)$ vs. Normalized longitudinal position $\left( {\hat{x}} \right)$, for several fluid front positions, provide useful information to carry out this analysis (Figs. 27, 28, 29, 30). The slopes of these curves in the partially saturated region account for the sink effect, in such a way that the bigger the slopes, the faster the liquid absorption into the tows regarding the fluid front velocity, leading to a more significant change of $S_{t}$ with $\hat{x}$. The evolution of the fully saturated length is another indication of the difference between the impregnation velocities of tows and channels. For the extreme case of full air compressibility, $\lambda = 1$, where total tows saturation is not possible, the evolution of the inlet saturation allows elucidating the behaviour of the sink effect until the equilibrium is reached. In this point, it is important to highlight that the sink effect, as analyzed in this section, refers to the magnitude of the liquid absorption into the tows relative to the fluid front velocity; this means, for instance, that steeper slopes for lower injection pressures does not necessarily represents a larger absolute value of the sink term, $S_{g}$, but a greater value relative to the fluid front velocity; in other words, the higher the sink effect, the higher the tows saturation rate relative to the channels filling. Bearing this in mind, despite the tows saturation rate,$\dot{S}_{t}$, and consequently the sink term,$S_{g}$, for a given saturation level, $S_{t}$, always increases with the injection pressure $\left( {P_{inj} } \right)$, vacuum pressure $\left( {P_{vac} } \right)$ and injection flow rate $\left( {Q_{inj} } \right)$, since the fluid front velocity increases with these parameters as well, the slope of the non-dimensional saturation curves for a given longitudinal position, $\hat{x}$, does not necessarily increase with these injection parameters.

Fig. 27

Saturation $\left( {S_{t} } \right)$ vs. Normalized longitudinal position $\left( {\hat{x}} \right)$ for simulations of Set 1. a $\lambda = 0$, b $\lambda = 0.75$, c $\lambda = 1$

Fig. 28

Saturation $\left( {S_{t} } \right)$ vs. Normalized longitudinal position $\left( {\hat{x}} \right)$ for simulations of Set 2. a $\lambda = 0$, b $\lambda = 0.75$, c $\lambda = 1$

Fig. 29

Saturation $\left( {S_{t} } \right)$ vs. Normalized longitudinal position $\left( {\hat{x}} \right)$ for simulations of Set 3. a $\lambda = 0$, b $\lambda = 0.75$, c $\lambda = 1$

Fig. 30

Saturation $\left( {S_{t} } \right)$ vs. Normalized longitudinal position $\left( {\hat{x}} \right)$ for simulations of Set 4. a $P_{inj} = 100\;{\text{kPa}}$, b $Q_{inj} = 1 \times 10^{ - 6} m^{3} /s$

5.3.4.1 Results of Set 1: Change of injection pressure, $P_{inj}$

Some simulations of Set 1 of Table 8 are now deemed. In Figs. 27a–c, $S_{t}$ vs. $\hat{x}$ curves for $P_{inj} = \left[ {10\;{\text{kPa}},100\;{\text{kPa}}} \right]$ and $\lambda = \left[ {0,0.75,1} \right]$ are presented. When total saturation is possible, namely, for $\lambda = \left[ {0,0.75} \right]$, Figs. 27a, b show that the slopes for all curves are very steep at points near the fluid front, which means a significant sink effect; as points move away from the fluid front (from right to left in the figures), the saturation curves for $P_{inj} = 10\;{\text{kPa}}$ and $P_{inj} = 100\;{\text{kPa}}$ diverge from each other. Accordingly, for $\lambda = 0$ (Fig. 27a), in the partially saturated region, the sink effect is more important in the simulation with $P_{inj} = 10\;{\text{kPa}}$ for the second, third and fourth fluid front positions; on the other hand, from the five fluid front position onwards, it is more relevant in the simulation with $P_{inj} = 100\;{\text{kPa}}$. For $\lambda = 0.75$ (Fig. 27b), the sink effect is more important with $P_{inj} = 10\;{\text{kPa}}$ for all fluid front positions, which in turn leads to larger fully saturated lengths for this injection pressure. In the case of full air compressibility ($\lambda = 1$), Fig. 27c, the sink effect near the fluid front is not as significant as in previous cases ($\lambda = 0$ and $\lambda = 0.75$); namely, curve slopes are lower for all fluid front positions. For such a case (Fig. 27c), the change of the sink effect (curve slope) as points get away from the fluid front is not monotonic and depends on the inlet saturation. Accordingly, for a given fluid front position, if the behaviour of $S_{t}$ vs. $\hat{x}$ curve is analysed from right to left, it can be noticed that sink effect (curve slope) experiences an increase, is kept almost constant, and then it decreases from a determined point until the inlet (this is more perceptible for the curves of the last fluid front positions with $P_{inj} = 100 {\text{kPa}}$). For a determined fluid front position and $\lambda = 1$, lower slopes are expected for the minor injection pressure, $P_{inj} = 10\;{\text{kPa}}$, since the tows saturation is bounded by the equilibrium saturation, $S_{t}^{eq}$, which in turn is lower for this injection pressure.

5.3.4.2 Results of Set 2: Change of vacuum pressure, $P_{vac}$

The influence of the vacuum pressure,$P_{vac}$, on the behaviour of the $S_{t}$ vs. $\hat{x}$ curves can be figured out in Figs. 28a–c, which corresponds to some simulation of Set 2 of Table 8. General findings previously obtained in Figs. 27a–c can be extended to this particular case, inferring that the positive $\left( {P_{inj} } \right)$ and negative pressure ($P_{vac}$) have a similar influence on the sink effect. Accordingly, for the total and partial dissolution cases ($\lambda = 0$ and $\lambda = 0.75$, respectively), Figs. 28a, b, sink effect is considerably more significant near the fluid front than for the full compressibility cases ($\lambda = 1$), Fig. 28c. Moreover, when $\lambda = 0$, in the partially saturated region, sink effect is lower for the greater vacuum pressure, $P_{vac} = - 75\;{\text{kPa}}$, from the second to the fifth fluid front positions, but this tendency is reversed from the sixth fluid front position onwards; when $\lambda = 0.75$, the initial trend is kept for all fluid front positions, entailing larger fully saturated lengths for the smaller vacuum pressure, $P_{vac} = 0\;{\text{kPa}}$. For the full compressibility case ($\lambda = 1$), Fig. 28c, $S_{t}$ vs. $\hat{x}$ curves behave in a similar manner as in Fig. 27c, namely, sink effect is small near the fluid front, then it increases as points move away from the fluid front, there is a region where it is almost constant and finally, it decreases from a determined point until the inlet. For a determined fluid front position and $\lambda = 1$, lower slopes are obtained for the inferior vacuum pressure, $P_{vac} = 0\;{\text{kPa}}$, because equilibrium saturation, $S_{t}^{eq}$, is lower as well.

5.3.4.3 Results of Set 3: Change of injection flow rate, ${\varvec{Q}}_{{{\varvec{inj}}}}$

The $S_{t}$ vs. $\hat{x}$ curves of Fig. 29a–c correspond to a constant flow rate regime, Set 3 of Table 8. The behaviour of these curves has some similarities to the curves previously analysed for the three dissolution factors, $\lambda = \left[ {0,0.75,1} \right]$, but some differences can be identified too. In general, for $\lambda = 0$ (Fig. 29a) and $\lambda = 0.75$ (Fig. 29b), the sink effect (curve slope) and consequently, the saturation $\left( {S_{t} } \right)$ for a given longitudinal position ($\hat{x}$), as well as the fully saturated length, are greater for the lower injection flow rate, $Q_{inj} = 7 \times 10^{ - 7} {\text{m}}^{3} /{\text{s}}$, for all fluid front positions. For the full compressibility case ($\lambda = 1$), Fig. 29c, the main difference with curves of Figs. 27c and 28c lies on the inlet saturation. For the constant pressure regimes (Figs. 27c and 28c), the inlet saturation threshold is the equilibrium saturation,$S_{t}^{eq}$, which does not change since the injection and vacuum pressures remain constant during the whole filling; on the other hand, for the constant flow rate regime (Fig. 29c), the equilibrium saturation is not reached at the inlet, in such a way that if the unidirectional injection continues indefinitely, $P_{inj} \to \infty$ as $S_{t} \to 1$.

5.3.4.4 Result of Set 4: Influence of vacuum pressure, ${\varvec{P}}_{{{\varvec{vac}}}}$, for the full compressibility case $\left( {\lambda = 1} \right)$

The influence of the vacuum pressure, $P_{vac}$, on the saturation curves for the full compressibility case $\left( {{\uplambda } = 1} \right)$ can be investigated from the results of simulations of Set 4 of Table 8, which are shown in Fig. 30a, b. The general behaviour of the sink effect (curve slope) is analogous to the one of the formerly analysed curves (Figs. 27c, 28c, and 29c): sink effect is small near the fluid front, it grows and then remains almost constant until a certain point, from which it reduces until the inlet. For the constant pressure regime $\left( {P_{inj} = 100\;{\text{kPa}}} \right)$, Fig. 30a, for a determined fluid front position, the relationship between the sink effect (curve slope) and the vacuum pressure, $P_{vac}$, is not equal at all longitudinal positions, $\hat{x}$. For instance, the three curves corresponding to the last fluid front position are analyzed. For points very close to the fluid front, the lower sink effect is reached for the greater vacuum pressure (green curve), $P_{vac} = - 75\;{\text{kPa}}$, whereas the bigger one is achieved for the intermediate vacuum pressure (red curve), $P_{vac} = - 50\;{\text{kPa}}$. This causes a higher tow saturation, $S_{t}$, for the case of $P_{vac} = - 50\;{\text{kPa}}$ than for the other two cases ($P_{vac} = - 75\;{\text{kPa}}$ and $P_{vac} = 0\;{\text{kPa}}$). As points move away from the fluid front, the sink effect increases for all curves and, from a determined point, this increment is more notorious for the greater vacuum pressure (green curve), $P_{vac} = - 75\;{\text{kPa}}$. From a determined longitudinal position to the inlet, a common trend is maintained: the greater $P_{vac}$, the more significant the sink effect and, consequently, the higher the tow saturation, $S_{t}$. As it is logical, the inlet saturation is always higher as the vacuum pressure is greater. For the constant flow rate regime $\left( {Q_{inj} = 1 \times 10^{ - 6} {\text{m}}^{3} /{\text{s}}} \right)$, Fig. 30b, the last analysis is applicable for the $S_{t}$ vs. $\hat{x}$ curves, but it is worth noting that, for a determined fluid front position, the differences between the three curves (green, blue and red curve) are not as considerable as for the constant pressure regime (Fig. 30a), which is associated with the continuous increment of the inlet pressure in the constant flow rate regime.

5.3.4.5 Pressure profiles for constant pressure and constant flow rate regimes

Another verification of the macroscopic simulations using the present sink term approach can be carried out by comparing the numerical pressure profiles with the profiles presented in Fig. 3. According to [1], the sink effect in the partially saturated region determines whether the pressure profile is convex or concave. As mentioned above, for the full and partial air dissolution cases (λ = 0 and λ = 0.75, respectively), the sink effect is very significant at points very close to the fluid front, which, according to [1], leads to a concave pressure profile, as shown in Fig. 3a. Accordingly, the pressure profiles for several fluid front positions corresponding to a constant-pressure-regime simulation ($P_{inj} = 10\;{\text{kPa}}$, $P_{vac} = 0\;{\text{kPa}}$, $\lambda = 0.75$) and a constant-flow-rate-regime simulation ($Q_{inj} = 2 \times 10^{ - 6} {\text{m}}^{3} /{\text{s}}$, $P_{vac} = 0\;{\text{kPa}}$, $\lambda = 0$) are represented in Fig. 31a, b, respectively, where marker points are added to some profiles to indicate the transition between the fully saturated and the partially saturated zones; some dotted lines are also shown indicating the projection of the linear part of these profiles. As can be observed, the change of the pressure from the inlet until the marker point is linear, but from the marker point until the fluid front, the curve is concave, coinciding with the results reported in [1, 70, 71].

Fig. 31

Normalized pressure $\left( {\hat{p}} \right)$ vs. Normalized longitudinal position $\left( {\hat{x}} \right)$. a Constant pressure regime with $P_{inj} = 10\;{\text{kPa}}$, $P_{vac} = 0\;{\text{kPa}}$, $\lambda = 0.75$, b Constant flow rate regime with $Q_{inj} = 2 \times 10^{ - 6} \;{\text{m}}^{3} /{\text{s}}$,$P_{vac} = 0\;{\text{kPa}}$, $\lambda = 0$

On the other hand, the slope of the pressure profiles in the fully saturated region for the constant flow rate regime (Fig. 31b) is another parameter that can be used to validate the numerical results. As $S_{g} = 0$ in this region, according to Eqs. (19) and (21), and considering that the horizontal velocity is $u_{g} = Q_{inj} /A$, the slope of the pressure profile in the fully saturated region shall be the same for all fluid front positions where this region is present and equal to:

$$ m_{linear} = \frac{{\left( {p_{sat} - P_{inj} \left( t \right)} \right)}}{{x_{sat} }} = - \frac{{Q_{inj} \mu }}{{AK_{g} }}, $$

(94)

where the point $\left( {x_{sat} ,p_{sat} } \right)$ is the coordinate corresponding to the threshold of the fully saturated region in each pressure profile (this threshold is represented in non-dimensional form by the marker points of Fig. 31a, b). If $x_{sat}$ and $p_{sat}$ are non-dimensionalized using Eqs. (22) and (28), respectively, the non-dimensional slope shall be $\hat{m}_{linear} = - 1$, which is in agreement with the slopes obtained in Fig. 31b. It is important to notice that $\hat{p}_{sat}$ is practically constant during the whole injection for the constant flow rate regime (Fig. 31b), whereas it decreases as the injection develops for the constant pressure regime (Fig. 31a).

6 Conclusions

In the present work, BEM techniques were applied to the problem of impregnation of dual-scale fibrous reinforcements used in the processing of composite materials. A Stokes-Darcy formulation was used to conduct filling simulations of RUC´s under different parameters complying with predetermined scale constraints; lumped functions for the sink term, $S_{g}$, and the effective unsaturated permeability, $K_{eff}$, were obtained from these simulations. It is important to highlight that the fitting parameters of the lumped functions $S_{g}$ and $K_{eff}$ are dependent on the geometry configuration of the RUC and tows. Modifications of resin viscosity, injection pressure, injection flow rate and/or vacuum pressure do not have any influence on these fitting parameters, as long as these physical variables remain inside the ranges considered here.

The methodology used to conduct the RUC filling simulations allows considering the fluid pressure gradient at channels (fluid motion), air compressibility, air dissolution, flow-direction dependent capillary pressure, and vacuum pressure, as well as capturing several phenomena involved in the dynamic evolution of intra-tow voids, such as compression, displacement and migration, with the last phenomenon having a time scale several orders of magnitude lower than the other two phenomena. The present methodology can be extended to any well-characterized microstructure since the fitting parameters are directly obtained from numerical BEM results. However, it is worth noting that the air dissolution phenomenon is accounted here in a lumped fashion by means of the prescribed factor λ, which does depict the complex dynamics of the air dissolution mechanism and whose estimation could imply non-trivial experimental tests [69, 88] that are out of the scope of the present work. In further works, the modelling of the air dissolution phenomenon could be included to enhance the robustness of the present methodology.

The main conclusions obtained from the RUC filling simulations (mesoscopic scale) can be summarized as follows:

• When any fraction of air dissolution is considered $\left( {\lambda < 1} \right)$, the total tows saturation is possible $\left( {S_{t} = 1} \right)$, with the saturation rate, $\dot{S}_{t}$, inversely proportional to $\lambda$. However, in the extreme scenario of full air compressibility $\left( {\lambda = 1} \right)$, total saturation is not possible $\left( {S_{t} < 1} \right)$ and an equilibrium saturation, $S_{t}^{eq}$, which depends on the channel, vacuum, and capillary pressure, is reached instead.

• The prescription of a pressure gradient, $\Delta P/\Delta x$, along the RUC length, instead of a uniform channel pressure, induces several phenomena that are more consistent with experiments, namely, velocity field in the channel is present, decentered voids can be obtained in the tows, displacement and migration of intra-tow voids is possible, among others. However, saturation curves seem to be not very sensible to $\Delta P/\Delta x$ for the small gap Reynolds numbers, $R_{eg}$, considered here.

• The lumped functions obtained for the sink term, $S_{g}$, and the effective unsaturated permeability, $K_{eff}$, describe properly the behaviour of these variables with the saturation, $S_{t}$, for any combination of average channel pressure $\left( {\left\langle {P_{g} } \right\rangle^{g} } \right)$, vacuum pressure $\left( {P_{vac} } \right)$ and air entrapment parameter $\left( \lambda \right)$. In the particular case of $S_{g}$, the lumped function was obtained by modifying an existing function with the addition of a potential-type term that improves the data fit and is physically consistent with the saturation behaviour.

Afterwards, a DR-BEM scheme was implemented to perform macroscopic simulations (mold filling). Firstly, this scheme was validated with a benchmark analytical solution of a constant-pressure unidirectional injection, considering a pressure-dependent linear function for the sink term, $S_{g}$; satisfactory results were obtained for the non-dimensional position of the macroscopic fluid front and non-dimensional length of the unsaturated region. Once validated with an analytical solution, the DR-BEM scheme was used to conduct macroscopic simulations using two lumped approaches (sink term and Richards approach), where the non-linear lumped functions computationally obtained for $S_{g}$ and $K_{eff}$ were implemented in the corresponding governing equations. These approaches were compared with each other, achieving the following conclusions:

• Both approaches describe a similar general behaviour of the saturation, $S_{t}$, along the longitudinal direction of the mold, although the Richards approach overpredicts the saturation at points far from the fluid front, as well as the fully saturated length for a particular fluid front position, regarding the sink term approach.

• The curves of Normalized fluid front position $\left( {\hat{L}_{ff} } \right)$ vs. Dimensionless time $\left( {\hat{t}} \right)$ predicted by both approaches are in acceptable agreement with experimental curves obtained in constant-pressure unidirectional tests, allowing to figure out the importance of considering the sink effect in the filling of dual-scale fibrous reinforcements when compared to a single-scale approximation. In general, it was found a better agreement with experimental results in the sink-term approach.

• The consideration of the air dissolution phenomenon is critical to obtained to obtain numerical results consistent with experimental tests. Extreme conditions of full air dissolution (λ = 0) and full air compressibility (λ = 1) seems not to be achievable in LCM processes.

The sink term approach was then used to conduct a parametric study on the influence of the inlet pressure, vacuum pressure, inlet flow rate, and air dissolution factor on the saturation behaviour, obtaining the following conclusions:

• When $\lambda < 1$, the general behavior of the saturation curves is similar for the two dissolution factors considered, $\lambda = \left[ {0,0.75} \right]$, in both constant-pressure and constant-flow rate regimes: sink effect (curve slope) near the fluid front is very high, then it decreases and remains almost constant in a portion of the partially saturated region, to decrease again until it becomes zero in the fully saturated region.

• When $\lambda < 1$, the sink effect, which refers to the rate of liquid absorption into the tows relative to the fluid front velocity, does not have a unique behaviour with the injection and vacuum pressures during the whole mold filling, since this depends on the fluid front position and air dissolution factor, $\lambda$. On the other hand, for the constant flow rate simulations, results showed that the sink effect and injection flow rate are inversely proportional for all fluid front positions and dissolution factors, $\lambda$. For this injection regime, the saturation ($S_{t}$) for a given longitudinal position ($\hat{x}$), as well as the fully saturated length, also decreases with the injection flow rate.

• In the extreme scenario of full air compressibility, $\lambda = 1$, the general behaviour of the saturation curves is similar in both constant-pressure and constant-flow rate regimes: sink effect near the fluid front is not significant, but then it considerably increases and is kept almost constant in a portion of the partially saturated region, to then decreases until the inlet.

• In the extreme scenario of full air compressibility, $\lambda = 1$, the lower the injection pressure, vacuum pressure and injection flow rate, the lower the saturation and sink effect for points far from the fluid front. The main difference between the constant-pressure and constant- flow rate injections when $\lambda = 1$ lies in the inlet saturation, which is bounded by the equilibrium saturation $S_{t}^{eq}$ for the former injection regime, whereas it is continuously increasing for the second one due to the inlet pressure increment.

Finally, it is worth mentioning that the present computational development will be implemented in future works for other RUC and mold geometries, as well as for different processing and material parameters, to evaluate the scope of the present conclusions.