Introduction

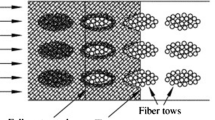
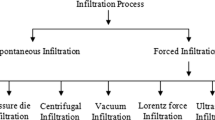
Liquid route processing is the most promising technology for manufacturing fiber-reinforced metal matrix composites (MMCs) both in terms of cost and the mass production of composite parts. Impregnation of the fibrous preform via the liquid route consists of injecting the metal in a liquid state into a mold containing the fibers. The principle may be simple, but with only a few very specific exceptions,[1] it comes up against problems related to the wetting of the mineral fibers by the liquid metal.[2] To ensure that impregnation is carried out successfully, either the wetting process can be improved or the pressures used must be sufficiently high to force the metal to penetrate. There are several solutions to the first case: the addition of chemical elements to the matrix to reduce the surface tension of the liquid metal or the application of a pretreatment to the fibers. For example, the fibers can be coated with ceramic or metal deposits. Metallic coatings mainly of nickel or copper are used to improve the wettability of fibers by aluminum.[3,4] These coatings can be obtained through electrolytic methods, with current, or by electroless techniques.[5,6] Other techniques consist of the chemical activation of wetting by fluoride treatments with K2ZrF6[7] or K2TiF6.[8] After improving the wetting, the fibrous preform can then be impregnated by gravity casting or by exerting a low pressure directly with the aid of a piston or a pressurized inert gas (Figure 1). These techniques generate additional costs, however (time, pollution), and leave residual impurities in the final product. Another technique is to carry out medium pressure die casting: after creating a vacuum in the different parts of the system (mold and preform), the preform and the metal are preheated; gas pressure of around 10 MPa is then applied to the metal to introduce it into the mold and penetrate the preform. Using low pressures has the advantage of not damaging the fibrous preform during processing; however, it generates slow cooling rates that favor chemical reactions between the matrix and the reinforcement. The chemical interaction between the fibers and the matrix causes interfacial zones to form, which may affect the characteristics of the composite, as can be seen, for example, in the case of titanium MMCs.[9]

Fig. 1
figure 1

Production of MMCs by the liquid route under low pressure

Full size image

The use of high pressures (of around 100 MPa) is interesting in several respects, mainly because it is then possible to overcome problems related to wetting (Figure 2), to limit chemical interactions between the fibers and the metal, and also to minimize the formation of microporosities during impregnation. All the techniques used to produce MMCs by infiltration of a fibrous preform have been described and compared by Sree Manu et al. in a recent bibliographic article.[10]

Fig. 2
figure 2

Production of MMCs by forced infiltration

Full size image

The liquid route can also be used to produce semiproducts: coating ceramic filaments by a matrix consists of encasing the filaments with a layer of liquid alloy by passing them at high speed through an induction heated bath.[11,12] After recalling the governing phenomena induced in the liquid metal infiltration of the reinforcement, we go on to present the contribution of different studies in the literature to the numerical modeling of infiltration for MMC manufacture.

Physical Phenomena

Heat and Mass Transfer

The infiltration of liquid metal into a fiber preform is a problem that couples fluid mechanics in porous medium with heat transfer. Perfecting liquid route processing techniques to produce MMCs is complex because of the appearance of metal solidification phenomena as the fibrous preform is being impregnated[13,14] or as the filament is being coated with metal to produce a semiproduct. In order to minimize chemical reactions between the matrix and the reinforcement by increasing the cooling rate of the metal, the initial temperatures of the fibers, and of the mold in the case of techniques for infiltrating the fibrous reinforcement, are lower than the solidification temperature of the metal. Thus, phase change phenomena appear as soon as the fibers and the metal are brought into contact, leading to changes in the permeability of the porous medium, which complicates metal flow.[15] For example, this interaction between the matrix and the reinforcement can result in various phenomena: gaps in impregnation;[16] appearance of microporosities;[17,18] chemical reaction at the interface between the matrix and the solid, which leads to a modification of the permeability;[19] and deformation of the porous medium.[20] In addition to this type of defect, we must mention problems of heterogeneities of the material due to alloy segregation phenomena during impregnation of the fibrous preform or to species diffusion phenomena.[21,22,23]

Capillary Phenomena

When the liquid metal and the air are in contact with the reinforcement, the wetting behavior is defined by an angle θ, which depends on the surface energies between the fluids and the solid, according to Young’s Eq. [1]:

$$ \sigma_{\text{sv}} - \sigma_{\text{sl}} = \sigma_{\text{lv}} \cos \theta $$
(1)

where \( \sigma_{\text{sv}} \), \( \sigma_{\text{sl}} \), and \( \sigma_{\text{lv}} \) are, respectively, the solid/vapor, solid/liquid, and liquid/vapor interfacial energies.

A liquid metal can spontaneously penetrate into the reinforcement when the metal wets the solid. The wetting sometimes results in the formation of a third phase at the interface between the matrix and solid (SiC in the case of an NiSi or SiCo alloy matrix and a solid graphite preform[24,25] or TiC in the case of a titanium alloy matrix and a solid SiC filament coated with a thin carbon layer[12]). However, in most cases, molten metal does not wet the reinforcement phases and a minimum external threshold pressure is then necessary to force the liquid into the reinforcement.[26] In the case of particle reinforcement with a spherical shape, the capillary pressure Pc is obtained by relation Eq. [2]:[27]

$$ P_{\text{C}} = \sigma_{\text{lv}} \cos \theta \frac{{AV_{\text{f}} }}{{(1 - V_{\text{f}} )D}} $$
(2)

where \( \sigma_{\text{lv}} \) is the liquid metal surface tension; D is the average diameter of the particles; and A is a factor, which depends on the deviation in the average geometry of the particles and on the surface roughness of the particles. Studies have shown that roughly 1 MPa of pressure is necessary to infiltrate Saffil preform with pure molten aluminum.[28,29] However, the reinforcement permeability is not constant and depends on its saturation.[20,30] Thus, the slug-flow assumption is not sufficient to describe the infiltration process correctly. Indeed, experimental isothermal infiltrations of a fibrous preform by a molten metal have enhanced the presence of a porous zone upstream of the liquid front, mixing liquid metal and gas, and have shown that flow is dependent on pore morphology.[29,31] This is also observed with particles.[32] Studies have shown that semiempirical models such as the Brooks–Corney model (Eq. [3]), which is used to describe drainage phenomena in soil mechanics, were adapted to represent the evolution of the metal fraction in the fibrous preform, initially saturated with air, as a function of the pressure exerted on metal:[33,34]

$$ S = - \left( {\frac{{P_{\text{b}} }}{P}} \right)^{\lambda } $$
(3)

where λ is a parameter that depends on the pore size of the reinforcement, Pb is the liquid front pressure (the “bubbling pressure”), and P is the applied pressure. However, the parameter λ can depend on the saturation, and thus, the Brooks–Corney cannot represent phenomena for the entire pore size distribution.[35,36] This suggests that in certain cases, the definition of an average preform permeability may still be a good approximation. In conclusion, the infiltration of molten metal is highly dependent on the matrix/reinforcement couple, on the geometry of the solid (fibers, particles), and on the size and distribution of the pores. Experimental tests for both reactive and nonreactive infiltration have shown that the results obtained from these two methods (slug-flow assumption and Brooks–Corney model) are ultimately not very different.[35]

Interest of Numerical Simulation of the Process

The processes for producing MMCs generate phenomena coupled with mass transfers (liquid metal in motion, species diffusion, and alloy segregation) and heat transfers with phase change phenomena related to solidification and also to the melting of the metal during the process. The complexity of the phenomena involved in these processes and the coupling of these phenomena has prompted some authors to develop numerical modeling and simulations not only to describe and explain certain phenomena but also to optimize the processes. Capillary pressures allow the fibrous preform to be infiltrated only when there are no solidification phenomena during the saturation. To produce MMCs by infiltration, external pressures are used to force the penetration of the metal into the porous reinforcement. As these pressures are very much higher than the capillary pressure, wetting problems are avoided. Thus, capillary phenomena were not taken into account in the numerical studies of MMCs processed by infiltration.

Numerical simulations and the associated equations, which are presented in the last sections, concern the gas pressure infiltration system (Figure 1). While only macroscopic scale models can meet this last objective, microscopic studies can prove essential in some cases for understanding certain physical phenomena or to justify certain hypotheses.

Numerical Simulation of the Infiltration of a Fibrous Preform by a Pure Metal

Microscopic-Scale Models

Models at the fiber scale can be used to describe the kinetics of heat transfers between a fiber and the matrix (a pure metal) in a static configuration in the case of two constituents brought into contact that have been first preheated to different temperatures. A model was used to study change in the metal solidification front for different fiber/matrix couples, taking thermal contact resistance into account.[37,38] Other models can be used to study the time taken for the fibers and the matrix to reach thermal equilibrium and to justify the instantaneous equilibrium hypothesis between the fibers and the matrix during impregnation of the fibrous reinforcement by the liquid metal.[39] The studied domain is made up of a periodic stacking of parallel layers, which is reduced by symmetry to a bidimensional domain bounded by two parallel slabs with the thickness of a half stratum (Figure 3). The flow problem is solved using the Brinkman equation, taking into account modifications due to the apparition of solidification:

Fig. 3
figure 3

Studied domain for the microscopic scale dynamic model

Full size image
$$ \rho \frac{DV}{Dt} = \rho g - {\mathbf{\nabla }}P + \mu {\mathbf{\nabla }}^{2} V - \frac{\mu }{K}V $$
(4)

where V is the velocity and P is the pressure; ρ and μ are, respectively, the density and the dynamic viscosity of the liquid metal. \( \frac{\mu }{K}V \) is a penalization term used to define the nature of the medium: if the terms of K are equal to 0, the metal is liquid, and if the terms of K tend to infinity, the metal is solid. Mass conservation is coupled with the heat equation, with phase change phenomena:

$$ \rho C\left( {\frac{\partial T}{\partial t} + V \cdot \nabla T} \right) = \nabla \cdot (\lambda \nabla T) + Q $$
(5)

where λ is the tensor of thermal conductivity of the medium, ρC is the volumetric heat capacity of the medium, T is the temperature, and Q is a source term, which includes the enthalpy release due to phase change.

Macroscopic-Scale Models

Studies at the microscopic scale have shown that production of MMCs by impregnation could be modeled with the traditional continuum mechanics approach: the fibrous preform saturated with metal is treated as a single continuous medium. The infiltration process of the liquid metal through the fibrous reinforcement, therefore, can be simulated at the scale of the process.

If we assume that the forces of inertia and gravity are negligible, then Darcy’s law governs the flow of metal through the fibrous preform according to the relation

$$ V = \frac{{ - {\mathbf{K}}}}{\mu }\;\nabla P $$
(6)

where P is the macroscopic pressure, V is the Darcy velocity, μ is the dynamic viscosity of the liquid metal, and K is the permeability tensor.

If we assume that the liquid metal and the solid metal are incompressible and of equal volume mass, and hypothesize that a fibrous reinforcement is nondeformable, we have the following conservation of mass equation:

$$ {\mathbf{\nabla }} \cdot V = 0\; $$
(7)

A numerical two-dimensional (2-D) finite element model, based on the coupled resolution of Eqs. [6] and [7], was used to describe metal flow as a function of parameters, such as orientation of the fiber network and injection pressure of the metal, in the case of isothermal impregnation where all the constituents (fibers, metal, and mold) are at the same temperature.[40,41]

The presence of a “cold” fibrous preform inside the mold results in the appearance of metal solidification around the fibers from the beginning of the production process, irrespective of the geometry of the mold. This strong interaction between fibers and metal must be taken into account in the numerical simulations of the process by coupling the equations that describe thermal phenomena and metal flow through the porous medium. Producing MMCs by the infiltration process, therefore, generates heat exchanges by conduction and convection with phase changes. The heat equation formulated according to temperature and taking conduction and convection heat exchanges into account can be written in the form

$$ (\rho c)^{*} \frac{\partial T}{\partial t} = {\mathbf{\nabla }}.({\varvec{\uplambda}}^{*} {\mathbf{\nabla }}T) + {\mathbf{\nabla }}.((\rho c)_{l} VT) + {\text{S}} $$
(8)

where T represents the temperature; (ρc)* and (ρc) t the volume heat of the equivalent medium and the liquid metal, respectively; \( {\varvec{\uplambda}}{*} \) the thermal conductivity tensor of the equivalent medium; and S a source term to take phase change phenomena into account.

One-dimensional (1-D) axisymmetric finite element models have been developed to simulate the squeeze casting process (Figure 2).[38,42] The model by You et al.[38] is based on the resolution of the heat Eq. [8] in conduction only, i.e., without the convective term. In fact, in this model, the fillings of the fibrous preform phase and the metal cooling phase are uncoupled. The model by Jung et al.[42] is based on an enthalpy formulation of Eq. [8], where the metal flow rate is assumed to be constant and equal to the piston speed. Using numerical simulations, change in solidification can be monitored as a function of the initial temperatures of the constituents (preform, liquid metal, and mold) and the volume fraction of the fibers. A 1-D model has been developed to simulate the impregnation of a fibrous preform by a liquid metal.[43] In this model, only exchanges between the fibers and the metal are taken into account and the walls of the mold are, therefore, assumed to be insulating.

A 2-D finite volume numerical model based on the coupled resolution of Eqs. [6] through [8] shows the influence of the different parameters of the process—operational parameters, such as the initial temperatures of the injected metal, the fibers, and the mold, the metal injection rate, the characteristics of the metal and the fibers (thermal conductivity, etc.), and the porosity of the fibrous preform—on the impregnation of the fibrous preform by the liquid metal for a simple geometry (Figure 3).[44,45] Another 2-D finite difference numerical model demonstrates the impregnation of a fibrous preform by a liquid metal injected at constant pressure in an insulated mold.[46] These models are also able to describe the evolution of phase changes throughout the process and to obtain the theoretical results put forward by Mortensen et al.[13] The results clearly show the existence of three zones: (1) one close to the injection face of the metal where the metal is totally liquid; (2) one containing a liquid/solid mixture due to heat exchanges between the fibers and the metal, resulting in the partial solidification of the metal around the fibers; and (3) one where the metal is totally solidified, due to exchanges between the fibers and the metal and between the metal and the walls of the mold.

In many models, the metal front is assumed to remain planar throughout the infiltration of the fibrous preform. This hypothesis is justified in the case of impregnation of thin plates in a fibrous preform assumed to be rigid in a system where the metal is injected across an entire face of the conduit (Figure 4). In other cases, depending on the geometry of the parts and the injection systems, it is essential to take account of the change in the geometry of the front during infiltration. Two-dimensional,[47] three-dimensional,[16] or axisymmetric[30,48] numerical models, based on the coupled resolution of Eqs. [6] through [8] and the advection Eq. [9], can take account simultaneously of phase change phenomena and the geometry of the metal front during infiltration.

Fig. 4
figure 4

Geometry of the macroscopic model

Full size image
$$ \frac{\partial F}{\partial t} + \;\frac{V}{\phi }\; \cdot \;{\mathbf{\nabla }}F = 0 $$
(9)

where F represents the metal volume fraction contained in a given volume and ϕ the porosity of the fibrous preform.

Numerical Simulation of Infiltration of a Fibrous Preform by an Alloy

In cases where the matrix is an alloy, modeling MMC processing by infiltration is much more complex, mainly because of segregation phenomena and the variation in temperature of the phase change in the alloy as a function of concentration during impregnation of the fibrous preform. Models should, therefore, take these phenomena combinations into account.

Segregation Phenomena

Phase changes in metals result in an enthalpy jump (release or absorption of heat). In the case of pure metal, this transition takes place at a given constant temperature. In the case of alloys, however, the situation is different as the phase change occurs across a temperature range, and these temperatures depend on the percentage of solute present in the liquid. Thus, when the alloy, which is initially in its liquid state with a given composition, solidifies, the solid formed is less rich in solute than the original mixture. This phenomenon is accompanied by solute enrichment of the liquid, called solute rejection, which is in contact with the solid formed. Over time, the solute concentration in the solid formed will increase and the liquid in contact will continue to be enriched. In the case of composite processing by infiltration, these phenomena of enrichment of the liquid during the flow will lead to heterogeneities in the part, phenomena that will be partly attenuated at the microscopic scale by diffusion phenomena, but which may be intensified at the macroscopic scale by convection.

Models at Fiber Scale

At fiber scale, metal flow between fibers is described by the conservation Eq. [4]. The phenomena of solute rejection and species diffusion in the liquid phase are described by Eqs. 10 and [11]:

$$ C_{\text{s}} = kC_{\text{l}} $$
(10)
$$ \frac{{\partial C_{\text{l}} }}{\partial t} + V \cdot {\mathbf{\nabla }}C_{\text{l}} = {\mathbf{\nabla }} \cdot (D_{\text{l}} {\mathbf{\nabla }}C_{\text{l}} ) + q $$
(11)

where Cl and Cs are concentrations of the liquid and the solid, respectively; and k is the partition coefficient of the alloy. q is the solute rejection at the interface, and Dl is the diffusion coefficient in the liquid.

Cantarel et al. developed a model based on the coupled resolution of Eqs. [4], [5], [10], and [11] with which they were able to simulate metal flow in a domain consisting of a periodic stack of parallel layers representing the reinforcement and the metal (or the vacuum) alternately (Figure 3).[49] In this model, the metal front is assumed to be planar and diffusion in the solid is disregarded. A numerical simulation is used to monitor the change in temperature distribution and the average concentration of the alloy (solid and liquid) during injection of a binary aluminum-copper alloy (Al-Cu 4.5) into alumina fibers. In particular, this model shows that there is alloy enrichment at the injection front.

Models at Macroscopic Scale

To describe an infiltration process, Mortensen and Michaud[21] proposed a theoretical model based on Eqs. [6] through [8] and the following mass transport equation:

$$ \frac{{\partial \overline{C} }}{\partial t} + \frac{V}{\phi }.{\mathbf{\nabla }}C_{\text{l}} = 0 $$
(12)

where \( \overline{C} \) represents the average composition of the matrix, and Cl is the composition of the liquid metal. V is the Darcy velocity, and ϕ is the porosity of the fibrous preform.

Based on this model and the Lever rule model for diffusion (infinite diffusion in the liquid and solid phases), to express composition \( \overline{C} \) as a function of Cl, Khan and Tong put in place a numerical model with finite volumes to simulate the impregnation of a fibrous preform in a 2-D configuration (Figure 4).[50] The authors take into account heat transfers between the fibers and the metal, and the walls of the mold are assumed to be insulated. With this model, it is possible to determine the presence of the different zones highlighted in the theoretical model, where the metal is in a liquid state, solid state, or eutectic composition.

Models to Simulate the Coating Process

Processing metal-coated SiC filaments (titanium alloy) by the liquid route, such as the reinforcement infiltration processes, involves coupled mass and heat transfer phenomena. During the coating process, contact between the carbon coating and the liquid titanium alloy results in a transfer of carbon into the liquid metal and the formation of TiC. This formation of TiC is essential to ensure the wetting of the filament by the liquid metal. However, the presence of TiC alters the mechanical characteristics of the final product. Lacoste et al. suggested a model with finite volumes to simulate the coating process.[51] This model is based on the coupled resolution of the heat Eq. [8] and Eqs. [10] and [11] for mass transfer, as these equations are formulated in an axisymmetric configuration. Equation [10] can be used to monitor carbon rejection at the liquid/solid interface and the thickness of the TiC that forms during the process. Using numerical simulations, the influence of the operational parameters of the process on the formation of TiC can be studied. This model is used as a basis from which to study different technological configurations in order to optimize the process.[52]

Numerical Simulation of the Formation of Microporosities

Types of Defect in the Part after Processing

In processing by impregnation, the processes are in two successive stages: first is the saturation of the fibrous preform, accompanied by solidification around the fibers, and second is the solidification of the metal saturating the reinforcement before the final unmolding of the part. During these stages, saturation defects may appear. These can be classified into two categories: (1) defects resulting from an imperfect impregnation of the fibrous preform during the filling phase by the metal and (2) microporosities associated with solidification shrinkage.[17,18]

The formation of defects during the filling phase, which can be reduced by the use of high pressures, is due to capillary mechanisms that may lead to the trapping of gas (trapping in nodules, for example). The saturation value obtained depends on pressure, interfacial tensions, the morphology of the fibrous preform, and the flow conditions, which are strongly disturbed because of the presence of the fibrous preform and metal solidification phenomena during the filling phase.

The solidification of most bodies is accompanied by volumetric shrinkage. This solidification shrinkage causes cavities or microporosities when the liquid metal is unable to compensate for the loss of volume generated by this shrinkage. The formation of microporosities can be explained by two predominant phenomena: poor interdendritic feeding, on the one hand, and dissolved gas rejection at the liquid/solid interface, on the other. In the case of MMC processing, during the metal solidification phase, the fibrous preform, present throughout the area, acts as the mushy zone found locally when the alloy solidifies, thus causing microporosities to form. The poor supply of liquid metal, combined with the presence of fibers, is accentuated by metal solidification phenomena that occur around the fibers and that lead to a decrease in porosity and a drop in the permeability of the medium.

Models for Microporosities Associated with Infiltration

Equations [6] and [7] can be used to describe the liquid metal flow through the porous medium, characterized by its permeability. This macroscopic approach to the flow neglects flows likely to coexist at different microscopic scales. For example, if the reinforcement is a fabric, then there are strands of fiber within which there are porosities (interfiber spaces). The saturation kinetics of porosities at the microscopic scale (interfiber spaces of the order of 1 μm) are different from those of porosities at the macroscopic scale (distance between the strands of fiber of around 1 mm), thus creating a pressure imbalance between micropores and macropores. To take into account these different scales of metal flow, two types of model have been developed.

Dopler et al. considered permeability as a function of saturation by introducing the concept of relative permeability.[30] They produced a numerical simulation of the change in the saturation of a fibrous preform by a metal during isothermal infiltration (temperature higher than the melting temperature of the metal) under low pressure (of the order of 1 MPa) based on a finite element model developed to describe drainage phenomena in hydrogeology. The metal flow is described by the conservation Eq. [13], and to resolve it requires knowledge of the change in permeability of the porous medium as a function of its saturation, and also the drainage curve (saturation as a function of pressure):

$$ (1 - \varepsilon_{f} )\frac{dS}{dP}\frac{\partial P}{\partial t} - {\mathbf{\nabla }} \cdot \left( {\frac{{{\mathbf{K}}(S)}}{\mu }{\mathbf{\nabla }}P} \right) = 0 $$
(13)

where S represents saturation and εf is the fiber volume rate.

Wang and Pillai developed a model in which the permeability field varies according to the position in the porous medium: the model is thus able to take into account flow between the fibers (macroflow front) and within the fibers (microflow front)[16] (Figure 5). Numerical simulations show the presence of gas trapped inside the fibers. The size and position of the areas with trapped gas depend on the metal injection pressure and the permeability fields.

Fig. 5
figure 5

Geometry of the dual-scale model

Full size image

Models for Microporosities Associated with Solidification Shrinkage

Mantaux et al. developed a model to describe the formation of microporosities due to solidification shrinkage and to the difficulty of feeding the solidifying zones during infiltration.[53] The physical model is based on mass transfer conservation of the metal (Eq. [14]), on a relation between the volume fraction of each component, knowing that the porous medium, solid metal, and fibers are assumed to be incompressible (Eq. [15]). Moreover, the liquid metal with trapped gas is assimilated as a compressible equivalent fluid, which follows a law of compressibility (Eq. [16]):

$$ \frac{{\partial (\rho_{\text{s}} \varepsilon_{\text{s}} )}}{\partial t} + \frac{{\partial (\rho_{\text{l}} \varepsilon_{\text{l}} )}}{\partial t} + \vec{\nabla }.(\rho_{\text{l}} \vec{u}) = 0 $$
(14)
$$ \frac{{\partial (\varepsilon_{l} + \varepsilon_{v} )}}{\partial t} = - \frac{{\partial \varepsilon_{s} }}{\partial t} $$
(15)
$$ \frac{{\partial \rho_{\text{l}} }}{\partial t} = \rho_{\text{l}} \beta_{\text{l}} \frac{\partial P}{\partial t} $$
(16)

In these equations, βl represents the coefficient of apparent compressibility of the liquid, εs the volume fraction of the solid metal, εf the volume fraction of the fibers, and εv the volume fraction of the microporosities (or vacuum). ρl and ρs represent, respectively, the density of liquid and solid.

After combining the Darcy law (Eq. [6]) with Eqs. [14] through [16], we obtain Eq. [17] describing mass transfers:

$$ {\mathbf{\nabla }}.\left( { - \rho_{\text{l}} \frac{{\mathbf{K}}}{\mu }{\mathbf{\nabla }}P} \right) + (\rho_{\text{s}} - \rho_{\text{l}} )\frac{{\partial \varepsilon_{\text{s}} }}{\partial t} - \rho_{\text{l}} \frac{{\partial \varepsilon_{\text{v}} }}{\partial t} + \rho_{\text{l}} \varepsilon_{\text{l}} \beta_{\text{l}} \frac{\partial P}{\partial t} = 0 $$
(17)

The term \( \left( {\rho_{\text{s}} - \rho_{\text{l}} } \right)\frac{{\partial \varepsilon_{\text{s}} }}{\partial t} \) represents volume contraction that corresponds to solidification shrinkage, and \( - \rho_{\text{l}} \frac{{\partial \varepsilon_{\text{v}} }}{\partial t} \) is a volume source term corresponding to the appearance of microporosities. The final model is based on the coupled resolution of the heat Eq. [8] and Eq. [17].

Conclusions

The numerical models and simulations found in the literature can be used to study different physical phenomena involved in MMC processing by the liquid route. Some models can be used to describe heat and mass transfer during the gas infiltration process or to explain phenomena such as the segregation or appearance of microporosities during the process. These numerical models are very interesting and are an indispensable complement to the theoretical and experimental studies carried out elsewhere on these processes. The knowledge acquired about the process provides a solid base not only for an understanding of the physical phenomena and their coupling but also for optimizing the operational parameters. However, due to the strong interactions between mass and heat transfers leading especially to phase change phenomena and segregation phenomena, the numerical simulations of these processes remain complicated to implement. In addition, the simulations require some parameters, such as permeability, which are difficult to characterize. Conversely, some more complete models exist, which simulate the infiltration of a resin into a fibrous preform to manufacture polymer matrix composites.